Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2014 Mar 20;10(3):e1003524.
doi: 10.1371/journal.pcbi.1003524. eCollection 2014 Mar.

Computational analyses of synergism in small molecular network motifs

Yili Zhang  1 , Paul Smolen  1 , Douglas A Baxter  1 , John H Byrne  1
Affiliations

Computational analyses of synergism in small molecular network motifs

Yili Zhang et al. PLoS Comput Biol. .

Abstract

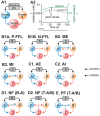
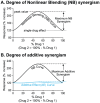
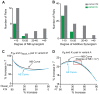
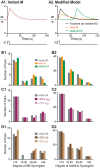
Cellular functions and responses to stimuli are controlled by complex regulatory networks that comprise a large diversity of molecular components and their interactions. However, achieving an intuitive understanding of the dynamical properties and responses to stimuli of these networks is hampered by their large scale and complexity. To address this issue, analyses of regulatory networks often focus on reduced models that depict distinct, reoccurring connectivity patterns referred to as motifs. Previous modeling studies have begun to characterize the dynamics of small motifs, and to describe ways in which variations in parameters affect their responses to stimuli. The present study investigates how variations in pairs of parameters affect responses in a series of ten common network motifs, identifying concurrent variations that act synergistically (or antagonistically) to alter the responses of the motifs to stimuli. Synergism (or antagonism) was quantified using degrees of nonlinear blending and additive synergism. Simulations identified concurrent variations that maximized synergism, and examined the ways in which it was affected by stimulus protocols and the architecture of a motif. Only a subset of architectures exhibited synergism following paired changes in parameters. The approach was then applied to a model describing interlocked feedback loops governing the synthesis of the CREB1 and CREB2 transcription factors. The effects of motifs on synergism for this biologically realistic model were consistent with those for the abstract models of single motifs. These results have implications for the rational design of combination drug therapies with the potential for synergistic interactions.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

Figure 1
Figure 1. Canonical model and variations.
(A1) The canonical model describes the convergence of two signaling pathways (elements A and B) onto target (T). A single stimulus (S) activates both A and B. Then, A and B positively regulate the activation of T. (A2) For the canonical model, the stimulus-response curves are transient in both model variants M and A (S = 1). (B–E) Various network motifs derived from the canonical model. (B1) Two types of coherent feed-forward loop (FFL). (B2) Positive feed-back loop between A and B (i.e., mutual excitation, ME). (B3) Negative feed-back loop between A and B (i.e., mutual inhibition, MI). (C1) Positive auto-regulation loop of A (i.e., auto-excitation, AE). (C2) Negative auto-regulation loop of A (i.e., auto-inhibition, AI). (D1) Negative feedback between A and B (NF (B-A)). (D2) Negative feedback from T to A and B (NF (T-A/B)). (E) Positive feedback from T to A and B (PF (T-A/B)).
Figure 2
Figure 2. A schematic of NB synergism (A) and additive synergism (B).
Response for AE curve = effect of drug 1 alone+effect of drug 2 alone. The maximal difference between peak value and endpoints of NB curves determines the maximum NB synergism. The maximal difference between NB and AE curves determines maximum additive synergism.
Figure 3
Figure 3. Histograms of NB synergism (A) and additive synergism (B) degrees from 91 parameter pairs for Variant M (grey bars) and Variant A (green bars) (S = 1).
(C) Variation of the parameter pair KTA/kbasal_A in Variant M shows that additive synergism can exist in the absence of NB synergism. kbasal_A increases from 0 to 90% as KTA concurrently decreases from 90 to 0%. (D) Variation of KB/KT in Variant A shows that NB synergism can exist in the absence of additive synergism (red box, concave-down NB curve is below AE curve).
Figure 4
Figure 4. For Variant M (S = 1), the histograms of synergism degrees from 91 parameter pairs were compared between standard parameter values and varied parameter values.
(A) The stimulus and response curves of A (see Eq. 1) and B (see Eq. 2) with standard parameter values (A1) and with parameters altered to give slower B dynamics (orange trace), or delayed B dynamics (green trace), with dynamics of A unchanged (black trace) (A2). (B) The histograms of NB synergism (B1) and additive synergism (B2) degrees with standard parameter values (grey bars) and with parameters altered to give slower B dynamics (orange bars) or delayed B dynamics (green bars). (C) The histograms of NB synergism (C1) and additive synergism (C2) degrees with standard parameter values (grey bars), with kST increased by 25% (red bars), and with kST reduced by 25% (pink bars). (D) The histograms of NB synergism (D1) and additive synergism (D2) degrees with standard values (grey bars), KT increased by 25% (dark brown bars), and KT reduced by 25% (light brown bars).
Figure 5
Figure 5. Simulations with Variant M generated NB curves and AE curves for three pairs of parameters, which show strong NB synergism (kdA/kdB) (A), moderate NB synergism (kdA/kST) (B), and weak NB (kdA/KT) (C).
S = 1 in the left column, and S = 10 in the right column.
Figure 6
Figure 6. Simulations of three parameter pairs with Variant M generated dose-effect curves that describe the relationships between NB synergism and stimulus strength (A), and between additive synergism and stimulus strength (B).
The strength of stimulus (S) was varied from 1 to 40.
Figure 7
Figure 7. Summary of the degrees of NB and additive synergism observed for all motifs for S = 1 and S = 10.
Degrees of synergism are plotted for kdA/kdB (A), kdA/kST (B), and kdA/KT (C). Motif abbreviations are as in Fig. 1. Vertical dashed lines delineate each motif and its associated synergism degrees (four for each combination of a motif and a parameter pair). For each motif and parameter pair, the degrees of additive synergism are plotted as blue and light green bars, and the degrees of additive synergism are plotted as black and grey bars, for S = 1 and S = 10 respectively. Negative values represent degrees of antagonism. In a few cases, the NB and AE curves were intertwined (e.g., Fig. S1B1) and exhibited both additive synergism and additive antagonism. For those cases only positive values (synergism) are plotted. The values of some data are too small to be easily visualized.
Figure 8
Figure 8. The model of Song et al. and simulations.
(A1) The feedback loops described by the model. (A2) After 5 pulses of 5-HT treatment, CREB1 and CREB2 switch from a LOW state to a HIGH state. (B) The NB curve and AE curve for the parameter pair Vx/kdy. This pair shows strong NB synergism, and additive synergism.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chkiovskii D, et al. (2002) Network motifs: simple building blocks of complex networks. Science 298: 824–827. - PubMed
    1. Goemann B, Wingender E, Potapov AP (2009) An approach to evaluate the topological significance of motifs and other patterns in regulatory networks. BMC Syst Biol 3: 53 doi:10.1186/1752-0509-3-53 - DOI - PMC - PubMed
    1. Kaizu K, Ghosh S, Matsuoka Y, Moriya H, Shimizu-Yoshida Y, et al. (2010) A comprehensive molecular interaction map of the yeast cell cycle. Mol Syst Biol 6: 415 doi:10.1038/msb.2010.73 - DOI - PMC - PubMed
    1. Cui Q, Ma Y, Jaramillo M, Bari H, Awan A, et al. (2007) A map of human cancer signaling. Mol Syst Biol 3: 152 doi:10.103/msb4100200 - DOI - PMC - PubMed
    1. Gerstein MB, Kundaje A, Hariharan M, Landt SG, Yan KK, et al. (2012) Architecture of the human regulatory network derived from ENCODE data. Nature 489: 91–100. - PMC - PubMed

Publication types

Substances

LinkOut - more resources