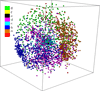
Background: Protein function is closely intertwined with protein structure. Discovery of meaningful structure-function relationships is of utmost importance in protein biochemistry and has led to creation of high-quality, manually curated classification databases, such as the gold-standard SCOP (Structural Classification of Proteins) database. The SCOP database and its counterparts such as CATH provide a detailed and comprehensive description of the structural and evolutionary relationships of the proteins of known structure and are widely employed in structural and computational biology. Since manual classification is both subjective and highly laborious, automated classification of novel structures is increasingly an active area of research. The design of methods for automated structure classification has been rendered even more important since the recent past, due to the explosion in number of solved structures arising out of various structural biology initiatives. In this paper we propose an approach to the problem of structure classification based on creating and tessellating low dimensional maps of the protein structure space (MPSS). Given a set of protein structures, an MPSS is a low dimensional embedding of structural similarity-based distances between the molecules. In an MPSS, a group of proteins (such as all the proteins in the PDB or sub-samplings thereof) under consideration are represented as point clouds and structural relatedness maps to spatial adjacency of the points. In this paper we present methods and results that show that MPSS can be used to create tessellations of the protein space comparable to the clade systems within SCOP. Though we have used SCOP as the gold standard, the proposed approach is equally applicable for other structural classifications.

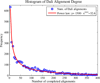
Methods: In the proposed approach, we first construct MPSS using pairwise alignment distances obtained from four established structure alignment algorithms (CE, Dali, FATCAT and MATT). The low dimensional embeddings are next computed using an embedding technique called multidimensional scaling (MDS). Next, by using the remotely homologous Superfamily and Fold levels of the hierarchical SCOP database, a distance threshold is determined to relate adjacency in the low dimensional map to functional relationships. In our approach, the optimal threshold is determined as the value that maximizes the total true classification rate vis-a-vis the SCOP classification. We also show that determining such a threshold is often straightforward, once the structural relationships are represented using MPSS.

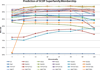
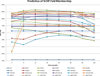
Results and conclusion: We demonstrate that MPSS constitute highly accurate representations of protein fold space and enable automatic classification of SCOP Superfamily and Fold-level relationships. The results from our automatic classification approach are remarkably similar to those found in the distantly homologous Superfamily level and the quite remotely homologous Fold levels of SCOP. The significance of our results are underlined by the fact that most automated methods developed thus far have only managed to match the closest-homology Family level of the SCOP hierarchy and tend to differ considerably at the Superfamily and Fold levels. Furthermore, our research demonstrates that projection into a low-dimensional space using MDS constitutes a superior noisereducing transformation of pairwise distances than do the variety of probability- and alignment-length-based transformations currently used by structure alignment algorithms.