Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2013 Jul 25;8(7):e69374.
doi: 10.1371/journal.pone.0069374. Print 2013.

A network integration approach to predict conserved regulators related to pathogenicity of influenza and SARS-CoV respiratory viruses

Hugh D Mitchell  1 , Amie J Eisfeld, Amy C Sims, Jason E McDermott, Melissa M Matzke, Bobbi-Jo M Webb-Robertson, Susan C Tilton, Nicolas Tchitchek, Laurence Josset, Chengjun Li, Amy L Ellis, Jean H Chang, Robert A Heegel, Maria L Luna, Athena A Schepmoes, Anil K Shukla, Thomas O Metz, Gabriele Neumann, Arndt G Benecke, Richard D Smith, Ralph S Baric, Yoshihiro Kawaoka, Michael G Katze, Katrina M Waters
Affiliations

A network integration approach to predict conserved regulators related to pathogenicity of influenza and SARS-CoV respiratory viruses

Hugh D Mitchell et al. PLoS One. .

Abstract

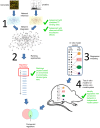
Respiratory infections stemming from influenza viruses and the Severe Acute Respiratory Syndrome corona virus (SARS-CoV) represent a serious public health threat as emerging pandemics. Despite efforts to identify the critical interactions of these viruses with host machinery, the key regulatory events that lead to disease pathology remain poorly targeted with therapeutics. Here we implement an integrated network interrogation approach, in which proteome and transcriptome datasets from infection of both viruses in human lung epithelial cells are utilized to predict regulatory genes involved in the host response. We take advantage of a novel "crowd-based" approach to identify and combine ranking metrics that isolate genes/proteins likely related to the pathogenicity of SARS-CoV and influenza virus. Subsequently, a multivariate regression model is used to compare predicted lung epithelial regulatory influences with data derived from other respiratory virus infection models. We predicted a small set of regulatory factors with conserved behavior for consideration as important components of viral pathogenesis that might also serve as therapeutic targets for intervention. Our results demonstrate the utility of integrating diverse 'omic datasets to predict and prioritize regulatory features conserved across multiple pathogen infection models.

PubMed Disclaimer

Conflict of interest statement

Competing Interests: The authors have declared that no competing interests exist.

Figures

Figure 1
Figure 1. Network Terminology.
Association networks capture both physical and regulatory interactions between gene pairs. Network hubs are identified by the degree centrality metric, which is the number of edges (i.e. relationships, represented by connecting lines) associated with any given vertex (elements being connected, e.g. genes, identified as circles). Network bottlenecks have high values for the betweenness centrality metric, which is the number of shortest paths between all pairs of vertices that pass through a given vertex. Network neighbors are vertices connected by a single edge.
Figure 2
Figure 2. Workflow for prediction of conserved regulators.
Step 1: Network inference. Network relationships are reconstructed from transcript and protein quantification data by finding similar expression patterns across multiple conditions. Protein and transcript networks are integrated to form a unified network (in the case of the SARS-CoV data; see text). Step 2: Ranking approaches. Network genes were ranked using three distinct measures: network betweenness, degree centrality, and differential expression between pathogenicity levels. Gene set enrichment analysis (GSEA) was used to test each individual ranking, and each combination of rankings, for how effectively they prioritize genes known to be relevant to viral infection. Step 3: Model construction. Multivariate regression was used to build regulatory models using the union of known transcription factors and top prioritized genes from step 2 as candidate regulators. The modeling process predicts a small set of regulatory genes that are likely to regulate each target (cluster of genes). Step 4: Cross-system comparison. Performance of the resulting models was tested in either an in vivo mouse model (influenza virus) or an ex vivo human primary lung epithelial model (SARS-CoV). In vivo and ex vivo models are both represented by the outlined mouse shape in the figure. Genes with conserved regulation in the new system were prioritized as conserved regulators for the respective virus infection (Tables 4 and 5). Green check marks indicate steps validated through comparison to/integration with outside experimental data.
Figure 3
Figure 3. Inferred network edge validation.
A) Network edges were compared to a predicted transcription factor – target database. The number of transcriptome network edges for each virus that was also present in the database (red) was compared with the number of matching edges in 1000 random networks (gray) to estimate the number of matching edges expected from chance. B) Relationships between genes targeted in a large siRNA-targeting study and the downstream affected genes were compared to relationships predicted from our network inference approach. Results show the number of genes that exhibited statistically significant overlap between their network neighbors and perturbed genes from the siRNA targeting study. Red designates the overlap with neighbors from the actual network; grey designates overlap with neighbors from 500 random networks (see Materials and Methods). Error bars represent standard deviation of the distribution of gene percentages with significant overlaps.
Figure 4
Figure 4. Overlap between rankings.
Genes were ranked according to betweenness, degree and differential expression (DE) as described in Materials and Methods. Venn diagrams indicate the overlap in the top 10% of each of these rankings for both viruses as indicated.
Figure 5
Figure 5. GSEA-based enrichment analysis of influenza rankings.
Seven distinct rankings of genes from the influenza network were evaluated for their enrichment in various influenza-related gene lists. The seven rankings consisted of network betweenness centrality, network degree centrality, differential gene expression (DE), combined betweenness and degree, combined betweenness and DE, combined degree and DE, and a combined ranking from all three. The average enrichment score in all influenza gene lists is shown for each of the seven rankings. Average enrichments were also calculated for 100 scrambled rankings of the same genes. P-values are calculated by comparing each ranking’s enrichment score to the distribution of enrichment scores of random rankings (see Methods). Single star indicates p-value below .05; double star indicates p-value below .001.
Figure 6
Figure 6. GSEA-based enrichment analysis of SARS-CoV rankings.
Seven rankings of genes from the SARS-CoV network were assessed for enrichment as in figure 5, this time using the 299 gene sets from the Molecular Signatures Database matching the search keys “viral” or “virus”. Average scores are compared to random rankings. Double stars indicate p-values <0.001.
Figure 7
Figure 7. Model system comparison based on Inferelator regression models.
Regulatory influence models for each gene cluster of both viruses were applied to comparable datasets from distinct model systems. For SARS-CoV, regulatory influences inferred from Calu3 data were applied to SARS-CoV infection data from a primary human airway epithelial cell model system. For influenza, the Calu3 model was applied to influenza infection data from C57BL/6 mice. The observed gene expression profile of the non-Calu3 data clusters was compared to the predicted gene expression profile based on the Calu3 model. Correlations were calculated for this comparison from each cluster and are shown in A. In B, a sample expression profile from a highly-predictive cluster from each virus is shown with the observed non-Calu3 expression profile shown in red, compared to the predicted expression profile from the Calu3 model in green. In C, the average cluster correlation for the SARS-CoV and influenza comparisons is shown, in comparison to the correlation obtained from applying 100 random models to the corresponding alternative model system. P-values were obtained by comparing each correlation with the distribution of 100 correlations based on random models.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Ideker T, Krogan NJ (2012) Differential network biology. Mol Syst Biol 8: 565. - PMC - PubMed
    1. McDermott JE, Diamond DL, Corley C, Rasmussen AL, Katze MG, et al. (2012) Topological analysis of protein co-abundance networks identifies novel host targets important for HCV infection and pathogenesis. BMC Syst Biol 6: 28. - PMC - PubMed
    1. Faith JJ, Hayete B, Thaden JT, Mogno I, Wierzbowski J, et al. (2007) Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles. PLoS Biol 5: e8. - PMC - PubMed
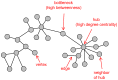
    1. McDermott JE, Taylor RC, Yoon H, Heffron F (2009) Bottlenecks and hubs in inferred networks are important for virulence in Salmonella typhimurium. J Comput Biol 16: 169–180. - PubMed
    1. McDermott JE, Archuleta M, Stevens SL, Stenzel-Poore MP, Sanfilippo A (2011) Defining the players in higher-order networks: predictive modeling for reverse engineering functional influence networks. Pac Symp Biocomput: 314–325. - PMC - PubMed

Publication types

MeSH terms

Associated data