Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2013:3:2171.
doi: 10.1038/srep02171.

Global efficiency of local immunization on complex networks

Laurent Hébert-Dufresne  1 , Antoine Allard, Jean-Gabriel Young, Louis J Dubé
Affiliations

Global efficiency of local immunization on complex networks

Laurent Hébert-Dufresne et al. Sci Rep. 2013.

Abstract

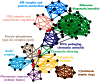
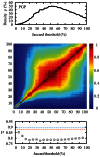
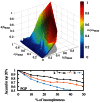
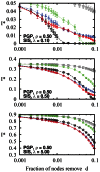
Epidemics occur in all shapes and forms: infections propagating in our sparse sexual networks, rumours and diseases spreading through our much denser social interactions, or viruses circulating on the Internet. With the advent of large databases and efficient analysis algorithms, these processes can be better predicted and controlled. In this study, we use different characteristics of network organization to identify the influential spreaders in 17 empirical networks of diverse nature using 2 epidemic models. We find that a judicious choice of local measures, based either on the network's connectivity at a microscopic scale or on its community structure at a mesoscopic scale, compares favorably to global measures, such as betweenness centrality, in terms of efficiency, practicality and robustness. We also develop an analytical framework that highlights a transition in the characteristic scale of different epidemic regimes. This allows to decide which local measure should govern immunization in a given scenario.

PubMed Disclaimer

Figures

Figure 1
Figure 1. Protein interactions of S. cerevisiae (subset).
The three black nodes correspond to the ones with the highest degree, and the three red ones have the highest membership number. In this particular example, it is readily seen that the latter are structurally more influent.
Figure 2
Figure 2. Robustness of structural hubs in the PGP network.
(top) Community density (ρ) obtained through different Jaccard thresholds. (middle) Robustness of the structural hubs identification methods. Element (i,j) gives the overlap (normalized) between the structural hubs (top 1%) selected with thresholds i and j. The highest line and last column of the matrix correspond to the case where the membership number equals the degree. (bottom) Prevalence I* of SIS epidemics with λ = 5 when the top 1% of structural hubs are removed (compared with the results without removal in blue or with random targets in orange).
Figure 3
Figure 3. Difference in immunization targets for the PGP network.
(top) We present correlations between the degree (k, right axis), the coreness (c, left axis), the betweenness centrality (b, vertical axis) and the membership number (m, color) for each nodes. Each measure is normalized according to the highest value found in the network. Each node is represented in this 4-dimensional space and a simple triangulation procedure then yields a more intelligible appearance. Structural hubs (dark red) can be found even at relatively small degree (~ kmax/2), coreness (~ cmax/5) and centrality (~ bmax/3). (bottom) Jaccard coefficient between the ensemble of nodes identified as part of the top 20% according to a given measure (k, m or b) on two versions of the network: the original complete network and a network ensemble where a certain percentage of links has been randomly removed (horizontal axis). The shorter the range of a measure, the more robust it is to incomplete information.
Figure 4
Figure 4. Efficiency of the immunization methods against an SIS epidemics on the PGP network.
Nodes are removed in decreasing order of their score according to each method: coreness (green pentagons), degree (black circles), betweenness centrality (blue triangles) and memberships (red diamonds) and the effect of removal is then quantified in terms of the decrease of the prevalence I*. The prevalence of the epidemics when the removed nodes are chosen at random (grey squares) has been added for comparison. Figures are presented in increasing order of transmissibility (λ) from top to bottom.
Figure 5
Figure 5. k-core decomposition of the PGP network.
Representation (based on26) of the k-shells in the PGP network with nodes colored according to their total infectious period during a given time interval. Red nodes are more likely to be infectious at any given time than green nodes as the color is given by the square of the fraction of time spent in infectious state. Note how the central nodes (the core) of the network are most at risk.
Figure 6
Figure 6. Efficiency of the immunization methods against SIS and SIR epidemics on several networks.
Nodes are removed in decreasing order of their score according to each method: coreness (green pentagons), degree (black circles), betweenness centrality (blue triangles) and memberships (red diamonds) to measure efficiency by the decrease of I* or Rf. The size of the epidemics for random removal of nodes (gray squares) is added for comparison. Error bars have been omitted for clarity of the SIR results on the Power Grid, but are shown in the SI.
Figure 7
Figure 7. Synthetic networks with tunable community structure.
Orange links belong to motifs of size M = 4, and single links are shown in blue. The degree k and membership m of a few selected nodes are indicated. They belong to i = (k − m)/(M − 2) motifs and have j = [(M − 1)m − k]/(M − 2) single links.
Figure 8
Figure 8. Results of local immunization methods on synthetic networks.
Final sizes of SIR epidemics after immunization of various fractions ε of nodes on synthetic networks with M = 4 and an heterogeneous degree distribution (details in SI). Near the epidemic threshold, targeting by degree (dotted curves) is the better choice whereas targeting by memberships (solid curve) should be preferred for higher transmissibility. Monte Carlo simulations were also performed to validate the formalism and indicated on the curves (the case ε = 0.05 is omitted not to clutter the graph) with circles (targeting by degree) and squares (targeting by membership).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Caldarelli G. & Vespignani A. Large Scale Structure and Dynamics of Complex Networks. World Scientific Publishing Company, Singapore (2007).
    1. Keeling M. J. & Rohani P. Modeling Infectious Diseases in Humans and Animals Princeton University Press, Princeton (2008).
    1. Anderson R. M. & May R. M. Infectious Diseases of Humans: Dynamics and Control Oxford University Press, New York (1991).
    1. Keeling M. J. & Eames K. T. D. Networks and epidemic models. J R Soc Interface 2, 295–307 (2005). - PMC - PubMed
    1. Pastor-Satorras R. & Vespignani A. Epidemic Spreading in Scale-Free Networks. Phys. Rev. Lett. 86, 3200–3203 (2001). - PubMed

Publication types