GWIS--model-free, fast and exhaustive search for epistatic interactions in case-control GWAS
- PMID: 23819779
- PMCID: PMC3665501
- DOI: 10.1186/1471-2164-14-S3-S10
GWIS--model-free, fast and exhaustive search for epistatic interactions in case-control GWAS
Abstract
Background: It has been hypothesized that multivariate analysis and systematic detection of epistatic interactions between explanatory genotyping variables may help resolve the problem of "missing heritability" currently observed in genome-wide association studies (GWAS). However, even the simplest bivariate analysis is still held back by significant statistical and computational challenges that are often addressed by reducing the set of analysed markers. Theoretically, it has been shown that combinations of loci may exist that show weak or no effects individually, but show significant (even complete) explanatory power over phenotype when combined. Reducing the set of analysed SNPs before bivariate analysis could easily omit such critical loci.
Results: We have developed an exhaustive bivariate GWAS analysis methodology that yields a manageable subset of candidate marker pairs for subsequent analysis using other, often more computationally expensive techniques. Our model-free filtering approach is based on classification using ROC curve analysis, an alternative to much slower regression-based modelling techniques. Exhaustive analysis of studies containing approximately 450,000 SNPs and 5,000 samples requires only 2 hours using a desktop CPU or 13 minutes using a GPU (Graphics Processing Unit). We validate our methodology with analysis of simulated datasets as well as the seven Wellcome Trust Case-Control Consortium datasets that represent a wide range of real life GWAS challenges. We have identified SNP pairs that have considerably stronger association with disease than their individual component SNPs that often show negligible effect univariately. When compared against previously reported results in the literature, our methods re-detect most significant SNP-pairs and additionally detect many pairs absent from the literature that show strong association with disease. The high overlap suggests that our fast analysis could substitute for some slower alternatives.
Conclusions: We demonstrate that the proposed methodology is robust, fast and capable of exhaustive search for epistatic interactions using a standard desktop computer. First, our implementation is significantly faster than timings for comparable algorithms reported in the literature, especially as our method allows simultaneous use of multiple statistical filters with low computing time overhead. Second, for some diseases, we have identified hundreds of SNP pairs that pass formal multiple test (Bonferroni) correction and could form a rich source of hypotheses for follow-up analysis.
Availability: A web-based version of the software used for this analysis is available at http://bioinformatics.research.nicta.com.au/gwis.
Figures
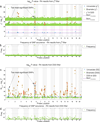

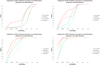


Similar articles
-
BridGE: a pathway-based analysis tool for detecting genetic interactions from GWAS.Nat Protoc. 2024 May;19(5):1400-1435. doi: 10.1038/s41596-024-00954-8. Epub 2024 Mar 21. Nat Protoc. 2024. PMID: 38514837 Free PMC article. Review.
-
Performance of epistasis detection methods in semi-simulated GWAS.BMC Bioinformatics. 2018 Jun 18;19(1):231. doi: 10.1186/s12859-018-2229-8. BMC Bioinformatics. 2018. PMID: 29914375 Free PMC article.
-
High-throughput analysis of epistasis in genome-wide association studies with BiForce.Bioinformatics. 2012 Aug 1;28(15):1957-64. doi: 10.1093/bioinformatics/bts304. Epub 2012 May 21. Bioinformatics. 2012. PMID: 22618535 Free PMC article.
-
Stability of bivariate GWAS biomarker detection.PLoS One. 2014 Apr 30;9(4):e93319. doi: 10.1371/journal.pone.0093319. eCollection 2014. PLoS One. 2014. PMID: 24787002 Free PMC article.
-
Detecting epistasis in human complex traits.Nat Rev Genet. 2014 Nov;15(11):722-33. doi: 10.1038/nrg3747. Epub 2014 Sep 9. Nat Rev Genet. 2014. PMID: 25200660 Review.
Cited by
-
High performance computing enabling exhaustive analysis of higher order single nucleotide polymorphism interaction in Genome Wide Association Studies.Health Inf Sci Syst. 2015 Feb 24;3(Suppl 1 HISA Big Data in Biomedicine and Healthcare 2013 Con):S3. doi: 10.1186/2047-2501-3-S1-S3. eCollection 2015. Health Inf Sci Syst. 2015. PMID: 25870758 Free PMC article.
-
BridGE: a pathway-based analysis tool for detecting genetic interactions from GWAS.Nat Protoc. 2024 May;19(5):1400-1435. doi: 10.1038/s41596-024-00954-8. Epub 2024 Mar 21. Nat Protoc. 2024. PMID: 38514837 Free PMC article. Review.
-
A new method for exploring gene-gene and gene-environment interactions in GWAS with tree ensemble methods and SHAP values.BMC Bioinformatics. 2021 May 4;22(1):230. doi: 10.1186/s12859-021-04041-7. BMC Bioinformatics. 2021. PMID: 33947323 Free PMC article.
-
A survey about methods dedicated to epistasis detection.Front Genet. 2015 Sep 10;6:285. doi: 10.3389/fgene.2015.00285. eCollection 2015. Front Genet. 2015. PMID: 26442103 Free PMC article. Review.
-
Interactions within the MHC contribute to the genetic architecture of celiac disease.PLoS One. 2017 Mar 10;12(3):e0172826. doi: 10.1371/journal.pone.0172826. eCollection 2017. PLoS One. 2017. PMID: 28282431 Free PMC article.
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

