Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2013 May;35(5):452-61.
doi: 10.1002/bies.201200131. Epub 2013 Mar 27.

Microtubule dynamic instability: a new model with coupled GTP hydrolysis and multistep catastrophe

Hugo Bowne-Anderson  1 , Marija Zanic, Monika Kauer, Jonathon Howard
Affiliations
Free PMC article

Microtubule dynamic instability: a new model with coupled GTP hydrolysis and multistep catastrophe

Hugo Bowne-Anderson et al. Bioessays. 2013 May.
Free PMC article

Erratum in

  • Bioessays. 2013 Jun;35(6):579

Abstract

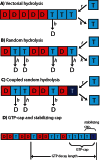
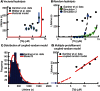
A key question in understanding microtubule dynamics is how GTP hydrolysis leads to catastrophe, the switch from slow growth to rapid shrinkage. We first provide a review of the experimental and modeling literature, and then present a new model of microtubule dynamics. We demonstrate that vectorial, random, and coupled hydrolysis mechanisms are not consistent with the dependence of catastrophe on tubulin concentration and show that, although single-protofilament models can explain many features of dynamics, they do not describe catastrophe as a multistep process. Finally, we present a new combined (coupled plus random hydrolysis) multiple-protofilament model that is a simple, analytically solvable generalization of a single-protofilament model. This model accounts for the observed lifetimes of growing microtubules, the delay to catastrophe following dilution and describes catastrophe as a multistep process.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Microtubule dynamic instability. Microtubules are 13-protofilament cylindrical polymers, which switch between phases of growth and shrinkage. Tubulin dimers are incorporated into the growing lattice in the GTP-bound form and stochastically hydrolyze to GDP-tubulin, thus forming a GTP-cap. It is thought that the switching from growth to shrinkage occurs due to the loss of the GTP-cap.
Figure 2
Figure 2
Timeline of milestones in modeling microtubule dynamics.
Figure 3
Figure 3
Measuring microtubule lengths and lifetimes. A: Kymograph made from a DIC movie, depicting typical microtubule growth and shrinkage using GMPCPP-stabilized microtubule seed and 12 µM tubulin. B: The measured length of a microtubule depends on the imaging technique used.
Figure 4
Figure 4
Schematic of single protofilament models. A: Vectorial hydrolysis, in which hydrolysis occurs only at the GDP-/GTP-tubulin-interface. B: Random hydrolysis, in which at any time, each GTP-tubulin dimer in the microtubule has the same probability of hydrolyzing. C: Coupled-random hydrolysis, in which the hydrolysis occurs randomly except that the terminal dimer cannot hydrolyze. D: The distinction between the stabilizing cap, the GTP-cap (the length of uninterrupted GTP-tubulin at the end), and the GTP-tubulin decay length, over which the fraction of GTP-tubulin drops e-fold.
Figure 5
Figure 5
Predictions of the main models alongside experimental data from Walker et al. and Gardner et al. . A: Vectorial hydrolysis with rates kon = 3.2 µM−1 s−1, k = 0.1 s−1, and h = 43.5 s−1. This value of h satisfies h > r − k ≍ 42 s. The data from Walker et al. are the points for which the authors had >10 observations. Error bars represent SE. B: Random hydrolysis: Simulation 1 rates are kon = 3.2 µM−1 s−1, k = 1 s−1, and h = 1.43 s−1; Simulation 2 rates are kon = 3.2 µM−1 s−1, k = 24 s−1, and h = 0.26 s−1. C: The multiple-protofilament coupled-random model fitted to 12 µM data from Gardner et al. . To do so, we used the mle MATLAB function. We did so for n = 2, 3, 4, with free parameter T′. The closest fit was given by n = 3 and a step time T′ = 1,580 ± 30 s. D: Analytic solution to the multiple-protofilament coupled-random model (Equation 2a), fitted to the lifetime data from Gardner et al. and the dilution data from Walker et al. (solid line); kon = 3.2 µM−1 s−1, k = 0.2 s−1, h = 0.12 s−1. Microtubules are not observed to nucleate below 5 µM. Our model predicts lifetimes of microtubules when diluted to concentrations above 0 µM and below the critical concentration for growth (dashed line). The arrow points to the predictions for dilution experiments to 0 µM in the model.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Mitchison T, Kirschner M. Dynamic instability of microtubule growth. Nature. 1984;312:237–42. - PubMed
    1. Walker R, O'Brien E, Pryer N, Soboero M, et al. Dynamic instability of individual microtubules analyzed by video light-microscopy – rate constants and transition frequencies. J Cell Biol. 1988;107:1437–48. - PMC - PubMed
    1. Gardner MK, Zanic M, Gell C, Bormuth V, et al. Depolymerizing kinesins Kip3 and MCAK shape cellular microtubule architecture by differential control of catastrophe. Cell. 2011;147:1092–103. - PubMed
    1. Odde DJ, Cassimeris L, Buettner HM. Kinetics of microtubule catastrophe assessed by probabilistic analysis. Biophys J. 1995;69:796–802. - PMC - PubMed
    1. Verde F, Dogterom M, Stelzer E, Karsenti E, et al. Control of microtubule dynamics and length by cyclin A-and cyclin B-dependent kinases in Xenopus egg extracts. J Cell Biol. 1992;118:1097–108. - PMC - PubMed

Publication types

LinkOut - more resources