Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2013 Feb;10(1):016004.
doi: 10.1088/1478-3975/10/1/016004. Epub 2013 Jan 28.

Branching and capping determine the force-velocity relationships of branching actin networks

Daniel B Smith  1 , Jian Liu
Affiliations

Branching and capping determine the force-velocity relationships of branching actin networks

Daniel B Smith et al. Phys Biol. 2013 Feb.

Abstract

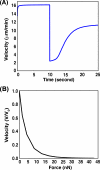
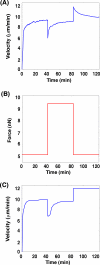
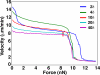
A branching actin network is the major engine that drives cell motility. A measure of the effectiveness of an engine is the velocity the engine is able to produce at a given resistance-the force-velocity relationship. Concave force-velocity relationships consist of a force-insensitive region, indicative of an adaptive response. In contrast, convex force-velocity relationships would reflect a passive response. Even in in vitro experiments, branching actin networks can exhibit both concave and convex force-velocity curves. However, the exact mechanism that can explain both force-velocity curves is not yet known. We carried out an agent-based stochastic simulation to explore such a mechanism. We discovered an emergent behavior of a branching actin network: Upon resistance, it remodels itself by increasing the number of filaments growing in contact with the load. The remodeling is favored by branching events and limited by capping. The force-velocity relationship hinges on the relative time-scale between the intrinsic kinetics of the branching actin network and the loading. Shortly after encountering resistance (∼seconds), the force-velocity relationship of the actin network is always convex, as it does not have enough time to remodel itself. A concave force-velocity relationship requires network remodeling at longer time-scales (∼tens of seconds to minutes) and the faster branching event relative to capping. Furthermore, our model explains the observed hysteresis in the force-velocity relationship of actin networks. Our model thus establishes a unified mechanism that can account for both convex and concave force-velocity relationships observed in branching actin networks.

PubMed Disclaimer

Figures

Figure 1
Figure 1
The force-velocity relationship of branching actin network at short timescale. (A): A characteristic time trace of the velocity response to force applied at ~10 seconds. (B): The convex force-velocity curve generated by the initial response of the network to force. For (A) and (B), the simulations were run with capping rate κ=1/s/filament and branching rate λ=200/s.
Figure 2
Figure 2
The increase in the number of contacting filaments dictates the convex and the concave force-velocity relationships at long timescale. (A) The change of the force-velocity curves from convex to concave is continuous upon the reduction of capping rates. (B) Snapshots of the evolution of actin network growth against a constant load force 6.8nN. The low capping rate is 3 per sec per filament; and the high capping rate is 7 per sec per filament. The “t” refers the time after the application the load force. The blue lines represent the actin filaments, the red solid line represents the load surface, and the black dash line denotes the position of one actin subunit length away from the load surface (the contacting zone). For illustration purposes, only 1/10 of the filaments are shown in each snapshot. (C) The number of contacting filaments increases upon load force, where the capping rates are kept the same as in (B). For (A)-(C), the ratio of branching rate vs. capping rate is kept fixed as λ/κ=200 filaments. The error bars in (A) and (C) represent the standard deviation estimated from 10 simulations.
Figure 3
Figure 3
The schematic diagram on the role of “reserved filaments” in the reinforcement of branching actin network growth against load force. Filaments are represented by black lines; the red line is the leading edge; the blue circles are actively growing barbed ends; and the yellow circle represents a barbed end that has been capped. (A): A hypothetical scenario involving one filament barbed contacting the leading edge with a second filament growing behind the leading edge. (B): When the capping rate is high, the reserve filament is capped (yellow circle) before it reaches the leading edge. (C): When the capping rate is low, sufficiently long filaments can grow and contact the leading edge, increasing the leading edge velocity.
Figure 4
Figure 4
Hysteresis in force-velocity relationships of branching actin network. (A): Without “sticky” load surface, a typical simulation result in a transient hysteresis effect. (B): The time-dependent load force as the model input used in both (A) and (C). (C) A typical simulation with “sticky” load surface, i.e., filaments reaching the leading edge stuck to the leading edge. For (A)-(C): The capping rate is 1/s/filament, the branching rate is 200/s.
Figure 5
Figure 5
The width of branching zone does not qualitatively affect the force-velocity relationship. Except that filaments are only branched in a zone of Nδ away from the leading edge, where δ is the length of actin subunit – 2.7nm, we kept all of the conditions identical to simulations as in Figure 2(B), in which the capping rate = 3/s/filament and branching rate =600/s. Note that, restricting the branching zone width gives rise to a concave force-velocity curve similar to the unrestricted case as in Figure 2(B).
Figure 6
Figure 6
The calculated phase diagram on the dependence of force-velocity relationships of branching actin network on branching rates and capping rates. For each pair of branching rate and capping rate, we quantitatively calculated the f1/2 from the force-velocity curves, averaged over 20 simulations. The color bar represents the calculated f1/2 for a variety of branching and capping rates. The cases with concave force-velocity curves are labeled with white stars. Decreasing the capping rate and increasing the branching rate serve to generate more filaments, which shift f1/2 rightward, meaning a more concave curve.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Abraham VC, Krishnamurthi V, Taylor DL, Lanni F. The Actin-Based Nanomachine at the Leading Edge of Migrating Cells. Biophysical journal. 1999;77:1721–32. - PMC - PubMed
    1. Akin O, Mullins RD. Capping Protein Increases the Rate of Actin-Based Motility by Promoting Filament Nucleation by the Arp2/3 Complex. Cell. 2008;133:841–51. - PMC - PubMed
    1. Amann KJ, Pollard TD. The Arp2/3 complex nucleates actin filament branches from the sides of pre-existing filaments. Nat Cell Biol. 2001;3:306–10. - PubMed
    1. Atilgan E, Wirtz D, Sun SX. Morphology of the Lamellipodium and Organization of Actin Filaments at the Leading Edge of Crawling Cells. Biophysical journal. 2005;89:3589–602. - PMC - PubMed
    1. Bohnet S, Ananthakrishnan R, Mogilner A, Meister J-J, Verkhovsky AB. Weak Force Stalls Protrusion at the Leading Edge of the Lamellipodium. Biophysical journal. 2006;90:1810–20. - PMC - PubMed

Publication types

LinkOut - more resources