Tuning genetic clocks employing DNA binding sites
- PMID: 22859962
- PMCID: PMC3409220
- DOI: 10.1371/journal.pone.0041019
Tuning genetic clocks employing DNA binding sites
Abstract
Periodic oscillations play a key role in cell physiology from the cell cycle to circadian clocks. The interplay of positive and negative feedback loops among genes and proteins is ubiquitous in these networks. Often, delays in a negative feedback loop and/or degradation rates are a crucial mechanism to obtain sustained oscillations. How does nature control delays and kinetic rates in feedback networks? Known mechanisms include proper selection of the number of steps composing a feedback loop and alteration of protease activity, respectively. Here, we show that a remarkably simple means to control both delays and effective kinetic rates is the employment of DNA binding sites. We illustrate this design principle on a widely studied activator-repressor clock motif, which is ubiquitous in natural systems. By suitably employing DNA target sites for the activator and/or the repressor, one can switch the clock "on" and "off" and precisely tune its period to a desired value. Our study reveals a design principle to engineer dynamic behavior in biomolecular networks, which may be largely exploited by natural systems and employed for the rational design of synthetic circuits.
Conflict of interest statement
Figures

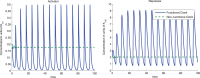
 ,
,  ,
,  and
and  . In the Functional Clock,
. In the Functional Clock,  whereas in the Non-Functional Clock,
whereas in the Non-Functional Clock,  . Parameters
. Parameters  and
and  were chosen to give about 500–2000 copies of protein per cell for activated promoters. Parameters
were chosen to give about 500–2000 copies of protein per cell for activated promoters. Parameters  and
and  were chosen to give about 1–10 copies per cell for non-activated promoters.
were chosen to give about 1–10 copies per cell for non-activated promoters.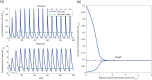
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  . The amount of DNA binding sites in the system with no load is
. The amount of DNA binding sites in the system with no load is  whereas in the system with activator load is
whereas in the system with activator load is  . (b) Bifurcation diagram with load as parameter. A continuation of the equilibrium as a function of the load parameter
. (b) Bifurcation diagram with load as parameter. A continuation of the equilibrium as a function of the load parameter  shows that, for this set of parameters, the amount of load to the activator required to stop the clock is on the order of the affinity coefficient
shows that, for this set of parameters, the amount of load to the activator required to stop the clock is on the order of the affinity coefficient  , with the bifurcation occurring at
, with the bifurcation occurring at  . The analysis was made on the full system (5) with the same parameters as before. The solid lines indicate a stable trajectory (the limit cycle to the left side of the Hopf bifurcation point and the equilibrium point to the right side of the Hopf bifurcation point). The dotted line indicates an unstable equilibrium point.
. The analysis was made on the full system (5) with the same parameters as before. The solid lines indicate a stable trajectory (the limit cycle to the left side of the Hopf bifurcation point and the equilibrium point to the right side of the Hopf bifurcation point). The dotted line indicates an unstable equilibrium point.
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  . The amount of DNA binding sites in the system with no load is
. The amount of DNA binding sites in the system with no load is  whereas in the system with repressor load is
whereas in the system with repressor load is  . (b)
. (b)  as a parameter. A continuation of the equilibrium as a function of the load parameter
as a parameter. A continuation of the equilibrium as a function of the load parameter  shows that, for this set of parameters, the amount of load required to activate the clock is in the same order of magnitude as that of the the affinity coefficient
shows that, for this set of parameters, the amount of load required to activate the clock is in the same order of magnitude as that of the the affinity coefficient  , with bifurcation occurring at
, with bifurcation occurring at  . This plot was obtained via continuation of system (14) with the same parameters as before. Solid lines indicate a stable trajectory (limit cycle to the right of the Hopf bifurcation and the equilibrium to its right). The dotted line indicates an unstable equilibrium point. (c)
. This plot was obtained via continuation of system (14) with the same parameters as before. Solid lines indicate a stable trajectory (limit cycle to the right of the Hopf bifurcation and the equilibrium to its right). The dotted line indicates an unstable equilibrium point. (c)  .
.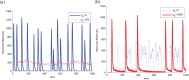
 and containing 5 copies of activator and repressor genes. (a) Functional clock stops with load to the activator. We show that, with the chosen parameters, it is possible to stop the clock with an amount of load that is roughly 100 times higher than the copy number of the circuit. (b) Load to the repressor leads to robust oscillation. We show that, the it is possible to generate robust oscillation with roughly 400 times the number of circuit genes with the choice of parameters above.
and containing 5 copies of activator and repressor genes. (a) Functional clock stops with load to the activator. We show that, with the chosen parameters, it is possible to stop the clock with an amount of load that is roughly 100 times higher than the copy number of the circuit. (b) Load to the repressor leads to robust oscillation. We show that, the it is possible to generate robust oscillation with roughly 400 times the number of circuit genes with the choice of parameters above.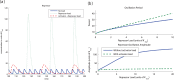
 ,
,  ). However, if we simultaneously add DNA binding sites with affinity to the activator, the amplitude is not affected as much (
). However, if we simultaneously add DNA binding sites with affinity to the activator, the amplitude is not affected as much ( ). (b) The period of system (20) can be changed with no effect on the amplitude when DNA binding sites with affinity to both the repressor and the activator are added simultaneously. The upper plot shows that a similar increase of period observed via the addition of repressor load can be obtained via the simultaneous addition of activator and repressor load. This second method has the advantage of not generating an increase in the amplitude, as shown in the lower plot. In this simulation we assumed the ratio
). (b) The period of system (20) can be changed with no effect on the amplitude when DNA binding sites with affinity to both the repressor and the activator are added simultaneously. The upper plot shows that a similar increase of period observed via the addition of repressor load can be obtained via the simultaneous addition of activator and repressor load. This second method has the advantage of not generating an increase in the amplitude, as shown in the lower plot. In this simulation we assumed the ratio  . Parameters of the activator repressor system used in the simulation were
. Parameters of the activator repressor system used in the simulation were  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  ,
,  . In the traces showing only repressor load
. In the traces showing only repressor load  , while the traces showing simultaneous repressor and activator load,
, while the traces showing simultaneous repressor and activator load,  .
.Similar articles
-
A simple negative interaction in the positive transcriptional feedback of a single gene is sufficient to produce reliable oscillations.PLoS One. 2011;6(11):e27414. doi: 10.1371/journal.pone.0027414. Epub 2011 Nov 10. PLoS One. 2011. PMID: 22205920 Free PMC article.
-
Interactivating feedback loops within the mammalian clock: BMAL1 is negatively autoregulated and upregulated by CRY1, CRY2, and PER2.Biochem Biophys Res Commun. 2002 Jan 25;290(3):933-41. doi: 10.1006/bbrc.2001.6300. Biochem Biophys Res Commun. 2002. PMID: 11798163
-
Feedback loops interlocked at competitive binding sites amplify and facilitate genetic oscillations.J Theor Biol. 2017 Sep 7;428:56-64. doi: 10.1016/j.jtbi.2017.06.005. Epub 2017 Jun 15. J Theor Biol. 2017. PMID: 28625476
-
[Synchronization and genetic redundancy in circadian clocks].Med Sci (Paris). 2008 Mar;24(3):270-6. doi: 10.1051/medsci/2008243270. Med Sci (Paris). 2008. PMID: 18334175 Review. French.
-
Molecular cogs of the insect circadian clock.Zoolog Sci. 2003 Aug;20(8):947-55. doi: 10.2108/zsj.20.947. Zoolog Sci. 2003. PMID: 12951399 Review.
Cited by
-
Molecular stripping, targets and decoys as modulators of oscillations in the NF-κB/IκBα/DNA genetic network.J R Soc Interface. 2016 Sep;13(122):20160606. doi: 10.1098/rsif.2016.0606. Epub 2016 Sep 28. J R Soc Interface. 2016. PMID: 27683001 Free PMC article.
-
Comparison between Effects of Retroactivity and Resource Competition upon Change in Downstream Reporter Genes of Synthetic Genetic Circuits.Life (Basel). 2019 Mar 26;9(1):30. doi: 10.3390/life9010030. Life (Basel). 2019. PMID: 30917535 Free PMC article.
-
Stochastic resonances in a distributed genetic broadcasting system: the NFκB/IκB paradigm.J R Soc Interface. 2018 Jan;15(138):20170809. doi: 10.1098/rsif.2017.0809. J R Soc Interface. 2018. PMID: 29343631 Free PMC article.
-
Sequestration of gene products by decoys enhances precision in the timing of intracellular events.Sci Rep. 2024 Nov 8;14(1):27199. doi: 10.1038/s41598-024-75505-y. Sci Rep. 2024. PMID: 39516495 Free PMC article.
-
Enhancement of gene expression noise from transcription factor binding to genomic decoy sites.Sci Rep. 2020 Jun 4;10(1):9126. doi: 10.1038/s41598-020-65750-2. Sci Rep. 2020. PMID: 32499583 Free PMC article.
References
-
- Alon U (2007) An introduction to systems biology. Design principles of biological circuits. Chapman-Hall.
-
- Dunlap JC (1999) Molecular Bases for Circadian Clocks Review. Cell 96: 271–290. - PubMed
-
- Ukai H, Ueda HR (2010) Systems biology of mammalian circadian clocks. Annual review of physiology 72: 579–603. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

