Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2012 Aug;9(4):046005.
doi: 10.1088/1478-3975/9/4/046005. Epub 2012 Jul 11.

Regimes of wave type patterning driven by refractory actin feedback: transition from static polarization to dynamic wave behaviour

W R Holmes  1 , A E Carlsson, L Edelstein-Keshet
Affiliations

Regimes of wave type patterning driven by refractory actin feedback: transition from static polarization to dynamic wave behaviour

W R Holmes et al. Phys Biol. 2012 Aug.

Abstract

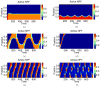
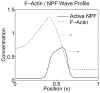
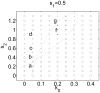
Patterns of waves, patches, and peaks of actin are observed experimentally in many living cells. Models of this phenomenon have been based on the interplay between filamentous actin (F-actin) and its nucleation promoting factors (NPFs) that activate the Arp2/3 complex. Here we present an alternative biologically-motivated model for F-actin-NPF interaction based on properties of GTPases acting as NPFs. GTPases (such as Cdc42, Rac) are known to promote actin nucleation, and to have active membrane-bound and inactive cytosolic forms. The model is a natural extension of a previous mathematical mini-model of small GTPases that generates static cell polarization. Like other modellers, we assume that F-actin negative feedback shapes the observed patterns by suppressing the trailing edge of NPF-generated wave-fronts, hence localizing the activity spatially. We find that our NPF-actin model generates a rich set of behaviours, spanning a transition from static polarization to single pulses, reflecting waves, wave trains, and oscillations localized at the cell edge. The model is developed with simplicity in mind to investigate the interaction between nucleation promoting factor kinetics and negative feedback. It explains distinct types of pattern initiation mechanisms, and identifies parameter regimes corresponding to distinct behaviours. We show that weak actin feedback yields static patterning, moderate feedback yields dynamical behaviour such as travelling waves, and strong feedback can lead to wave trains or total suppression of patterning. We use a recently introduced nonlinear bifurcation analysis to explore the parameter space of this model and predict its behaviour with simulations validating those results.

PubMed Disclaimer

Figures

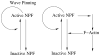
Figure 1
Figure 1
Schematic diagrams of models discussed in this paper. Left: The pure NPF system is based on the wave-pinning model of Mori et al. [25]. Right: NPF/refractory actin system with a constant pool of G-actin G.
Figure 2
Figure 2
The FitzHugh Nagumo model provides motivation for our representation of F-actin and nucleation promoting factor (NPF) system. A wave-generator induces a travelling wave-front, which separates high and low states. A refractory variable suppresses the high trailing edge of the wave on a longer timescale, leading to a spatially localized wave.
Figure 3
Figure 3
Simulations of our NPF/F-actin model, (Eqs. (1), (3b), (3a), (4) with a local perturbation at x = 0 used to initiate patterning. Parameter sets are drawn from Fig. 5 with remaining parameters in Table D1. For example, panel a is simulated with the parameter set labelled ‘a’ in that figure. Panels a – d are computed at fixed k0 with s2 varied. As s2 is increased patterns go from stable boundary localized (a), to oscillating boundary localized (b), to reflecting waves (c), to a single terminating wave (d), to no patterning. Panel e shows a wave train and panel f a more exotic pattern.
Figure 4
Figure 4
Snapshot of the localized travelling wave profile of F and A from Fig. 3d at time T = 95. The wave of NPF leads, and is followed by a wave of F-actin. The F-actin suppresses the trailing edge of the NPF wave, producing a localized profile.
Figure 5
Figure 5
The k0, s2 parameter plane, showing regimes of distinct patterning for our NPF/F-actin model (Eqs. (1), (3b), (3a), (4)), as determined by full simulations of the PDE model. Here, s1 = .5, ε = .1, and all other parameters as in SM Table 1. Initial conditions: HSS with a raised region of A (local perturbation) superimposed at the x = 0 boundary. Letters (a–f) correspond to patterns shown in the corresponding panels of Fig 3. Symbols: ○ - no patterning, ⋄ - boundary localized pattern, + -persistent reflecting wave, x - single terminating wave, * - persistent wave trains. The gray curve shows a two parameter continuation of the Hopf bifurcations in the LPA bifurcation plot of Fig. 6(b). The closed loop that forms represents an approximate boundary of a region where an oscillatory instability exists for the PDE system.
Figure 6
Figure 6
Nonlinear bifurcation analysis. Panel (a) the wave pinning model (Equations (1), (2)). Panel (b) our NPF/F-actin model, (Eqs. (1), (3b), (3a), (4)). Thick lines: HSS of the well-mixed system; thin lines: additional local states in the local perturbation system. Solid lines: stable states; dashed lines: unstable states. Panel (a) Three patterning regions are observed: I, III - wave pinning excitable response requiring a positive (resp. negative) valued perturbation, II - unstable response. In Region IV, the well mixed state is stable to all perturbations. Parameters used are γ = K = δ = 1 with the conserved quantity A + I = 2.27, taken from [25]. Panel (b) Structure similar to panel (a) but with two new Hopf bifurcations (H). These result from F-actin feedback. Between these, there is an oscillatory instability leading to wave dynamics. Parameters: s1 = 0.7, s2 = 0.7, τ = 0.1, and others as in SM Table 1. Gray arrows indicate the stability of branches.
Figure 7
Figure 7
Schematic diagram of the local perturbation of u on which the ‘Local Perturbation Analysis’ (LPA) approximation is based. In the limit Du ≪ Dv, u takes on a local behaviour ul near the perturbation and ug globally. The fast diffusing variable v (not depicted) takes on a uniform global level, vg as any inhomogeneities are quickly smoothed out. The dashed line depicts the idealized local perturbation in the LPA diffusion limit, and the solid line is its realistic counterpart, where small but finite diffusion of u causes a slight outwards spread.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Mackay Deborah JG, Hall Alan. Rho GTPases. Journal of Biological Chemistry. 1998;273(33):20685–20688. - PubMed
    1. Vicker MG. F-actin assembly in dictyostelium cell locomotion and shape oscillations propagates as a self-organized reaction-diffusion wave. FEBS Lett. 2002;510:5–9. - PubMed
    1. Vicker MG. Eukaryotic cell locomoation depends on the propagation of self-organized reaction-diffusion waves and oscillations of actin filament assembly. J Expt Cell Res. 2002;275:54–66. - PubMed
    1. Weiner OD, Marganski WA, Wu LF, Altschuler SJ, Kirschner MW. An actin-based wave generator organizes cell motility. PLoS biology. 2007;5(9):e221, 2053–2063. - PMC - PubMed
    1. Millius Arthur, Dandekar Sheel N, Houk Andrew R, Weiner Orion D. Neutrophils establish rapid and robust wave complex polarity in an actin-dependent fashion. Current Biology. 2009;19:253–259. - PMC - PubMed

Publication types