A framework for mapping, visualisation and automatic model creation of signal-transduction networks
- PMID: 22531118
- PMCID: PMC3361003
- DOI: 10.1038/msb.2012.12
A framework for mapping, visualisation and automatic model creation of signal-transduction networks
Abstract
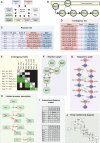
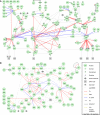
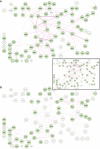
Intracellular signalling systems are highly complex. This complexity makes handling, analysis and visualisation of available knowledge a major challenge in current signalling research. Here, we present a novel framework for mapping signal-transduction networks that avoids the combinatorial explosion by breaking down the network in reaction and contingency information. It provides two new visualisation methods and automatic export to mathematical models. We use this framework to compile the presently most comprehensive map of the yeast MAP kinase network. Our method improves previous strategies by combining (I) more concise mapping adapted to empirical data, (II) individual referencing for each piece of information, (III) visualisation without simplifications or added uncertainty, (IV) automatic visualisation in multiple formats, (V) automatic export to mathematical models and (VI) compatibility with established formats. The framework is supported by an open source software tool that facilitates integration of the three levels of network analysis: definition, visualisation and mathematical modelling. The framework is species independent and we expect that it will have wider impact in signalling research on any system.
Conflict of interest statement
The authors declare that they have no conflict of interest.
Figures



Similar articles
-
Reaction-contingency based bipartite Boolean modelling.BMC Syst Biol. 2013 Jul 8;7:58. doi: 10.1186/1752-0509-7-58. BMC Syst Biol. 2013. PMID: 23835289 Free PMC article.
-
Information content and scalability in signal transduction network reconstruction formats.Mol Biosyst. 2013 Aug;9(8):1993-2004. doi: 10.1039/c3mb00005b. Epub 2013 May 2. Mol Biosyst. 2013. PMID: 23636168 Review.
-
Metabolic and signalling network maps integration: application to cross-talk studies and omics data analysis in cancer.BMC Bioinformatics. 2019 Apr 18;20(Suppl 4):140. doi: 10.1186/s12859-019-2682-z. BMC Bioinformatics. 2019. PMID: 30999838 Free PMC article.
-
2.5D visualisation of overlapping biological networks.J Integr Bioinform. 2008 Nov 10;5(1). doi: 10.2390/biecoll-jib-2008-90. J Integr Bioinform. 2008. PMID: 20134057
-
Biological Network Inference and analysis using SEBINI and CABIN.Methods Mol Biol. 2009;541:551-76. doi: 10.1007/978-1-59745-243-4_24. Methods Mol Biol. 2009. PMID: 19381531 Review.
Cited by
-
A detailed molecular network map and model of the NLRP3 inflammasome.Front Immunol. 2023 Nov 15;14:1233680. doi: 10.3389/fimmu.2023.1233680. eCollection 2023. Front Immunol. 2023. PMID: 38077364 Free PMC article. Review.
-
MOSBIE: a tool for comparison and analysis of rule-based biochemical models.BMC Bioinformatics. 2014 Sep 25;15(1):316. doi: 10.1186/1471-2105-15-316. BMC Bioinformatics. 2014. PMID: 25253680 Free PMC article.
-
Rule-based modeling: a computational approach for studying biomolecular site dynamics in cell signaling systems.Wiley Interdiscip Rev Syst Biol Med. 2014 Jan-Feb;6(1):13-36. doi: 10.1002/wsbm.1245. Epub 2013 Sep 30. Wiley Interdiscip Rev Syst Biol Med. 2014. PMID: 24123887 Free PMC article. Review.
-
Modeling for (physical) biologists: an introduction to the rule-based approach.Phys Biol. 2015 Jul 16;12(4):045007. doi: 10.1088/1478-3975/12/4/045007. Phys Biol. 2015. PMID: 26178138 Free PMC article. Review.
-
Systems Level Analysis of the Yeast Osmo-Stat.Sci Rep. 2016 Aug 12;6:30950. doi: 10.1038/srep30950. Sci Rep. 2016. PMID: 27515486 Free PMC article.
References
-
- Ai W, Bertram PG, Tsang CK, Chan TF, Zheng XF (2002) Regulation of subtelomeric silencing during stress response. Mol Cell 10: 1295–1305 - PubMed
-
- Alepuz PM, Jovanovic A, Reiser V, Ammerer G (2001) Stress-induced map kinase Hog1 is part of transcription activation complexes. Mol Cell 7: 767–777 - PubMed
-
- Andrews BJ, Herskowitz I (1989) Identification of a DNA binding factor involved in cell-cycle control of the yeast HO gene. Cell 57: 21–29 - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

