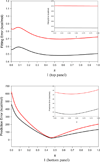
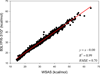
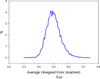
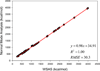
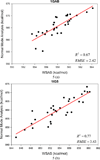
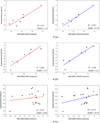
It is of great interest in modern drug design to accurately calculate the free energies of protein-ligand or nucleic acid-ligand binding. MM-PBSA (molecular mechanics Poisson-Boltzmann surface area) and MM-GBSA (molecular mechanics generalized Born surface area) have gained popularity in this field. For both methods, the conformational entropy, which is usually calculated through normal-mode analysis (NMA), is needed to calculate the absolute binding free energies. Unfortunately, NMA is computationally demanding and becomes a bottleneck of the MM-PB/GBSA-NMA methods. In this work, we have developed a fast approach to estimate the conformational entropy based upon solvent accessible surface area calculations. In our approach, the conformational entropy of a molecule, S, can be obtained by summing up the contributions of all atoms, no matter they are buried or exposed. Each atom has two types of surface areas, solvent accessible surface area (SAS) and buried SAS (BSAS). The two types of surface areas are weighted to estimate the contribution of an atom to S. Atoms having the same atom type share the same weight and a general parameter k is applied to balance the contributions of the two types of surface areas. This entropy model was parametrized using a large set of small molecules for which their conformational entropies were calculated at the B3LYP/6-31G* level taking the solvent effect into account. The weighted solvent accessible surface area (WSAS) model was extensively evaluated in three tests. For convenience, TS values, the product of temperature T and conformational entropy S, were calculated in those tests. T was always set to 298.15 K through the text. First of all, good correlations were achieved between WSAS TS and NMA TS for 44 protein or nucleic acid systems sampled with molecular dynamics simulations (10 snapshots were collected for postentropy calculations): the mean correlation coefficient squares (R²) was 0.56. As to the 20 complexes, the TS changes upon binding; TΔS values were also calculated, and the mean R² was 0.67 between NMA and WSAS. In the second test, TS values were calculated for 12 proteins decoy sets (each set has 31 conformations) generated by the Rosetta software package. Again, good correlations were achieved for all decoy sets: the mean, maximum, and minimum of R² were 0.73, 0.89, and 0.55, respectively. Finally, binding free energies were calculated for 6 protein systems (the numbers of inhibitors range from 4 to 18) using four scoring functions. Compared to the measured binding free energies, the mean R² of the six protein systems were 0.51, 0.47, 0.40, and 0.43 for MM-GBSA-WSAS, MM-GBSA-NMA, MM-PBSA-WSAS, and MM-PBSA-NMA, respectively. The mean rms errors of prediction were 1.19, 1.24, 1.41, 1.29 kcal/mol for the four scoring functions, correspondingly. Therefore, the two scoring functions employing WSAS achieved a comparable prediction performance to that of the scoring functions using NMA. It should be emphasized that no minimization was performed prior to the WSAS calculation in the last test. Although WSAS is not as rigorous as physical models such as quasi-harmonic analysis and thermodynamic integration (TI), it is computationally very efficient as only surface area calculation is involved and no structural minimization is required. Moreover, WSAS has achieved a comparable performance to normal-mode analysis. We expect that this model could find its applications in the fields like high throughput screening (HTS), molecular docking, and rational protein design. In those fields, efficiency is crucial since there are a large number of compounds, docking poses, or protein models to be evaluated. A list of acronyms and abbreviations used in this work is provided for quick reference.