Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2011;1(4):295-308.
doi: 10.1089/brain.2011.0055.

The brain as a complex system: using network science as a tool for understanding the brain

Qawi K Telesford  1 , Sean L Simpson, Jonathan H Burdette, Satoru Hayasaka, Paul J Laurienti
Affiliations
Review

The brain as a complex system: using network science as a tool for understanding the brain

Qawi K Telesford et al. Brain Connect. 2011.

Abstract

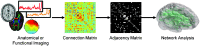
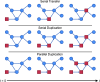
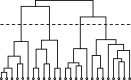
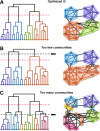
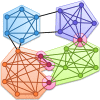
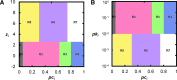
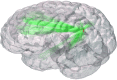
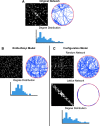
Although graph theory has been around since the 18th century, the field of network science is more recent and continues to gain popularity, particularly in the field of neuroimaging. The field was propelled forward when Watts and Strogatz introduced their small-world network model, which described a network that provided regional specialization with efficient global information transfer. This model is appealing to the study of brain connectivity, as the brain can be viewed as a system with various interacting regions that produce complex behaviors. In practice, graph metrics such as clustering coefficient, path length, and efficiency measures are often used to characterize system properties. Centrality metrics such as degree, betweenness, closeness, and eigenvector centrality determine critical areas within the network. Community structure is also essential for understanding network organization and topology. Network science has led to a paradigm shift in the neuroscientific community, but it should be viewed as more than a simple "tool du jour." To fully appreciate the utility of network science, a greater understanding of how network models apply to the brain is needed. An integrated appraisal of multiple network analyses should be performed to better understand network structure rather than focusing on univariate comparisons to find significant group differences; indeed, such comparisons, popular with traditional functional magnetic resonance imaging analyses, are arguably no longer relevant with graph-theory based approaches. These methods necessitate a philosophical shift toward complexity science. In this context, when correctly applied and interpreted, network scientific methods have a chance to revolutionize the understanding of brain function.

PubMed Disclaimer

Figures

FIG. 1.
FIG. 1.
Network analysis schematic. Anatomical and functional brain imaging data are analyzed to produce a connection matrix, denoting the strength of connection between nodes. A threshold is commonly applied to the matrix to generate a binary adjacency matrix. From the adjacency matrix, various graph metric analyses can be performed.
FIG. 2.
FIG. 2.
Patterns of information flow. Information is passed through a network by using one of three processes: serial transfer, serial duplication, and parallel duplication. In this schematic, information (squares) is either moved or copied to an adjacent node (circles). Arrows indicate where information will flow at the next time point. The brain most resembles parallel duplication, where multiple copies are propagated from a node.
FIG. 3.
FIG. 3.
Hierarchical clustering tree. Community structure in a network can be expressed as a hierarchical tree (dendrogram) with the circles at the bottom indicating the nodes and the tree indicating the order in which the nodes form a community. A demarcation line can be drawn across the tree at any level (dashed line), indicating communities below the line.
FIG. 4.
FIG. 4.
Modularity analysis. Depending on the level where the hierarchical tree is cut (dashed line), the number of communities can change. (A) In this example network, the optimal Q yields four communities (indicated by the dashed line). Shifting this line up or down (indicated by the dashed line with an arrow) produces a lower Q value that yields suboptimal communities. (B) As the line shifts higher, fewer communities are formed (approaching every node in a single community). (C) As the line shifts lower, more communities are formed (approaching every node in their own community).
FIG. 5.
FIG. 5.
Overlapping communities in a network. One limitation of Newman's analysis is that a given node can only be assigned to one community; however, a node may exist in more than one community. A node that serves in more than one community is akin to a node with more than one membership or role within a network. Image adapted from Palla et al. (2005).
FIG. 6.
FIG. 6.
Functional cartography maps. (A) Functional cartography classifies nodes as hubs and nonhubs based on its within-module degree (zi) (Guimerà and Amaral, 2005); if zi≥2.5, then the node is classified as a hub. (B) An alternative method based on the distribution of the data uses a within-module degree probability pki instead of a Z-score classifying a node as a hub if pki≤0.01 (Joyce et al., 2010). The combination of a node's participation coefficient (pci) and pki classifies the node as one of seven types: (R1) ultra-peripheral nodes, (R2) peripheral nodes, (R3) nonhub connector nodes, (R4) nonhub kinless nodes, (R5) provincial hubs, (R6) connector hubs, and (R7) kinless hubs.
FIG. 7.
FIG. 7.
Connections originating from the highest degree node. The highest degree node in a resting-state functional magnetic resonance imaging network is denoted by a sphere. Edges originating from the node, denoted by lines, extend to the brain areas known as the default mode network. Focusing solely on the degree of each node fails to acknowledge the regions to which it is connected. It is important to acknowledge the complex relationship between highly central nodes and the rest of the network.
FIG. 8.
FIG. 8.
Network null models with corresponding degree distribution. In network analysis, null models are used to better assess network topology. (A) The original network (represented as an adjacency matrix and circular graph) is often compared with random network models. Popular random network models include the (B) Erdős-Rényi (ER) random model and the (C) random network with preserved degree distribution. Although less popular, lattice network models can also be used to assess network topology. Null models with preserved degree distribution are generally preferred, as the degree distribution of the ER model does not match that of the original network.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Achard S. Bullmore E. Efficiency and cost of economical brain functional networks. PLoS Comput Biol. 2007;3:e17. - PMC - PubMed
    1. Achard S. Salvador R. Whitcher B. Suckling J. Bullmore E. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J Neurosci. 2006;26:63–72. - PMC - PubMed
    1. Alexander-Bloch AF, et al. Disrupted modularity and local connectivity of brain functional networks in childhood-onset schizophrenia. Front Syst Neurosci. 2010;4:147. - PMC - PubMed
    1. Balenzuela P, et al. Modular organization of brain resting state networks in chronic back pain patients. Front Neuroinform. 2010;4:116. - PMC - PubMed
    1. Bassett DS, et al. Hierarchical organization of human cortical networks in health and schizophrenia. J Neurosci. 2008;28:9239–9248. - PMC - PubMed

LinkOut - more resources