Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2012 Aug;33(1):53-75.
doi: 10.1007/s10827-011-0374-4. Epub 2011 Dec 21.

Improved measures of phase-coupling between spikes and the Local Field Potential

Martin Vinck  1 , Francesco Paolo Battaglia, Thilo Womelsdorf, Cyriel Pennartz
Affiliations

Improved measures of phase-coupling between spikes and the Local Field Potential

Martin Vinck et al. J Comput Neurosci. 2012 Aug.

Abstract

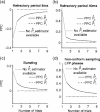
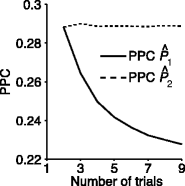
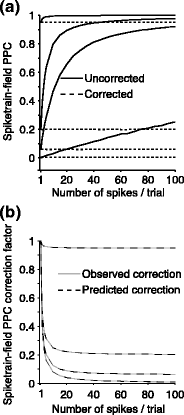
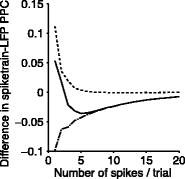
An important tool to study rhythmic neuronal synchronization is provided by relating spiking activity to the Local Field Potential (LFP). Two types of interdependent spike-LFP measures exist. The first approach is to directly quantify the consistency of single spike-LFP phases across spikes, referred to here as point-field phase synchronization measures. We show that conventional point-field phase synchronization measures are sensitive not only to the consistency of spike-LFP phases, but are also affected by statistical dependencies between spike-LFP phases, caused by e.g. non-Poissonian history-effects within spike trains such as bursting and refractoriness. To solve this problem, we develop a new pairwise measure that is not biased by the number of spikes and not affected by statistical dependencies between spike-LFP phases. The second approach is to quantify, similar to EEG-EEG coherence, the consistency of the relative phase between spike train and LFP signals across trials instead of across spikes, referred to here as spike train to field phase synchronization measures. We demonstrate an analytical relationship between point-field and spike train to field phase synchronization measures. Based on this relationship, we prove that the spike train to field pairwise phase consistency (PPC), a quantity closely related to the squared spike-field coherence, is a monotonically increasing function of the number of spikes per trial. This derived relationship is exact and analytic, and takes a linear form for weak phase-coupling. To solve this problem, we introduce a corrected version of the spike train to field PPC that is independent of the number of spikes per trial. Finally, we address the problem that dependencies between spike-LFP phase and the number of spikes per trial can cause spike-LFP phase synchronization measures to be biased by the number of trials. We show how to modify the developed point-field and spike train to field phase synchronization measures in order to make them unbiased by the number of trials.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
Illustration of point-field phase synchronization measures. Spikes (vertical, solid lines) are related to LFPs by determining the instantaneous LFP phases at the times of spiking by centering a window (horizontal, solid lines) around every spike. Thus, the phase for each spike is determined from the LFP snippet that is centered around it. The instantaneous LFP phase at the time of spiking can be directly gauged by using the dotted lines that connect the spikes to the LFP. The frequency resolution, which is inversely proportional to time resolution, is proportional to the window length, which needs to be sufficiently large. However, if the windows are too long, then the loss of time-resolution may lead to a decrease in spike-LFP phase consistency. The instantaneous spike-LFP phases are depicted by the unit arrows that originate from the spikes. The LFP was modeled as band-stop filtered Gaussian white noise, as in Zeitler et al. (2006). Here, we show only two (m = 1 and m = 2) out of M available trials. The measures of point-field phase consistency are computed over the n relative spike-LFP phases. By vector addition of the n spike-LFP phase vectors, a resultant vector is obtained, whose length is conventionally taken as a measure of point-field phase consistency
Fig. 2
Fig. 2
Illustration of spike train to field phase synchronization measures. Spikes (vertical, solid lines) are related to LFPs by computing, using the Fast Fourier Transform, the respective phase offsets of the spike train and the LFP at a particular frequency (grey arrows) and subsequently determining the relative phase between these phase offsets (black arrows). Thus, the relative phases are computed for a time-period, not for an individual spike. The LFP was generated using the same model as in Fig. 1. Shown here are two trials (m = 1 and m = 2). The measures of spike train to field phase consistency are computed over the M relative phases. By vector addition of the M relative phase vectors, a resultant vector is obtained, whose length is conventionally taken as a measure of the consistency of the relative phases between LFPs and spike trains
Fig. 3
Fig. 3
Illustration of the point-field PPC formula image and the point-field PPC formula image. (a) Nine spike-LFP phases from four different trials are recorded. These spike-LFP phases are depicted by the arrows, which are duplicated on the x- and y-axis. This gives 9 ·9 = 81 potential 2-combinations of spike-LFP phases across trials. The extent to which two spike-LFP phase vectors coincide is measured by the dot product. The point-field PPC formula image equals the average dot product of spike-LFP phase vectors across all 2-combinations of different spikes. The nine 2-combinations of spikes with themselves are not taken into account, which is indicated by the diagonal patterns. (b) Same as in (a), but the point-field PPC formula image equals the average dot product of spike-LFP phase vectors across all 2-combinations of spikes from different trials.The 2-combinations of spikes from the same trial are not taken into account, which is indicated by the diagonal patterns
Fig. 4
Fig. 4
Influence of dependence between spike-LFP phases on point-field phase synchronization measures. (a) Estimated, expected point-field PPC formula image (solid), and point-field PPC formula image values (dotted) (y-axis) as a function of the number of trials (x-axis), in the presence of an absolute refractory period of 8 ms. The grey portion of the solid formula image curve highlights that no formula image estimate exists when only one trial is available. (b) Similar to (a), but now in the presence of an absolute refractory period of 40 ms. (c) Influence of burstiness on point-field phase synchronization measures. Estimated expected point-field PPC formula image (solid), and point-field PPC formula image value (dotted) (y-axis) as a function of the number of trials (x-axis). For every spike fired, we added one extra spike with the same phase. (d) Influence of incomplete coverage of LFP phases on estimated, expected point-field PPC formula image (solid), and point-field PPC formula image values (dotted) (y-axis) as a function of number of trials (x-axis), with the neuron firing only during 20% of the cycle duration
Fig. 5
Fig. 5
Influence of dependence of spike-LFP phase consistency and spike count on point-field phase synchronization measures. Estimated, expected point-field PPC formula image (solid), and point-field PPC formula image values (black, dotted) (y-axis) as a function of the number of trials (x-axis), where trials with a large number of spikes have a noisier phase distribution
Fig. 6
Fig. 6
Comparison of uncorrected and corrected spike train to field PPC formula image. (a) Y-axis: corrected spike train to field PPC formula image (dotted) and uncorrected spike train to field PPC formula image (solid). X-axis: number of spikes per trial. Different lines represent different coupling strength, with the von Mises dispersion parameter κ ∈ { 0.1, 0.5, 1, 20 }. (b) Empirically observed and analytically predicted correction factor for spike train to field PPC formula image (y-axis) as a function of the number of spikes per trial (x-axis), again for κ ∈ { 0.1, 0.5, 1, 20 }
Fig. 7
Fig. 7
Influence of firing rate variance on spike train to field phase synchronization measures. Dashed: spike train to field PPC formula image for Poisson distribution minus spike train to field PPC formula image for zero-variance distribution, as a function of the number of spikes per trial. Positive values indicate a larger formula image value for Poisson distribution. Solid: as for dashed, but now for spike train to field PPC formula image. Dashed-dotted: as solid, but now for spike train to field PPC formula image
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Abeles M. Role of the cortical neuron: Integrator or coincidence detector? Israel Journal of Medical Sciences. 1982;18:83. - PubMed
    1. Adey WR, Walter DO, Hendrix CE. Computer techniques in correlation and spectral analyses of cerebral slow waves during discriminative behavior. Experimental Neurology. 1961;3:501–524. - PubMed
    1. Azouz R, Gray CM. Adaptive coincidence detection and dynamic gain control in visual cortical neurons in vivo. Neuron. 2003;37:513–523. - PubMed
    1. Battaglia FP, Benchenane K, Sirota A, Pennartz CM, Wiener SI. The hippocampus: Hub of brain network communication for memory. Trends in Cognitive Science. 2011;15:310–318. - PubMed
    1. Benchenane K, Peyrache A, Khamassi M, Tierney PL, Gioanni Y, Battaglia FP, et al. Coherent theta oscillations and reorganization of spike timing in the hippocampal- prefrontal network upon learning. Neuron. 2010;66:921–936. - PubMed

LinkOut - more resources