Emergence of long timescales and stereotyped behaviors in Caenorhabditis elegans
- PMID: 21502536
- PMCID: PMC3088607
- DOI: 10.1073/pnas.1007868108
Emergence of long timescales and stereotyped behaviors in Caenorhabditis elegans
Abstract
Animal behaviors often are decomposable into discrete, stereotyped elements, well separated in time. In one model, such behaviors are triggered by specific commands; in the extreme case, the discreteness of behavior is traced to the discreteness of action potentials in the individual command neurons. Here, we use the crawling behavior of the nematode Caenorhabditis elegans to demonstrate the opposite view, in which discreteness, stereotypy, and long timescales emerge from the collective dynamics of the behavior itself. In previous work, we found that as C. elegans crawls, its body moves through a "shape space" in which four dimensions capture approximately 95% of the variance in body shape. Here we show that stochastic dynamics within this shape space predicts transitions between attractors corresponding to abrupt reversals in crawling direction. With no free parameters, our inferred stochastic dynamical system generates reversal timescales and stereotyped trajectories in close agreement with experimental observations. We use the stochastic dynamics to show that the noise amplitude decreases systematically with increasing time away from food, resulting in longer bouts of forward crawling and suggesting that worms can use noise to modify their locomotory behavior.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
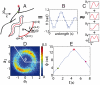
 . (E) The phase trajectories exhibit abrupt reversals, moments when ω ≡ dϕ/dt change sign. The red cross marks the onset of a body wave reversal and the green and magenta dots mark times prior to and during a reversal. These same times are also marked in A demonstrating that phase reversals correspond to reversals in the crawling direction.
. (E) The phase trajectories exhibit abrupt reversals, moments when ω ≡ dϕ/dt change sign. The red cross marks the onset of a body wave reversal and the green and magenta dots mark times prior to and during a reversal. These same times are also marked in A demonstrating that phase reversals correspond to reversals in the crawling direction.

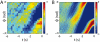
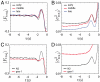
Similar articles
-
Reversal frequency in Caenorhabditis elegans represents an integrated response to the state of the animal and its environment.J Neurosci. 2003 Jun 15;23(12):5319-28. doi: 10.1523/JNEUROSCI.23-12-05319.2003. J Neurosci. 2003. PMID: 12832557 Free PMC article.
-
Dimensionality and dynamics in the behavior of C. elegans.PLoS Comput Biol. 2008 Apr 25;4(4):e1000028. doi: 10.1371/journal.pcbi.1000028. PLoS Comput Biol. 2008. PMID: 18389066 Free PMC article.
-
Caenorhabditis elegans selects distinct crawling and swimming gaits via dopamine and serotonin.Proc Natl Acad Sci U S A. 2011 Oct 18;108(42):17504-9. doi: 10.1073/pnas.1108673108. Epub 2011 Oct 3. Proc Natl Acad Sci U S A. 2011. PMID: 21969584 Free PMC article.
-
Automated imaging of C. elegans behavior.Methods Mol Biol. 2006;351:241-51. doi: 10.1385/1-59745-151-7:241. Methods Mol Biol. 2006. PMID: 16988438 Review.
-
The Si elegans project at the interface of experimental and computational Caenorhabditis elegans neurobiology and behavior.J Neural Eng. 2016 Dec;13(6):065001. doi: 10.1088/1741-2560/13/6/065001. Epub 2016 Oct 14. J Neural Eng. 2016. PMID: 27739402 Review.
Cited by
-
Multistability and metastability: understanding dynamic coordination in the brain.Philos Trans R Soc Lond B Biol Sci. 2012 Apr 5;367(1591):906-18. doi: 10.1098/rstb.2011.0351. Philos Trans R Soc Lond B Biol Sci. 2012. PMID: 22371613 Free PMC article. Review.
-
Social behavioral profiling by unsupervised deep learning reveals a stimulative effect of dopamine D3 agonists on zebrafish sociality.Cell Rep Methods. 2023 Jan 5;3(1):100381. doi: 10.1016/j.crmeth.2022.100381. eCollection 2023 Jan 23. Cell Rep Methods. 2023. PMID: 36814839 Free PMC article.
-
Time Irreversibility and Criticality in the Motility of a Flagellate Microorganism.Phys Rev Lett. 2018 Aug 3;121(5):058103. doi: 10.1103/PhysRevLett.121.058103. Phys Rev Lett. 2018. PMID: 30118294 Free PMC article.
-
A Cohesive Framework for Motor Stereotypy in Typical and Atypical Development: The Role of Sensorimotor Integration.Front Integr Neurosci. 2017 Aug 25;11:19. doi: 10.3389/fnint.2017.00019. eCollection 2017. Front Integr Neurosci. 2017. PMID: 28890690 Free PMC article.
-
Multistability and Long-Timescale Transients Encoded by Network Structure in a Model of C. elegans Connectome Dynamics.Front Comput Neurosci. 2017 Jun 13;11:53. doi: 10.3389/fncom.2017.00053. eCollection 2017. Front Comput Neurosci. 2017. PMID: 28659783 Free PMC article.
References
-
- Bullock TH, Orkand R, Grinnell A. Introduction to Nervous Systems. San Francisco: WH Freeman; 1977.
-
- Korn H, Faber DS. The Mauthner cell half a century later: A neurobiological model for decision making? Neuron. 1990;47:13–28. - PubMed
-
- Dayan P, Abbott LF. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. Cambridge, MA: MIT Press; 2001.
-
- Croll N. Components and patterns in the behavior of the nematode Caenorhabditis elegans. J Zool . 1975;176:159–176.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

