Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2009 Dec;19(4):043123.
doi: 10.1063/1.3270261.

Epidemics with multistrain interactions: the interplay between cross immunity and antibody-dependent enhancement

Simone Bianco  1 , Leah B Shaw, Ira B Schwartz
Affiliations

Epidemics with multistrain interactions: the interplay between cross immunity and antibody-dependent enhancement

Simone Bianco et al. Chaos. 2009 Dec.

Abstract

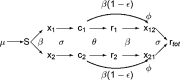
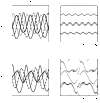
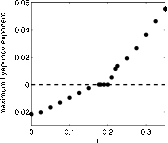
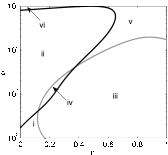
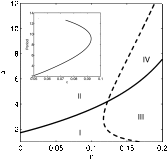
This paper examines the interplay of the effect of cross immunity and antibody-dependent enhancement (ADE) in multistrain diseases. Motivated by dengue fever, we study a model for the spreading of epidemics in a population with multistrain interactions mediated by both partial temporary cross immunity and ADE. Although ADE models have previously been observed to cause chaotic outbreaks, we show analytically that weak cross immunity has a stabilizing effect on the system. That is, the onset of disease fluctuations requires a larger value of ADE with small cross immunity than without. However, strong cross immunity is shown numerically to cause oscillations and chaotic outbreaks even for low values of ADE.

PubMed Disclaimer

Figures

FIG. 1.
FIG. 1.
Flow diagram of how an individual would proceed through the model in the case of two serotypes. Note the reduction of susceptibility to a secondary infection through the cross immunity factor (1−ϵ) and the enhancement of secondary infectiousness due to the ADE factor ϕ. Death terms for each compartment are not included in the graph for ease of reading.
FIG. 2.
FIG. 2.
Bifurcation diagram in ADE (ϕall) for the multistrain system with no cross immunity. For each ADE value, we show the local maxima (black) and local minima (gray) of the susceptibles during a 100 year time series after removal of transients. [Reprinted with permission from Schwartz et al., Phys. Rev. E 72, 066201 (2005). Copyright © 2005, American Physical Society.]
FIG. 3.
FIG. 3.
Predicted and actual location for Hopf bifurcation as a function of ϵ and ϕ for weak cross immunity in the case of no mortality (μd=0). The full curve is the analytic approximation [zeros of Eq. (11)], while the dashed curve is the actual location of the Hopf bifurcation obtained numerically for the full system in the case of no mortality. The number of strains is n=4, and other parameters are as listed in the text.
FIG. 4.
FIG. 4.
Bifurcation diagram for the system of ordinary differential equations [Eq. (1)] in the absence of ADE (ϕ=1). The cross immunity parameter ϵ is varied from 0 to 1. For each cross immunity value we plot the maxima (black) and the minima (gray) of the susceptibles during a 100 year time series after removal of a transient. A transition to chaos occurs at ϵ≈0.2.
FIG. 5.
FIG. 5.
Poincaré section showing ln x2(n+1) vs ln x2(n). ϵ=0.179, ϕ=0. See text for details.
FIG. 6.
FIG. 6.
Quasiperiodic attractors for ϵ=0.179 [panels (a) and (b)] and ϵ=0.2 [panels (c) and (d)]. Time series of primary infectives (log variables) are shown in (a) and (c). Phase differences of primary infectives x2,x3,x4 relative to primary infective x1 are shown in (b) and (d). The time series in (a) and (c) are the beginning of those used to generate (b) and (d). The reference strain x1 is the lightest gray curve in (a) and (c). Other parameters: ϕ=1.
FIG. 7.
FIG. 7.
Maximum Lyapunov exponent of Eq. (1) for ϕ=1 as a function of cross immunity strength ϵ. Equations were integrated for 104 yr after removal of transients.
FIG. 8.
FIG. 8.
Chaotic attractor for ϵ=0.35, ϕ=1. (a) Time series of all four primary infectives (log variables). Black dashed curve: x1; darkest gray curve: x2. (b) Histogram of phase differences of primary infective x2 relative to primary infective x1. (c) Time series of the first primary infective x1 and the secondary infectives currently infected with strain 1 xj,1 (log variables). Black dashed curve: x1. (d) Histogram of phase differences of secondary infective x2,1 relative to primary infective x1. Phase difference histograms are collected for 2000 yr time series.
FIG. 9.
FIG. 9.
Full bifurcation diagram in cross immunity ϵ and ADE ϕ. Curves indicate location of Hopf bifurcations. See text for details.
FIG. 10.
FIG. 10.
Blowup of bifurcation diagram in Fig. 9 for small cross immunity ϵ and ADE ϕ. Curves indicate location of Hopf bifurcations. Only region I has stable steady states. The inset shows the period of a branch of unstable orbits as a function of ϵ for ϕ≈3.877 in region II. See text for details.
FIG. 11.
FIG. 11.
Bifurcation diagrams in ADE for cases with nonzero cross immunity. For each ADE value, we show maxima (black) and minima (gray). (a) Weak cross immunity, ϵ=0.05. (b) Strong cross immunity, ϵ=0.6. (For comparison, Fig. 2 shows the case of no cross immunity.)
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Abu-Raddad, L. J. and Ferguson, N. M. , “The impact of cross-immunity, mutation and stochastic extinction on pathogen diversity,” Proc. R. Soc. London, Ser. B PRLBA4271, 2431–2438 (2004).10.1098/rspb.2004.2877 - DOI - PMC - PubMed
    1. Adams, B. and Boots, M., “Modelling the relationship between antibody-dependent enhancement and immunological distance with application to dengue,” J. Theor. Biol. JTBIAP242, 337–346 (2006).10.1016/j.jtbi.2006.03.002 - DOI - PubMed
    1. Adams, B., Holmes, E. C. , Zhang, C., Mammen, M. P. , Nimmannitya, S., Kalayanarooj, S., and Boots, M., “Cross-protective immunity can account for the alternating epidemic pattern of dengue virus serotypes circulating in Bangkok,” Proc. Natl. Acad. Sci. U.S.A. PNASA6103, 14234–14239 (2006).10.1073/pnas.0602768103 - DOI - PMC - PubMed
    1. Adams, B. and Sasaki, A., “Cross-immunity, invasion and coexistence of pathogen strains in epidemiological models with one-dimensional antigenic space,” Math. Biosci. MABIAR210, 680–699 (2007).10.1016/j.mbs.2007.08.001 - DOI - PubMed
    1. Aguiar. M. and Stollenwerk, N., “A new chaotic attractor in a basic multi-strain epidemiological model with temporary cross-immunity,” e-print arXiv:cond-mat/0704.3174

Publication types

MeSH terms