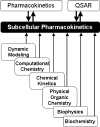
Modeling kinetics of subcellular disposition of chemicals
- PMID: 19265398
- PMCID: PMC2682929
- DOI: 10.1021/cr030440j
Modeling kinetics of subcellular disposition of chemicals
Figures

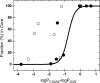


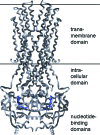
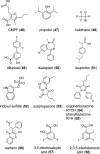
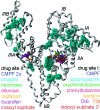





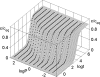
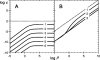
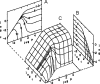
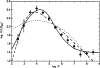
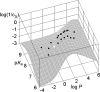

Similar articles
-
Domain formation in the plasma membrane: roles of nonequilibrium lipid transport and membrane proteins.Phys Rev Lett. 2008 May 2;100(17):178102. doi: 10.1103/PhysRevLett.100.178102. Epub 2008 Apr 28. Phys Rev Lett. 2008. PMID: 18518341
-
The 'double lives' of membrane lipids. Workshop: Anno 2000. A lipid milestone.EMBO Rep. 2001 Feb;2(2):91-5. doi: 10.1093/embo-reports/kve029. EMBO Rep. 2001. PMID: 11258718 Free PMC article. No abstract available.
-
Cooperative dynamics of quasi-1D lipid structures and lateral transport in biological membranes.Gen Physiol Biophys. 1997 Dec;16(4):311-9. Gen Physiol Biophys. 1997. PMID: 9595300
-
Thermodynamics of lipid interactions in complex bilayers.Biochim Biophys Acta. 2009 Jan;1788(1):72-85. doi: 10.1016/j.bbamem.2008.08.007. Epub 2008 Aug 15. Biochim Biophys Acta. 2009. PMID: 18775410 Review.
-
Capacities of membrane lipids to accumulate neutral organic chemicals.Environ Sci Technol. 2011 Jul 15;45(14):5912-21. doi: 10.1021/es200855w. Epub 2011 Jun 28. Environ Sci Technol. 2011. PMID: 21671592 Review.
Cited by
-
Convergence of Free Energy Profile of Coumarin in Lipid Bilayer.J Chem Theory Comput. 2012 Apr 10;8(4):1200-1211. doi: 10.1021/ct2009208. Epub 2012 Feb 24. J Chem Theory Comput. 2012. PMID: 22545027 Free PMC article.
-
Structural determinants of drug partitioning in n-hexadecane/water system.J Chem Inf Model. 2013 Jun 24;53(6):1424-35. doi: 10.1021/ci400112k. Epub 2013 May 21. J Chem Inf Model. 2013. PMID: 23641957 Free PMC article.
-
Bioanalysis of eukaryotic organelles.Chem Rev. 2013 Apr 10;113(4):2733-811. doi: 10.1021/cr300354g. Chem Rev. 2013. PMID: 23570618 Free PMC article. Review. No abstract available.
-
Structure-based prediction of drug distribution across the headgroup and core strata of a phospholipid bilayer using surrogate phases.Mol Pharm. 2014 Oct 6;11(10):3577-95. doi: 10.1021/mp5003366. Epub 2014 Sep 18. Mol Pharm. 2014. PMID: 25179490 Free PMC article.
-
A Permeability Study of O2 and the Trace Amine p-Tyramine through Model Phosphatidylcholine Bilayers.PLoS One. 2015 Jun 18;10(6):e0122468. doi: 10.1371/journal.pone.0122468. eCollection 2015. PLoS One. 2015. PMID: 26086933 Free PMC article.
References
-
- Bio-Loom Database and Software; Biobyte Corp.: Claremont, CA, 2006. (www.biobyte.com)
-
- Kurup A. J. Comput. Aid. Mol. Des. 2003, 17, 187. - PubMed
-
- Hansch C.; Steward A. R.; Iwasa J.; Deutsch E. W. Mol. Pharmacol. 1965, 1, 205. - PubMed
-
- Hansch C. Farmaco 1968, 23, 293. - PubMed
-
- Hansch C.; Dunn W. J. J. Pharm. Sci. 1972, 61, 1. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

