Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2009 Jan 9;385(1):91-8.
doi: 10.1016/j.jmb.2008.09.078. Epub 2008 Oct 9.

Correlated evolution of interacting proteins: looking behind the mirrortree

Maricel G Kann  1 , Benjamin A Shoemaker, Anna R Panchenko, Teresa M Przytycka
Affiliations

Correlated evolution of interacting proteins: looking behind the mirrortree

Maricel G Kann et al. J Mol Biol. .

Abstract

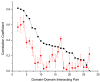
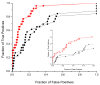
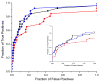
It has been observed that the evolutionary distances of interacting proteins often display a higher level of similarity than those of noninteracting proteins. This finding indicates that interacting proteins are subject to common evolutionary constraints and constitutes the basis of a method to predict protein interactions known as mirrortree. It has been difficult, however, to identify the direct cause of the observed similarities between evolutionary trees. One possible explanation is the existence of compensatory mutations between partners' binding sites to maintain proper binding. This explanation, though, has been recently challenged, and it has been suggested that the signal of correlated evolution uncovered by the mirrortree method is unrelated to any correlated evolution between binding sites. We examine the contribution of binding sites to the correlation between evolutionary trees of interacting domains. We show that binding neighborhoods of interacting proteins have, on average, higher coevolutionary signal compared with the regions outside binding sites; however, when the binding neighborhood is removed, the remaining domain sequence still contains some coevolutionary signal. In conclusion, the correlation between evolutionary trees of interacting domains cannot exclusively be attributed to the correlated evolution of the binding sites or to common evolutionary pressure exerted on the whole protein domain sequence, each of which contributes to the signal measured by the mirrortree approach.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Comparing signals from the binding neighborhood against randomly selected MSA columns. (1) The binding neighborhoods are extracted from crystal structures of interacting domains and projected onto the multiple sequence alignment (MSA) of orthologous sequences. (2) The distance matrices are constructed using the MSA columns corresponding to the binding neighborhoods, and separately, for the sequences constructed by randomly selecting the same number of non-binding MSA columns. The upper triangle of the distance matrix is represented as a vector. Subsequently, (3) each vector is corrected by subtracting the speciation vector (s→, depicted in gray). (4) The correlation coefficient between the resulting vectors is computed (dashed and dotted vectors for randomly selected and binding neighborhood respectively). (5) Finally, it is tested whether the correlation between vectors computed using the binding neighborhood lead to better retrieval results than vectors computed using randomly selected MSA columns.
Figure 2
Figure 2
Comparison of the correlation coefficients for each domain-domain interacting pair using the binding neighborhood (black), and an equivalent number of randomly selected columns (red). The values in the x-axis, labeled 1 to 26, represent each of the domain-domain interacting pairs sorted in descending order by the corresponding correlation coefficient when using the binding neighborhood. Results in panels a and b were obtained using the orthogonal and non-orthogonal speciation corrections respectively. For randomized experiments we plot the mean value and represent the standard deviation based on 100 trials as the error bar.
Figure 2
Figure 2
Comparison of the correlation coefficients for each domain-domain interacting pair using the binding neighborhood (black), and an equivalent number of randomly selected columns (red). The values in the x-axis, labeled 1 to 26, represent each of the domain-domain interacting pairs sorted in descending order by the corresponding correlation coefficient when using the binding neighborhood. Results in panels a and b were obtained using the orthogonal and non-orthogonal speciation corrections respectively. For randomized experiments we plot the mean value and represent the standard deviation based on 100 trials as the error bar.
Figure 3
Figure 3
Comparison of the performance of the mirrortree method on the binding neighborhood and on the randomly selected MSA columns set of the same size. The red lines correspond to the performance using the binding neighborhood with corrections from the orthogonal speciation subtraction (circles) and non-orthogonal speciation subtraction (squares). The corresponding graphs for randomly selected residues are drawn in black. Insert shows ROC curves for up to 20% false positive rate.
Figure 4
Figure 4
Dependence of ROC results on the columns used in the alignment and on the speciation correction used in the analysis. Results for ROCtotal and ROC50 show the following trends. Regardless of the region of the sequence used, the performance of the method with the correction for speciation (darker colors) is better than that of the original mirrortree without the correction (lighter colors). In particular, using the full length sequence with speciation correction yields, for ROC50, the best results (grey), and substracting a set of randomly selected non-binding columns (brown) represents only a slight decrease in the performance, while subtracting the binding neighborhood (cyan) to the full sequence represents a significant decrease on the overall performance of the method. Finally, performance using the binding neighborhood alone (green) is significantly better than using a randomly selected set of columns of the same size but not belonging to the binding neighborhood (yellow).
Figure 5
Figure 5
Comparison of the performance of the mirrortree method using the full sequence (black), full sequence without the binding neighborhood (red), and sequence without the set of randomly selected columns of the same number as the binding neighborhood (blue). Figure 5a corresponds to the orthogonal speciation correction and Figure 5b corresponds to the non-orthogonal correction. Inserts show ROC curves for up to 20% false positive rate.
Figure 5
Figure 5
Comparison of the performance of the mirrortree method using the full sequence (black), full sequence without the binding neighborhood (red), and sequence without the set of randomly selected columns of the same number as the binding neighborhood (blue). Figure 5a corresponds to the orthogonal speciation correction and Figure 5b corresponds to the non-orthogonal correction. Inserts show ROC curves for up to 20% false positive rate.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Goh CS, Bogan AA, Joachimiak M, Walther D, Cohen FE. Co-evolution of proteins with their interaction partners. J Mol Biol. 2000;299:283–93. - PubMed
    1. Pazos F, Helmer-Citterich M, Ausiello G, Valencia A. Correlated mutations contain information about protein-protein interaction. J Mol Biol. 1997;271:511–23. - PubMed
    1. Pazos F, Valencia A. Similarity of phylogenetic trees as indicator of protein-protein interaction. Protein Eng. 2001;14:609–14. - PubMed
    1. Goh CS, Cohen FE. Co-evolutionary analysis reveals insights into protein-protein interactions. J Mol Biol. 2002;324:177–92. - PubMed
    1. Jothi R, Kann MG, Przytycka TM. Predicting protein-protein interaction by searching evolutionary tree automorphism space. Bioinformatics. 2005;21(Suppl 1):i241–50. - PMC - PubMed

Publication types

LinkOut - more resources