Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2009 May 6;6(34):447-54.
doi: 10.1098/rsif.2008.0258. Epub 2008 Aug 15.

Sharing the burden: antigen transport and firebreaks in immune responses

Andreas Handel  1 , Andrew Yates, Sergei S Pilyugin, Rustom Antia
Affiliations

Sharing the burden: antigen transport and firebreaks in immune responses

Andreas Handel et al. J R Soc Interface. .

Abstract

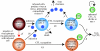
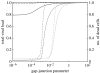
Communication between cells is crucial for immune responses. An important means of communication during viral infections is the presentation of viral antigen on the surface of an infected cell. Recently, it has been shown that antigen can be shared between infected and uninfected cells through gap junctions, connexin-based channels, that allow the transport of small molecules. The uninfected cell receiving antigen can present it on its surface. Cells presenting viral antigen are detected and killed by cytotoxic T lymphocytes. The killing of uninfected cells can lead to increased immunopathology. However, the immune response might also profit from killing those uninfected bystander cells. One benefit might be the removal of future 'virus factories'. Another benefit might be through the creation of 'firebreaks', areas void of target cells, which increase the diffusion time of free virions, making their clearance more likely. Here, we use theoretical models and simulations to explore how the mechanism of gap junction-mediated antigen transport (GMAT) affects the dynamics of the virus and immune response. We show that under the assumption of a well-mixed system, GMAT leads to increased immunopathology, which always outweighs the benefit of reduced virus production due to the removal of future virus factories. By contrast, a spatially explicit model leads to quite different results. Here we find that the firebreak mechanism reduces both viral load and immunopathology. Our study thus shows the potential benefits of GMAT and illustrates how spatial effects may be crucial for the quantitative understanding of infection dynamics and immune responses.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Schematic of GMAT between target cells. Uninfected cells become infected. The infected cells produce free virus, and they also transfer viral antigen via gap junctions to neighbouring uninfected cells, turning these into antigen-presenting, uninfected bystander cells. CTL can recognize antigen on both infected and bystander cells, form complexes with those cells and, after some time, kill the complexed cells. The specific meaning and values of the rates indicated by the symbols are described in §2.
Figure 2
Figure 2
Viral load and dead cells for different values of the gap-junction parameter, immediate killing by CTL. Shown are total viral load, integrated over the whole infection (solid lines) and number of dead cells at the end of the infection (dashed lines) as a function of the gap-junction parameter. For better representation, each curve is scaled by its maximum value. The model used to obtain the results is the set of ODEs described in §2, with δ→∞, corresponding to the immediate killing of target or bystander cells by CTL. The virion clearance rates corresponding to slow (black lines), medium (dark grey lines) and fast (light grey lines) virus clearances are c=2 d−1, c=4 d−1 and c=8 d−1, respectively.
Figure 3
Figure 3
Viral load and dead cells for different values of the gap-junction parameter, delayed killing by CTL. Same scenario as shown in figure 2, but with δ=48 d−1, corresponding to approximately 30 min between complex formation and killing by CTL.
Figure 4
Figure 4
Snapshots of the infection simulation for (a) low and (b) high GMAT. Uninfected cells are green, infected cells red, bystander cells yellow, virus is blue and CTL are white. The black area represents tissue where epithelial cells have died. (New susceptible epithelial cells regenerate on a time scale that is slower than the time scale of acute viral infections such as influenza; this process is therefore neglected in the simulation.) In (b) FBs between the virions and uninfected cells are clearly visible (e.g. see the orange ellipse).
Figure 5
Figure 5
Normalized (a) total viral load and (b) number of dead cells obtained from the ABM for three different parameter combinations. Shown are averages of 200 simulations for different values of the gap-junction parameter. Parameters for scenario 1 (squares) are pv=0.28, pk=1, pi=1, pc=0.5, mv=0.25 and mt=2; parameters for scenario 2 (diamonds) are pv=0.34, pk=1, pi=0.3, pc=1, mv=0.5 and mv=2; and parameters for scenario 3 (circles) are pv=0.28, pk=0.63, pi=1, pc=1, mv=0.25 and mt=2.
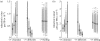
Figure 6
Figure 6
Reduction in (a) normalized viral load and (b) normalized number of dead cells per FB. A FB is defined as a bystander cell that gets killed by a CTL. The differences are between no GMAT and maximum GMAT. The notation (−/+) indicates an increase in that parameter. Clearance is increasing with values pv=0.15, 0.22, 0.28 and 0.34, corresponding to c=4, 6, 8 and 10. Other parameters are pk=1, pi=1, pc=1, mv=0.2 and mt=2. Values for the increasing diffusion rate are mv=0.25, 0.3, 0.35 and 0.4. Other parameters for this scenario are pv=0.28, pk=1, pi=0.3, pc=1 and mt=2. Values for complex killing are pk=0.39, 0.63, 0.86 and 1, corresponding to δ=12, 24, 48 and ∞. Other parameters are pv=0.28, pi=1, pc=1, mv=0.2 and mt=2. The black squares show the mean and the grey crosses show individual results for 1000 simulations.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Alves L.A., Nihei O.K., Fonseca P.C., Campos-de- Carvalho A.C., Savino W. Gap junction modulation by extracellular signaling molecules: the thymus model. Braz. J. Med. Biol. Res. 2000;33:457–465. doi: 10.1590/S0100-879X2000000400012. - DOI - PubMed
    1. Baccam P., Beauchemin C., Macken C.A., Hayden F.G., Perelson A.S. Kinetics of influenza A virus infection in humans. J. Virol. 2006;80:7590–7599. doi: 10.1128/JVI.01623-05. - DOI - PMC - PubMed
    1. Beauchemin C. Probing the effects of the well-mixed assumption on viral infection dynamics. J. Theor. Biol. 2006;242:464–477. doi: 10.1016/j.jtbi.2006.03.014. - DOI - PubMed
    1. Beauchemin C., Samuel J., Tuszynski J. A simple cellular automaton model for influenza A viral infections. J. Theor. Biol. 2005;232:223–234. doi: 10.1016/j.jtbi.2004.08.001. - DOI - PubMed
    1. Belz G.T., Xie W., Doherty P.C. Diversity of epitope and cytokine profiles for primary and secondary influenza a virus-specific CD8+T cell responses. J. Immunol. 2001;166:4627–4633. - PubMed

Publication types

Substances

LinkOut - more resources