Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2008 May 6;5(22):545-53.
doi: 10.1098/rsif.2007.1152.

Antiviral treatment for the control of pandemic influenza: some logistical constraints

N Arinaminpathy  1 , A R McLean
Affiliations

Antiviral treatment for the control of pandemic influenza: some logistical constraints

N Arinaminpathy et al. J R Soc Interface. .

Abstract

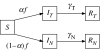
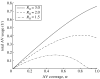
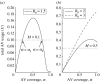
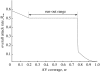
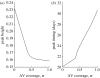
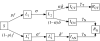
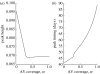
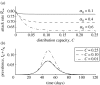
Disease control programmes for an influenza pandemic will rely initially on the deployment of antiviral drugs such as Tamiflu, until a vaccine becomes available. However, such control programmes may be severely hampered by logistical constraints such as a finite stockpile of drugs and a limit on the distribution rate. We study the effects of such constraints using a compartmental modelling approach. We find that the most aggressive possible antiviral programme minimizes the final epidemic size, even if this should lead to premature stockpile run-out. Moreover, if the basic reproductive number R(0) is not too high, such a policy can avoid run-out altogether. However, where run-out would occur, such benefits must be weighed against the possibility of a higher epidemic peak than if a more conservative policy were followed. Where there is a maximum number of treatment courses that can be dispensed per day, reflecting a manpower limit on antiviral distribution, our results suggest that such a constraint is unlikely to have a significant impact (i.e. increasing the final epidemic size by more than 10%), as long as drug courses sufficient to treat at least 6% of the population can be dispensed per day.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Summary of the basic model, where f=β(IT+IN). A proportion α of infected cases receive treatment (class IT) and recover in 1/γT days. The remainder of infected cases (class IN) recover in 1/γN days, where γT>γN.
Figure 2
Figure 2
Plots of AV usage U (or minimum required stockpile) versus coverage α, for different values of R0.
Figure 3
Figure 3
Illustration of different run-out scenarios. (a) Stockpile of 10% and R0=1.5. There are precisely two values of AV coverage, marked α1 and α2, such that U(α)=M. Run-out may be avoided by α<α1 or by α>α2. (b) Stockpile of 30% and R0=2, 3. Here R0 is sufficiently large for the antiviral usage U(α) to be monotonically increasing with respect to α. Run-out can be avoided only by a sufficiently low AV coverage.
Figure 4
Figure 4
Attack rate versus AV coverage α. For R0=1.5 and a stockpile M=0.1.
Figure 5
Figure 5
Numerical plots of epidemic peak properties, where prevalence is IT+IN. The ‘kinks’ in both plots arise because, for sufficiently high α, the epidemic peak occurs after run-out. Parameters: γT=0.4, γN=0.25, M=0.2 and R0=0.25. (a) Peak height and (b) peak timing.
Figure 6
Figure 6
Schematic illustration of the extended model, where f=βCTICT+βCNICN+βN(L2+L2′+IAN).
Figure 7
Figure 7
Numerical plots of epidemic peak properties for the extended model, measuring ICT+ICN. The ‘kinks’ arise because, for sufficiently high α, the peak occurs after run-out. (a) Peak height versus AV coverage. In the run-out range (α>0.32), peak height is an increasing function of α. (b) Peak timing in days versus AV coverage. Parameters: p=0.67, σ=σ′=1/1.2, δ=δ′=1/0.7, γT=0.4, γN=0.25, βCT=0.3, βCN=0.6, βN=0.39, M=0.1 and R0=2.5.
Figure 8
Figure 8
(a) Calculated attack rate versus distribution capacity C, for different values of α0. (b) Prevalence versus time under a limited distribution capacity, α0=0.6, for different values of C. Parameters: γN=0.25, γT=0.4 and R0=2.
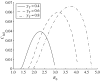
Figure 9
Figure 9
Minimum required distribution capacity Cfail, to ensure that attack rate is within 10% of the case of unlimited distribution capacity, versus R0, for different values of γT. The ‘termination’ of each curve is where R0 is sufficiently high that the percentage difference in attack rate between even the two most extreme cases, C=0 and C→∞, is less than 10%. γN=0.25.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Arino J, Brauer F, van den Driessche P, Watmough J, Wu J. Simple models for containment of a pandemic. J. R. Soc. Interface. 2006;3:453–457. doi: 10.1098/rsif.2006.0112. - DOI - PMC - PubMed
    1. Barnes, B., Glass, K. & Becker, N. G. In press. The role of health care workers and antiviral drugs in the control of pandemic influenza. Math. Biosci (10.1016/j.mbs.2007.02.008). - DOI - PubMed
    1. Beigel J.H, et al. Avian influenza A (H5N1) in humans. N. Engl. J. Med. 2005;353:1374–1385. doi: 10.1056/NEJMra052211. - DOI - PubMed
    1. Chowell G, Ammon C.E, Hengartner N.W, Hyman J.M. Transmission dynamics of the great influenza pandemic of 1918 in Geneva Switzerland: assessing the effects of hypothetical interventions. J. Theor. Biol. 2006;241:193–204. doi: 10.1016/j.jtbi.2005.11.026. - DOI - PubMed
    1. Chowell G, Nishiura H, Bettencourt L.M.A. Comparative estimation of the reproduction number for pandemic influenza from daily case notification data. J. R. Soc. Interface. 2007;4:155–166. doi: 10.1098/rsif.2006.0161. - DOI - PMC - PubMed

Publication types

MeSH terms

Substances