Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2007 Mar;16(3):449-64.
doi: 10.1110/ps.062655907.

A unified mechanism for protein folding: predetermined pathways with optional errors

Mallela M G Krishna  1 , S Walter Englander
Affiliations

A unified mechanism for protein folding: predetermined pathways with optional errors

Mallela M G Krishna et al. Protein Sci. 2007 Mar.

Abstract

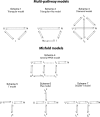
There is a fundamental conflict between two different views of how proteins fold. Kinetic experiments and theoretical calculations are often interpreted in terms of different population fractions folding through different intermediates in independent unrelated pathways (IUP model). However, detailed structural information indicates that all of the protein population folds through a sequence of intermediates predetermined by the foldon substructure of the target protein and a sequential stabilization principle. These contrary views can be resolved by a predetermined pathway--optional error (PPOE) hypothesis. The hypothesis is that any pathway intermediate can incorporate a chance misfolding error that blocks folding and must be reversed for productive folding to continue. Different fractions of the protein population will then block at different steps, populate different intermediates, and fold at different rates, giving the appearance of multiple unrelated pathways. A test of the hypothesis matches the two models against extensive kinetic folding results for hen lysozyme which have been widely cited in support of independent parallel pathways. The PPOE model succeeds with fewer fitting constants. The fitted PPOE reaction scheme leads to known folding behavior, whereas the IUP properties are contradicted by experiment. The appearance of a conflict with multipath theoretical models seems to be due to their different focus, namely on multitrack microscopic behavior versus cooperative macroscopic behavior. The integration of three well-documented principles in the PPOE model (cooperative foldons, sequential stabilization, optional errors) provides a unifying explanation for how proteins fold and why they fold in that way.

PubMed Disclaimer

Figures

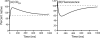
Figure 1.
Figure 1.
Lysozyme folding followed by CD225 (A) and fluorescence (B). The smoothed traces shown are from Dobson et al. (1994; reprinted with permission from Elsevier). The dashed lines show the native signal.
Figure 2.
Figure 2.
The reaction schemes invoked here. Schemes 1–3 represent the independent unrelated pathway (IUP) models found by Kiefhaber and coworkers (Kiefhaber et al. 1997; Wildegger and Kiefhaber 1997; Bieri et al. 1999; Bieri and Kiefhaber 2001). Scheme 4 represents a predetermined pathway–optional error (PPOE) model. Diagonal steps may also occur. The pathway may branch when the sequential stabilization principle allows two or more alternative next steps. (Similar models have been used to explain the complex folding kinetics of cytochrome c and staphylococcal nuclease [Elöve et al. 1994; Sosnick et al. 1994; Colón et al. 1996; Walkenhorst et al. 1997; Englander et al. 1998].) Schemes 5–7 show the limiting cases used here. Ii and Iix are pictured to have essentially the same native-like structured regions, but Iix has in addition some misfolding error that interferes with the formation and docking of an incoming foldon unit. It may act immediately or can be incipient and block at a later step (e.g., misisomerized proline).
Figure 3.
Figure 3.
Lysozyme folding data (fluorescence) obtained in the low-salt condition (from Wildegger and Kiefhaber 1997). (A,D) The chevron plots show measured macroscopic relaxation rates as a function of GdmCl concentration. (B,E) The data show the U, I, and N populations as a function of folding time (in 0.6 M GdmCl), measured in interrupted folding experiments. (C,F) The folding models and their fitted microscopic rate constants (at 0.6 M GdmCl); m-values needed for the chevrons are in parentheses; m = d(RT ln k)/d[GdmCl]). The parameters fully constrained by the data fitting are in boldface. Also shown are χR 2 values for the global fit and the fluorescence signal strength (S) of the populated intermediates calculated relative to the previous results (from Fig. 1 of Wildegger and Kiefhaber 1997; see Materials and Methods). The red curves in panels A and B fit the Triangular model to the data using the rate constants given in Figure 3 of Wildegger and Kiefhaber (1997). Black curves show the global refitting done here. (D) The T model predicts another faster phase whose rates are, however, very poorly determined because of the minimal population of I, as suggested by the multiple predicted chevrons shown (dotted lines). Note that S for the populated intermediate, the folding flux away from U, the unfolding flux away from N, and the flux into the blocked intermediate populations is the same in the two different models. The rate constants (seconds−1) and m-values (kilocalories/mole per molar GdmCl) used in constructing the red lines in the Triangular model are: k UN = 14 (−1.9), k NU = 9E − 7 (0.7), k UI = 19 (−1.2), k IU = 3.5 (0.3), k IN = 2.5 (−0.5), k NI = 9E − 7 (0.7), where E indicates powers of 10.
Figure 4.
Figure 4.
Comparison of the fitted macroscopic relaxation rates (solid lines) with the calculated microscopic rate constants (black dashed lines) determined for the (A) Triangular and the (B,C) T models. Data are from Wildegger and Kiefhaber (1997). The dashed red lines show that the extrapolation of the fast-phase unfolding arm intersects the measured slow-phase folding data, which was used by Wildegger and Kiefhaber (1997) to reject the conventional off-pathway intermediate possibility, assumed as an Ix ↔ U ↔ N sequence. In comparison, the Ix-to-I curves (k I x I in panels B and C) show that the measured data are not inconsistent with the T model.
Figure 5.
Figure 5.
Extension of Figure 3 (open symbols) to include the additional data for two-phase unfolding for the populated intermediate (filled symbols) (from Figs. 3 and 4A of Kiefhaber et al. 1997). For the Triangular model, the additional fast unfolding phase requires an added intermediate (Nu) that was not measured in the folding direction. The unmodified PPOE model already predicts the additional fast unfolding phase, and the new unfolding data fix its previously underdetermined parameters. In this case, the fitting adjusts the signal proportionality constants (S-values) for the silent intermediates differently in the two models so that the fluxes at corresponding points do not match. The two models require eight and six fitting rate constants, respectively.
Figure 6.
Figure 6.
Three phase folding data obtained at the high-salt condition (from Bieri et al. 1999), which requires two populated intermediates. Fits obtained for the Diamond model are shown in red for the rate constants given in Figure 7 of Bieri et al. (1999) (m-values adjusted for best fit) and in black when globally refit. The Diamond and PPOE models require 12 and eight fitting rate constants, respectively. Other notes are as for Figure 3. The rate constants used in constructing the red lines in the Diamond model are (at 0.6 M GdmCl; m-values in parenthesis): k UN = 1.2 (−1.5), k NU = 9E − 9 (1.0), k UI1 = 9.7 (−1.4), k I1U = 4.3 (0.2), k UI2 = 6.9 (−1.6), k I2U = 0.9 (2E − 5), k I1I2 = 1.4 (−4E−5), k I2I1 = 1.8 (1E−5), k I1N = 0.3 (−6E − 5), k NI1 = 5E−8 (0.9), k I2N = 0.2 (−7E − 3), k NI2 = 2E − 9 (0.1).
Figure 7.
Figure 7.
Three-phase folding data obtained at the high pH condition (from Bieri and Kiefhaber 2001), which requires two populated intermediates. Fits obtained for the Diamond model are shown in red for the rate constants given in Figure 3 of Bieri and Kiefhaber (2001) (m-values adjusted for best fit) and in black when globally refit. The Diamond and PPOE models require 12 and eight fitting rate constants, respectively. Other notes are as for Figure 3. The rate constants used in constructing the red lines in the Diamond model are (at 0.6 M GdmCl; m-values in parenthesis): k UN = 1.8 (−1.6), k NU = 2E − 6 (0.7), k UI1 = 46 (−1.4), k I1U = 4.0 (0.2), k UI2 = 13 (−1.4), k I2U = 0.1 (0.4), k I1I2 = 6.9 (−0.13), k I2I1 = 1.7 (6E − 6), k I1N = 0.8 (−0.1), k NI1 = 3E − 6 (0.6), k I2N = 2E − 6 (−0.03), k NI2 = 2E − 6 (0.7).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Anderson E., Bai, Z., Bischof, C., Blackford, S., Demmel, J., Dongarra, J., Du Croz, J., Greenbaum, A., Hammarling, S., and McKenney, A., et al. 1999. LAPACK users’ guide. Society for Industrial and Applied Mathematics, Philadelphia.
    1. Bai Y.. 1999. Kinetic evidence for an on-pathway intermediate in the folding of cytochrome c . Proc. Natl. Acad. Sci. 96: 477–480. - PMC - PubMed
    1. Bai Y., Sosnick, T.R., Mayne, L., and Englander, S.W. 1995. Protein folding intermediates: Native-state hydrogen exchange. Science 269: 192–197. - PMC - PubMed
    1. Baldwin R.L.. 1995. The nature of protein folding pathways: The classical versus the new view. J. Biomol. NMR 5: 103–109. - PubMed
    1. Barshop B.A., Wrenn, R.F., and Frieden, C. 1983. Analysis of numerical methods for computer simulation of kinetic processes: Development of KINSIM—A flexible, portable system. Anal. Biochem. 130: 134–145. - PubMed

Publication types

LinkOut - more resources