Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Review
. 2006 Nov;39(4):325-60.
doi: 10.1017/S0033583506004446. Epub 2006 Oct 16.

Determination of thermodynamics and kinetics of RNA reactions by force

Ignacio Tinoco Jr  1 , Pan T X Li, Carlos Bustamante
Affiliations
Review

Determination of thermodynamics and kinetics of RNA reactions by force

Ignacio Tinoco Jr et al. Q Rev Biophys. 2006 Nov.

Abstract

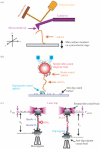
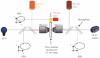
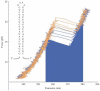
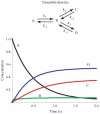
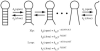
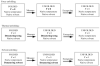
Single-molecule methods have made it possible to apply force to an individual RNA molecule. Two beads are attached to the RNA; one is on a micropipette, the other is in a laser trap. The force on the RNA and the distance between the beads are measured. Force can change the equilibrium and the rate of any reaction in which the product has a different extension from the reactant. This review describes use of laser tweezers to measure thermodynamics and kinetics of unfolding/refolding RNA. For a reversible reaction the work directly provides the free energy; for irreversible reactions the free energy is obtained from the distribution of work values. The rate constants for the folding and unfolding reactions can be measured by several methods. The effect of pulling rate on the distribution of force-unfolding values leads to rate constants for unfolding. Hopping of the RNA between folded and unfolded states at constant force provides both unfolding and folding rates. Force-jumps and force-drops, similar to the temperature jump method, provide direct measurement of reaction rates over a wide range of forces. The advantages of applying force and using single-molecule methods are discussed. These methods, for example, allow reactions to be studied in non-denaturing solvents at physiological temperatures; they also simplify analysis of kinetic mechanisms because only one intermediate at a time is present. Unfolding of RNA in biological cells by helicases, or ribosomes, has similarities to unfolding by force.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
Experiment set-ups for mechanical studies of RNA. (a) Atomic force microscopy (Rief et al. 1997). The ‘pulling’ AFM consists of a cantilever, a laser detection system and a moveable surface. The silicon nitride tip of the cantilever picks up RNA molecules by ‘tapping’ on the surface. The position of the cantilever is monitored by the deflection of a detecting laser. RNA samples are placed on a mica surface mounted on a 3D translational stage. Moving the mica in the x and y direction allows scanning the surface to find RNA molecules. Then the mica is moved in the z direction to exert force on the molecule. (b) Magnetic tweezers (Strick et al. 1996). Two short pieces of dsRNA, labeled either with digoxigenins or biotins, are ligated to a long dsRNA (Abels et al. 2005). The RNA is deposited on a surface coated with anti-digoxigenin antibody. The other end of the molecule is tethered to a magnetic bead coated with streptavidin. By applying a magnetic field, the bead and therefore the RNA can be pulled. (c) Optical tweezers (Smith et al. 2003). The RNA is tethered to a pair of beads coated either with streptavidin or anti-digoxigenin antibody (Liphardt et al. 2001). The former bead is held in a force-measuring optical trap, shown in purple. The other bead is sucked on the tip of a micropipette by applying vacuum. Position of the micropipette is controlled by a piezo-electric stage. By moving the stage, the RNA is extended and tension is generated.
Fig. 2
Fig. 2
Basic design of a dual-beam optical trap (Smith et al. 2003). The reaction occurs in a flow chamber, which is placed between two high numerical aperture objectives and mounted on a piezo-electric stage. Two co-aligned laser beams, generated by a pair of 830 nm lasers (orange and coffee), enter the back of the objectives and are focused in a spot in the flow chamber to create an optical trap. After passing the trap, the beams enter the other objective and become parallel. These rays are then redirected to a pair of photosensitive detectors (PSD), which measure the total intensity and positions of the beams. An LED is used to illuminate the chamber and image the focal plane on a CCD camera. To detect the position of the chamber, a light-lever system is used. This system consists of a low power fiber-coupled 630 nm laser, a PSD and a lens with focal length of 1·45 mm mounted on the flow chamber. The lens directs the laser beam on to the PSD. Therefore, the movement of the chamber is monitored by the PSD.
Fig. 3
Fig. 3
A force-extension curve for a RNA hairpin. A single RNA hairpin flanked by ∼500 bp DNA/RNA handles was pulled at a constant rate of 1 pN/s. First, the force increases monotonically as the handles are stretched. The force-extension relationship can be modeled (left dashed curve) using a WLC interpolation formula (Bustamante et al. 1994) with a persistence length of 10 nm and a contour length of 0·34 nm/bp (Liphardt et al. 2001). A rip at 13·5 pN indicates that the hairpin unfolded - the base pairs broke - in a single step with an increase in extension of 18 nm. The breaking of the base pairs decreases the force and produces a rip with a slope approximately equal to the spring constant of the trap (κ). After the rip, both handles and the unfolded RNA are stretched. The force-extension of this region also fits the WLC model (right dashed curve) with addition of the effect of the single-stranded region. The mechanical work to unfold the hairpin is the area under the rip. Under reversible condition, the mechanical work equals the unfolding/folding free-energy change of the hairpin (Liphardt et al. 2001).
Fig. 4
Fig. 4
Force-extension curves of irreversible unfolding/refolding. Five cycles of pulling (orange) and relaxation (blue) curves of a hairpin (inset) at a loading rate of 7·5 pN/s show stochastic nature of the unfolding/refolding process (adapted from Collin et al. 2005). The hysteresis between the unfolding and refolding indicates the irreversibility. The mechanical work to stretch or relax the RNA plus handles from 355 nm to 380 nm was determined by integrating the area under each trajectory during pulling and relaxation. The area under the lowest refolding curve is shown in blue. The measured mechanical work values were analyzed using Jarzynski’s equality and Crooks fluctuation theorem (Collin et al. 2005).
Fig. 5
Fig. 5
Free-energy recovery by Crooks fluctuation theorem (adapted from Collin et al. 2005). Unfolding (solid lines) and refolding (dashed lines) work distributions for wild-type (purple) and mutant (orange) S15 three-helix junctions are shown. The intersections of the distributions for folding and unfolding (large empty circles) provide ΔG for the reactions. Over 900 and 1200 trajectories were collected for the wild-type and mutant RNA, respectively. The inset shows the logarithmic ratio of unfolding to refolding work probabilities as a function of total work done on the molecule. The solid line is a fit to Eq. (3.16).
Fig. 6
Fig. 6
Hopping kinetics of a hairpin (Li et al. 2006). (a) A time trace of the extension of a TAR RNA hairpin that hops between folded and unfolded states at a constant force of 12·4 pN in 250 mm KCl (pH 22 °C). A change in extension of about 18 nm occurs as the 22-bp helix forms and is broken. (b) The probability that the reaction has not occurred (fraction of reactant present) is plotted as a function of time. Lifetimes of the unfolded or folded states (>100 observations each) are binned in 5 s intervals to generate the probability density function and the cumulative probability. The mean lifetime of the unfolded state gives the folding rate; the mean lifetime of the folded state gives the unfolding rate. The solid lines represent fits to a single exponential. The first-order rate constant for folding the RNA is 43±1 ms-1, and that for unfolding is 33±1 ms-1. Rare lifetimes over 100 s were observed for the folding reaction; these points do not fit the single exponential and are not shown.
Fig. 7
Fig. 7
The concentrations versus time of four species that follow the kinetic scheme shown. Note that in the usual ensemble experiments all four species are present at all times; and there is no unique way to extract the rate constants from the measured data.
Fig. 8
Fig. 8
The same scheme used in Fig. 7 studied one molecule at a time. Obviously, only one species is present at any time. Each rate constant is uniquely characterized by the average lifetime of each species, as it transits to another species.
Fig. 9
Fig. 9
Examples of force-jump-drop experiments (adapted from Li et al. 2006). (a) A time trace of force in two force-jump-drop events. Each cycle starts at 6 pN, at which the hairpin is folded. The force is quickly raised to 14 pN and held constant until the unfolding occurs. After the unfolding, the force is further ramped to 20 pN and held there for 3 s to insure complete unfolding. Then the force is quickly dropped to 12·7 pN to monitor the refolding. In the last step, the force is decreased to 6 pN. (b) A time trace of extension for the same experiments shown in panel (a). At the unfolding force, the extension of the molecule remained constant until the unfolding, at which time the extension suddenly increased by ∼18 nm. At the refolding force, the formation of the hairpin was indicated by the quick decrease in the extension. Lifetimes of the species, tfolded and tunfolded, were used to calculate the rate constants of unfolding and refolding, respectively.
Fig. 10
Fig. 10
Calculated free-energy landscape at 25 °C for RNA hairpin P5ab at zero force and at Fm, the melting force. At zero force the free energies are calculated from nearest-neighbor values (Mathews et al. 1999); at the Fm the WLC model is used to obtain the effect of force on each partially unfolded species. At zero force the hairpin is the only species present. At Fm the species present in significant amounts are now the hairpin, the single strand, and the hairpin with 3 bp broken caused by the destabilizing effect of the bulged U. (This figure from Tinoco, 2004.)
Fig. 11
Fig. 11
A simple kinetic mechanism for the unfolding of RNA secondary structure. There are four elementary steps, but only two are independent because the ratio of rate constants equal equilibrium constants. The assumptions are that helix free energies depend only on the nearest-neighbor base pairs, and loop free energies depend only on loop size. Base-pair opening is assumed to be essentially independent of force because the distance to the transition state for base-pair opening is of order 0·1 nm (Cocco et al. 2003a).
Fig. 12
Fig. 12
Force-jump kinetic data for the unfolding of TAR RNA (adapted from Li et al. 2006). (a) Plots of fraction of folded RNA versus time at 13·6 pN and 14·2 pN; the curves fit well with single exponentials consistent with first-order kinetics. (b) Plot of the logarithm of the rate constants versus force for unfolding and refolding. The slopes of the linear plots give the distances to the transition state from the folded state (ΔX‡=8·2 nm), and from the unfolded state (ΔX‡=8 nm), The transition state is roughly halfway between the folded and unfolded species.
Fig. 13
Fig. 13
Schematic diagram illustrating the differences in initial and final states for force, thermal, and solvent unfolding. For each experiment the environment is adjusted to produce measurable amounts of two species, such as folded and unfolded. Then the ratio of species is measured to give an equilibrium constant and free energy, or the work necessary to convert one species to the other is measured.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Abbondanzieri E, Greenleaf W, Shaevitz J, Landick R, Block S. Direct observation of base-pair stepping by RNA polymerase. Nature. 2005;438:460–465. - PMC - PubMed
    1. Abels J, Moreno-Herrero F, van der Heijden T, Dekker C, Dekker N. Single-molecule measurements of the persistence length of double-stranded RNA. Biophysical Journal. 2005;88:2737–2744. - PMC - PubMed
    1. Allison D, Hinterdorfer P, Han W. Biomolecular force measurements and the atomic force microscope. Current Opinion in Biotechnology. 2002;13:47–51. - PubMed
    1. Ashkin A. Methods in Cell Biology. Vol. 55. Academic Press; San Diego: 1998. Forces of a single-beam gradient laser trap on a dielectric sphere in the ray optics regime; pp. 1–27. - PubMed
    1. Ashkin A, Dziedzic J, Bjorkholm J, Chu S. Observation of a single-beam gradient force optical trap for dielectric particles. Optical Letters. 1986;11:288–290. - PubMed

Publication types