Inferring global topology from local juxtaposition geometry: interlinking polymer rings and ramifications for topoisomerase action
- PMID: 16537549
- PMCID: PMC1403174
- DOI: 10.1529/biophysj.105.076778
Inferring global topology from local juxtaposition geometry: interlinking polymer rings and ramifications for topoisomerase action
Abstract
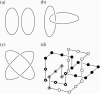
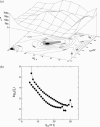
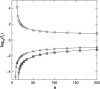
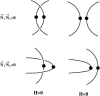
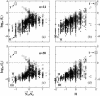
Lattice modeling is applied to investigate how the configurations of local chain juxtapositions may provide information about whether two ring polymers (loops) are topologically linked globally. Given a particular juxtaposition, the conditional probability that the loops are linked is determined by exact enumeration and extensive Monte Carlo sampling of conformations satisfying excluded volume constraints. A discrimination factor fL, defined as the ratio of linked to unlinked probabilities, varies widely depending on which juxtaposition is presumed. /log fL/s that are large for small loop size n tend to decrease, signaling diminishing topological information content of the juxtapositions, with increasing n. However, some juxtaposition geometries can impose sufficient overall conformational biases such that /log fL/ remains significant for large n. Notably, for two loops as large as n=200 in the model, the probability that passing the segments of a hooked juxtaposition would unlink an originally linked configuration is remarkably high, approximately 85%. In contrast, segment-passage of a free juxtaposition would link the loops from an originally unlinked configuration more than 90% of the time. The statistical mechanical principles emerging from these findings suggest that it is physically possible for DNA topoisomerases to decatenate effectively by acting selectively on juxtapositions with specific "hooked" geometries.
Figures
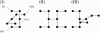


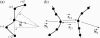
Similar articles
-
Topological information embodied in local juxtaposition geometry provides a statistical mechanical basis for unknotting by type-2 DNA topoisomerases.J Mol Biol. 2006 Aug 11;361(2):268-85. doi: 10.1016/j.jmb.2006.06.005. Epub 2006 Jun 19. J Mol Biol. 2006. PMID: 16842819
-
Consistent rationalization of type-2 topoisomerases' unknotting, decatenating, supercoil-relaxing actions and their scaling relation.J Phys Condens Matter. 2015 Sep 9;27(35):354103. doi: 10.1088/0953-8984/27/35/354103. Epub 2015 Aug 20. J Phys Condens Matter. 2015. PMID: 26291958
-
Efficient chain moves for Monte Carlo simulations of a wormlike DNA model: excluded volume, supercoils, site juxtapositions, knots, and comparisons with random-flight and lattice models.J Chem Phys. 2008 Apr 14;128(14):145104. doi: 10.1063/1.2899022. J Chem Phys. 2008. PMID: 18412482
-
Single-molecule measurements of DNA topology and topoisomerases.J Biol Chem. 2010 Jun 18;285(25):18967-71. doi: 10.1074/jbc.R109.092437. Epub 2010 Apr 9. J Biol Chem. 2010. PMID: 20382732 Free PMC article. Review.
-
Tracking topoisomerase activity at the single-molecule level.Annu Rev Biophys Biomol Struct. 2005;34:201-19. doi: 10.1146/annurev.biophys.34.040204.144433. Annu Rev Biophys Biomol Struct. 2005. PMID: 15869388 Review.
Cited by
-
DNA supercoiling and its role in DNA decatenation and unknotting.Nucleic Acids Res. 2010 Apr;38(7):2119-33. doi: 10.1093/nar/gkp1161. Epub 2009 Dec 21. Nucleic Acids Res. 2010. PMID: 20026582 Free PMC article. Review.
-
Action at hooked or twisted-hooked DNA juxtapositions rationalizes unlinking preference of type-2 topoisomerases.J Mol Biol. 2010 Jul 30;400(5):963-82. doi: 10.1016/j.jmb.2010.05.007. Epub 2010 May 10. J Mol Biol. 2010. PMID: 20460130 Free PMC article.
-
DNA supercoiling inhibits DNA knotting.Nucleic Acids Res. 2008 Sep;36(15):4956-63. doi: 10.1093/nar/gkn467. Epub 2008 Jul 25. Nucleic Acids Res. 2008. PMID: 18658246 Free PMC article.
-
Local site preference rationalizes disentangling by DNA topoisomerases.Phys Rev E Stat Nonlin Soft Matter Phys. 2010 Mar;81(3 Pt 1):031902. doi: 10.1103/PhysRevE.81.031902. Epub 2010 Mar 4. Phys Rev E Stat Nonlin Soft Matter Phys. 2010. PMID: 20365765 Free PMC article.
-
How do type II topoisomerases use ATP hydrolysis to simplify DNA topology beyond equilibrium? Investigating the relaxation reaction of nonsupercoiling type II topoisomerases.J Mol Biol. 2009 Feb 6;385(5):1397-408. doi: 10.1016/j.jmb.2008.11.056. Epub 2008 Dec 7. J Mol Biol. 2009. PMID: 19094994 Free PMC article.
References
-
- Sumners, D. W., and S. G. Whittington. 1988. Knots in self-avoiding walks. J. Phys. A.-Math. Gen. 21:1689–1694.
-
- Lickorish, W. B. R. 1997. An Introduction to Knot Theory. Springer-Verlag, New York.
-
- Buck, G. 1998. Four-thirds power law for knots and links. Nature. 392:238–239.
-
- Gambini, R., and J. Pullin. 2000. Loops, Knots, Gauge Theories and Quantum Gravity. Cambridge University Press, Cambridge, UK.
-
- Ladd, A. M., and L. E. Kavraki. 2004. Using motion planning for knot untangling. Int. J. Robot Res. 23:797–808.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

