Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2006 May 15;90(10):3410-27.
doi: 10.1529/biophysj.105.078030. Epub 2006 Feb 10.

Forced-unfolding and force-quench refolding of RNA hairpins

Changbong Hyeon  1 , D Thirumalai
Affiliations

Forced-unfolding and force-quench refolding of RNA hairpins

Changbong Hyeon et al. Biophys J. .

Abstract

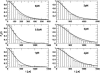
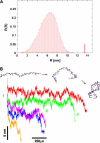
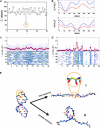
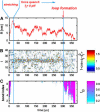
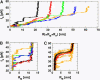
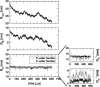
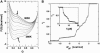
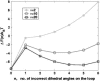
Nanomanipulation of individual RNA molecules, using laser optical tweezers, has made it possible to infer the major features of their energy landscape. Time-dependent mechanical unfolding trajectories, measured at a constant stretching force (f(S)) of simple RNA structures (hairpins and three-helix junctions) sandwiched between RNA/DNA hybrid handles show that they unfold in a reversible all-or-none manner. To provide a molecular interpretation of the experiments we use a general coarse-grained off-lattice Gō-like model, in which each nucleotide is represented using three interaction sites. Using the coarse-grained model we have explored forced-unfolding of RNA hairpin as a function of f(S) and the loading rate (r(f)). The simulations and theoretical analysis have been done both with and without the handles that are explicitly modeled by semiflexible polymer chains. The mechanisms and timescales for denaturation by temperature jump and mechanical unfolding are vastly different. The directed perturbation of the native state by f(S) results in a sequential unfolding of the hairpin starting from their ends, whereas thermal denaturation occurs stochastically. From the dependence of the unfolding rates on r(f) and f(S) we show that the position of the unfolding transition state is not a constant but moves dramatically as either r(f) or f(S) is changed. The transition-state movements are interpreted by adopting the Hammond postulate for forced-unfolding. Forced-unfolding simulations of RNA, with handles attached to the two ends, show that the value of the unfolding force increases (especially at high pulling speeds) as the length of the handles increases. The pathways for refolding of RNA from stretched initial conformation, upon quenching f(S) to the quench force f(Q), are highly heterogeneous. The refolding times, upon force-quench, are at least an order-of-magnitude greater than those obtained by temperature-quench. The long f(Q)-dependent refolding times starting from fully stretched states are analyzed using a model that accounts for the microscopic steps in the rate-limiting step, which involves the trans to gauche transitions of the dihedral angles in the GAAA tetraloop. The simulations with explicit molecular model for the handles show that the dynamics of force-quench refolding is strongly dependent on the interplay of their contour length and persistence length and the RNA persistence length. Using the generality of our results, we also make a number of precise experimentally testable predictions.

PubMed Disclaimer

Figures

FIGURE 1
FIGURE 1
Coarse-grained representation of a molecule of RNA using three interaction sites per nucleotide—phosphate (P), sugar (S), and base (B). On the left we present the secondary structure of the 22-nt P5GA hairpin, in which the bonds formed between basepairs are labeled from 1 to 9. The PDB structure (17) and the lowest energy structure obtained with the coarse-grained model are shown on the right.
FIGURE 2
FIGURE 2
(A) Schematic illustration of laser optical tweezer (LOT) setup for RNA stretching. A single RNA molecule is held between two polystyrene beads via molecular handles with one of the polystyrene beads being optically trapped in the laser light. The location of the other bead is changed by micropipette manipulation. The extension of the molecule through the molecular handles induces the deviation in the position of the polystyrene bead held in the force-measuring optical trap. (B) Both LOT and AFM can be conceptualized as schematically shown. The RNA molecule is sandwiched between the linkers and one end of the linker is pulled. The spring constant of the harmonic trap in LOT (or the cantilever in AFM experiments) is given by k and v is the pulling speed.
FIGURE 3
FIGURE 3
Unfolding pathways upon temperature and force jump. (A) The time-dependence of rupture of the bonds is monitored when the temperature is raised from T = 100 K < Tm ≈ 341 K to T = 346 K > Tm. The nine-bond set is disrupted stochastically. (B) In forced unfolding, bonds rip from the ends to the loop regions in an apparent staircase pattern. For both A and B, the scale indicating the probability of a given bond being intact is given below. (C) Free energy F(Q) as a function of Q. The stable hairpin with Q ≈ 1 at T = 100 K becomes unstable upon rapid temperature jump to T = 346 K (blue asterisks). Subsequent to the T-jump, the hairpin relaxes to the new equilibrium state by crossing a small free energy barrier (≈0.5 kcal/mol) with Q ≈ 0.2. The inset shows the equilibrium free energy profile at T = 346 K and f = 0. (D) Deformation of the free energy profile upon application of force. The R-dependent free energy F(R) = F(R; fS = 0) – fS × R favors the stretched state at R = 12 nm when f = 42 pN (see inset). The activation barrier separating the UBA and NBA is ∼ 1–2 kcal/mol.
FIGURE 4
FIGURE 4
Constant loading rate force unfolding. (A) The unfolding force distributions at different pulling speeds with hard (k = 70 pN/nm, top) and soft springs (k = 0.7 pN/nm, bottom). For the hard spring, the pulling speeds from right to left are v = 8.6 × 104, 8.6 × 103, and 8.6 × 102 μm/s. For the soft spring, the pulling speeds are v = 8.6 × 104, 1.7 × 104, 8.6 × 103, 8.6 × 102, and 8.6 × 101 μm/s from right to left force peaks. The peak in the distributions which are fit to a Gaussian is the most probable force f*. (B) The dependence of f* as a function of the loading rates, rf. The results from the hard spring and soft spring are combined using the loading rate as the relevant variable. The inset illustrates the potential difficulties in extrapolating from simulations at large rf to small values of rf.
FIGURE 5
FIGURE 5
Kinetics of forced-unfolding and force-quench refolding. (A) Plot of force-induced unfolding times (τU) as a function of the stretching force. Over a narrow range of force τU decreases exponentially as f increases. (B) Refolding time τF as a function of fQ. The initial value of the stretching force is 90 pN. By fitting τF using formula image exp(formula image), in the range of 0.5 pN < fQ < 4 pN, we obtain formula image and formula image. (C) Changes in the equilibrium free energy profiles at T = 290 K F(R) as a function of the variable R. We show F(R) at various fS values. For emphasis, the free energies at fS = 0 and at the transition midpoint fS = 7.5 pN (dashed line) are drawn in thick lines.
FIGURE 6
FIGURE 6
Time-dependence of the probability that RNA is unfolded upon force-quench. In these simulations, T = 290 K, and the initial stretching force, fS = 90 pN, and fQ, the quench force, is varied (values are given in each panel). The simulation results are fit using Eq. 14, which is obtained using the kinetic scheme formula image. Here, I represents conformations within certain fractions of incorrect dihedral angles. The time constants (τ1,τ2), in μs, at each force are: (81.2, 101.3) at fQ = 0 pN; (159.5, 160.8) at fQ = 0.5 pN; (180.0, 174.8) at fQ = 1 pN; (237.6, 240.5) at fQ = 2 pN; (326.8, 335.6) at fQ = 3 pN; and (347.7, 329.7) at fQ = 4 pN.
FIGURE 7
FIGURE 7
(A) The equilibrium distribution of the end-to-end distance at extremely high temperature (T = 1500 K). Even at this elevated temperature, the fully stretched conformations of R = 13.5 nm (arrow) are not found in the ensemble of thermally denatured conformations. (B) Refolding is initiated by a force-quench from the initial value fS = 90 pN to fQ = 4 pN. The five time-traces show great variations in the relaxation to the hairpin conformation. However, in all trajectories, R decreases in at least three distinct stages that are explicitly labeled for the trajectory in green.
FIGURE 8
FIGURE 8
(A) The dihedral angles of the P5GA hairpin in the native state. All the dihedral angles are in the trans form except the 19th position of the dihedral angle, which is in the gauche (+) conformation (indicated by orange circle). (B) The dihedral angle potentials for trans (top) and gauche (+) forms (bottom) are plotted using Eq. 3. The red lines show the potentials in the loop region. (C and D) The average deviation of the ith dihedral angle relative to the native state is computed using the 100 different structures generated by high temperature (T = 500 K) (C) and by force (R = 13.5 nm) (D). To express the deviations of the dihedral angles from their native-state values, we used 1 – cos(formula image) for ith dihedral angle φI, where formula image is the ith dihedral angle of the native state. (E) A snapshot of a fully stretched hairpin (I). Note the transition in the 19th dihedral angle undergoes g+→t transition when the hairpin is stretched. This is an example of a partially stretched conformation (II) with the GAAA tetraloop and bond-9 intact. Refolding times starting from these conformations are expected to be shorter than those that start from fully stretched states.
FIGURE 9
FIGURE 9
(A) A sample refolding trajectory starting from the stretched state. The hairpin was initially unfolded to a fully stretched state and fQ was set to zero at t ≈ 20 μs. End-to-end distance monitored as a function of time shows that refolding occurs in steps. (B) The deviation of dihedral angles from their values in native state as a function of time. The large deviation of the dihedral angles in the loop region can be seen in the red strip. Note that this strip disappears around t ≈ 300 μs, which coincides with the formation of bonds shown in C. The value fB is the fraction of bonds with pink color, indicating that the bond is fully formed.
FIGURE 10
FIGURE 10
The force extension curves (FECs) of RNA hairpin at constant pulling speed and varying linker lengths and flexibilities. Pulling speed is v = 0.86 × 102 μm/s; spring constant is k = 0.7 pN/nm. FECs from different linker lengths are plotted in black (10 nm), red (20 nm), green (30 nm), blue (40 nm), and orange (50 nm). (A) Shows the experimentally relevant plots, namely, FECs for H-RNA-H construct. The signature for the hairpin opening transition region is ambiguous at large LH values. (B) FECs only, for P5GA corresponding to different LH values. The FEC for the linker is subtracted from A. The gradual increase of rupture force is observed as L increases. The value of kA (Eq. 9) of linker polymer used in A and B is 80 kcal/(mol · Å). (C) Comparison between FECs with LH (= 40 nm) fixed, but at different kA-values. The red curve is the average of seven individual FECs, which are shown in orange (80 kcal/(mol · Å)). The black curve is the average of nine individual FECs in gray (20 kcal/(mol × Å)). A less-stiff linker leads to a slightly larger unfolding force. It should be stressed that, for both values of kA, the λ-ratio is large.
FIGURE 11
FIGURE 11
Refolding trajectory of RNA that is attached to the handles. Linkers with formula image and formula image are attached to both sides of the RNA hairpin. The initial force (90 pN) stretched P5GA to 14 nm. The value of fQ = 2 pN. The top panel shows the dynamics of the end-to-end distance, Rsys, of H-P5GA-H. The middle panel corresponds to the end-to-end distance of P5GA. The end-to-end distances, RH, of the 3′ and 5′-side handles, fluctuate around its equilibrium value of 14 nm after the initial rapid relaxation. The right panels show the decomposition of RH into the longitudinal and the transverse components. The value of formula image agrees well with the equilibrium value obtained by solving formula image with fQ = 2 pN.
FIGURE 12
FIGURE 12
(A) Free energy profiles of Q at different temperatures. Note that the positions of the transition states over the temperature variation almost remain constant. (B) The movement of transition state measured in terms of the Leffler parameter (Eq. 17). The structural nature of a transition state is monitored by the free energy difference between NBA and UBA when f is an external variable. The inset shows the variation of α with respect to force; value of T = 290 K.
FIGURE 13
FIGURE 13
The free energy as a function of the number of incorrect dihedral angles calculated using the Zwanzig model (see text for details). As the number of distinct values (ν) that the dihedral angle can take increases the entropic barrier increases. For P5GA, ν = 13 provides the best fit of the model to simulations (see text).
FIGURE 14
FIGURE 14
(A) Sketch of the one-dimensional potential E(x) as a function of x for several values of fS. The transition-state location is obtained using E′(xts) = 0. The boundary separating bound and unbound states is given by |E(xts)/kBT| = 1. (B) Dependence of the most probable unbinding force f* as a function of rf. The (f*, log rf) plot for the artificial potential is similar to that shown in Fig. 4 B.
FIGURE 15
FIGURE 15
Persistence length lp as a function of contour length L for linkers at 290 K. The number of monomers N (Eq. 9) is also shown. The values of lp and L are obtained by fitting the end-to-end distance distribution function P(R) generated by simulations to the theoretical expression based on a mean field model (Eq. 23). An example of such a fit for a linker with N = 50, using two different values of kA (see Eq. 9), is shown in the top inset. For large N, lp converges to a constant value. The fit of simulated P(R) for P5GA computed at T = 500 K > Tm is shown in the bottom inset. From the WLC fit, we obtain lp ≈ 1.5 nm and L = 12.5 nm for P5GA.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Doudna, J., and T. Cech. 2002. The chemical repertoire of natural ribozymes. Nature. 418:222–228. - PubMed
    1. Onoa, B., and I. Tinoco, Jr. 2004. RNA folding and unfolding. Curr. Opin. Struct. Biol. 14:374–379. - PubMed
    1. Tinoco, I., Jr. 2004. Force as a useful variable in reactions: unfolding RNA. Annu. Rev. Biophys. Biomol. Struct. 33:363–385. - PMC - PubMed
    1. Bustamante, C., Y. R. Chemla, N. R. Forde, and D. Izhaky. 2004. Mechanical processes in biochemistry. Annu. Rev. Biochem. 73:705–748. - PubMed
    1. Liphardt, J., B. Onoa, S. B. Smith, I. Tinoco, Jr., and C. Bustamante. 2001. Reversible unfolding of single RNA molecules by mechanical force. Science. 292:733–737. - PubMed

Publication types

LinkOut - more resources