Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 1999 Apr;113(4):525-40.
doi: 10.1085/jgp.113.4.525.

Energetic and spatial parameters for gating of the bacterial large conductance mechanosensitive channel, MscL

S I Sukharev  1 , W J Sigurdson, C Kung, F Sachs
Collaborators, Affiliations

Energetic and spatial parameters for gating of the bacterial large conductance mechanosensitive channel, MscL

S I Sukharev et al. J Gen Physiol. 1999 Apr.

Abstract

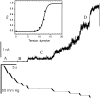
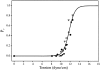
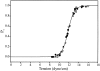
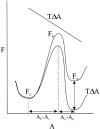
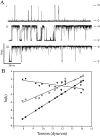
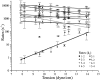
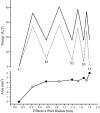
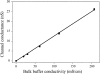
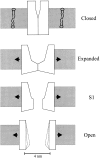
MscL is multimeric protein that forms a large conductance mechanosensitive channel in the inner membrane of Escherichia coli. Since MscL is gated by tension transmitted through the lipid bilayer, we have been able to measure its gating parameters as a function of absolute tension. Using purified MscL reconstituted in liposomes, we recorded single channel currents and varied the pressure gradient (P) to vary the tension (T). The tension was calculated from P and the radius of curvature was obtained using video microscopy of the patch. The probability of being open (Po) has a steep sigmoidal dependence on T, with a midpoint (T1/2) of 11.8 dyn/cm. The maximal slope sensitivity of Po/Pc was 0.63 dyn/cm per e-fold. Assuming a Boltzmann distribution, the energy difference between the closed and fully open states in the unstressed membrane was DeltaE = 18.6 kBT. If the mechanosensitivity arises from tension acting on a change of in-plane area (DeltaA), the free energy, TDeltaA, would correspond to DeltaA = 6.5 nm2. MscL is not a binary channel, but has four conducting states and a closed state. Most transition rates are independent of tension, but the rate-limiting step to opening is the transition between the closed state and the lowest conductance substate. This transition thus involves the greatest DeltaA. When summed over all transitions, the in-plane area change from closed to fully open was 6 nm2, agreeing with the value obtained in the two-state analysis. Assuming a cylindrical channel, the dimensions of the (fully open) pore were comparable to DeltaA. Thus, the tension dependence of channel gating is primarily one of increasing the external channel area to accommodate the pore of the smallest conducting state. The higher conducting states appear to involve conformational changes internal to the channel that don't involve changes in area.

PubMed Disclaimer

Figures

Figure 1
Figure 1
The current (top) activated in a multichannel patch by increasing suction (bottom). The highest suction reached in this experiment was 54 mmHg, at which point the patch ruptured (vertical current spike at the right margin). The patch conductance derived from this trace was corrected for the series pipette resistance R s and the MscL open probability (see methods) was then plotted against pressure (inset). The labels on the current trace correspond to the images shown in Fig. 2.
Figure 2
Figure 2
The geometry of the patch at pressure gradients of 0 (A), 20 (B), 42 (C), and 52 (D) mmHg, imaged simultaneously with the current recording shown in Fig. 1. (A) At zero pressure, the patch membrane (*) was practically flat. As the pressure gradient increased, the radius of curvature decreased and the geometry became stable beyond 40 mmHg. A and B show a fragment of membrane located toward the tip, but not bearing tension as shown by the opposite curvature. The vertical striped bars located on the left side of the images are analogue data records multiplexed onto the video signal (see Zhang et al., 1997). Scale bar, 10 μm.
Figure 3
Figure 3
Curve fitting images of the patch. (A) Increasing pipette suction produces only small changes in the radius of curvature while the patch membrane slowly creeps upward into the pipette. The amount of pipette suction (mmHg) is indicated in each frame. (B) The location of the pipette walls and the patch membrane, as determined by the image-fitting program, are superimposed onto the images. Scale bar, 9 μm.
Figure 4
Figure 4
Partial dose–response (open probability–tension) curves measured for four independent patches. The curvature of each individual patch was fit as shown in Fig. 3. Using the patch radius and the pressure, P o(P ) curves were transformed into P o(T) curves according to Laplace's law. The simultaneous fit of all these curves with a Boltzmann distribution gave a midpoint T 1/2 of 11.8 dyn/cm and a slope of 0.61 dyn/cm per e-fold (P o/P c ratio).
Figure 5
Figure 5
A statistical evaluation of the slope for dose–response curves. 11 P o(P) curves taken without patch imaging were converted to P o(T) dependencies by rescaling to the same midpoint T 1/2 of 11.81 dyn/cm and fit to the Boltzmann two-state model (Sachs and Morris, 1998). The mean slope factor for this set of curves is 0.63 dyn/cm (per e-fold change of P o/P c).
Figure 6
Figure 6
An energy diagram of the two-state channel model as a function of the in-plane area A of the channel. F represents the Helmholtz free energies of the closed (c) and open (o) states and the barrier peak (b). TΔA is the change in energy between the closed and open channels at tension T. Relative to the model in the text, a = (A c − A b)/k B T, where the A is the area of the channel in the relevant parts of the reaction path, ΔA = A o − A c. The tension does the work of TΔA when the channel (in either state) changes area by ΔA (upper linear curve).
Figure 7
Figure 7
MscL kinetics at different tensions, analyzed with a two-state model. (A) Representative traces obtained on one patch containing a single MscL at three different membrane tensions. Tension and P o for A, i–iii, were 9.6, 12.3, and 14.1 dyn/cm and 0.028, 0.689, and 0.976, respectively. Data were decimated fivefold and low-pass filtered at 2 kHz. (B) Logarithms of rate constants for opening (k on, ○) and closing (k off, ▾) as a function of tension. The ln(P o/P c) for all data sets (•) is shown for comparison. The slopes, m, and correlation coefficients are: ln(P o/P c) m = 1.59, r2 = 0.999; ln(k on) m = 1.093, r2 = 0.90; ln(k off) m = −0.34, r2 = 0.48.
Figure 8
Figure 8
A plot of the single channel currents from MscL at different time scales illustrating multiple conducting states. The state amplitudes are noted as C1, S2, S3, S4, and O5 for the closed, subconductance 1–3, and open states, respectively. (A) Low-time resolution showing average MscL gating activity (P o = 0.67). O and C represent the fully open and closed states, respectively. Time scale bar, 800 ms. (B) An expanded segment of A demonstrates the multiple conductance levels typical of this channel (time scale bar, 80 ms). Two expanded segments of B are shown in Ci and Di, showing in more detail the four open conductance levels and MscL opening and closing via substates, some of which have been marked with *. Time scale, 15 and 20 ms, respectively. Below the current traces are idealizations (Cii and Dii) produced by SKM for segments Ci and Di. These show the relative amplitudes of each of the four conductance classes. (Solutions: symmetrical 200 mM KCl 40 mM MgCl2, 10 mM HEPES, pH 7.2; membrane potential, 20mV; membrane tension, 12.3 dyn/cm).
Scheme I
Scheme I
Figure 9
Figure 9
The rate constants vs. tension for the linear sequential model (inset, the respective rate constant symbols). The rate constants were obtained using the program MIL and the regression lines were calculated as fits to single exponential functions of tension with weights determined by the estimated variance of the parameters produced by MIL. The rate-limiting step in opening is k 12, corresponding to the rate of going from closed to the smallest conductance substate. The plot includes data from five different patches.
Figure 10
Figure 10
The energy profiles and area changes of MscL states. (Top) The energy of the states at rest (solid line) and at a tension of 11.8 dyn/cm, midway in the activation curve (dotted line). The energies have been referenced to the closed state. The resting state energies were calculated from the preexponential term of the rate constants assuming the Eyring form of a rate: k = k B T/h exp(−ΔS/k B), where h is Planck's constant and ΔS is the entropy of the reaction. The energies while under tension were calculated from k = k B T/h exp(TΔA/k B T − ΔS/k B). The effective pore radii were calculated from our conductance data assuming a cylindrical pore 4.2-nm long and arbitrarily giving the closed channel a radius of 0.1 nm (see discussion). (Bottom) The integrated change of in-plane area as the channel moves from closed to open (calculated from α = TΔA in Table III).
Figure 11
Figure 11
The dependence of single-channel conductance on the conductivity of the bathing solution. Hille's equation, G ch = ρπa 2/(l + πa/2), linking the channel conductance to the length of the pore (l), its radius (a), and specific electrolyte conductance (ρ) was used to fit the curve. The corresponding pore diameter (d) and cross-sectional area (s), were estimated from the slope of the curve are shown in Table IV.
Figure 12
Figure 12
Cartoon of a cross-sectional view of the channel as it opens suggested by the calculated energy landscape. The channel progresses from the closed conformation (Closed), experiences an increase in membrane tension (Expanded), gates to the first substate (S1), and, through a series of internally reorganized substates, to the fully open state (Open). Open shows the pore diameters for the subconductance states as dashed lines. The channel outer diameter increases primarily in the closed-to-S1 transition. The gating process is likely preceded by an elastic deformation of the entire channel complex, noted as expanded. The opening rate is limited by the first gating transition to S1. The subsequent transitions are largely tension independent and lead to the open state. The drawing of the open state is to scale with the outer diameter of the fully open state ∼6 nm with a pore diameter of 3.6 nm, corresponding to a ring of five to six alpha helices surrounding the pore.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Akinlaja, J. 1997. Electromechanical rupture of cell-attached patches. Physics. Thesis/Dissertation. SUNY at Buffalo, Buffalo, NY. 1–56.
    1. Arkin IT, Sukharev S, Blount P, Kung C, Brunger AT. Helicity, membrane incorporation, orientation and thermal stability of the large conductance mechano-sensitive ion channel from E. coli. . Biochim Biophys Acta. 1998;1369:131–140. - PubMed
    1. Awayda MS, Ismailov II, Berdiev BK, Benos DJ. A cloned renal epithelial Na+channel protein displays stretch activation in planar lipid bilayers. Am J Physiol. 1995;268:C1450–C1459. - PubMed
    1. Berrier C, Besnard M, Ajouz B, Coulombe A, Ghazi A. Multiple mechanosensitive ion channels from Escherichia coli,activated at different thresholds of applied pressure. J Membr Biol. 1996;151:175–187. - PubMed
    1. Bloom M, Evans E, Mouritsen OG. Physical properties of the fluid lipid-bilayer component of cell membranes: a perspective. Q Rev Biophys. 1991;24:293–397. - PubMed

Publication types