Abstract
Persistence of HIV in people living with HIV (PWH) on suppressive antiretroviral therapy (ART) has been linked to physiological mechanisms of CD4+ T cells. Here, in the same 37 male PWH on ART we measure longitudinal kinetics of HIV DNA and cell turnover rates in five CD4 cell subsets: naïve (TN), stem-cell- (TSCM), central- (TCM), transitional- (TTM), and effector-memory (TEM). HIV decreases in TTM and TEM but not in less-differentiated subsets. Cell turnover is ~10 times faster than HIV clearance in memory subsets, implying that cellular proliferation consistently creates HIV DNA. The optimal mathematical model for these integrated data sets posits HIV DNA also passages between CD4 cell subsets via cellular differentiation. Estimates are heterogeneous, but in an average participant’s year ~10 (in TN and TSCM) and ~104 (in TCM, TTM, TEM) proviruses are generated by proliferation while ~103 proviruses passage via cell differentiation (per million CD4). In simulations, therapies blocking proliferation and/or enhancing differentiation could reduce HIV DNA by 1-2 logs over 3 years. In summary, HIV exploits cellular proliferation and differentiation to persist during ART but clears faster in more proliferative/differentiated CD4 cell subsets and the same physiological mechanisms sustaining HIV might be temporarily modified to reduce it.
Subject terms: HIV infections, Computational models, Retrovirus, Bioinformatics
The authors used mathematical modeling of human data to study how HIV persists despite suppressive antiretroviral therapy. They found that when latently infected CD4+ T cells proliferate or differentiate, they can create HIV DNA and passage it into other subsets. More mature CD4 cell subsets then clear HIV DNA faster.
Introduction
The persistence of chromosomally-integrated HIV DNA in CD4+ T cells is the primary barrier preventing people living with HIV (PWH) from achieving viral remission after stopping antiretroviral therapy (ART)1,2. HIV persistence has been associated to physiological mechanisms of CD4 cells3,4 (e.g., homeostatic5–7 and antigen-driven proliferation8, cellular differentiation/maturation9, and death). To help elucidate persistence mechanisms, it is critical to compare HIV DNA and CD4 cell dynamics as directly as possible.
To that end it is important to consider that integrated HIV DNA can be found in multiple CD4 cell subsets6,9–11 (categorized by surface markers12–14) which have different physiological functions (phenotypes) and maturational levels. For instance, at certain time points, higher proportions of HIV DNA have been found in more mature memory and effector CD4 cells, suggesting they are preferentially infected and/or expand HIV DNA through cellular proliferation6,15–17. On the other hand, longitudinally across individuals, HIV DNA appears to accumulate over time in less mature subsets that turn over less frequently18. However, no study to date has measured both CD4 cell turnover and HIV kinetics across subsets in the same individuals.
Mathematical modeling has continually proven useful to understand the kinetics and kinetic heterogeneity of HIV levels within a person over time during suppressive ART19–22. In addition, modeling studies have sometimes inferred cellular rates using HIV as a molecular tag23,24. Our methodology builds upon a rigorous body of work using dynamical systems and population mixed effects modeling to quantitatively describe viral dynamics and recently, for multiple simultaneous data types25–27.
Previously, most CD4 cell subsets have been shown to turn over several times per year in individuals without HIV28,29. These rates have been compared to HIV DNA decay rates (generally >4 year half-lives30–32), with the implication that HIV DNA in the reservoir must be replenished consistently while CD4 cells are born and die. Yet, a further complication is that genetically intact proviruses generally decay faster than defective ones22,33,34, suggesting extrinsic factors like immune selection35,36 may also influence viral persistence. Overall, the precise balance of processes that support reservoir maintenance remain incompletely characterized.
Here we measured cellular turnover in each of five resting CD4 cell subsets and changes in integrated HIV DNA levels within these subsets over 3 years in the same participants. We directly compared HIV DNA kinetics and cellular turnover rates within each subset and identified how these rates contribute to overall slow HIV DNA clearance. By selecting the most parsimonious mechanistic model for these combined data, we inferred the degree to which cellular proliferation and differentiation contribute to maintenance of integrated HIV DNA levels during suppressive ART. Finally, we simulated temporary modulations of proliferation and differentiation to highlight how minor changes in these processes might result in meaningful changes to HIV kinetics.
Results
Study cohort
The HOPE cohort consists of 37 PWH on suppressive ART (clinical and demographic information in Supplementary Table 1), 24 of whom underwent a 45-day deuterium labeling study to measure CD4+ T cell turnover rates and were reported previously17 in a cross-sectional study. Here, we report a prospective 3-year longitudinal analysis of levels of integrated HIV DNA in distinct maturational CD4 cell subsets from all 37 HOPE participants and integrated these data with measured CD4 cell subset turnover rates. Follow up began 1–10 years after achieving viral suppression. Levels of integrated HIV DNA per million CD4+ T cells tended to be stable over time within individuals but differed between individuals by several orders of magnitude (Supplementary Fig. 1).
Quantifying HIV DNA in CD4+ T cell subsets
From these longitudinal samples, resting (HLA-DR-) CD4+ T cells were isolated and sorted by flow cytometry into six CD4 cell subsets (sort schematic in Supplementary Fig. 2): naïve (TN), stem-cell memory (TSCM), central memory (TCM), transitional memory (TTM), effector memory (TEM) cells, and a putative terminally differentiated (TTD) population. As we observed contamination with TN in TTD, the present analysis was focused on the first five sorted populations, each of which was sorted with high purity17.
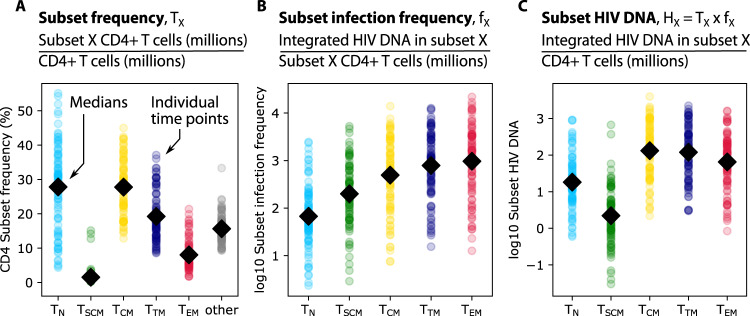
CD4+ T cell subset frequency was calculated as the ratio of subset cells per resting CD4 cells (Fig. 1A). TN and TCM were most common, each with a median across participants and time of ~25% of all resting CD4 cells. The infection frequency was then calculated as the number of integrated HIV DNA copies per million resting cells within each subset (Fig. 1B). Typically, ~1 in 1000 resting TTM and TEM harbored integrated HIV DNA, whereas the other subsets less commonly harbored HIV DNA16. Finally, by multiplying the subset frequency by the infection frequency, we derived the subset HIV DNA level which reflects the relative contribution of each subset to the measured HIV DNA, i.e., the number of integrated HIV DNA copies in a given subset per million total CD4 cells (Fig. 1C). Although not the highest in infection frequency, given its high subset frequency, TCM contributed the highest median HIV DNA levels, with ~100 infected TCM for every million CD4 cells. Median HIV DNA levels were generally lower but not significantly different in other memory phenotypes (TTM and TEM). Considerable variability was noted within each subset and for each data type.
Fig. 1. Definitions and representation of study data.
From 37 PWH in the HOPE cohort, samples were taken at 1–3 time points over a 3-year period. Resting CD4+ T cells were sorted into five phenotypic subsets including naïve (TN), stem-cell memory (TSCM), central memory (TCM), transitional memory (TTM), and effector memory cells (TEM). Three measurements were observed or calculated (panel headings): (A) subset frequency—the proportion of cells in each subset relative to total resting CD4 cells (“other” represents resting cells not among the five sorted subsets), (B) subset infection frequency—integrated HIV DNA in each subset per million subset cells, and (C) subset HIV DNA—the number of HIV DNA copies in a given subset per million CD4 cells. Colored dots indicate values from all participant time points and black diamonds represent means across all dots.
HIV infected cells decay faster than non-infected cells in TTM and TEM (but not other) subsets
To determine if HIV DNA cleared differently in each subset, we used a statistical framework (log-linear mixed effects model) to assess changes in subset infection frequency over the 3-year study period (Fig. 2A). Although the decay rates were heterogeneous (and even positive, i.e., growing, in certain individuals), the average integrated DNA levels within TN, TSCM, and TCM did not significantly change over time (t test p > 0.05 against null hypothesis of no change), while those within TTM and TEM decayed slowly but significantly over time (t test p < 1e-8) (Fig. 2B). Accordingly, TN and TCM rates were significantly different from TTM and TEM rates (pairwise t tests p < 0.005 according to Bonferroni correction for multiple comparisons). Estimated median half-lives were 81 and 59 months for TTM and TEM, respectively. A declining subset infection frequency implies that HIV-infected cells decay faster than non-HIV-infected cells in that subset, suggesting an active process whereby HIV-infected cells are selectively removed.
Fig. 2. The kinetics of subset HIV frequency vary by subset and are generally slower than cellular turnover.
A Longitudinal kinetics of HIV subset infection frequency in each cell subset: thin lines and dots are individual trajectories and thick solid lines represent the estimated average slopes from a log-linear mixed effects model. B Box plots of participants’ decay rates—note that some are positive, meaning that HIV frequency increased. P-values indicate one-sided t-test against null hypothesis of no clearance. For scale, the decay rate equivalent to the QVOA reservoir benchmark 44 month half-life30 is denoted with the dashed gray line. C Cellular turnover rates derived from deuterated water labeling in 24 of these 37 individuals. P values indicated paired two-sided t-tests with non-equal variance. Magnitudes of cellular turnover rates (in non-TN subsets) are much higher than HIV decay rates—note difference in y-axis scales in (C) versus (B). D The % of cellular turnover that is accompanied by HIV turnover (Methods). Values close to 100% indicate that HIV is typically repopulated when cells turn over. In (B–D) box plots indicate median (center line), interquartile range (box), 1.5x interquartile range (whiskers), and outliers (gray diamonds). Each dot (N = 24) represents an individual. E Cartoon example for TEM: in a year, there is frequent cellular turnover, which is infrequently (~5% of events) accompanied by elimination of HIV-infected cells, resulting in the observed slight decay of HIV DNA.
Measuring cellular turnover via deuterium labeling
We used deuterated water labeling37 performed on 24 of the 37 HOPE participants to estimate cellular turnover rates in each subset17. In these experiments, the cellular turnover rate is derived from modeling the proportion of cells that take up a deuterium label during a 45-day labeling period (model schematic in Supplementary Fig. 3). More specifically, the fraction of cells that divided during exposure to deuterated water is calculated37–39. Although what is initially measured from deuterium incorporation into genomic DNA is S-phase cell division, or proliferation40, we instead use the term turnover rate here because this rate represents the combination of all mechanisms that impact levels of deuterium in a subset, including migration/trafficking and/or differentiation. For instance, labels in a given subset can rise due to maturation of a labeled progenitor cell or fall due to further maturation41. Cellular turnover rates ranged across subsets from slowest (TN median 0.2/year) to most rapid (TEM median 2.6/years) (Fig. 2C). Turnover rates were generally more rapid in more differentiated subsets, with the greatest differences between TN to TSCM and TCM to TTM (pairwise t-test p-values in Fig. 2C). A turnover rate of 1 per year corresponds to a half-life of 8.3 months, so these CD4 subsets have median half-lives of 35, 5.3, 4.3, 3.4, and 3.1 months, respectively. Considerable variability was noted within each subset.
CD4+ T cell turnover is often but not always accompanied by HIV DNA turnover in certain subsets
In all subsets except TN, the cellular turnover rate was roughly an order of magnitude faster than the rate of decay of HIV-infected cells (compare Fig. 2B, C). This suggests that cellular turnover of HIV-infected cells does not usually result in removal of HIV DNA. We therefore estimated the percentage of cellular turnover events that might also be accompanied by HIV turnover rather than HIV clearance (Methods). For the five subsets respectively, we calculated medians of 112, 94, 99, 96, and 94% (Fig. 2D). In TN, this number is greater than 100% suggesting some increases in HIV DNA in this subset; however, there was very high variability across participants making the median less reliable. Additionally, the much lower cellular turnover rates invoke lower signal compared to noise in the deuterium labeling measurements, potentially reducing precision. In the TCM subset, we estimate that cellular turnover almost always results in HIV turnover, so HIV DNA does not necessarily decline. Finally, in TSCM, TTM, and TEM, 94–96% of cellular turnover can be associated with HIV turnover. That is, roughly 5% of cellular turnover events are accompanied by clearance of HIV DNA in these subsets (see example for TEM in Fig. 2E). Together, these results indicate that most, but not all, events that increase cell numbers—cellular proliferation and other mechanisms contributing to turnover—are accompanied by concomitant increases in HIV DNA. Any slight imbalance towards cell number increases without HIV increases could drive decay of HIV DNA in certain CD4 subsets.
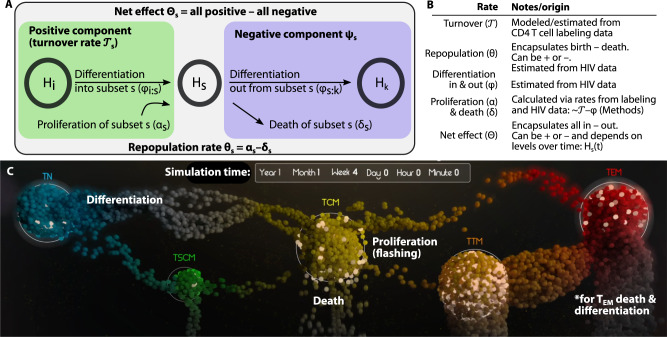
Mechanistic modeling of subset HIV DNA suggests differentiation rapidly passages HIV through CD4+ T cell subset maturation pathways
CD4+ T cell subsets are connected to one another by known steps of lineage maturation14. Previously, in this cohort, we found HIV DNA integrated into identical human chromosomal sites among TCM and TTM and TTM and TEM subsets, a strong sign that differentiation of HIV-infected cells can occur17. Moreover, HIV DNA frequencies and levels were found to correlate between certain subsets (Supplementary Fig. 4). Yet, the relative degree to which differentiation into a given CD4 cell subset versus proliferation within that subset contributes to HIV DNA persistence remains unclear. Therefore, we next sought to model HIV DNA levels with a mechanistic model that included specific rules of cellular proliferation, death, and differentiation.
We developed a variety of models inclusive of different mechanistic processes and degrees of complexity (Table 1, see Methods for equations and text describing assumptions). The list of models encodes scenarios in which HIV DNA levels are governed by one or more mechanisms including slow decay, proliferation, and cell differentiation between subsets. A schematic and table of definitions illustrates the rates we consider (Fig. 3A, B). We then tested these models for fit against levels of subset HIV DNA (e.g., Fig. 1C). Importantly, this is a different data type than in Fig. 2 and provides a common denominator of million CD4+ T cells for each subset. In our model, the levels of HIV DNA are linked across subsets, allowing proliferation and differentiation rates to be directly compared.
Table 1.
Results of information theoretic mathematical model selection on integrated HIV DNA per million CD4+ T cells
| Rank | Model | ΔLL | N rates | ΔAIC | ΔBIC |
|---|---|---|---|---|---|
| 1 | Differentiation with skips: subsets can proliferate and die and are connected from least to most differentiated but additional connections are possible (e.g., TN > TCM).) | 0 | 11 | 0 | 0 |
| 2 | Constrained differentiation with skips: same as 1 but with limits on maximal differentiation rates (no greater than cell turnover) based on biological plausibility. | 10.5 | 11 | 10.5 | 10.4 |
| 3 | Linear differentiation: subsets can proliferate and die and are connected from least to most differentiated. | 25.4 | 9 | 17.4 | 10.9 |
| 4 | Carrying capacity: integrated HIV DNA in each subset is assumed to have an equilibrium value such that levels away from this value return through logistic growth/shrinking. | 28.7 | 10 | 24.7 | 21.4 |
| 5 | Linear differentiation linked to proliferation: a mathematical formulation in which some proportion of proliferation leads to differentiation. | 44.9 | 10 | 40.9 | 37.6 |
| 6 | No differentiation: subsets can only proliferate and die. | 84 | 5 | 60 | 40.6 |
| 7 | Constrained linear differentiation: same as #3 but with limits on maximal differentiation rates based on biological plausibility. | 75 | 9 | 67 | 60.5 |
| 8 | Carrying capacity 2: same as #4 with a different mathematical form for equilibration. | 73.2 | 10 | 69.2 | 65.9 |
| 9 | Only differentiation: subsets have no proliferation/death or net repopulation rates. | 113.1 | 4 | 85.1 | 62.5 |
| 10 | Forced clearance: repopulation rates must be negative, and no differentiation is included. | 136.4 | 5 | 112.4 | 93 |
Constrained differentiation with skips was chosen as the optimal model (see bolded rank 2) as best BIC given biologically realistic parameters. Δ denotes differences from the absolute best model (rank 1). N rates is included to indicate model complexity (more estimated rates is more complex).
LL log likelihood, AIC Akaike information criterion, BIC Bayesian information criterion.
Fig. 3. Modeling subset HIV DNA dynamics via physiological mechanisms of T cells including proliferation, differentiation, and death.
Model schematic (A) and definitions (B) of model rates for a single subset. Net effect rates describes the total kinetic rate summing all modeled mechanisms governing HIV DNA so can be positive or negative for each subset. The turnover rate represents the positive contribution to cellular turnover, estimated via the labeling study. Our mathematical model estimates the repopulation (θ) and differentiation (φ) rates in and out of each subset. Therefore, we can calculate the proliferation (α) and death (δ) rates for each subset from turnover and differentiation. C The most parsimonious model of all combined subset HIV DNA levels included infected cell proliferation (dots flashing), death (dots falling and fading), and differentiation between certain subsets (dots moving). This image is a screenshot of the Supplementary Movie 1 which visualizes the system over time. The differentiation pattern that was most parsimonious included a general flow from least to most mature subsets, but also some “skip” patterns, i.e., TN-to-TCM and TCM-to-TEM. With no further measured subset past TEM, death and differentiation out could not be distinguished for TEM so we combined the two phenomena (see *).
Models were ranked by their accuracy (fit to data) but also penalized for complexity using information criterion. The selected model (Fig. 3C, Supplementary Movie 1) ranked best by both Akaike and Bayesian information criteria42 (AIC and BIC, Table 1). In this best model, each subset level of HIV DNA has a repopulation rate that encapsulates the balance of cell proliferation and death. Cellular differentiation passages HIV DNA between subsets to with rate . Because we did not include the terminally differentiated subset (TTD) due to TN experimental contamination, we could not estimate TEM clearance and differentiation rates simultaneously. Therefore, we explicitly note a combination of the two phenomena (see * in Fig. 3C). We also constrained parameter estimation to ensure rates for each subset were no larger than observed cellular turnover rates for that subset (Supplementary Fig. 5A, B). When this constraint on parameter space was relaxed, some models performed slightly better, but our initial best model remained second only to a model with the same structure but including biologically unrealistic rates (Table 1). Therefore, for the remainder of the analysis, we proceeded with this more conservative model.
Qualitative features of model selection provide several mechanistic results. First, all models lacking differentiation had significantly poorer fit compared to the optimal model (ΔAIC > 2, Table 1). A model that attempted to explain HIV levels through differentiation without cell proliferation was substantially worse than the optimal model (ΔAIC = 85). The selected model includes passaging of HIV DNA along CD4 maturation pathways (i.e., linearly from least to most differentiated subsets) but additionally was improved by the addition of “skip” differentiation from TN to TCM, and from TCM to TEM. A simpler model with purely linear differentiation TN > TSCM > TCM > TTM > TEM was ranked 3rd but did not provide as strong a fit to data (Table 1). Together, these findings suggest differentiation is necessary but not sufficient to precisely describe HIV DNA dynamics in CD4 cell subsets over time.
To potentially broaden the applicability of this model, we provide a table of initial conditions, mean and standard deviation of population rates, and estimated variability of HIV DNA data (Supplementary Table 2).
Sensitivity analysis on model selection
To assess whether the sparse 3-year sampling could have resulted in observations favoring a model with skip differentiation, we simulated the best-fit version of the model with linear differentiation, added appropriate noise, and sampled time points per the 3-year study scheme (Supplementary Fig. 6). We then refit this model to the linear- and skip-differentiation models. As expected, the linear differentiation model fit these data better than the skip-differentiation model (ΔLL = 1.5, ΔAIC = 10 compared to skip-differentiation model). This sensitivity analysis illustrates how model selection can be self-consistent, such that data generated with a given model contains enough information to recover the same model via model selection. In addition, it supported that the skip differentiation model was not innately favored based on noise or the sampling scheme.
Estimating HIV DNA decay half-lives in the model inclusive of cellular differentiation
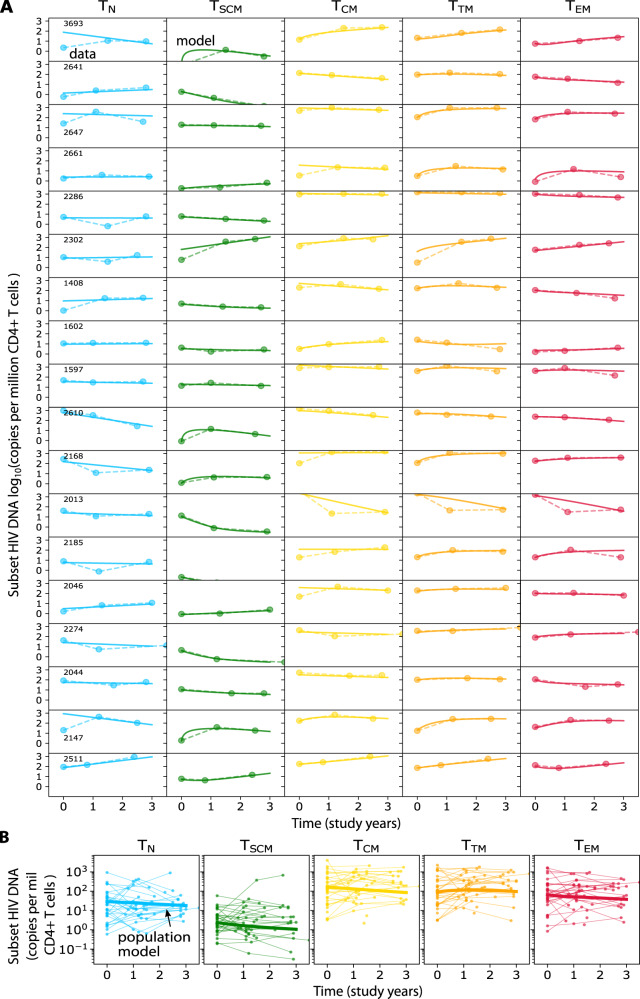
With some exceptions, model fits were excellent across highly variable subset trajectories (see 18 of 37 fits for participants with three time points, Fig. 4A). The overall population trends for each subset show that, notwithstanding some degree of heterogeneity, the average integrated HIV DNA level decays per million CD4+ T cells in 4/5 subsets with a half-life of: 4.3 years in TN, 2.6 years in TSCM, 3.2 years in TCM and 3.7 years in TEM (Fig. 4B). At the same time, HIV DNA levels in TTM appeared to increase (which implies no half-life). When HIV DNA levels in all subsets were summed, the net half-life across all subsets was calculated to be 5.4 years. Although these data are not inclusive of all CD4 cell subsets capable of harboring HIV genomes, and individuals have different timeframes of ART (i.e., see trajectories in Supplementary Fig. 1), these half-life estimates are within ranges of previously-estimated HIV DNA decay22,32,43.
Fig. 4. Modeling including proliferation and differentiation recapitulates individual subset HIV DNA kinetics.
A Model fits (solid lines) of subset HIV DNA levels (dots/dashed lines) for all participants having 3 longitudinal measurements (N = 18). B Population model (solid lines) estimates of subset HIV DNA (copies per million CD4 T cells) to all longitudinal participant data (dots with thin lines).
Quantifying the contribution of cell proliferation, death, and differentiation to integrated HIV DNA persistence
To compare and contrast the mechanisms underlying HIV persistence in the best model, we next directly applied the cellular turnover data to estimate the absolute number of integrated HIV DNA copies (per million CD4+ T cells) that enter and leave each subset pool during a typical year due to proliferation, differentiation in and out, and death (Methods, Fig. 3A, B).
In a typical year in the average individual, we calculated (Methods) that 1–10 HIV DNA copies per million CD4 T cells are generated by proliferation of TN and TSCM while 100–1000 copies are generated by proliferation in TCM, TTM, and TEM (Fig. 5B). Meanwhile, similar numbers of HIV DNA copies are removed by death (Fig. 5D). These numbers imply that HIV DNA persists in a rapid and dynamic near-equilibrium state (Supplementary Movie 1). At the same time, few HIV DNA copies per million CD4+ T cells enter TN and TSCM (Fig. 5A), and 1–10 copies exit those subsets (Fig. 5C) due to differentiation. On average, ten copies enter, and 100 copies leave TCM due to differentiation (Fig. 5C). The unequal differentiation in and out then requires a slight imbalance favoring proliferation over death (Fig. 5B vs. Fig. 5D) to maintain TCM near equilibrium. TTM differentiation was almost balanced (mean ~100 copies in, ~70 copies out in Fig. 5A vs. Fig. 5C). We could not distinguish TEM outward differentiation from death using these data since terminally differentiated cells were not studied in this analysis. Considerable variability was noted across participants within each subset.
Fig. 5. Absolute and relative contribution to HIV reservoirs by cell proliferation, death, and differentiation.
A–D Absolute contributions to HIV subset DNA by differentiation in, proliferation, differentiation out, and death of each subset. E Relative contribution of each mechanism to each subset. Positive (persistence) and negative (clearance) contributions are treated separately for % calculations. Differentiation out and death of TEM are grouped together because the lack of terminally differentiated cells in this analysis precluded identification of both rates. In A–E, estimate for each individual (N = 24) are shown as colored dots and black diamonds indicate means across individuals. F The absolute contribution of each mechanism averaged across all individuals.
Next, we compared mechanisms relative to one another by calculating the percentage of creation (differentiation in and proliferation) and removal (differentiation out and death) events from each mechanism and for each cell subset (Fig. 5E). Proliferation was the dominant mechanism contributing to the persistence of integrated HIV DNA in TN, TCM, and TTM. However, differentiation inward may play an important role in maintaining HIV genomes in TSCM and TEM. Differentiation outward was an important mechanism particularly for TN and TCM, in which removal was projected to occur more through differentiation than death. TEM are known to proliferate frequently and had the highest cellular turnover rates. However, the absolute contribution of proliferation estimated here was lower than differentiation in. If HIV DNA dynamics mirror cellular dynamics measured with deuterated water experiments, this suggests that cellular turnover of HIV-infected TEM may particularly be influenced by differentiation.
In summary the model portrays typical HIV DNA levels as a rapidly proliferating, dying, and differentiating population that, in aggregate, maintains a nearly equilibrated system such that integrated HIV DNA only decays slowly and only in more mature CD4 subsets (Supplementary Movie 1). Importantly, proliferation remains the predominant mechanism in the generation of integrated HIV DNA. TN and TSCM contain less HIV DNA; therefore, the absolute HIV DNA creation and removal in those subsets is orders of magnitude smaller than that found in memory subsets. Proliferation is of particular impact in the context of TCM and TTM: when coupled with differentiation outward (to one or more subsets), these subsets contribute meaningfully to HIV DNA persistence in the rapidly dying/differentiating TEM pool (Fig. 5F).
Modeling cell-associated HIV RNA
We also fit models with no differentiation, linear differentiation, and our favored model with skip differentiation to cell-associated HIV RNA (caRNA) levels measured in the same participants (Supplementary Fig. 7). For these data, the model without differentiation was optimal via AIC. In line with observations for HIV DNA, caRNA levels per million CD4 T cells appeared to increase slightly in TCM and decrease in TEM in these participants. But unlike for DNA, RNA increased in TTM. Together, these data suggest that RNA levels are less tightly connected across subsets, potentially because RNA is generated by DNA and additional variability in this process reduces correlations.
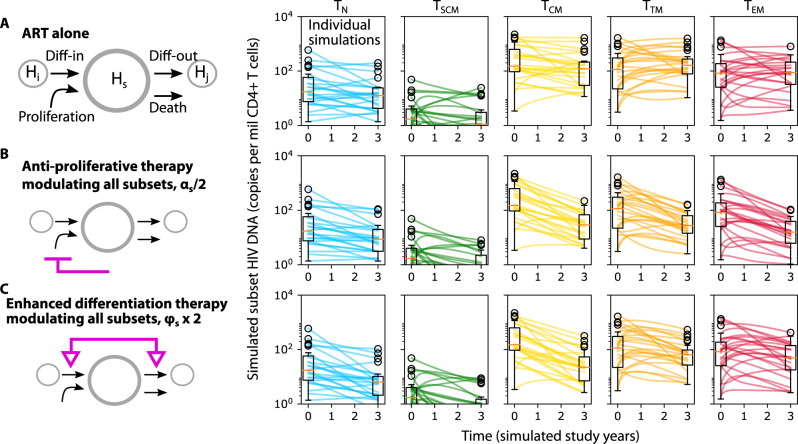
In silico knockout demonstrates the theoretical capacity of reservoir reduction through reduced cell proliferation and/or enhanced cell differentiation
Mechanistic modeling provides the valuable ability to project the dynamics of HIV DNA persistence in the context of perturbed CD4+ T cell subset proliferation and/or differentiation. Thus, we used the model to simulate three therapeutic scenarios over a period of three years: ART alone (Fig. 6A), ART with anti-proliferative therapy that reduces cellular proliferation for all subsets by a factor of 2 (Fig. 6B), and ART with enhanced differentation therapy that increases differentiation for all subsets by a factor of 2 (Fig. 6C). We calculated changes in HIV DNA per million CD4+ T cells over time. For ART alone, (as observed in the raw experimental data) we projected a relatively minimal median change and wide variability inclusive of increases and decreases in all subsets. For ART and anti-proliferative therapy, median HIV DNA across subsets dropped by 300 copies (or ~90%) with most simulations resulting in overall decrease. For ART and enhanced differentiation therapy, median HIV DNA across subsets dropped by 200-300 copies (or ~80–90%) with slightly more simulations inclusive of no change or increase versus anti-proliferative therapy.
Fig. 6. Simulations of modulated HIV persistence mechanisms.
Projections of subset HIV DNA levels in all resting CD4+ T cell subsets during three theoretical therapeutic interventions: A ART alone, (B) ART and anti-proliferative therapy: 2-fold reduction in cell proliferation in all subsets, and (C) ART and enhanced differentiation therapy: 2-fold increase in cell differentiation in and out of all subsets. Box plots indicate median (center line), interquartile range (box), 1.5x interquartile range (whiskers), and outliers (open circles). Each line (N = 24) represents a simulation using parameters from each individual.
Discussion
Here, we addressed the mechanistic basis for HIV persistence during ART in different phenotypic subsets of CD4 + T cells. We measured both longitudinal levels of integrated HIV DNA and cellular turnover rates in five resting CD4 cell subsets in ART-suppressed people living with HIV (PWH). In agreement with previous studies in adults and children6,15,17,44, HIV DNA in these individuals was most commonly found in central, transitional, and effector memory subsets (TCM, TTM, and TEM). Although total levels of naïve CD4 T cells (TN) were as high, if not higher than those with a memory phenotype, TN were much less frequently found to harbor integrated HIV DNA, consistent with observations that memory subsets are easier to infect45,46 and/or that HIV DNA accumulates more quickly within them7.
We documented that HIV decays more rapidly in differentiated CD4 cell subsets (TTM and TEM) vs. less mature subsets (TCM and TN). This explains why HIV DNA appears to accumulate in less-differentiated subsets, as observed in a prior cross-sectional study17. It is possible that proliferation and/or differentiation in these subsets promotes HIV expression and immune recognition47, leading to preferential removal of latently infected cells48. However, TCM also commonly proliferated, so more experiments are needed to refine mechanisms in each subset.
Deuterium labeling data from these PWH demonstrated that turnover rates of predominantly uninfected memory CD4 cells were approximately tenfold faster than HIV DNA decay rates. Therefore, we concluded that HIV-infected cells must frequently die and repopulate by cellular proliferation (and/or differentiation). Additionally, TN turned over substantially less frequently, such that in this subset cellular longevity of latently infected cells is a potential mechanism of reservoir persistence. Most importantly, HIV-infected cells must be slightly balanced towards death during cellular turnover to allow for the HIV DNA decay we observed in the most differentiated subsets.
Cellular differentiation naturally occurs in the context of homeostasis of the total CD4+ T cell population13,14,49. However, the contribution of CD4 cell differentiation to HIV persistence has mostly been discerned indirectly9 and the magnitude of differentiation, especially as compared to cellular proliferation, has not been quantified. We also observed strong associations between HIV levels in different cell subsets over time. Therefore, we tested mathematical models of HIV DNA levels that directly linked subsets and found that models inclusive of differentiation allowed for the best agreement with the data, strengthening the evidence that integrated HIV DNA is passaged from one subset to another through physiologic pathways of CD4 T cellular differentiation.
Our optimal model included “skips” in which HIV DNA was passaged from TN to TCM and TCM to TEM without going through intermediate TSCM and TTM subsets. There may be a mechanistic explanation for why apparent “skipping” is a better fit than linear differentiation. Indeed, it is hard to reconcile the speed of antigenic response with a model in which TCM must become TTM (with 3 months half-lives) before becoming TEM. As different viral infections are controlled by phenotypically different CD8+ T cell subsets50, it may be that certain CD4 cell subsets respond to different antigens.
On an absolute scale, cellular proliferation was confirmed to be the dominant mechanism of reservoir persistence51, accounting (using the best model) for 10–10,000s of new HIV DNA copies per million CD4 cells in a given year. The upper end of this range is comparable to estimates of total reservoir sizes such that, in 1 year, individual cells carrying integrated HIV DNA may be completely refreshed while HIV DNA levels remain nearly constant. In addition to proliferation, the persistence of HIV DNA was also found to be driven by cell differentiation. An implication is that differentiation does not necessarily re-activate HIV expression and result in immune recognition. The overall picture from the model is one in which all subsets proliferate (and TCM in particular proliferate and differentiate rapidly), creating HIV DNA and passaging it onto more mature progeny.
Though we did not study HIV provirus clonality, the best model helps to mechanistically explain past observations of clonal HIV proviruses detected in different CD4 cell subsets9–11,52. Other recent data showed predominantly unique HIV sequences isolated from TN, whereas those retrieved from TEM were mainly clonal53,54. Previously, we reported on HIV clonality in some HOPE study participants17. Oligoclonality was generally higher in more mature subsets and these subsets also had the highest degree of sharing of the same clonotypes. The present modeling provides some mechanistic insight for these observations: we estimate that much of the integrated HIV DNA found in TEM and TTM was likely generated upon cell proliferation and/or passaged onward from the highly proliferative (and therefore highly clonal) progenitor TCM subset. Thus, these subsets are both highly likely (in absolute terms) to be clonal and to share clones in common. However, while TN is still predominantly sustained by proliferation, their lower proliferation rates mean TN is relatively less clonal than other subsets.
Armed with the mechanistic model55, we simulated in silico therapeutics and found that continually reducing cellular proliferation (anti-proliferative therapy7) or enhancing differentiation (akin to “rinse and replace”56) during suppressive ART could substantially reduce HIV DNA levels relative to the use of ART alone. These approaches achieve reduction in HIV DNA differently. It is assumed that the natural (slow) HIV DNA clearance rate in each subset arises from a balance of cell proliferation and death. Anti-proliferative therapies imbalances each subset individually, and HIV DNA clearance is projected to be faster in subsets with higher natural death (turnover) rates. Alternatively, enhancing differentiation does not increase clearance in each subset but rather pushes HIV DNA into the most differentiated compartments, in which HIV DNA clears more rapidly.
In all our simulations, sustained therapy for several years was required to meaningfully reduce HIV DNA, which presents both clinical and experimental challenges for validation. Nevertheless, a human study on IL-15 superagonist N-803, an anti-cancer drug that might promote differentiation57, achieved a small but significant reduction in inducible HIV proviruses58. Individuals taking Dasatinib, a different anti-cancer agent that restricts antigen-driven and homeostatic proliferation of CD4+ T cells in PWH59, also appeared to have lower HIV DNA levels than those taking ART alone, but whether this effect is driven by anti-proliferation requires more research60.
Predictions about anti-proliferative or pro-differentiation therapy from the in silico models should be interpreted carefully. For instance, larger HIV clones found during ART were observed to be less likely to reactivate when ART was stopped (with a continuous relationship between probability and size61), perhaps because they are either genetically defective62–65 or integrated within epigenetically silenced locations (graveyards)35,36,66. This could suggest that more proliferative clonotypes, which in turn might be more affected by anti-proliferative therapy, may be less relevant for predicting viral rebound. Because we did not have viral rebound data, we did not explore models that included viral reactivation67–69 (also precluding simulation of latency reversal agents70).
There are also experimental caveats to this work. CD4 cell subset categorization is inherently imperfect because identifying cells by cell surface markers requires defining thresholds and dichotomizing what is likely a continuum of cell maturation states71. In particular, TN may be heterogeneous to the point of resembling other phenotypes72. We could not distinguish the loss of HIV genomes in TEM through cell death or migration or differentiation outward because we did not successfully sort high-purity terminally differentiated cells.
On the modeling side, our absolutely best scored model admitted rates that were not necessarily biologically plausible. By constraining these rates, we derived a reasonable model that still fits data accurately. Going forward, it would be ideal to collect more temporally resolved data to refine these rates. Other simplifications include that we did not model HIV DNA influx into TN cells -- although small numbers of recent thymic emigrants and/or bone marrow progenitors can be infected73,74. Cellular trafficking to other anatomic compartments and the role of resident memory CD4+ T cells75 were not explicitly modeled; on the other hand, the composite movement of cells in and out of tissues are likely balanced over the multi-year study timescales in our study. Finally, on a conceptual level, cell differentiation and proliferation are fundamentally single cell/lineage properties, whereas we interpreted estimated rates as frequencies of cellular processes averaged over cell populations, which inherently minimizes within-host stochastic effects.
A strength of this study is the direct comparison of CD4 cell turnover and HIV DNA decay in the same participants and subsets. Still, most CD4 cells during ART are not HIV-infected, so it is unclear whether measured turnover rates precisely represent those of HIV-infected cells. HIV-infected cells that persist may be particularly biased toward cell survival and/or proliferation76,77, or more likely to express signatures indicating resistance to immune-mediated killing35,36,66. Our modeling does not reach this level of genetic precision, but our observations of proportional DNA decay in more differentiated CD4 cell subsets (TTM and TEM) indicate that survival mechanisms are likely insufficient to overcome clearance mechanisms in these subsets.
Finally, it would be desirable to estimate mechanistic contributions specifically to the persistence of intact proviruses, which are much more rare but known to clear more rapidly than defective HIV proviruses in the first years of ART33,34,62,65,78. Depth remains a challenge in many HIV reservoir studies, and filtering HIV DNA into both subsets and by intactness has admitted very low proviral counts16. We hope this limitation can be overcome in the future.
In summary, by examining HIV DNA levels and cellular turnover in CD4+ T cell subsets, we found that HIV DNA decays faster in differentiated CD4 cell subsets and quantified how both cellular proliferation and differentiation contribute to HIV persistence. Our simulations suggest that the same mechanisms that HIV exploits for its persistence might also be leveraged for its elimination.
Methods
Inclusion and ethics
All participants were over 18 years old and provided written informed consent for inclusion before they participated in the study. The study (NCT00187512) is an observational, prospective study of HIV-1 infected volunteers designed to provide a specimen bank of samples with carefully characterized clinical data. The study was conducted in accordance with the Declaration of Helsinki, and the protocol was approved by the University of California San Francisco Committee on Human Research.
Study participant characteristics
Thirty-seven persons living with HIV (PWH) on ART were recruited between 2015 and 2019 from the clinic-based SCOPE and OPTIONS cohorts at Zuckerberg San Francisco General Hospital. Study participants returned yearly for 1-3 time points of follow up. The SCOPE cohort enrolls PWH with chronic HIV, whereas the OPTIONS cohort enrolls PWH < 12 months (before 2003) and <6 months (after 2003) following HIV antibody seroconversion. Viral suppression by ART was a requirement for study entry. Duration of viral suppression was estimated based on clinic records (typically assessed every 3–6 months). HIV acquisition timing for each participant was estimated as previously described79.
Isolation of CD4+ T cell subpopulations
All participants underwent leukaphereses performed as outpatients. PBMC were isolated and viably cryopreserved. Frozen PBMC were thawed and CD4 T cells enriched with the EasySep™ Human CD4 + T Cell Negative Selection Enrichment Kit (Stemcell). Cells were stained with Live/Dead Fixable Aqua (Life Technologies) and the following monoclonal antibodies cocktail: anti-CD3-FITC, anti-CD4-AlexaFluor700, anti-CCR7-PE-Cyanine7, anti-CD27-APC, anti-HLA-DR-APC H7, anti-CD57-Brilliant Violet 421, and anti-CD95-PE (Becton Dickinson) as well as anti-CD45RA-ECD (Beckman Coulter). HLA-DR- CD4 + T cell subpopulations were sorted on a FACS ARIA II flow cytometer (BD Biosciences) at >97% purity. Dry pellets were snap-frozen at −80 °C. Flow cytometry data were analyzed on FACSDiva v8.0.1 (BD Biosciences) and FlowJo v8.7 (Tree Star). Sorting schema is provided in Supplementary Fig. 2.
Integrated HIV DNA quantification
Total DNA was extracted using the Allprep DNA/RNA/miRNA Universal Kit (Qiagen). Integrated HIV DNA copies were quantified with a two-step PCR reaction80 using isolated genomic DNA for PCR amplification instead of whole cell lysates. Integrated HIV DNA was pre-amplified with two Alu primers and a primer specific for the HIV LTR region, in addition to primers specific for the CD3 gene to determine cell counts. Nested qPCR was then used to amplify HIV and CD3 sequences from the first round of amplification. Specimens were assayed with up to 500 ng cellular DNA in triplicate and copy number was determined by extrapolation against a 5-point standard curve (3–30,000 copies), using extracted DNA from ACH-2 cells.
Cell-associated HIV RNA quantification
Total RNA was extracted using the Allprep DNA/RNA/miRNA Universal Kit (Qiagen) with on-column DNase treatment (Qiagen RNase-Free DNase Set). HIV RNA levels were quantified with a qPCR TaqMan assay using LTR-specific primers F522-43 (5′ GCC TCA ATA AAG CTT GCC TTG A 3′; HXB2 522-543) and R626-43 (5′ GGG CGC CAC TGC TAG AGA 3′; 626-643) coupled with a FAM-BQ probe (5′ CCA GAG TCA CAC AAC AGA CGG GCA CA 3) on a StepOne Plus Real-time PCR System (Applied Biosystems, Inc.)81. Up to 500 ng of total RNA per sample were characterized in triplicate, and copy numbers were determined by extrapolation against a 7-point standard curve (1–10,000 copies). The input cell number in each PCR well was estimated using independent qPCR measurement of the cellular housekeeping human RPLP0 gene.
Estimating the slope of subset infection fraction
To estimate the slope of HIV subset infection frequency (per million cells of each resting subset), we assumed that the longitudinal kinetics of each subset infection frequency followed an independent exponential model:
| 1 |
So that each subset (denoted by ) has a rate of change per year (or log-linear slope) . Using MONOLIX25, we estimated the five values of . Importantly, we did not assume this rate was negative, such that increases (rather than clearance) were possible. Then, for subsets with negative values of this rate, the half-life in years could be estimated as .
Calculating the percentage of cellular turnover events that result in HIV repopulation
In Fig. 2D, we used each subset infection frequency decay rate and its matching cellular turnover rate to calculate the percentage of cellular turnover events resulting in HIV repopulation. Assuming the net decay can be accounted for as a balance of turnover and repopulation , the repopulation percentage is or:
| 2 |
Normalized correlations between subset levels
Further evidence for connections between subsets emerged from a correlation analysis (Supplementary Fig. 4). For both subset frequencies and subset HIV DNA data, values were normalized to each individual’s longitudinal average value (i.e., ). This procedure prevents spurious correlations (Simpson’s paradox) related to large or small absolute reservoir sizes. Then, pairwise Spearman correlations were computed using the SciPy Stats package.
Mechanistic mathematical models for subset HIV DNA
Our general model of the connected system of HIV DNA in each subset is governed by a system of differential equations that splits the kinetics of HIV DNA into the processes of proliferation, death, and differentiation between subsets. Others have used similar equations82. Each model can be written in vector form as:
| 3 |
Where subset HIV DNA in each subset is the vector , and the clearance and differentiation rates are written with the vectors as and , respectively. Differentiation could be generally from different compartments into others so it is not necessarily the same sized vector in each model. The models tested are numbered as follows:
Model 1 assumes each subset is independent and decays or grows independently (similar to the model used for subset infection frequency in Eq.(1)):
| 4 |
Based on past observations of a net decrease in HIV DNA over years of ART, Model 2 tested the hypothesis that all subset HIV DNA decays independently by using the same structure as Model 1 but forcing .
Model 3 assumes a linear differentiation model whereby each subset had a decay term and differentiation terms in and out from most proximal subsets. There are, therefore, four differentiation terms: .
| 5 |
Model 4 assumed a more complex differentiation pattern derived from the significant correlations between subsets observed in Supplementary Fig. 4. In this model, there are 6 differentiation terms, the same four linear differentiation rates as in Model 3, and two additional skip terms: and .
For models including differentiation, we generally assumed that the differentiation rate of HIV DNA into naïve cells from some unknown/unobserved compartment was zero: . This assumption is based on TREC content observations suggesting thymic emigrants are not carrying HIV DNA frequently, if at all17. We also assumed differentiation out from TEM was zero:. There may be other terminally differentiated cells that TEM can transition into, but these were not observed in the study. Therefore, the clearance rate of TEM effectively covers death and differentiation out and is denoted rather than to make this explicit in Fig. 3.
As another approach, Model 5 assumes each subset was independent and followed a logistic growth term with a carrying capacity. This tests the hypothesis that decay was not occurring and that HIV DNA levels in each subset had a rough equilibrium:
| 6 |
Yet another approach (Model 6) more explicitly tested the hypothesis that proliferation and differentiation were linked. We assumed that some fraction of repopulation events are associated with differentiation:
| 7 |
As a final note, multiphasic decay is well documented for HIV DNA clearance after initiation of ART32,83. However, these phases are generally equilibrated within a year or two of ART initiation, which was irrelevant to our data.
Model fitting and selection with population non-linear mixed effects modeling (pNLME)
Model fit and selection was performed using MONOLIX25 software, which employs a population nonlinear mixed-effects (pNLME) approach. We assumed assay variability (noise) was log normal. Repopulation parameters were generally assumed to be normally distributed (allowing for negative values), and differentiation rates were generally assumed to be lognormally distributed. Population parameters were found to be uncorrelated, but across individuals, certain parameters were strongly correlated (Supplementary Fig. 5C). This finding suggests that those with higher rates in one subset tend to also have higher rates in others. Individual best fit parameters for each participant using the optimal model are collected in Supplementary Data 1.
Imputing turnover rate to define mechanistic components
The underlying assumption of the repopulation rate is that it is a balance of proliferation and death, . To estimate these component rates, we use the cellular turnover data (Fig. 3B). We begin with a general equation for the -th HIV DNA subset level from the best model and use a quasistatic assumption to indicate that cellular turnover mitigates a balance inward and outward of each subset. Yet, this balance has an absolute value such that in some subsets, although net zero change occurs, there is more inward and outward flow. We therefore set inward and outward mechanisms (from Eq. (5)) equal and split repopulation into proliferation and death, leaving:
| 8 |
The turnover rate (per year) then can be factored out of the rhs as , such that the death rate can be defined as the turnover rate minus the differentiation rate out:
| 9 |
And similarly solving , leads to:
| 10 |
Which we approximate by using the values of .
Tracking equations to distinguish mechanistic contributions
After imputing the turnover rates to define the mechanistic compartments, the HIV DNA created at any time (instantaneously in the interval ) due to each mechanism was computed. This computation occurs independently after solving the differential equations. Thus, the proliferation and death terms follow
| 11 |
While the differentiation terms follow:
| 12 |
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Supplementary information
Description of additional Supplementary files
Acknowledgements
The authors sincerely thank each one of the HOPE study participants who devoted their time and bodies to our research and the clinical staff from the SCOPE and OPTIONS cohorts who made this project possible: Monika Deswal, Montha Pao, Heather Hartig, Marian Kerbleski, and Viva Tai. We thank Alex Carvidi, Elizabeth Sinclair, and Jeff Milush from the Core Immunology Lab for their assistance on this study; Mike Busch as well as the “Reservoir Assay Validation and Evaluation Network” (RAVEN) study group for their contribution to the collection of leukaphereses; and the DARE U19 Consortium for their support. This study was supported by the following NIH grants: K25 AI155224 (D.B.R.), R01 AI116368 and K24 AI145806 (P.W.H.), UM1 AI126611 (S.G.D.), and P30 AI027763. D.B.R. is extremely grateful for the support of the University of Washington/Fred Hutch Center for AIDS Research (CFAR, P30 AI027757) through a New Investigator Award that initiated this project.
Author contributions
D.B.R., C.B.S., P.W.H., and J.T.S. conceived the project. C.B.S performed and oversaw all experiments with help from R.H., H.A., M.S., R.H., and J.M. D.B.R. performed all modeling, analysis, and generated all figures. M.F. and M.K.H. performed deuterium labeling experiments and analysis. P.W.H., S.G.D., J.M.M., and J.T.S. supervised the project. D.B.R. wrote the manuscript with many revisions from C.B.S., P.W.H., M.M., and J.T.S. All authors revised the manuscript.
Peer review
Peer review information
Nature Communications thanks Eugenio Montini, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
Data used to generate figures is available at https://github.com/dbrvs/HOPE-modeling and in Supplementary Data 1.
Code availability
All model code is freely available at https://github.com/dbrvs/HOPE-modeling. Python and in particular the Seaborn package were used to generate all figures.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Daniel B. Reeves, Charline Bacchus-Souffan, Joshua T. Schiffer, Peter W. Hunt.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-023-41521-1.
References
- 1.Chun TW, et al. Presence of an inducible HIV-1 latent reservoir during highly active antiretroviral therapy. Proc. Natl Acad. Sci. USA. 1997;94:13193–13197. doi: 10.1073/pnas.94.24.13193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Finzi D, et al. Identification of a reservoir for HIV-1 in patients on highly active antiretroviral therapy. Science. 1997;278:1295–1300. doi: 10.1126/science.278.5341.1295. [DOI] [PubMed] [Google Scholar]
- 3.Murray AJ, Kwon KJ, Farber DL, Siliciano RF. The latent reservoir for HIV-1: how immunologic memory and clonal expansion contribute to HIV-1 persistence. J. Immunol. 2016;197:407–417. doi: 10.4049/jimmunol.1600343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cohn LB, Chomont N, Deeks SG. Review the biology of the HIV-1 latent reservoir and implications for cure strategies. Cell Host Microbe. 2020;27:519–530. doi: 10.1016/j.chom.2020.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Reeves, D. B. et al. A majority of HIV persistence during antiretroviral therapy is due to infected cell proliferation. Nat. Commun.9, 4811 (2018). [DOI] [PMC free article] [PubMed]
- 6.Chomont N, et al. HIV reservoir size and persistence are driven by T cell survival and homeostatic proliferation. Nat. Med. 2009;15:893–900. doi: 10.1038/nm.1972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Reeves DB, et al. Anti-proliferative therapy for HIV cure: a compound interest approach. Sci. Rep. 2017;7:4011. doi: 10.1038/s41598-017-04160-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Simonetti FR, et al. Antigen-driven clonal selection shapes the persistence of HIV-1 infected CD4+ T cells in vivo. J. Clin. Invest. 2020;131:e145254. doi: 10.1172/JCI145254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Horsburgh BA, et al. Cellular activation, differentiation, and proliferation influence the dynamics of genetically intact proviruses over time. J. Infect. Dis. 2022;225:1168–1178. doi: 10.1093/infdis/jiab291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gantner P, et al. Single-cell TCR sequencing reveals phenotypically diverse clonally expanded cells harboring inducible HIV proviruses during ART. Nat. Commun. 2020;11:1–9. doi: 10.1038/s41467-020-17898-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.von Stockenstrom S, et al. Longitudinal genetic characterization reveals that cell proliferation maintains a persistent HIV Type 1 DNA pool during effective HIV therapy. J. Infect. Dis. 2015;1:596–607. doi: 10.1093/infdis/jiv092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sallusto F, Lenig D, Förster R, Lipp M, Lanzavecchia A. Two subsets of memory T lymphocytes with distinct homing potentials and effector functions. Nature. 1999;401:708–712. doi: 10.1038/44385. [DOI] [PubMed] [Google Scholar]
- 13.Lanzavecchia A, Sallusto F. Understanding the generation and function of memory T cell subsets. Curr. Opin. Immunol. 2005;17:326–332. doi: 10.1016/j.coi.2005.04.010. [DOI] [PubMed] [Google Scholar]
- 14.Mahnke YD, Brodie TM, Sallusto F, Roederer M, Lugli E. The who’s who of T-cell differentiation: human memory T-cell subsets. Eur. J. Immunol. 2013;43:2797–2809. doi: 10.1002/eji.201343751. [DOI] [PubMed] [Google Scholar]
- 15.Buzon MJ, et al. HIV-1 persistence in CD4+ T cells with stem cell–like properties. Nat. Med. 2014;20:139–142. doi: 10.1038/nm.3445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Morcilla V, et al. HIV-1 genomes are enriched in memory CD4+ T-Cells with short half-lives. MBio. 2021;12:e0244721. doi: 10.1128/mBio.02447-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bacchus-Souffan C, et al. Relationship between CD4 T cell turnover, cellular differentiation and HIV persistence during. PLoS Pathog. 2021;17:e1009214. doi: 10.1371/journal.ppat.1009214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jaafoura S, et al. Progressive contraction of the latent HIV reservoir around a core of less-differentiated CD4+ memory T cells. Nat. Commun. 2014;5:1–8. doi: 10.1038/ncomms6407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Perelson AS, et al. Decay characteristics of HIV-1-infected compartments during combination therapy. Nature. 1997;387:188–191. doi: 10.1038/387188a0. [DOI] [PubMed] [Google Scholar]
- 20.Blankson JN, et al. Biphasic decay of latently infected CD4+ T cells in acute human immunodeficiency virus type 1 infection. J. Infect. Dis. 2000;182:1636–1642. doi: 10.1086/317615. [DOI] [PubMed] [Google Scholar]
- 21.Luo R, et al. Modelling HIV-1 2-LTR dynamics following raltegravir intensification. J. R. Soc. Interface. 2013;10:20130186. doi: 10.1098/rsif.2013.0186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.White JA, et al. Complex decay dynamics of HIV virions, intact and defective proviruses, and 2LTR circles following initiation of antiretroviral therapy. Proc. Natl Acad. Sci. Usa. 2022;119:e2120326119. doi: 10.1073/pnas.2120326119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Althaus CL, Joos B, Perelson AS, Günthard HF, Günthard HF. Quantifying the turnover of transcriptional subclasses of HIV-1-infected cells. PLoS Comput. Biol. 2014;10:e1003871–11. doi: 10.1371/journal.pcbi.1003871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Imamichi H, et al. Lifespan of effector memory CD4+ T cells determined by replication-incompetent integrated HIV-1 provirus. AIDS. 2014;28:1091–1099. doi: 10.1097/QAD.0000000000000223. [DOI] [PubMed] [Google Scholar]
- 25.Kuhn E, Lavielle M. Maximum likelihood estimation in nonlinear mixed effects models. Comput. Stat. Data Anal. 2005;49:1020–1038. doi: 10.1016/j.csda.2004.07.002. [DOI] [Google Scholar]
- 26.Reeves DB, et al. Timing HIV infection with a simple and accurate population viral dynamics model. J. R. Soc. Interface. 2021;18:20210314. doi: 10.1098/rsif.2021.0314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cardozo-Ojeda EF, et al. Thresholds for post-rebound SHIV control after CCR5 gene-edited autologous hematopoietic cell transplantation. Elife. 2021;10:1–25. doi: 10.7554/eLife.57646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Macallan DC, et al. Rapid turnover of effector memory CD4+ T cells in healthy humans. J. Exp. Med. 2004;200:255–260. doi: 10.1084/jem.20040341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ahmed R, et al. Reconciling estimates of cell proliferation from stable isotope labeling experiments. PLoS Comput. Biol. 2015;11:e1004355. doi: 10.1371/journal.pcbi.1004355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Siliciano JD, et al. Long-term follow-up studies confirm the stability of the latent reservoir for HIV-1 in resting CD4+ T cells. Nat. Med. 2003;9:727–728. doi: 10.1038/nm880. [DOI] [PubMed] [Google Scholar]
- 31.Bruner KM, et al. A quantitative approach for measuring the reservoir of latent HIV-1 proviruses. Nature. 2019;566:120–125. doi: 10.1038/s41586-019-0898-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Besson GJ, et al. HIV-1 DNA decay dynamics in blood during more than a decade of suppressive antiretroviral therapy. Clin. Infect. Dis. 2014;59:1312–1321. doi: 10.1093/cid/ciu585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gandhi RT, et al. Selective decay of intact HIV-1 proviral DNA on antiretroviral therapy. J. Infect. Dis. 2021;223:225–233. doi: 10.1093/infdis/jiaa532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Peluso MJ, et al. Differential decay of intact and defective proviral DNA in HIV-1-infected individuals on suppressive antiretroviral therapy. JCI Insight. 2020;5:e132997. doi: 10.1172/jci.insight.132997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lian X, et al. Signatures of immune selection in intact and defective proviruses distinguish HIV-1 elite controllers. Sci. Transl. Med. 2021;13:eabl4097. doi: 10.1126/scitranslmed.abl4097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sun W, et al. Phenotypic signatures of immune selection in HIV-1 reservoir cells. Nature. 2023;614:309–317. doi: 10.1038/s41586-022-05538-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Busch R, Neese RA, Awada M, Hayes GM, Hellerstein MK. Measurement of cell proliferation by heavy water labeling. Nat. Protoc. 2007;2:3045–3057. doi: 10.1038/nprot.2007.420. [DOI] [PubMed] [Google Scholar]
- 38.McCune JM, et al. Factors influencing T-cell turnover in HIV-1–seropositive patients. J. Clin. Invest. 2000;105:R1–R8. doi: 10.1172/JCI8647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Neese RA, et al. Measurement in vivo of proliferation rates of slow turnover cells by 2H2O labeling of the deoxyribose moiety of DNA. Proc. Natl Acad. Sci. 2002;99:15345–15350. doi: 10.1073/pnas.232551499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Macallan DC, et al. Measurement and modeling of human T cell kinetics. Eur. J. Immunol. 2003;33:2316–2326. doi: 10.1002/eji.200323763. [DOI] [PubMed] [Google Scholar]
- 41.Gossel G, Hogan T, Cownden D, Seddon B, Yates AJ. Memory CD4 T cell subsets are kinetically heterogeneous and replenished from naive T cells at high levels. Elife. 2017;6:182. doi: 10.7554/eLife.23013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Burnham, K. P. & Anderson, D. R. Model Selection and Inference: A Practical Information-Theoretic Approach. 65, (Springer, New York, 2001).
- 43.Golob JL, et al. HIV DNA levels and decay in a cohort of 111 long-term virally suppressed patients. AIDS. 2018;32:2113–2118. doi: 10.1097/QAD.0000000000001948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Luzuriaga K, et al. HIV Type 1 (HIV-1) proviral reservoirs decay continuously under sustained virologic control in HIV-1–infected children who received early treatment. J. Infect. Dis. 2014;210:1529–1538. doi: 10.1093/infdis/jiu297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Xie G, et al. Characterization of HIV-induced remodeling reveals differences in infection susceptibility of memory CD4+ T cell subsets in vivo. Cell Rep. 2021;35:109038. doi: 10.1016/j.celrep.2021.109038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Okoye A, et al. Progressive CD4+ central memory T cell decline results in CD4+ effector memory insufficiency and overt disease in chronic SIV infection. J. Exp. Med. 2007;204:2171–2185. doi: 10.1084/jem.20070567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Pollack RA, et al. Defective HIV-1 proviruses are expressed and can be recognized by cytotoxic T Lymphocytes, which shape the proviral landscape. Cell Host Microbe. 2017;21:494–506.e4. doi: 10.1016/j.chom.2017.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Wonderlich ER, et al. Effector memory differentiation increases detection of replication-competent HIV-l in resting CD4+ T cells from virally suppressed individuals. PLoS Pathog. 2019;15:e1008074. doi: 10.1371/journal.ppat.1008074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Geginat J, Sallusto F, Lanzavecchia A. Cytokine-driven proliferation and differentiation of human naïve, central memory and effector memory CD4+ T cells. Pathol. Biol. 2003;51:64–66. doi: 10.1016/S0369-8114(03)00098-1. [DOI] [PubMed] [Google Scholar]
- 50.Appay V, et al. Memory CD8+ T cells vary in differentiation phenotype in different persistent virus infections. Nat. Med. 2002;8:379–385. doi: 10.1038/nm0402-379. [DOI] [PubMed] [Google Scholar]
- 51.Virgilio MC, Collins KL. The impact of cellular proliferation on the HIV-1 reservoir. Viruses. 2020;12:1–24. doi: 10.3390/v12020127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Josefsson L, et al. The HIV-1 reservoir in eight patients on long-term suppressive antiretroviral therapy is stable with few genetic changes over time. Proc. Natl Acad. Sci. 2013;110:E4987–E4996. doi: 10.1073/pnas.1308313110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Venanzi Rullo E, et al. Persistence of an intact HIV reservoir in phenotypically naive T cells. JCI Insight. 2020;5:e133157. doi: 10.1172/jci.insight.133157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Gartner MJ, et al. Persistence of envelopes in different CD4+ T-cell subsets in antiretroviral therapy-suppressed people with HIV. AIDS. 2023;37:247–257. doi: 10.1097/QAD.0000000000003424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Handel A, La Gruta NL, Thomas PG. Simulation modelling for immunologists. Nat. Rev. Immunol. 2020;20:186–195. doi: 10.1038/s41577-019-0235-3. [DOI] [PubMed] [Google Scholar]
- 56.Grossman Z, et al. ‘Rinse and Replace’: boosting T cell turnover to reduce HIV-1 reservoirs. Trends Immunol. 2020;41:466–480. doi: 10.1016/j.it.2020.04.003. [DOI] [PubMed] [Google Scholar]
- 57.Waickman AT, et al. CD4 effector T cell differentiation is controlled by IL-15 that is expressed and presented in trans. Cytokine. 2017;99:266–274. doi: 10.1016/j.cyto.2017.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Miller JS, et al. Safety and virologic impact of the IL-15 superagonist N-803 in people living with HIV: a phase 1 trial. Nat. Med. 2022;28:392–400. doi: 10.1038/s41591-021-01651-9. [DOI] [PubMed] [Google Scholar]
- 59.Innis EA, et al. Pharmacologic control of homeostatic and antigen-driven proliferation to target HIV-1 persistence. Biochem. Pharmacol. 2021;194:114816. doi: 10.1016/j.bcp.2021.114816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Vigón L, et al. Provirus reactivation is impaired in HIV-1 infected individuals on treatment with dasatinib and antiretroviral therapy. Biochem. Pharmacol. 2021;192:114666. doi: 10.1016/j.bcp.2021.114666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Lorenzi JCC, et al. Paired quantitative and qualitative assessment of the replication-competent HIV-1 reservoir and comparison with integrated proviral DNA. Proc. Natl Acad. Sci. 2016;113:E7908–E7916. doi: 10.1073/pnas.1617789113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Antar AR, et al. Longitudinal study reveals HIV-1-infected CD4+ T cell dynamics during long-term antiretroviral therapy. J. Clin. Invest. 2020;130:29–32. doi: 10.1172/JCI135953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Huang S-HH, et al. Latent HIV reservoirs exhibit inherent resistance to elimination by CD8+ T cells. J. Clin. Invest. 2018;128:876–889. doi: 10.1172/JCI97555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Bender AM, et al. The Landscape of Persistent Viral Genomes in ART-Treated SIV, SHIV, and HIV-2 Infections. Cell Host Microbe. 2019;26:73–85.e4. doi: 10.1016/j.chom.2019.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Bruner KM, et al. Defective proviruses rapidly accumulate during acute HIV-1 infection. Nat. Med. 2016;22:1043–1049. doi: 10.1038/nm.4156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Einkauf KB, et al. Parallel analysis of transcription, integration, and sequence of single HIV-1 proviruses. Cell. 2022;185:266–282.e15. doi: 10.1016/j.cell.2021.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Hill AL, Rosenbloom DIS, Fu F, Nowak MA, Siliciano RF. Predicting the outcomes of treatment to eradicate the latent reservoir for HIV-1. Proc. Natl Acad. Sci. 2014;111:15597–15597. doi: 10.1073/pnas.1406663111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Conway JM, Perelson AS. Post-treatment control of HIV infection. Proc. Natl Acad. Sci. Usa. 2015;6:4–9. doi: 10.1073/pnas.1419162112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Saha, A. & Dixit, N. M. Pre-existing resistance in the latent reservoir can compromise VRC01 therapy during chronic HIV-1 infection. PLoS Comput. Biol.16, e1008434 (2020). [DOI] [PMC free article] [PubMed]
- 70.Bashiri K, Rezaei N, Nasi M, Cossarizza A. The role of latency reversal agents in the cure of HIV: a review of current data. Immunol. Lett. 2018;196:135–139. doi: 10.1016/j.imlet.2018.02.004. [DOI] [PubMed] [Google Scholar]
- 71.Eizenberg-Magar I, et al. Diverse continuum of CD4+ T cell states is determined by hierarchical additive integration of cytokine signals. Proc. Natl Acad. Sci. 2017;114:E6447–E6456. doi: 10.1073/pnas.1615590114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Caccamo N, Joosten SA, Ottenhoff THM, Dieli F. Atypical human effector/memory CD4+ T Cells with a naive-like phenotype. Front. Immunol. 2018;9:1–6. doi: 10.3389/fimmu.2018.02832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Fabre-Mersseman V, et al. CD4+ recent thymic emigrants are infected by HIV in vivo, implication for pathogenesis. AIDS. 2011;25:1153–1162. doi: 10.1097/QAD.0b013e3283471e89. [DOI] [PubMed] [Google Scholar]
- 74.Sebastian NT, Collins KL. Targeting HIV latency: resting memory T cells, hematopoietic progenitor cells and future directions. Expert Rev. Anti. Infect. Ther. 2014;12:1187–1201. doi: 10.1586/14787210.2014.956094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Schenkel JMM, Masopust D. Tissue-resident memory T Cells. Immunity. 2014;41:886–897. doi: 10.1016/j.immuni.2014.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Clark IC, et al. HIV silencing and cell survival signatures in infected T cell reservoirs. Nature. 2023;614:318–325. doi: 10.1038/s41586-022-05556-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Wagner TA, et al. Proliferation of cells with HIV integrated into cancer genes contributes to persistent infection. Science. 2014;345:570–573. doi: 10.1126/science.1256304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Cho A, et al. Longitudinal clonal dynamics of HIV-1 latent reservoirs measured by combination quadruplex polymerase chain reaction and sequencing. Proc. Natl Acad. Sci. USA. 2022;119:e2117630119. doi: 10.1073/pnas.2117630119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Pilcher CD, et al. A generalizable method for estimating duration of HIV infections using clinical testing history and HIV test results. AIDS. 2019;33:1231–1240. doi: 10.1097/QAD.0000000000002190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Vandergeeten C, et al. Cross-clade ultrasensitive PCR-based assays to measure HIV persistence in large-cohort studies. J. Virol. 2014;88:12385–12396. doi: 10.1128/JVI.00609-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Kumar AM, Borodowsky I, Fernandez B, Gonzalez L, Kumar M. Human immunodeficiency virus type 1 RNA levels in different regions of human brain: quantification using real-time reverse transcriptase-polymerase chain reaction. J. Neurovirol. 2007;13:210–224. doi: 10.1080/13550280701327038. [DOI] [PubMed] [Google Scholar]
- 82.Hapuarachchi T, Lewis J, Callard RE. A mechanistic model for naive CD4 T cell homeostasis in healthy adults and children. Front. Immunol. 2013;4:2–7. doi: 10.3389/fimmu.2013.00366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Spivak AM, et al. Short communication: dynamic constraints on the second phase compartment of HIV-infected cells. AIDS Res. Hum. Retrovir. 2011;27:759–761. doi: 10.1089/aid.2010.0199. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Description of additional Supplementary files
Data Availability Statement
Data used to generate figures is available at https://github.com/dbrvs/HOPE-modeling and in Supplementary Data 1.
All model code is freely available at https://github.com/dbrvs/HOPE-modeling. Python and in particular the Seaborn package were used to generate all figures.