Exploring meteorological impacts based on Köppen-Geiger climate classification after reviewing China's response to COVID-19

Fangyuan Chen; Siya Chen; Mengmeng Jia; Mingyue Jiang; Zhiwei Leng; Libing Ma; Yanxia Sun; Ting Zhang; Luzhao Feng; Weizhong Yang

doi:10.1016/j.apm.2022.09.008

. 2022 Oct 3;114:133–146. doi: 10.1016/j.apm.2022.09.008

Exploring meteorological impacts based on Köppen-Geiger climate classification after reviewing China's response to COVID-19

Fangyuan Chen ^a,^b,^#,^⁎, Siya Chen ^b,^#, Mengmeng Jia ^b,^#, Mingyue Jiang ^b, Zhiwei Leng ^b, Libing Ma ^b, Yanxia Sun ^b, Ting Zhang ^b, Luzhao Feng ^b, Weizhong Yang ^b

PMCID: PMC9528067 PMID: 36212726

Abstract

More than 30 months into the novel coronavirus 2019 (COVID-19) pandemic, efforts to bring this prevalence under control have achieved tentative achievements in China. However, the continuing increase in confirmed cases worldwide and the novel variants imply a severe risk of imported viruses. High-intensity non-pharmaceutical interventions (NPIs) are the mainly used measures of China's early response to COVID-19, which enabled effective control in the first wave of the epidemic. However, their efficiency is relatively low across China at the current stage. Therefore, this study focuses on whether measurable meteorological variables be found through global data to learn more about COVID-19 and explore flexible controls. This study first examines the control measures, such as NPIs and vaccination, on COVID-19 transmission across 189 countries, especially in China. Subsequently, we estimate the association between meteorological factors and time-varying reproduction numbers based on the global data by meta-population epidemic model, eliminating the aforementioned anthropogenic factors. According to this study, we find that the basic reproduction number of COVID-19 transmission varied wildly among Köppen-Geiger climate classifications, which is of great significance for the flexible adjustment of China's control protocols. We obtain that in southeast China, Köppen-Geiger climate sub-classifications, Cwb, Cfa, and Cfb, are more likely to spread COVID-19. In August, the R_SIM of Cwb climate subclassification is about three times that of Dwc in April, which implies that the intensity of control efforts in different sub-regions may differ three times under the same imported risk. However, BSk and BWk, the most widely distributed in northwest China, have smaller basic reproduction numbers than Cfa, distributed in southeast coastal areas. It indicates that northwest China's control intensity could be appropriately weaker than southeast China under the same prevention objectives.

Keywords: COVID-19, China's response, NPIs and vaccination, Köppen-Geiger climate classification

Introduction

By the end of June 2022, the novel coronavirus 2019 (COVID-19) pandemic caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) has spread globally for more than 30 months, resulting in more than 550,000,000 infections and more than 6000,000 deaths [1], which means more than 7% of the world's population had been infected by the coronavirus. This pandemic covers more than 180 countries or regions. However, the incidence of COVID-19 is not evenly distributed across the world due to regional heterogeneity in natural and social environments [1]. In the mainland of China, where the epidemic emerged earlier, the national incidence was about 7 × 10⁻⁵ from December 2019 to October 2021, which was much lower than the average number around the world [2]. China has continued to implement facilitated actions, for instance, strict non-pharmaceutical interventions and nationwide free vaccination strategy to keep its population safe [3]. 3411,903,000 doses of COVID-19 vaccines have been given in the mainland of China [4] as of July 15, 2021.

The combination of non-pharmaceutical interventions (NPIs) [5], [6], [7], [8], [9] and the vaccination strategy [4,10] have contained another large-scale prevalence of COVID-19 in the mainland of China. Although a few local cases caused by imported viruses have been reported in China, the average monthly incidence of confirmed symptomatic cases in each province is less than 1/10,000 [2]. On April 8, 2020, Wuhan, the original epicenter of the epidemic in China, announced the lifting of 76-day outbound traffic restrictions [3,5], indicating the end of the first nationwide wave of COVID-19 in China. Since then, China has entered an ongoing stage with lower incidence. During this stage, 10,149 confirmed cases [4] have been reported in the mainland of China, but 546,121 close contacts [4] have been traced to medical isolation, with an efficiency of only 1.86%. Compared with the first quarter in 2020, the tracking efficiency decreases by 83.84%. Meanwhile, the proportion of imported confirmed cases increases from 1.03% to 86.67%.

Currently, China confronts a high risk of external imported viruses and difficult tracking of close internal contacts due to the prevalence of pre-symptomatic and asymptomatic infections [11]. High-intensity NPIs are the mainly used measures of China's early response to COVID-19, which enabled effective control in the first wave of the epidemic, but the proportion of infected people tracked is relatively lower at the ongoing stage with a low incidence. Public health institutions must invest much workforce and material resources to get fewer latent infections, which is inefficient. Meanwhile, the data analysis of domestic cases has not been able to obtain more information, such as the spatial-temporal heterogeneous effect of meteorological factors, due to the absence of continuous data. Therefore, this study focused on whether measurable risk variables could be found through global COVID-19 data in order to implement epidemic control more efficiently in China. Previous studies [12], [13], [14], [15], [16] about the association between COVID-19 transmission and meteorological conditions have been published over the last years. However, diversity of selected regions, data sets, and mathematical methods might contribute to specific results, leading to significantly different from each other [17], [18].

Using the similar generalized additive models based on similar epidemiological data sets from cities in China, Yao et al. [19] showed no significant correlation between relative humidity, temperature, and cumulative incidence or reproduction number of COVID-19. However, Zhu et al. [20] found the correlation between average temperature and confirmed COVID-19 cases was approximately linear below 3 °C. For every 1 °C increase in average temperature below 3 °C, the number of confirmed COVID-19 cases increased by 4.861% every day. Wei et al. [21] concluded that a higher average temperature had a significant negative effect on the risk of COVID-19 when the temperature was below 10 °C. However, the effect was insignificant when the temperature was over 10 °C. It is observed that the results of these studies on COVID-19 data at the city level in China are quite different and even contradictory. After carefully reviewing the research objects of these studies, we found that the data deadlines of these studies are February 10, February 29, and March 11 in 2020, respectively. Due to China's location in the Northern Hemisphere, winter fell between December 2019 and March 2020, and the average temperature of most cities in China was below 15℃. Then, as the hours of daily sunshine increased, most of China's cities would become warmer. Therefore, it is suspected that the reason for the differentiation of correlation studies based on micro-meteorological daily data and COVID-19 epidemiology daily data is the regional heterogeneity limited by the uneven time-varying prevalence of the disease. At least that doubt exists in China's study, where the first wave of the COVID-19 epidemic ended in May 2020 without experiencing year-round climate changes.

Appropriate temperature and humidity conditions provided a suitable external environment for the survival of the SARS-CoV-2 virus and more opportunities to invade the human body for further reproduction. The stability of pathogens in the environment could directly affect their transmission efficiency, among which temperature and humidity were important environmental factors. The SARS-CoV-2 virus was most stable at 4℃, but its stability decreased with an increase in temperature [22]. The virus could survive no more than 1 day at 35–40℃. When the temperature increased to 40℃, the inactivation time of the virus decreased to 6 h. As the temperature increased to 70 °C, the survival time of the virus was reduced to 5 min [23]. However, the isolation time of live viruses at 20℃ was up to 28 days for common surfaces such as glass, stainless steel, paper, and polymer banknotes [24]. At the same time, the humidity verified the sensitivity of the SARS-CoV-2 virus. However, the analysis of meteorological factors differed from virus sensitivity for the population level. For 166 countries, Wu et al. [25] examined the influence of temperature and relative humidity on the daily new cases and new deaths of COVID-19. The results showed that the daily new cases and deaths negatively correlated the temperature and relative humidity, which were stable when different model structures and sensitivity has been used. It suggested that the COVID-19 pandemic might suppress partially with increasing temperature and humidity. Similar results could be found in the article [26], [27]. Regardless, Sera et al. [28] found no evidence that meteorological conditions influenced the early stages of local epidemics. It concluded that population behavior and government intervention were more important transmission drivers by the COVID-19 daily data in 26 countries from January 1, 2020, to May 31, 2020. Most of the selected cities were in Europe and North America at the outbreak's primary stage.

Dynamic models suggested that meteorological variables are unlikely to be a dominant spread risk factor for the early stages of the COVID-19 pandemic, given population's high sensitivity. [29], [30] But, SARS-CoV-2 has been circulating globally for more than two years, with more than 500 million reported cases, not including unreported data from some parts of Africa. With the lifting of in-bound restrictions and social contact restrictions in some countries, non-pharmaceutic interventions are becoming weaker. Studies on weakly correlated factors such as climate factors are worth rethinking. Due to the heterogeneity among existing studies, this study will analyze the correlation between meteorological factors and COVID-19 transmission based on the climate classification. Inspired by the sub-systematic microanalysis of the data set in a limited period or region of some existing studies, this study will quantitatively analyze the spatial-temporal heterogeneous effect of some natural and social factors on the spread of COVID-19, integrate data-driven and model-driven findings, to illustrate the multifactorial risks of the COVID-19 pandemic and its implications for China from mathematical theory to data analysis practice. The findings might advise the epidemic control in the period of a low incidence in China. Unlike most previous studies, this study characterizes the prevalence of COVID-19 in different climate zones to reduce the impact of administrative district divisions on disease data collection.

Methods

In this study, we construct a meta-population epidemic model (Supplementary Fig. 1) that reflects the transmission mechanism of COVID-19 among subpopulations and find out the functional relationship between different influencing factors and reproduction numbers, which might be linear or nonlinear. Then, we estimate the social multifactorial effects during the disease transmission, jointly actual epidemiological data [1,2,4,[31], [32], [33], [34], [35], [36]], demographic data [37], [38], [39], [40], geographical data [38], [39], [40], meteorological data [41], [42], [43], [44], [45], and other measurable sociological data [46], [47], [48], [49] for analysis. At last, this study integrates data-driven and model-driven findings, then subtracts social factors, restoring the transmission without human intervention, and further analyzes the effects of some natural factors.

Meta-population epidemic model

The model includes seven compartments, which are susceptibles (S), pre-symptomatic infections (E), symptomatic infections (I), asymptomatic infections (A), isolated individuals (O), treated cases in hospital (T), and recovered individuals (R) to describe the global transmission of COVID-19. Supplementary Fig. 1 and Supplementary Table 1 show the specific flowchart and parameter definitions. The mathematical model can be shown as

{\begin{matrix} \frac{d S_{i} (t)}{d t} = - β_{i} C_{i} (I_{i} (t) + θ_{i} A_{i} (t) + ϕ_{i} E (t)) \frac{S_{i} (t)}{N_{i} (t)} - q_{S_{i}} S_{i} (t) + \frac{α_{S_{i}} O_{i} (t)}{δ_{i}} + d_{S_{i}} \sum_{j = 1}^{n} L_{i j} S_{j} (t), \\ \frac{d E_{i} (t)}{d t} = β_{i} C_{i} (I_{i} (t) + θ_{i} A_{i} (t) + ϕ_{i} E (t)) \frac{S_{i} (t)}{N_{i} (t)} - \frac{E_{i} (t)}{σ_{i}} - q_{E_{i}} E_{i} (t) + d_{E_{i}} \sum_{j = 1}^{n} L_{i j} E_{j} (t), \\ \frac{d A_{i} (t)}{d t} = \frac{η_{i}}{σ_{i}} E_{i} (t) - \frac{A_{i} (t)}{γ_{A_{i}}} - q_{A_{i}} A_{i} (t) + d_{A_{i}} \sum_{j = 1}^{n} L_{i j} A_{j} (t), \\ \frac{d I_{i} (t)}{d t} = \frac{1 - η_{i}}{σ_{i}} E_{i} (t) - (Δ_{I_{i}} + e_{i} + \frac{1}{γ_{I_{i}}}) I_{i} (t) + d_{I_{i}} \sum_{j = 1}^{n} L_{i j} I_{j} (t), \\ \frac{d O_{i} (t)}{d t} = q_{S_{i}} S_{i} (t) + q_{E_{i}} E_{i} (t) + q_{A_{i}} A_{i} (t) - \frac{O_{i} (t)}{δ_{i}}, \\ \frac{d T_{i} (t)}{d t} = Δ_{I_{i}} I_{i} (t) + \frac{α_{E_{i}} O_{i} (t)}{δ_{i}} - (e_{T_{i}} + \frac{1}{γ_{T_{i}}}) T_{i} (t), \\ \frac{d R_{i} (t)}{d t} = \frac{A_{i} (t)}{γ_{A_{i}}} + \frac{I_{i} (t)}{γ_{I_{i}}} + \frac{T_{i} (t)}{γ_{T_{i}}} + \frac{α_{A_{i}} O_{i} (t)}{δ_{i}} + d_{R_{i}} \sum_{j = 1}^{n} L_{i j} R_{j} (t), \\ N_{i} (t) = (ν_{i} p_{i} + Q_{i} - ν_{i} p_{i} Q_{i}) N_{i} (0) + S_{i} (t) + E_{i} (t) + A_{i} (t) + I_{i} (t) + O_{i} (t) + T_{i} (t) + R_{i} (t), \\ S_{i} (0) = (1 - ν_{i} p_{i}) (1 - Q_{i}) N_{i} (0), i = 1, 2, \dots, n . \end{matrix}

It is assumed that susceptible individuals can only get infected through contact with infections, including direct and indirect contact. However, these contacts do not develop symptoms immediately after infection. They will come into the pre-symptomatic compartment first. The effective isolation of suspected cases is attributed to identifying the pre-symptomatic or asymptomatic infection. Then, the individuals who are suspected to be infected by the virus should be placed in an isolation compartment. In contrast, those diagnosed with COVID-19 are re-placed in the infection compartment until recovery. If necessary, infections requiring hospitalization are placed in the treatment compartment. All recovered cases are finally placed in the recovered compartment. The subscript of variables refers to the specific compartments in different regions. If there is no subscript, the parameter represents the global average level. It should be noted that due to insufficient evidence, secondary infection is not considered in this study.

In this study, the cumulative daily confirmed cases, cumulative daily recovered cases, and cumulative daily death cases in 189 countries or regions (Supplementary Table 2) from January 23, 2020, to September 31, 2021, are selected as the basic dataset [1,2,4,[31], [32], [33], [34], [35], [36]] for calculating the spread of COVID-19. Therefore, i = 1,2, 3, …,189, n = 189, representing 189 sub-populations.

In addition to the parameter definitions shown in Supplementary Table 1, essential parameters related to some influencing factors need to be further explained. Inspired by the models in the works of literature [19], [20], [21], this paper used the commonly linear model to describe the statistical correlation between the probability of infection and meteorological variables. The notation β represents the probability of infection per contact with a symptomatic infectious individual driven by natural factors and its mathematical formula is

β = β (T E M, H U M) = B_{0} + B_{1} * T E M + B_{2} * H U M + ε_{0}, ε_{0} \sim i . i . d . N (0, σ_{ε_{0}}) .

The notation TEM represents the temperature (℃), HUM represents the relative humidity (%), B ₀ represents stable probability among local populations determined by different climate classifications. The parameters, B ₁ and B ₂, are the regression coefficients of temperature and relative humidity. ε₀ represents random disturbance by other environmental factors not influenced by temperature and relative humidity. C = C(ICC) represents the average number of contacts an individual has per day, controlled by interior containment and closure measures (ICC). Q = Q(PIC) represents the efficacy of healthy consciousness on reducing the infection rate, controlled by public information campaign and facial coverings (PIC).

According to the definition of basic reproduction number [50,51] by next-generation matrix, we obtain that

R_{0} = ρ (F V^{- 1}) |_{E^{0}},

where ρ(A) denotes the spectral radius of a matrix A. If J is the Jacobian matrix of infective compartments, then let J = F − V, F be the rate of appearance of new infections in compartment I, V be the rate of transfer of individuals out of compartment I. We call FV ⁻¹ be the next generation matrix and set ρ(FV ⁻¹) at disease-free equilibrium point E ⁰ be the basic reproduction number.

By calculation, we can obtain that

F = (\begin{matrix} A_{11} & \dots & A_{1 n} \\ ⋮ & ⋱ & ⋮ \\ A_{n 1} & \dots & A_{n n} \end{matrix}), V = (\begin{matrix} B_{11} & \dots & 0 \\ 0 & ⋱ & 0 \\ 0 & \dots & B_{n n} \end{matrix}),

where

A_{i i} = (\begin{matrix} β_{i} C_{i} ϕ_{i} & β_{i} C_{i} θ_{i} & β_{i} C_{i} \\ η_{i} / σ_{i} & 0 & 0 \\ (1 - η_{i}) / σ_{i} & 0 & 0 \end{matrix}), A_{i j, j \neq i} = (\begin{matrix} d_{E} L_{i j} & 0 & 0 \\ 0 & d_{A} L_{i j} & 0 \\ 0 & 0 & d_{I} L_{i j} \end{matrix}),

B_{i i} = (\begin{matrix} 1 / σ_{i} + q_{E_{i}} - d_{E} L_{i i} & 0 & 0 \\ 0 & 1 / γ_{A} + q_{A_{i}} - d_{A} L_{i i} & 0 \\ 0 & 0 & Δ_{I} + e_{i} + 1 / γ_{I} - d_{I} L_{i i} \end{matrix}) .

Then we can obtain the sub basic reproduction number in sub-population i,

R_{0}^{i} = \frac{β_{i} C_{i} ϕ_{i} σ_{i}}{(1 - σ_{i} d_{E} L_{i i})} + \frac{β_{i} C_{i} θ_{i} η_{i} γ_{A_{i}}}{(1 - σ_{i} d_{E} L_{i i}) (1 - γ_{A_{i}} d_{A} L_{i i})} + \frac{β_{i} C_{i} γ_{I} (1 - η_{i})}{(1 - σ_{i} d_{E} L_{i i}) (γ_{I} Δ_{I} + γ_{I} e_{i} + 1 - γ_{I} d_{I} L_{i i})},

and sub effective reproduction number in sub-population i,

\begin{matrix} R_{E}^{i} & = & \frac{(1 - ν_{i} p_{i}) (1 - Q_{i}) β_{i} C_{i} ϕ_{i} σ_{i}}{(1 + σ_{i} q_{E_{i}} - σ_{i} d_{E} L_{i i})} + \frac{(1 - ν_{i} p_{i}) (1 - Q_{i}) β_{i} C_{i} θ_{i} η_{i} γ_{A_{i}}}{(1 + σ_{i} q_{E_{i}} - σ_{i} d_{E} L_{i i}) (1 + γ_{A_{i}} q_{A_{i}} - γ_{A_{i}} d_{A} L_{i i})} \\ + \frac{(1 - ν_{i} p_{i}) (1 - Q_{i}) β_{i} C_{i} γ_{I} (1 - η_{i})}{(1 + σ_{i} q_{E_{i}} - σ_{i} d_{E} L_{i i}) (γ_{I} Δ_{I} + γ_{I} e_{i} + 1 - γ_{I} d_{I} L_{i i})} . \end{matrix}

The first line of the formula represents the contribution of pre-symptomatic infections to reproduction number, the second line represents the contribution of asymptomatic infections, and the third line represents the contribution of symptomatic cases. The difference between the basic and effective reproduction numbers lies in the influence of prevention and control measures. $R_{0}^{i}$ indicates the speed of COVID-19 transmission in the absence of human intervention. In comparison, $R_{E}^{i}$ notes the speed of COVID-19 transmission under control measures. It is obvious that $R_{0}^{i} > R_{E}^{i}$ . Furthermore, if $ν_{i} = Q_{i} = q_{E_{i}} = 0$ , then $R_{0}^{i} = R_{E}^{i} .$

Finally, using the definition of the spectral radius, we can obtain the global reproduction numbers

R_{0} \geq max {R_{0}^{i}}, R_{E} \geq max {R_{E}^{i}},

which determines the stability of the disease-free equilibrium point in the meta-population model. The specific proof is omitted here, please refer to References [50], [51], [52], [53].

This result answers a question about the meta-population model. When classifying populations, if sub-populations have different reproduction numbers, the total population's reproduction number is greater than the maximum reproduction number in sub-population. It theoretically answers that even if the average of $R_{0}^{i}$ falls below 1 in some sub-regions, it does not imply the extinction of the disease globally. If the population flow between sub-regions is considered, the threshold value of global disease control is the maximum value of $R_{0}^{i}$ . For a fixed time, the effective reproduction number in all sub-regions of the world should be less than 1 to ensure the extinction of the COVID-19 transmission.

Estimations of ICC, PIC, CTI, RIT, VAC

We use the dataset of non-pharmaceutical interventions collected and assembled from a global panel database of pandemic policies (Oxford COVID-19 Government Response Tracker, OxCGRT) [48]. The ICC (Interior Containment and Closure measures) index consists of interior containment and closure measures, including school closing, workplace closing, canceling public events, restrictions on gathering size, public transport closing, stay-at-home requirements, restrictions on internal movement. The PIC (Public Information Campaign) index consists of public information campaigns and their results in an increase of facial covering. The CTI (Contact Tracing and Isolation) index consists of testing policy and contact tracing. The RIT (Restrictions on International Travel) represents the intensity of restrictions on international travel. Based on the OxCGRT index values, we calculate the OxCGRT index score of ICC, PIC, CTI, RIT by the equation 1 and 2 in Methods of Reference [48]. VAC represents the efficient coverage of COVID-19 vaccine, which is collected from the website of OurWorldInData [33].

Estimations of reproduction numbers

We can obtain the continuity epidemiological dataset, which includes confirmed cases, recovery cases, and deaths at the country level [1,2,4,[31], [32], [33], [34], [35], [36]]. Hence, we include susceptible individuals, infected individuals, and recovered individuals in an endemic SIR model to estimate the actual time-varying reproduction number, which is similar to the time-varying effective reproduction number in the meta-population model above. It should be noted that constant parameters in the endemic SIR model will also be replaced by variables dependent on time and space than the meta-population model.

In order to better preserve and transmit data information, this study uses the discrete dynamical model to estimate parameters. According to a differential equation representing the change over time of infected cases, we can obtain that

I_{i, j + 1} - I_{i, j} = β_{i, j} I_{i, j} S_{i, j} / N_{i, j} - 1 / γ_{i, j} I_{i, j} - d_{i, j} I_{i, j},

where S _i,j, I _i,j, and N _i,j represent the number of susceptibles, infections and total population in sub-region i at time j. R _i,j = 1/γ_i,j I _i,j represents the newly increased number of recovered in sub-region i at time j. D _i,j = d _i,j I _i,j represents the new number of deaths caused by COVID-19 in sub-region i at time j. Then we can obtain

β_{i, j} = (I_{i, j + 1} - I_{i, j} + 1 / γ_{i, j} I_{i, j} + d_{i, j} I_{i, j}) N_{i, j} / (I_{i, j} S_{i, j}) .

Finally, the actual time-varying reproduction number is represented by

R_{A C T}^{i, j} = (I_{i, j + 1} - I_{i, j} + 1 / γ_{i, j} I_{i, j} + d_{i, j} I_{i, j}) N_{i, j} / (I_{i, j} S_{i, j}) / (1 / γ_{i, j} + d_{i, j}) .

This study adopts the time-delay correlation of reported cases and the sum of recovered cases and deaths cases to estimate the reporting delays. It is selected the time delay with the strongest Pearson correlation as the recovery time of the confirmed cases in the sub-region at that month. If the data is missing or abnormal, the global average recovery time delay at that quarter is selected instead. The longest time-delay around the year is defined as the approximate subregion's individual duration of COVID-19.

It can be represented by

r (R p_{i, j - τ_{0}^{i}}, R_{i, j} + D_{i, j}) = max (r (R p_{i, j - τ}, R_{i, j} + D_{i, j})),

where j > 30, 0 < τ < 30,

r (X, Y) = \frac{C o v (X, Y)}{\sqrt{V a r [X] V a r [Y]}} .

Rp_i,j represents the number of reported cases in sub-region j at time i. It should be noted that the delays in reporting recovered individuals and deaths is ignored here. Then we obtain the reporting delay days between infection and confirmation is that $τ_{1}^{i} = \max (τ_{0}^{i}) - τ_{0}^{i}$ . Individual duration days of COVID-19 infection is that $τ_{2}^{i} = \max (τ_{0}^{i})$ . Unfortunately, according to such an algorithm, the estimation value of $τ_{2}^{i}$ may be smaller than the actual value, but we have not found a better way at the country level globally by existing data. And the recovery days from confirmation is $τ_{0}^{i}$ . Finally, we can obtain the actual time-varying reproduction number, which can be represented by

R_{A C T}^{i, j} = (R p_{i, j + 1 + τ_{1}^{i}} - R p_{i, j + τ_{1}^{i}} + 1 / τ_{2}^{i} R p_{i, j + τ_{1}^{i}} + d_{i, j} R p_{i, j + τ_{1}^{i}}) N_{i, j} / (R p_{i, j + τ_{1}^{i}} S_{i, j}) / (1 / τ_{2}^{i} + d_{i, j}) .

This is essentially the same as the algorithm in Reference [35] by a Bayesian latent variable approach, which is reflected that the uniform distribution replaces the prior distribution of each estimation, and the estimation results in this study are also adequate, as shown in Supplementary Fig. 3A. However, the difference of R_t and R_ACT (Fig. 2B) is that this study did not make data smooth in order to retain more data information but used the monthly average reproduction number to reduce the random perturbation of data. At the same time, this algorithm is easier and faster to operate. Therefore, the reproduction number mentioned in this study is generally processed by the mean monthly, representing the spread rate of COVID-19 in subregions in different months.

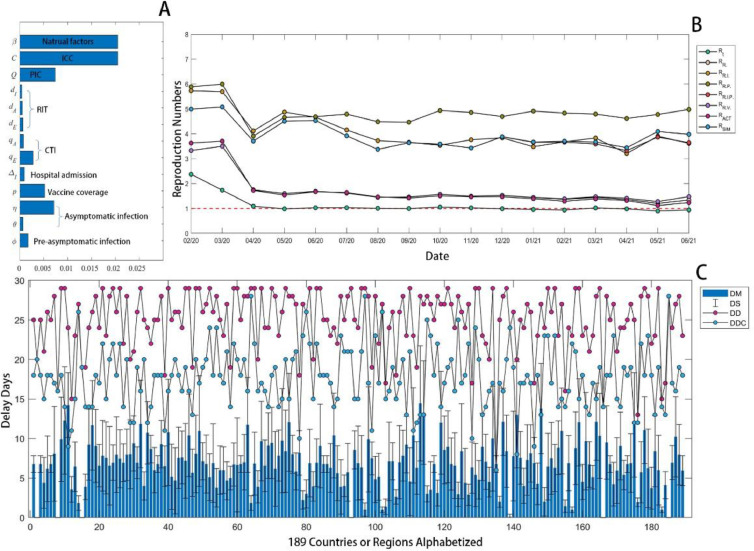
Fig 2 — Some results of parameter estimation

A Global sensitivity analysis of the parameters, which represent the different effects on the change of effective reproduction number.

B Reproduction numbers calculated in different scenarios.

R_t: Monthly average of instantaneous reproduction number calculated by a Bayesian latent variable approach [35];

R_ACT: Monthly average of the instantaneous reproduction number based on global data as shown in Method;

R_R.: Monthly average of the instantaneous reproduction number, subtracting imported cases estimated by international tourism data [46,49];

R_R.I.: Adjustment of R_R. by subtracting the effect of ICC;

R_R.P.: Adjustment of R_R. by subtracting the effect of PIC;

R_R.V.: Monthly average of the instantaneous reproduction number, subtracting imported cases and population vaccinated [33].

R_R.I.P.: Adjustment of R_R. by subtracting the effects of ICC and PIC;

R_SIM: Adjustment of R_R.V. by subtracting the effects of ICC and PIC.

C Some estimated results around 189 countries or regions selected in this study

DM: Average of reporting delay days between infection and confirmation;

DS: Standard deviation of reporting delay days;

DD: Average duration days of COVID-19 infection;

DDC: Average recovery days from confirmation.

Next, we will discuss the estimation of R_R _., R_R.I., R_R.P., R_R.V., R_R.I.P., and R_SIM.

For the estimation of R_R _., which is the instantaneous reproduction number, subtracting imported cases, we collect the data about the number of arrivals and departures in 2019 from the dataset on the world bank website [46], then adjust it by the percentage change in 2020 and 2021 of international tourist arrivals by country of destination [49] over the same period of 2019. Finally, we estimate the imported cases worldwide approximate, which is represented by

I_{i (I m p o r t), j} = (I_{W o r l d, j} - I_{i, j}) A r r i v a l s_{i, j} / (P o p u l a t i o n_{W o r l d, j} - P o p u l a t i o n_{i, j}),

then the imported cases is represented by

I_{i (L o c a l), j} = I_{i, j} - I_{i (I m p o r t), j} .

Furthermore, the reproduction number is adjusted by

R_{R .}^{i, j} = \frac{(R p_{i (L o c a l), j + 1 + τ_{1}^{i}} - R p_{i (L o c a l), j + τ_{1}^{i}} + 1 / τ_{2}^{i} R p_{i (L o c a l), j + τ_{1}^{i}} + d_{i, j} R p_{i (L o c a l), j + τ_{1}^{i}}) N_{i, j}}{(R p_{i (L o c a l), j + τ_{1}^{i}} S_{i, j}) (1 / τ_{2}^{i} + d_{i, j})} .

For the estimation of R_R.V., which is the instantaneous reproduction number, subtracting imported cases and population vaccinated, we replace the susceptibles S _i,j to S _i,j − νV _i,j, where V _i,j represents the number of the vaccinated people [14].

For the estimation of R_R.I., R_R.P., R_R.I.P., and R_SIM, we design a new algorithm. R_R.I. and R_R.P. represent the instantaneous reproduction number, subtracting the effect of ICC or PIC. R_R.I.P. is the instantaneous reproduction number, subtracting the effect of ICC and PIC, but R_SIM is adjusted of R_R.V. by subtracting the effects of ICC and PIC. According to definition of $R_{E}^{i}$ above, we obtain that the parameters C and Q are linearly correlated with the effective reproduction number. Meanwhile, it is supposed that parameter C is controlled by ICC and parameter Q is controlled by PIC. Therefore, our objective is to find the strongest linear correlation coefficient between ICC, PIC, and reproduction numbers. Firstly, according to the time-delay linear correlation analysis, which is similar to the method of estimating the reporting delays, we get the average monthly lag time of ICC and PIC acting on the reproduction number. On this foundation, we search for the maximum regression coefficient with P value less than 0.001 to indicate the intensity of ICC, or PIC, or their combination acting on reproduction numbers. Finally, the value of the reproduction numbers subtracted the effects of ICC, or PIC, or their combination is derived by inverse function. It should be noted that this algorithm is not absolutely strict, so we delete the unreasonable results, such as a reproduction number greater than 10.

Processing of gridded data

The difficulty of integrating epidemiological and meteorological data lies in the difference of statistical caliber. COVID-19 cases are counted at the country level, but global meteorological data is in the grid box. Accordingly, in this study, we will assume that the distribution of reproduction numbers is uniform at the country level. Then we can grid epidemiological data correspondence with meteorological or geographical data to analyze the heterogeneity of climate classification, temperature, humidity, and other factors in the spread of COVID-19.

Köppen-Geiger climate classification in this study is one of the most widely used classification. This classification divides the world into five primary climatic zones and 13 major climate subclassifications. In addition, each climate subclassification may contain two to four secondary subgroups, and 30 climate subclassification are assembled around the world. Compared with the synchronous impact of temperature and humidity on the transmission of COVID-19, the heterogeneous effect of living conditions in different climate classifications on the social behavior of populations is more reflected in the COVID-19 transmission in long time scales. Over an extended period, human beings formed fixed patterns of production and life in relatively stable climate classifications. Therefore, in this study, we select the spatial distribution data of the global Köppen–Geiger climate classification from 1901 to 2000 to study the correlation between different climate classifications and the reproduction number of COVID-19 transmission. At the same time, to weaken the effects of seasonal factors, we analyze the data of the various countries from July 2020 to June 2021.

In addition, this study uses monthly meteorological data of global temperature, humidity, precipitation, wind speed, and common atmospheric pollutants to analyze the impact of some climatic factors on the spread of COVID-19 in the same time scale. The primary meteorological data of this study comes from the ERA5 reanalysis, the latest weather data produced by the ECMWF (European centre for Medium-Range Weather Forecasts), which integrates observational data around the world. We obtain ERA5 data [44] at a spatial resolution of 0.25° (about 28 km at the equator), including 2 m temperature (℃), total precipitation (m), 10 m wind speed (m/s), and relative humidity (%) at 1000 hPa.

We obtain the gridded population data at the website of SEDAC [40], including the population count of the world in 2020 at a spatial resolution of 0.5°, then rasterize the epidemiological data depending on the positive population in the gridded box, mm × nn (1440 × 720), at the country level. mm represents longitude coordinates, nn represents latitude coordinates. Raster data of reproduction number R_SIM is represented by

R_{S I M} (m m, n n) = R_{S I M}^{i} (m m, n n) |_{P o p u l a t i o n (m m, n n)} > 0,

where R_SIM(mm,nn) represents the reproduction number at the gridded box, mm × nn; $R_{S I M}^{i} (m m, n n)$ represents the reproduction number of the country i at the gridded box, mm × nn; Population(mm, nn) represents the population count at the gridded box, mm × nn.

Furthermore, we can get the same spatial resolution of the gridded reproduction numbers, the climate grid data, and the meteorological grid data by scaling up. The results of Fig. 4-5, Supplementary Fig. 4–8 can be obtained by comparing these data sets.

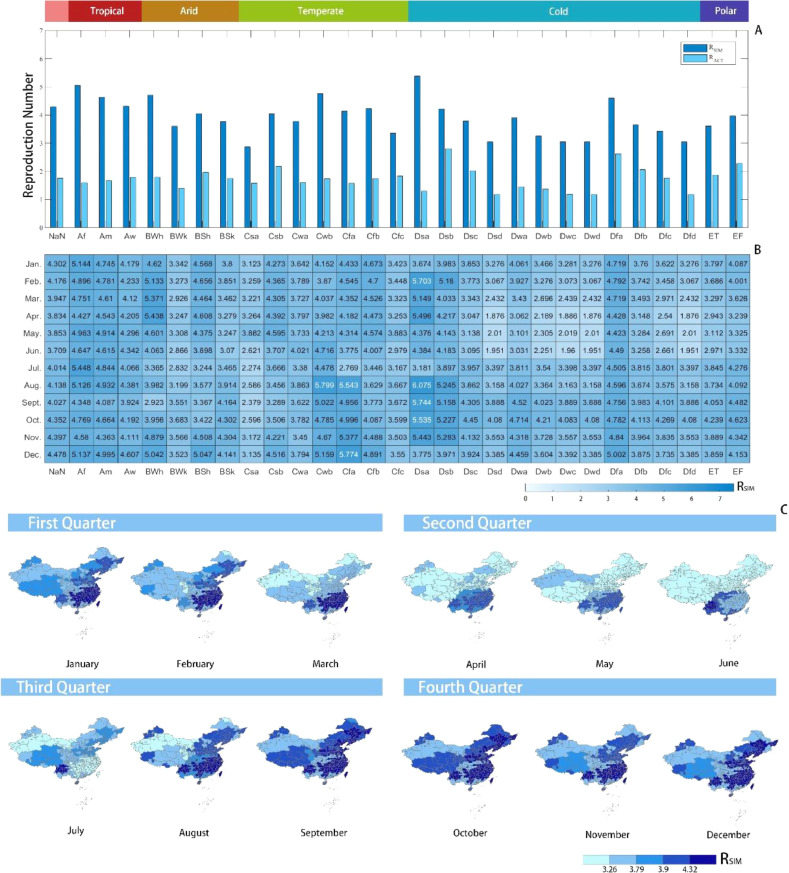
Fig 4 — Heterogeneity of Köppen–Geiger climate classifications

A Distribution of *R_SIM* and *R_ACT* based on Köppen–Geiger climate classifications

B Monthly distribution of *R_SIM* based on Köppen–Geiger climate classifications

C China city-level map of *R_SIM* based on Köppen–Geiger climate classifications in different months.

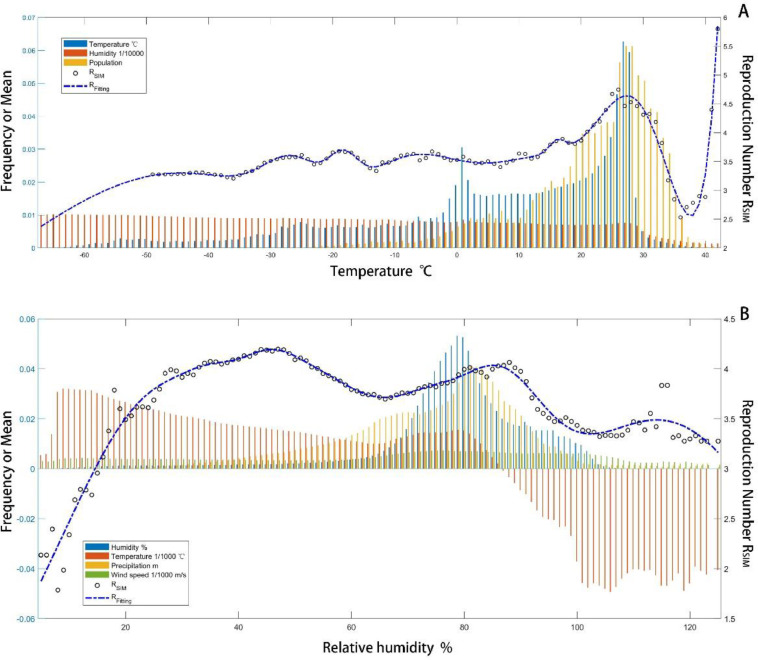
Fig 5 — Heterogeneity of temperature and relative humidity

A Distribution of *R_SIM* based on temperature. Frequency of temperature, mean of 1/1000 relative humidity, mean of population density, and mean of *R_SIM* spacing between 1℃ of temperature.

B Distribution of *R_SIM* based on relative humidity. Frequency of relative humidity, mean of 1/1000 temperature, mean of precipitation, mean of 1/1000 wind speed, and mean of *R_SIM* spacing between 1% of relative humidity.

Results

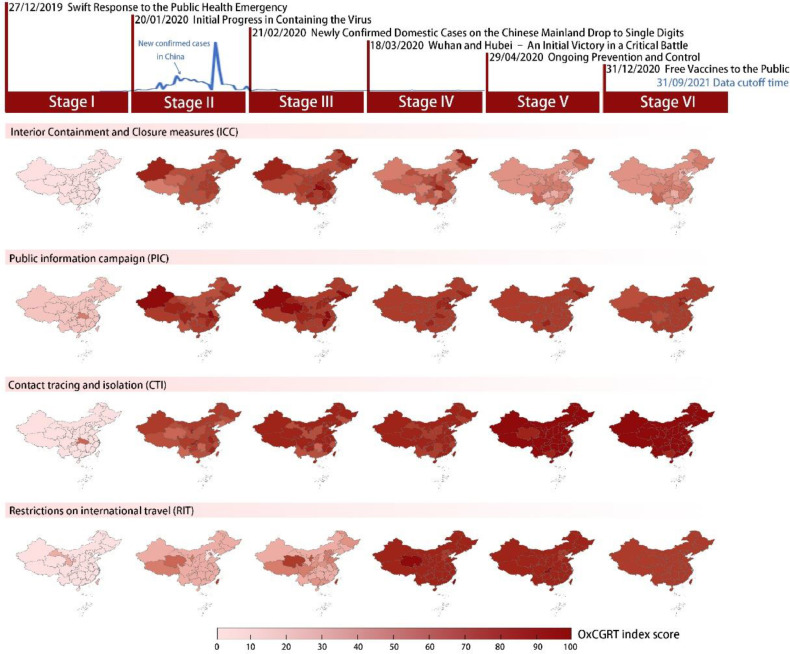
Intensity of NPIs in different control stages in China

China's response to COVID-19 can be divided into six stages (Fig. 1 ). In the first stage, we knew little about COVID-19, and only weaker PIC and CTI measures were adopted in Hubei province. Since January 20, 2020, the number of newly confirmed cases has increased rapidly, then control efforts of different provinces in China were strengthened simultaneously. At the national level, the intensity of ICC, CTI, and PIC increased to 71.79, 69.27, and 78.51, respectively, which ranged from 0 to 100 (100 represents implementing the strictest measures) as OxCGRT index score [47,48]. The second stage witnessed the sharpest growth in confirmed cases. The monthly increase in the number of confirmed cases was about 53,000, more than half of all cases in China. After the third stage, the epidemic was almost contained in China, with ICC intensity reaching the highest score of 82.55. On April 26, 2020, all hospitalized cases of COVID-19 in Wuhan were cleared, and the mainland of China entered the fifth stage to prevent the prevalence. Since then, CTI has become the most critical control measure, and the high intensity of ICC has gradually decreased. It is also evident from Fig. 1 that the intensity of NPIs in China has not weakened due to the free vaccination strategies.

Assessments of NPIs and vaccination on global reproduction number

Based on global data, we find that between February 2020 and June 2021, the incorporated efforts of ICC and PIC reduced the reproduction number of COVID-19 by about 57.42% (Fig. 2 B) and the number of confirmed cases by approximately 78.52% worldwide. In this study, the reproduction number is the average number of secondary cases generated by a symptomatic infectious individual over his/her entire course of the infectious period in a fully susceptible population in different scenarios defined as Fig. 2B. The bigger the reproduction number is, the faster the COVID-19 spreads. In general, it means the disease can be controlled when the reproduction number is less than 1. RIT changed the reproduction number from –7.77% to 9.03% (Fig. 2B), limited by the balance between domestic and foreign prevalence. The functional effect of CTI is shown in the figure by simulation (Supplementary Fig. 2). COVID-19 vaccination controls the reproduction number increased from 0.5% to 11.2% from January to June 2021. However, this result may be low since we used the lowest vaccine effectiveness 67% to estimate [33].

Reporting and NPIs delays

By time-delay correlation analysis, the average individual duration of COVID-19 infection globally is about 25 days (Fig. 2C). It takes 17.57 days on average for confirmed cases to recover. The average reporting delay is about 6.74 days (Fig. 2C). Using a similar algorithm, we estimate the response delay of NPIs is 14.98 days behind the variation in R_ACT, while the reaction of NPI adjustments on the change in R_ACT takes about 16.04 days on average (Supplementary Fig. 3B). Significantly, these two delays do not show a strict positive correlation. This study also calculates rigorously the time-delay correlation between NPIs response and incidence or cases in each country and globality, as well as global R_ACT. However, the results are imperfect for weaker time-delay correlation.

Heterogeneity of Köppen–Geiger climate classifications

In terms of natural factors, this study mainly considered the impact of climate factors. The difference between this study and previous studies [12,13] is reflected in excluding social factors. The reproduction number R_SIM without NPIs and VAC is derived reverse based on the above results. After excluding ICC, PIC, RIT, and VAC, the reproduction number R_SIM of COVID-19 in different sub-regions and months is obtained from July 2020 to June 2021. As shown in Fig. 4, the average annual R_SIM in Dsa is higher than that of other climate classifications. For the Northern Hemisphere (Supplementary Fig. 4), Dsa has more potential to transmit SARS-CoV-2, either. However, this sub-climate does not exist in the Southern Hemisphere.

Rainforest sub-classification with P_dry ≥ 60 mm have a higher R_SIM in the tropical climate. In the arid climate, a hot sub-climate with MAT ≥ 18℃ is more potential to transmit SARS-CoV-2. The warm summer sub-climate is more likely to spread the disease in the temperate climate. However, the risk decreases by lower summer temperate in the cold climate. We estimated the monthly R_SIM for the seasonal heterogeneity of different Köppen–Geiger climate classifications. The findings in Fig. 4B, Supplementary Fig. 5 can provide a basis of modifying control measures in different seasons.

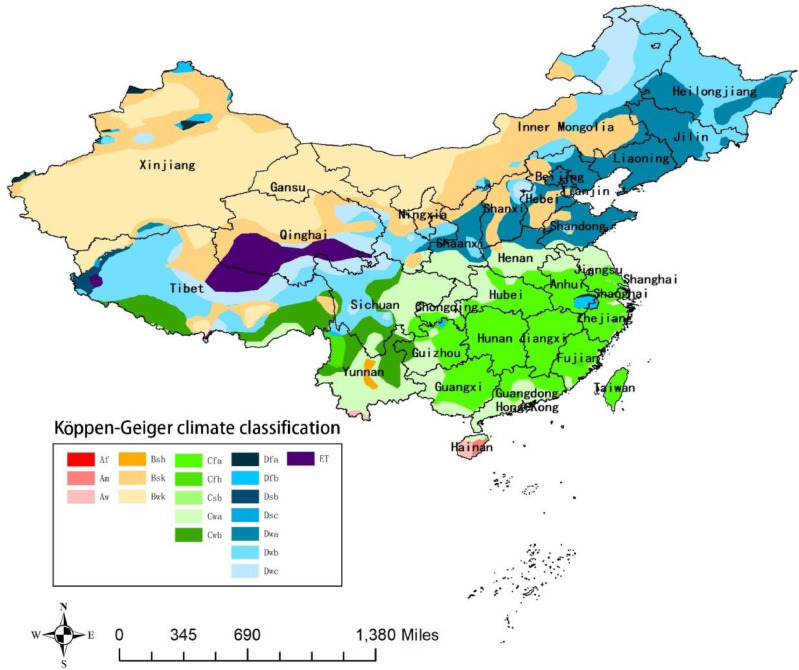
China has a vast territory, and it covers 19 Köppen–Geiger climate sub-classifications in it (Fig. 3 ). We obtain the R_SIM distribution maps in different months in China at the city level (Fig. 4 C) which shows the maximum of R_SIM is 5.799 (Cwb, August), and the minimum of R_SIM is 1.886 (Dwc, April), with a threefold distinction.

Heterogeneity of temperature, humidity, and other meteorological factors

As shown in Fig. 5 , the optimal temperature for COVID-19 transmission among the population is 27℃–28℃, consistent with the optimal living temperature of human beings, and the population density is the largest in this temperature range. R_SIM increases sharply at the extreme temperature of 42℃–43℃, and slightly increasing between –30℃ and −10℃, which may be related to the increased transmission with cold chain logistics. For humidity part, the relative humidity of 40%–50% and 80%–90% are the most suitable conditions for COVID-19 spread. The functional relationship between relative humidity and R_SIM value is not strictly monotonous, which may be caused by the interference of temperature, precipitation, wind speed, and other meteorological factors.

The sensitivity of temperature and humidity to R_SIM is not only for showing evident regional heterogeneity (Supplementary Fig. 6–8), but also for depicting the heterogeneity with different climate classifications. We also divide the results into winter and summer to reflect the seasonal heterogeneity more detailly. For example, Af and Am subclassifications had a larger reproduction number in tropical climate zones (Supplementary Fig. 6). However, for 30–40% relative humidity, the reproduction number in Am region was significantly higher than that in other climate regions. It implies that the heterogeneous impact of climate on the spread of COVID-19 may need to be delineated more carefully in order to adjust the intensity of controls more appropriately.

Discussion

This study involves the multifactorial analysis of the COVID-19 global pandemic. We incorporate more actual data applications into parameter estimation to reduce the rigid influence of assumptions before model construction. This study analyzes the impact of control measures, such as ICC, PIC, CTI, RIT, and VAC, on the reproduction number of COVID-19 transmission across 189 countries, including China. Furthermore, the global spatial-temporal heterogeneous effect of some natural factors on the spread of COVID-19 based on meteorological data in the absence of the aforementioned social factors is calculated by reverse derivation, which is more pronounced and reasonable than the study without excluding social factors. The variables associated with the incidence of COVID-19 and time-varying reproduction numbers revealed the risks in different climatic regions globally. As the host of SARS-CoV-2, the human lifestyle ultimately affects the epidemic's prevalence within a fixed pattern of life and production limited by their survival climate circumstances. In terms of natural factors, the difference between this study and previous studies is reflected in excluding social factors and more detailed Köppen–Geiger climate sub-classifications. The Köppen–Geiger climate classification used in this study is one of the most widely used and influential climate classification methods worldwide [41,42], dividing the global map by temperature, precipitation, and seasonal variation and taking monthly average temperature and precipitation as classification indexes. In Reference [54], global COVID-19 data were used to examine the dynamical variations across the five climate regions: tropical, arid, temperate, and cold. A new approach named Yi Hua Jie Mu is proposed to find that the temperate and cold climate regions have higher infection rates than the tropical and arid climate regions, which indicates that climate may modulate the transmission of COVID-19. This paper further analyzed the correlation between different meteorological factors, including temperature and humidity, depending on various climate sub-classifications. It is found that Dsa is the sub-classification of Köppen–Geiger climate in which COVID-19 is spreading fastest, which indicates that Dsa has more potential to transmit SARS-CoV-2 either. However, this sub-climate does not exist in the Southern Hemisphere. It may partly explain the more severe state of early COVID-19 in the Northern hemisphere.

According to this study, we could only face a genuinely safe environment if the global disease extinction ensued, and this aspiration required concerted, sustained, and synchronized efforts by all countries around the world. By the analysis results, we found that the intensity of NPIs response depends more on domestic COVID-19 reproduction numbers but not on the overall of the world, which is contradictory with the analysis above that the global reproduction number depended on the maximum of sub-region reproduction numbers. It indicates that currently global control may be challenging to achieve through non-global collaboration. The global sensitivity analysis of parameters reveals that natural factors and ICC may primarily affect COVID-19 transmission, followed by PIC and vaccine coverage (Fig. 2A). Nevertheless, these results are theoretical and subject to the choice of parameter values (Supplementary Fig. 2 and Supplementary Table 1). The greater significance of these theoretical results is to answer the functional relationship between control measures and reproduction numbers. We have theoretically obtained that the threshold value of global control is the maximum value of $R_{0}^{i}$ in the sub-region i, that is $R_{0} \geq max (R_{0}^{i})$ . If international travel is considered, all of the sub-region effective reproduction numbers ( $R_{E}^{i}$ ) should be less than 1 to ensure the extinction of the pandemic (Method). Combining the numerical simulations (Supplementary Fig. 2), we find that the quantitative relationship between ICC, PIC, and $R_{E}^{i}$ is linear, beneficial to our parameter estimations. However, the relationship between RIT, CTI, and $R_{E}^{i}$ is nonlinear.

Within the same climate sub-classification, the spread of COVID-19 will also change with the season, temperature, and humidity. The results in Fig. 4C illustrate the distribution of the basic reproduction number of COVID-19 in different months in China. It is evident that the disease spreads faster in winter than in summer. This conclusion is consistent with the laboratory results of SARS-CoV-2, which is the pathogen of COVID-19. Some laboratory results show that the virus was most stable at 4℃, but its stability decreased with an increase in temperature [22]. The virus could survive no more than one day at 35–40℃ [23]. As shown in Supplementary Fig. 6–8, sub-classifications show evident regional heterogeneity for the sensibility of temperature and humidity. We obtain that Cwb, Cfa, and Cfb in southeast China are more potential to spread the disease. In August, the RSIM of Cwb climate subclassification is about three times that of Dwc in April, which implies that the intensity of control efforts in different sub-regions may differ three times under the same imported risk. Taking Cfa as an example, it is susceptible to temperature (Supplementary Fig. 7). The higher the temperature is, the larger the reproduction number of COVID-19 increases. However, for Cwb and Cfb, humidity is more sensitive than the temperature for the COVID-19 transmission. We can obtain the heterogeneous association of meteorological conditions from the disease outbreaks. Based on existing climate zoning and the weather forecast, combining with monitoring abnormal weather on the sensitivity of the reproduction number can also offer some suggestions for the prevention and control protocol adjustments. Finally, formulate flexible control measures reasonably and effectively based on different sensitivity temperature, humidity and seasonality.

The distribution of different climatic sub-classifications will determine the transmission of COVID-19 and further affect the formulation of prevention and control measures. Although China has a vast territory, it does not cover all the Köppen-Geiger climate classifications, as shown in Fig. 3. There is almost no tropical climate distribution in the mainland of China. No tropical rainforest climate exists in China, and only a few tropical sparse forest grassland climates and tropical monsoon climates are distributed in the south of Hainan. The dry environment in mainland China belongs to the cold sub-classification. The warm belt is widely distributed south of the Qinling Mountains and Huaihe River and most of the east of the Qinghai-Tibet Plateau. The cold zone is mainly distributed north of Qinling Mountains and the Huaihe River. The highland tundra climate is widely distributed in the Qinghai-Tibet Plateau. Bsk, Bwk, Cwa, Cwb, Cfa, Dwa, Dwb, Dwc, and ETG were mainly included in China, while Am, Aw, Csa, Cfb, Dfa, Dfb, Dfc, and EFG were less distributed. This study showed that Bsk and Bwk, widely distributed in Northwest China, are less sensitive to the spread of COVDI-19 than Cfa in Southeast China. It implies that the intensity of control measures in Northwest China could be lower than that in southeast coastal areas. Depending on global meteorological data, we find that the reproduction number of COVID-19 transmission varied wildly among climate classifications, which is of great significance for the flexible adjustment of China's prevention and control protocols. However, this speculation is based on the linear effect of control measures on the reproduction number. A marginal effect of control measures may exist in reality, but this study did not draw specific conclusions regarding numerical value.

Rapid and sustained implementation of NPIs is the practical measure for China to achieve the initial victory. On January 19, 2020, the epidemiological experts confirmed that the coronavirus had been transmitted in Wuhan from person to person. At 10 o'clock on January 23, the airport and railway stations were temporarily closed only four days later. The data analysis in our results shows that the time delay of NPIs response is about 14.98 days on average worldwide, nearly 11 days later than China's control speed. Therefore, the timeliness of the control response in the outbreak stage is crucial. The sustainability, diversification, and rhythmicity of prevention and control measures are essential for China to maintain the low prevalence of COVID-19 in the ongoing epidemic stage. China has developed corresponding prevention and control measures in different periods, sub-regions, and scenarios. China adopts more stringent ICC control measures in the strict control stage, however more implements of PIC and CTI strategies in the stable control stage. RIT measures are stringent while the global epidemic is not stable. Importantly, the NPIs are synchronized across the country at the province level. In China, traveling tracks of the confirmed positive cases will be used to identify individuals with different degrees of close contact. Afterward, they will be subjected to polymerase chain reaction (PCR) testing or isolation in a limited time at different levels. The containment, control, and prevention zones shall be regulated differently for the region where the positive cases live or work. These measures have achieved remarkable results in the current stage of ongoing epidemic control in China [5], [6], [7], [8], [9], but no clear quantitative plan existed to support the length of the tracking chain for closing contacts and the demarcation of risk areas to identify potential cases. Accordingly, some adjustments based on natural factors’ effect may be practical in shortening the close contact tracking chain and reducing the isolation risk areas with small R_SIM, then reducing control efforts, and achieving more economic benefits.

This study answers some questions about the global epidemic control of COVID-19, but it still has many deficiencies. We inevitably set some assumptions in our research. For example, people in different countries are evenly mixed, without considering the effects of population heterogeneity, such as age. At the same time, we also need to make some assumptions of uniformity to complete the analysis due to the large scale of data selected and the large gap between interfaces of multi-source data. As our understanding of the novel coronavirus increases, many parameters in this study may be changed, which requires exploring better mathematical methods in our future study. No model can perfectly restore the real world, and diversity of mathematical methods might contribute to specific results. The meta-population model adopted in this study also has many defects. It assumed that the number of secondary infections was evenly distributed in the disease course for patients in the infection stage. The daily effective reproduction number in different regions was calculated using the daily reported and recovered case data, and then the monthly average of the obtained results was calculated to reduce the influence of random interference factors. According to the heterogeneity of the obtained monthly mean effective reproduction number in different Köppen–Geiger climate zones, the results of this study were more reflected in the macro impact of meteorological classification on the spread of COVID-19. In addition, many parameters were considered in the model, some of which were estimated, and others were from literature. These parameters would change with the development of COVID-19, which also required further tracking calculations to improve. Therefore, a more detailed model and more realistic algorithm design are necessary for our further study and discussion.

Author contributions

F.C. designed the study, built the model, collected data, finalized the analysis, interpreted the findings, and wrote the manuscript. S.C., M.M.J., and W.Y. commented on and revised drafts of the manuscript. M.Y.J., Z.L., L.M., Y.S., T.Z., L.F. revised drafts of the manuscript. All authors read and approved the final manuscript. The corresponding authors had full access to all of the data in the study and had final responsibility for the decision to submit for publication.

Declaration of Competing Interests

The authors declare no competing interests.

Acknowledgements

This study was supported by funding from Chinese Academy of Medical Sciences (CAMS) Innovation Fund for Medical Sciences (2020-I2M-1–001). The funder of the study had no role in study design, data collection, data analysis, data interpretation, or writing of the report.

Footnotes

Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.apm.2022.09.008.

Appendix. Supplementary materials

mmc1.docx^{(2.4MB, docx)}

Data Availability

Data will be made available on request.

References

1.World Health Organization, WHO Coronavirus (COVID-19) Dashboard, 31 June 2022. https://covid19.who.int/
2.Chinese Center for Disease Control. Distribution of COVID-19, 31 October 2021. http://2019ncov.chinacdc.cn/2019-nCoV/
3.The State Council Information Office of the People's Republic of China, Fighting COVID-19: China in Action, June 2020. http://www.scio.gov.cn/zfbps/ndhf/42312/Document/1682142/1682142.htm
4.National Health Commission of the People's Republic of China, Progress in COVID-19 prevention and control, 31 October 2021. http://www.nhc.gov.cn/ [DOI] [PMC free article] [PubMed]
5.Chen Q., Rodewald L., Lai S., Gao G.F. Rapid and sustained containment of covid-19 is achievable and worthwhile: implications for pandemic response. BMJ. 2021;375 doi: 10.1136/BMJ-2021-066169. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Tang J., Li L. Importance of public health tools in emerging infectious diseases. BMJ. 2021;375:n2374. doi: 10.1136/bmj.n2374. [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Zhang Y., Quigley A., Wang Q., MacIntyre C.R. Non-pharmaceutical interventions during the roll out of covid-19 vaccines. BMJ. 2021;375:n2314. doi: 10.1136/bmj.n2314. [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Zhou Y., Jiang H., Wang Q., Yang M., Chen Y., Jiang Q., et al. Use of contact tracing, isolation, and mass testing to control transmission of covid-19 in China. BMJ. 2021;375:n2330. doi: 10.1136/bmj.n2330. [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Tu H., Hu K., Zhang M., Zhuang Y., Song T. Effectiveness of 14 day quarantine strategy: chinese experience of prevention and control. BMJ. 2021;375 doi: 10.1136/BMJ-2021-066121. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.An Z., Wang F., Pan A., Yin Z., Rodewald L., Feng Z., et al. Vaccination strategy and challenges for consolidating successful containment of covid-19 with population immunity in China. BMJ. 2021;375 doi: 10.1136/bmj-2021-066125. [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Gao W., Lv J., Pang Y., Li L. Role of asymptomatic and pre-symptomatic infections in covid-19 pandemic. BMJ. 2021;375:n2342. doi: 10.1136/bmj.n2342. [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Mecenas P., Bastos R., Vallinoto A.C.R., et al. Effects of temperature and humidity on the spread of COVID-19: a systematic review. PLoS ONE. 2021;15(9) doi: 10.1371/journal.pone.0238339. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Briz-Redón I., Serrano-Aroca A. The effect of climate on the spread of the COVID-19 pandemic: a review of findings, and statistical and modelling techniques. Prog. Phys. Geogr. 2020;44(18) [Google Scholar]
14.Kerr G.H., Badr H.S., Gardner L M L.M., et al. Associations between meteorology and COVID-19 in early studies: inconsistencies, uncertainties, and recommendations. One. Health. 2021;12 doi: 10.1016/j.onehlt.2021.100225. [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Zheng H.L., Guo Z.L., Wang M.L., Yang C., An S.Y., Wu W. Effects of climate variables on the transmission of COVID-19: a systematic review of 62 ecological studies. Environ. Sci. Pollut. Res. 2021;28:54299–54316. doi: 10.1007/s11356-021-15929-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Yan X., Wang Z., Wang X., Zhang X., Wang L., Lu Z., et al. Association between human coronaviruses' epidemic and environmental factors on a global scale. Environ. Sci. Pollut. Res. 2022;29:14333–14347. doi: 10.1007/s11356-021-16500-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Babin S. Use of weather variables in SARS-CoV-2 transmission studies. Int. J. Infect. Dis. 2020;100:333–336. doi: 10.1016/j.ijid.2020.09.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Zaitchik B.F., Sweijd N., Shumake-Guillemot J., et al. A framework for research linking weather, climate and COVID-19. Nat. Commun. 2020;11:5730. doi: 10.1038/s41467-020-19546-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Yao Y., Pan J.H., Liu Z.X. No association of COVID-19 transmission with temperature or UV radiation in Chinese cities. Eur. Respir. J. 2020;55(5) doi: 10.1183/13993003.00517-2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Zhu Y., Xie J. Association between ambient temperature and COVID-19 infection in 122 cities from China. Sci. Total Environ. 2020;724 doi: 10.1016/j.scitotenv.2020.138201. [DOI] [PMC free article] [PubMed] [Google Scholar]
21.Wei J., Liu Y., Zhu Y., et al. Impacts of transportation and meteorological factors on the transmission of COVID-19. Int. J. Hyg. Envir. Heal. 2020;230 doi: 10.1016/j.ijheh.2020.113610. [DOI] [PMC free article] [PubMed] [Google Scholar]
22.Lv Q., Liu M., Qi F., et al. Sensitivity of SARS-CoV-2 to different temperatures. Animal Models Experiment. Med. 2020;3(4):3. doi: 10.1002/ame2.12141. [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Reza D., Mohammad A. Stability of SARS-CoV-2 in different environmental conditions. Lancet. Microbe. 2020;1:e145. doi: 10.1016/S2666-5247(20)30093-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Riddell S., Goldie S., Hill A., et al. The effect of temperature on persistence of SARS-CoV-2 on common surfaces. Virol. J. 2020;17(1):145. doi: 10.1186/s12985-020-01418-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Wu Y., Jing W.Z., Liu J., et al. Effects of temperature and humidity on the daily new cases and new deaths of COVID-19 in 166 countries. Sci. Total. Environ. 2020;792 doi: 10.1016/j.scitotenv.2020.139051. [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Sobral M., Duarte G.B., da Penha Sobral A., et al. Association between climate variables and global transmission oF SARS-CoV-2. Sci. Total. Environ. 2020;729 doi: 10.1016/j.scitotenv.2020.138997. [DOI] [PMC free article] [PubMed] [Google Scholar]
27.Guo C., Bo Y., Lin C., et al. Meteorological factors and COVID-19 incidence in 190 countries: an observational study. Sci. Total. Environ. 2021;757 doi: 10.1016/j.scitotenv.2020.143783. [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Sera F., Armstrong B., Abbott S., et al. A cross-sectional analysis of meteorological factors and SARS-CoV-2 transmission in 409 cities across 26 countries. Nat. Commun. 2021;12:5968. doi: 10.1038/s41467-021-25914-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Carlson C.J., Gomez A.C.R., Bansal S., et al. Misconceptions about weather and seasonality must not misguide COVID-19 response. Nat. Commun. 2021;11:4312. doi: 10.1038/s41467-020-18150-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Baker R.E., Yang W., Vecchi G.A., et al. Susceptible supply limits the role of climate in the early SARS-CoV-2 pandemic. Science. 2020;369:315–319. doi: 10.1126/science.abc2535. [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Dong E., Du H., Gardner L. An interactive web-based dashboard to track COVID-19 in real time. Lancet. Inf. Dis. 2020;20(5):533–534. doi: 10.1016/S1473-3099(20)30120-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
32.Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU), COVID-19 Dashboard, 31 September 2021. https://gisanddata.maps.arcgis.com/apps/dashboards/bda7594740fd40299423467b48e9ecf6
33.H. Ritchie, E. Mathieu, L. Rodés-Guirao, C. Appel, C. Giattino, E. Ortiz-Ospina, et al. Coronavirus Pandemic (COVID-19). Published online at OurWorldInData.org. https://ourworldindata.org/coronavirus
34.European Centre for Disease Prevention and Control, COVID-19. https://www.ecdc.europa.eu/en/covid-19
35.S. Abbott, J. Hellewell, R.N. Thompson, K. Sherratt, H.P. Gibbs, N.I. Bosse, et al. Temporal variation in transmission during the COVID-19 outbreak. https://epiforecasts.io/covid/
36.GISAID, covSPECTRUM, https://cov-spectrum.org/
37.National Bureau of Statistics of China . China Statistics Press; 2021. China Statistical Yearbook. [Google Scholar]
38.WorldPop, Open Spatial Demographic Data and Research. https://www.worldpop.org/
39.Population Division of the Department of Economic and Social Affairs of the United Nations Secretariat, 2019 Revision of World Population Prospects, https://population.un.org/wpp/
40.CIESIN at Columbia University, Socioeconomic Data and Application Center (SEDAC). https://sedac.ciesin.columbia.edu/
41.Kottek M., Grieser J., Beck C., Rudolf B., Rubel F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006;15:259–263. [Google Scholar]
42.Peel M.C., Finlayson B.L., McMahon T.A. Updated world map of the Koppen-Geiger climate classification. Hydrol. Earth. Syst. Sci. 2007;11:1633–1644. [Google Scholar]
43.National Earth System Science Data Center, National Science & Technology Infrastructure of China. http://www.geodata.cn
44.ECMWF, Atmosphere Data Store, https://ads.atmosphere.copernicus.eu/
45.ECMWF, Climate Data Store, https://cds.climate.copernicus.eu/
46.IBRD•IDA, World Bank Open Data, https://data.worldbank.org.cn/
47.Zhang Y., Hale T., Wood A., Philips T., Petherick A., Folco M.D., et al. Chinese provincial government responses to COVID-19. Blavatnik School of Government Working Paper. 2021 www.bsg.ox.ac.uk/covidtracker Available: [Google Scholar]
48.Hale T., Angrist N., Goldszmidt R., Kira B., Petherick A., Phillips T., et al. A global panel database of pandemic policies (Oxford COVID-19 Government Response Tracker) Nat. Hum. Behav. 2021;5:529–537. doi: 10.1038/s41562-021-01079-8. [DOI] [PubMed] [Google Scholar]
49.UNWTO, UNWTO tourism data dashboard. https://www.unwto.org/unwto-tourism-dashboard
50.Driessche P.V., Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002;180:29–48. doi: 10.1016/s0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
51.Diekmann O., Heesterbeek J.A.P., Metz J.A. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990;28:365–382. doi: 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]
52.Hsieh Y., Driessche P.V., Wang L. Impact of travel between patches forspatial spread of disease. Bull. Math. Biol. 2007;69:1355–1375. doi: 10.1007/s11538-006-9169-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
53.Gao D. Travel Frequency and Infectious Diseases. SIAM. J. Appl. Math. 2019;79:1581–1606. [Google Scholar]
54.Wang X., Yin G., Z. Hu Z., et al. Dynamical Variations of the Global COVID-19 Pandemic Based on a SEICR Disease Model: a New Approach of Yi Hua Jie Mu. Geohealth. 2021;5(8) doi: 10.1029/2021GH000455. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

mmc1.docx^{(2.4MB, docx)}

Data Availability Statement

Data will be made available on request.

[bib0001] 1.World Health Organization, WHO Coronavirus (COVID-19) Dashboard, 31 June 2022. https://covid19.who.int/

[bib0002] 2.Chinese Center for Disease Control. Distribution of COVID-19, 31 October 2021. http://2019ncov.chinacdc.cn/2019-nCoV/

[bib0003] 3.The State Council Information Office of the People's Republic of China, Fighting COVID-19: China in Action, June 2020. http://www.scio.gov.cn/zfbps/ndhf/42312/Document/1682142/1682142.htm

[bib0004] 4.National Health Commission of the People's Republic of China, Progress in COVID-19 prevention and control, 31 October 2021. http://www.nhc.gov.cn/ [DOI] [PMC free article] [PubMed]

[bib0005] 5.Chen Q., Rodewald L., Lai S., Gao G.F. Rapid and sustained containment of covid-19 is achievable and worthwhile: implications for pandemic response. BMJ. 2021;375 doi: 10.1136/BMJ-2021-066169. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0006] 6.Tang J., Li L. Importance of public health tools in emerging infectious diseases. BMJ. 2021;375:n2374. doi: 10.1136/bmj.n2374. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0007] 7.Zhang Y., Quigley A., Wang Q., MacIntyre C.R. Non-pharmaceutical interventions during the roll out of covid-19 vaccines. BMJ. 2021;375:n2314. doi: 10.1136/bmj.n2314. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0008] 8.Zhou Y., Jiang H., Wang Q., Yang M., Chen Y., Jiang Q., et al. Use of contact tracing, isolation, and mass testing to control transmission of covid-19 in China. BMJ. 2021;375:n2330. doi: 10.1136/bmj.n2330. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0009] 9.Tu H., Hu K., Zhang M., Zhuang Y., Song T. Effectiveness of 14 day quarantine strategy: chinese experience of prevention and control. BMJ. 2021;375 doi: 10.1136/BMJ-2021-066121. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0010] 10.An Z., Wang F., Pan A., Yin Z., Rodewald L., Feng Z., et al. Vaccination strategy and challenges for consolidating successful containment of covid-19 with population immunity in China. BMJ. 2021;375 doi: 10.1136/bmj-2021-066125. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0011] 11.Gao W., Lv J., Pang Y., Li L. Role of asymptomatic and pre-symptomatic infections in covid-19 pandemic. BMJ. 2021;375:n2342. doi: 10.1136/bmj.n2342. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0012] 12.Mecenas P., Bastos R., Vallinoto A.C.R., et al. Effects of temperature and humidity on the spread of COVID-19: a systematic review. PLoS ONE. 2021;15(9) doi: 10.1371/journal.pone.0238339. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0013] 13.Briz-Redón I., Serrano-Aroca A. The effect of climate on the spread of the COVID-19 pandemic: a review of findings, and statistical and modelling techniques. Prog. Phys. Geogr. 2020;44(18) [Google Scholar]

[bib0014] 14.Kerr G.H., Badr H.S., Gardner L M L.M., et al. Associations between meteorology and COVID-19 in early studies: inconsistencies, uncertainties, and recommendations. One. Health. 2021;12 doi: 10.1016/j.onehlt.2021.100225. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0015] 15.Zheng H.L., Guo Z.L., Wang M.L., Yang C., An S.Y., Wu W. Effects of climate variables on the transmission of COVID-19: a systematic review of 62 ecological studies. Environ. Sci. Pollut. Res. 2021;28:54299–54316. doi: 10.1007/s11356-021-15929-5. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0016] 16.Yan X., Wang Z., Wang X., Zhang X., Wang L., Lu Z., et al. Association between human coronaviruses' epidemic and environmental factors on a global scale. Environ. Sci. Pollut. Res. 2022;29:14333–14347. doi: 10.1007/s11356-021-16500-y. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0017] 17.Babin S. Use of weather variables in SARS-CoV-2 transmission studies. Int. J. Infect. Dis. 2020;100:333–336. doi: 10.1016/j.ijid.2020.09.032. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0018] 18.Zaitchik B.F., Sweijd N., Shumake-Guillemot J., et al. A framework for research linking weather, climate and COVID-19. Nat. Commun. 2020;11:5730. doi: 10.1038/s41467-020-19546-7. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0019] 19.Yao Y., Pan J.H., Liu Z.X. No association of COVID-19 transmission with temperature or UV radiation in Chinese cities. Eur. Respir. J. 2020;55(5) doi: 10.1183/13993003.00517-2020. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0020] 20.Zhu Y., Xie J. Association between ambient temperature and COVID-19 infection in 122 cities from China. Sci. Total Environ. 2020;724 doi: 10.1016/j.scitotenv.2020.138201. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0021] 21.Wei J., Liu Y., Zhu Y., et al. Impacts of transportation and meteorological factors on the transmission of COVID-19. Int. J. Hyg. Envir. Heal. 2020;230 doi: 10.1016/j.ijheh.2020.113610. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0022] 22.Lv Q., Liu M., Qi F., et al. Sensitivity of SARS-CoV-2 to different temperatures. Animal Models Experiment. Med. 2020;3(4):3. doi: 10.1002/ame2.12141. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0023] 23.Reza D., Mohammad A. Stability of SARS-CoV-2 in different environmental conditions. Lancet. Microbe. 2020;1:e145. doi: 10.1016/S2666-5247(20)30093-8. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0024] 24.Riddell S., Goldie S., Hill A., et al. The effect of temperature on persistence of SARS-CoV-2 on common surfaces. Virol. J. 2020;17(1):145. doi: 10.1186/s12985-020-01418-7. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0025] 25.Wu Y., Jing W.Z., Liu J., et al. Effects of temperature and humidity on the daily new cases and new deaths of COVID-19 in 166 countries. Sci. Total. Environ. 2020;792 doi: 10.1016/j.scitotenv.2020.139051. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0026] 26.Sobral M., Duarte G.B., da Penha Sobral A., et al. Association between climate variables and global transmission oF SARS-CoV-2. Sci. Total. Environ. 2020;729 doi: 10.1016/j.scitotenv.2020.138997. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0027] 27.Guo C., Bo Y., Lin C., et al. Meteorological factors and COVID-19 incidence in 190 countries: an observational study. Sci. Total. Environ. 2021;757 doi: 10.1016/j.scitotenv.2020.143783. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0028] 28.Sera F., Armstrong B., Abbott S., et al. A cross-sectional analysis of meteorological factors and SARS-CoV-2 transmission in 409 cities across 26 countries. Nat. Commun. 2021;12:5968. doi: 10.1038/s41467-021-25914-8. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0029] 29.Carlson C.J., Gomez A.C.R., Bansal S., et al. Misconceptions about weather and seasonality must not misguide COVID-19 response. Nat. Commun. 2021;11:4312. doi: 10.1038/s41467-020-18150-z. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0030] 30.Baker R.E., Yang W., Vecchi G.A., et al. Susceptible supply limits the role of climate in the early SARS-CoV-2 pandemic. Science. 2020;369:315–319. doi: 10.1126/science.abc2535. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0031] 31.Dong E., Du H., Gardner L. An interactive web-based dashboard to track COVID-19 in real time. Lancet. Inf. Dis. 2020;20(5):533–534. doi: 10.1016/S1473-3099(20)30120-1. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0032] 32.Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU), COVID-19 Dashboard, 31 September 2021. https://gisanddata.maps.arcgis.com/apps/dashboards/bda7594740fd40299423467b48e9ecf6

[bib0033] 33.H. Ritchie, E. Mathieu, L. Rodés-Guirao, C. Appel, C. Giattino, E. Ortiz-Ospina, et al. Coronavirus Pandemic (COVID-19). Published online at OurWorldInData.org. https://ourworldindata.org/coronavirus

[bib0034] 34.European Centre for Disease Prevention and Control, COVID-19. https://www.ecdc.europa.eu/en/covid-19

[bib0035] 35.S. Abbott, J. Hellewell, R.N. Thompson, K. Sherratt, H.P. Gibbs, N.I. Bosse, et al. Temporal variation in transmission during the COVID-19 outbreak. https://epiforecasts.io/covid/

[bib0036] 36.GISAID, covSPECTRUM, https://cov-spectrum.org/

[bib0037] 37.National Bureau of Statistics of China . China Statistics Press; 2021. China Statistical Yearbook. [Google Scholar]

[bib0038] 38.WorldPop, Open Spatial Demographic Data and Research. https://www.worldpop.org/

[bib0039] 39.Population Division of the Department of Economic and Social Affairs of the United Nations Secretariat, 2019 Revision of World Population Prospects, https://population.un.org/wpp/

[bib0040] 40.CIESIN at Columbia University, Socioeconomic Data and Application Center (SEDAC). https://sedac.ciesin.columbia.edu/

[bib0041] 41.Kottek M., Grieser J., Beck C., Rudolf B., Rubel F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006;15:259–263. [Google Scholar]

[bib0042] 42.Peel M.C., Finlayson B.L., McMahon T.A. Updated world map of the Koppen-Geiger climate classification. Hydrol. Earth. Syst. Sci. 2007;11:1633–1644. [Google Scholar]

[bib0043] 43.National Earth System Science Data Center, National Science & Technology Infrastructure of China. http://www.geodata.cn

[bib0044] 44.ECMWF, Atmosphere Data Store, https://ads.atmosphere.copernicus.eu/

[bib0045] 45.ECMWF, Climate Data Store, https://cds.climate.copernicus.eu/

[bib0046] 46.IBRD•IDA, World Bank Open Data, https://data.worldbank.org.cn/

[bib0047] 47.Zhang Y., Hale T., Wood A., Philips T., Petherick A., Folco M.D., et al. Chinese provincial government responses to COVID-19. Blavatnik School of Government Working Paper. 2021 www.bsg.ox.ac.uk/covidtracker Available: [Google Scholar]

[bib0048] 48.Hale T., Angrist N., Goldszmidt R., Kira B., Petherick A., Phillips T., et al. A global panel database of pandemic policies (Oxford COVID-19 Government Response Tracker) Nat. Hum. Behav. 2021;5:529–537. doi: 10.1038/s41562-021-01079-8. [DOI] [PubMed] [Google Scholar]

[bib0049] 49.UNWTO, UNWTO tourism data dashboard. https://www.unwto.org/unwto-tourism-dashboard

[bib0050] 50.Driessche P.V., Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002;180:29–48. doi: 10.1016/s0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]

[bib0051] 51.Diekmann O., Heesterbeek J.A.P., Metz J.A. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990;28:365–382. doi: 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]

[bib0052] 52.Hsieh Y., Driessche P.V., Wang L. Impact of travel between patches forspatial spread of disease. Bull. Math. Biol. 2007;69:1355–1375. doi: 10.1007/s11538-006-9169-6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0053] 53.Gao D. Travel Frequency and Infectious Diseases. SIAM. J. Appl. Math. 2019;79:1581–1606. [Google Scholar]

[bib0054] 54.Wang X., Yin G., Z. Hu Z., et al. Dynamical Variations of the Global COVID-19 Pandemic Based on a SEICR Disease Model: a New Approach of Yi Hua Jie Mu. Geohealth. 2021;5(8) doi: 10.1029/2021GH000455. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Exploring meteorological impacts based on Köppen-Geiger climate classification after reviewing China's response to COVID-19

Fangyuan Chen

Siya Chen

Mengmeng Jia

Mingyue Jiang

Zhiwei Leng

Libing Ma

Yanxia Sun

Ting Zhang

Luzhao Feng

Weizhong Yang

Abstract

Introduction

Methods

Meta-population epidemic model

Estimations of ICC, PIC, CTI, RIT, VAC

Estimations of reproduction numbers

Fig. 2.

Processing of gridded data

Fig. 4.

Fig. 5.

Results

Intensity of NPIs in different control stages in China

Fig. 1.

Assessments of NPIs and vaccination on global reproduction number

Reporting and NPIs delays

Heterogeneity of Köppen–Geiger climate classifications

Fig. 3.

Heterogeneity of temperature, humidity, and other meteorological factors

Discussion

Author contributions

Declaration of Competing Interests

Acknowledgements

Footnotes

Appendix. Supplementary materials

Data Availability

References

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases