Abstract
Cellular protrusions, invaginations, and many intracellular organelles have strongly curved membrane regions. Transmembrane and peripheral membrane proteins that induce, sense, or stabilize such regions cannot be properly fitted into a single flat bilayer. To treat such proteins, we developed a new method and a web tool, PPM 3.0, for positioning proteins in curved or planar, single or multiple membranes. This method determines the energetically optimal spatial position, the hydrophobic thickness, and the radius of intrinsic curvature of a membrane‐deforming protein structure by arranging it in a single or several sphere‐shaped or planar membrane sections. In addition, it can define the lipid‐embedded regions of a protein that simultaneously spans several membranes or determine the optimal position of a peptide in a spherical micelle. The PPM 3.0 web server operates with 17 types of biological membranes and 4 types of artificial bilayers. It is publicly available at https://opm.phar.umich.edu/ppm_server3. PPM 3.0 was applied to identify and characterize arrangements in membranes of 128 proteins with a significant intrinsic curvature, such as BAR domains, annexins, Piezo, and MscS mechanosensitive channels, cation‐chloride cotransporters, as well as mitochondrial ATP synthases, calcium uniporters, and TOM complexes. These proteins form large complexes that are mainly localized in mitochondria, plasma membranes, and endosomes. Structures of bacterial drug efflux pumps, AcrAB‐TolC, MexAB‐OrpM, and MacAB‐TolC, were positioned in both membranes of the bacterial cell envelop, while structures of multimeric gap‐junction channels were arranged in two opposed cellular membranes.
Keywords: annexins, ATP synthase, BAR domains, ion channels, membrane curvature, membrane proteins, TOM complex, transporters, web server
Abbreviations
- 3D
three‐dimensional
- APC
acid‐polyamine‐organocation (superfamily)
- CCC
cation‐chloride cotransporter
- CG
coarse‐grained
- cryo‐EM
cryo‐electron microscopy
- IM
inner membrane
- KUP
K+‐uptake permease
- LHC
light harvesting complex
- MCU
mitochondrial calcium uniporter
- MD
molecular dynamics
- MIM
mitochondrial inner membrane
- MOM
mitochondrial outer membrane
- OM
outer membrane
- OPM
orientations of proteins in membranes (database); ORG, organelle membrane
- PDB
Protein Data Bank
- PPM
positioning of proteins in membranes (method and a web server)
- PM
plasma membrane
- PSI
photosystem I
- PSII
photosystem II
- RND
resistance‐nodulation‐cell division (family); THYL, thylakoid membrane
- TM
transmembrane
- TOM
the translocase of the outer membrane
1. INTRODUCTION
Biological membranes separate living cells from the outside environment and create intracellular compartments. They serve as selective permeability barriers to regulate ionic and metabolic homeostasis and response of cells to external signals. While membranes are formed from a wide variety of lipids, membrane functions are mainly associated with proteins, which either span the lipid bilayer (transmembrane [TM] proteins), or are inserted permanently or transiently from one membrane side (monotopic or peripheral proteins). The interplay between proteins and lipids determines the membrane shape, curvature, thickness, elasticity, and other physical properties that regulate processes in membranes.
Recent progress in structure determination techniques, such as X‐ray, NMR, and cryo‐electron microscopy (cryo‐EM), have led to nearly an exponential growth of three‐dimensional (3D) structures of membrane proteins at atomic resolution that have been deposited into the Protein Data Bank (PDB), 1 EMDataBank, 2 and other resources. However, the spatial arrangements of proteins with respect to the lipid bilayer and their hydrophobic thicknesses are not immediately obvious from these structures.
To define the spatial positions of protein structures within membranes, several fast computational methods have been developed and provided to the public as web tools or open‐source software. These methods include PPM (positioning of proteins in membranes), 3 , 4 MEMEMBED, 5 Ez‐3D, 6 , 7 , 8 TMDET, 9 , 10 ANVIL, 11 and the HDGB‐based approach. 12 Around 14,000 structures of TM and peripheral membrane proteins and peptides with membrane boundaries precalculated by PPM were deposited in the orientations of proteins in membranes (OPMs) database. 4 The PDBTM database, which focuses only on TM proteins, provides more than 6,300 protein structures positioned in the lipid bilayer by TMDET. 13 Recently, the PDB database has made available ANVIL‐predicted orientations of TM proteins using the Mol* viewer. 14
However, all these computational methods operate only with a flat bilayer and neglect the membrane curvature. Therefore, they cannot properly define the location of membrane boundaries for curvature‐promoting proteins that induce membrane bending, vesicularization, or tubulation. Among these proteins are various peripheral scaffolding and TM proteins that work as extrinsic and intrinsic factors, respectively, for generation or stabilization of membrane curvature. 15
Protein‐induced membrane distortions can be modeled using the coarse‐grained (CG) and all‐atom molecular dynamics (MD) simulations of TM proteins in lipid bilayers. To facilitate these complex and computationally extensive simulations, they were organized in a pipeline for automated generation of membrane positions for newly released protein structures. 16 Currently, around 5,000 TM proteins have been simulated in a single‐component lipid bilayer, and their 3D models have been collected in the MemProtMD database. 17 However, these calculations were focused on local membrane deformation and did not address global changes of membrane curvature on nanometer or micrometer scales. Reproducing the large‐scale membrane bending induced by scaffolding proteins requires millisecond simulations of multi‐million atom systems or application of the specific shape‐based CG approach that allows reaching systems sizes of 100 nm and time scales of 100 μs. 18
Another drawback of the existing web servers for positioning proteins in membranes is overlooking protein structures that are simultaneously embedded into several membranes, such as multidrug efflux pumps of Gram‐negative bacteria that span both outer and inner bacterial membranes. Fast computational tools usually calculate boundaries of only one membrane for such proteins.
To address these problems, we developed PPM 3.0, the first method implemented as a web server for positioning TM and peripheral membrane proteins not only in a single flat lipid bilayer, but also in sphere‐shaped vesicles, multiple membranes, or in a spherical micelle. Here, we describe the PPM 3.0 method and illustrate its performance in identifying and characterizing membrane‐deforming proteins.
2. RESULTS AND DISCUSSION
PPM 3.0 determines the optimal spatial position of a protein structure by minimizing its free energy of transfer from water to the membrane environment considered as a fluid anisotropic solvent. The methodology and empirical parameters for calculating the transfer energy from water to the membrane environment (∆G transf) were previously tested against experimental data available for many hundred proteins, peptides, and small molecules. 3 , 19 , 20 PPM 3.0 operates with the same energy as PPM 2.0, but implements new procedures for the positioning of proteins in curved or multiple membranes and uses 17 types of biological membranes and 4 types of artificial lipid bilayers characterized by the specified thicknesses and stretching stiffness coefficients (Table S1). The radius of intrinsic protein curvature is defined as the optimal radius of a spherical lipid vesicle that accommodates the protein with the minimal ∆G transf value. For each membrane‐deforming protein, PPM 3.0 calculates its hydrophobic thickness, TM segments, radius of its intrinsic curvature and provides coordinates of curved membrane boundaries.
We applied PPM 3.0 to calculate spatial positions in membranes for a set of 1,362 and 748 structures representing different families of TM and peripheral proteins, respectively. Among them, we tested structures of BAR domains that were not previously included to the OPM database because of their significant intrinsic curvature and small binding energies to the flat lipid bilayer. For each structure, PPM 3.0 determined the lowest transfer energies from water to both flat (∆G flat) and curved (∆G curv) membranes. In most cases, both values were rather similar: the difference between ∆G curv and ∆G flat values was less than 10%. TM proteins with a more significant energy gain in curved membranes were selected for comparison with other structures of the same protein, with other proteins from the same family, and with published data. Visual inspection of selected protein structures showed that they had significantly nonplanar hydrophobic regions and, therefore, could be better accommodated in a curved membrane. We also recalculated membrane boundaries for structures of bacterial multidrug efflux pumps that span both outer and inner membranes of Gram‐negative bacteria and for gap‐junction channels that bridge plasma membranes of two adjacent cells. The results of these calculations were deposited to the OPM database, summarized in Tables S2–S4, and discussed below.
2.1. BAR domains
The Bin‐Amphiphysin‐Rvs167 (BAR) domain superfamily includes peripheral membrane proteins containing the BAR domain at N‐terminus (N‐BAR), the extended FCH (EFC)/FCH‐BAR domain (F‐BAR), or the IRSp53‐MIM homology domain (IMD)/inverse BAR domain (I‐BAR). 21 , 22 These proteins deform membranes to a geometry that corresponds to the structure of their membrane‐binding face. 23 The BAR domain consists of an extended coiled‐coil structure forming a long “banana shaped” dimer. It has a curved membrane‐binding surface rich in positively charged residues that interacts with acidic phospholipids. N‐BAR domains of some proteins, such as endophilin and amphiphysin, also have hydrophobic amino acids in the amphiphilic N‐terminal helix that contribute to the membrane binding. 24 Both N‐BAR and F‐BAR domains promote the positive membrane curvature and are involved in plasma membrane invaginations leading to endocytosis and phagocytosis. 21 Proteins with F‐BAR domains also regulate the formation of filopodium, lamellipodium, and podosome. 25 In contrast, I‐BAR domains with inverted curvature likely sense or induce negative membrane curvature and stabilizes plasma membrane protrusions, such as filopodia, by interacting with the membrane from the inner side of the bend. 26
The calculations with PPM 3.0 allowed us to evaluate radii of the intrinsic curvature for members of various families from the BAR domain superfamily. The radii vary widely, from around 120 Å for N‐BAR domains to around 410 and 540 Å for F‐BAR and I‐BAR domains, respectively (Tables 1, S2, and Figure 1a–d). These calculation results are consistent with previous estimates for these proteins. 23 The calculated binding energies for many BAR domains are small, especially for protein structures with missing hydrophobic anchor residues. In such cases, the reliability of PPM 3.0 is lower.
TABLE 1.
Average parameters of spatial positions in spherical membranes of peripheral and TM proteins calculated by PPM 3.0: hydrophobic thickness or depths (D), radius of intrinsic curvature (R), sign of curvature (J), and binding energy to curved membrane (∆G curv)
| Protein family | PDB ID | D, Å | R, Å | J | ∆G curv, kcal/mol | Membrane type a |
|---|---|---|---|---|---|---|
| Peripheral proteins | ||||||
| N‐BAR domains | 2c08, 1uru, 1zww, 2d4c, 2z0v, 2fic, 3caz, 4avm | 2.5 ± 1.8 | 116 ± 33 | >0 | −6 ± 2 | END, PM |
| F‐BAR domains | 2v0o, 2efk, 2efl, 2x3v, 3i2w, 3lll, 3qe6, 3qni, 3q0k, 4bne, 4wpe, 5c1f, 6ikn, 6xj1 | 1.9 ± 1.3 | 412 ± 140 | >0 | −4 ± 2 | END, LYS, PM, ER |
| I‐BAR domains | 1wdz, 1y2o | 0.4 ± 0 | 540 ± 60 | <0 | −4 ± 0 | PM |
| Annexins | 1ann, 1aow, 1anx, 1axn,1dk5, 1dm5, 1hm6, 1w45, 1xjl, 1yii, 2ie6, 2q4c, 2zhj, 2zoc, 3brx, 4mdv, 6b3i, 6tu2 | 3.0 ± 0.9 | 107 ± 41 | <0 | −9 ± 6 | PM |
| TM proteins | ||||||
| V‐type and F‐type ATPases | 6rd4, 6tmk, 6yny | 28.1 ± 0.2 | 143 ± 39 | >0 | −194 ± 67 | MIM |
| Piezo channels | 5z10, 6b3r, 6bpz, 6lqi, 6kg7 | 31.6 ± 0.4 | 114 ± 8 | >0 | −214 ± 72 | PM |
| MscS channels | 5y4o, 6urt, 6zyd, 3t9n, 3udc, 7onl, 7oo8, 7oo6, 4hw9, 6vyk, 7oo0, 7ooa, 7onj, 2oau, 6rld, 5aji, 2vv5, 4age, 4agf, 4hwa, 6pwn, 6pwo, 6pwp, 6uzh, 7a46, 6vym, 6vyl | 29.4 ± 2.4 | 85 ± 7 | >0 | −126 ± 25 | G− IM, G+ PM |
| Tom40 translocases | 6jnf, 6ucv, 6ucu, 7ck6, 7ck9 | 22.2 ± 0.2 | 142 ± 52 | <0 | −128 ± 17 | MOM |
| Cation‐chloride cotransporters | 6kkr, 6kkt, 6kku, 6m1y, 6m22, 6m23, 6nph, 6npk, 6npl, 6pzt, 6y5r, 6y5v,7d8z, 7d10, 7d14, 7d90, 7d99, 7aip, 7ain, 7aio, 7aiq, 7air, 7ngb | 31.9 ± 0.5 | 103 ± 16 | >0 | −137 ± 18 | PM |
| KimA, proton‐coupled K+ transporter | 6s3k | 29.5 | 70 | >0 | −131 | G+ PM |
| Respiratory complex I‐ | 6h8k, 6zka, 6ztq, 7a23, 7b93, 7b0h | 27.8 ± 0.6 | 450 ± 28 | <0 | −240 ± 67 | MIM |
| Photosystem I and II | 6tcl, 6jlu,7d0j | 30.7 ± 0.4 | 490 ± 71 | >0 | −539 ± 59 | THYL |
Membrane types: END, endosomal membrane; ER, membrane of endoplasmic reticulum; G+ PM, plasma membrane of Gram‐positive bacteria; LYS, lysosomal membrane; MIM, mitochondrial inner membrane; MOM, mitochondrial outer membrane; PM, plasma membrane; THYL, thylakoid membrane. Average values of parameters with standard deviations are shown for proteins from the second column.
FIGURE 1.
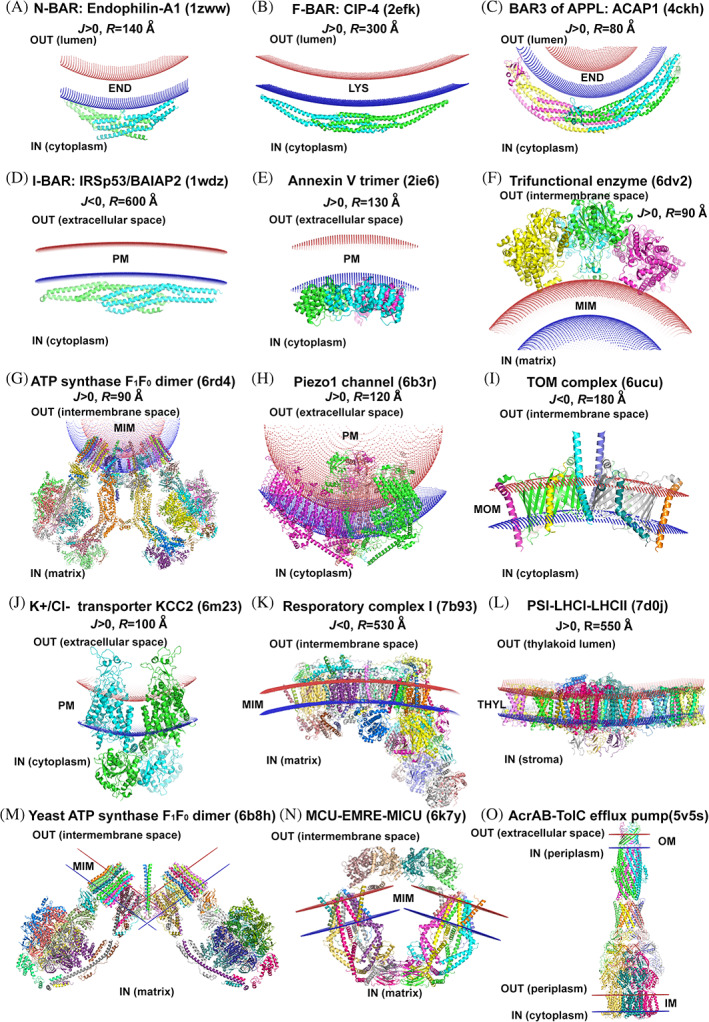
Positioning by PPM 3.0 of membrane‐deforming proteins in sphere‐shaped membranes (a–l) and in two flat membranes (m–o)
2.2. Annexins
Annexins are a family of peripheral membrane proteins that bind to anionic membranes containing phosphatidylserine in the presence of Ca2+‐ions. In humans, this family has 12 members (ANXA1‐11, ANXA13) that are involved in plasma membrane vesiculation and repair. 27 The conserved C‐terminal core domain of annexins consists of four similar repeats (eight in ANXA6), each having five α‐helices that form Ca2+‐binding sites. Some annexins act as monomers, other form dimers (ANXA1, ANXA2), trimer (ANXA4, ANXA5), or larger aggregates. It was shown that annexins can induce negative curvature on anionic membranes in Ca2+‐dependent manner, which leads to membrane aggregation, folding, blebbing, roll‐up, and fusion. 27
Our calculations with PPM 3.0 demonstrated that available structures of monomers and trimers of different annexins have a negative intrinsic curvature (J <0) with average radii of around 100 Å (Figure 1e, Tables 1 and S2).
2.3. Mitochondrial ATP synthases
F‐type mitochondrial adenosine triphosphate (ATP) synthase is a multiprotein complex located in mitochondrial cristae that converts the proton motive force generated by proteins from the electron transport chain into ATP. In yeast and mammals, ATP synthase is composed of a soluble catalytic F1 region containing α3β3γσε subunits and a TM F0 region containing a, b, e, f, g, i/j, k, l, 8 subunits and a ring of 10 c‐subunits. During ATP synthesis, protons move across the mitochondrial inner membrane (MIM) from the intramembrane space into the matrix via F0 region, which leads to rotation of the central rotor (γσεc10), conformational changes in α3β3 subunits, and ATP synthesis from ADP and phosphate.
The mitochondrial ATP synthase complexes from plants, fungi, and mammals assemble into dimers forming rows along the ridges of the cristae. 28 Dimer organization in long ribbons stabilizes the highly curved cristae ridges, which is essential for MIM morphology. 29
PPM 3.0 was used to calculate spatial positions in membranes of V‐shaped dimers of F1F0‐ATP synthases from different organisms. It appeared that dimers from unicellular organisms (protozoa and algae), which are held together by hydrophilic helices, can be arranged in a spherical membrane bent toward the mitochondrial matrix (J >0) with average radii of 140 Å (Figure 1g, Tables 1 and S3). In contrast, two halves of the yeast ATP synthase dimer, which associate via the membrane‐embedded F0 region, can be optimally positioned in two separate planar membrane sections that intersect under nearly a right angle (Figure 1m, Tables 2 and S4). These calculations agree with the previous analysis of cryo‐EM‐maps. 28
TABLE 2.
Average parameters of spatial positions of TM proteins in two intersecting or parallel membranes calculated by PPM 3.0: hydrophobic thickness (D) and binding energies to flat membranes (∆G flat)
| Protein name | PDB ID | First membrane | 2nd membrane | Membrane type a | ||
|---|---|---|---|---|---|---|
| D, Å | ∆G flat, kcal/Mol | D, Å | ∆G flat, kcal/Mol | |||
| TM proteins positioned in two intersecting membranes | ||||||
| Mitochondrial ATP synthase (yeast) | 6b2z, 6b8h | 29.5 ± 0.7 | −143 ± 9 | 29.3 ± 0.1 | −140 ± 8 | MIM |
| MCU‐EMRE‐MICU transporter complex (human) | 6k7x, 6k7y, 6o58, 6wdo, 6xjv | 28.7 ± 0.3 | −76 ± 9 | 29.0 ± 0.5 | −76 ± 10 | MIM |
| TM proteins positioned in two parallel membranes | ||||||
| AcrAB‐TolC efflux pump | 5v5s, 5o66, 5ng5 | 24.8 ± 0.1 | −54 ± 4 | 29.4 ± 0.4 | −171 ± 27 | OM/IM |
| MexAB‐OprM efflux pump | 6iol, 6iok, 6ta5 | 25.1 ± 0.2 | −70 ± 2 | 29.4 ± 0.5 | −160 ± 8 | OM/IM |
| MacAB‐TolC efflux pump | 5nik | 25.3 | −69 | 31.9 | −93 | OM/IM |
| Connexin gap‐junction channels | 2zw3, 5er7, 6uvs, 7jkc, 7jmd, 7jn0, 7jn1, 7jjp, 7jlw, 7jkc, 7jm9, 7jmc, 6mhq, 6mhy | 33.1 ± 0.5 | −180 ± 29 | 33.2 ± 0.5 | −180 ± 29 | PM/PM |
| CALHM gap‐junction channels | 6uix, 6vai, 6lom, 6ytl, 6ytk | 33.2 ± 0.3 | −298 ± 33 | 33.3 ± 0.3 | −299 ± 33 | PM/PM, PM/ORG |
| Innexin gap‐junction channel | 5hlr | 33.0 | −230 | 33.0 | −226 | PM/PM |
| Pannexin gap‐junction channel | 6wbn | 34.6 | −292 | 34.6 | −292 | PM/PM |
Membrane types: IM, bacterial inner membrane; MIM, mitochondrial inner membrane; OM, bacterial outer membrane; ORG, organelle membrane; PM, plasma membrane; Average values of parameters with standard deviations are shown for proteins from the second column.
Noteworthy, ATP synthase of chloroplasts predominantly exist as monomers and can be generally accommodated in flat membranes. Indeed, localization of chloroplast ATP synthase is confined to minimally curved membrane regions at the grana end and stroma lamellae. 30
2.4. Mechanically activated Piezo and MscS ion channels
The mechanically activated Piezo channels are key eukaryotic mechanotransducers that convert mechanical force into cation permeation. 31 They mediate touch perception, mechanical nociception, proprioception, and vascular development. Piezo1 and Pezo2 are mainly expressed in nonsensory and sensory tissues of vertebrates, respectively. They are evolutionary and structurally unrelated to mechanosensitive channels of prokaryotes.
Several atomic models based on cryo‐EM density maps have been constructed for the mouse Piezo 1 31 , 32 and Piezo 2 channels. 33 Each channel represents a propeller‐like trimeric complex, where each subunit consists of 38 TM α‐helices organized in nine 4‐TM α‐bundles (first 12 TM α‐helices are not resolved in EM maps of Piezo 1; PDB ID: 6b3r) and two central helices connected by a regulatory C‐terminal extracellular domain. Pairs of central TM α‐helices form a narrow pore that deforms the membrane into a dome. 31
Calculation with PPM 3.0 demonstrated that all available structures of trimetric complexes of Piezo channels can be accommodated in a spherically deformed membrane bent toward the cytoplasm (J >0, R ~114 Å; Figure 1h). Similar results were obtained for heptameric bacterial mechanosensitive channels of small‐conductance, MscS (Tables 1 and S3).
2.5. Mitochondrial import receptor complex
The translocase of the outer membrane (TOM) represents the mitochondrial protein‐conducting channel that coordinates translocation of nuclear‐encoded proteins with mitochondrial target sequences from cytosol into mitochondria. 34 The core TOM complex is a dimer of 10 TM subunits composed of two β‐barrels of TOM40 pore, each surrounded by single‐α‐helical TM subunits: TOM5, TOM6, TOM7, and TOM22. Recently, cryo‐EM structures of TOM complexes from Homo sapiens and Saccharomyces cerevisiae have been reported. 35 , 36 Further, dimeric TOM complexes were shown to associate in tetramers 36 , 37 or trimers. 35
Calculations with PPM 3.0 demonstrated that the dimeric and tetrameric complexes of TOM bend MOM toward the intermembrane space, away from the cytoplasm, thus inducing a significant negative curvature (J <0). Importantly, the hydrophobic thickness of MOM was calculated as being reduced from ~30 to ~22 Å in the area of TOM40 β‐barrels (Figure 1I, Tables 1 and S2). The shallow membrane depression at the cytoplasmic site of the TOM complex may help preprotein binding and guiding to TOM40 translocation pores.
2.6. Mitochondrial calcium uniporter
Mitochondrial calcium uniporter (MCU) is a highly selective calcium channel localized in MIM. It mediates Ca2+‐uptake by mitochondria, which is critical for the regulation of Ca2+‐homeostasis in eukaryotes. MCU was found in all major eukaryotic taxa. However, only in metazoa, MCU forms a functional complex with EMRE and MICU1‐MICU2 heterodimer that blocks the channel at low Ca2+ concentration. 38 , 39 Several structures of dimeric forms of human MCU‐EMRE and MCU‐EMRE‐MICU1‐MICU2 complexes have been recently determined. 38 , 39 , 40 , 41
Positioning of these structures in membranes by PPM 3.0 showed that monomeric MCU complexes can be accommodated in the flat lipid bilayer. However, the dimeric forms of MCU‐EMRE and MCU‐EMRE‐MICU1‐MICU2 complexes did not fit well to a single flat or a spherically deformed membrane. Apparently, they are located in a strongly bent region of mitochondrial cristae where they can be approximated by two flat membrane sections intersecting at an obtuse angle (Figure 1n, Tables 2 and S4).
The membrane deformation caused by dimerization of MCU‐EMRE complexes is a likely reason of MCU enrichment at the curved surfaces of MIM between the inner boundary membranes and the cristae membranes that are close to contact points with MOM. 41 , 42 Such localization of uniporter complexes may increase their accessibility to Ca2+ ions from the cytosol.
2.7. Cation‐chloride cotransporters
The cation‐chloride cotransporters (CCCs) move Cl− ions into or out of cells using the Na+ and/or K+ gradients generated by the Na+‐K+‐ATPase. NKCC1, the most experimentally studied CCC, participates in chloride homeostasis, regulation of cell volume, and neuronal excitability. 43 Each CCC assembles into a dimer, where each subunit has the first 10 TM α‐helices forming the transport core and TM11‐TM12 helices participating in the dimerization interface. Similar to other members of the amino acid‐polyamine‐organocation (APC) superfamily of secondary active transporters, CCCs display the pseudo‐symmetric topology of two inverted repeats of five TM α‐helices (with broken TM1 and TM6) that form the central ligand binding cavity of the 10‐helical TM core. Cryo‐EM models of CCC dimers in the inward‐facing state demonstrate a similar architecture, with the peripheral TM4‐TM5 α‐helices located ~9 Å above the central TM11–TM12 α‐helices. 43
Our calculations with PPM 3.0 demonstrated that all 23 available structures of CCCs can be better accommodated in highly curved sphere‐shaped membranes that are bent toward the cytoplasmic side of the PM (J >0, R ~105 Å; Figure 1j, Tables 1 and S3). Perhaps the local membrane deformation that appears as a “depression” in the middle of these protein complexes facilitates the TM transport.
2.8. Proton‐coupled K+ transporter
K+‐uptake permeases (KUPs) represent another family of the APC superfamily. KimA, a high affinity proton‐coupled K+ importer from Bacillus subtilis, shares a similar fold with CCCs. 44 It functions as a homodimer, where each subunit is composed of 10‐helical core and TM11‐TM12 helices, which together with C‐terminal cytoplasmic domains form the dimerization interface. PPM 3.0 calculations revealed that, similar to CCCs, KimA in the inward‐facing state can be better accommodated in the significantly curved membrane bent toward the cytoplasm (J >0, R = 70 Å; Tables 1 and S3). Based on results of CG and MD simulations, it was suggested that the extent of the membrane bending by KimA dimer could be altered during transporter activity. 44
2.9. Respiratory complex I
Mitochondrial respiratory complex I (NADH:ubiquinone oxidoreductase) is an essential enzyme for mitochondrial energy metabolism. It converts energy released by electron transfer from NADH to ubiquinone to the proton flux out of the matrix across the MIM, which is used for ATP synthesis. Mammalian respiratory complex I is the largest of respiratory complexes; it is composed of 45 subunits: 14 “core” subunits conserved in prokaryotes and eukaryotes that are sufficient for catalysis, and 31 “supernumerary” species‐specific subunits that are required for complex assembly, stability, and regulation. 45 The L‐shape of the complex I is created by the matrix‐exposed hydrophilic part, which provides electron transfer between NADH and ubiquinone, and the TM domain, which is responsible for proton translocation.
Calculations by PPM 3.0 of mitochondrial respiratory complexes I of plant and mammals demonstrate that the difference between transfer energies for curved and flat membranes is smaller (∆∆G ~12%) than for other calculated membrane‐deforming proteins (∆∆G from 20% to 80%). Therefore, respiratory complexes I can be accommodated either in flat or slightly curved membranes that bend toward the intermembrane space (J <0, R ~450 Å; Figure 1k, Tables 1 and S3). Such results are consistent with localization of these complexes in flat or slightly curved regions of inner membranes of cristae. 28 On the other hand, the bacterial respiratory complex I (PDB ID: 3rko) has a slightly larger curvature (J <0, R = 270 Å) compared to the mitochondrial complex I. The structures of all other components of the respiratory chain (complexes II, III, and IV) were found to be planar.
2.10. Photosystems I and II
Photosystem I and II (PSI and PSII) are two multisubunit pigment‐protein complexes embedded in the thylakoid membranes of higher plants, algae, and cyanobacteria that capture light energy and transform it to photochemical reactions of oxygenic photosynthesis. In higher plants and algae, the core complexes of PSI and PSII form large supercomplexes with peripheral antennae, the light‐harvesting complexes (LHCs): PSI‐LHCI, PSII‐LHCII (or PSII‐FCPII), and PCI‐LHCI‐LHCII at state 2. 46 In plant and algae, PSI exists as monomers, while in bacteria, it usually forms trimers, but also may exist as tetramers, possibly as adaptation to high light levels. 47 PSII‐LHCs supercomplexes are formed by two protomers, each composed of multisubunits PSII core and a complex antenna systems. 48
Calculation by PPM 3.0 of all available structures of PSI and PSII complexes with or without LHCs revealed that almost all of them fit to a planar lipid bilayer. A few exceptions are: the tetrameric PSI from cyanobacteria (PDB ID: 6tcl 47 ), the PSI‐LHCI‐LCHII supercomplex from green algae (PDB ID: 7d0j 46 ), and the PSII‐FCPII supercomplex of diatoms (PDB ID: 6jlu 48 ). These complexes can be better arranged in slightly curved membranes (average R of 490 Å) than in a flat lipid bilayer (Figure 1l, Tables 1 and S3). The physiological relevance of a small intrinsic curvature of these proteins is not completely clear, but it might reflect the slight bend of thylakoids in unicellular algae and cyanobacteria.
2.11. Tripartite multidrug efflux pumps
In Gram‐negative bacteria, tripartite multidrug efflux pumps export biological metabolites and antimicrobial compounds out of the cell, thereby contributing to bacterial resistance. Models of three such pumps, which span both inner (IM) and outer (OM) bacterial membranes, were experimentally determined: AcrAB‐TolC efflux pump of Escherichia coli, MexAB‐OprM complex of Pseudomonas aeruginosa, and MacAB–TolC assembly of Escherichia coli. AcrAB‐TolC and MexAB‐OprM belong to the Resistance‐Nodulation‐cell Division (RND) family, while MacAB‐TolC complex is a FtsX‐like permease. RND transporters operate as a secondary proton/drug antiporter using the energy of proton transport in TM domains located in the IM to power the export of substrates through the periplasm and the OM. 49 , 50 MacAB‐TolC contains the dimeric MacB ATPase, an ABC‐transporter from IM that energizes the drug transport. 51 The boundaries of both membranes of the bacterial cell envelop were determined by PPM 3.0 for these structures (Figure 1o, Tables 2 and S4).
2.12. Gap‐junctions channels
Gap‐junction proteins, such as connexins, innexins, pannexins, leucine‐rich repeat‐containing 8 (LRRC8) proteins, and calcium homeostasis modulators (CALHM), are large‐pore channels with a pore diameter more than 14 Å. These proteins are composed of TM 4‐α‐helical bundles organized in multimers: 6‐mers (connexins, LRRC8), 7‐mers (pannexins), 8‐mers (innexines, CALHM1), and 9, 10, 11‐mers (CALHMs). Multimeric hemichannels connecting through their extracellular regions form gap‐junction channels between adjacent cells, while hemichannels of CALHM1 and CALMH4 interacting through their cytoplasmic regions may form channels between the plasma membrane and the organelle membrane. 52 Boundaries of two opposed membranes connected via gap‐junction channels were calculated by PPM 3.0 for 21 multimeric structures of connexins, CALHMs, innexins, and pannexins (Tables 2 and S4).
3. CONCLUSIONS
Here we present PPM3.0, the first web tool for calculating the spatial positions of proteins in curved and multiple membranes. This fast computational approach was applied to identify a set of 128 membrane proteins that induced significant membrane curvature. Most of these proteins were known to bend membranes, but their intrinsic curvatures and exact locations of membrane boundaries have not been assessed. Now, structures of these proteins are included in the OPM database along with PPM 3.0‐produced parameters of their spatial arrangement in membranes, including radii of their intrinsic curvature, hydrophobic thicknesses, TM segments, and coordinates of membrane boundaries.
Membrane bending is especially important for the function of transport proteins, formation of membrane protrusions and invaginations, and stabilization of vesicular and tubular shapes of cell organelles. 15 Indeed, the screening of a large set of membrane proteins by PPM 3.0 demonstrated that curved peripheral proteins mainly belong to the BAR domain and annexin families involved in the formation of protrusions, invagination, vesicles, and tubules. We found that less than 5% of TM proteins of known structure induce significant local or global curvature, while the majority of them can be accommodated in flat membranes. TM proteins with significant intrinsic curvature mostly belong to families of CCC, KUP, and MCU transporters, mitochondrial ATP synthases, Piezo and MscS channels, and TOM protein translocases. These proteins usually form large complexes that are located predominantly in mitochondrial cristae membranes, but also in eukaryotic PM, endosomes, and lysosomes.
Interestingly, the majority of calculated curvature‐promoting proteins were satisfactorily accommodated in spherical vesicles, though some of these proteins are known to induce tubular membrane structures. This result indicates that the simplified approximation of curved membranes by spheres is sufficiently accurate in most cases. However, certain mitochondrial proteins located in crista edges cannot be properly accommodated in a sphere‐shaped bilayer and require an approximation of a bent membrane by two intersecting bilayers. Thus, our method can be further advanced by implementing more complex membrane shapes, such as spheroids, ellipsoids, and cylinders.
The results of our calculations with PPM 3.0 can be affected by the quality, resolution and completeness of the experimental protein structures. The best results were obtained for structures of the largest protein complexes with resolution better than 3.5 Å and fewer missing loops and side chains. The radii of protein curvatures may depend on the protein state and crystallization conditions.
Finally, we should emphasize that while PPM 3.0 is helpful in evaluating intrinsic curvatures of protein structures in crystals, the real deformations of diverse biological membranes depend on the interplay of proteins and lipids. Therefore, the 3D models of protein complexes in curved membranes produced by our method can be used as a starting point for the refinement of protein‐membrane systems using MD simulations with explicit lipids corresponding to natural compositions of biological membranes.
4. METHODS
4.1. PPM 3.0 method
The PPM 3.0 method determines orientations in membranes of proteins and peptides by optimizing their transfer free energies from water to the membrane environment (∆G transf). Since the PPM 2.0 method was previously extensively tested, 3 , 19 , 20 we used the same approach for calculating ∆G transf, but added the following new options: (a) fitting a protein structure into a sphere‐shaped bilayer with an adjustable radius of curvature and hydrophobic thickness; (b) positioning of proteins in several lipid bilayers; (c) using different membrane systems; and (d) positioning of peptides or small proteins in a spherical micelle.
The transfer free energy is calculated as a sum of short‐range ASA‐dependent contributions for all atoms (H‐bonds, van der Waals, and hydrophobic interactions with solvent), long‐range electrostatic contributions of dipole moments and charged groups, and the ionization penalty for ionizable groups. 19 The solvation properties of a membrane as an anisotropic solvent are described by hydrogen bonding capacity and dielectric permittivity profiles along the bilayer normal. These profiles were calculated based on the experimentally determined distributions of different lipid groups along the normal of the 1,2‐dioleoyl‐sn‐glycero‐3‐phosphocholine (DOPC) bilayer. 53
4.1.1. Positioning of protein structures in a spherical lipid vesicle or a micelle
To evaluate whether a protein structure fits better to a planar or a curved membrane, PPM 3.0 calculates the optimal transfer energy of the protein from water to both systems. The optimization procedure in a flat membrane uses a combination of grid scan and local energy minimization, as in OPPM 2.0. 19 The transfer energy minimization in a spherical lipid vesicle employs a grid scan with a gradually decreasing step in the space of protein rigid‐body variables (d, τ, φ), the adjustable hydrophobic thickness of the bilayer (D), and the radius of curvature of the vesicle (R). The protein variables include its shift d along the bilayer normal, the tilt angle τ, and the rotation angle φ, as described previously. 3 The origin of coordinates corresponds to the center of the vesicle, while the radius R represents the distance from the origin of coordinates to the middle of the spherically curved bilayer. The position of every atom i of the protein along the bilayer normal is defined as r i –R (r i is the distance of atom i from the origin of coordinates), instead of the z i coordinate used for a flat bilayer with a normal coinciding with Z axis. The value of R is optimized with the step of 10 Å in the interval from 80 to 600 Å. Positioning of a peptide in a spherical micelle is performed as previously described. 20
4.1.2. Curvature sign (J)
Peripheral proteins that can be accommodated on convex or concave membrane surfaces better than on a flat surface are designated as proteins inducing positive (J >0) or negative (J <0) membrane curvature, respectively. 54 For TM proteins, the positive or negative intrinsic curvature corresponds to the protein's ability to bend a membrane toward or away, respectively, from its “inner” (e.g., cytoplasmic) side. 15
4.1.3. Positioning of a protein structure in several lipid bilayers
PPM 3.0 is able to determine the hydrophobic boundaries of several lipid bilayers for a single protein structure. The procedure starts from protein positioning with respect to the first membrane. Then the structure together with the DUMMY atoms marking boundaries of the first membrane (at the area of lipid carbonyl groups) is re‐positioned with respect to the second membrane, and so on. This option can also be applied to proteins located in adjacent intersecting parts of a deformed membrane that can be approximated by several flat or curved surfaces.
4.1.4. Different membrane types
Insertion of a TM protein in a lipid bilayer can alter the local hydrophobic thickness of a bilayer to match the hydrophobic thickness of a protein. The corresponding membrane deformation energy is described as:
where N L is the number of annular lipids in two leaflets around a TM protein structure, 19 D 0 and D are the equilibrium and the adjusted hydrophobic thickness of the bilayer, and is the empirical stretching stiffness coefficient. is included in the transfer energy.
Currently, PPM 3.0 operates with 17 types of biological membranes and four artificial bilayers, characterized by the specified hydrophobic thicknesses D 0 and stretching stiffness coefficients, (Table S1).
4.2. PPM 3.0 web server
The PPM 3.0 web server provides fast calculation of spatial positions and intrinsic curvatures of TM and peripheral proteins in flat and curved biological and artificial membranes. It also allows calculating boundaries of several membranes (or several independent sections of the same membrane) where the protein complex is located. The web server is located at the OPM database web site (https://opm.phar.umich.edu/ppm_server3).
The input includes: (a) a coordinate file (in pdb format) of a 3D structure of a protein or a peptide of interest that can be provided by a user or taken from the PDB or the OPM databases; (b) a choice between one to four membranes; (c) a choice of each membrane type (from 17 types of biological membranes, four types of lipid bilayer, and a DPC micelle); (d) lists of protein subunits assigned to each membrane in the multiple membranes option; (e) designation of protein topology (location of N‐terminus of the first subunit relative to the “in” or “out” membrane side); and (f) an option to include curvature in calculation. With the “curvature allowed” option selected, PPM 3.0 automatically defines whether a protein fits better to a planar or a spherically deformed bilayer. The option with positioning in a spherical micelle can be used only for peptides and small amphiphilic proteins, but not for TM proteins.
The output includes: (a) a downloadable coordinate file (in pdb format) of a protein structure supplemented by calculated membrane boundaries; (b) the membrane binding energy for peripheral proteins or the transfer free energies of TM proteins from water to flat (∆G flat) and curved (∆G curv) membranes; (c) the radius of curvature for proteins in curved membranes (R); (d) the membrane penetration depth for peripheral proteins or hydrophobic thickness (D) for TM proteins; and (e) the tilt angle between the membrane normal and the protein axis.
For structures with a single planar bilayer, the origin of the coordinates corresponds to the center of the lipid bilayer. Z axis coincides with the membrane normal; atoms with a positive sign for its Z coordinate are arranged in the outer leaflet as defined by the user‐specified topology. The center of the spherical vesicle or the micelle corresponds to the origin of coordinates. The radius of curvature of a sphere‐shaped membrane (R) denotes the distance from the origin of coordinates to the middle of the lipid bilayer, which includes only the inner leaflet and excludes the other leaflet with a 35 Å‐thicknesses (15 Å thick hydrophobic core plus 20 Å thick head group region). Thus, R of 100 Å would correspond to the diameter of a spherical vesicle of 270 Å. The protein axis is calculated as the sum of TM secondary structure segment vectors (for TM proteins) or as the principal inertia axis (for peripheral proteins).
Visualization of calculated protein structures positioned in planar or curved membranes is provided by Jmol, a platform‐independent Java‐viewer, and a WebGL‐based 3D viewer iCn3D.
CONFLICT OF INTEREST
The authors declare no potential conflict of interest.
AUTHOR CONTRIBUTIONS
Andrei L. Lomize: Conceptualization (lead); data curation (equal); formal analysis (equal); funding acquisition (equal); investigation (equal); methodology (equal); project administration (equal); resources (equal); software (equal); supervision (equal); validation (equal); visualization (equal); writing – original draft (equal); writing – review and editing (equal). Spencer C. Todd: Methodology (supporting); resources (lead); software (equal); visualization (lead); writing – review and editing (supporting). Irina D. Pogozheva: Funding acquisition (equal); investigation (equal); methodology (equal); validation (equal); writing – original draft (lead); writing – review and editing (equal).
Supporting information
Appendix S1: Supporting Information
ACKNOWLEDGMENT
This work was supported by the Division of Biological Infrastructure of the National Science Foundation (Award # 2010851 to Andrei L. Lomize and Irina D. Pogozheva).
Lomize AL, Todd SC, Pogozheva ID. Spatial arrangement of proteins in planar and curved membranes by PPM 3.0. Protein Science. 2022;31:209–220. 10.1002/pro.4219
Funding information National Science Foundation, Grant/Award Number: 2010851
REFERENCES
- 1. Burley SK, Berman HM, Kleywegt GJ, Markley JL, Nakamura H, Velankar S. Protein Data Bank (PDB): The single global macromolecular structure archive. Methods Mol Biol. 2017;1607:627–641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Lawson CL, Baker ML, Best C, et al. EMDataBank.org: Unified data resource for CryoEM. Nucleic Acids Res. 2011;39:D456–D464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Lomize AL, Pogozheva ID, Lomize MA, Mosberg HI. Positioning of proteins in membranes: A computational approach. Protein Sci. 2006;15:1318–1333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Lomize MA, Pogozheva ID, Joo H, Mosberg HI, Lomize AL. OPM database and PPM web server: Resources for positioning of proteins in membranes. Nucleic Acids Res. 2012;40:D370–D376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Nugent T, Jones DT. Membrane protein orientation and refinement using a knowledge‐based statistical potential. BMC Bioinform. 2013;14:276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Senes A, Chadi DC, Law PB, Walters RF, Nanda V, Degrado WF. E(z), a depth‐dependent potential for assessing the energies of insertion of amino acid side‐chains into membranes: Derivation and applications to determining the orientation of transmembrane and interfacial helices. J Mol Biol. 2007;366:436–448. [DOI] [PubMed] [Google Scholar]
- 7. Schramm CA, Hannigan BT, Donald JE, et al. Knowledge‐based potential for positioning membrane‐associated structures and assessing residue‐specific energetic contributions. Structure. 2012;20:924–935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Hsieh D, Davis A, Nanda V. A knowledge‐based potential highlights unique features of membrane alpha‐helical and beta‐barrel protein insertion and folding. Protein Sci. 2012;21:50–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Tusnady GE, Dosztanyi Z, Simon I. Transmembrane proteins in the Protein Data Bank: Identification and classification. Bioinformatics. 2004;20:2964–2972. [DOI] [PubMed] [Google Scholar]
- 10. Tusnady GE, Dosztanyi Z, Simon I. TMDET: Web server for detecting transmembrane regions of proteins by using their 3d coordinates. Bioinformatics. 2005;21:1276–1277. [DOI] [PubMed] [Google Scholar]
- 11. Postic G, Ghouzam Y, Guiraud V, Gelly J‐C. Membrane positioning for high‐ and low‐resolution protein structures through a binary classification approach. Prot Eng Des Sel. 2015;29:87–92. [DOI] [PubMed] [Google Scholar]
- 12. Dutagaci B, Feig M. Determination of hydrophobic lengths of membrane proteins with the HDGB implicit membrane model. J Chem Inf Model. 2017;57:3032–3042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Kozma D, Simon I, Tusnady GE. PDBTM: Protein Data Bank of transmembrane proteins after 8 years. Nucleic Acids Res. 2013;41:D524–D529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Sehnal D, Bittrich S, Deshpande M, et al. Mol* viewer: Modern web app for 3D visualization and analysis of large biomolecular structures. Nucleic Acids Res. 2021;49:W431–W437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Jarsch IK, Daste F, Gallop JL. Membrane curvature in cell biology: An integration of molecular mechanisms. J Cell Biol. 2016;214:375–387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Stansfeld PJ, Goose JE, Caffrey M, et al. MemProtMD: Automated insertion of membrane protein structures into explicit lipid membranes. Structure. 2015;23:1350–1361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Newport TD, Sansom MSP, Stansfeld PJ. The MemProtMD database: A resource for membrane‐embedded protein structures and their lipid interactions. Nucleic Acids Res. 2019;47:D390–d397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Yin Y, Arkhipov A, Schulten K. Simulations of membrane tubulation by lattices of amphiphysin N‐BAR domains. Structure. 2009;17:882–892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Lomize AL, Pogozheva ID, Mosberg HI. Anisotropic solvent model of the lipid bilayer. 2. Energetics of insertion of small molecules, peptides, and proteins in membranes. J Chem Inf Model. 2011;51:930–946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Lomize AL, Schnitzer KA, Todd SC, Pogozheva ID. Thermodynamics‐based molecular modeling of α‐helices in membranes and micelles. J Chem Inf Model. 2021;61:2884–2896. [DOI] [PubMed] [Google Scholar]
- 21. Suetsugu S. The proposed functions of membrane curvatures mediated by the BAR domain superfamily proteins. J Biochem. 2010;148:1–12. [DOI] [PubMed] [Google Scholar]
- 22. Suetsugu S, Toyooka K, Senju Y. Subcellular membrane curvature mediated by the BAR domain superfamily proteins. Sem Cell Dev Biol. 2010;21:340–349. [DOI] [PubMed] [Google Scholar]
- 23. Lemmon M. Membrane recognition by phospholipid‐binding domains. Nat Rev Mol Cell Biol. 2008;9:99–111. [DOI] [PubMed] [Google Scholar]
- 24. Gallop JL, Jao CC, Kent HM, et al. Mechanism of endophilin N‐BAR domain‐mediated membrane curvature. EMBO J. 2006;25:2898–2910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Liu S, Xiong X, Zhao X, Yang X, Wang H. F‐BAR family proteins, emerging regulators for cell membrane dynamic changes‐from structure to human diseases. J Hematol Oncol. 2015;8:47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Carlson B, Soderling SH. Mechanisms of cellular protrusions branch out. Dev Cell. 2009;17:307–309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Boye TL, Jeppesen JC, Maeda K, et al. Annexins induce curvature on free‐edge membranes displaying distinct morphologies. Sci Rep. 2018;8:10309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Davies KM, Anselmi C, Wittig I, Faraldo‐Gómez JD, Kühlbrandt W. Structure of the yeast F1F0‐ATP synthase dimer and its role in shaping the mitochondrial cristae. Proc Natl Acad Sci U S A. 2012;109:13602–13607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Guo H, Bueler SA, Rubinstein JL. Atomic model for the dimeric F0 region of mitochondrial ATP synthase. Science. 2017;358:936–940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Daum B, Nicastro D, Austin J 2nd, McIntosh JR, Kühlbrandt W. Arrangement of photosystem II and ATP synthase in chloroplast membranes of spinach and pea. Plant Cell. 2010;22:1299–1312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Guo YR, MacKinnon R. Structure‐based membrane dome mechanism for Piezo mechanosensitivity. Elife. 2017;6:e33660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Saotome K, Murthy SE, Kefauver JM, Whitwam T, Patapoutian A, Ward AB. Structure of the mechanically activated ion channel Piezo1. Nature. 2018;554:481–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Wang L, Zhou H, Zhang M, et al. Structure and mechanogating of the mammalian tactile channel Piezo2. Nature. 2019;573:225–229. [DOI] [PubMed] [Google Scholar]
- 34. Bausewein T, Mills DJ, Langer JD, Nitschke B, Nussberger S, Kühlbrandt W. Cryo‐EM structure of the TOM core complex from neurospora crassa. Cell. 2017;170:693–700. [DOI] [PubMed] [Google Scholar]
- 35. Araiso Y, Tsutsumi A, Qiu J, et al. Structure of the mitochondrial import gate reveals distinct preprotein paths. Nature. 2019;575:395–401. [DOI] [PubMed] [Google Scholar]
- 36. Tucker K, Park E. Cryo‐EM structure of the mitochondrial protein‐import channel TOM complex at near‐atomic resolution. Nat Struct Mol Biol. 2019;26:1158–1166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Wang W, Chen X, Zhang L, et al. Atomic structure of human TOM core complex. Cell Discov. 2020;6:67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Wang Y, Nguyen NX, She J, et al. Structural mechanism of EMRE‐dependent gating of the human mitochondrial calcium uniporter. Cell. 2019;177:1252–1261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Wang Y, Han Y, She J, et al. Structural insights into the Ca(2+)‐dependent gating of the human mitochondrial calcium uniporter. Elife. 2020;9:e60513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Zhuo W, Zhou H, Guo R, et al. Structure of intact human MCU supercomplex with the auxiliary MICU subunits. Protein Cell. 2021;12:220–229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Fan M, Zhang J, Tsai C‐W, et al. Structure and mechanism of the mitochondrial Ca(2+) uniporter holocomplex. Nature. 2020;582:129–133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. De La Fuente S, Fernandez‐Sanz C, Vail C, et al. Strategic positioning and biased activity of the mitochondrial calcium uniporter in cardiac muscle. J Biol Chem. 2016;291:23343–23362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Yang X, Wang Q, Cao E. Structure of the human cation‐chloride cotransporter nkcc1 determined by single‐particle electron cryo‐microscopy. Nat Commun. 2020;11:1016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Tascón I, Sousa JS, Corey RA, et al. Structural basis of proton‐coupled potassium transport in the KUP family. Nat Commun. 2020;11:626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Agip AA, Blaza JN, Bridges HR, et al. Cryo‐EM structures of complex I from mouse heart mitochondria in two biochemically defined states. Nat Struct Mol Biol. 2018;25:548–556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Huang Z, Shen L, Wang W, et al. Structure of photosystem I‐LHCI‐LHCII from the green alga Chlamydomonas Reinhardtii in state 2. Nat Commun. 2021;12:1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Chen M, Perez‐Boerema A, Zhang L, et al. Distinct structural modulation of photosystem I and lipid environment stabilizes its tetrameric assembly. Nature Plants. 2020;6:314–320. [DOI] [PubMed] [Google Scholar]
- 48. Pi X, Zhao S, Wang W, et al. The pigment‐protein network of a diatom photosystem II‐light‐harvesting antenna supercomplex. Science. 2019;365:eaax4406. [DOI] [PubMed] [Google Scholar]
- 49. Wang Z, Fan G, Hryc CF, et al. An allosteric transport mechanism for the AcrAB‐TolC multidrug efflux pump. Elife. 2017;6:e24905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Glavier M, Puvanendran D, Salvador D, et al. Antibiotic export by MexB multidrug efflux transporter is allosterically controlled by a MexA‐OprM chaperone‐like complex. Nat Commun. 2020;11:4948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Fitzpatrick AWP, Llabrés S, Neuberger A, et al. Structure of the MacAB‐TolC ABC‐type tripartite multidrug efflux pump. Nat Microbiol. 2017;2:17070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Syrjanen J, Michalski K, Kawate T, Furukawa H. On the molecular nature of large‐pore channels. J Mol Biol. 2021;433:166994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Pogozheva ID, Tristram‐Nagle S, Mosberg HI, Lomize AL. Structural adaptations of proteins to different biological membranes. Biochim Biophys Acta. 2013;1828:2592–2608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Campelo F, McMahon HT, Kozlov MM. The hydrophobic insertion mechanism of membrane curvature generation by proteins. Biophys J. 2008;95:2325–2339. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1: Supporting Information


