Modeling the dynamics of viral infections in presence of latently infected cells

1. Introduction

Dangerous viruses have been appearing from time to time attacking the human body and causing several health problems, deaths and socio-economic damage worldwide. For instance, a novel coronavirus (nCoV) was identified on January 7, 2020 responsible for the initial cases of pneumonia occurred in Wuhan, China. This virus has recently been reported as extreme acute respiratory syndrome coronavirus 2 (SARS-CoV-2) by the Coronavirus Study Group of the International Committee on Taxonomy of Viruses [7]. Because its genetic sequence is very similar to that of severe acute respiratory syndrome (SARS), another coronavirus that appeared for first time in 2002 and caused a pandemic with more than 8000 infected people and 800 deaths. Another coronavirus that causes severe disease in humans is middle east respiratory syndrome (MERS), identified for the first time in 2012 in the Middle East having connection with camels. As of 24 March 2020, more than 372,757 cases of SARS-CoV-2 have been confirmed in 196 countries and territories, including 195,511 cases in European region, and the number of deaths from the virus has reached 16,231 globally, according to the World Health Organization (WHO) [27]. Also, already existing viruses like hepatitis B virus (HBV) and human immunodeficiency virus (HIV) are still causing large numbers of deaths worldwide. As per an estimation in 2015, 257 million people were living with chronic hepatitis B infection (defined as hepatitis B surface antigen positive), and death of 887,000 people, mostly due to cirrhosis and hepatocellular carcinoma (i.e. primary liver cancer) [28]. Also, 770,000 people died from HIV-related causes and 1.7 million people were newly infected in 2018 [29].

The rapid spread of viruses has been attracting the attention of researchers to carry out new researches to understand various associated aspects. It has been shown biologically that viruses can spread by both modes, viz., virus-to-cell mode via the extracellular environment and through cell-to-cell transmission mode by direct cell-cell contact [13], [14], [23]. During cell-to-cell transmission, it is possible for several viral particles to be transferred from infected to uninfected cells via structures called infectious or virological synapses [13]. In the case of HIV infection, cell-to-cell transmission may be 10–1000 times more effective than the passive dissemination of virons via the extracellular environment [2], [4], [5]. In [30], HIV is used as a model virus in understanding the processes that consequence in viral spread via virus-to-cell or cell contact dependent mode. In the same work, it is demonstrated that HIV can spread by virus-to-cell mode if all steps of the viral replication cycle are efficient. If any of these steps is impaired, then co-cultures of HIV donor cells with specific target cells allow effective viral spreading.

Latently infected cells are those cells which include the viruses but do not producing them due to time lag between both the moment of infection and the moment when the infected cell becomes active to create new infectious viruses. For some viruses like herpesvirus, latency is an essential mechanism for immune evasion and viral persistence [16], [17]. One of the major hurdles in eliminating HIV infection completely is the presence of a small reservoir of latently infected cells that can survive through long-term suppression of viral replication by extremely active anti-retroviral therapy (HAART) [6], [21], [22]. A recent study found that cell-to-cell transmission contributes to the production of latently infected cells [1]. This mode of viral transmission is found to contribute to both the spread and pathogenesis of the virus in vivo and to the production and maintenance of latent reservoirs that represent a serious barrier to the curing of the infection [19].

The above biological studies inspire to propose the following model:

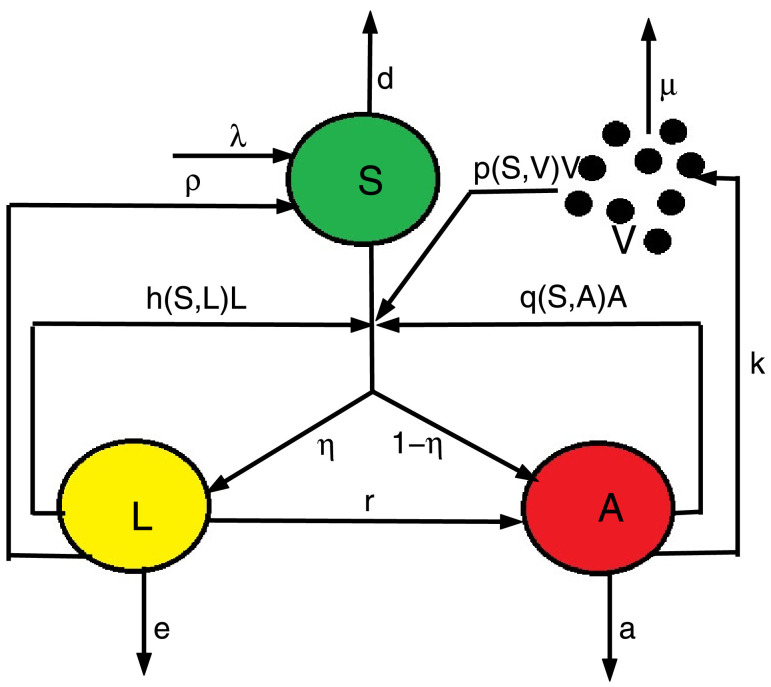
where S(t), L(t), A(t) and V(t) respectively indicate the concentration of susceptible cells, latently infected cells, actively infected cells and free virus particles at time t. It is also considered that susceptible cells are generated at a constant rate of λ, die at a rate of dS and become infected either through free virus at a rate of p(S, V)V, or through direct contact with actively infected cells at a rate of q(S, A)A, or by direct contact with latently infected cells at a rate of h(S, L)L. The term $p(S,V)V+q(S,A)A+h(S,L)L$ then describes the total infection rate of susceptible cells. It is assumed a fraction η of infected cells to be latently infected cells and the remaining $(1-\eta )$ becomes actively infected cells, where 0 < η ≤ 1. We take e and a as the parameters for the death rates of latently and actively infected cells. Also, r, k and μ are the parameters respectively for the production rate of virus from actively infected cells, the rate at which the latently infected cells are transmitted to actively infected cells, and the clearance rate of virus. Fig. 1 is an illustration of the schematic diagram of model (1).

As in Hattaf and Yousfi [10], 11], the general incidences p(S, V), q(S, A) and h(S, L) are assumed to be continuously differentiable in the interior of $\text{I}{\text{R}}_{+}^2$ and also satisfy the following hypotheses:

• (H₁)

  $p(0,V)=0,$ ${\displaystyle \frac{\partial p}{\partial S}(S,V)>0,}$ ${\displaystyle \frac{\partial p}{\partial V}(S,V)\le 0}$   ∀ S, V ≥ 0.

• (H₂)

  $q(0,A)=0,$ ${\displaystyle \frac{\partial q}{\partial S}(S,A)>0,}$ ${\displaystyle \frac{\partial q}{\partial A}(S,A)\le 0}$   ∀ S, A ≥ 0.

• (H₃)

  $h(0,L)=0,$ ${\displaystyle \frac{\partial h}{\partial S}(S,L)>0,}$ ${\displaystyle \frac{\partial h}{\partial L}(S,L)\le 0}$   ∀ S, L ≥ 0.

It should be noted that model (1) extends as well as generalizes many special cases available in the literature. As example, one can get the latent infection model of Pankavich [18] with $p(S,V)={\beta }_{1}S,$ $q(S,A)=0,$ $h(S,L)=0$ and $\rho =0,$ where β ₁ is the virus-to-cell infection rate. Also, the model of Callaway and Perelson [3] with $p(S,V)=(1-ϵ){\beta }_{1}S,$ $q(S,A)=0,$ $h(S,L)=0$ and $\rho =0,$ where ϵ is an overall drug efficacy. Furthermore, the model (1) includes the class of HIV infection models for different rates of infection and latently infected cells as investigated in Wang et al. [26].

The model (1) reduces to

when all of infected cells become latently infected cells (i.e. $\eta =1$).

This system includes the following viral models:

• •

  Model of Rong et al. [20] with $p(S,V)={\beta }_{1}S$ and $q(S,A)=h(S,L)=0$.

• •

  Model of Hu et al. [9] with $p(S,V)=\frac{{\beta }_{1}S}{1+{\alpha }_{2}V}$ and $q(S,A)=h(S,L)=0$.

• •

  Model of Sun et al. [24] with $p(S,V)=\frac{{\beta }_{1}S}{S+V},$ $q(S,A)=h(S,A)=0$ and $\rho =0$.

• •

  Model of Wang et al. [25] with $p(S,V)=\frac{{\beta }_{1}S}{1+{\alpha }_{1}S+{\alpha }_{2}V},$ $q(S,A)=0$ and $h(S,L)=0$.

• •

  Model of Maziane et al. [15] with $p(S,V)=\frac{{\beta }_{1}S}{1+{\alpha }_{1}S+{\alpha }_{2}V+{\alpha }_{3}SV},$ $q(S,A)=0$ and $h(S,L)=0,$ where α ₁, α ₂ and α ₃ are nonnegative constants measuring the saturation or inhibitory effect.

The paper has been organized as follows: In Section 2, the existence of equilibria and the well-posedness of the model including nonnegativity and boundedness of the solutions have been established. The stability analysis of the equilibria has been presented in Section 3. An application and illustrative numerical simulations have been given in Section 4. The Section 5 is for conclusion in terms of both mathematical and biological perspectives of the findings.

2. Well-posedness and equilibria

This section first establishes the well-posedness of our model (1) by proving the nonnegativity and boundedness of solutions. Then we derive the threshold parameter for the existence of equilibria.

Theorem 2.1

All solutions of model (1) with nonnegative initial conditions remain nonnegative and bounded ∀ t > 0.

Proof

We have

$$\begin{array}{ccc}\hfill \dot{S}{|}_{S=0}& =& \lambda >0,\dot{L}{|}_{L=0}=\eta (p(S,V)V+q(S,A)A)\ge 0\text{for}\text{all}S,A,V\ge 0,\hfill \\ \hfill \dot{A}{|}_{A=0}& =& (1-\eta )\left(p\right(S,V)V+h(S,L\left)L\right)+rL\ge 0\text{for}\text{all}S,L,V\ge 0,\hfill \\ \hfill \dot{V}{|}_{V=0}& =& kA\ge 0\text{for}\text{all}A\ge 0.\hfill \end{array}$$

Then $\text{I}{\text{R}}_{+}^5$ is positively invariant with regard to (1). Next, we prove the boundedness of solutions. Denote

$${\displaystyle F\left(t\right)=S\left(t\right)+L\left(t\right)+A\left(t\right)+\frac{a}{2k}V\left(t\right).}$$

Then

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dF}{dt}}& =& {\displaystyle \lambda -dS\left(t\right)-eL\left(t\right)-\frac{a}{2}A\left(t\right)-\frac{a\mu }{2k}V\left(t\right)}\hfill \\ & \le & \lambda -\delta F\left(t\right),\hfill \end{array}$$

where ${\displaystyle \delta =\min \{d,e,\frac{a}{2},\mu \}}$. Therefore,

$${\displaystyle \underset{t\to \infty }{lim\; sup}F\left(t\right)\le \frac{\lambda }{\delta },}$$

which implies that S(t), L(t), A(t) and V(t) are bounded. □

It is obvious that model (1) has always one infection-free equilibrium E_p(S ₀, 0, 0, 0), where ${\displaystyle S_0=\frac{\lambda }{d}}$. Then we define the basic reproduction number of (1) as follows:

where $\theta =r+(1-\eta )(e+\rho )$. This number can be rewritten as follows

where

The other equilibrium of model (1) satisfies the following system

From (4)-(7), we have ${\displaystyle L=\frac{\eta (\lambda -dS)}{\theta +\eta e},}$ ${\displaystyle A=\frac{\theta (\lambda -dS)}{a(\theta +\eta e)},}$ ${\displaystyle V=\frac{k\theta (\lambda -dS)}{a\mu (\theta +\eta e)}}$ and

Since ${\displaystyle L=\frac{\eta (\lambda -dS)}{\theta +\eta e}\ge 0,}$ we have ${\displaystyle S<\frac{\lambda }{d}}$. This implies that there is no biological equilibrium when ${\displaystyle S\ge \frac{\lambda }{d}}$. Let G be a function defined on the closed interval ${\displaystyle [0,\frac{\lambda }{d}]}$ as follows

We have $G\left(0\right)=-a\mu (e+r+\rho )<0,$ ${\displaystyle G\left(\frac{\lambda }{d}\right)=a\mu (e+r+\rho )({\mathcal{R}}_0-1)}$ and

Then the equation $G\left(S\right)=0$ admits a unique solution ${\displaystyle S^{*}\in (0,\frac{\lambda }{d})}$ if ${\mathcal{R}}_0>1$. Therefore, model (1) has a unique chronic infection equilibrium E*(S*, L*, A*, V*) when ${\mathcal{R}}_0>1$.

The pervious discussions are summarized in the following theorem.

Theorem 2.2

• (i)

  If ${\mathcal{R}}_0\le 1,$ then model (1) has a unique infection-free equilibrium E_p(S ₀, 0, 0, 0), where ${\displaystyle S_0=\frac{\lambda }{d}}$ .

• (ii)

  If ${\mathcal{R}}_0>1,$ then model (1) has a unique chronic infection equilibrium E*(S*, L*, A*, V*) besides E_p, where ${\displaystyle S^{*}\in (0,\frac{\lambda }{d}),}$ ${\displaystyle L^{*}=\frac{\eta (\lambda -d{S}^{*})}{\theta +\eta e},}$ ${\displaystyle A^{*}=\frac{\theta (\lambda -d{S}^{*})}{a(\theta +\eta e)}}$ and ${\displaystyle V^{*}=\frac{k\theta (\lambda -d{S}^{*})}{a\mu (\theta +\eta e)}}$ .

3. Stability analysis

This section deals with the stability analysis of two equilibria E_p and E*. For more details, the local stability is obtained by analyzing the characteristic equation. However, the global stability is established by using two techniques, the first is based on the definition which consists to prove that the solution of the model converges to the equilibrium point independently of the initial conditions. The second technique is based on the direct Lyapunov method which aims to construct an appropriate Lyapunov functional.

Theorem 3.1

The infection-free equilibrium E_p is locally asymptotically stable if ${\mathcal{R}}_0<1$ and unstable if ${\mathcal{R}}_0>1$ .

Proof

The characteristic equation of model (1) at E_p is given by

$$\left|\begin{array}{cccc}-d-\xi & -h(S_0,0)+\rho & -q(S_0,0)& -p(S_0,0)\\ 0& \eta h(S_0,0)-(e+r+\rho )-\xi & \eta q(S_0,0)& \eta p(S_0,0)\\ 0& (1-\eta )h(S_0,0)+r& (1-\eta )q(S_0,0)-a-\xi & (1-\eta )p(S_0,0)\\ 0& 0& k& -\mu -\xi \end{array}\right|=0,$$

which lead to

$$(\xi +d)({\xi }^3+a_1{\xi }^2+a_2\xi +a_3)=0,$$

(8)

where

$$\begin{array}{ccc}\hfill a_1& =& \mu +a(1-{\mathcal{R}}_{02})+(e+r+\rho )(1-{\mathcal{R}}_{03})+\frac{ar\eta }{\theta }{\mathcal{R}}_{02},\hfill \\ \hfill a_2& =& \mu (e+r+\rho )(1-{\mathcal{R}}_{03})+a(e+r+\rho )(1-{\mathcal{R}}_{02}-{\mathcal{R}}_{03})+a\mu (1-{\mathcal{R}}_0)\hfill \\ & & +\frac{a}{\theta }[r\eta {\mathcal{R}}_0+\mu (1-\eta )(e+r+\rho ){\mathcal{R}}_{03}],\hfill \\ \hfill a_3& =& a\mu (e+r+\rho )(1-{\mathcal{R}}_0).\hfill \end{array}$$

It is obvious that $\xi =-d$ is a negative root of Eq. (8). The other roots are determined by the following equation:

$${\xi }^3+a_1{\xi }^2+a_2\xi +a_3=0.$$

(9)

If ${\mathcal{R}}_0<1,$ then a ₁ > 0, a ₂ > 0, a ₃ > 0 and

$$\begin{array}{ccc}\hfill a_1{a}_2-a_3& =& a\mu (e+r+\rho ){\mathcal{R}}_{01}+(a_1-\mu )a_2\hfill \\ & & +\mu [a_2-a(e+r+\rho )(1-{\mathcal{R}}_{02}-{\mathcal{R}}_{03})]>0.\hfill \end{array}$$

By the Routh-Hurwitz Theorem [8], we know that all roots of (9) have negative real parts. Thus, the infection-free equilibrium E_p is locally asymptotically stable if ${\mathcal{R}}_0<1$.

If ${\mathcal{R}}_0>1,$ then a ₃ < 0. So, Eq. (9) has at least one positive root. This implies that the infection-free equilibrium E_p becomes unstable when ${\mathcal{R}}_0>1$. □

The following theorem characterizes the global stability of the infection-free equilibrium E_p when ${\mathcal{R}}_0<1$.

Theorem 3.2

The infection-free equilibrium E_p is globally asymptotically stable when ${\mathcal{R}}_0<1$ .

Proof

We have the following inequality from the first equation of (1)

$$\dot{S}\le \lambda -dS,$$

which implies that

$${\displaystyle \underset{t\to \infty }{lim\; sup}S\left(t\right)\le \frac{\lambda }{d}.}$$

Then for arbitrary ϵ > 0, there exist a t ₁ > 0 such that

$$S\left(t\right)\le S_0+ϵ,\forall t\ge t_1.$$

From the last three equations of (1), for t ≥ t ₁, we have

$$\{\begin{array}{cc}\dot{L}\hfill & \le \eta (p(S_0+ϵ,0)V+q(S_0+ϵ,0)A+h(S_0+ϵ,0)L)-(e+r+\rho )L,\hfill \\ \dot{A}\hfill & \le (1-\eta )(p(S_0+ϵ,0)V+q(S_0+ϵ,0)A+h(S_0+ϵ,0)L)+rL-aA,\hfill \\ \dot{V}\hfill & =kA-\mu V,\hfill \end{array}$$

Consider the following comparison system

$$\{\begin{array}{cc}\dot{u_1}\hfill & =\eta (p(S_0+ϵ,0)u_3+q(S_0+ϵ,0)u_2+h(S_0+ϵ,0)u_1)-(e+r+\rho )u_1,\hfill \\ \dot{u_2}\hfill & =(1-\eta )(p(S_0+ϵ,0)u_3+q(S_0+ϵ,0)u_2+h(S_0+ϵ,0)u_1)+r{u}_1-a{u}_2,\hfill \\ \dot{u_3}\hfill & =k{u}_2-\mu u_3,\hfill \end{array}$$

This system can be rewritten as follows

$$\dot{u}\left(t\right)=Mu\left(t\right),$$

where $u=(u_1,u_2,u_3){}^T$ and

$$M=\left(\begin{array}{ccc}\eta h(S_0+ϵ,0)-(e+r+\rho )& \eta q(S_0+ϵ,0)& \eta p(S_0+ϵ,0)\\ (1-\eta )h(S_0+ϵ,0)+r& (1-\eta )q(S_0+ϵ,0)-a& (1-\eta )p(S_0+ϵ,0)\\ 0& k& -\mu \end{array}\right).$$

The eigenvalues of the matrix M satisfy the following equation:

$${\xi }^3+b_1{\xi }^2+b_2\xi +b_3=0,$$

$$\begin{array}{ccc}\hfill b_1& =& \mu +a(1-R_{02}\left(ϵ\right))+(e+r+\rho )(1-R_{03}\left(ϵ\right))+\frac{ar\eta }{\theta }{R}_{02}\left(ϵ\right),\hfill \\ \hfill b_2& =& \mu (e+r+\rho )(1-R_{03}\left(ϵ\right))+a(e+r+\rho )(1-R_{02}\left(ϵ\right)-R_{03}\left(ϵ\right))+a\mu (1-R_0\left(ϵ\right))\hfill \\ & & +\frac{a}{\theta }[r\eta R_0\left(ϵ\right)+\mu (1-\eta )(e+r+\rho )R_{03}\left(ϵ\right)],\hfill \\ \hfill b_3& =& a\mu (e+r+\rho )(1-R_0\left(ϵ\right)),\hfill \end{array}$$

with

$${\displaystyle R_{01}\left(ϵ\right)=\frac{k\theta p(S_0+ϵ,0)}{a\mu (e+r+\rho )},R_{02}\left(ϵ\right)=\frac{k\theta q(S_0+ϵ,0)}{a(e+r+\rho )},R_{03}\left(ϵ\right)=\frac{\eta h(S_0+ϵ,0)}{e+r+\rho }}$$

and

$$R_0\left(ϵ\right)=R_{01}\left(ϵ\right)+R_{02}\left(ϵ\right)+R_{03}\left(ϵ\right).$$

Clearly, $R_0\left(0\right)={\mathcal{R}}_0$. Since ${\mathcal{R}}_0<1,$ we can fix an ϵ > 0 small enough such that R ₀(ϵ) < 1. Thus, b ₁ > 0, b ₂ > 0, b ₃ > 0 and

$$\begin{array}{ccc}\hfill b_1{b}_2-b_3& =& a\mu (e+r+\rho )R_{01}\left(ϵ\right)+(b_1-\mu )b_2\hfill \\ & & +\mu [b_2-a(e+r+\rho )(1-R_{02}\left(ϵ\right)-R_{03}\left(ϵ\right))]>0.\hfill \end{array}$$

It follows from the Routh-Hurwitz Theorem that all eigenvalues of M have negative real parts. Therefore,

$$\underset{t\to +\infty }{\lim }{u}_i\left(t\right)=0.$$

Hence, we conclude that (L(t), A(t), V(t)) → (0, 0, 0) as $t\to +\infty$ for ${\mathcal{R}}_0<1$.

From the first equation of (1), for t ≥ t ₁, we can get

$$\lambda -dS-p(S_0+ϵ,0)V-q(S_0+ϵ,0)A-h(S_0+ϵ,0)L+\rho L\le \dot{S}\le \lambda -dS,\forall t\ge t_1.$$

Consequently,

$$\underset{t\to +\infty }{\lim }S\left(t\right)=S_0.$$

This completes the proof of Theorem 3.2. □

Next, we investigate the global asymptotic stability of the chronic infection equilibrium E*(S*, L*, A*, V*) by assuming that ${\mathcal{R}}_0>1$ and the incidence functions p, q and h satisfy,  ∀ S, L, A, V > 0, the following further hypothesis:

Theorem 3.3

Suppose that ${\mathcal{R}}_0>1$ and (H ₄ ) holds. Then the chronic infection equilibrium E* is globally asymptotically stable for $\rho =0$ and $\eta =1$ .

Proof

Consider the following Lyapunov functional

$$\begin{array}{ccc}\hfill W(S,L,A,V)& =& S-S^{*}-{\int }_{S^{*}}^S\frac{p(S^{*},V^{*})}{p(s,V^{*})}ds+L^{*}\Phi \left(\frac{L}{L^{*}}\right)\hfill \\ & & {\displaystyle +\frac{p(S^{*},V^{*})V^{*}+q(S^{*},A^{*})A^{*}}{r{L}^{*}}{A}^{*}\Phi \left(\frac{A}{A^{*}}\right)+\frac{p(S^{*},V^{*})}{\mu }{V}^{*}\Phi \left(\frac{V}{V^{*}}\right),}\hfill \end{array}$$

where $\Phi \left(z\right)=z-1-\ln z,$ for z > 0. It is clear that Φ(z) ≥ 0 for all z > 0, and $\Phi \left(z\right)=0$ if and only if $z=1$. Thus, W(S, L, A, V) > 0 for all S, L, A, V > 0 and $W(S^{*},L^{*},A^{*},V^{*})=0$. By a simple computation, we get

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dW}{dt}}& =& d{S}^{*}(1-\frac{S}{S^{*}})(1-\frac{p(S^{*},V^{*})}{p(S,V^{*})})\hfill \\ & & +p(S^{*},V^{*})V^{*}(-1-\frac{V}{V^{*}}+\frac{p(S,V)V}{p(S,V^{*})V^{*}}+\frac{p(S,V^{*})}{p(S,V)})\hfill \\ & & +q(S^{*},A^{*})A^{*}(-1-\frac{A}{A^{*}}+\frac{p(S^{*},V^{*})q(S,A)A}{p(S,V^{*})q(S^{*},A^{*})A^{*}}+\frac{p(S,V^{*})q(S^{*},A^{*})}{p(S^{*},V^{*})q(S,A)})\hfill \\ & & +h(S^{*},L^{*})L^{*}(-1-\frac{L}{L^{*}}+\frac{p(S^{*},V^{*})h(S,L)L}{p(S,V^{*})h(S^{*},L^{*})L^{*}}+\frac{p(S,V^{*})h(S^{*},L^{*})}{p(S^{*},V^{*})h(S,L)})\hfill \\ & & -p(S^{*},V^{*})V^{*}\left[\Phi \right(\frac{p(S^{*},V^{*})}{p(S,V^{*})})+\Phi (\frac{p(S,V^{*})}{p(S,V)})+\Phi (\frac{p(S,V)V{L}^{*}}{p(S^{*},V^{*})V^{*}L})\hfill \\ & & +\Phi \left(\frac{A^{*}L}{A{L}^{*}}\right)+\Phi \left(\frac{A{V}^{*}}{A^{*}V}\right)]-q(S^{*},A^{*})A^{*}[\Phi \left(\frac{p(S^{*},V^{*})}{p(S,V^{*})}\right)\hfill \\ & & +\Phi \left(\frac{p(S,V^{*})q(S^{*},A^{*})}{p(S^{*},V^{*})q(S,A)}\right)+\Phi \left(\frac{q(S,A)A{L}^{*}}{q(S^{*},A^{*})A^{*}L}\right)+\Phi \left(\frac{A^{*}L}{A{L}^{*}}\right)]\hfill \\ & & -h(S^{*},L^{*})L^{*}\left[\Phi \right(\frac{p(S^{*},V^{*})}{p(S,V^{*})})+\Phi (\frac{p(S,V^{*})h(S^{*},L^{*})}{p(S^{*},V^{*})h(S,L)})+\Phi (\frac{h(S,L)}{h(S^{*},L^{*})}\left)\right].\hfill \end{array}$$

Since the incidence function p(S, V) is strictly monotonically increasing with respect to S, we deduce that

$$(1-\frac{S}{S^{*}})(1-\frac{p(S^{*},V^{*})}{p(S,V^{*})})\le 0.$$

By (H ₄), we obtain

$${\displaystyle -1-\frac{V}{V^{*}}+\frac{p(S,V)V}{p(S,V^{*})V^{*}}+\frac{p(S,V^{*})}{p(x,v)}=(1-\frac{p(S,V)}{p(S,V^{*})})(\frac{p(S,V^{*})}{p(S,V)}-\frac{V}{V^{*}})\le 0,}$$

$$\begin{array}{c}\hfill -1-\frac{A}{A^{*}}+\frac{p(S^{*},V^{*})q(S,A)A}{p(S,V^{*})q(S^{*},A^{*})A^{*}}+\frac{p(S,V^{*})q(S^{*},A^{*})}{p(S^{*},V^{*})q(S,A)}\\ \hfill {\displaystyle =(1-\frac{p(S^{*},V^{*})q(S,A)}{p(S,V^{*})q(S^{*},A^{*})})(\frac{p(S,V^{*})q(S^{*},A^{*})}{p(S^{*},V^{*})q(S,A)}-\frac{A}{A^{*}})\le 0,}\end{array}$$

and

$$\begin{array}{ccc}& & -1-\frac{L}{L^{*}}+\frac{p(S^{*},V^{*})h(S,L)L}{p(S,V^{*})h(S^{*},L^{*})L^{*}}+\frac{p(S,V^{*})h(S^{*},L^{*})}{p(S^{*},V^{*})h(S,L)})\hfill \\ & & {\displaystyle =(1-\frac{p(S^{*},V^{*})h(S,L)}{p(S,V^{*})h(S^{*},L^{*})})(\frac{p(S,V^{*})h(S^{*},L^{*})}{p(S^{*},V^{*})h(S,L)}-\frac{L}{L^{*}})\le 0.}\hfill \end{array}$$

Since Φ(x) ≥ 0, we have ${\displaystyle \frac{dW}{dt}\le 0}$ with equality if and only if $S=S^{*},$ $L=L^{*},$ $A=A^{*}$ and $V=V^{*}$. From LaSalle’s invariance principle [12], we conclude that the chronic infection equilibrium E* is globally asymptotically stable when ${\mathcal{R}}_0>1$. □

4. Application and numerical simulations

In this section, we first apply our main results to the following HIV infection model:

which is a special case of model (1) by choosing $f(S,V)=\frac{{\beta }_{1}S}{1+{\alpha }_{1}V},$ $q(S,A)=\frac{{\beta }_{2}S}{1+{\alpha }_{2}A}$ and $h(S,L)=\frac{{\beta }_{3}S}{1+{\alpha }_{3}L}$ with β ₂ and β ₃ are the cell-to-cell transmission rates through actively and latently infected cells, respectively.

Obviously, the hypotheses $\left(H_1\right)-\left(H_3\right)$ are satisfied. Further, we have

and

Then the assumption (H ₄) is also satisfied. In this special case, the basic reproduction number has the following form:

According to Theorems 3.2 and 3.3, we deduce the following result.

Corollary 4.1

Let ${\mathcal{R}}_0$ defined by (11) .

• (i)

  If ${\mathcal{R}}_0<1,$ then the infection-free equilibrium E_p of model (10) is globally asymptotically stable.

• (ii)

  If ${\mathcal{R}}_0>1,$ then the infection-free equilibrium E_p becomes unstable and the chronic infection equilibrium E* of model (10) is globally asymptotically stable for $\rho =0$ and $\eta =1$ .

Now, we carry out numerical simulations to confirm the above analytical results concerning the dynamics of model with the parameter values given in Table 1 .

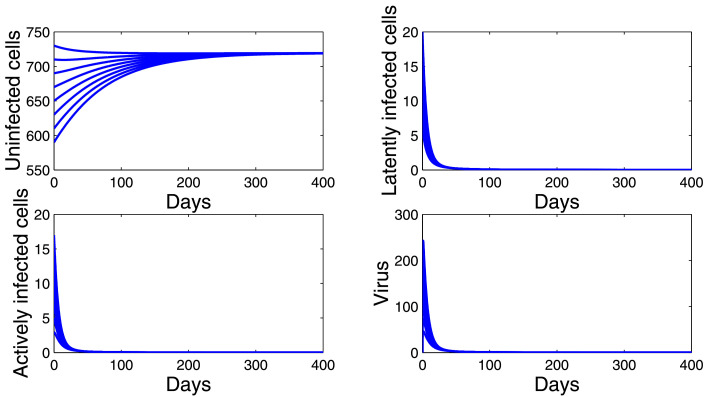
Firstly, we choose ${\beta }_1=5.2\times {10}^{-5},$ $\rho =0.01$ and $\eta =0.7$. By a simple computation, we have ${\mathcal{R}}_0=0.9733<1$. Hence, model (10) has an infection-free equilibrium E_p(719.4245, 0, 0, 0). Fig. 2 shows that the trajectories of (10) starting from different initial values tend to E_p. This supports the global stability result given by Corollary 4.1(i).

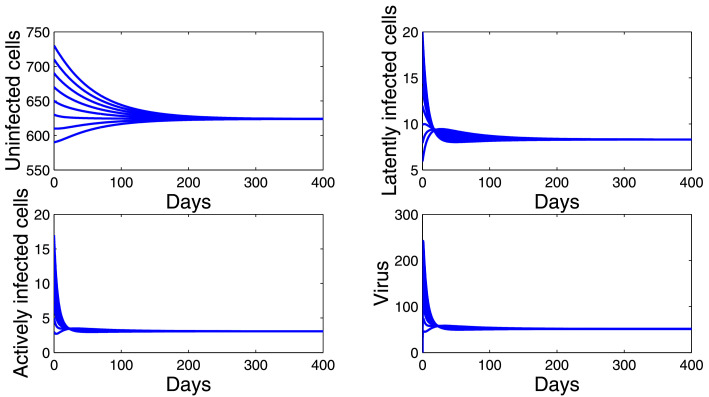
Secondly, we choose ${\beta }_1=2.4\times {10}^{-4},$ $\rho =0$ and $\eta =1$. In this case, we have ${\mathcal{R}}_0=6.7313>1$. Fig. 3 shows that the trajectories of model (10) starting from different initial values converge to E*(628.2521, 8.3904, 3.1097, 51.8294). This confirms the global stability result given by Corollary 4.1(ii).

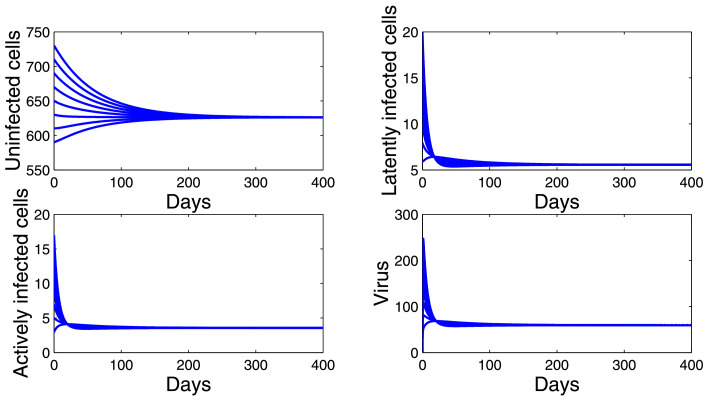
Thirdly, we choose ${\beta }_1=2.4\times {10}^{-4},$ $\rho =0.01$ and $\eta =0.7$. Then ${\mathcal{R}}_0=7.6442>1$. Fig. 4 shows that E*(618.5765, 5.4708, 3.5012, 58.3445) is globally asymptotically stable despite ρ ≠ 0 and η ≠ 1. Thus, the conditions $\rho =0$ and $\eta =1$ are not necessary for the global asymptotic stability of the chronic infection equilibrium E*. We will prove analytically this open problem in future work.

5. Conclusions

The work developed a model by using tools and techniques of mathematics for infection by viruses with latently infected cells and cell-to-cell transmission. The well-posedness of the model, including nonnegativity and boundedness of solutions have been established. It also identified two equilibria, viz. an infection-free equilibrium E_p and chronic infection equilibrium E*. It is proved that E_p is globally asymptotically stable if the basic reproduction number is less than one, which implies that the virus is eradicable and the infection is curable. And, when the basic reproduction number is greater than one, E_p becomes unstable and E* is globally asymptotically stable for $\rho =0$ and $\eta =1$. In this case, the virus persists in the host. On the other hand, the models and results presented in Callaway and Perelson [3], Hu et al. [9], Maziane et al. [15], Pankavich [18], Rong et al. [20], Sun et al. [24], Wang et al. [25], 26] are improved and generalized.

It is observed from the explicit formula of the basic reproduction number ${\mathcal{R}}_0$ given in (3) that ${\mathcal{R}}_0$ is as sum of the basic reproduction numbers for the classical virus-to-cell infection mode ${\mathcal{R}}_{01},$ cell-to-cell transmission mode via actively infected cells ${\mathcal{R}}_{02}$ and cell-to-cell transmission mode via latently infected cells ${\mathcal{R}}_{03}$. Hence, ignoring the cell-to-cell transmission in viral infections dynamics will underestimate ${\mathcal{R}}_0$. Further, the study of this paper can be of help for the biologists to develop effective treatments against viral infections in order to reduce the patients’ basic reproduction number to less than one and eliminate the latent reservoirs which represent the main obstacle to the eradication of virus from the human body.

Credit statement

Author 1 discussed the research problem with Author 2 first. Author 2 gave his opinion on the formulation of the model and possible solutions. All the authors contributed in developing the main results and their proofs. All authors contributed in each section of the paper and approved the paper for submission.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.