Abstract
Experimental studies on intrinsically disordered and unfolded proteins have shown that in isolation they typically have low populations of secondary structure, and exhibit distance scaling suggesting they are at near theta-solvent conditions. Until recently however, all-atom force fields failed to reproduce these fundamental properties of intrinsically disordered proteins (IDPs). Recent improvements by refining against ensemble averaged experimental observables for polypeptides in aqueous solution have addressed deficiencies including secondary structure bias, global conformational properties, and thermodynamic parameters of biophysical reactions such as folding and collapse. To date, studies utilizing these improved all-atom force fields have mostly been limited to a small set of unfolded or disordered proteins. Here, we present data generated for a diverse library of unfolded or disordered proteins using three progressively-improved generations of Amber03 force fields, and we explore how global and local properties are acted by each successive change in the force field. We find that the most recent force field refinements significantly improve the agreement of the global properties such as radii of gyration and end-end distances with experimental estimates. However, these global properties are largely independent of the local secondary structure propensity. This result stresses the need to validate force fields with reference to a combination of experimental data providing information about both local and global structure formation.
Graphical Abstract
Introduction
Studies of protein structure and function have historically focused on folded proteins or protein domains, in a large part because they were amenable to experimental structure determination. However, it is now well appreciated that proteins which are either partially or fully disordered perform vital functions .1,2 In contrast to folded proteins, these so-called intrinsically disordered proteins (IDPs), lacking a well-defined three-dimensional structure, can adopt a broad distribution of conformations3,4 and cannot easily be studied by conventional structural biology methods. Only a limited number of experimental methods are applicable, most notably nuclear magnetic resonance (NMR),5 Förster resonance energy transfer (FRET)6 and small-angle X-ray scattering (SAXS).7 In addition, experimental IDP data sets are typically averaged over a broad conformational ensemble,3,4 increasing the difficulty of extracting the underlying structural properties.8–12
In this context, molecular simulation is clearly a useful tool, as it can potentially yield information on the structural and dynamic properties of IDPs associated with their functions with high spatiotemporal resolution .13–15 Experimental data may also be incorporated in molecular simulations, either as a bias or to reweight the configurations sampled in an existing trajectory.8,16–20 Regardless of whether or not such a bias is used, having an accurate simulation force field is expected to improve the quality of the resulting structural ensemble.14,15,21–23
However, as has been well documented in recent years, many force fields in current usage have significant shortcomings when applied to unfolded and disordered proteins ,22,24–26 often being too compact or giving a poor reproduction of partial secondary structure content in unfolded states (reviewed in27–30). This is not because they were explicitly optimized to reproduce folded protein structures: in fact, the parameters were usually optimized to describe the properties of small molecule fragments containing functional groups common in proteins, and then assumed to be mostly “transferable” to the macromolecular force field31–34 although more recent efforts at backbone parameterization have included data derived from the Protein Data Bank.35–37 Nonetheless, the focus of the systems used in testing and in applications was on folded states. As a result of some 40 years of optimization, all-atom force fields have now been shown to be of sufficient quality to reversibly fold many small proteins (less than 100 residues), a strong validation of the optimization strategy used,38–41notwithstanding the remaining deficiencies for unfolded states, mentioned above.
Disordered proteins populate a diverse ensemble of conformers of similar free energy and their population is sensitive to small errors in the energy function used for all-atom simulations. Therefore, ensemble-averaged experimental data for IDPs and weakly structured peptides in different solvent conditions are a good target to optimize force fields. Two major shortcomings of force fields with respect to reproducing IDP properties have been identified: incorrect prediction of secondary structure and a tendency to be too collapsed with respect to experiment. The former problem had long been recognized, leading in the case of the Amber force fields to a succession of changes in which the secondary structure propensity was altered by modifying torsion angle parameters (Amber ff94 to Amber ff96, Amber ff99, Amber ff99SB and beyond).42–48 With the development of advanced sampling techniques and improved computer power, it became practical to use equilibrium data for weakly structured peptides in order to optimize secondary structure propensity, as was done in the Amber ff03*,49 Amber ff99SB*,49 CHARMM 22*.50 and CHARMM 3651 force fields, to give just a few examples. As a consequence of these and related efforts, force fields can now more accurately capture the propensity for local, α, β or extended structures in disordered proteins.
More recently, it was found that the radius of gyration and related properties of disordered proteins were poorly reproduced by current force-fields: simulations of unfolded or disordered proteins frequently resulted in collapsed structures, often barely larger than folded states,24,52–54 pointing to insufficiently favorable solvation, a picture that was supported by overly favorable protein-protein interactions in several simulation force fields.55,56Initial attempts to correct this by changing from the widely-used TIP3P water model57 to more accurate models such as TIP4P-Ew25,52 or TIP4P/200558 yielded some improvements, but disordered states were still too collapsed.52
Two main approaches have been taken to address the issue of collapsed unfolded states. In the first, the strength of the protein-water Lennard-Jones term22,25 is directly modified, while in the second the water model itself is reparametrized to have a stronger contribution from dispersion interactions.59 In both of these instances, and other related studies,60 the major change from previous force fields has been to make protein solvation more favorable. These efforts have resulted in significant improvements in capturing not only dimensions of unfolded protein but also intrachain peptide dynamics in disordered peptides.61 These models have been used extensively to obtain molecular insights into the equilibrium structural ensemble of disordered proteins which otherwise is challenging to obtain solely from experimental data.13,14,27 In addition to the above efforts, a host of recent studies have been directed at further improvements in reproducing the properties of both folded and disordered proteins in all-atom simulations.15,23,62–66
Because of the known deficiencies of force fields, many investigators now compare their simulation results to experimental data in order to identify potential problems. However, as we will show, agreement with one set of data is not necessarily a strong validation of the results, as different observables can reflect different properties of the ensemble. In order to systematically address this issue, we focus on comparing a series of sequential modifications of the Amber ff03 force field45 which have been developed in our laboratories, and for which we have a large set of data available. Using a large data set of disordered and unfolded proteins, we provide a comprehensive survey of Amber ff03*, ff03w, and ff03ws, the evolution of which will be detailed in the next section. We find that the degree of compaction is most significantly affected over this series, with the chain dimensions from Amber ff03ws being most similar to experimental estimates.
Force Field Evolution
The modified versions of the Amber ff03 force field considered here are ff03*, ff03w, and ff03ws. The parent force field ff03 is an all-atom molecular mechanical potential based on the original Amber ff94 force field,31 but with atomic partial charges refitted to an electrostatic potential calculated from a quantum chemistry calculation including an implicit solvation model, as well as refitted dihedral potentials.45 The model is coupled with a 3-site water model, TIP3P,57 to represent the proteins in an explicit aqueous solution. Over the last decade, our groups have developed a number of cumulative improvements to this force field. Prior to the introduction of empirical backbone torsional correction term,49 secondary structure bias was a well-known problem. The backbone correction term adjusted for the very small, but nonetheless significant, biases towards one or other secondary structure. A single additional torsion term was applied to the Ψ torsion angle and its parameters optimized to match helix populations inferred from chemical shift data for the (AAQAA)3 peptide.49 This simple correction has been made in the context of the original force fields Amber ff99SB, ff03 and CHARMM22, yielding respectively the ff99SB* and ff03*49 and CHARMM22*39 and have been shown to allow the use of same force field to fold both helix and β-strand-dominant peptides.39–41
Protein-water interactions and water-mediated interactions are clearly important driving forces behind biological assembly processes. Therefore, both protein-water and water-water interactions are critical components in the modeling of biomolecules in aqueous solutions. Explicit modeling of water has been area of intense research activity which has led to much improved models .67–69 We have focused on the TIP4P/2005 water model,69 one of the most accurate four-site point-charge models for liquid water. As a first step, this water model was combined with Amber ff03, together with a backbone correction for secondary structure propensity, resulting in the ff03w force field (a similar approach was applied to Amber ff99SB to give ff99SBw).58 This combination yielded some immediate improvements in the thermodynamics of protein folding as well as aqueous solution properties of IDPs such as the temperature-dependent collapse seen in SAXS and FRET experiments.70–72
Despite the improvements obtained through the backbone torsion corrections and the use of better water models such as TIP4P/2005 and TI4P-Ew, it was found that unfolded and disordered proteins were still overly compact compared to experimental estimates ,24–26,52,53,58 suggesting that (in simulations) water acts as a poor solvent for polypeptides.
In an effort to remedy the poor solvation of proteins, we proposed a simple and minimal force field change, by introducing a general scaling factor included in the geometric combination rule for the Lennard-Jones ε parameters between the oxygen atoms in water and every types of atoms in protein.22 Note that in principle an amino acid-based, or atom-based scaling factor could be introduced,25 but would require more experimental data for optimization. We found that for Amber ff03w, a scaling factor of 1.10 (10% increase in the protein-water interactions) has been found to be optimal for matching the simulated and experimental Rg of a fragment of CspTm. Amber ff03w with this scaling of protein-water interactions was named Amber ff03ws.22 The same change in the context of Amber ff99SB-ildn-Q73 was termed Amber ff99SBws. Amber ff03ws has then been shown to reproduce experimentally measured sizes of a number of unfolded or disordered proteins and resolve the nonspecific protein-protein interactions problem.14,22,26 For compatibility with the new Amber ff03ws, we have also optimized protein-denaturant interactions based on the KBFF denaturant force field74,75 and extended Amber ff03ws to work with both urea and GdmCl (i.e. KBFFs).76
In this work, we have used the Amber ff03-series of force field modifications described above to sample a broad variety of proteins, spanning a range of sizes and sequence characteristics. We will discuss how each of these successive improvements to Amber ff03 family affect the local and global structural properties of IDPs in the next two sections. Methodological details, such as the advanced sampling methods, algorithms, ensembles, and analysis are provided in Supporting Information. A summary of the properties of all the sequences in this work are presented in Figure S1 and simulation run lengths are summarized in Table S1–S4.
In general, any polymer is able to undergo a collapse transition as conditions such as temperature or solvent are varied, from a state in which it forms a completely collapsed globule and attractive interactions dominate, to one in which repulsive interactions dominate and the chain is expanded, the self-avoiding walk limit. At a point in between these extremes, known as the θ state, the attractive and repulsive interactions effectively cancel, yielding chain statistics similar to those of a ghost chain.78 Thus, the degree of collapse and its response to changes in environmental conditions such as temperature or solvents is an important global property of intrinsically disordered proteins.
The degree of collapse of a polymer chain can be characterized using a scaling law of the form79
| (1) |
in which Rg is the radius of gyration, k is a prefecture, ν is a scaling exponent, and N is the chain length (here we follow the convention in the protein biophysics literature80 that N is the number of residues rather than the number of bonds N −1; in practice, this makes a negligible difference). By measuring the internal distance scaling within different proteins, Schuler and coworkers determined average scaling exponents of 0.46 and 0.62 in aqueous solution and in high denaturant solution, respectively, by using FRET experiments,6 although there is more variation in water than in denaturant .6,81 Similarly, Plaxo and coworkers have reported a scaling exponent of about 0.6 when fitting Rg from SAXS experiments under denaturing conditions.80 More recent analysis of SAXS and FRET data confirmed these conclusions, although the estimated scaling exponents in water were slightly larger.9,12,14,82 Thus, proteins in water are close to the θ-state, which is characterized by scaling exponent ν = 0.5 while in denaturant they are closer to a self-avoiding walk, for which ν= 0.6.
To address the scaling behavior in simulations, we compiled simulation data for proteins with a broad range of characteristics. In Figure S1, we list the hydrophobicity, net charge, and praline content for each sequence. The proteins are either intrinsically disordered, or for foldable proteins, in which case we analyze only their equilibrium unfolded ensembles. For small peptides where a folding equilibrium was sampled in the simulations (such as GB1 and TrpCage), we decide the unfolded population according to a cutup using a standard metric such as Cα RMSD or backbone dRMS. For other foldable proteins (such as CSP, NTL9, Ubiquitin, Barstar, etc.) we did not observe folding transitions within the time scales of the simulation. In Figure 1A we compile the average radii of gyration as a function of the chain length for each protein, and with each force field variant, at 300 K. The average Rg’s approximately follow a power law dependence (Eq. 1) with the fitted parameters and statics tabulated in Table 1. The older generations of the force field, ff03* and ff03w, yield fairly compact ensembles which are much more compact than the experimentally observed unfolded or disordered protein size with scaling exponents of 0.38 and 0.39 respectively, close to those of a compact globule, inconsistent with experiment which shows the chains to be more expanded in water. By contrast, the scaling exponent in water for the latest generation, ff03ws, is much closer to the experimental estimates, with ν = 0.53. In addition, the scaling exponent for ff03ws in denaturant is close to the theoretical value for a self-avoiding walk (due to the finite length of the chain it is slightly larger than that infinite-chain limit). While the trend approximately follows a power law, there are small deviations from the perfect fit, presumably reflecting the broad range of sequence characteristics represented by these peptides (Figure 1A). Notably, the scatter is larger for proteins in water than in denaturant, consistent with a picture in which the denaturant effectively cancels the sequence-specific attractive features of each chain; a similar picture has been observed in experiments .6,81 We note that we exclude several proteins from Figure 1A as extreme outliers due to their unusually high charge or proline content (Figure S1). These include PROT-C (03w), PROT-N (03w) and tau174−183 (03*). Proline has computationally been shown to have an impact on the dimension of the disordered proteins in a recent study.83 An all-inclusive version of Fig. 1A is presented in Figure S2.
Figure 1:
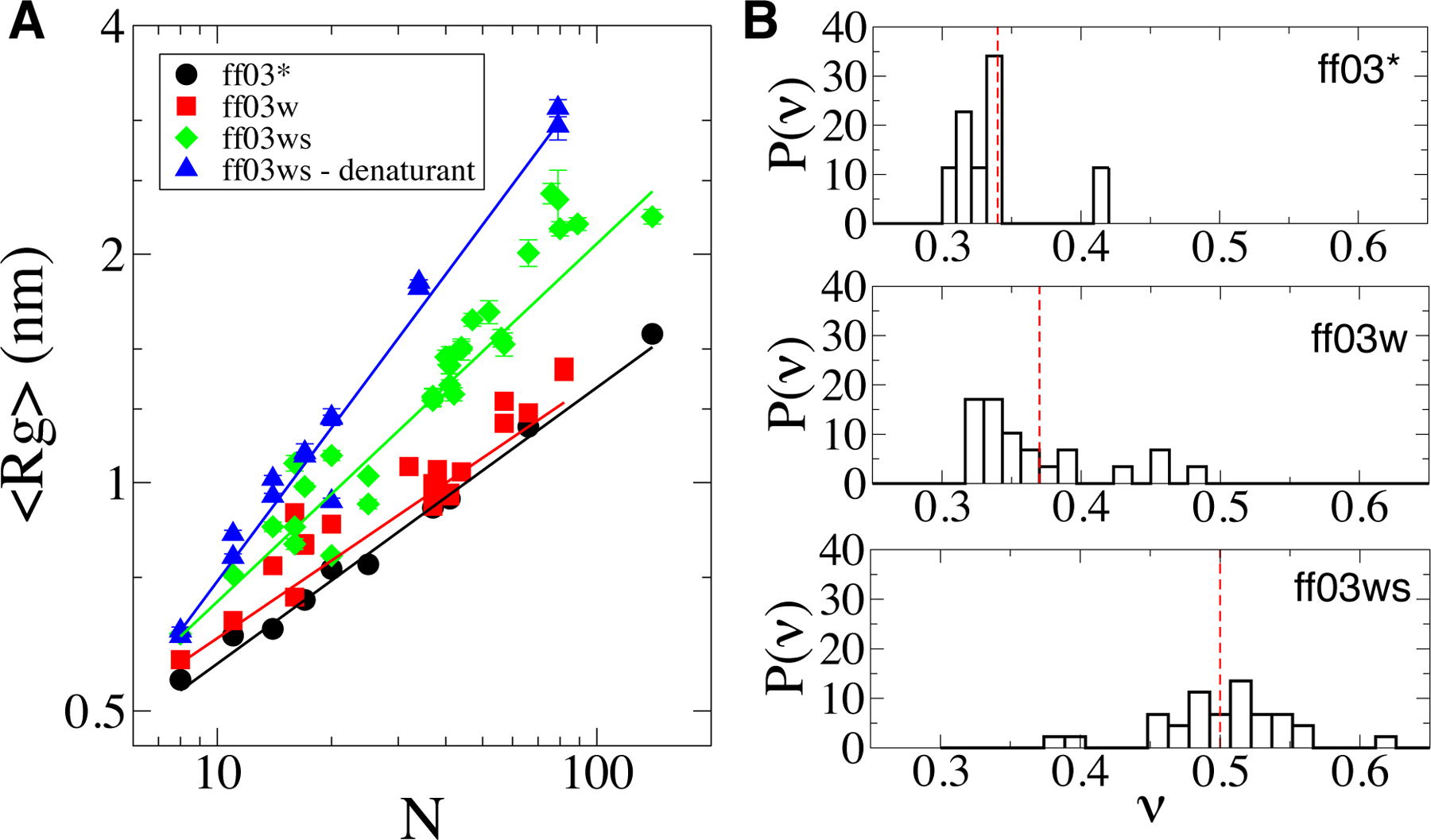
Chain size characteristics of the unfolded and disordered protein ensembles. A) Radius of gyration, Rg, with respect to peptide length, N for the deferent proteins in the data set. Symbols denote the ensemble-averaged values whereas solid lines represent power law _fits. Fit parameters are reported in Table 1. B) Normalized distribution of scaling exponents as evaluated from internal distance scaling. Broken red lines indicate the average scaling exponent, ν, for each force _field. Errors are calculated blocked standard error using two equal, non-overlapping blocks of data.77 Symbol sizes are larger than the error bars for the data points whose error bars are not visible.
Table 1:
Fit parameters from the least-squares fitting of the data in Fig. 1A. Exponents and prefectures of power law function (Eq. 1) presented together with the statistics of the fits including the correlation coincident and the number ofsamples used for _fitting. Standard errors are shown in brackets.
| Force field | Exponent v | Prefactor k (nm) | Correlation coefficient | number of samples |
|---|---|---|---|---|
| ff03* | 0.38 [0.01] | 0.25 [0.01] | 0.99 | 10 |
| ff03w | 0.39 [0.03] | 0.24 [0.03] | 0.90 | 29 |
| ff03ws | 0.53 [0.03] | 0.21 [0.02] | 0.90 | 32 |
| ff03ws-denaturant | 0.64 [0.02] | 0.18 [0.01] | 0.99 | 15 |
We have also calculated internal distance scaling separately for each protein, by computing the root mean square distance Ri,j between the C β carbon of every pair of residues(i, j) (where i ≠ j), as a function of sequence separation |i - j|. The scaling of the averaged distances as a function of |i − j| can be approximated by a power law
| (2) |
with b and ∨ the fitting parameters, providing an independent estimate of compactness of the protein.78,84 Individual fits of the power law function to the scaling of intra-chain distances with sequence separation are presented in Figures S3, S4 and S5, and the distribution of the scaling exponents obtained for each force field is in Figure 1B. The exponent of 0.5 corresponds to a so-called θ -state of the chain in which the effective interactions between monomers are on average neither repulsive nor attractive. Exponents smaller than 0.5 indicate a net attractive interaction between monomers, therefore, a more compact overall conformation. When the interactions between monomers become repulsive, the scaling exponent approaches the limiting value of Ȉ 0.6 for long chains .78 Consistent with the scaling of the Rg of the proteins, the average of these exponents is significantly increased when protein-water interactions were optimized in ff03ws. Similarly, there is only a slight increase in ν moving from ff03* to ff03w. This confirms that using a water model which more accurately reproduces the properties of water is not sufficient to improve the accuracy of the all-atom protein simulations in explicit water.
The improvement in the reproduction of the sizes of unfolded and disordered proteins by the newest generation of the force field (ff03ws) is striking. We emphasize that this improvement is not limited to the ensemble-averaged global structural quantities. In earlier work, we have investigated the diffusionand reaction-controlled rates of contact formation within disordered peptides, finding that simulations with the newest generation of the force field more accurately reproduce the experimentally determined dynamics.61,76 On the other hand, the rates obtained from the older generations of the force field deviate from the experimental data by up to an order of magnitude. We have rationalized this improvement as due to the
We selected three of larger unfolded/disordered proteins in our data set, with a partial secondary structure content, to investigate trends in secondary structure across the series ff03*-ff03w-ff03ws. While the Islet Amyloid PolyPeptide (IAPP)85 and the 310–350 fragment from a TAR-DNA binding protein (TDP-43310−350)13 are intrinsically disordered, cold-shock protein (CSP) from Thermotoga maritama72 can fold into a five-stranded β -barrel, but only its unfolded state has been sampled in our simulations. We calculate the secondary structure content of the proteins following the widely used DSSP algorithm.86 DSSP assigns seven structure types (α -helix, 3(10)-helix, 5-helix, β-sheet, β -bridge, turn, and bend) according to the backbone hydrogen bonds of each residue of each conformer. If the given residue does not satisfy any of these seven types, DSSP assigns it as coil. In order to concisely summarize the differences between the force fields, we broadly classify DSSP structure types into three groups in Figure 2: (i) helix: α-helix, 3(10)-helix and 5-helix, (ii) beta: β-sheet and (iii) disordered: everything else. DSSP analysis with all eight types is presented in Figure S7–S9 for all of the proteins. Fig. 2, top row shows the average of the total structure content and it indicates that all the proteins studied are predominantly disordered with some helical content. While the helix fraction is essentially zero for CSP, it reaches 0.3 for IAPP and TDP-43310−350. Helix fractions from the three force fields are similar to each
Figure 2:
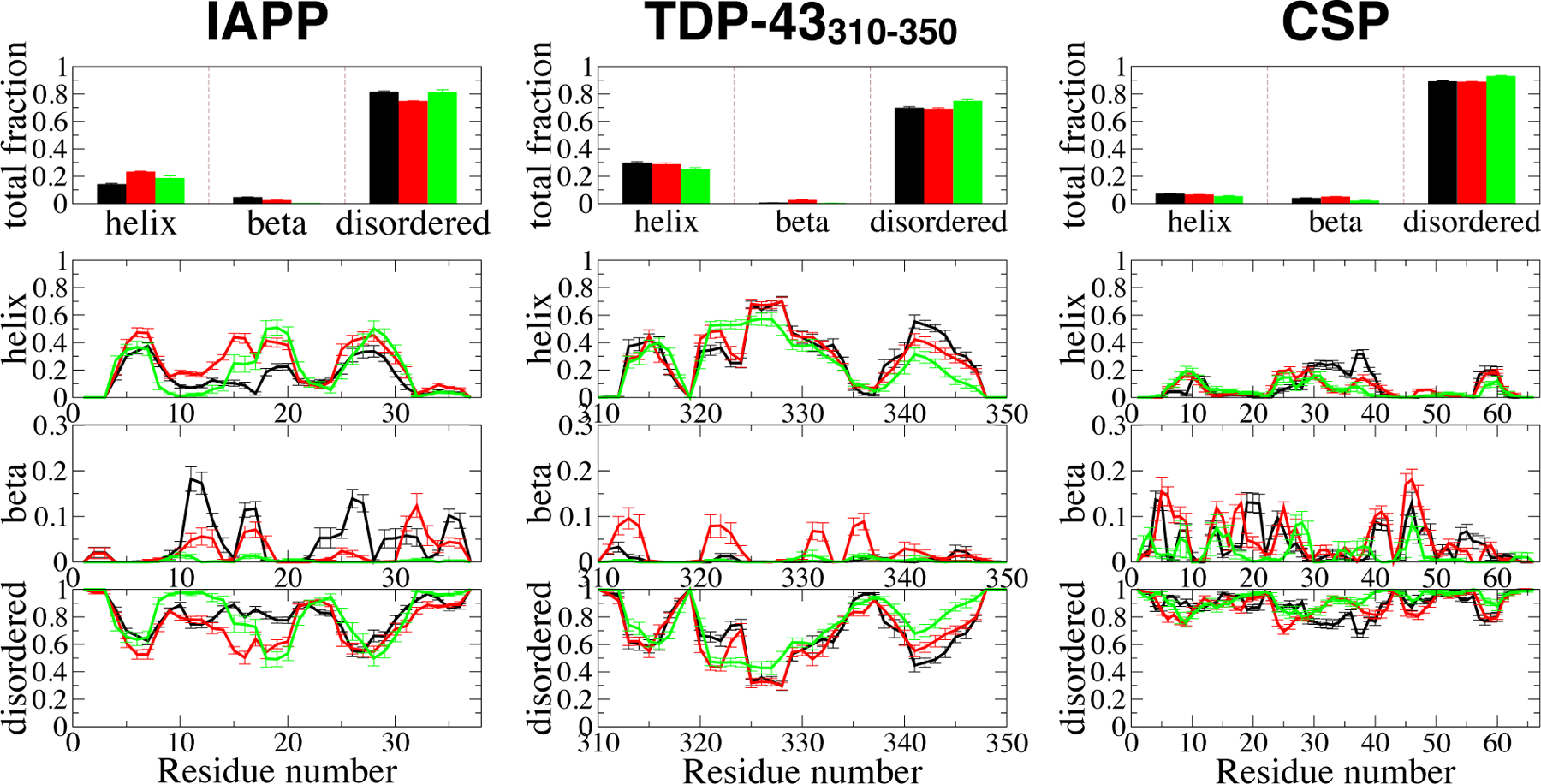
DSSP based secondary propensities for three polypeptides, IAPP, TDP-43310-350and CSP. Top panels represent the total fractions of the structures sampled and the other panels show the per-residue secondary structure propensities including alpha, beta and disordered secondary structures. Note we have reduced the DSSP-defined secondary structures into three types for the clarity of interpreting the differences between the three force fields (see the text), black: ff03* (black), ff03w (red), and _03ws (green). Errors are calculated blocked standard error using two equal, non-overlapping blocks of data.
other, with the differences being comparable to the statistical error in the simulations. This is not unexpected, because in each of 03*, 03w and 03ws, a dihedral correction term on the ψ dihedral was optimized to reproduce helical propensity in model peptides; much larger differences would be expected when comparing to earlier force fields.53,87 The per-residue analysis of the structure content (three bottom rows of Fig. 2) reveals that the difference in helical fractions of IAPP for different versions of the force field mainly comes from fluctuations in the middle region of the peptide, whereas the helix fractions of the two termini are mainly conserved. The TDP-43310−350 fragment has the largest secondary structure content of all the three sequences, a significant fraction of α-helix, which is nearly identical for all three force fields (Fig. 2). CSP, on the other hand, barely has any α helix or β-sheet fraction, which is quantitatively consistent in all three force fields. In summary, therefore, three force fields with very different degrees of overall chain compaction nevertheless populate very similar secondary structures.
We note that each of these force fields have already been extensively validated against experimental NMR data for different systems. To give an illustrative example, we present NMR secondary chemical shifts and J-couplings for the TDP-43310−350 peptide for which solution experimental data is available (Fig. 3). All calculated chemical shift deviations with respect to random coil (ΔδCA, ΔδCB, Δδ C, Δδ N, ΔδHN, Δδ HA) can be found in Figure S10,together with experimental data. We note the good consistency between the experimental and simulation CSDs (Fig. 3A) data for all force fields as evident from the average root- mean-square difference (RMSD) between experimental and simulation data for CA− CB (reported on legends, Fig. 3A). All of the force fields yield an RMSD (i.e. 0.94, 0.99 and 0.72 ppm), less than the prediction error of SPARTA+ (±1 ppm for carbon chemical shifts88).CSD estimates from ff03ws are closest to the experimental data with the lowest RMSD of 0.72 ppm. Fig. 3B shows the per-residue deviation of simulated 3JHNH coupling constant from experiment calculated for each of the three force fields, also indicating a reasonable agreement between simulation and experiment for all the three force fields. Simulated 3JHNHA values are predicted employing the Karplus equation with a parameter set suitable for IDPs89 (see also SI Text, Analysis). The x2 difference between simulation and experiment is calculated using the experimental uncertainties,89 the smaller the value the better the agreement between simulation and experiment. The x2 from the three force fields are very similar to each other, suggesting similar performance of these force fields in reproducing the 3JHNH coupling constant closely relevant to local torsional angles. Raw data for the three force fields and the experiment are shown in Figure S11.
Figure 3:
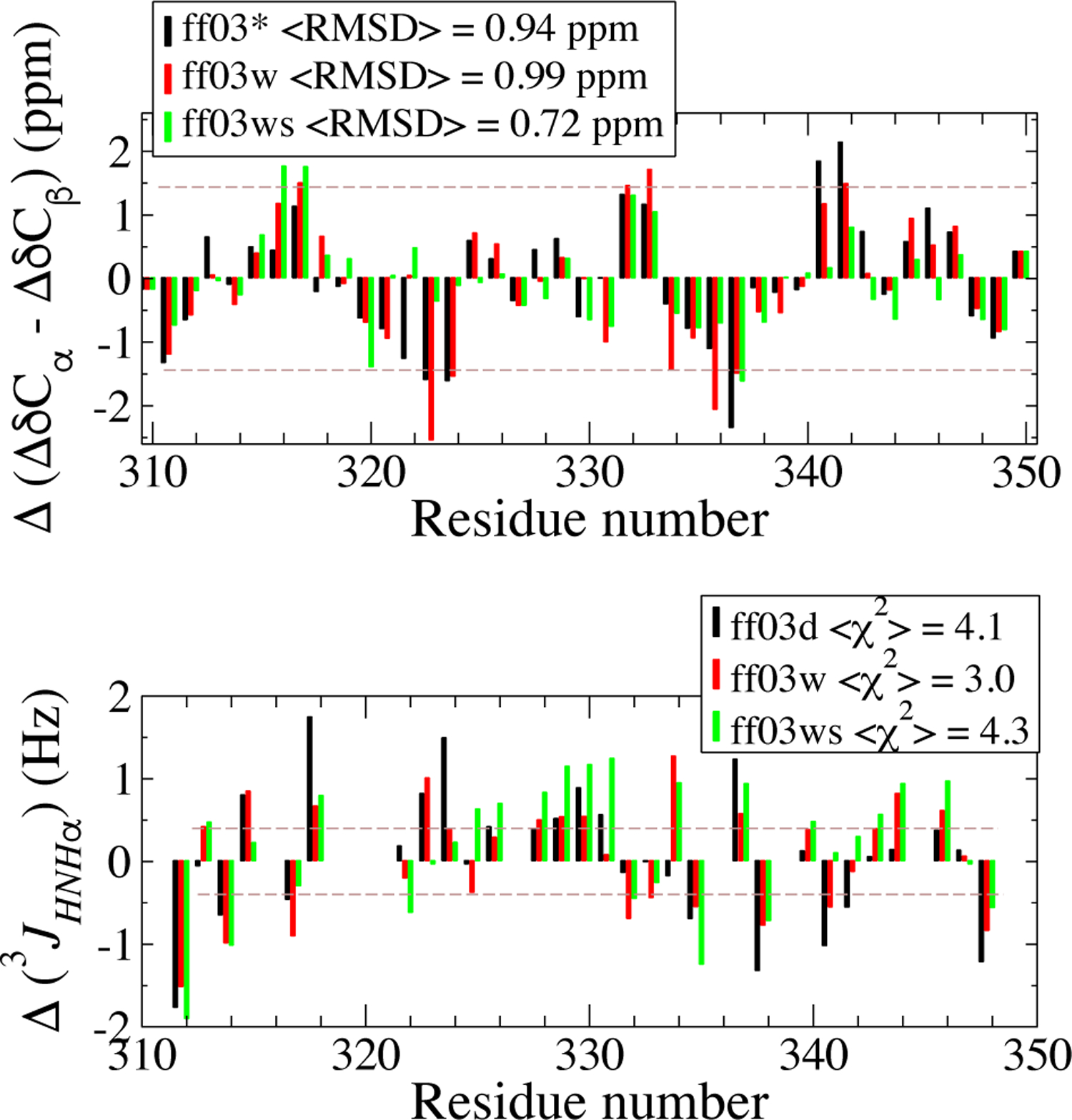
NMR order parameters of TDP-43310–350 are evaluated from simulation ensembles. The difference between experiment and simulation (Δ) is reported for all three force fields with the color code shown in the legend. Top panel shows the C α and C β chemical shift deviations (as ΔδCα - ΔδCβ). Average root mean square deviation, hRMSDi, between the simulation and experimental values are reported in the legends. Bottom panel shows the comparison between the scalar coupling constant 3JHNH_ from experiment and simulations.X2 values are shown in the legend. Brown dash lines indicate the errors associated with the prediction methods88,89 to show the reliability of such prediction, the magnitude of which is larger than the differences between the three force fields.14
Here, we emphasize that differences between the three Amber ff03 force fields (as well as the difference between the experiment and simulation) are small for both for both local structure content and NMR measurable which reflect mainly such local structure. We conclude that it is possible to match these experimental properties, essentially irrespective of how favorable the protein solvation is.
Conclusions
An accurate atomistic simulation ensemble (rigorously validated against experimental data) provides the most detailed microscopic information on IDP structure, which is diff cult to obtain solely from experimental data. We have previously shown that recent force field modifications yielded improved results in specific cases; here we have generalized to a large group of disordered proteins, finding that with the most recent ff03ws force field we are able to capture the same polymer scaling properties in water and chemical denaturant as seen in experiment. In particular, scaling exponents in water are close to 0.5, while those in high concentrations of denaturant are closer to 0.6. In contrast, older force fields yield scaling exponents in the range 0.3–0.4, characteristic of collapsed chains.
Of note is that the effects of the different force field changes appear to befforthogonal. The degree of collapse is essentially only affected by improving the solvation of the chain, here accomplished by introducing the scaling of protein-water Lennard-Jones interactions. On the other hand, however favorable the solvation model, it is still possible to reproduce local structure by altering backbone dihedral terms. Thus, dihedral angle modifications and protein solvation affect (primarily) the local structure formation and degree of collapse respectively. This stresses the need to use data reflecting both local and global structure formation in force field parameterization and validation; showing agreement with one type of data holds no guarantee for the other.
Supplementary Material
Acknowledgement
This work was supported by the U.S. Department of Energy, Office of Basic Energy Science, Division of Material Sciences and Engineering under Award (DE-SC0013979). This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported under Contract No. DE-AC02-05CH11231. Use of the high-performance computing capabilities of the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the National Science Foundation, project no. TG-MCB120014, is also gratefully acknowledged. RBB was supported by the Intramural Research Program of the National Institute of Diabetes and Digestive and Kidney Diseases of the National Institutes of Health. This work utilized the computational resources of the NIH HPC Biowulf cluster (http://hpc.nih.gov).
Footnotes
Supporting Information Available
Supporting methods (Simulation details and Analysis), 4 tables and 11 figures are available
References
- (1).van der Lee R; Buljan M; Lang B; Weatheritt RJ; Daughdrill GW; Dunker AK; Fuxreiter M; Gough J; Gsponer J; Jones DT et al. Classification of intrinsically disordered regions and proteins. Chem. Rev 2014, 114, 6589–6631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Wright PE; Dyson HJ Intrinsically disordered proteins in cellular signaling and regulation. Nat. Rev. Mol. Cell Biol 2015, 16, 18–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Ozenne V; Bauer F; Salmon L; Huang J.-r.; Jensen MR; Segard S; Bernadó P; Charavay C; Blackledge M. Flexible-meccano: a tool for the generation of explicit ensemble descriptions of intrinsically disordered proteins and their associated experimental observables. Bioinformatics 2012, 28, 1463–1470. [DOI] [PubMed] [Google Scholar]
- (4).Schneider R; Huang J.-r.; Yao M; Communie G; Ozenne V; Mollica L; Salmon L; Jensen MR; Blackledge M. Towards a robust description of intrinsic protein disorder using nuclear magnetic resonance spectroscopy. Mol. BioSyst 2012, 8, 58–68. [DOI] [PubMed] [Google Scholar]
- (5).Jensen MR; Ruigrok RW; Blackledge M Describing intrinsically disordered proteins at atomic resolution by NMR. Current opinion in structural biology 2013, 23, 426–435. [DOI] [PubMed] [Google Scholar]
- (6).Hofmann H; Soranno A; Borgia A; Gast K; Nettels D; Schuler B Polymer scaling laws of unfolded and intrinsically disordered proteins quantified with single-molecule spectroscopy. Proc. Natl. Acad. Sci. U.S.A 2012, [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Bernadó P; Svergun DI Structural analysis of intrinsically disordered proteins by small-angle X-ray scattering. Mol. BioSyst 2012, 8, 151–167. [DOI] [PubMed] [Google Scholar]
- (8).Borgia A; Zheng W; Buholzer K; Borgia MB; Schuler A; Hofmann H; Soranno A; Nettels D; Gast K; Grishaev A et al. Consistent view of polypeptide chain expansion in chemical denaturants from multiple experimental methods. J. Am. Chem. Soc 2016, 138, 11714–11726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Riback JA; Bowman MA; Zmyslowski AM; Knoverek CR; Jumper JM; Hinshaw JR; Kaye EB; Freed KF; Clark PL; Sosnick TR Innovative scattering analysis shows that hydrophobic proteins are expanded in water. Science 2017, 358, 238–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Zheng W; Zerze GH; Borgia A; Mittal J; Schuler B; Best RB Inferring properties of disordered chains from FRET transfer e ciencies. J Chem. Phys 2018, 148, 123329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Zheng W; Best RB An extended Guinier analysis for intrinsically disordered proteins. J. Mol. Biol 2018, 430, 2540–2553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Best RB; Zheng W; Borgia A; Buholzer K; Borgia MB; Hofmann H; Soranno A; Nettels D; Gast K; Grishaev A et al. Comment on “Innovative scattering analysis shows that hydrophobic disordered proteins are expanded in water”, in press. Science 2018, [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Conicella AE; Zerze GH; Mittal J; Fawzi NL ALS mutations disrupt phase separation mediated by α-helical structure in the TDP-43 low-complexity C-terminal domain. Structure 2016, 24, 1537–1549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Zheng W; Borgia A; Buholzer K; Grishaev A; Schuler B; Best RB Probing the action of chemical denaturant on an intrinsically disordered protein by simulation and experiment. J. Am. Chem. Soc 2016, 138, 11702–11713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Robustelli P; Piana S; Shaw DE Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. U.S.A 2018, 201800690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Dedmon MM; Lindor-Larsen K; Christodoulou J; Vendruscolo M; Dobson CM Mapping long-range interactions in α-synuclein using spin-label NMR and ensemble molecular dynamics simulations. J. Am. Chem. Soc 2005, 127, 476–477. [DOI] [PubMed] [Google Scholar]
- (17).Lindor-Larsen K; Best RB; DePristo MA; Dobson CM; Vendruscolo M Simultaneous determination of protein structure and dynamics. Nature 2005, 433, 128. [DOI] [PubMed] [Google Scholar]
- (18).Ganguly D; Chen J Structural interpretation of paramagnetic relaxation enhancement-derived distances for disordered protein states. J. Mol. Biol 2009, 390, 467–477. [DOI] [PubMed] [Google Scholar]
- (19).Hummer G; Jürgen Köfinger, Bayesian ensemble refinement by replica simulations and reweighting. J. Chem. Phys 2015, 143, 243150. [DOI] [PubMed] [Google Scholar]
- (20).Fisher CK; Stultz CM Constructing ensembles for intrinsically disordered proteins. Curr. Opin. Struct. Biol 2011, 21, 426–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Mittal J; Yoo TH; Georgiou G; Truskett TM Structural ensemble of an intrinsically disordered polypeptide. J. Phys. Chem. B 2012, 117, 118–124. [DOI] [PubMed] [Google Scholar]
- (22).Best RB; Zheng W; Mittal J Balanced protein-water interactions improve properties of disordered proteins and non-specific protein association. J. Chem. Theor. Comput 2014, 10, 5113–5124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Huang J; Rauscher S; Nawrocki G; Ran T; Feig M; de Groot BL; Grubmüller H; MacKerell AD Jr CHARMM36m: an improved force field for folded and intrinsically disordered proteins. Nat. Met 2016, 14, 71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Piana S; Klepeis JL; Shaw DE Assessing the accuracy of physical models used in protein folding simulations: quantitative evidence from long molecular dynamics simulations. Curr. Opin. Struct. Biol 2014, 24, 98–105. [DOI] [PubMed] [Google Scholar]
- (25).Nerenberg PS; Head-Gordon T Optimizing protein-solvent force fields to reproduce intrinsic conformational preferences of model peptides. J. Chem. Theor. Comput 2011, 7, 1220–1230. [DOI] [PubMed] [Google Scholar]
- (26).Henriques J; Cragnell C; Skepo M Molecular dynamics simulations of intrinsically disordered proteins: force field evaluation and comparison with experiment. J. Chem. Theory Comput 2015, 11, 3420–3431. [DOI] [PubMed] [Google Scholar]
- (27).Best RB Computational and theoretical advances in studies of intrinsically disordered proteins. Current opinion in structural biology 2017, 42, 147–154. [DOI] [PubMed] [Google Scholar]
- (28).Nerenberg PS; Head-Gordon T New developments in force fields for biomolecular simulations. Curr. Opin. Struct. Biol 2018, 49, 129–138. [DOI] [PubMed] [Google Scholar]
- (29).Huang J; MacKerell AD Force field development and simulations of intrinsically disordered proteins. Curr. Opin. Struct. Biol 2018, 48, 40–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Levine ZA; Shea J-E Simulations of disordered proteins and systems with conformational heterogeneity. Curr. Opin. Struct. Biol 2017, 43, 95–103 [DOI] [PubMed] [Google Scholar]
- (31).Cornell WD; Cieplak P; Bayly CI; Gould IR; Merz KM; Ferguson DM; Spellmeyer DC; Fox T; Caldwell JW; Kollman PA A second generation force field for the simulation of proteins, nucleic acids and organic molecules. J. Am. Chem. Soc 1995, 117, 5179–5197. [Google Scholar]
- (32).Jorgensen WL; Maxwell DS; Tirado-Rives J Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. Journal of the American Chemical Society 1996, 118, 11225–11236. [Google Scholar]
- (33).MacKerell AD Jr; Bashford D; Bellott M; Dunbrack RL Jr; Evanseck JD; Field MJ; Fischer S; Gao J; Guo H; Ha S et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. The Journal of Physical Chemistry B 1998, 102, 3586–3616. [DOI] [PubMed] [Google Scholar]
- (34).Scott WR; Hünenberger PH; Tironi IG; Mark AE; Billeter SR; Fennen J; Torda AE; Huber T; Krüger P; van Gunsteren WF The GROMOS biomolecular simulation program package. The Journal of Physical Chemistry A 1999, 103, 3596–3607. [Google Scholar]
- (35).MacKerell AD Jr; Feig M; Brooks CL Improved treatment of the protein backbone in empirical force fields. J. Am. Chem. Soc 2003, 126, 698–699. [DOI] [PubMed] [Google Scholar]
- (36).Jiang F; Zhou C-Y; Wu Y-D Residue-specific force field based on the protein coil library. RSFF1: Modification of OPLS-AA/L. J. Phys. Chem. B 2014, 118, 6983–6998. [DOI] [PubMed] [Google Scholar]
- (37).Zhou C-Y; Jiang F; Wu Y-D Residue-specific force field based on protein coil library. RSFF2: modification of AMBER 99SB. J. Phys. Chem. B 2014, 119, 1035–1047. [DOI] [PubMed] [Google Scholar]
- (38).Shaw DE; Maragakis P; Lindor-Larsen K; Piana S; Dror RO; Eastwood MP; Bank JA; Jumper JM; Salmon JK; Shan Y et al. Atomic-level characterization of the structural dynamics of proteins. Science 2010, 330, 341–346. [DOI] [PubMed] [Google Scholar]
- (39).Lindor-Larsen K; Piana S; Dror RO; Shaw DE How fast-folding proteins fold. Science 2011, 334, 517–520. [DOI] [PubMed] [Google Scholar]
- (40).Best RB; Mittal J Balance between α and β structures in ab initio protein folding.J. Phys. Chem. B 2010, 114, 8790–8798. [DOI] [PubMed] [Google Scholar]
- (41).Mittal J; Best RB Tackling force-field bias in protein folding simulations: folding of Villin HP35 and Pin WW domains in explicit water. Biophys. J 2010, 99, L26–L28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Cornell WD; Cieplak P; Bayly CI; Gould IR; Merz KM; Ferguson DM; Spellmeyer DC; Fox T; Caldwell JW; Kollman PA A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc 1995, 117, 5179–5197. [Google Scholar]
- (43).Kollman P; Dixon R; Cornell W; Fox T; Chipot C; Pohorille A Computer simulation of biomolecular systems; Springer, 1997; pp 83–96. [Google Scholar]
- (44).Wang J; Cieplak P; Kollman PA How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? J. Comput. Chem 2000, 21, 1049–1074. [Google Scholar]
- (45).Duan Y; Wu C; Chowdhury S; Lee MC; Xiong G; Zhang W; Yang R; Cieplak P; Luo R; Lee T et al. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem 2003, 24, 1999–2012. [DOI] [PubMed] [Google Scholar]
- (46).Garcia AE; Sanbonmatsu KY α-Helical stabilization by side chain shielding of backbone hydrogen bonds. Proc. Natl. Acad. Sci. U.S.A 2002, 99, 2782–2787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Sorin EJ; Pande VS Exploring the helix-coil transition via all-atom equilibrium ensemble simulations. Biophys. J 2005, 88, 2472–2493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Hornak V; Abel R; Okur A; Strockbine B; Roitberg A; Simmerling C Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins: Struct., Funct., Bioinf 2006, 65, 712–725 [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Best RB; Hummer G Optimized molecular dynamics force fields applied to the helix-coil transition of polypeptides. J. Phys. Chem. B 2009, 113, 9004–9015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Piana S; Lindor-Larsen K; Shaw DE How robust are protein folding simulations with respect to force field parameterization. Biophys. J 2011, 100, L47–L49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Best RB; Zhu X; Shim J; Lopes P; Mittal J; Feig M; Mackerell AD Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone ϕ, ψ and side-chain X1 and X2 dihedral angles. J. Comp.Theor. Comput 2012, 8, 3257–3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (52).Nettels D; Müller-Spath S; Küster F; Hofmann H; Haenni D; Rüegger S; Reymond L; Ho mann A; Kubelka J; Heinz B et al. Single-molecule spectroscopy of the temperature-induced collapse of unfolded proteins. Proc. Natl. Acad. Sci. U.S.A 2009, 106, 20740–20745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Best RB; Mittal J Free-energy landscape of the GB1 hairpin in all-atom explicit solvent simulations with different force fields: Similarities and differences. Proteins: Struct., Funct., Bioinf 2011, 79, 1318–1328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Baxa MC; Yu W; Adhikari AN; Ge L; Xia Z; Zhou R; Freed KF; Sosnick TR Even with nonnative interactions, the updated folding transition states of the homologs proteins G & L are extensive and similar. Proc. Natl. Acad. Sci. U. S. A 2015, 112, 8302–8307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Petrov D; Zagrovic B Are current atomistic force fields accurate enough to study proteins in crowded environments? PLoS Comput. Biol 2014, 10, e1003638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (56).Abriata LA; Peraro MD Assessing the potential of atomistic molecular dynamics simulations to probe reversible protein-protein recognition and binding. Sci. Rep 2015, 5, 10549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (57).Jorgensen WL Transferable intermolecular potential functions for water, alcohols, and ethers. Application to liquid water. J. Am. Chem. Soc 1981, 103, 335–340. [Google Scholar]
- (58).Best RB; Mittal J Protein simulations with an optimized water model: cooperative helix formation and temperature-induced unfolded state collapse. J. Phys. Chem. B 2010, 114, 14916–14923. [DOI] [PubMed] [Google Scholar]
- (59).Piana S; Donchev AG; Robustelli P; Shaw DE Water dispersion interactions strongly influence simulated structural properties of disordered protein states. J. Phys. Chem. B 2015, 119, 5113–5123. [DOI] [PubMed] [Google Scholar]
- (60).Ploetz EA; Bentenitis N; Smith PE Developing force fields from the microscopic structure of solutions. Fluid phase equilibria 2010, 290, 43–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (61).Zerze GH; Mittal J; Best RB Diffusive dynamics of contact formation in disordered polypeptides. Phys. Rev. Lett 2016, 116, 068102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (62).Li S; Elcock AH Residue-Specific Force Field (RSFF2) Improves the Modeling of Conformational Behavior of Peptides and Proteins. The journal of physical chemistry letters 2015, 6, 2127–2133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (63).Robertson MJ; Tirado-Rives J; Jorgensen WL Improved peptide and protein torsional energetics with the OPLS-AA force field. Journal of chemical theory and computation 2015, 11, 3499–3509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (64).Yoo J; Aksimentiev A Refined Parameterization of Nonbonded Interactions Improves Conformational Sampling and Kinetics of Protein Folding Simulations. The journal of physical chemistry letters 2016, 7, 3812–3818 [DOI] [PubMed] [Google Scholar]
- (65).Debiec KT; Cerutti DS; Baker LR; Gronenborn AM; Case DA; Chong LT Further along the road less traveled: AMBER 15ipq, an original protein force field built on a self-consistent physical model. Journal of chemical theory and computation 2016, 12, 3926–3947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (66).Song D; Luo R; Chen H-F The IDP-specific force field 14IDPSFF improves the conformer sampling of intrinsically disordered proteins. Journal of chemical information and modeling 2017, 57, 1166–1178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (67).Berendsen H; Grigera J; Straatsma T The missing term in effective pair potentials. J. Phys. Chem 1987, 91, 6269–6271. [Google Scholar]
- (68).Horn HW; Swope WC; Pitera JW; Madura JD; Dick TJ; Hura GL; Head-Gordon T Development of an improved four-site water model for bio molecular simulations: TIP4P-Ew. J. Chem. Phys 2004, 120, 9665–9678. [DOI] [PubMed] [Google Scholar]
- (69).Abascal JL; Vega C A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys 2005, 123, 234505. [DOI] [PubMed] [Google Scholar]
- (70).Kjaergaard M; Norholm A-B; Hendus-Altenburger R; Pedersen SF; Poulsen FM; Kragelund BB Temperature-dependent structural changes in intrinsically-disordered proteins: formation of -helices or loss of polyproline II? Protein Sci. 2010, 19, 1555–1564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (71).Wuttke R; Hofmann H; Nettels D; Borgia MB; Mittal J; Best RB; Schuler B Temperature-dependent solvation modulates the dimensions of disordered proteins. Proceedings of the National Academy of Sciences 2014, 201313006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (72).Zerze GH; Best RB; Mittal J Sequence and temperature-dependent properties of unfolded and disordered proteins from atomistic simulations. J. Phys. Chem. B 2015, 119, 14622–14630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (73).Best RB; de Sancho D; Mittal J Residue-specific α-helix propensities from molecular simulation. Biophys. J 2012, 102, 1462–1467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (74).Weerasinghe S; Smith PE A Kirkwood-Buff derived force field for mixtures of urea and water. J. Phys. Chem. B 2003, 107, 3891–3898. [Google Scholar]
- (75).Weerasinghe S; Smith PE A Kirkwood-Buff derived force field for the simulation of aqueous guanidinium chloride solutions. J. Chem. Phys 2004, 121, 2180–2186. [DOI] [PubMed] [Google Scholar]
- (76).Zheng W; Borgia A; Borgia MB; Schuler B; Best RB Empirical Optimization of Interactions between Proteins and Chemical Denaturants in Molecular Simulations. J. Chem. Theor. Comput 2015, 11, 5543–5553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (77).Flyvbjerg H; Petersen HG Error estimates on averages of correlated data. J. Chem. Phys 1989, 91, 461–466 [Google Scholar]
- (78).de Gennes P-G Scaling Concepts in Polymer Physics; Cornell University Press, 1978. [Google Scholar]
- (79).Flory PJ Principles of polymer chemistry; Cornell University Press, 1953. [Google Scholar]
- (80).Kohn JE; Millett IS; Jacob J; Zagrovic B; Dillon TM; Cingel N; Dothager RS; Seifert S; Thiyagarajan P; Sosnick TR et al. Random-coil behavior and the dimensions of chemically unfolded proteins. Proc. Natl. Acad. Sci. U.S.A 2004, 101, 12491–12496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (81).Marsh JA; Forman-Kay JD Sequence determinants of compaction in intrinsically disordered proteins. Biophys. J 2010, 98, 2383–2390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (82).Fuertes G; Banterle N; Ru KM; Chowdhury A; Mercadante D; Koehler C; Kachala M; Girona GE; Milles S; Mishra A et al. Decoupling of size and shape fluctuations in heteropolymeric sequences reconciles discrepancies in SAXS vs. FRET measurements. PNAS 2017, 114, E6342–E6351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (83).Martin EW; Holehouse AS; Grace CR; Hughes A; Pappu RV; Mittag T Sequence determinants of the conformational properties of an intrinsically disordered protein prior to and upon multisite phosphorylation. Journal of the American Chemical Society 2016, 138, 15323–15335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (84).Rubinstein M; Colby RH Polymer physics; Oxford University Press New York, 2003; Vol. 23. [Google Scholar]
- (85).Miller C; Zerze GH; Mittal J Molecular simulations indicate marked differences in the structure of amylin mutants, correlated with known aggregation propensity. J. Phys. Chem. B 2013, 117, 16066–16075 [DOI] [PubMed] [Google Scholar]
- (86).Kabsch W; Sander C Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637. [DOI] [PubMed] [Google Scholar]
- (87).Lindor-Larsen K; Maragakis P; Piana S; Eastwood MP; Dror RO; Shaw DE Systematic validation of protein force fields against experimental data. PloS one 2012, 7, e32131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (88).Shen Y; Bax A SPARTA+: a modest improvement in empirical NMR chemical shift prediction by means of an artificial neural network. J. Biomol. NMR 2010, 48, 13–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (89).Vögeli B; Ying J; Grishaev A; Bax A Limits on variations in protein backbone dynamics from precise measurements of scalar couplings. J. Am. Chem. Soc 2007, 129, 9377–9385. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


