Abstract
Human DNA Pol κ is a polymerase enzyme, specialized for near error-free bypass of certain bulky chemical lesions to DNA that are derived from environmental carcinogens present in tobacco smoke, automobile exhaust and cooked food. By employing ab initio QM/MM–MD (Quantum Mechanics/Molecular Mechanics–Molecular Dynamics) simulations with umbrella sampling, we have determined the entire free energy profile of the nucleotidyl transfer reaction catalyzed by Pol κ and provided detailed mechanistic insights. Our results show that a variant of the Water Mediated and Substrate Assisted (WMSA) mechanism that we previously deduced for Dpo4 and T7 DNA polymerases is preferred for Pol κ as well, suggesting its broad applicability. The hydrogen on the 3′-OH primer terminus is transferred through crystal and solvent waters to the γ-phosphate of the dNTP, followed by the associative nucleotidyl transfer reaction; this is facilitated by a proton transfer from the γ-phosphate to the α,β-bridging oxygen as pyrophosphate leaves, to neutralize the evolving negative charge. MD simulations show that the near error-free incorporation of dCTP opposite the major benzo[a]pyrene—derived dG lesion is compatible with the WMSA mechanism, allowing for an essentially undisturbed pentacovalent phosphorane transition state, and explaining the bypass of this lesion with little mutation by Pol κ.
INTRODUCTION
The Y family translesion synthesis (TLS) DNA polymerases are generally low fidelity on undamaged DNA (1) and have functions which include, among others, to bypass distorting bulky DNA lesions (2–7) that primarily stall high fidelity replicative polymerases; one or more members of the Y family TLS polymerases may then replace the high fidelity polymerase to bypass the region of distortion (7–9). This bypass may be error-free or error-prone, depending on the nature of the lesion and the specific polymerase (1–3,7).
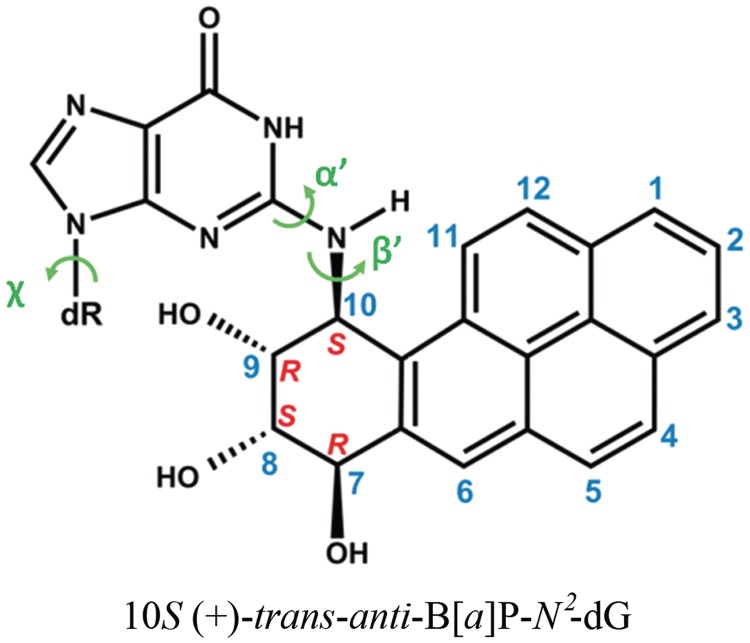
Human Pol κ, a member of the Y-family polymerases, has the striking capacity for near error-free bypass in vitro (10–12) and in mammalian cells (13), of bulky lesions linked to the amino group of guanine that reside in the B-DNA minor groove. Particularly interesting is a series of studies of the major benzo[a]pyrene (B[a]P)-derived adduct, 10S (+)-trans-anti-B[a]P-N2-dG (B[a]P-dG) (Figure 1). Benzo[a]pyrene is an ubiquitous environmental carcinogen, present in tobacco smoke, automobile exhaust and cooked foods (14–16), and the B[a]P-dG adduct is highly mutagenic (17,18). The studies showed mostly error-free bypass of this carcinogen-induced lesion by Pol κ in vitro (11,19–22). Furthermore, in mouse embryonic fibroblasts it has been shown that Pol κ bypasses this adduct with higher efficiency and accuracy than other Y family polymerases (23), and mutagenic bypass depends on other polymerases in the system (24). In addition, it was shown that mouse embryonic stem cells are protected against mutations targeted to guanine by the diol-epoxide metabolite (B[a]PDE) of B[a]P (25). NMR solution studies have shown that the B[a]P-dG adduct resides in the B-DNA minor groove, directed 5′ along the modified strand (17,26–29). While minor groove lesions are bypassed near error-free by Pol κ, lesions residing on the major groove side tend to cause the polymerase to stall (11,30,31).
Figure 1.
Structure of the 10S (+)-trans-anti-B[a]P-N2-dG (B[a]P-dG) adduct. The absolute configurations of the four chiral atoms C7, C8, C9 and C10 are indicated. Torsion angles are defined as χ = O4′(dR) – C1′(dR) – N9 – C4 (dR is deoxyribose), α′ = N1 – C2 – N2 – C10(B[a]P-dG), β′ = C2 – N2 – C10(B[a]P-dG) – C9(B[a]P-dG).
Structurally, high fidelity replicative and the Y family bypass polymerases, including Pol κ, share common features: they are shaped like a hand with palm, fingers and thumb domains; however, the bypass polymerases all have an additional domain known as the little finger or PAD (Polymerase Associated Domain) (2,6). Another notable difference is the absence of an induced fit mechanism upon the entry of a dNTP. In high fidelity polymerases the fingers close so that the nascent base pair is in van der Waals contact with the polymerase prior to reaction. In Y-family polymerases the active site is preformed, without the opening/closing induced fit motion in going from the binary to the ternary complex; the active site is more open and solvent exposed, particularly on the minor groove side of the nascent duplex (1,2,4). These structural differences account for the low fidelity of the bypass polymerases on undamaged DNA and also their functionality in lesion bypass, in which only small numbers of nucleotides are synthesized to transit the region of lesion-induced distortion (1,2,7). DNA polymerase κ is unique in having an additional domain, known as the N-Clasp (an N-terminal extension of ∼75 residues) on the major groove side of the nascent duplex; as a result a region of the DNA near the active site is completely encircled by Pol κ, as shown in the crystal structure containing the ternary complex with template–primer and incoming dNTP; without the N-Clasp DNA synthesis by Pol κ is severely impaired (32).
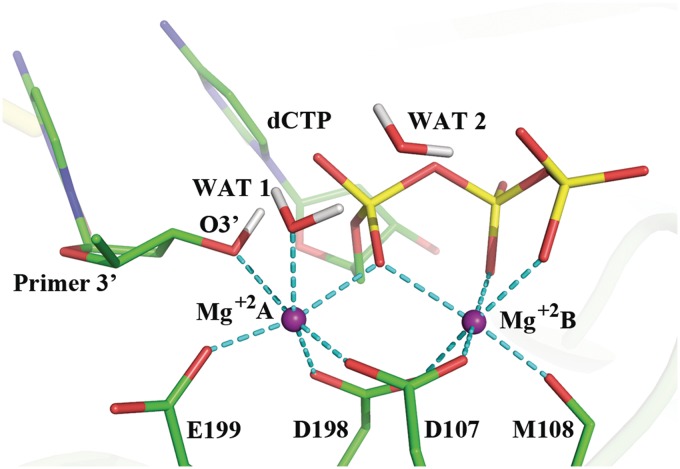
Pol κ has an active site for catalysis of the nucleotidyl transfer reaction that shares common features with all DNA polymerases. Overall, the 3′-OH group on the sugar of the primer terminus reacts with the α-phosphate of a deoxyribonucleoside triphosphate, pyrophosphate is released and the chemical step of nucleotide insertion is achieved. A pair of universally conserved divalent metal ions (normally Mg+2) has been suggested to play key catalytic roles in this essential process: the catalytic ion, Mg+2 A (Figure 2), lowers the pKa of the 3′-OH and facilitates the nucleophilic attack; the nucleotide-binding ion, Mg+2 B, assists the leaving of the pyrophosphate (33). Both ions organize the active site in octahedral coordination with a triad of conserved carboxylate-containing amino acid residues, water, the primer O3′ and phosphate oxygens of the dNTP (33). A high resolution view of a well-organized active site in Pol β was obtained by Batra and coworkers (Supplementary Figure S1) (34); this structure contained the 3′OH group of the sugar and utilized a non-hydrolyzable deoxynucleotide analog to inhibit the extension reaction, instead of the dideoxy termini that had been commonly employed and did not provide organized active sites.
Figure 2.
Active site of Pol κ ternary complex ((32) and PDB ID: 2OH2) remodeled with MD as described in Computational Methods section. This structure was utilized to initiate the QM/MM–MD simulations. The octahedral coordination of the two Mg+2 ions is shown with the dashed lines and their distances are shown in Supplementary Figure S2. Hydrogen atoms are not displayed for clarity except for the H(O3′) and the crystal water hydrogens.
A Water Mediated and Substrate Assisted mechanism (WMSA) has been previously delineated for the low-fidelity lesion-bypass polymerase Dpo4 (Y-family) and the high-fidelity replicative DNA polymerase T7 (A-Family) (35,36). The mechanistic details revealed a stepwise mechanism with essential common features: the general base for the H(O3′) is the γ-phosphate of the dNTP; this protonation takes place first via proton transfer through a shuttle of two mediating water molecules. The subsequent associative nucleophilic attack of the O3′ on Pα is accompanied by a transfer of the proton from the γ-phosphate to the α,β-bridging oxygen via a water molecule. This mechanism is consistent with the work of Castro, Cameron and coworkers (37) which revealed that there are two proton transfers in the overall chemical reaction in a number of polymerases, one of which was suggested to correspond to the deprotonation of the 3′-OH and the other to protonation of the pyrophosphate leaving group.
The goal of the present work was to determine if a WMSA-type mechanism was feasible for human Pol κ and to gain insights on the near error-free lesion bypass of the B[a]P-dG adduct by Pol κ. We thoroughly explored the nucleotidyl transfer mechanism of undamaged Pol κ and assessed whether the characterized mechanism obtained in our extensive searches remained feasible in the presence of the lesion. We used advanced ab initio quantum mechanics/molecular mechanics–molecular dynamics simulations (QM/MM–MD) with the umbrella sampling method (38,39) to calculate free energy profiles for the mechanisms investigated. At each MD time step, the atomic forces as well as the total energy of the enzyme system are calculated with the pseudobond ab initio QM/MM method (40,41), in which the bond forming/breaking process is treated by the ab initio QM method, while the rest of the system is described by the molecular mechanical force field; the pseudobond approach provides a robust treatment of the QM/MM boundary across covalent bonds. From a series of biased simulations (42), which are employed to enhance the sampling of lower probability states, the free energy profile along the reaction coordinate is obtained with the weighted histogram analysis method (WHAM) (43–45). This state-of-the-art approach provides a first-principle QM description of the chemical reaction, adequately accounts for the biological environment, and takes account of the fluctuations of the reaction active site and the surrounding enzyme system. The method has been demonstrated to be powerful in determining the mechanism of various enzymes (38–43).
Previous molecular dynamics (MD) simulations have shown that in the ternary complex prior to reaction the B[a]P-dG adduct, linked to a templating guanine, is well accommodated on the minor groove side in Pol κ; a dCTP incoming nucleotide maintains normal Watson–Crick pairing with the damaged guanine, and the active site appears well-organized (30). By contrast, the analogous adenine adduct (10S (+)-trans-anti-B[a]P-N6-dA), directed towards the N-clasp on the major groove side of the evolving duplex, probably impedes translocation sterically, preventing the damaged template from entering the insertion site; this is consistent with experimentally observed blockage at the pre-insertion site (11,30). Our present results showed that the WMSA mechanism provides the lowest free energy path for the reaction among the multiple mechanisms we investigated for Pol κ; furthermore, the B[a]P ring system in the B[a]P-dG adduct does not disrupt the pentacovalent phosphorane transition state nor the water network required for the proton transfer steps that are essential for the mechanism.
COMPUTATIONAL METHODS
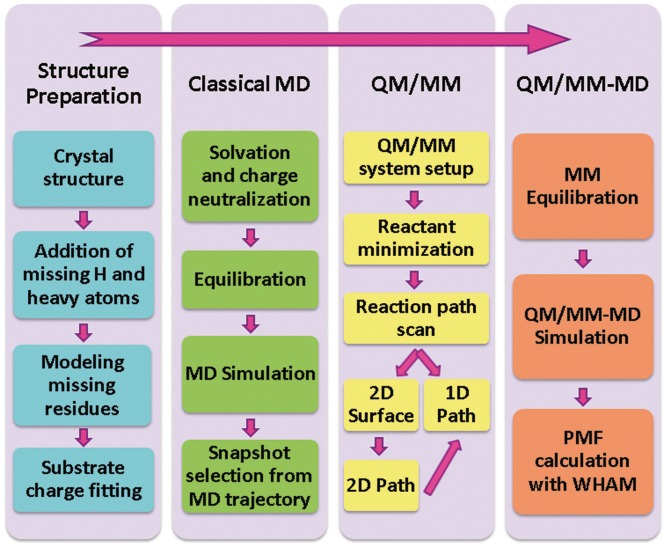
Scheme 1 summarizes our computational protocol.
Scheme 1.
Computational protocol.
Structure preparation
The ternary crystal structure (PDB ID (46): 2OH2) of Pol κ19-526 with DNA and incoming dTTP (32) was the basis for our prepared enzyme-substrate model. Details are given in Supplementary Data including Supplementary Scheme S1.
Classical MD
The initial model was subjected to 3 ns of MD simulations using AMBER 9 (47). We employed the Amber99SB (48–50) force field with modification for DNA by parmbsc0 (51), and previously calculated parameters for the dCTP (52). The structure was neutralized by 10 Na+ counterions and was solvated with a periodic rectangular box of TIP3P water (53,54) with 10 Å buffer around the enzyme-substrate complex. Details of the MD protocols are given in Supplementary Materials. A random snapshot from the last 0.5 ns of the 3 ns trajectory was utilized for the subsequent QM/MM–MD stage. In this snapshot the Mg+2 coordination, Mg+2–Mg+2 distance, and O3′–Pα distance were similar to those in the high resolution X-ray crystal structure of pol β (34), in our previous Pol κ model (30), and in the initial models utilized for our previous polymerase mechanism studies with Dpo4 (35) and T7 (36) (shown in Figure 2 and Supplementary Figure S2).
QM/MM and QM/MM–MD
The QM subsystem (81 atoms) was comprised of the dCTP, the primer 3′-nucleotide (excluding the C5′ phosphate group), the glutamic acid (E199), the catalytic and nucleotide-binding Mg+2 ions (Mg+2 A and Mg+2 B, respectively), and two water molecules (Supplementary Figure S3). While the QM subsystem did not include all the ligands of the two Mg+2 ions (Figure 2), the critical ones for the chemistry of the nucleotidyl transfer reaction are included: E199, the crystal water molecule, the attacking O3′ and the dNTP phosphate oxygens. The other ligands, which do not participate in the chemistry per se but act to maintain the active site structure in a reaction-ready organization, are simulated through the MM component of our computations. Hence, the overall treatment of the Mg+2 ion ligands is sufficiently robust. This subsystem was treated by the hybrid density functional B3LYP (55–57) with a medium split valence basis set and polarization functions 6–31G* (58,59). All other residues and the surrounding water molecules (11 774 atoms), constituting the MM subsystem, were described by the TIP3P water model and the modified Amber99SB force field that was used in the classical MD simulations. Spherical boundary conditions were applied in all QM/MM calculations and all atoms outside the 20 Å radius centered at the primer 3′-end oxygen atom were frozen. A cutoff of 12.0 Å was used for van der Waals interactions, and a cutoff of 18.0 Å was employed for electrostatic interactions among the MM atoms. There was no cutoff for electrostatic interactions between the QM and MM atoms. Solvent molecules outside of a 27 Å sphere centered at the primer 3′-end oxygen atom were removed. The pseudobond approach (40,41) with improved parameters (60) was employed to treat the partition between QM and MM subsystems (Supplementary Figure S3). All QM/MM calculations were carried out utilizing the modified QChem (61) and Tinker (62) programs. The reactant was minimized by the efficient iterative optimization QM/MM approach. We mapped the minimum energy path for the investigated mechanisms utilizing the reaction coordinate driving method (42). For each determined structure along the path, a 500 ps MD simulation with the MM force field was carried out to equilibrate the MM sub-system. The resulting snapshot was used as the starting structure for ab initio QM/MM–MD simulations with umbrella sampling (38,39,63) that applies a harmonic potential to constrain the reaction coordinate (RC) at successive values. In order to ensure sufficient overlap between the successive windows, force constants in the range of 0 to 300 kcal/mol-Å2 were employed; these were chosen based on the estimated slope of the free energy curve at the reaction coordinate. The potential of mean force (PMF) was calculated from the probability distributions along a reaction coordinate using WHAM (43–45).
Pol κ containing the B[a]P-dG lesion in the pentacovalent phosphorane transition state
For the studies involving the B[a]P-dG adduct we began with the pentacovalent phosphorane transition state structure of the characterized WMSA mechanism. We modeled the B[a]P-dG lesion by docking the B[a]P moiety to the amino group of the templating guanine, placing the B[a]P on the minor groove side in Pol κ, oriented in the 5′-direction of the modified strand as in the NMR solution structure (26). Because the transition state contains five covalent bonds about the α-phosphate, it was necessary to develop an Amber-compatible force field to simulate this transient chemical state for the unmodified Pol κ. A new residue comprised of the incoming dCTP and the 3′-terminal nucleotide of the primer DNA strand was defined. This residue contained four new atom types: one for the protonated γ-phosphate oxygen of the dCTP, a second for the γ protonating hydrogen, a third for the α-phosphate of the dCTP and the fourth atom type was defined to describe both the dCTP α,β-bridging oxygen and the primer O3′. Topology assignments, geometries and partial charge parameters were characterized on the basis of the QM/MM–MD calculations for the transition state (data are listed in Supplementary Tables S1 and S2). The force constants were chosen to be large enough to maintain the transition state bond lengths, bond angles and dihedral angles in the unmodified Pol κ. Partial charges were taken from the QM calculations. The force field parameters for the guanine lesion, B[a]P-dG, were taken from Jia and coworkers (30). The MD protocol was the same as described in Supplementary Data.
All initial model constructions were carried out using the INSIGHT II 2005 program (Accelrys Software, Inc.). PyMOL (Delano Scientific, LLC) (64) was employed to make molecular images and movies.
RESULTS
We investigated many reaction schemes which considered the destination and pathways open to the H(O3′) as it is taken up by a base, the roles of amino acid residues in the active site in the mechanism, and the order of events in the nucleotidyl transfer reaction. The minimum energy path was calculated for each scheme employing the reaction coordinate driving method and B3LYP(6–31G*) QM/MM calculations. For several mechanisms two-dimensional minimum potential energy surfaces were mapped in order to locate an optimal path with the lowest energy barriers and stable intermediates (Scheme 1 and Supplementary Figures S4B, S5B and S6E). The most promising schemes were further investigated with B3LYP(6–31G*) QM/MM–MD simulations. This hierarchy of strategies allowed us to examine numerous mechanistic paths (Scheme 1). The lowest energy pathway that we obtained was a variant of the WMSA mechanism, while those that involved an amino acid as the base and/or utilized an amino acid to protonate the dCTP γ-phosphate were unfavorable due to uphill paths or unstable intermediates.
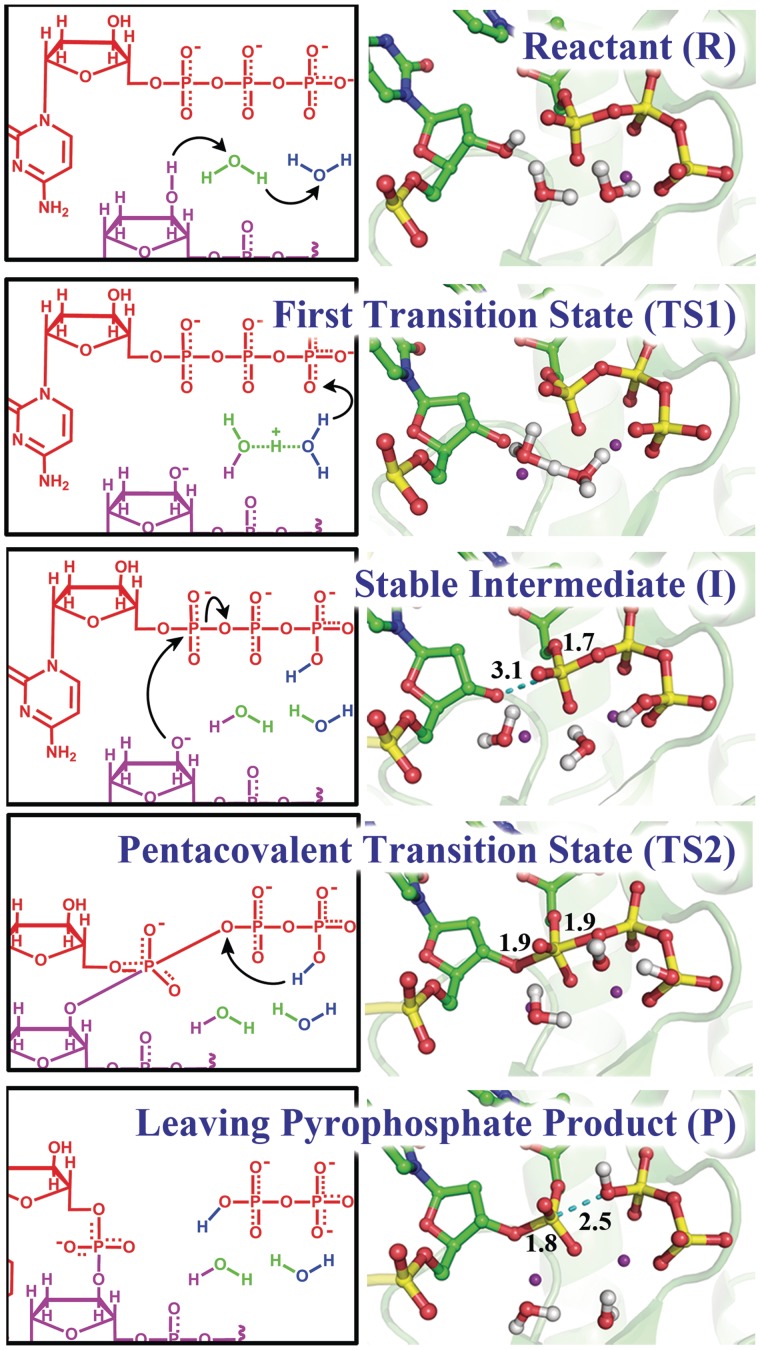
In the WMSA mechanism the γ-phosphate of the incoming dNTP serves as the base for the H(O3′) which shuttles through water molecules
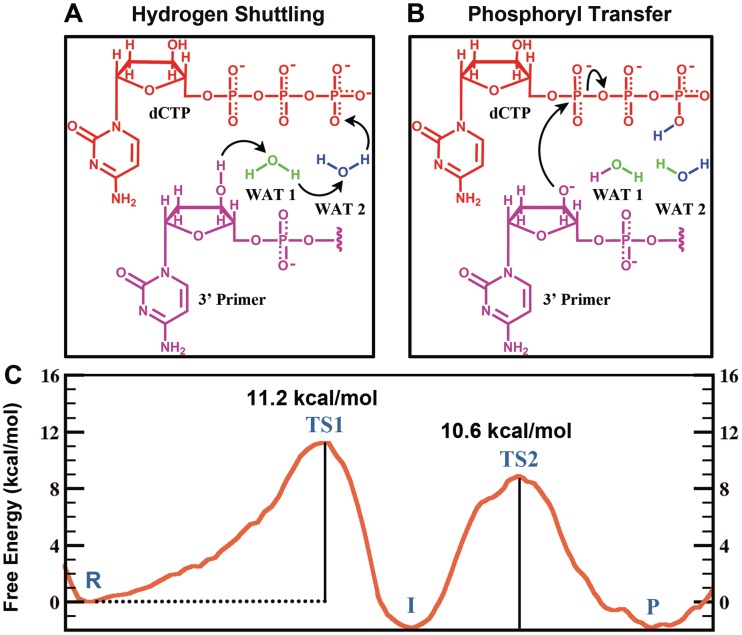
We found that a variant of the WMSA mechanism, which was previously proposed for the bypass DNA polymerase Dpo4 (35) and the high-fidelity replicative T7 DNA polymerase (36), is preferred for the human bypass DNA polymerase κ over the many explored schemes. Two steps are involved in this mechanism. In the first step, the H of O3′ is transferred to the oxygen on the γ-phosphate of the dCTP via two mediating water molecules (Figures 3 and 4). Hydrogen bond analysis revealed stable interactions throughout the reaction pathway between the β-phosphate group of the dCTP with Thr138, Arg144 and Phe111, while the γ-phosphate group hydrogen bonds with Arg144 and Lys328 and with the Ala110 backbone (Figure 5 and Supplementary Figure S7). The γ-phosphate has the most negative partial charge among the phosphate groups of dCTP (52), and this is relieved by protonation (Figure 6). In addition, the α-phosphate maintained stable hydrogen bonds with the two water molecules and helped anchor the second water (not coordinated with Mg+2) throughout the reaction. The proton transfers in this shuttle are: from the O3′ to the crystal water molecule that participates in the Mg+2 coordination; from this water to a solvent water, that is stably held by hydrogen bonds with oxygen atoms of the substrate, and from the second water to the γ-phosphate of the dCTP (Figures 3A and 4). The crystal water found in Pol κ (32) is also observed in a number of other polymerases (34,65–70). In the organized active site of Pol β (34) and in several other DNA polymerases (66,68–70) a second crystal water is located at the same position as the solvent water (WAT2) in our model (Supplementary Figure S1). A free energy profile was calculated for the first step of this mechanism by employing 37 umbrella windows along the reaction coordinate, each simulated for 30 ps of B3LYP(6–31G*) QM/MM–MD. An activation barrier of 11.2 ± 0.4 kcal/mol was determined for this free energy profile (Figure 3C). (Supplementary Movie S1).
Figure 3.
WMSA mechanism: (A, B) Reaction schemes and (C) Free energy profile. R: reactant; TS1: transition state 1; I: intermediate; TS2: transition states 2; P: product. These are illustrated in Figure 4.
Figure 4.
Key structures of the nucleotidyl transfer reaction catalyzed by Pol κ: reaction mechanism (left) and critical structures (right). See Supplementary Movies S1 and S2 for mechanism details.
Figure 5.
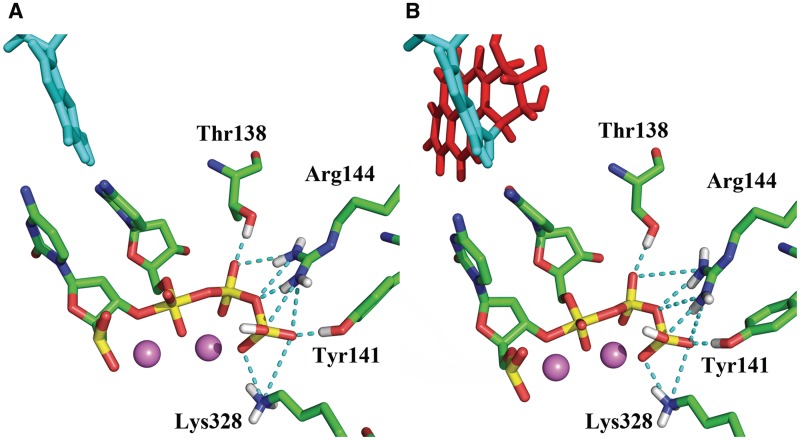
Key stabilizing hydrogen-bonding interactions (dashed lines) between active site amino acid residues and the pentacovalent phosphorane transition state. (A) Unmodified system simulated with QM/MM–MD (B) Modified system simulated with classical MD. The unmodified system simulated with classical MD preserves the same hydrogen bonding interactions as shown in Supplementary Table S3.
Figure 6.
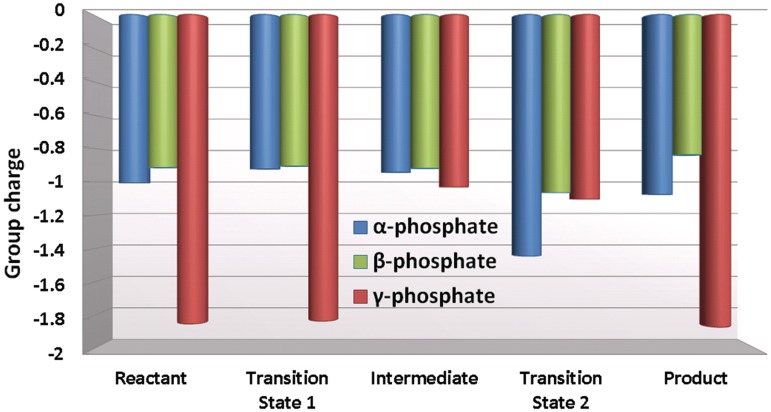
The α, β and γ phosphate group charges during key stationary points of the reaction (Figure 4). The partial charge of the bridging oxygen atoms is considered to be evenly shared between the neighboring phosphate groups.
In an associative mechanism a pentacovalent phosphorane is the transition state of the nucleotidyl transfer reaction
With a protonated γ-phosphate as a stable intermediate the reaction proceeds to the second step with a nucleophilic attack of the naked O3′ on the α-phosphate and leaving of the pyrophosphate (Figures 3B and 4). The transition state is a pentacovalent phosphorane structure, which results from an associative nucleotidyl transfer reaction; that is, the O3′–Pα bond forms before the Pα–Oα,β-bridge breaks (Supplementary Figure S8). The free energy barrier obtained for this step is 10.6 ± 0.3 kcal/mol, calculated using 50 umbrella sampling windows along the reaction coordinate each for 35 ps of B3LYP(6–31G*) QM/MM–MD (Figure 3C) (Supplementary Movie S2). As the reaction progresses the distance between the catalytic Mg+2 A and the nucleotide-binding Mg+2 B becomes shorter and achieves a minimum of 3.59 ± 0.09 Å at the transition state (Supplementary Figure S2A) which promotes the formation of the O3′–Pα bond; it subsequently elongates again to facilitate the breaking of the Pα–Oα,β-bridge bond. By approaching metal B, metal A brings the nucleophile O3′ within attack distance of the Pα, as was suggested by Yang et al. (71).
Stabilization of the pentacovalent phosphorane transition state involves interactions with nearby amino acid residues
We wished to elucidate the roles of the amino acid residues in the active site in facilitating the WMSA mechanism. We analyzed hydrogen bonding interactions, and calculated intermolecular interactions (including van der Waals and electrostatic energies). We also analyzed group partial charges of each of the three phosphates in the dCTP along the reaction pathway for the nucleophilic attack. We compared the transition state values with those for the intermediate in which the γ-phosphate was protonated but phosphoryl transfer had not been initiated, in order to reveal the specific interactions that stabilize the transition state.
Key hydrogen bonding interactions present in the transition state are shown in Figure 5A. The partial charge analysis showed that negative charge builds up on the α and also to some extent on the β phosphates as the pentacovalent phosphorane forms during the nucleophilic attack (Figure 6). This motivates the proton on the γ-phosphate to migrate toward the α,β-bridge. Consequently the γ-phosphate group becomes highly negatively charged (Figure 6). This negative charge provokes stronger electrostatic interactions between Arg144, Tyr141 and Lys328 and the γ-phosphate group compared to their interactions in the γ-protonated intermediate (Figure 7, Supplementary Figures S9 and S10). In addition there is a water mediated hydrogen bond involving Tyr141 with the γ-phosphate throughout both steps of the reaction. In the transition state the hydrogen bond is direct without water mediation (Supplementary Figure S11).
Figure 7.
Stabilizing interactions (electrostatic and van der Waals) between Pol κ amino acid residues and the QM active site region (defined in Supplementary Figure S3) for the attack-ready O3′ intermediate and the pentacovalent phosphorane transition state (Figure 4). See also Supplementary Figures S9 and S10.
Transition state alignment is facilitated by C3′-endo sugar pucker
The conformation of the sugar pucker of the primer terminus through the progression of the reaction is shown in Supplementary Figure S12. In the original crystal structure, which had a hydrogen in place of the 3′OH, the sugar pucker was C2′-endo, but upon remodeling and MD simulation (see ‘Computational Methods’ section) the pucker changed to C3′-endo. Supplementary Figure S12 shows the pseudorotation parameter P (72,73) during the QM/MM–MD as a function of the reaction coordinate. We see that the pucker remains near C3′-endo until the neighborhood of the intermediate (Figure 4), where it oscillates around C1′-exo but returns to C3′-endo in the transition state, providing the proper alignment for the transition state geometry. Crystal structures of pre-reactant polymerase ternary complexes have been predominantly C3′-endo (34,66,68–70,74–76) except for Y-Family polymerases (2).
Spontaneous proton transfer from the γ-phosphate to the α,β-bridging oxygen occurs during leaving of the pyrophosphate
Under the influence of the QM/MM–MD the dynamics revealed spontaneous proton transfer from the γ-phosphate to the α,β phosphate bridge during the leaving of the pyrophosphate (Figure 4). This protonation accompanied the nucleotidyl transfer reaction step after formation of the pentacovalent phosphorane transition state and before the pyrophosphate left completely. The leaving of the pyrophosphate is assisted by this proton transfer, which relieves the accumulating negative charge on the α,β-bridging oxygen during the elongation of the Pα–Oα,β-bridge bond (Figure 6).
Other mechanisms provide unstable intermediates or higher energy barriers
Other pathways that we explored for the deprotonation of the H(O3′) included: (i) Amino acids as the general base for H(O3 ′). There are two carboxylate-containing amino acids within a short distance of the primer (E199 and D198). Both are part of the conserved amino acid triad in polymerase active sites (4). We considered the closer one, E199 as a natural candidate for the base that absorbs the O3′ proton. While the potential energy for this transfer revealed a promising activation barrier of 30.1 kcal/mol, the E199 protonated intermediate was not stable and the hydrogen quickly returned to the O3′ upon an unrestrained QM/MM–MD of 0.5ps (Supplementary Figure S13). This contrasts with the case for the WMSA mechanism discussed above where the O3′ proton remained stably on the γ-phosphate during 35 ps of unrestrained QM/MM–MD. We next tried a one-step mechanism in which the O3′ donates its proton to E199 while it simultaneously approaches the α-phosphate for the nucleophilic attack. This mechanism always produced an uphill reaction energy profile (Supplementary Figure S14).
(ii) Amino Acids as donor to protonate the dNTP. Experimental evidence indicates that the incoming dNTP must become protonated to ease the phosphoryl transfer and the leaving of the pyrophosphate, and it has been suggested that an amino acid could be the donor in the case of certain other polymerases (77). In Pol κ a suitable donor amino acid could be Arg144 because a guanidino group proton is 2.8 Å from the γ phosphate oxygen (Figure 5 and Supplementary Figure S7). Therefore, we explored a path that involves protonation of the γ-phosphate by this Arg144 (Supplementary Figure S15A). Another path we explored for the γ-phosphate protonation combined proton donation by Arg144 with E199 serving as the base for the H(O3′) (Supplementary Figure S15B). In addition we considered the possibility that each of these two paths occurred simultaneously with the nucleophilic attack. All produced uphill reaction energy profiles (Supplementary Figure S15C).
(iii) The α-phosphate of the dNTP as the base or an intermediate in the path of H(O3′) to the γ-phosphate. Mechanisms involving protonation of the α-phosphate were examined: either a direct protonation or protonation via a water were considered (Supplementary Figure S6). The protonated α-phosphate did not provide a stable intermediate as found for the Dpo4 WMSA mechanism (35); upon a short unrestrained QM/MM–MD the hydrogen went back to the primer O3′ to produce the reactant structure. By contrast the protonated γ-phosphate intermediate in the WMSA mechanism was stable during 35 ps of unrestrained QM/MM–MD simulation.
Disfavored mechanisms remain so irrespective of H(O3′) orientation
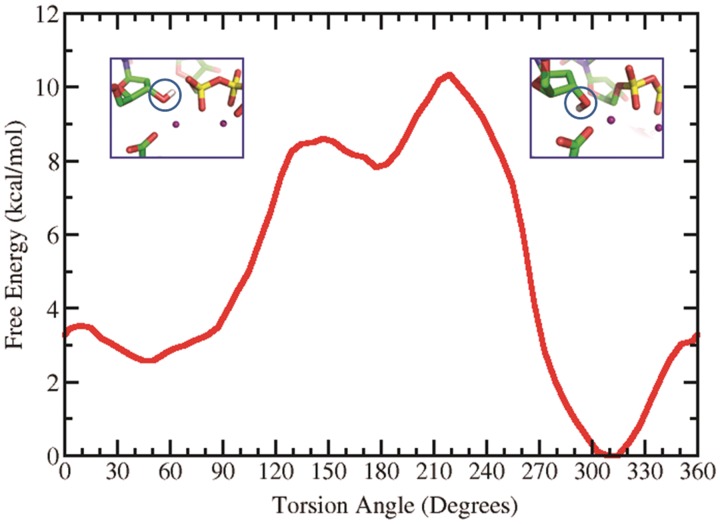
We made an extensive investigation of the H(O3′) orientation and its effect on the reaction mechanisms that we studied. We carried out a survey of the free energy profile of the C2′–C3′–O3′–H torsion angle which governs the orientation of the hydrogen of the O3′. This was carried out with AMBER 9 (47) by restraining this torsion angle at 10° intervals from 0° to 360° with 2 ns MD simulations for each window, utilizing a force constant of 30 kcal/mol-rad2. The WHAM method was then utilized to obtain the free energy profile (78). Figure 8 shows minima at 45°, 177° and 309° with relative energies of 2.6, 7.8 and 0 kcal/mol, respectively. Our results showed that for the WMSA mechanism it was necessary for the H(O3′) to be near the 60° energy well, which allows the proton to shuttle through the water molecule, as in our earlier work (35,36); however, the disfavored mechanisms remained disfavored irrespective of the H(O3′) orientation (e.g. Supplementary Figure S14).
Figure 8.
Free energy profile of the torsion angle C2′–C3′–O3′–H determining the orientation of the H(O3′). At the 45° minimum the hydrogen is oriented towards the α-phosphate while at the 309° minimum it is directed toward E199.
The pentacovalent phosphorane transition state structure is preserved in the presence of the B[a]P-dG adduct
We wished to evaluate whether the pentacovalent phosphorane transition state in our characterized WMSA mechanism is preserved in the presence of the B[a]P-dG adduct, modeled on the minor groove side of the templating base in Pol κ, as in the NMR solution structure (26). For this purpose, we developed a new Amber-compatible force field for the transition state structure in the unmodified Pol κ (see ‘Computational Methods’ section and Supplementary Tables S1 and S2). Transition states are extremely transient, with a lifetime of the order of 0.01 to 0.1 ps, in the same time frame as a single bond vibration (79). We carried out an MD simulation of the transition state structure in the presence of the B[a]P-dG adduct, and for an unmodified control transition state structure. We wished to determine if the geometric properties of the QM/MM–MD determined transition state for the unmodified Pol κ are preserved when the lesion is present. Supplementary Figure S16 and Supplementary Table S3 shows that the characteristic phosphorane transition state geometry, after 1 ns of classical MD, is preserved as in the QM/MM–MD transition state for both unmodified and modified systems. Figure 5 shows the QM/MM–MD transition state and that of the B[a]P-containing structure simulated by MD. These data reveal that the transition state is maintained in the presence of the lesion as well as it is in the unmodified case, and as found in the QM/MM–MD computations for the unmodified system. Figures 9 and 10, and Supplementary Movie S3 show the adduct structures prior to reaction and in the transition state after the 1 ns MD, revealing that they are very similar. Supplementary Figure S17 shows the linkage site torsion angles χ, α’ and β’; 242 ± 12°, 204 ± 39° and 58 ± 9°, respectively (as defined in Figure 1) that govern the carcinogen orientation on the minor groove side. They are very close to those obtained previously by Jia and coworkers, who performed MD simulations (30) for this adduct positioned in Pol κ on the templating guanine opposite dCTP prior to the nucleotidyl transfer reaction (χ, α′ and β′; 225 ± 13.0°, 187 ± 8.1° and 64.4 ± 9.4°, respectively). These results indicate that the lesion does not interfere with the formation of the transition state as the reaction progresses from its initial state.
Figure 9.
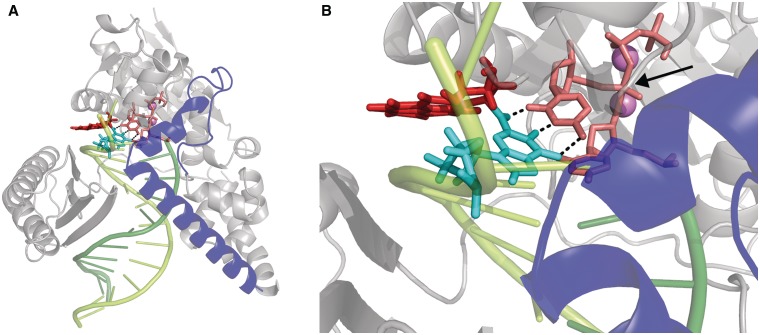
Pol κ containing the B[a]P-dG adduct in the minor groove at the pentacovalent phosphorane transition state. View is towards the major groove and emphasizes the maintained Watson–Crick base pairing between B[a]P-dG and the incoming dCTP. (A) Zoom-out view (B) Close-up view. Color scheme: N-clasp domain, blue; B[a]P ring system, red; lesion-containing guanine, cyan; Primer-linked dCTP, pink. Watson–Crick hydrogen bonds between B[a]P-dG and dCTP, black dashed lines. The pentacovalent phosphorane is indicated by an arrow. See Supplementary Movie S3.
Figure 10.
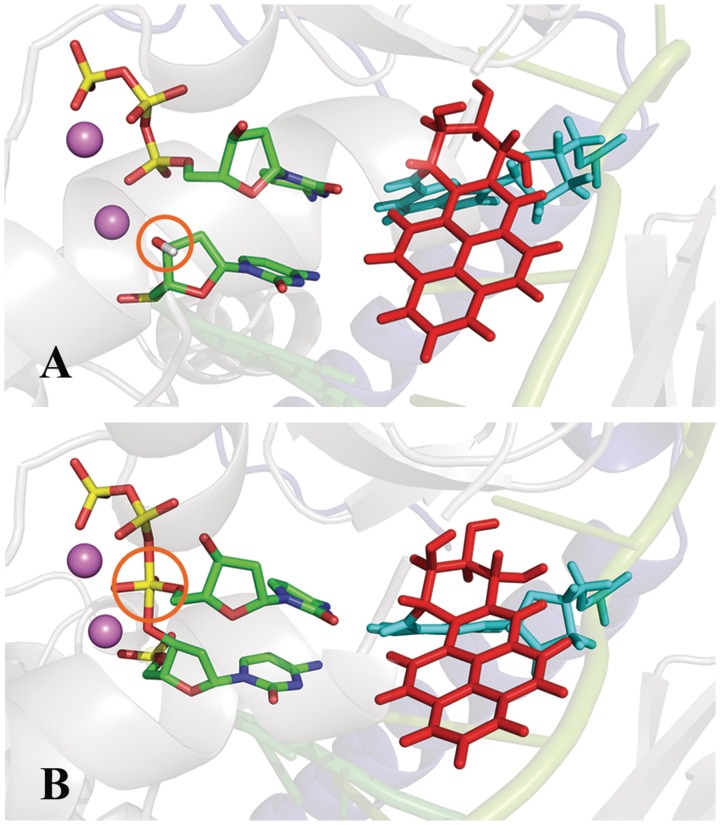
Pol κ containing the B[a]P-dG adduct viewed into the minor groove in close-up (A) Prior to reaction with the O3′H designated by an orange circle (B) At the transition state with pentacovalent phosphorane designated by an orange circle; Color scheme: N-clasp domain, blue; B[a]P ring system, red; lesion-containing guanine, cyan; dCTP and the primer are colored by atom. See Supplementary Movie S3.
DISCUSSION
We have carried out a very comprehensive investigation of the mechanism for the nucleotidyl transfer reaction in human DNA Pol κ utilizing cutting edge ab initio QM/MM–MD methods. Examined mechanisms considered the identity of the general base for the H(O3′) and different possibilities for the protonation of the dCTP. The roles of the amino acids in the vicinity of the dCTP in these investigated mechanisms were extensively explored, as were the functions of crystal and solvent waters. Our previous work utilizing QM/MM methods determined that a WMSA mechanism had the lowest free energy reaction path for the Y-family polymerase Dpo4 (35) and the A-family polymerase T7 (36). Here we used the more advanced QM/MM–MD method which has the advantage of taking account of dynamics of the enzyme active site and its environment on an equal footing.
We find that a variant of the WMSA mechanism again provides the lowest free energy path and that all other mechanisms investigated were not energetically feasible. The mechanism proceeds in two steps: (i) deprotonation of the H(O3′) with nearly concerted shuttling of the proton through a crystal and a solvent water to the γ-phosphate of dCTP; the latter acts as the general base and the barrier is 11.2 ± 0.4 kcal/mol (Supplementary Movie S1); (ii) nucleophilic attack of O3′ on the α-phosphate of the dCTP in an associative manner, to produce a pentacovalent phosphorane transition state; this is followed by pyrophosphate leaving accompanied by proton transfer from the γ-phosphate to the α,β-oxygen bridge. The barrier for the second step is 10.6 ± 0.3 kcal/mol (Supplementary Movie S2). These barriers may be compared with the experimentally observed kcat values in the range of 0.46 to 0.28 s−1 (10,80–82); this kcat range corresponds to a barrier upper bound for the reaction of 18.7 to 19.0 kcal/mol according to transition state theory: kcat(T) = kBT/h exp[−ΔG++(T)/RT] (where kcat is the catalytic rate constant, KB is the Boltzmann constant, h is the Planck constant, R is the universal gas constant, T is the temperature (310 K) and ΔG++ is the free energy of activation). The mechanism is essentially the same as the WMSA mechanism determined for both T7 and Dpo4, with minor differences in paths taken by the migrating protons. However, the barriers for steps (i) and (ii), respectively were 13.0 and 10.5 kcal/mol for Dpo4 and 14.2 and 5.5 for T7, indicating that deprotonation of the H(O3′) was rate limiting in those two cases. In Pol κ the barriers for the two steps are very close in energy, although step (ii) appears to be slightly lower energy. Our current results point to the likelihood that the WMSA mechanism could be widely applicable, but that the details can differ in different polymerases as governed by the specific local structural details.
Overall, the WMSA mechanism is consistent with the experimental findings that the chemical reaction in several polymerases entails transfer of two protons, involving 3′OH deprotonation and protonation of the leaving pyrophosphate (37,77). However, for Pol κ our extensive investigations did not locate a low energy pathway that utilized a basic amino acid residue in the active site as a general acid to donate a proton to pyrophosphate, as experimentally suggested for a number of other polymerases (77). In Pol κ candidate amino acid residues might be Arg144 and Lys328, but they are positioned differently than in the experimentally investigated polymerases (Figure 5). Nonetheless, we find that the local amino acids, Arg144, Lys328 and Thr138 play a key role in anchoring the dCTP throughout the reaction and provide added stabilization to the transition state by a network of hydrogen bond interactions. Particularly important is the role of Arg144 whose multiple hydrogen bonding opportunities are dynamically utilized as the reaction progresses (Figure 5). Another important stabilizing hydrogen bonding interaction is provided by Tyr141; this amino acid is hydrogen bonded with the γ-phosphate via a water throughout the reaction, but is hydrogen bonded directly at the transition state. Accordingly one could propose that mutating Arg144, Lys328, Thr138 and Tyr141, would impact the catalytic power of the enzyme, with Arg144 perhaps having the greatest effect. These proposed mutations offer suggestions for future experimental studies. However, none of them would be required to directly act as a general acid. It is entirely plausible, since local organization of amino acid residues is polymerase dependent (77), and that these residues can function in different ways to facilitate the nucleotidyl transfer reaction in different polymerases.
The nature of the general base for the deprotonation of the H(O3′) has been considered in previous calculations for other polymerases and attention has centered mainly on amino acids as the general base (83–86). However, a water mediated shuttle to the γ-phosphate was confirmed for Dpo4 (87) as in our WMSA mechanism (35). Our previous studies did not support an amino acid as general base for Dpo4 or T7 DNA polymerase (35,36), and the current results do not support it for Pol κ. However, polymerase dependence certainly remains possible and experimental insights could provide further elucidation.
Of particular significance is our determination that the pentacovalent phosphorane transition state structure that we computed with QM/MM–MD methods for the unmodified DNA in Pol κ remains intact in the presence of the B[a]P-dG lesion, covalently linked to the templating guanine and oriented in the 5′-direction of the modified strand as in the NMR solution structure (26). The lesion has been shown to be bypassed near error-free in vitro by DNA Pol κ (11), and Pol κ bypasses this lesion with higher efficiency and accuracy than other Y family polymerases (23). Furthermore, we have shown previously using MD simulations of dCTP Watson–Crick paired with the templating B[a]P-dG in Pol κ, that the pre-reactant state remains organized for nucleotidyl transfer (30). Our current work shows, importantly, that the transient pentacovalent phosphorane transition state, whose stability would be in the 0.01–0.1 ps time range (79), remains stable for over a nanosecond of MD simulation both with and without the presence of the B[a]P-dG lesion. These findings provide key determinations that this minor groove bulky lesion disturbs neither the pre-reactant nor the critical transition state on the reaction pathway. An experimental comparison is provided by steady state kinetic studies with this B[a]P-dG stereoisomeric lesion and incoming dCTP in Pol κ. These studies (80) showed an increase in overall barrier to reaction from 18.7 to 21.5 kcal/mol, i.e. 2.8 kcal/mol, according to transition state theory. This modest difference does not appear to stem from impediments to the nucleotidyl transfer chemical reaction, but to other factors that are subsumed in the overall kcat that derive from the presence of the bulky polycyclic ring system, such as perhaps translocation (88).
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online: Supplementary Tables 1–3, Supplementary Figures 1–17, Supplementary Movies 1–3, Supplementary Computational Details, Supplementary Scheme 1 and Supplementary References [30,32,34,46,47,54,65,89–97].
FUNDING
National Institutes of Health (NIH) [R01-CA-28038 to S.B., R01-GM079223 to Y.Z. and CA-099194 to N.E.G.]; NSF [CHE-CAREER-0448156 to Y.Z.]. Computational infrastructure and systems management were partially supported by NIH [R01-CA-75449 to S.B.]. Funding for open access charge: NIH [R01-CA-28038 to S.B.].
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation (NSF) and the Multi-purpose High Performance Computing resource of New York University (NYU-ITS). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Cancer Institute or the National Institutes of Health.
REFERENCES
- 1.McCulloch SD, Kunkel TA. The fidelity of DNA synthesis by eukaryotic replicative and translesion synthesis polymerases. Cell Res. 2008;18:148–161. doi: 10.1038/cr.2008.4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Yang W, Woodgate R. What a difference a decade makes: insights into translesion DNA synthesis. Proc. Natl Acad. Sci. USA. 2007;104:15591–15598. doi: 10.1073/pnas.0704219104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lange SS, Takata K, Wood RD. DNA polymerases and cancer. Nat. Rev. Cancer. 2011;11:96–110. doi: 10.1038/nrc2998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Broyde S, Wang L, Rechkoblit O, Geacintov NE, Patel DJ. Lesion processing: high-fidelity versus lesion-bypass DNA polymerases. Trends Biochem. Sci. 2008;33:209–219. doi: 10.1016/j.tibs.2008.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Guo C, Kosarek-Stancel JN, Tang TS, Friedberg EC. Y-family DNA polymerases in mammalian cells. Cell Mol. Life Sci. 2009;66:2363–2381. doi: 10.1007/s00018-009-0024-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Prakash S, Johnson RE, Prakash L. Eukaryotic translesion synthesis DNA polymerases: specificity of structure and function. Annu. Rev. Biochem. 2005;74:317–353. doi: 10.1146/annurev.biochem.74.082803.133250. [DOI] [PubMed] [Google Scholar]
- 7.Sale JE, Lehmann AR, Woodgate R. Y-family DNA polymerases and their role in tolerance of cellular DNA damage. Nat. Rev. Mol. Cell Biol. 2012;13:141–152. doi: 10.1038/nrm3289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Livneh Z, Ziv O, Shachar S. Multiple two-polymerase mechanisms in mammalian translesion DNA synthesis. Cell Cycle. 2010;9:729–735. doi: 10.4161/cc.9.4.10727. [DOI] [PubMed] [Google Scholar]
- 9.Friedberg EC, Lehmann AR, Fuchs RP. Trading places: how do DNA polymerases switch during translesion DNA synthesis? Mol. Cell. 2005;18:499–505. doi: 10.1016/j.molcel.2005.03.032. [DOI] [PubMed] [Google Scholar]
- 10.Choi JY, Angel KC, Guengerich FP. Translesion synthesis across bulky N2-alkyl guanine DNA adducts by human DNA polymerase kappa. J. Biol. Chem. 2006;281:21062–21072. doi: 10.1074/jbc.M602246200. [DOI] [PubMed] [Google Scholar]
- 11.Rechkoblit O, Zhang Y, Guo D, Wang Z, Amin S, Krzeminsky J, Louneva N, Geacintov NE. trans-Lesion synthesis past bulky benzo[a]pyrene diol epoxide N2-dG and N6-dA lesions catalyzed by DNA bypass polymerases. J. Biol. Chem. 2002;277:30488–30494. doi: 10.1074/jbc.M201167200. [DOI] [PubMed] [Google Scholar]
- 12.Poon K, Itoh S, Suzuki N, Laxmi YR, Yoshizawa I, Shibutani S. Miscoding properties of 6alpha- and 6beta-diastereoisomers of the N(2)-(estradiol-6-yl)-2′-deoxyguanosine DNA adduct by Y-family human DNA polymerases. Biochemistry. 2008;47:6695–6701. doi: 10.1021/bi7022255. [DOI] [PubMed] [Google Scholar]
- 13.Yasui M, Dong H, Bonala RR, Suzuki N, Ohmori H, Hanaoka F, Johnson F, Grollman AP, Shibutani S. Mutagenic properties of 3-(deoxyguanosin-N2-yl)-2-acetylaminofluorene, a persistent acetylaminofluorene-derived DNA adduct in mammalian cells. Biochemistry. 2004;43:15005–15013. doi: 10.1021/bi048279+. [DOI] [PubMed] [Google Scholar]
- 14.Phillips DH. Fifty years of benzo(a)pyrene. Nature. 1983;303:468–472. doi: 10.1038/303468a0. [DOI] [PubMed] [Google Scholar]
- 15.Phillips DH. Polycyclic aromatic hydrocarbons in the diet. Mutat. Res. 1999;443:139–147. doi: 10.1016/s1383-5742(99)00016-2. [DOI] [PubMed] [Google Scholar]
- 16.Clapp RW, Jacobs MM, Loechler EL. Environmental and occupational causes of cancer: new evidence 2005-2007. Rev. Environ. Health. 2008;23:1–37. doi: 10.1515/reveh.2008.23.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Geacintov NE, Cosman M, Hingerty BE, Amin S, Broyde S, Patel DJ. NMR solution structures of stereoisometric covalent polycyclic aromatic carcinogen-DNA adduct: principles, patterns, and diversity. Chem. Res. Toxicol. 1997;10:111–146. doi: 10.1021/tx9601418. [DOI] [PubMed] [Google Scholar]
- 18.Hanrahan CJ, Bacolod MD, Vyas RR, Liu T, Geacintov NE, Loechler EL, Basu AK. Sequence specific mutagenesis of the major (+)-anti-benzo[a]pyrene diol epoxide-DNA adduct at a mutational hot spot in vitro and in Escherichia coli cells. Chem. Res. Toxicol. 1997;10:369–377. doi: 10.1021/tx9601925. [DOI] [PubMed] [Google Scholar]
- 19.Huang X, Kolbanovskiy A, Wu X, Zhang Y, Wang Z, Zhuang P, Amin S, Geacintov NE. Effects of base sequence context on translesion synthesis past a bulky (+)-trans-anti-B[a]P-N2-dG lesion catalyzed by the Y-family polymerase pol kappa. Biochemistry. 2003;42:2456–2466. doi: 10.1021/bi026912q. [DOI] [PubMed] [Google Scholar]
- 20.Zhang Y, Wu X, Guo D, Rechkoblit O, Geacintov NE, Wang Z. Two-step error-prone bypass of the (+)- and (-)-trans-anti-BPDE-N2-dG adducts by human DNA polymerases eta and kappa. Mutat. Res. 2002;510:23–35. doi: 10.1016/s0027-5107(02)00249-x. [DOI] [PubMed] [Google Scholar]
- 21.Zhang Y, Wu X, Guo D, Rechkoblit O, Wang Z. Activities of human DNA polymerase kappa in response to the major benzo[a]pyrene DNA adduct: error-free lesion bypass and extension synthesis from opposite the lesion. DNA Repair. 2002;1:559–569. doi: 10.1016/s1568-7864(02)00055-1. [DOI] [PubMed] [Google Scholar]
- 22.Zhang Y, Yuan F, Wu X, Wang M, Rechkoblit O, Taylor JS, Geacintov NE, Wang Z. Error-free and error-prone lesion bypass by human DNA polymerase kappa in vitro. Nucleic Acids Res. 2000;28:4138–4146. doi: 10.1093/nar/28.21.4138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Avkin S, Goldsmith M, Velasco-Miguel S, Geacintov N, Friedberg EC, Livneh Z. Quantitative analysis of translesion DNA synthesis across a benzo[a]pyrene-guanine adduct in mammalian cells: the role of DNA polymerase kappa. J. Biol. Chem. 2004;279:53298–53305. doi: 10.1074/jbc.M409155200. [DOI] [PubMed] [Google Scholar]
- 24.Hashimoto K, Cho Y, Yang IY, Akagi JI, Ohashi E, Tateishi S, de Wind N, Hanaoka F, Ohmori H, Moriya M. The vital role of pol zeta and REV1 in mutagenic, but not correct, DNA synthesis across benzo[a]pyrene-dG and the recruitment of pol zeta by REV1 to a replication-stalled site. J. Biol. Chem. 2012;287:9613–9622. doi: 10.1074/jbc.M111.331728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Conney AH. Induction of microsomal enzymes by foreign chemicals and carcinogenesis by polycyclic aromatic hydrocarbons: G. H. A. Clowes Memorial Lecture. Cancer Res. 1982;42:4875–4917. [PubMed] [Google Scholar]
- 26.Cosman M, de los Santos C, Fiala R, Hingerty BE, Singh SB, Ibanez V, Margulis LA, Live D, Geacintov NE, Broyde S, et al. Solution conformation of the major adduct between the carcinogen (+)-anti-benzo[a]pyrene diol epoxide and DNA. Proc. Natl Acad. Sci. USA. 1992;89:1914–1918. doi: 10.1073/pnas.89.5.1914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cho BP. Dynamic conformational heterogeneities of carcinogen-DNA adducts and their mutagenic relevance. J. Environ. Sci. Health C. Environ. Carcinog. Ecotoxicol. Rev. 2004;22:57–90. doi: 10.1081/LESC-200038217. [DOI] [PubMed] [Google Scholar]
- 28.Stone MP, Huang H, Brown KL, Shanmugam G. Chemistry and structural biology of DNA damage and biological consequences. Chem. Biodivers. 2011;8:1571–1615. doi: 10.1002/cbdv.201100033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lukin M, de Los Santos C. NMR structures of damaged DNA. Chem. Rev. 2006;106:607–686. doi: 10.1021/cr0404646. [DOI] [PubMed] [Google Scholar]
- 30.Jia L, Geacintov NE, Broyde S. The N-clasp of human DNA polymerase kappa promotes blockage or error-free bypass of adenine- or guanine-benzo[a]pyrenyl lesions. Nucleic Acids Res. 2008;36:6571–6584. doi: 10.1093/nar/gkn719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sherrer SM, Sanman LE, Xia CX, Bolin ER, Malik CK, Efthimiopoulos G, Basu AK, Suo Z. Kinetic analysis of the bypass of a bulky DNA lesion catalyzed by human Y-family DNA polymerases. Chem. Res. Toxicol. 2012;25:730–740. doi: 10.1021/tx200531y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lone S, Townson SA, Uljon SN, Johnson RE, Brahma A, Nair DT, Prakash S, Prakash L, Aggarwal AK. Human DNA polymerase kappa encircles DNA: implications for mismatch extension and lesion bypass. Mol. Cell. 2007;25:601–614. doi: 10.1016/j.molcel.2007.01.018. [DOI] [PubMed] [Google Scholar]
- 33.Steitz TA. DNA polymerases: structural diversity and common mechanisms. J. Biol. Chem. 1999;274:17395–17398. doi: 10.1074/jbc.274.25.17395. [DOI] [PubMed] [Google Scholar]
- 34.Batra VK, Beard WA, Shock DD, Krahn JM, Pedersen LC, Wilson SH. Magnesium-induced assembly of a complete DNA polymerase catalytic complex. Structure. 2006;14:757–766. doi: 10.1016/j.str.2006.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wang L, Yu X, Hu P, Broyde S, Zhang Y. A water-mediated and substrate-assisted catalytic mechanism for Sulfolobus solfataricus DNA polymerase IV. J. Am. Chem. Soc. 2007;129:4731–4737. doi: 10.1021/ja068821c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wang L, Broyde S, Zhang Y. Polymerase-tailored variations in the water-mediated and substrate-assisted mechanism for nucleotidyl transfer: insights from a study of T7 DNA polymerase. J. Mol. Biol. 2009;389:787–796. doi: 10.1016/j.jmb.2009.04.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Castro C, Smidansky E, Maksimchuk KR, Arnold JJ, Korneeva VS, Gotte M, Konigsberg W, Cameron CE. Two proton transfers in the transition state for nucleotidyl transfer catalyzed by RNA- and DNA-dependent RNA and DNA polymerases. Proc. Natl Acad. Sci. USA. 2007;104:4267–4272. doi: 10.1073/pnas.0608952104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hu P, Wang S, Zhang Y. How do SET-domain protein lysine methyltransferases achieve the methylation state specificity? Revisited by Ab initio QM/MM molecular dynamics simulations. J. Am. Chem. Soc. 2008;130:3806–3813. doi: 10.1021/ja075896n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hu P, Wang SL, Zhang YK. highly dissociative and concerted mechanism for the nicotinamide cleavage reaction in sir2tm enzyme suggested by ab initio QM/MM molecular dynamics simulations. J. Am. Chem. Soc. 2008;130:16721–16728. doi: 10.1021/ja807269j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhang Y, Lee T, Yang W. A pseudobond approach to combining quantum mechanical and molecular mechanical methods. J. Chem. Phys. 1999;110:46–54. [Google Scholar]
- 41.Zhang Y. Pseudobond ab initio QM/MM approach and its applications to enzyme reactions. Theor. Chem. Acc. 2006;116:43–50. [Google Scholar]
- 42.Zhang Y, Liu H, Yang W. Free energy calculation on enzyme reactions with an efficient iterative procedure to determine minimum energy paths on a combined ab initio QM/MM potential energy surface. J. Chem. Phys. 2000;112:3483–3492. [Google Scholar]
- 43.Kumar S, Bouzida D, Swendsen RH, Kollman PA, Rosenberg JM. The weighted histogram analysis method for free-energy calculation on biomolecules .1. The method. J. Comput. Chem. 1992;13:1011–1021. [Google Scholar]
- 44.Souaille M, Roux B. Extension to the weighted histogram analysis method: combining umbrella sampling with free energy calculations. Comput. Phys. Commun. 2001;135:40–57. [Google Scholar]
- 45.Ferrenberg AM, Swendsen RH. New Monte Carlo technique for studying phase transitions. Phys. Rev. Lett. 1988;61:2635–2638. doi: 10.1103/PhysRevLett.61.2635. [DOI] [PubMed] [Google Scholar]
- 46.Berman HM, Battistuz T, Bhat TN, Bluhm WF, Bourne PE, Burkhardt K, Feng Z, Gilliland GL, Iype L, Jain S, et al. The protein data bank. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2002;58:899–907. doi: 10.1107/s0907444902003451. [DOI] [PubMed] [Google Scholar]
- 47.Case DA, Darden TA, Cheatham TE, III, Simmerling CL, Wang J, Duke RE, Luo R, Merz KM, Pearlman DA, Crowley M, et al. AMBER 9. San Francisco: University of California; 2006. [Google Scholar]
- 48.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]
- 49.Wang J, Cieplak P, Kollman PA. How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? J. Comput. Chem. 2000;21:1049–1074. [Google Scholar]
- 50.Hornak V, Abel R, Okur A, Strockbine B, Roitberg A, Simmerling C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins. 2006;65:712–725. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Perez A, Marchan I, Svozil D, Sponer J, Cheatham TE, 3rd, Laughton CA, Orozco M. Refinement of the AMBER force field for nucleic acids: improving the description of alpha/gamma conformers. Biophys. J. 2007;92:3817–3829. doi: 10.1529/biophysj.106.097782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Perlow RA, Broyde S. Toward understanding the mutagenicity of an environmental carcinogen: structural insights into nucleotide incorporation preferences. J. Mol. Biol. 2002;322:291–309. doi: 10.1016/s0022-2836(02)00751-9. [DOI] [PubMed] [Google Scholar]
- 53.Jorgensen WL, Chandrasekhar J, Madura J, Klein ML. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 54.Price DJ, Brooks CL., 3rd A modified TIP3P water potential for simulation with Ewald summation. J. Chem. Phys. 2004;121:10096–10103. doi: 10.1063/1.1808117. [DOI] [PubMed] [Google Scholar]
- 55.Lee C, Yang W, Parr RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B: Condens. Matter. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 56.Becke AD. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A. 1988;38:3098–3100. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- 57.Becke AD. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993;98:5648–5652. [Google Scholar]
- 58.Petersson GA, Bennett A, Tensfeldt TG, Al-Laham MA, Shirley WA, Mantzaris J. A complete basis set model chemistry. I. The total energies of closed-shell atoms and hydrides of the first-row atoms. J. Chem. Phys. 1988;89:2193–2218. [Google Scholar]
- 59.Al-Laham Mohammad A, Petersson GA. A complete basis set model chemistry. II. Open-shell systems and the total energies of the first-row atoms. J. Chem. Phys. 1991;94:6081–6090. [Google Scholar]
- 60.Zhang Y. Improved pseudobonds for combined ab initio quantum mechanical/molecular mechanical methods. J. Chem. Phys. 2005;122:024114. doi: 10.1063/1.1834899. [DOI] [PubMed] [Google Scholar]
- 61.Shao Y, Molnar LF, Jung Y, Kussmann J, Ochsenfeld C, Brown ST, Gilbert ATB, Slipchenko LV, Levchenko SV, O'Neill DP, et al. Advances in methods and algorithms in a modern quantum chemistry program package. Phys. Chem. Chem. Phys. 2006;8:3172–3191. doi: 10.1039/b517914a. [DOI] [PubMed] [Google Scholar]
- 62.Ponder JW. TINKER, software Tools for molecular design. 2004 doi: 10.1021/acs.jctc.8b00529. Version 4.2 ed, Washington University in St. Louis, St. Louis, WA. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Hu H, Yang W. Free energies of chemical reactions in solution and in enzymes with ab initio quantum mechanics/molecular mechanics methods. Annu. Rev. Phys. Chem. 2008;59:573–601. doi: 10.1146/annurev.physchem.59.032607.093618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. DeLano, W.L. (2002). DeLano Scientific, Palo Alto, CA, USA.
- 65.Ling H, Sayer JM, Plosky BS, Yagi H, Boudsocq F, Woodgate R, Jerina DM, Yang W. Crystal structure of a benzo[a]pyrene diol epoxide adduct in a ternary complex with a DNA polymerase. Proc. Natl Acad. Sci. USA. 2004;101:2265–2269. doi: 10.1073/pnas.0308332100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Doublie S, Tabor S, Long AM, Richardson CC, Ellenberger T. Crystal structure of a bacteriophage T7 DNA replication complex at 2.2 A resolution. Nature. 1998;391:251–258. doi: 10.1038/34593. [DOI] [PubMed] [Google Scholar]
- 67.Brieba LG, Eichman BF, Kokoska RJ, Doublie S, Kunkel TA, Ellenberger T. Structural basis for the dual coding potential of 8-oxoguanosine by a high-fidelity DNA polymerase. EMBO J. 2004;23:3452–3461. doi: 10.1038/sj.emboj.7600354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Wang F, Yang W. Structural insight into translesion synthesis by DNA Pol II. Cell. 2009;139:1279–1289. doi: 10.1016/j.cell.2009.11.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Berman AJ, Kamtekar S, Goodman JL, Lazaro JM, de Vega M, Blanco L, Salas M, Steitz TA. Structures of phi29 DNA polymerase complexed with substrate: the mechanism of translocation in B-family polymerases. EMBO J. 2007;26:3494–3505. doi: 10.1038/sj.emboj.7601780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Garcia-Diaz M, Bebenek K, Krahn JM, Pedersen LC, Kunkel TA. Role of the catalytic metal during polymerization by DNA polymerase lambda. DNA Repair. 2007;6:1333–1340. doi: 10.1016/j.dnarep.2007.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Yang W, Lee JY, Nowotny M. Making and breaking nucleic acids: two-Mg2+-ion catalysis and substrate specificity. Mol. Cell. 2006;22:5–13. doi: 10.1016/j.molcel.2006.03.013. [DOI] [PubMed] [Google Scholar]
- 72.Altona C, Sundaralingam M. Conformational analysis of the sugar ring in nucleosides and nucleotides. A new description using the concept of pseudorotation. J. Am. Chem. Soc. 1972;94:8205–8212. doi: 10.1021/ja00778a043. [DOI] [PubMed] [Google Scholar]
- 73.Saenger W. Defining Terms for the Nucleic Acids. In: Cantor CR, editor. Principles of Nucleic Acid Structure. New York: Springer-Verlag; 1984. pp. 19–20. [Google Scholar]
- 74.Li Y, Korolev S, Waksman G. Crystal structures of open and closed forms of binary and ternary complexes of the large fragment of Thermus aquaticus DNA polymerase I: structural basis for nucleotide incorporation. EMBO J. 1998;17:7514–7525. doi: 10.1093/emboj/17.24.7514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Franklin MC, Wang J, Steitz TA. Structure of the replicating complex of a pol alpha family DNA polymerase. Cell. 2001;105:657–667. doi: 10.1016/s0092-8674(01)00367-1. [DOI] [PubMed] [Google Scholar]
- 76.Johnson SJ, Taylor JS, Beese LS. Processive DNA synthesis observed in a polymerase crystal suggests a mechanism for the prevention of frameshift mutations. Proc. Natl Acad. Sci. USA. 2003;100:3895–3900. doi: 10.1073/pnas.0630532100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Castro C, Smidansky ED, Arnold JJ, Maksimchuk KR, Moustafa I, Uchida A, Gotte M, Konigsberg W, Cameron CE. Nucleic acid polymerases use a general acid for nucleotidyl transfer. Nat. Struct. Mol. Biol. 2009;16:212–218. doi: 10.1038/nsmb.1540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Grossfield A. WHAM: the Weighted Histogram Analysis Method. version 2.0.4 ed. [Google Scholar]
- 79.Schramm VL. Enzymatic transition states, transition-state analogs, dynamics, thermodynamics, and lifetimes. Annu. Rev. Biochem. 2011;80:703–732. doi: 10.1146/annurev-biochem-061809-100742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Sassa A, Niimi N, Fujimoto H, Katafuchi A, Gruz P, Yasui M, Gupta RC, Johnson F, Ohta T, Nohmi T. Phenylalanine 171 is a molecular brake for translesion synthesis across benzo[a]pyrene-guanine adducts by human DNA polymerase kappa. Mutat. Res. 2011;718:10–17. doi: 10.1016/j.mrgentox.2010.11.002. [DOI] [PubMed] [Google Scholar]
- 81.Choi JY, Lim S, Kim EJ, Jo A, Guengerich FP. Translesion synthesis across abasic lesions by human B-family and Y-family DNA polymerases alpha, delta, eta, iota, kappa, and REV1. J. Mol. Biol. 2010;404:34–44. doi: 10.1016/j.jmb.2010.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Choi JY, Chowdhury G, Zang H, Angel KC, Vu CC, Peterson LA, Guengerich FP. Translesion synthesis across O6-alkylguanine DNA adducts by recombinant human DNA polymerases. J. Biol. Chem. 2006;281:38244–38256. doi: 10.1074/jbc.M608369200. [DOI] [PubMed] [Google Scholar]
- 83.Cisneros GA, Perera L, Garcia-Diaz M, Bebenek K, Kunkel TA, Pedersen LG. Catalytic mechanism of human DNA polymerase lambda with Mg2+ and Mn2+ from ab initio quantum mechanical/molecular mechanical studies. DNA Repair. 2008;7:1824–1834. doi: 10.1016/j.dnarep.2008.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Florian J, Goodman MF, Warshel A. Computer simulations of protein functions: searching for the molecular origin of the replication fidelity of DNA polymerases. Proc. Natl Acad. Sci. USA. 2005;102:6819–6824. doi: 10.1073/pnas.0408173102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Florian J, Goodman MF, Warshel A. Computer simulation of the chemical catalysis of DNA polymerases: discriminating between alternative nucleotide insertion mechanisms for T7 DNA polymerase. J. Am. Chem. Soc. 2003;125:8163–8177. doi: 10.1021/ja028997o. [DOI] [PubMed] [Google Scholar]
- 86.Lin P, Pedersen LC, Batra VK, Beard WA, Wilson SH, Pedersen LG. Energy analysis of chemistry for correct insertion by DNA polymerase b. Proc. Natl. Acad. Sci. USA. 2006;103:13294–13299. doi: 10.1073/pnas.0606006103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Wang Y, Schlick T. Quantum mechanics/molecular mechanics investigation of the chemical reaction in Dpo4 reveals water-dependent pathways and requirements for active site reorganization. J. Am. Chem. Soc. 2008;130:13240–13250. doi: 10.1021/ja802215c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Zhang L, Rechkoblit O, Wang L, Patel DJ, Shapiro R, Broyde S. Mutagenic nucleotide incorporation and hindered translocation by a food carcinogen C8-dG adduct in Sulfolobus solfataricus P2 DNA polymerase IV (Dpo4): modeling and dynamics studies. Nucleic Acids Res. 2006;34:3326–3337. doi: 10.1093/nar/gkl425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Uljon SN, Johnson RE, Edwards TA, Prakash S, Prakash L, Aggarwal AK. Crystal structure of the catalytic core of human DNA polymerase kappa. Structure. 2004;12:1395–1404. doi: 10.1016/j.str.2004.05.011. [DOI] [PubMed] [Google Scholar]
- 90.Gordon JC, Myers JB, Folta T, Shoja V, Heath LS, Onufriev A. H++: a server for estimating pKas and adding missing hydrogens to macromolecules. Nucleic Acids Res. 2005;33:W368–W371. doi: 10.1093/nar/gki464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Anandakrishnan R, Onufriev A. Analysis of basic clustering algorithms for numerical estimation of statistical averages in biomolecules. J. Comput. Biol. 2008;15:165–184. doi: 10.1089/cmb.2007.0144. [DOI] [PubMed] [Google Scholar]
- 92.Dolinsky TJ, Nielsen JE, McCammon JA, Baker NA. PDB2PQR: an automated pipeline for the setup of Poisson-Boltzmann electrostatics calculations. Nucleic Acids Res. 2004;32:W665–W667. doi: 10.1093/nar/gkh381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Mezei M. A new method for mapping macromolecular topography. J. Mol. Graph. Model. 2003;21:463–472. doi: 10.1016/s1093-3263(02)00203-6. [DOI] [PubMed] [Google Scholar]
- 94.Darden TY, York D, Pedersen L. Particle mesh Ewald: an NlogN method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 95.Essmann UP, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen L. A smooth particle mesh Ewald method. J. Chem. Phys. 1995;103:8577–8593. [Google Scholar]
- 96.Ryckaert JPC, Ciccotti G, Berendsen HJ. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977;23:327–341. [Google Scholar]
- 97.Berendsen HJC, Postma JPM, van Gunsteren WF, DiNola A, Haak JR. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984;81:3684–3690. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.