Abstract
Sedimentation velocity analytical ultracentrifugation has experienced a significant transformation, precipitated by the possibility of efficiently fitting Lamm equation solutions to the experimental data. The precision of this approach depends on the ability to account for the imperfections of the experiment, both regarding the sample and the instrument. In the present work, we explore in more detail the relationship between the sedimentation process, its detection, and the model used in the mathematical data analysis. We focus on configurations that produce steep and fast-moving sedimentation boundaries, such as frequently encountered when studying large multi-protein complexes. First, as a computational tool facilitating the analysis of heterogeneous samples, we introduce the strategy of partial boundary modeling. It can simplify the modeling by restricting the direct boundary analysis to species with sedimentation coefficients in a predefined range. Next, we examine factors related to the experimental detection, including the magnitude of optical aberrations generated by out-of-focus solution columns at high protein concentrations, the relationship between the experimentally recorded signature of the meniscus and the meniscus parameter in the data analysis, and the consequences of the limited radial and temporal resolution of the absorbance optical scanning system. Surprisingly, we find that large errors can be caused by the finite scanning speed of the commercial absorbance optics, exceeding the statistical errors in the measured sedimentation coefficients by more than an order of magnitude. We describe how these effects can be computationally accounted for in SEDFIT and SEDPHAT.
Keywords: Analytical ultracentrifugation, Hydrodynamics, Direct boundary modeling, Lamm equation
Introduction
In the 1980s, analytical ultracentrifugation reemerged as an important tool of physical biochemistry, partly due to the development of computerized data acquisition systems and the commercial availability of a new generation of analytical ultracentrifuges (Schachman 1989). Building on this advance, in the last decade, modern computational methods of data analysis have substantially expanded the capabilities and widened the application in particular of sedimentation velocity (SV) analytical ultracentrifugation, chiefly due to the ability to more efficiently and more accurately solve the Lamm equation (Lamm 1929) (the partial differential equation that describes the evolution of the macromolecular concentration distributions) (Philo 1997; Schuck 1998; Schuck et al. 1998; Demeler et al. 2000; Behlke and Ristau 2002; Stafford and Sherwood 2004; Cao and Demeler 2005; Dam et al. 2005; Brown and Schuck 2008), and the consideration of sample heterogeneity through diffusion-deconvoluted size-distribution approaches (Schuck 2000; Schuck et al. 2002; Balbo et al. 2005; Brown and Schuck 2006) that allow one to distinguish with unprecedented resolution the contributions from diffusion, heterogeneity, and chemical reactions to the evolution of the shape of the sedimentation boundary. In the biological sciences, examples for areas of significant interest in the Lamm equation modeling of SV data include protein self- and hetero-associations and the characterization of multi-protein complex assemblies with regard to the number, populations, and stoichiometry of species; the binding energy and kinetics; the hydrodynamic shape of proteins, protein complexes, and other biomacromolecules; the characterization of drug delivery nano-particles; and the quality control of protein pharmaceuticals. For recent, more general reviews on this technique, see Lebowitz et al. (2002), Howlett et al. (2006), Schuck (2007), and Brown et al. (2008a, b).
It is obvious that in order to obtain reliable and detailed results, it is necessary to apply close scrutiny to the limitations of the experimental data and their faithful representation in the data analysis model. For example, a key for the detailed direct modeling of the experimental signal profiles was the introduction of the explicit systematic time-invariant (TI) and radial-invariant (RI) noise offsets into the mathematical model (Schuck and Demeler 1999). Similarly, inclusion of the acceleration phase of the rotor allowed for the model to better match the actual experiment (Schuck et al. 2000), as did the consideration of pressure gradients from solvent compressibility (Schuck 2004). With these tools, in conjunction with size-distribution methods that account for imperfections in the sample, it is frequently possible to fit the experimental data within the error of data acquisition. However, with increasingly detailed questions being addressed by SV and increasingly sophisticated analysis models being applied, it is necessary to critically reassess the relationship between experiment and theoretical model and to refine their correspondence in order to obtain accurate results. Accordingly, many recent studies have explored the limitations of detection of SV from theoretical and experimental perspectives and were aimed at identifying potential factors that when properly controlled or accounted for could further improve SV methodology (Gonzalez et al. 2003; Liu et al. 2006; Gabrielson et al. 2007a, b; Pekar and Sukumar 2007; Brown et al. 2008a, b; Gabrielson et al. 2009).
In the present work, we have focused on several aspects that currently appear to be limiting the precision or that impact the practical application of SV analysis of steep, fast-moving boundaries. These are among the most challenging experimental SV configurations, yet also promise to provide the highest resolution sedimentation coefficient distributions and the highest precision of sedimentation coefficients.
An experimental concern for such configurations is the finite radial and temporal resolution of the commercial absorbance optical system caused by its relatively slow scanning speed. One distortion immediately apparent is the movement of the boundary during the time required by the scanner to record the boundary shape. A perhaps not as apparent, but equally important problem is that the time-stamp of the scans generally does not reflect the time when the boundary position is actually recorded. One of the goals in the present work was to test the magnitude of these effects experimentally and to derive corrections in the mathematical model of SV analyses that allow describing the recorded data more faithfully.
Another experimental concern when generating steep boundaries is aberrations in the optical system from refractive index gradients, which unavoidably always accompany the macromolecular sedimentation boundary. By bending the path of light through the solution (“Wiener skewing”, Wiener 1893), the imaged radial positions experience a distortion dependent on the magnitude of the refractive index gradient and the focus of the optical system (see below). The effect on the recorded data has been shown to be minimal when the optical system is focused to the 2/3 plane of the solution column, a condition usually fulfilled when using standard 12-mm centerpieces. Unfortunately, this is not easily possible for the 3-mm centerpieces that are commonly used at higher protein concentrations, requiring either refocusing the optical system or the use of custom-made spacers, neither being practical to apply. In the present work, we describe experiments that explore the permissible magnitude of refractive index gradients in the standard experimental configuration.
For further developing the data analysis models, one current practical limitation is the ubiquitous presence of trace populations of aggregates and other degradation products in protein samples. They also become most apparent when the macromolecule of interest forms a well-defined, narrow boundary. The exquisite sensitivity of SV does allow for the detection of trace species, and in fact, requires their incorporation into the model such that they do not bias the parameters of interest. While for some studies, such as the quality control of protein pharmaceuticals, this is the result of primary interest (Berkowitz 2006; Liu et al. 2006; Gabrielson et al. 2007a, b; Pekar and Sukumar 2007; Brown et al. 2008a, b), for other applications their description is more cumbersome and a nuisance in the modeling. In the present work, we describe an alternative strategy to accomplish this, termed “partial boundary modeling” (PBM). It is based on the idea of setting different fitting limits for each measured concentration profile at different time-points, such that species whose sedimentation takes place outside the main sedimentation boundary of interest (e.g., the faster sedimenting aggregates) do not need to be considered in the model. As will be shown in the present work, PBM lends itself particularly well to modeling steep boundaries. Because it can be applied to the same data subsets, PBM also allows for a detailed comparison with the approach of analyzing SV data in a transformed data space using a g(s*) “data transformation.”
Finally, we addressed what currently seem to be two major experimental limitations, one being the possible effect of low level convection on the sedimentation process, and one arising from the inability to determine experimentally the precise meniscus position. The difficulty of determining the meniscus position is due to both the presence of significant local optical artifacts at the liquid/air interface and the limited radial resolution of the experimental scans (Gropper 1964; Philo 1997; Pekar and Sukumar 2007). As has been emphasized by Philo (1997), it is not clear how to determine the true meniscus parameter, yet it seems an essential model parameter for predicting the boundary position. From experiments conducted under conditions promoting exaggerated convection, we were able to demonstrate that the meniscus problem and the convection problem can be interrelated, and that it can be advantageous not to attempt incorporating a graphically determined meniscus position into the analysis. This topic is also closely related to the problem of the finite temporal resolution of the absorbance system, as well as the choice of data analysis mode: treating the meniscus parameter as a freely adjustable fitting parameter can compensate for offsets in the apparent boundary positions introduced by the finite speed of the absorbance scanner. Further, we found that, in contrast to g(s*), using PBM or whole boundary modeling allows incorporating sufficiently large numbers of scans spanning the whole experiment such that the meniscus parameter is well-determined from the time-course of the observed boundary displacement.
The goal of the present work was to study these interrelated problems, clarify experimental limitations, and develop tools to improve the reliable data interpretation in SV analytical ultracentrifugation.
Theory
Modeling the central slope of the sedimentation boundary
The initial motivation was to develop a modern analogue to the analysis of the area/height ratio of Schlieren peaks in terms of apparent diffusion coefficients, in order to obtain a very robust tool for boundary analysis in the presence of significant sample heterogeneity. We were inspired by the use of this analysis as a highly sensitive approach to study, for example, the lifetime of complexes in systems with ligand-induced conformational changes such as aspartate transcarbamoylase (Werner and Schachman 1989). In this sense, the approach should serve as a “model-free” tool to quantitatively assess the degree of boundary spreading.
The Schlieren optical detection system directly detects concentration gradients, whereas the absorbance and Rayleigh interference optical systems measure concentrations or concentration differences, respectively. In order to apply the area/height ratio approach from Schlieren analysis to the latter detection systems, it is desirable to translate the area/height ratio of the gradient peaks into the data space of concentrations. (The alternative approach of radial differentiation to transform the concentration data computationally to Schlieren peaks would unavoidably result in severe noise amplification.) In the data space of the absorbance and the interference system, the area of a Schlieren peak corresponds to the plateau concentration, and the height of the Schlieren peak corresponds to the maximum slope of the sedimentation boundary. The plateau concentration can be easily determined from the concentration profiles. In order to extract the maximum slope, we can fit a straight line to a narrow region in the center of the sedimentation boundary. A sufficiently linear portion of the sedimentation boundary may be, for example, the central 20% of the boundary (i.e., data points with concentration values between 0.4 and 0.6-fold the plateau concentration); in our implementation in SEDPHAT, the boundary portion can be refined by the user after inspection of the fit for sufficient linearity of the boundary region used.
We globally fit the central scan section of all scans with straight lines with the slopes
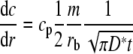 |
1 |
(with the rotor angular velocity ω, plateau concentration cp, meniscus position m, time t, radial coordinate r, boundary position 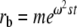 , sedimentation coefficient s, and apparent diffusion coefficient D*). Equation 1 represents the radial derivative of the first term of the Faxén solution to the Lamm equation (Faxén 1929). The apparent diffusion coefficient D* describes the broadening of the boundary, i.e., its decreasing slope, as it migrates towards the bottom of the cell. It corresponds to the true molecular diffusion coefficient only for ideally sedimenting, monodisperse samples. In this case, one could apply the Svedberg equation
, sedimentation coefficient s, and apparent diffusion coefficient D*). Equation 1 represents the radial derivative of the first term of the Faxén solution to the Lamm equation (Faxén 1929). The apparent diffusion coefficient D* describes the broadening of the boundary, i.e., its decreasing slope, as it migrates towards the bottom of the cell. It corresponds to the true molecular diffusion coefficient only for ideally sedimenting, monodisperse samples. In this case, one could apply the Svedberg equation
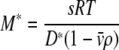 |
2 |
to estimate the molar mass M*. However, in practice this estimate can be a substantial underestimate for heterogeneous systems (which exhibit boundary broadening in significant excess over that caused by diffusion), or an overestimate in the presence of repulsive nonideality (which will cause steeper boundaries) or optical artifacts from Wiener skewing (which will cause steepening and translation of the signal gradients).
A disadvantage of this model for interference optical data is that it is not compatible with the algebraic determination of TI and RI noise. Incompatibility arises when the central boundary portions of sequential scans are not overlapping, thus not providing an opportunity to distinguish the concentration signal from the systematic noise. Further, the algorithm for the algebraic noise subtraction developed in Schuck and Demeler (1999) thus far requires all scans to be analyzed over identical radial ranges. Therefore, an empirical TI and RI noise subtraction method does need to be applied prior to the central slope model when using interference optical data (such as the application of another ad hoc model to prefit the data for the analysis of TI and RI signals). To overcome this drawback, we developed a strategy of calculating TI and RI noise parameters when using wider radial analysis windows, modeled with numerical Lamm equation solutions (Brown and Schuck 2008) instead of Eq. 1. This was achieved with the new approach of PBM.
Partial boundary modeling and systematic noise decomposition
For very heterogeneous samples, it can be desirable to confine the analysis to just the main boundary component, but to characterize that in great detail and with high precision. A very useful and rational way to define the radial limits of the moving data window is to follow the transport flux of ideally sedimenting nondiffusing particles. For each scan n, the smallest radius value ln and highest radius value un are described by hypothetical particles sedimenting with a lower and upper s-value, sl and su, respectively, propagating from the meniscus according to the well-known expressions 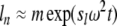 and
and 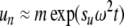 (with the approximation sign meant to indicate that we take the closest point on the radial grid of experimental data points). With this design of the radial analysis illustrated in Figs. 1 and 2, we would need to consider in our boundary model only species with s-values in the range between sl and su if it were not for diffusion and attractive or repulsive intermolecular interactions taking place. Since the diffusion of small particles can be very high, leading to migration comparably fast to the sedimentation of large particles, we envision that the most useful models to be applied in PBM may likely describe species with s-values from 0 to su, but not species sedimenting much faster than su.
(with the approximation sign meant to indicate that we take the closest point on the radial grid of experimental data points). With this design of the radial analysis illustrated in Figs. 1 and 2, we would need to consider in our boundary model only species with s-values in the range between sl and su if it were not for diffusion and attractive or repulsive intermolecular interactions taking place. Since the diffusion of small particles can be very high, leading to migration comparably fast to the sedimentation of large particles, we envision that the most useful models to be applied in PBM may likely describe species with s-values from 0 to su, but not species sedimenting much faster than su.
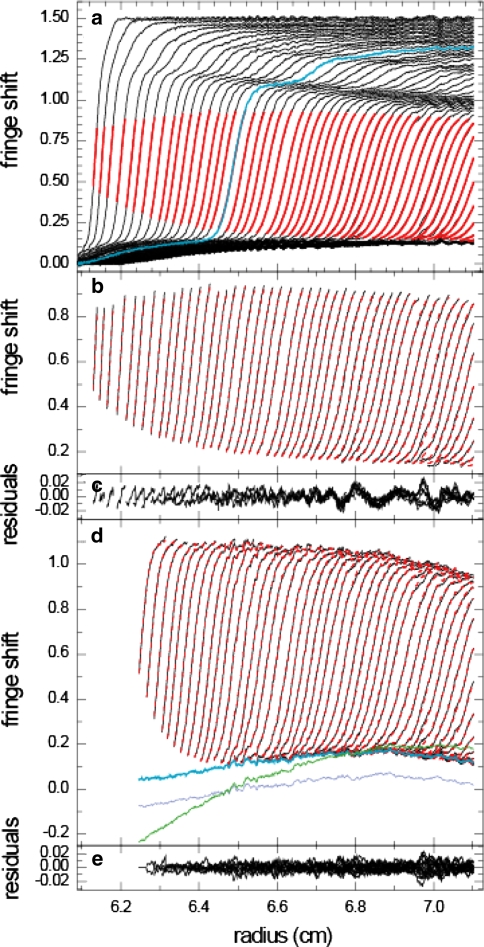
Fig. 1.
a Sedimentation profiles of thyroglobulin sedimenting at 50,000 rpm. For clarity, TI and RI noise contributions initially estimated from a standard c(s) analysis of the whole profiles were subtracted. Highlighted in red are the partial boundary segments defined with the apparent s-values of 17 and 20 S. In order to demonstrate the shape of the boundary and the relative location of the slow- and fast-moving boundaries at a single point in time, one profile is highlighted in blue. b The PBM region of the raw data (black lines) being fit with the partial boundary model (dashed red lines) using a single-species model. The residuals are shown in c. d A larger analysis window in PBM (15–21 S) is used for PBM accounting directly for TI and RI noise. The data are shown in black, the fit as red dashed line. The first several scans are eliminated due to insufficient overlap. The best-fit TI noise profile is shown as a green line, which can be compared to the TI noise estimate from the whole boundary c(s) model in gray. After eliminating the RI noise from scan alignment with a preliminary whole boundary analysis, the TI noise estimate derived from PBM is shown as a blue solid line. e Residuals from d
Fig. 2.
Schematic of the selection of PBM limits for heterogeneous systems that exhibit both small and large species. To illustrate the recommended strategy, the black solid lines are simulated sedimentation data for three species of 0.3, 6, and 20 S. The red portion highlights the partial boundary for apparent s-values ranging from 1 to 8 S, which includes a large portion of the boundary spread from the small species, such that their influence on the main boundary can be accurately assessed, but no signal from the large species that can be excluded from consideration in the model
Provided that this design leads to overlapping radial regions covering each radial position with at least two scans, the data do provide information for calculating TI and RI signal offsets. (Otherwise the systematic noise contributions must be predetermined and/or absent.) The following describes an approach for determining the systematic TI noise contributions bi = b(ri) at the radial points ri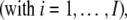 and the systematic RI noise contributions βn = β(tn) at the time of the nth scan, tn
and the systematic RI noise contributions βn = β(tn) at the time of the nth scan, tn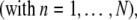 given data an,i in a moving radial window reaching from the lower radial limit i = ln to an upper limit i = un. The systematic noise will be part of a boundary model and added to the model for the sedimenting species, which may be expressed in general as
given data an,i in a moving radial window reaching from the lower radial limit i = ln to an upper limit i = un. The systematic noise will be part of a boundary model and added to the model for the sedimenting species, which may be expressed in general as 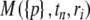 which is dependent on a set of parameters {p}. For example, for the case of TI noise, this leads to the minimization problem
which is dependent on a set of parameters {p}. For example, for the case of TI noise, this leads to the minimization problem
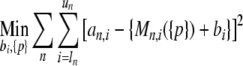 |
3 |
As outlined in Schuck and Demeler (1999), the best minimization strategy for fitting the data in a least-squares sense in the presence of systematic noise is the separation of linear and nonlinear parameters (Ruhe and Wedin 1980). Briefly, this strategy recognizes that the TI noise variables are linear and therefore can be analytically eliminated. For the full boundary model, this leads to 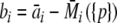 , with
, with 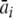 being the signal at radius ri averaged over all scans, and
being the signal at radius ri averaged over all scans, and 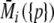 being the model at radius ri averaged over all scans, which allows us to rephrase the minimization problem as
being the model at radius ri averaged over all scans, which allows us to rephrase the minimization problem as
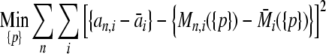 |
4 |
It is noteworthy that this appears as a fitting problem where both the data and the model appear as differences in individual profiles compared to the average profile. Once this is solved, explicit values for the systematic noise profiles bi can be calculated. (The case is similar for RI noise variables).
For PBM, a more complicated procedure has to be adopted, which we will illustrate for the case of RI and TI noise and a sedimentation model that consists of a linear combination of Lamm equation terms, 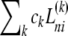 , with unknown coefficients ck
, with unknown coefficients ck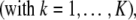 analogous to the problem of determining sedimentation coefficient distributions such as c(s). (However, any other explicit boundary model can be substituted, such as a single-species model, or a set of Lamm equation solutions coupled with reaction terms describing the sedimentation of rapidly interacting systems.) For this least-squares minimization problem of PBM,
analogous to the problem of determining sedimentation coefficient distributions such as c(s). (However, any other explicit boundary model can be substituted, such as a single-species model, or a set of Lamm equation solutions coupled with reaction terms describing the sedimentation of rapidly interacting systems.) For this least-squares minimization problem of PBM,
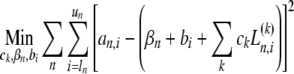 |
5 |
an optimal value of a specific RI parameter βp can be found by setting the partial derivative with regard to this parameter to 0, leading to
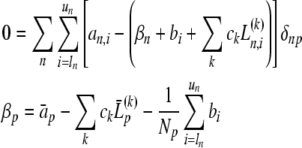 |
6 |
with the abbreviations 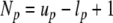 (the number of radial points in the window of scan p),
(the number of radial points in the window of scan p), 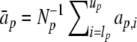 , and
, and 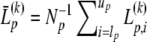 . Unfortunately, the average TI noise signal over the radial window of scan p does not vanish. This is in contrast to the simultaneous analysis of data on an identical radial grid, where the linear dependence of the set of bi, βn with regard to addition of a radially and temporally constant baseline b allowed to request per definition that
. Unfortunately, the average TI noise signal over the radial window of scan p does not vanish. This is in contrast to the simultaneous analysis of data on an identical radial grid, where the linear dependence of the set of bi, βn with regard to addition of a radially and temporally constant baseline b allowed to request per definition that 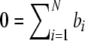 , which then led to a simple matrix operation determining at once all linear parameters, i.e., bi, βn, and ck (Schuck and Demeler 1999). In the present case, the optimal RI parameter estimates for a particular scan will be dependent on the particular TI parameters across the radial window analyzed from this scan. Similarly, setting the partial derivative with regard to a specific TI parameter bj to 0 leads to the relationship
, which then led to a simple matrix operation determining at once all linear parameters, i.e., bi, βn, and ck (Schuck and Demeler 1999). In the present case, the optimal RI parameter estimates for a particular scan will be dependent on the particular TI parameters across the radial window analyzed from this scan. Similarly, setting the partial derivative with regard to a specific TI parameter bj to 0 leads to the relationship
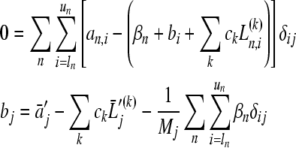 |
7 |
with the abbreviations  (the number of scans whose radial window includes rj),
(the number of scans whose radial window includes rj), 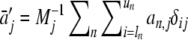 , and
, and 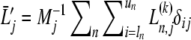 . As a consequence, the optimal TI parameter estimate bj will be dependent on the RI parameters of those scans that have analysis windows including the radial point rj.
. As a consequence, the optimal TI parameter estimate bj will be dependent on the RI parameters of those scans that have analysis windows including the radial point rj.
Because the TI and RI parameters are still linear parameters, they could in theory still be determined in a single-step matrix operation, but this would require the inversion of a matrix of the size (I + N + K – 1) × (I + N + K − 1), which is impractically large. However, we can solve Eqs. 6 and 7 iteratively in perpendicular steps by alternating the optimization of TI noise and ck for a given RI noise, and the optimization of RI noise and ck for a given TI noise. In each of these steps, Eqs. 6 and 7, respectively, can be reinserted into Eq. 5, and ck can be determined (requiring the inversion of only a K × K matrix), followed by using Eqs. 6 and 7 to evaluate the respective noise offsets. Starting estimates for both TI and RI noise parameters are easily obtained from an empirical fit of the data using the entire scans without PBM. We observed good convergence of this procedure, with usually in the order of 10 steps required to reach a precision in the root-mean-square-deviation (RMSD) of the fit of 10−6.
If this model were to be applied with a single-species Lamm equation solution, in the limit of very small analysis windows it would correspond to the central slope approach described above. However, it is more general and flexible in that it allows the consideration of larger radial regions and the application of any other boundary model.
Spatial resolution of the detection
A highly simplified mathematical model for how the finite radial bandwidth may affect the measured radial concentration profiles is averaging over the light intensity that would be detected across a radial interval Δr in an otherwise ideal optical system. Over this radial interval, we approximate the absorbance profile a(r) with the first term of a Taylor series 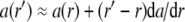 . Since the absorbance depends on the measured intensities as
. Since the absorbance depends on the measured intensities as 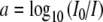 , the difference between the apparent absorbance a*(r) and the true absorbance a(r) is
, the difference between the apparent absorbance a*(r) and the true absorbance a(r) is
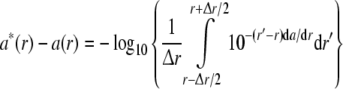 |
8 |
For example, with a radial bandwidth of 0.01 cm, only absorbance gradients greater than ~2.5 OD/mm would result in deviations in excess of the typical noise of the absorbance data acquisition. We can apply Eq. 8 for the apparent absorbance a*(r) to replace a(r) for the data analysis of single species. (For mixtures of multiple species, strictly, the apparent absorbance is a nonlinear function of the individual signals, but in the implementation in SEDFIT and SEDPHAT, we have approximated multiple signals a*(r) to be simply additive.)
This situation is better with the interference optical system (IF), first because the radial resolution is higher, and second because the error term should resemble a more symmetric box average, for which errors arise only for the quadratic and higher terms in the Taylor series of the concentration profile. However, there is a theoretical maximum gradient imposed by the continuity requirement for the fringe shifts recorded in neighboring pixel columns. In the simplest form, it would require neighboring fringe shifts to differ by less than half a fringe, 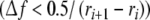 , which imposes an upper limit on the measurable slope of ~70 fringes/mm, corresponding to concentration gradients for proteins of ~20 (mg/ml)/mm. We have observed “skipping” of fringe counts in experiments with solutes at very high loading concentrations that formed strong gradients. To some extent, this can be addressed by post-centrifugal data processing, for example, requiring the continuity of fringe displacement profiles also of the higher derivatives of the fringe shift trace. Such data processing tools are implemented in SEDFIT.
, which imposes an upper limit on the measurable slope of ~70 fringes/mm, corresponding to concentration gradients for proteins of ~20 (mg/ml)/mm. We have observed “skipping” of fringe counts in experiments with solutes at very high loading concentrations that formed strong gradients. To some extent, this can be addressed by post-centrifugal data processing, for example, requiring the continuity of fringe displacement profiles also of the higher derivatives of the fringe shift trace. Such data processing tools are implemented in SEDFIT.
Temporal resolution of the detection
The frequency of scans in SV detection is usually uncritical, as a sufficiently large number of scans (>10–20, Balbo et al. 2005) representing the entire sedimentation process can ordinarily be taken even at high rotor speeds. However, of concern is the time required for completing a single scan when using the absorbance optics. In contrast to the interference optical system, where the fringe shift pattern is imaged simultaneously across the entire solution column, in the absorbance system the scanning movement of the slit across the photomultiplier is relatively slow. Because the sedimentation process continues during the time required for the scan, three concerns arise.
To what extent does the movement of the sedimentation boundary concurrent to the movement of the detection slit lead to an artificial spread of the measured boundaries? (Both movements are usually in the same orientation.) A back-of-the-envelope estimate can reveal the magnitude of this effect. For the present purpose, we may approximate the boundary shape as an error function of width σ. The time interval needed for scanning through the boundary is dt = σ/vscan, a time during which the boundary will have moved away from the scanner by
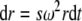 . As a result, the boundary will appear artificially broader, with the relative error given by
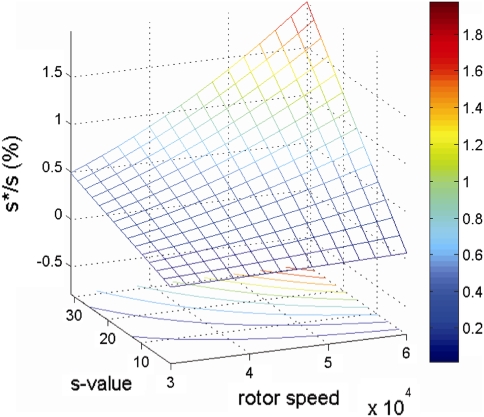
. As a result, the boundary will appear artificially broader, with the relative error given by 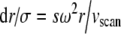 . We would expect the apparent diffusion coefficient D* characterizing the boundary spread to be overestimated by the square of this factor. A numerical evaluation with a typical scan speed of vscan ~40 μm/s for recommended scanner settings (Brown et al. 2008a, b) (see below) suggests that at a rotor speed of 50,000 rpm and radius of 7.0 cm, errors in the measured boundary spread in excess of 1% would be observed for particles >21 S.
. We would expect the apparent diffusion coefficient D* characterizing the boundary spread to be overestimated by the square of this factor. A numerical evaluation with a typical scan speed of vscan ~40 μm/s for recommended scanner settings (Brown et al. 2008a, b) (see below) suggests that at a rotor speed of 50,000 rpm and radius of 7.0 cm, errors in the measured boundary spread in excess of 1% would be observed for particles >21 S.- Despite the finite time interval required for a scan, there is only one time-stamp associated with the data. If that time-stamp is the elapsed time of the run at the start of the scan, the scans taken late in the run showing the boundary close to the bottom will have scanned through that boundary with an additional, unreported time–lag during which the boundary had a chance to migrate further. At the typical scan speeds and for a 12-mm column, this time–lag is ~30 s. The underestimate of the time it took for the boundary to migrate to the observed position in the scan will lead to an over-estimate of s-values. Quantitatively, the error in the s-value can be approximated as
(with the bottom position of the solution column at b). For example, with a solution column from 6.0 to 7.2 cm, a >0.5% relative error will be encountered at an s-value of >11.3 S or >17.7 S for rotor speeds of 50,000 or 40,000 rpm, respectively. It should be noted that this relative error is already fivefold higher than the typical precision of s-values in ultracentrifugal analyses.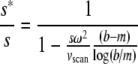
9 As the scanner moves forward into the plateau regions, the sedimentation continues and with it the radial dilution, such that scanning the solution “plateau” will produce a continually decaying signal. The magnitude of this effect can be a signal decrease in the order of 0.005–0.01 OD across the cell.
An accurate description of the absorbance data would incorporate all of these effects by recognizing the measured profiles to be a*(r, t) = a[r, tscan + (r−r0)/vscan] (with r0 being the starting radius of the scan). This correction was implemented in SEDFIT and SEDPHAT as modifications to the Lamm equation solutions (Brown and Schuck 2008) to be used when modeling absorbance optical data. The finite scan time was also considered in the theoretical expressions for the step-function boundaries of nondiffusing species, which will be affected by points (2) and (3). With the true boundary position of the nondiffusing species at 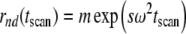 , due to the extra time delay in scanning with the absorbance system it will appear to be (in an excellent first-order approximation) at
, due to the extra time delay in scanning with the absorbance system it will appear to be (in an excellent first-order approximation) at
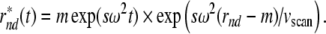 |
10 |
Similarly, the shape of the measured plateau is described by the decaying exponential
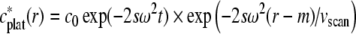 |
11 |
(with c0 the loading concentration). These corrections were implemented in the ls−g*(s) analysis (Schuck and Rossmanith 2000), which uses the step functions of nondiffusing species as the kernel. Similarly, the time delay 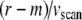 caused by the finite scan time of the absorbance optics has been accounted for in the least-squares based van Holde–Weischet model of SEDFIT (Schuck et al. 2002). Similarly, we envision that Eq. 11 will allow similar scan time corrections to be applied to the g(s*) transformation.
caused by the finite scan time of the absorbance optics has been accounted for in the least-squares based van Holde–Weischet model of SEDFIT (Schuck et al. 2002). Similarly, we envision that Eq. 11 will allow similar scan time corrections to be applied to the g(s*) transformation.
Experimental
SV experiments of thyroglobulin and bovine serum albumin samples
For most of the experiments examining the performance of the PBM analysis approach, the potential optical aberrations in 3-mm centerpieces at high concentrations, as well as the effect of the finite scan time in the absorbance optical data acquisition, we used electrophoretically heterogeneous thyroglobulin from bovine thyroid (Sigma–Aldrich, St. Louis, MO) dissolved into phosphate-buffered saline. Stock dilutions of 100 or 400 μL to concentrations between 0.5 and 8 mg/mL were loaded into the ultracentrifugal cell assemblies with 12- or 3-mm optical pathlength centerpieces, respectively, as described in “Results.” For the convection experiments, and the experiment in Fig. 5, samples of bovine serum albumin (Sigma–Aldrich, St. Louis, MO) were dissolved in 400 μL PBS. Unless otherwise mentioned in the “Results” we followed in detail the standard protocol (Balbo et al. 2007). In brief, samples were temperature equilibrated at 20.0°C in a resting An50-Ti rotor, and then accelerated to 50,000 rpm and the evolution of the concentration gradient was recorded using the interference and/or absorbance detection system until the boundary had moved to the bottom of the cell.
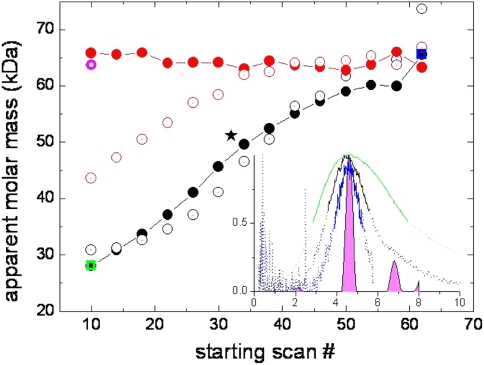
Fig. 5.
Dependence of the best-fit apparent molar mass value, as determined from a single-species Lamm equation model in PBM of the raw data (red), on the choice of scan subsets. For comparison, the results are shown of the analogous analysis when using the improved g(s*) fit with transformed Lamm equation solutions (black). All scan subsets use scan #69 as the last scan, with an interval starting with the scan number indicated in the abscissa (i.e., using 60 scans for the first data point, and only 8 scans for the last data point). The sedimentation coefficient range used in the analysis by both approaches was either fixed to the interval from 3.568 S to 5.593 S (filled circles), or adjusted for each scan selection such as to represent the width of the normalized g(s*) distribution at half-height (open circles). Shown at the coordinate 51.2 kDa/scan #32 (black star) is the best-fit apparent mass resulting from the single-species fit of the g(s*) distribution for the subset of scans from #32 to #43 suggested by the dcdt+ wizard. The fixed s-value interval from 3.5681 to 5.5933 S corresponds to the half-height of the g(s*) peak for these conditions. The inset shows the g(s*) curve for the wizard-selected conditions (dashed gray), with all scans included (green), and with the smallest subset (blue), all normalized to the same peak height. Solid lines indicate their adjusted s-range. A PBM c(s) distribution derived from the widest scan set with the adjusted s-range is shown as magenta area plot. It leads to a frictional ratio that yields a peak M-value as indicated by the magenta circle in the main plot
SV experiments of trp RNA-binding attenuating protein (TRAP)
The trp RNA-binding attenuating protein data are from the laboratory of Dr. James Cole. They served as example data in the analytical ultracentrifugation workshop at the University of Connecticut and are used here with kind permission. The samples were prepared and studied as described in Snyder et al. (2004). The g(s*) analyses were conducted with dcdt+ version 2.2.0, using the improved method as described in Philo (2006). The g(s*) analysis of the TRAP data as published in Philo (2006) was kindly provided by Dr. John Philo.
Results
Partial boundary modeling
Figure 1 shows fringe shift data of a sample of thyroglobulin, exhibiting a large number of aggregate species and other degradation products. If the intent for the SV experiment is to characterize with high precision the main boundary only, the conventional modeling approach would place significant computational effort on the contaminating species by requiring all sedimenting material to be accounted for in the model. In contrast, if the analysis is confined to the radial range highlighted in red (defined by the apparent sedimentation coefficients from 17 to 20 S), a much simpler model can be applied. Clearly, the displacement of the boundary and its decreasing slope with time can be assessed well, which allows one to determine apparent diffusion coefficient and molar mass values D* and M*, respectively. For the data shown in Fig. 1 in red, a single species model leads to an apparent molar mass estimate of 670 kDa, in good agreement with the literature value of 660 kDa (Mercken et al. 1985), with an RMSD of 0.0075 fringes.
One potential pitfall of PBM caused by too narrow boundary sections is the inability to define the height of the boundary component, which could potentially result in inaccurate implications for the modeled location of the boundary midpoint. This should be monitored, and, if necessary, addressed either by fixing the loading concentration parameter in the model, and/or by including some portions of the curved leading and trailing tails of the boundary into the analysis window.
A not-too-small analysis window is also desirable for several other reasons. In the fit shown in Fig. 1a and b, the systematic noise offsets had been removed after approximating them with a preliminary conventional, whole-boundary c(s) analysis. As an alternative to this ad hoc procedure, Fig. 1d and e show the analysis of the original raw data using slightly larger radial windows, (15–21 S) which leads to more overlap, such that now both TI and RI signals can be accounted for in the PBM model. A significant further improvement of the quality of fit can be observed, now leading to an apparent molar mass of 661 kDa with an RMSD of 0.0058 fringes.
A correlation between RI and TI noise parameters occurs when there is little overlap of radial segments from consecutive scans. This is because RI offsets are local to each scan, and if the TI noise profile is also predominantly a local property of only a few scans covering the same radial interval, the TI and RI noise overdetermine the offsets. This effect can be discerned from the drift of the calculated TI noise shown in green in Fig. 1d, as compared to the TI noise from a whole boundary c(s) analysis (gray line). Therefore, when forced to use PBM with only marginally overlapping radial regions, it is advantageous to use an empirical vertical prealignment of scans by an initial c(s) distribution fit to the entire set of scans across all data. This will define the RI noise well because the solution and solvent plateau regions containing most information about the RI offsets are trivial to fit and are not much correlated with the actual boundary model. (This approach seems statistically preferable and more precise than the procedure frequently applied in the context of dcdt analysis of vertical fringe alignment in a small radial region of the air-to-air space above both solution columns.) As illustrated in Fig. 1d, after such removal of RI offsets as free parameters, the remaining TI estimates from the PBM model shown in blue and from the whole-boundary c(s) model (in gray) are very similar (modulo an arbitrary constant offset).
Further, since the high diffusion coefficients of small species can cause migrations at rates comparable to the sedimentation of large species, it can be useful to include a significant portion of the trailing part of the boundary in the analysis, such as to gain more precise information on their signal gradients which may significantly modulate the shape of the boundary in the radial window of interest both in the trailing and leading (due to back-diffusion effects) parts of the boundary. An illustration for how the optimal application PBM is envisioned is shown in Fig. 2. A significant portion of the small species are included in the fit, but PBM affords the exclusion of the larger species.
PBM and data transformations
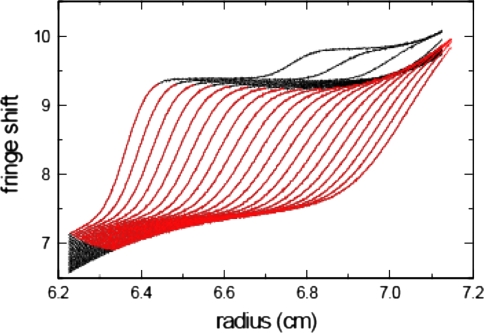
PBM establishes a new methodological relationship between data analyses in the original data space and those using the dcdt method for g(s*) (Stafford 1992), as for the first time both can be applied to similar data subsets. Of particular interest is the detailed comparison of the determination of the molar mass of a single, noninteracting species either by PBM analysis directly fitting a single-species Lamm equation solution, or by the two-stage analysis strategy of fitting transformed Lamm equation solutions (or traditionally Gaussians) to g(s*) apparent sedimentation coefficient distribution obtained through the dcdt “transform.” To illustrate this point, we examined a data set that was previously taken as a methodological model by Philo (Fig. 6 of 2006) from the SV experiments of trp TRAP.
The complete set of absorbance data is shown in Fig. 3a (gray lines). For this experiment, Philo reports the molar mass estimate for the TRAP complex to be 11.0 (10.7–11.4) monomer units, “exactly as expected” (Philo 2006) from the literature (Snyder et al. 2004). Revisiting this analysis using the same data and g(s*) analysis, we observe that it did rely on (1) a specific, fixed value of the meniscus, (2) a particular choice of fitting limits (from 4.39 to 6.28 S), and (3) the choice of a data subset consisting precisely of scans #23 to #34 (red lines in Fig. 3a) from a total of 60 meaningful scans (gray lines in Fig. 3a). The prior determination of these three factors is an intrinsic requirement for g(s*), but each can substantially influence the results. For example, a change in the meniscus position alone by −0.01 cm (still within the range of the meniscus artifact) already leads to an increase by ~0.41 monomer units. Figure 3b illustrates the strong dependence on small changes in meniscus, s-range, and scan selection, which could have led to best-fit results varying between at least 9 and 12 monomer units (excluding the data from early scans). This demonstrates that the errors reported by Philo, which appear to be just the statistical errors propagated from the noise of the data points included, grossly underestimate the uncertainty of the whole analysis.
Fig. 3a, b.
Analysis of the absorbance data from the sedimentation of TRAP used as a model system by Philo (2006). a Overlay of all experimental absorbance scans (gray) and the selection subjected to the data analysis by Philo (red) (Philo 2006), consisting of data with apparent s*-values between 4.39 and 6.28 S from scans #23 to #34. The meniscus value assumed in Philo’s analysis is indicated as bold vertical red line. b Dependence of the result from Philo’s approach on the particular set of scans included in the analysis. Shown are the molar mass estimates for sequences of scans starting with the number indicated in the abscissa, for total scan numbers of 8 scans (bold black line), 12 scans (green line), or 16 scans (blue line). Also indicated are the results obtained for 12 scans with a shift of the assumed meniscus position by –0.01 cm and a slightly narrower analysis interval including s*-values from 4.65 to 6.03 S (down triangles), and for 12 scans with a shift of the assumed meniscus position by +0.01 cm and a slightly wider analysis interval including s*-values from 4.03 to 6.91 S (up triangles). The thin black horizontal line indicates the expected value from the literature (11.0), and the red circle indicates the conditions for which the results were reported by Philo. The dashed black lines are the limits of the 95% confidence interval reported by Philo
A strong variation in best-fit results can be expected in any method that relies on preselected parameters and data subsets, which often bias the outcome in a way that is not accounted for in the statistical errors of the analysis. Therefore, it is desirable to use a method that does not have to rely on preselected data subsets and preselected fixed parameters.
The PBM approach allows the inclusion, without drawbacks, of all available scans. This, in turn, permits the optimization of the meniscus position by nonlinear regression. This leads to an excellent fit of a single-species model to the data with apparent s-range from 4.39 to 6.28 S, as shown in Fig. 4a–c. In this case, we obtain a best-fit M estimate of 9.7 monomer units, but with a wide minimum of the error surface (Fig. 4d, calculated with the projection method and F statistics). This shows that the information content of this noisy data set is not sufficient to determine the oligomer size well. Similar best-fit values of 9.8 and 9.7 were obtained with wider s-ranges (4.0–7.0 S) or smaller s-ranges (4.66–6.08 S), respectively. This molar mass estimate of 9.7 monomer units obtained here with PBM is consistent with the value of 10.1 obtained by c(M) analysis of the full data set (data not shown) and the value of 10.4 reported by Philo for the SEDPHAT hybrid discrete/continuous model, both explicitly accounting for the contaminating smaller and larger species.
Fig. 4a–d.
Analysis of the same absorbance data as in Fig. 3, but considering the information from all scans. a Overlay of all experimental absorbance scans (gray) and segments with apparent s*-values between 4.39 and 6.28 S (equivalent to those in Fig. 3). The PBM analysis permits calculating the best-fit meniscus position, as indicated by the black vertical line. The best-fit estimate of the TI noise profile is indicated by the blue line. b Enhanced view of the data (black lines) and fit (red lines) of the PBM analysis, for clarity with the TI noise estimates subtracted. c Residuals of the fit, using different colors in consecutive scans. d Normalized χ2 as a function of molar mass in monomer units, calculated with the error surface projection method of fixing the molar mass value to the values indicated while floating all other parameters. The horizontal dashed lines are the critical χ2-values for one and two standard deviation confidence levels
In order to proceed in comparing g(s*) and PBM results, we first observe the result of the g(s*) analysis when using all scans (#1 to #60), analogous to those shown in Fig. 4. This large number of scans would normally not be recommended for analysis with the standard g(s*) algorithm due to a conflict with the “rule of thumb.” However, this does not necessarily apply for the improved Lamm equation modeling of g(s*) curves, as pointed out by Philo (2006): “using this algorithm, it is actually possible to use the full span from the time the meniscus region is just cleared until the plateau region is about to disappear (Fig. 4a).” Although this would be impacted by unresolved heterogeneity (see below), the good quality of fit with the PBM model in Fig. 4 for a single-species model and the low sensitivity of the PBM result to the precise s-range chosen encouraged us that heterogeneity may not be a major factor for the present data, when the analysis is restricted to the central portion of the boundary (or peak, respectively), such as to exclude the signal contributions from the faster-sedimenting aggregates. In order to maintain this condition in the presence of the shift in peak maximum of the g(s*) distribution by ~1.5 S, we adjusted the s* range for the analysis to 3.02–6.28 S. This resulted in an estimate for M by g(s*) of only ~7.4 monomer units.
Vice versa, we can apply the PBM method to Philo’s scan selection, s-range, meniscus parameter, and best-fit estimates of M and s. This yields an RMSD of 0.00369 OD in the raw data space with PBM. Floating the s- and M-values (but keeping the meniscus fixed), results in a best-fit molar mass value of 12.0 monomer units, at a slightly improved RMSD (0.00358 OD, which is a statistically significant improvement). The error analysis with the Monte–Carlo method is not recommended for ill-behaved error surfaces. However, for comparison with the Monte–Carlo analysis reported by Philo for his SEDPHAT analysis, we performed a Monte–Carlo error analysis that suggested an error interval (95% confidence level) of about ±0.74 monomer units (requiring <10 min for 1,000 iterations on a modern desktop PC employing a single thread). Thus, for the present data the dcdt data-transform into the s*-space followed by the Lamm equation-based analysis in the s*-space, led to a difference, relative to the best-fit PBM results from Lamm equation modeling in the raw data space, in the best-fit molar mass by ~9%, and a smaller statistical error estimate by almost a factor of two.
Finally, we made a comparison of the results when using an intermediate scan range (#13 to #44), which does not yet cause a very large shift in the peak s*-value of g(s*). This results in an estimate of ~8.6 monomer units. When the PBM model was fixed to the same meniscus value and the best-fit s- and M-values from the g(s*) analysis, this led to an RMSD of 0.00508 OD in the raw data space. In comparison, when, in an otherwise identical model, the s and M parameters are optimized in the original data space with the PBM analysis (at a fixed meniscus), a significantly better fit with RMSD ~0.00474 OD was found with molar mass of ~9.7 monomer units. (Due to poor convergence on this ill-defined error surface, the precise values for the RMSD varied by ~0.00001 OD dependent on starting conditions, with a corresponding variation of M of ~0.7 monomer units). Again, the difference in the RMSD between the best-fit PBM model and that with parameters fixed to those determined by g(s*) shows that the g(s*) parameter values are nonoptimal when applied in the raw data space with the PBM model.
If a single-species model is applied to a boundary from a poorly resolved, heterogeneous mixture, a possible strategy might be to constrain the s-range of the analysis to a boundary fraction that represents mostly the species of interest and to choose a subset of scans late in the run where the different species are best resolved. Although we do not recommend the use of small scan ranges for PBM analysis, it is of interest to examine the apparent molar mass values returned from this “subset” single-species modeling approach as a function of the scan range. This also sheds additional light on the comparison of the properties of PBM and g(s*) and addresses the question how many scans should be included in a g(s*) analysis using the improved g(s*) fitting approach with transformed Lamm equation solutions.
To this end, a sample of BSA was sedimented at 50,000 rpm, using a loading concentration that produced ~0.2 OD280 in a 12-mm double-sector centerpiece, and absorbance profiles were acquired at ~3-min intervals. We analyzed the data with scan ranges of decreasing size, starting with scans #10–69, #14–69, 18–69, etc., until finally the smallest range of #62–69. For the s-range, we chose 3.57–5.60 S [which would correspond to the half-height of the g(s*) peaks under the conditions suggested by the dcdt+ wizard]. The apparent molar mass values as a function of scan range used in PBM are shown in Fig. 5 as red solid circles, resulting in estimates of ~65 kDa. There is a slight increase in the apparent molar mass with increasing scan range, but no apparent penalty in using a very large scan range. In contrast, for the equivalent analyses in g(s*) (keeping the meniscus value at the wizard-determined position), we observe a strong systematic decrease in the molar mass estimate to less than half the true value (black circles) when using the largest interval. The same trend was observed when adjusting the s-value range for each scan subset individually to encompass the half-width of each particular g(s*) peak (open black circles). These half-widths of the g(s*) peaks increase with increasing scan range (from 3.91–5.25 S at the smallest to 2.84–7.47 S) due to g(s*) peak broadening.
When the PBM model was executed in the raw data space using the same adjusted s-ranges as used in the corresponding g(s*) analysis, a drop in the molar mass estimate was also observed (open red circles), although significantly less than in the g(s*) analysis. However, we note that in this case the quality of fit with a single-species model is not acceptable, and a switch from the single-species PBM to a c(s) PBM model is indicated. For example, with the widened s-range of 2.82–7.47 S for the scan set #10–69, the single-species PBM model exhibits an RMSD of 0.00339 OD with systematic residuals, whereas the c(s) model for the otherwise identical PBM selection leads to a much improved RMSD of 0.00176 OD. The resulting c(s) sedimentation coefficient distribution fit to this PBM selection is as shown in the inset of Fig. 5 (magenta area graph); it has a peak molar mass of ~64 kDa (magenta circle).
Having characterized the properties of the PBM approach, it will be used in the following for the detailed analysis of the measured sedimentation data from the thyroglobulin sample similar to the data shown in Fig. 1.
Recording steep sedimentation boundaries in 3-mm centerpieces
One of the concerns of SV experiments with steep boundaries is the refractive index gradient dn/dr associated with the macromolecular concentration gradient, and whether it leads to optical aberrations (lensing effects) such as Wiener skewing (Wiener 1893). Clearly, dn/dr will be higher at higher protein concentrations, and an obvious approach to reduce dn/dr is to use shorter path-length centerpieces. Unfortunately, when using commercially available cell components with 3-mm centerpieces, another problem arises: the optical system of the analytical ultracentrifuge is aligned such that the focus is in the 2/3 plane of the solution column of the standard 12-mm centerpieces. This minimizes the Wiener skewing from the refractive index gradients of the sedimenting sample (Forsberg and Svensson 1954; Svensson 1954) when using these standard centerpieces. However, this condition cannot be easily fulfilled with common cell components when using 3-mm centerpieces.
In order to examine to what extent the location of the focus of the interference optical system relative to the solution column affects the quality of signal in 3-mm centerpieces, we assembled the ultracentrifugal cell in three alternate configurations: (1) using two standard 4.5-mm spacers on either side such that the filling holes are lined up with the aluminum housing, but the optics is focused at the lower end of the solution column, (2) with a custom-made 3-mm spacer below and a 6-mm spacer above the 3-mm centerpiece such as to lower the centerpiece and to maintain the 2/3 plane of the solution column in the optical focal plane, and (3) in the opposite combination raising the centerpiece and exacerbating the out-of-focus position, which will place the focal point 3 mm below the end of the solution column.
First, at a low concentration of thyroglobulin (0.5 mg/mL), no significant differences (within the error of replicate experiments) in the s-values, signal amplitudes, and frictional ratios were observed (data not shown). This is expected due to the small refractive index gradients formed. Next, we filled all centerpieces with the same thyroglobulin solution at 8 mg/mL, causing maximum slopes in the sedimentation boundary of ~100 fringes/cm. Here, the standard c(s) analysis cannot model the measured boundary shapes well due to the neglect of hydrodynamic nonideality in the c(s) model, and at the same time a single nonideal species model also fails due to the neglect of heterogeneity in the sample. Therefore, we applied PBM to fit only the central steep portion of the gradients using a single ideal-species model simply as an empirical measure for the boundary location and slope. In comparing the different cells, the apparent sedimentation and diffusion coefficient so obtained should capture any systematic distortions in the boundary shape caused by optical aberrations. The results of this analysis are summarized in Table 1. All the measured s-values and D-values were significantly lower than in dilute solution (Fig. 1), as expected in the presence of hydrodynamic nonideality. No significant differences between different cell configurations were found in the measured s-values. For the cells that were installed with the 2/3 plane matching the focus of the optics, we measured an apparent diffusion coefficient of 0.664 ± 0.005 F, which is within error identical to the values of 0.660 ± 0.006 F obtained in the configuration using the standard spacers. Only in the configuration exacerbating the offset of the centerpiece was the result significantly different, with the lower value of 0.583 F indicating the steepening of the recorded profiles. This suggests that the 1.5-mm offset between the 2/3 plane and the focal point of the optical system in the 3-mm centerpieces is not causing significant aberrations at gradients of up to ~100 fringes/cm.
Table 1.
Effect of the position of 3-mm centerpieces on the apparent boundary spread D*
| 2/3 Plane offset to focal point (mm) | Concentration (fringes)a | s (S)b | D* (F)b |
|---|---|---|---|
| 1.5 | 21.0 | 16.99 | 0.664 |
| 1.5 | 21.1 | 17.02 | 0.656 |
| 0 | 20.3 | 16.98 | 0.663 |
| 0 | 20.1 | 16.93 | 0.660 |
| 0 | 21.0 | 17.10 | 0.669 |
| 3.0 | 19.7 | 17.04 | 0.583 |
aCorrected for cell path-length
bSedimentation and diffusion coefficient were determined from a single-species PBM model from the data points contributing to the s-range of 16.5 to 17.5 S
The effect of finite time resolution when using the absorbance optical scanner
For numerous experimental reasons it can often be advantageous to use the absorbance optical detection system. It is not based on imaging but on scanning through the radial coordinate with a finite spatial detector width and relatively low time-resolution. Since only one time-stamp for the scan is available, as opposed to the exact times for each radial point when the local signals were recorded, a potential concern arises especially when observing steep and fast-moving boundaries. We first examined the effect of the relatively slow scanning speed, in order to test the predictions outlined in the “Theory” section.
In initial experiments, we determined the radial velocity of the absorbance optical scanner by measuring the duration of the audible lamp flashes when scanning the cell for a preset radial interval. As expected, this strongly depends on the radial increment and number of replicates. For our standard settings of “continuous mode” acquisition in radial increments of 0.003 cm with a single reading at each radius (Balbo et al. 2007), we arrived at a scan velocity of ~2.5 cm/min. (For 0.002- and 0.001-cm intervals and single acquisitions, the measured scan speeds were 1.65 and 0.94 cm/min, respectively.) From the comparison of the time-stamp of interference and absorbance data, we concluded that the time-stamp given to the absorbance data stems from the beginning of the scan. We observed no significant dependence on the rotor speed between 30,000 and 60,000 rpm.
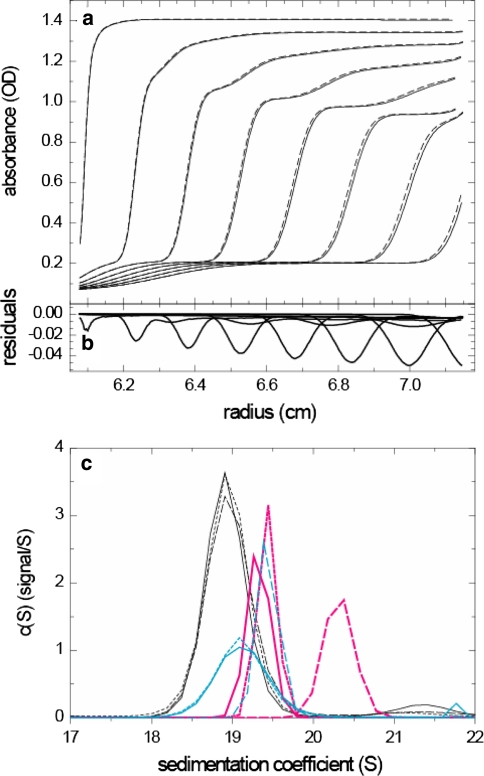
Next, we carried out an SV experiment at 50,000 rpm with the thyroglobulin sample, using standard absorbance optical acquisition parameters. The measured absorbance profiles are shown in Fig. 6a as solid lines. We fitted the data with a superposition of Lamm equation solutions that account for the scan velocity of 2.5 cm/min and then simulated with unchanged sedimentation parameters what absorbance profiles would have existed at the time points when the scans started (dashed lines in Fig. 6a). The difference is highly significant and reaches values >0.05 OD, which is 10-fold above the noise of the data acquisition. Even though the scan time is only on the order of 20–30 s, the boundary has migrated substantially during the time of the scan, mimicking a faster sedimentation rate. The apparent s-value without corrections for the scanning speed is 19.27 S, whereas the fit with the modified Lamm equations accounting for the scanner speed results in a value of 19.10 S. The relative difference (s* − s)/s is 0.89%, in excellent agreement with Eq. 9 which predicts a difference of 0.81%).
Fig. 6a–c.
The time-delay of scanning in the absorbance optical system. a Experimental absorbance profiles of thyroglobulin sedimenting at 50,000 rpm (solid lines) recorded with standard 0.003-cm radial increment. Data were fit with a superposition of Lamm equation solution accounting for the finite scanning velocity of 2.5 cm/min, which allowed to predict the theoretical absorbance profiles that would have been recorded with instantaneous detection (dashed line). b Difference between experimental and theoretical curves. c Best-fit uncorrected c(s) traces of SV data from three cells with absorbance optical data acquisition in radial increments of 0.003 cm and single (magenta solid line), double (magenta dotted line), and quadruple (magenta dashed line) acquisition at each radial point. The c(s) traces from the interference optical data acquired simultaneously from the same cells are shown in black. After corrections were applied to the c(s) distribution for the predicted scanner velocity, the blue curves were obtained
In the attempt to more directly visualize the time-delay from the scanner, we sedimented three identical samples side-by-side at 50,000 rpm and recorded concentration profiles by interference and absorbance optical detection. In the absorbance scans, we acquired one, two, and four readings per radial point (with the standard radial increment of 0.003 cm). While the c(s) distributions from the interference data demonstrate the usual reproducibility and superimpose very well (Fig. 6c, black lines), the c(s) traces without corrections (magenta lines) show the expected overestimate of the s-value, exacerbated at the higher number of replicates (dashed magenta line). Application of the corrections with the respective scanner speeds leads to c(s) peaks (blue lines in Fig. 6c) much closer throughout to those from the interference optics. For the data obtained at the slowest scanner speed, we note that the corrections do not account for the complete shift, although the absorbance c(s) traces after correction are still considerably more consistent.
The source of the remaining difference of 0.18 S between the interference peaks and the two well-aligned absorbance peaks is unclear. A likely source of systematic error between the two optical systems is the radial calibration. Statistical errors of the calibration can be assessed more easily with the interference optical system. In a rotor containing six counterbalances, we imaged the locations of the reference points and observed standard deviations between their radial positions of 0.003–0.004 cm. We can estimate the magnification error to be ~0.3%, which would result in an uncertainty of the absolute s-values of ~0.3%, or ~0.05 S at 19 S. Another possible source of error is the measurement of the scan times.
Another aspect of the time-delay from scanning in the absorbance data acquisition is the constant time offset caused by scanning the region outside the solution column, in particular the air-to-air region at small radii. At a rotor speed of 50,000 rpm, under our standard experimental conditions, during the time required for the scanner to traverse 1 mm, a 20 S species will migrate ~0.0008 cm. If we assume scanning a 3-mm air-to-air region, a 10 S species will have migrated by 0.0012 cm and show an apparent offset of this magnitude in the recorded radial position of the boundary. This offset is constant for each scan, and therefore can be largely compensated by an equivalent compensatory shift in the meniscus position of the model. The magnitude is small but can be significant relative to the width of the optical artifact at the meniscus and the required precision in the model. (Fixing the meniscus would be a worse alternative, since it would lead to worse fit and/or would transfer the error to compensatory errors in the estimates of the s-values, see below.) To address this problem more directly, we have implemented a routine in SEDFIT that explicitly calculates the time-delay caused by scanning between the first radial data point and the meniscus position, and applies this delay as a correction to the time-stamp of the scan.
The radial resolution of the absorbance system
In order to experimentally obtain an estimate for the radial resolution of the absorbance system, we scanned an empty six-channel centerpiece recording the radial intensity profile in the transition region from light to dark at the edges of the sectors (data not shown). Since ideally this transition should be sharp, we took the apparent width of this region of ~0.008 cm as an estimate for the effective radial resolution Δr.
We then used the experimental absorbance profiles shown in Fig. 6a and estimated the effect of a convolution via Eq. 8. For most of the scans, the difference compared to the original traces was negligible (<0.001 OD). However, for the steepest scan in the beginning, which has a maximum slope of ~30 OD/mm, deviations of ~0.014 OD were observed. For the second scan where the maximal slope has decayed to ~10 OD/mm, the calculated difference was only 0.002 OD, and diminished further for the following scans.
Convection and the meniscus position
The meniscus position is an important parameter for modeling the sedimentation process. Its optical determination is obscured by the fact that the meniscus creates large artifacts that only allow one to discern lower and upper bounds for the meniscus position. More precise information on the meniscus location is contained in the translation of the measured sedimentation boundaries, since the meniscus is the boundary position at time zero, and thus implicitly determined by the boundary movement. However, the accuracy of the best-fit value of the meniscus parameter of the model relies (among other factors, including the spatial and temporal resolution of data acquisition discussed above) on the regular boundary evolution and the absence of convection driven by temperature differences.
For this reason, we wanted to study in more detail the effect of convection on the best-fit meniscus position and the impact on the results of the data analysis. To this end, we conducted experiments where we intentionally caused convection, for example, by equilibrating the rotor at 25°C for several hours but then starting the run at 20°C. In this way the rotor would begin cooling as soon as the rotor started spinning and thereby create significant spatial and temporal temperature gradients. As shown in Fig. 7a, a characteristic feature for the presence of substantial convection is the visible distortions with increasing slopes in the leading edges of the early sedimentation boundaries, which highlight a transient local delay of sedimentation. This feature is superimposed to an initially overall faster sedimentation due to the lower solvent viscosity at the initially higher temperature.
Fig. 7a–e.
Interference optical data from a sedimentation experiment with convection. BSA was sedimented at 50,000 rpm at 20°C after preincubation of the rotor at 25°C. a Experimental fringe profiles (black lines) and best-fit c(s) model (red lines) with the meniscus fixed to the optical meniscus artifact. Due to the presence of convection, a poor fit is obtained with RMSD of 0.0195 fringes. b Residuals of the fit. c Constraining the analysis to the experimental scans recorded after 3,800 s (black lines) leads to an improved fit quality (red lines) with RMSD of 0.0061 fringes. The inset shows the meniscus region with the best-fit meniscus position indicated as a red vertical line. If the meniscus is fixed to the optical artifact (blue line in the inset), a significantly worse fit with RMSD of 0.0079 fringes is obtained (data not shown). d Residuals of the fit. ec(s) distributions from different analyses of the data: the complete data with graphically constrained meniscus as shown in a (solid black line) leading to s1 = 4.31 S, f/f0 = 1.54, and M1 = 77.4 kDa; the late data with floating meniscus as shown in c (solid magenta line) leading to s1 = 4.2 S, f/f0 = 1.47, and M1 = 69.2 kDa; the late data with constrained meniscus (dotted blue line) leading to s1 = 4.31 S, f/f0 = 1.47, and M1 = 71.4 kDa; and the c(s) distribution of a reference experiment without convection (dotted black line) leading to s1 = 4.21 S, f/f0 = 1.47, and M1 = 68.9 kDa
Not surprisingly, a naïve c(s) fit with the meniscus fixed to the optical artifact does not model the data well when using the complete data set (Fig. 7a, b). The best-fit distribution (Fig. 7e, black solid line) is surprisingly close to the distribution obtained in a properly conducted control experiment (black short-dashed line) but leads to an overestimation of the monomer s-value by 0.1 S, as well as an overestimate of the frictional ratio and the molar mass associated with the main peak by 12%. If the first 3,800 s are excluded from the analysis, a much better fit is obtained. Although this seems desirable, it is misleading in that the later scans still are influenced by the entire history of the physical sedimentation process. Therefore, although the fit improved, the error in the s-values persisted at the same magnitude (see blue dotted line in Fig. 7e). However, when we allowed the meniscus to freely adjust, it assumed a best-fit value clearly inside the solution column, compensating for the initially faster sedimentation in the lower viscosity conditions and allowing a significantly better fit (RMSD = 0.0061 fringes compared to 0.0079 fringes with the meniscus fixed to the optical artifact) (Fig. 7c, d, magenta line in Fig. 7e). The resulting s-values and Mw estimates are within error identical to those of a properly conducted control experiment (with differences of 0.01 S and 0.3 kDa, respectively). Similar results were obtained when the initial temperature of the rotor was lower than that during the run (data not shown), in this case moving the best-fit meniscus parameter towards smaller radii.
Discussion
Sedimentation velocity has undergone significant transformation over the last 10 years with the ability to solve the Lamm equation and with the development of direct boundary modeling. These techniques have the promise for unprecedented accuracy and detail. However, a careful adjustment of the mathematical model to the physical sedimentation process and its detection is required. In the present work, we have reassessed several basic elements of SV with regard to the relationship between the mathematical models and the imperfections of the experimental setup. In particular, we have focused on apparent limitations that would impact SV experiments with the most precise information on sedimentation coefficients—those that exhibit rapid migration of steep boundaries. Among the problems that do, or could be suspected to, limit the accuracy and precision of SV analyses are properties of the optical system with regard to its spatial and temporal resolution and aberrations in the presence of refractive index gradients, sample contamination, convection, and the meniscus position.
The meniscus position is often regarded as a key parameter for the analysis of boundary movement in the mathematical model of SV. Although a crude assignment can be made easily from visual inspection of the scans, it is notoriously difficult to determine the meniscus with sufficient accuracy commensurate with modern Lamm equation modeling. The required precision usually exceeds even the resolution of the experimental data points, and the radial region of measured optical meniscus artifacts often extends over a relatively wide radial range. The shape of the optical artifact itself can be expected to be highly sensitive to optical alignment, sample and solvent properties, sample concentration, rotor speed, centerpiece material, etc. as was studied in detail previously by several investigators (Trautman 1958; Erlander and Babcock 1961; Gropper 1963). Gropper has pointed out that with the focus of the optics being at the 2/3 plane of the solution column, the meniscus position will not appear at the correct image location (Gropper 1964). As emphasized by Philo (1997), “it is not entirely clear how to determine the true correct meniscus position from the experimental data.”
What can be assigned with higher confidence from graphical inspection are the limits for the region of possible meniscus positions. These may be used as constraints for the computational estimation of the meniscus position through the least-squares modeling of the sedimentation profiles. The latter usually produces a very well-defined value, since (especially for steep boundaries in high-speed experiments) the progression of boundary positions at the times of the available scans implies unambiguously the position of the boundary at time zero, provided that a sufficiently high number of scans is incorporated in the analysis, such that it represents the complete experiment. Accordingly, the correlation of the meniscus parameter is usually very low. With this approach, we found the typical precision for s-values measured in replicate experiments to be ~0.01 S. For some applications, however, some correlation with other model parameters may occur, as reported for example by Liu and co-workers (Liu et al. 2006), presumably also depending on other factors such as the steepness of the experimental sedimentation boundaries, the scan range considered, and likely also how closely the model describes the observed sedimentation process.
There are cases where the expected range for the meniscus position from visual inspection of the optical artifact is in conflict with the overall best-fit meniscus position. Even though our convection experiment is grossly exaggerating the extent of convection that may be encountered in a well-executed SV experiment, low level convection and detailed temperature control are considered the limiting factors for the accuracy of SV (Errington and Rowe 2003; Schuck 2007). The point of our experimental exercise was to show how convection can influence the estimated meniscus position (as well as the shape of the sedimentation boundaries and thus the quality of fit). (As a cautionary note, the visual patterns shown in Fig. 7 may possibly also be caused by other effects and should not be taken as a sole diagnostics for the presence of convection.) We also found that another factor influencing the best-fit value of the meniscus position would be (uncorrected for) constant offsets in the time-stamp of experimental absorbance scans.
Our data suggest that a floating meniscus parameter can help to compensate for these effects and prevent them from degrading the precision of the sedimentation coefficients and the quality of fit. We believe the estimated meniscus position should then be regarded as an apparent meniscus position. The advantage of this approach is that it honors the complete information of the later boundary positions as a function of time. In contrast, the approach of force-fitting the data with this parameter constrained to the visually discerned position, which is a prerequisite for many historic SV analysis methods, improves neither the analysis results nor the fit. However, the visually discerned value is very useful still. It is a significant advantage of the direct Lamm equation modeling approach over previous methods of SV analysis that it can flag convective sedimentation by poor fits and/or “impossible” best-fit meniscus positions, suggesting a failed SV run, despite the fact that a reasonably good fit may be achieved when using only a subset of the data (particularly late subsets).
A time-honored approach to eliminate signals from sample imperfections biasing the analysis of the species of interest is adjusting the radial fitting limits. In the present work, we have developed a PBM approach that allows one to selectively exclude from the analysis the ranges of data that would be influenced by faster sedimenting impurities or degradation products. Although ideally all data should be included into the analysis, in some cases the signals from aggregates would require significant extension of the model without producing a corresponding increase in relevant information. This is the case, for example, when modeling interacting systems with coupled Lamm equations with reaction terms (Stafford and Sherwood 2004; Dam et al. 2005). Another example is the sedimentation of heterogeneous mixtures of species with hydrodynamic nonideality. In this case, currently no rigorous theoretical description is available, but PBM can allow extending the utility of a single-species nonideal sedimentation model. (Errors in the nonideality terms and hydrodynamic interactions from neglect of the contaminating species can be expected to be much smaller than the bias that would be introduced into the fit from disregarding their signal contributions to the data analyzed.) Another potentially useful application of the PBM approach is the generation of prior knowledge on the monomer properties needed for the Bayesian enhancement of the characterization of monomer/oligomer systems (Brown et al. 2007). Finally, PBM in conjunction with an ideal single-species model with empirical s*-values and D*-values can serve as a direct analogue of the Schlieren peak area/height ratio approach applied previously with exquisite sensitivity to the study of the heterogeneity of the ATCase ensemble (Werner and Schachman 1989).
There are some practical considerations that suggest the boundary region should not be chosen too small: first, in case TI noise is to be estimated from the experimental data, clearly all included sections of the scans need to show at least twofold overlap throughout for the model to be well-posed. This can be achieved either by adjusting the boundary section to be fitted, or by the number of scans included into the analysis. Second, it is useful if the boundary sections are sufficiently large to include curvature in the leading edges, such as to carry more information about the total boundary height. Alternatively, the total signal would need to be constrained in order to avoid correlation of this parameter with s* and D* or RI signal offsets. Finally, it is very useful to keep in mind that the diffusion of small molecules can lead to migration exceeding the sedimentation of much larger particles. As a consequence, it is advantageous to retain the trailing edge of the boundary and the region of low s-values in the data to be analyzed in order to permit possible signal contributions from small molecules to be detectable and well-defined when accounted for in the model.
Although PBM is a useful tool to exclude visibly distinct boundaries from the analysis, such as those of faster-sedimenting aggregate species, it is generally not well-suited for isolating information on a single species in a boundary that is formed by an unresolved heterogeneous mixture.1 If multiple species do not separate, they should be accounted for by a suitable model describing heterogeneity, such as c(s). Vice versa, if the PBM s-limits are chosen on the basis of bracketing a single baseline-resolved peak in c(s), this does not necessarily mean that the PBM model can proceed with a single-species model, since the diffusional envelope of other species may contribute to signals in the same s-range.
Partial boundary modeling is a straightforward concept, but has not been implemented in the past, likely because of the increased computational difficulties it poses for the determination of TI and RI noise. This problem was tackled in the present work with an iterative algorithm that permits both systematic noise contributions, as well as linear concentration factors, to be separated from the optimization of the nonlinear parameters.
It is a significant advantage for RI noise offsets to be included in the model and to be determined by least-squares fit from the actual data sets subject to the analysis, as compared to the empirical alignment of scans to remove jitter in the air-to-air region above the solution column. The air-to-air alignment is based on only a small number of data points, providing poor statistics. Because it utilizes signals outside the analysis range, the alignment approach is also intrinsically very sensitive to slight periodic tilting of the scans due to vibrations in the optical system, which are not uncommon and can be readily identified in the residual bitmaps of direct boundary models.
Similarly, we find it is advantageous to account for TI signal contributions directly in the model as opposed to the alternative of the pair-wise subtraction of scans for removal of time-invariant features. A very useful direct comparison of the two methods can be made on the basis of Eq. 4, which shows that an arbitrary shape of TI profile can be folded into the analysis of the macromolecular sedimentation parameters, such that the latter appears as a model for the difference between each scan and an average scan. After fitting the macromolecular sedimentation parameters, their corresponding implicit TI profile can be determined. This is different from the time-difference approach, where the reference scan to be subtracted is a single partner scan in the particular scan pair, and the implicit TI profile information is lost.2 From the similar form of the optimization problem, both have similar degrees of freedom (or “model-dependence”) for the macromolecular sedimentation model. However, the time-difference procedure suffers unavoidably from stronger amplification of the statistical noise, which can be expected to be problematic, in particular, when modeling ill-conditioned error surfaces of complex models for interacting systems, making the unambiguous parameter determination even more difficult. Further, the pair-wise subtraction method is more permissive to small drifts (since the first pair does not need to have the same TI noise as the last pair) as compared to the more stringent requirement that all scans exhibit the same TI offsets. Finally, it is very useful to obtain an explicit estimate of the TI noise profile, since that can be compared to the water blank fringe profile of the instrument and may flag impostor fits that imply strongly curved TI profiles. The latter would go unnoticed in the differencing transformation, since it does not lead to an explicit TI trace, unless a method for reconstructing an explicit boundary model a posteriori is used, such as that described for the back-transformation of g(s*) fits into the raw data space (Schuck 2003).
The selection of the radial data-fitting range via the radial positions of particles with s-values sl and su in PBM is in correspondence with the selection of a predefined s*-range in the historic two-stage hierarchical approach of first “transforming” the data into g(s*) traces and then fitting these with Gaussians or transformed Lamm equation solutions. As pointed out by Philo (2006), this approach affords the possibility to focus exclusively on the radial values that correspond to any particular sedimentation coefficient range of interest, which was previously not directly possible with the whole boundary modeling techniques. The PBM technique can overcome this limitation. This opens the possibility to compare the data transform and direct boundary modeling approaches with regard to their statistical properties.
The first data set examined here for this purpose was the TRAP data previously chosen by Philo (2006) as a model system. It exhibits a very shallow minimum of the error surface, which is advantageous in the present context in that it emphasizes differences in data analysis approach. First, we observed that the g(s*) analysis is based on several factors chosen prior to and kept fixed during the analysis (including the choice of data subset and meniscus position) that have a significant influence on the analysis. They have to be skillfully chosen (see above for the meniscus problem), are then fixed in the analysis, and may lead the investigator to arrive at results with a wide range of values (Fig. 3b). Unfortunately, none of these paramount, preselected factors are considered in the statistical error analyses reported by Philo (2006).
Generally, a variation in results dependent on which values the preselected parameters are fixed at is not restricted to g(s*) and will likely be a problem for any analysis based on preconceived meniscus positions and narrow scan subsets, including PBM if it were to be artificially constrained in that way. However, the key advantage of the PBM approach is that it naturally allows all data to be incorporated and all unknowns to be included into the analysis. In this way, it can determine an unambiguous best-fit value for the set of unknown parameters, with error estimates that incorporate correlations of all unknowns. In particular, early scans may be included in the PBM approach, which makes the computational determination of the effective meniscus location by nonlinear regression better conditioned.
It is an open question to what extent the “improved” Lamm equation fitting method of the g(s*) transform does also allow inclusion of large scan ranges. While Philo has reported that the accuracy of the fitted parameters “becomes essentially independent of the time span,” and that “it is actually possible to use the full span from the time the meniscus region is cleared until the plateau region is about to disappear” (Philo 2006), this seems to apply only to data from strict mono-disperse samples or from samples that are fully described by the Lamm equation model. For very large time-ranges, the g(s*) peaks from all species become artificially broadened, and even though this broadening is mimicked for each species by modeling with the transformed Lamm equation solutions, the peaks can eventually merge. This strongly diminishes the possibility of focusing on a particular species of interest and using a single-species model for its description. This effect increases with larger scan intervals and the inclusion of earlier times [the effect being approximately proportional to ~Δt/tmid (Schuck and Rossmanith 2000)]. This interpretation is consistent with our observation of lower best-fit M values from g(s*) analyses compared to best-fit PBM results when considering scans #13–44 and scans #1–60 for the TRAP data, as well as the strong decrease in the apparent monomer molar mass estimates of g(s*) with larger scan numbers from the BSA data in Fig. 5.
Such an effect is absent in the PBM modeling. Even though unresolved and unaccounted for heterogeneity will also lower the apparent molar mass values, in particular when using large s-ranges, this effect is not exacerbated by artificial broadening of the contributions from the different boundary components. This allows one to use very large or entire data sets without drawbacks. This is unbiased and statistically optimal and presents residuals between the model and the raw data.
When we compared the results with the PBM analysis of equivalent scans and radial ranges using an equivalent model, we found that the parameter estimates from the g(s*) analysis are nonoptimal in the original data space. Contributing to this may be remaining subtle differences in the model, for example, with regard to the noise parameters (see above), and possibly the exact data points contributing to g(s*) curve versus those fitted to in PBM. However, we believe that the main contribution arises from the artificial broadening outlined above, which we suspect is ultimately a by-product of the reduction in the dimensionality of the data from signal as a function of space and time to a transformed signal as a function only of s*. From our point of view, a priori favoring the raw data and explicit direct boundary models, the nonoptimality of the g(s*)-derived parameters in the raw data space suggests a distortion of the error surface in the g(s*)-based approach, including obviously a translation of its minimum.
With regard to the TRAP analysis, we emphasize that the point of this exercise was not to re-determine the oligomeric state of TRAP, and it is apparent the data in Fig. 3 simply do not have the information to determine the oligomer size (in contrast to the data presented in Snyder et al. 2004). We have validated these PBM results in a detailed analysis. We believe that for the present data, a theoretical value of 11.0 cannot necessarily be referenced as the “true” value to be expected. Although the putative TRAP undecamer is within error consistent with the data, generally there may be important reasons why the sedimentation boundary, when modeled as a single species, gives best-fit estimates for the apparent molar mass lower than the putative true molar mass of the main species. For example, errors in the partial-specific volume can translate to systematic errors in M. Further, as is well-known, any unaccounted heterogeneity either from mixtures of 11mers and possibly co-existing 12mers (McCammon et al. 2004) (Watanabe et al. 2009) or from 11mers coexisting in different trp-ligation states [which exhibit different s-values (Snyder et al. 2004)] would serve to artificially lower the molecular weight estimate. From the data in Fig. 3a, we do not know to what extent these factors are relevant. It is certainly a boon of any data analysis method to reveal such problems if they exist, which allows one to address them and ultimately arrive at reliable results.
For deriving accurate detailed information from the analysis of SV experiments, it is crucially important to understand imperfections in the optical detection. One limitation is Wiener skewing, a curvature in the light path caused by refractive index gradients (Wiener 1893). As described by Svensson in the analysis of optical aberrations for interference optical imaging systems (Svensson 1954) and summarized by Rowe (2006), the most important term is of third power in the cell height and proportional to 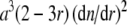 with a being the cell height and r the fractional distance of the focal plane along the cell (derived for the condition that the focus lies within the solution column). For 3-mm centerpieces, in the configuration with equal spacers that allow access to the standard filling holes, the focus is not maintained at the 2/3 plane, and therefore aberrations causing fringe displacements will arise. To assess the theoretically expected error, if we use—as an approximation—the above expression, its third power dependence on cell height would suggest that the position of the focus should be far less significant for 3-mm cells than it would be with 12-mm cells. This is consistent with the experimental observation by Yphantis that the focus plane is far more critical in 30-mm cells than in 12-mm cells (Yphantis 1964). Therefore, we asked whether at moderate protein concentrations with relatively steep gradients any aberrations would be experimentally detectable. In the standard configuration of 3-mm centerpieces, we found no evidence for optical aberrations affecting the measured sedimentation parameters for protein gradients of up to 100 fringes/mm. This is consistent with theoretical predictions (Lloyd 1974; Rowe 2006). At higher protein concentrations, however, this error would be expected to become more significant (along with even greater difficulties of analyzing the hydrodynamic nonideality).
with a being the cell height and r the fractional distance of the focal plane along the cell (derived for the condition that the focus lies within the solution column). For 3-mm centerpieces, in the configuration with equal spacers that allow access to the standard filling holes, the focus is not maintained at the 2/3 plane, and therefore aberrations causing fringe displacements will arise. To assess the theoretically expected error, if we use—as an approximation—the above expression, its third power dependence on cell height would suggest that the position of the focus should be far less significant for 3-mm cells than it would be with 12-mm cells. This is consistent with the experimental observation by Yphantis that the focus plane is far more critical in 30-mm cells than in 12-mm cells (Yphantis 1964). Therefore, we asked whether at moderate protein concentrations with relatively steep gradients any aberrations would be experimentally detectable. In the standard configuration of 3-mm centerpieces, we found no evidence for optical aberrations affecting the measured sedimentation parameters for protein gradients of up to 100 fringes/mm. This is consistent with theoretical predictions (Lloyd 1974; Rowe 2006). At higher protein concentrations, however, this error would be expected to become more significant (along with even greater difficulties of analyzing the hydrodynamic nonideality).
Together with the results from an experimental study of Wiener skewing effects in the absorbance optics by Gonzalez et al. (2003), we conclude that for proteins at concentrations that do not show either significant hydrodynamic nonideality or obvious “black bands” in the absorption optics, the magnitude of Wiener skewing is too small to affect the SV analysis when using centerpieces currently in general use. Even when it does occur, we would expect it to lead predominantly to distortions of the boundary shape, rather than introducing errors in the estimated radial displacement of the boundary with time, and thereby leave the determination of the s-value less affected. However, for the detailed study of high protein concentrations it may be possible in the future to apply numerical corrections in the model fitted to the data to mimic the effects of Wiener skewing.
Finally, a probably widely recognized problem with the absorbance optical system is the relatively poor spatial and temporal resolution (as compared to, for example, the interference optical system). We have studied in a simple model the effects of the limited radial resolution and found it not to significantly affect the gradients obtained under most conditions. However, our results do show the possibility of significant errors arising from the finite radial resolution for the steep slopes at the beginning of the run. Further, we detected very significant errors in the apparent s-values arising from the finite scanning velocity of the absorbance data acquisition. Under the conditions of our experimental test (a protein of 19 S sedimenting at 50,000 rpm), the error is ~1%, which is an order of magnitude above the usual precision in the determination of sedimentation coefficients. For proteins with other s-values, the dependence of the theoretically expected error on the rotor speed and s-value of the protein is shown in Fig. 8.
Fig. 8.
Predicted relative error in the apparent sedimentation coefficient as a function of true s-value (in S) and rotor speed (in rpm) when uncorrected for the finite time of scanning. Standard conditions are assumed, with a solution column corresponding to a 400 μl sample and a scanning speed of 2.5 cm/min, approximately that obtained with standard acquisition parameters with a 0.003 cm radial increment and continuous acquisition of a single reading per radial value
The problem is conceptually straightforward to illustrate: If a particle requires, for example, 100 min to travel from meniscus to a reference point close to the bottom, and it takes—hypothetically—1 min to complete one scan across the same distance, then a scan with the beginning time-stamp of 99 min will record the particle already at the reference point. Therefore, the particle will appear to have sedimented 1% faster than it really did. Surprisingly, this problem has to our knowledge not been previously analyzed in the published literature. Although it could be experimentally minimized by running experiments at a lower rotor speed, this is not desirable due to the shallower boundaries leading to lower precision of the sedimentation coefficients. We have shown that the error can be accounted for by appropriate theoretical corrections in the model functions. Most importantly, the fitted Lamm equation solutions can be adapted to the finite scanning speed by mimicking the evolution of sedimentation during the recording process of the concentration gradients. These corrections will allow improved hydrodynamic modeling, molar mass estimates, and improved correlation of the signals from the different optical systems in the global multi-signal ck(s) method (Balbo et al. 2005). The need for computational corrections accounting for the finite speed of the absorbance scanner will be particularly important when studying larger macromolecular assemblies that sediment fast.
Acknowledgments
We thank Dr. Cole for allowing us to use his data on the TRAP system, and thank Dr. Philo for providing us with a copy of his analysis (Philo 2006). This work was supported by the Intramural Research Program of the National Institute of Bioimaging and Bioengineering, NIH.
Open Access This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Footnotes
Whether or not two species contribute to the same boundary may be visually inspected, for example, with a c(s) analysis in SEDFIT, requesting the peak information by pressing control-M, and clicking on a peak button, which causes the diffusion-broadened contributions of this peak to different boundary fractions to be superimposed on the raw data.
Philo (2006) uses the term “algebraic” for the pair-wise subtraction. This is confusing, as we have introduced the terminology “algebraic noise decomposition” for the explicit calculation of TI and RI noise from the data set to be analyzed, which uses matrix algebra to directly calculate the least-squares optimal estimates for these parameters. This should be distinguished from the pair-wise subtraction in the Δc/Δt approach.
References
- Balbo A, Brown P et al (2007) Step-by-step protocol for sedimentation velocity analytical ultracentrifugation. http://www.analyticalultracentrifugation.com/svprotocols.htm
- Balbo A, Minor KH et al (2005) Studying multi-protein complexes by multi-signal sedimentation velocity analytical ultracentrifugation. Proc Natl Acad Sci USA 102:81–86 [DOI] [PMC free article] [PubMed]
- Behlke J, Ristau O (2002) A new approximate whole boundary solution of the Lamm differential equation for the analysis of sedimentation velocity experiments. Biophys Chem 95(1):59–68 [DOI] [PubMed]
- Berkowitz SA (2006) Role of analytical ultracentrifugation in assessing the aggregation of protein biopharmaceuticals. AAPS J 8(3):E590–E605 [DOI] [PMC free article] [PubMed]
- Brown PH, Schuck P (2006) Macromolecular size-and-shape distributions by sedimentation velocity analytical ultracentrifugation. Biophys J 90:4651–4661 [DOI] [PMC free article] [PubMed]
- Brown PH, Schuck P (2008) A new adaptive grid-size algorithm for the simulation of sedimentation velocity profiles in analytical ultracentrifugation. Comput Phys Commun 178(2):105–120 [DOI] [PMC free article] [PubMed]
- Brown P, Balbo A et al (2007) Using prior knowledge in the determination of macromolecular size-distributions by analytical ultracentrifugation. Biomacromolecules 8:2011–2024 [DOI] [PMC free article] [PubMed]
- Brown PH, Balbo A et al (2008a) Characterizing protein–protein interactions by sedimentation velocity analytical ultracentrifugation. Curr Protoc Immunol 81:18.15.1-18.15.39 [DOI] [PubMed]
- Brown PH, Balbo A et al (2008b) A bayesian approach for quantifying trace amounts of antibody aggregates by sedimentation velocity analytical ultracentrifugation. AAPS J 10(3):481–493 [DOI] [PMC free article] [PubMed]
- Cao W, Demeler B (2005) Modeling analytical ultracentrifugation experiments with an adaptive space–time finite element solution of the Lamm equation. Biophys J 89(3):1589–1602 [DOI] [PMC free article] [PubMed]
- Dam J, Velikovsky CA et al (2005) Sedimentation velocity analysis of protein–protein interactions: Lamm equation modeling and sedimentation coefficient distributions c(s). Biophys J 89:619–634 [DOI] [PMC free article] [PubMed]
- Demeler B, Behlke J et al (2000) Determination of molecular parameters from sedimentation velocity experiments: whole boundary fitting using approximate and numerical solutions of the Lamm equation. Methods Enzymol 321:36–66 [DOI] [PubMed]
- Erlander SR, Babcock GE (1961) Interface and meniscus widths and positions for low-speed ultracentrifuge runs. Biochem Biophys Acta 50(2):205–212 [DOI] [PubMed]
- Errington N, Rowe AJ (2003) Probing conformation and conformational change in proteins is optimally undertaken in relative mode. Eur Biophys J 32(5):511–517 [DOI] [PubMed]
- Faxén H (1929) Über eine Differentialgleichung aus der physikalischen Chemie. Ark Mat Astr Fys 21B:1–6
- Forsberg D, Svensson H (1954) The second-order aberrations in the interferometric measurement of concentration gradients. J Modern Optics 1(2):90–93 [DOI]
- Gabrielson JP, Brader ML et al (2007a) Quantitation of aggregate levels in a recombinant humanized monoclonal antibody formulation by size-exclusion chromatography, asymmetrical flow field flow fractionation, and sedimentation velocity. J Pharm Sci 96(2):268–279 [DOI] [PubMed]
- Gabrielson JP, Randolph TW et al (2007b) Sedimentation velocity analytical ultracentrifugation and SEDFIT/c(s): limits of quantitation for a monoclonal antibody system. Anal Biochem 361(1):24–30 [DOI] [PubMed]
- Gabrielson JP, Arthur KK et al (2009) Common excipients impair detection of protein aggregates during sedimentation velocity analytical ultracentrifugation. J Pharm Sci 98(1):50–62 [DOI] [PubMed]
- Gonzalez JM, Rivas G et al (2003) Effect of large refractive index gradients on the performance of absorption optics in the Beckman XL-A/I analytical ultracentrifuge: an experimental study. Anal Biochem 313(1):133–136 [DOI] [PubMed]
- Gropper L (1963) Correcting for cell tilt caused by differential expansion of rotors in the analytical ultracentrifuge. Anal Biochem 6(2):170–175 [DOI] [PubMed]
- Gropper L (1964) Optical alignment procedure for the analytical ultracentrifuge. Anal Biochem 7:401–428 [DOI] [PubMed]
- Howlett GJ, Minton AP et al (2006) Analytical ultracentrifugation for the study of protein association and assembly. Curr Opin Chem Biol 10(5):430–436 [DOI] [PubMed]
- Lamm O (1929) Die Differentialgleichung der Ultrazentrifugierung. Ark Mat Astr Fys 21B(2):1–4
- Lebowitz J, Lewis MS et al (2002) Modern analytical ultracentrifugation in protein science: a tutorial review. Protein Sci 11(9):2067–2079 [DOI] [PMC free article] [PubMed]
- Liu J, Andya JD et al (2006) A critical review of analytical ultracentrifugation and field flow fractionation methods for measuring protein aggregation. AAPS J 8(3):E580–E589 [DOI] [PMC free article] [PubMed]
- Lloyd PH (1974) Optical methods in ultracentrifugation, electrophoresis, and diffusion. Clarendon Press, Oxford
- McCammon MG, Hernandez H et al (2004) Tandem mass spectrometry defines the stoichiometry and quaternary structural arrangement of tryptophan molecules in the multiprotein complex TRAP. J Am Chem Soc 126(19):5950–5951 [DOI] [PubMed]
- Mercken L, Simons MJ et al (1985) Primary structure of bovine thyroglobulin deduced from the sequence of its 8, 431-base complementary DNA. Nature 316(6029):647–651 [DOI] [PubMed]
- Pekar A, Sukumar M (2007) Quantitation of aggregates in therapeutic proteins using sedimentation velocity analytical ultracentrifugation: practical considerations that affect precision and accuracy. Anal Biochem 367(2):225–237 [DOI] [PubMed]
- Philo JS (1997) An improved function for fitting sedimentation velocity data for low molecular weight solutes. Biophys J 72:435–444 [DOI] [PMC free article] [PubMed]
- Philo JS (2006) Improved methods for fitting sedimentation coefficient distributions derived by time-derivative techniques. Anal Biochem 354(2):238–246 [DOI] [PubMed]
- Rowe AJ (2006) [RASMB] 3mm centerpieces - the Svensson equation http://rasmb.bbri.org/pipermail/rasmb/2006/001271.html
- Ruhe A, Wedin PÅ (1980) Algorithms for separable nonlinear least squares problems. SIAM Rev 218122:318–337 [DOI]
- Schachman HK (1989) Analytical ultracentrifugation reborn. Nature 341:259–260 [DOI]
- Schuck P (1998) Sedimentation analysis of noninteracting and self-associating solutes using numerical solutions to the Lamm equation. Biophys J 75:1503–1512 [DOI] [PMC free article] [PubMed]
- Schuck P (2000) Size distribution analysis of macromolecules by sedimentation velocity ultracentrifugation and Lamm equation modeling. Biophys J 78:1606–1619 [DOI] [PMC free article] [PubMed]
- Schuck P (2003) On the analysis of protein self-association by sedimentation velocity analytical ultracentrifugation. Anal Biochem 320:104–124 [DOI] [PubMed]
- Schuck P (2004) A model for sedimentation in inhomogeneous media. II. Compressibility of aqueous and organic solvents. Biophys Chem 187:201–214 [DOI] [PubMed]
- Schuck P (2007) Sedimentation velocity in the study of reversible multiprotein complexes. In: Schuck P (ed) Protein interactions: biophysical approaches for the study of complex reversible systems. Springer, New York, pp 469–518
- Schuck P, Demeler B (1999) Direct sedimentation analysis of interference optical data in analytical ultracentrifugation. Biophys J 76:2288–2296 [DOI] [PMC free article] [PubMed]
- Schuck P, Rossmanith P (2000) Determination of the sedimentation coefficient distribution by least-squares boundary modeling. Biopolymers 54:328–341 [DOI] [PubMed]
- Schuck P, MacPhee CE et al (1998) Determination of sedimentation coefficients for small peptides. Biophys J 74:466–474 [DOI] [PMC free article] [PubMed]
- Schuck P, Taraporewala Z et al (2000) Rotavirus nonstructural protein NSP2 self-assembles into octamers that undergo ligand-induced conformational changes. J Biol Chem 276:9679–9687 [DOI] [PubMed]
- Schuck P, Perugini MA et al (2002) Size-distribution analysis of proteins by analytical ultracentrifugation: strategies and application to model systems. Biophys J 82(2):1096–1111 [DOI] [PMC free article] [PubMed]
- Snyder D, Lary J et al (2004) Interaction of the trp RNA-binding attenuation protein (TRAP) with anti-TRAP. J Mol Biol 338(4):669–682 [DOI] [PubMed]
- Stafford WF (1992) Boundary analysis in sedimentation transport experiments: a procedure for obtaining sedimentation coefficient distributions using the time derivative of the concentration profile. Anal Biochem 203:295–301 [DOI] [PubMed]
- Stafford WF, Sherwood PJ (2004) Analysis of heterologous interacting systems by sedimentation velocity: curve fitting algorithms for estimation of sedimentation coefficients, equilibrium and kinetic constants. Biophys Chem 108:231–243 [DOI] [PubMed]
- Svensson H (1954) The second-order abberations in the interferometric measurement of concentration gradients. J Modern Optics 1(1):25–32 [DOI]
- Trautman R (1958) Optical fine-structure of a meniscus in analytical ultracentrifugation in relation to the molecular-weight determinations using the Archibald principle. Biochim Biophys Acta 28:417–431 [DOI] [PubMed]
- Watanabe M, Heddle JG et al (2009) The nature of the TRAP-anti-TRAP complex. Proc Natl Acad Sci USA 106(7):2176–2181 [DOI] [PMC free article] [PubMed]
- Werner WE, Schachman HK (1989) Analysis of the ligand-promoted global conformational change in aspartate transcarbamoylase. Evidence for a two-state transition from boundary spreading in sedimentation velocity experiments. J Mol Biol 206(1):221–230 [DOI] [PubMed]
- Wiener O (1893) Darstellung gekruemmter Lichtstrahlen und Verwerthung derselben zur Untersuchung von Diffusion und Waermeleitung. Ann Physik 49:105–149 [DOI]
- Yphantis DA (1964) Equilibrium ultracentrifugation of dilute solutions. Biochemistry 3:297–317 [DOI] [PubMed]