Abstract
The leading edge of motile cells is propelled by polymerization of actin filaments according to a dendritic nucleation/array treadmilling mechanism. However, little attention has been given to the origin and maintenance of the dendritic array. Here we develop and test a population–kinetics model that explains the organization of actin filaments in terms of the reproduction of dendritic units. The life cycle of an actin filament consists of dendritic nucleation on another filament (birth), elongation by addition of actin subunits and, finally, termination of filament growth by capping protein (death). The regularity of branch angle between daughter and mother filaments endows filaments with heredity of their orientation. Fluctuations of branch angle that become fixed in the actin network create errors of orientation (mutations) that may be inherited. In our model, birth and death rates depend on filament orientation, which then becomes a selectable trait. Differential reproduction and elimination of filaments, or natural selection, leads to the evolution of a filament pattern with a characteristic distribution of filament orientations. We develop a procedure based on the Radon transform for quantitatively analyzing actin networks in situ and show that the experimental results are in agreement with the distribution of filament orientations predicted by our model. We conclude that the propulsive actin network can be understood as a self-organizing supramolecular ensemble shaped by the evolution of dendritic lineages through natural selection of their orientation.
A fundamental issue beyond genomics and proteomics is the origin of large-scale order in biomolecular ensembles. An important example of such an ensemble is the network of actin filaments responsible for the protrusive activity of motile cells. Actin filaments are intrinsically polar, with one end (the barbed end) favored for growth and the other end (the pointed end) favored for shortening (1). Actin polymerized in vitro forms populations of randomly organized filaments. In contrast, actin filaments at the leading edge of cells form branched arrays in a characteristic criss-cross pattern with filament barbed ends uniformly facing forward (2). How does this dendritic pattern arise? Why do the barbed ends face forward? Why are rearward-facing branches not seen? These questions prompted an inquiry into the organizing principles of the network.
The most general organizing principle in biology is natural selection. Higher-level biological systems will be shaped by natural selection whenever Darwin's conditions of variation and heritability of fitness are satisfied, regardless of the nature of the entities being selected (3). Not only speciation (4), but also development of immune and neural networks (5) and communication (6, 7), has been studied in an evolutionary framework. The question we consider here is whether self-organization by means of natural selection is a central mechanism for shaping the intracellular architecture of the motility machinery.
Model and Results
In lamellipodia of a moving cell, actin filaments are born as branches on existing filaments through nucleation by the Arp2/3 complex (1, 8–10). We term this process reproduction of filaments. The angle between a filament and its branch (Fig. 1) is quite regular and has a mean value, ψ, of 67° in Xenopus keratocytes (9) with similar values for branches formed in vitro (8, 11). The orientation of a new filament therefore depends on the orientation of the filament on which it was nucleated. We term this phenomenon inheritance of orientation. The angle between mother and daughter filaments varies about its mean, ψ, with standard deviation, σ, which equals 12° in Xenopus keratocytes (9). As revealed by high-speed imaging in vitro, a similar deviation results from thermal bending of the junction (11). In the dense actin network in vivo, we assume that a branch cannot fluctuate as freely as in dilute solution and that it can become trapped by the surrounding network in a deviated orientation. We term the variation of angle between a filament and its branch mutation of orientation. Reproduction, inheritance, and mutation set the stage for evolution by natural selection. What remains to be identified is the trait on which selection operates.
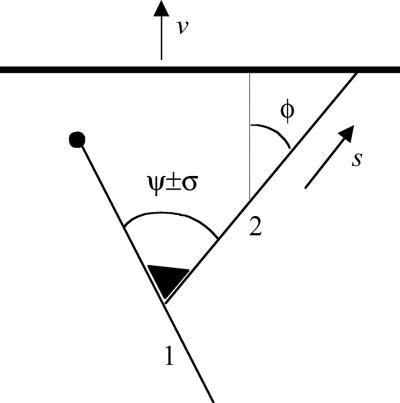
Figure 1.
Organizational unit of actin network at the leading edge. Near the leading edge (heavy line), filaments (solid lines) are nucleated on existing ones by the Arp2/3 complex (triangle). The angle between the mother (1) and daughter (2) filaments is ψ on average, with root-mean-square deviation σ. Filaments elongate and propel the plasma membrane and are stochastically terminated by capping protein (solid circle). Orientation of a filament is characterized by its incidence angle with the leading edge, φ (φ as shown is positive). Velocity of membrane advance is denoted by v; rate of filament elongation is denoted by s, which depends on φ.
Consider a filament nucleated at an angle φ with respect to the normal to the leading edge (Fig. 1). The membrane advances at a rate v, and the filament elongates by addition of actin monomers to its barbed end at a rate, s. If the filament is propelling the protrusion, it has to maintain contact with the advancing plasma membrane, and therefore its rate of elongation, s, is related geometrically to the rate of protrusion by scos φ = v. Neglecting the small rate of monomer dissociation at the growing tip, the rate of filament elongation is s = δkaMap, where δ is the elongation contributed by addition of a monomer actin molecule, ka is the polymerization rate constant, Ma is the concentration of monomer, and p is the probability that the filament tip is not obstructed by the membrane but open because of thermal fluctuations (12). For a filament propelling the leading edge, p = p0/cosφ, where p0 = v/δkaMa is the probability that a tip orthogonal to the leading edge is open. p0 is equivalent to the ratio of the rate of protrusion to the rate of elongation of a filament not in contact with the surface. p depends on filament orientation and reaches unity when |φ| increases to a critical angle, θ = arccos p0. For |φ| greater than the critical angle, polymerization does not keep up with protrusion, and the filament tip loses contact with the advancing membrane. Because nucleation of a filament depends on the Arp2/3 complex being activated by a WASP (Wiscott–Aldrich Syndrome Protein) (13–15) family member, which is localized at the leading edge, filaments oriented with |φ| > θ do not generate branches and are excluded from reproduction. Termination of filament growth also depends on orientation. For |φ| > θ, filament tips are not obstructed by the surface and are terminated by association of capping protein at a rate c, the rate of capping a free filament barbed end. For |φ| < θ, termination is possible only when the tip is open and occurs at a rate cp = cp0/cosφ. Hence, the smaller |φ|, the longer the filament tip is not capped, and the longer it stays at the leading edge and branches. Thus, the reproductive potential of a filament depends on its orientation, which makes orientation a selectable trait.
In the life cycle of filaments, dendritic nucleation leads to patterns of reproduction that depend on the magnitudes of ψ and θ. In general, filaments with orientation φ can be nucleated on filaments with orientation φ ± ψ. Although the following analysis can be generalized, it is written here for the biologically relevant values of ψ; namely, within the range 60–90° (8, 9, 11). Consider branching of filaments in the plane of the flat lamellipodium (Fig. 2). If θ < ψ/2, it means that the branch angle is greater than the acceptable range of angles (2θ) for filaments to maintain contact with the pushing surface. Consequently, a branch of any existing filament would be oriented beyond the critical angle, would not keep up with the catalytic surface and, therefore, reproduction could not be sustained. If ψ/2 < θ < ψ, filament branches can remain within the critical angle, and therefore reproduction can occur. However, not all filament orientations result in successful progeny. Filaments in the range θ − ψ to ψ − θ will generate branches beyond the critical angle and thus not be sustained. Filaments in the range −θ ≤ φ ≤ θ − ψ may generate branches of φ − ψ or φ + ψ, but only branches to one side, φ + ψ, give rise to filaments that are in the acceptable range ψ − θ ≤ φ ≤ θ. Similarly, filaments in the range ψ − θ ≤ φ ≤ θ give rise to fecund branches in the range −θ ≤ φ ≤ θ − ψ. Thus, within the regime, ψ/2 < θ < ψ, filaments reproduce in two-generation cycles of orientations. If θ > ψ, some filaments can nucleate a successful branch to either side, so sequences of three orientations in successive generations also become possible, for example (φ − ψ, φ, φ + ψ), |φ| < θ − ψ. Sequences of four or more orientations cannot exist for ψ larger than 60°, because this would require at least one branch to be oriented at >90° with respect to the normal to the surface. Thus, reproductive patterns for biologically relevant values of ψ occur as pairs or triplets of filaments. We term a given pair or triplet of orientations, which arise in the course of reproduction of filaments, a “type.” Because filaments can reproduce only within a type, reproductive potential is a property of a type, not of an individual filament.
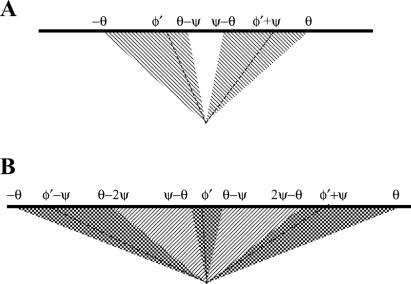
Figure 2.
Diagrams showing reproductive patterns of actin filaments at the leading edge. Heavy lines represent the leading edge. Angles noted are the incidence angles of lines and boundaries with respect to the leading edge. Hatched and crosshatched areas represent the range of the incidence angle φ, within which a filament is reproductively successful. The branching angle, ψ, is shown equal to 67°. (A) When the critical angle θ is larger than ψ/2 but smaller than ψ, two orientations alternate in successive generations. Dashed lines show an example of a pair of such orientations (φ′, φ′ + ψ). Filaments with these orientations form a particular two-orientation type. (B) When the critical angle θ is larger than ψ, in successive generations there can be three orientations (in the crosshatched area) as well as two (in the hatched area). Dashed lines show an example of a triplet of orientations (φ′ − ψ, φ′, φ′ + ψ). Filaments that have these orientations form a particular three-orientation type.
Let us evaluate the reproductive potential of a two-orientation type first. The abundance of filaments that belong to such a type is given by the number n1 of filaments whose orientation is φ and the number n2 of filaments whose orientation φ + ψ is complementary to φ. The rate at which the filaments proliferate depends on b, the rate of branching per filament and c, the rate of capping. When these numbers n are large, they can be treated as continuous functions of time t, so that the change of the abundance of the type with time can be represented by a system of differential equations:
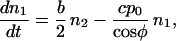 |
1 |
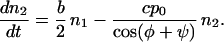 |
The coefficients reflect that first, filaments are born on one side (i.e., at the rate b/2) on filaments of the complementary orientation and, second, that filaments of orientation φ are capped at the rate cp0/cosφ. The solution to this system of equations is
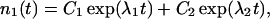 |
2 |
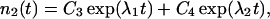 |
where C1 … C4 are constants that depend on initial conditions, and λ1, λ2 are functions of the kinetic coefficients in Eq. 1. Of the two exponential terms, the one with the larger λ will describe the proliferation in the long run, dominating over the other term. So, provided that branching prevails over capping, Eq. 2 reflects an asymptotically exponential increase in the abundance of the type. The rate of this asymptotic increase, that is the largest λ, is a function of orientation φ that enters the kinetic coefficients in Eq. 1:
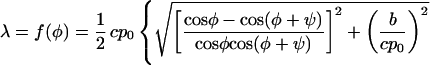 |
3 |
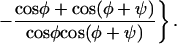 |
f(φ) is the required measure of the reproductive potential of filaments whose orientation is φ. Obviously, the filaments of the complementary orientation φ + ψ have the same reproductive potential. Being the rate of the exponential increase, f(φ) is by definition the Malthusian parameter of the type (3, 16, 17). As introduced by R. A. Fisher, it “measures fitness to survive by the objective fact of representation in future generations” (16) and can also be called the Fisherian fitness (3) of the type.
It must be emphasized that Eq. 3 is derived for the conditions for which Eq. 1 was written. A universal definition of the fitness function f(φ), which is valid for φ representing any orientation of any type, three as well as two orientation, is more complex and is given in Appendix 1. In general, fitness is not defined for |φ| ≥ θ, nor for any φ when p0 > cos(ψ/2), because filament reproduction cannot be sustained, and therefore types do not exist under these conditions. Differentiation of the function f(φ) shows that for cosψ < p0 < cos(ψ/2), it reaches maxima at φ = ±ψ/2. Therefore, the fittest under this condition is the two-generation type with symmetrically alternating orientations. Analogously, for p0 < cosψ, the type consisting of three orientations (0, ±ψ) has the greatest fitness. Thus, optimal orientations exist at which reproductive potential is maximized.
Mutations are necessary to provide the variation of orientation on which natural selection can operate. Let the variation be Gaussian with root-mean-square deviation σ from the mean angle ψ between the two filaments (11, 18). Then the number density n(φ, t) of filaments at the leading edge as a function of their orientation and time evolves according to the following equation:
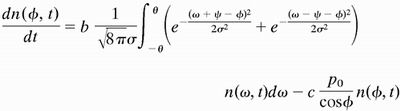 |
4 |
The kernel under the integral sign reflects the probability density that a filament at angle φ is nucleated on a filament at angle ω. In this dynamic equation, the pseudofirst-order rate constants of branching and capping, b and c, should be regarded as unknown functions of N, the total number of filaments in contact with the leading edge. This requirement is to reflect that the actin cytoskeleton of a steadily moving cell has to be in a steady state (9), but the mechanism of the establishment and maintenance of the steady state is not known. In general, the density function q(φ, t) of the distribution of angle φ is defined by n(φ, t) = q(φ, t)N(t). In the present work, we study the steady state as given, assuming that neither N nor q(φ) changes with time. Then it follows from Eq. 4 that the density function qss(φ), which is realized in a steady-state population of filaments, is the eigenfunction, and the steady-state ratio of capping and branching rates css/bss is the eigenvalue of what we call the branching–capping operator as expressed in the following eigenproblem:
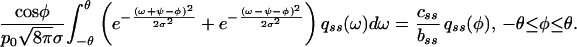 |
5 |
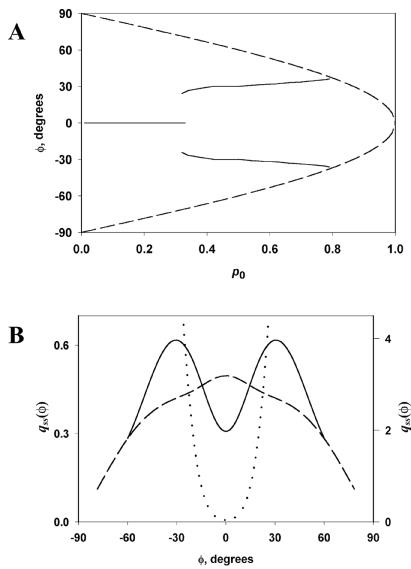
The quadrature method (19) yields for every p0 a unique solution with css/bss of the order of unity and qss(φ) depending on p0, as shown in Fig. 3. Maxima of qss(φ) correspond well to the maxima of f(φ). Thus, the fittest, as defined by the most rapidly proliferating, dominate in the population. According to the bifurcation diagram (Fig. 3A), the predominant orientations will be close to 0 when p0 is small, abruptly change to ±35° for intermediate values of p0, and gradually again become small when p0 is close to 1.
Figure 3.
Steady-state density (relative frequency) qss(φ) of filaments with the incidence angle φ at the leading edge. (A) Locations of the maxima of qss(φ) (solid lines) are incidence angles of the most abundant filaments under different p0, the probability that the filament with φ = 0 is not obstructed by the plasma membrane. Beyond the dashed line, qss(φ) is not defined, that is, existence of such angles is not predicted. (B) qss(φ) for p0 = 0.2 (dashed curve, left axis), p0 = 0.5 (solid curve, left axis), and p0 = 0.9 (dotted curve, right axis). ψ = 67°, σ = 12°.
The relationship between the fitness and steady-state density functions is crucial for the evolutionary explanation of the self-organization of the filaments. The filament types differ in their capacity to proliferate as expressed by Eq. 1 and f(φ) in terms of the underlying kinetics and geometry. The types transmute because of mutations of filament orientation, and the number of filaments is maintained constant, as expressed in Eq. 5, whose solution is qss(φ). So, the correspondence of maxima of the fitness function f(φ) to those of the steady-state density function qss(φ) has a dual meaning. First, it constitutes a theoretical demonstration of natural selection of actin filaments at the leading edge. Additionally, it provides a mechanistic explanation for the shape of qss(φ), which is the main prediction of the theory.
Comparing qss(φ) and f(φ) in more detail, it is necessary to take into account that in the three-orientation type, the middle orientation is twice as abundant as each of the two others, so for p0 < cosψ, there is only one maximum in qss(φ), as compared with three in f(φ). In addition, although under the condition p0 > cos(ψ/2), types do not reproduce themselves [f(φ) not defined], the assembly of the network can nevertheless persist [qss(φ) ≠ 0, Fig. 3], relying entirely on errors in the orientation inheritance. By the same reason, under the condition cosψ < p0 < cos(ψ/2), all angles −θ < φ < θ are represented, despite the fact that some types do not reproduce. Slight displacements of the maxima and bifurcation points of qss(φ) from their locations analytically determined for f(φ) can also be regarded as effects of orientation mutations.
A specific prediction on the distribution of the filament orientation that is realized in the cell can be made by considering the kinetic efficiency of the several protrusion regimes. Lower values of p0 imply lower velocity of protrusion under the same possible rate of polymerization. In contrast, for high p0, branching produces on average filaments that do not push because they do not keep up with the leading edge. Consequently, the regime of intermediate p0, which produces a bimodal distribution with maxima at φ = ±ψ/2, appears most physiological.
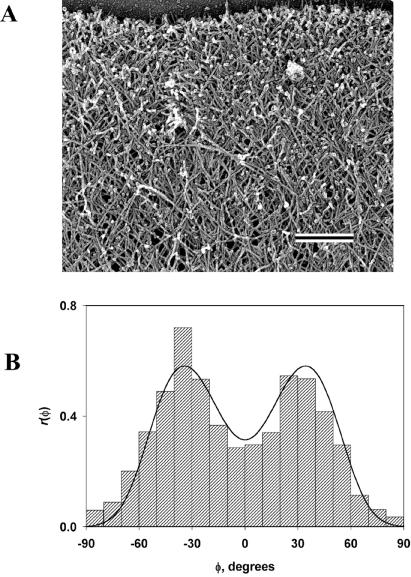
Our model predicts that the most probable filament orientations are given as ±half the branching angle. Thus, a branching angle ψ of ≈70° (8, 9) specifies that filament orientations of ±35° will be most frequent. Earlier qualitative observations estimated the most frequent orientation of filaments in lamellipodia as ±45° (2, 20), and a subsequent analysis (21) gave orientations of filaments at the margin of ±25°. Although these estimates bracket the predicted value of 35°, it seemed desirable to quantitatively test the prediction of our theory by measuring the distribution of angles φ formed by actin filaments and the normal to the leading edge of the lamellipodium. We carried out measurements on electron micrographs of lamellipodia from several kinds of motile cells including Xenopus keratocytes (Fig. 4A), fish (Hymnocorhymbus ternezii) keratocytes, and Xenopus fibroblasts (not shown) (see Appendix 2 for methods). Because filament orientation is expected to occur over a range of angles, it was important to use a measurement procedure that avoided subjectivity and that included a sufficiently large population to average natural variations. For this purpose, we initially used the Fourier transform to objectively analyze the digitized electron micrographs. However, in the course of the work, we found that the Radon transform (22, 23) used in computer vision algorithms and tomography provided a better approach. The Radon transform computes projections of an image matrix along specified directions. Thus, it is particularly useful in detecting lines or linear objects in an image. Before applying the Radon transform, filaments were enhanced by an edge-detection procedure based on the Canny algorithm (24). The Canny method is a particularly powerful edge-detection method, which uses two thresholds and is less likely to be confused by noise. Edges oriented at an angle to the direction of the projection give only weak signals that are filtered out, so that the integrated intensity of signal that remains in the projection becomes a function of the number of filaments in the direction of the projection. The resulting distribution, or empiric density function r(φ), of filament incidence angle in the Xenopus keratocyte is shown in Fig. 4B. It has two maxima at approximately ±35°, in agreement with the theory when cosψ < p0 < cos(ψ/2) and ψ = 70° (8, 9). The same angle values correspond to peaks in histograms obtained from the Hymnocorhymbus keratocyte and the Xenopus fibroblast (not shown). Similar distributions were obtained from deeper regions of the lamellipodium but showed greater fluctuations as filament density decreased. At the lamellipodial/cell body transition zone, filaments become oriented parallel to the leading edge. Accordingly, in this region, analysis yielded a narrow monomodal distribution of angles peaking at ≈90° to the normal.
Figure 4.
Orientation of actin filaments at the leading edge. (A) Platinum replica electron micrograph of the dendritic brush of actin filaments at the leading edge of a moving Xenopus keratocyte. The cell margin is at the top of the image. (Bar = 0.2 μm.) (B) Histogram of angles between filaments and the normal to the leading edge in the actin cytoskeleton of a Xenopus keratocyte lamellipodium (bars) and its theoretical approximation (curve). Negative and positive angles mean deviation to one and the other side from the normal. The region shown in A corresponds to approximately one-half the lamellipodial area from which the histogram was generated. The histogram is representative of histograms obtained from other regions of lamellipodia and other cells.
The theoretical density function of φ inside the lamellipodium is proportional to the flux of filaments off the leading edge, that is, to qss(φ)/cos(φ), and therefore has the same maxima and domain as qss(φ). If the so-far-unaccounted factors that influence the distribution of angles are numerous but each of them has only a small impact, that is, if the theory captures all essential features of the process, r(φ) has to be the convolution of the theoretical density function with a Gaussian. Least-squares optimization yields p0 = 0.57 (so that css/bss = 0.62) and the standard deviation of the Gaussian 12.5° for the best approximation (Fig. 4B). The obtained css/bss is within the range of 50kcMc/knMa = 0.4–4, where kc = 3.0 μM−1 ⋅ s−1 is the rate constant for capping (25), Mc = 0.2–2 μM is the concentration of the capping protein (25), kn = 6.4 μM−1 ⋅ s−1 is the rate constant of nucleation of actin filaments from monomer by the Arp2/3 complex (8), Ma = 12 μM is the concentration of monomer (26), and the numerical factor is the average number of unproductive decays of a nucleation complex before a successful elongation (8). The obtained value of p0 implies that if ka = 11.6 μM−1 ⋅ s−1 (27) and δ = 2.7 nm (28), the rate of protrusion is 0.21 μm s−1, which is within the range measured in keratocytes, 0.05–0.5 μm s−1 (29). Thus, the value of p0 computed from the experimentally determined distribution of filament angles is consistent with the literature data on the kinetics of actin polymerization and protrusion.
Discussion
Branching actin filaments at the leading edge of crawling cells satisfy Darwin's conditions of variation and heritability of fitness (3). Therefore, they must be subject to competition and natural selection. It is important to note that invoking natural selection as a directive force is more than a mere metaphor. Our purpose is to emphasize the point that the concept of natural selection applies more generally than to the origin of species, and that its application to supramolecular assemblies provides explanatory power for understanding their dynamic self-organization. Building on this idea, we have developed a quantitative population–kinetic theory of natural selection of actin filaments propelling the leading edge of a motile cell. The theory explains the structure of the propulsive array in agreement with measurements of the actin network in situ. It permits estimation of a single parameter, p0, which allows determination of the relative rates of elongation of free filaments and advance of the leading edge. It allows estimation of the relative rates of filament capping and branching in the steady state. Finally, it explains self-organization of the actin network as an evolutionary process on the basis of natural selection of filament orientation.
The model as developed uses only a two-dimensional treatment. This is a simplifying limitation, because actin filaments can presumably branch in three dimensions. The limitation, however, may be of minor consequence because of the thinness of the lamellipodium (≈200 nm) and the restriction of branch nucleation to the leading edge. Although the mechanism responsible for determining the depth of the lamellipodium has not been established, filaments branching into the third dimension would rapidly arrive at the limiting membrane and encounter an impediment to growth. Because such filaments would also fall behind the leading edge, they would be selected against both through failure to generate progeny and through termination by capping protein. Consequently, we believe our two-dimensional model captures the essential biological properties of actin filament self-organization.
Our population–kinetic model is consistent with the “elastic Brownian ratchet” model put forward by Mogilner and Oster (12) to explain quantitatively the protrusive mechanics of lamellipodia. The control parameter p0 used kinematically in our model may be interpreted as a Boltzmann factor, the exponential of the work in units of thermal energy that is done by a filament to advance the membrane by the length of a monomer unit. According to this interpretation of p0, its value will depend on load, approaching 0 at high load and approaching 1 as the resistance to protrusion vanishes. The Mogilner–Oster model focused on how the thermal motions of polymerizing filaments can produce a directed force. They developed a force–velocity relationship and showed that filament growth velocity was maximal at a particular orientation angle, which they estimated from assumptions of relevant parameters to be 48°. They suggested that, because filaments grow fastest in this direction, they would come to predominate in the population. Our model also concludes that a particular orientation will predominate, but we determine it to be half the branching angle, namely 35°. We do not feel much significance need be attached to this difference for several reasons. First, the Mogilner–Oster model was proposed before the dendritic organization of actin filaments with branching angle of 70° was known. Incorporation of the constraint of branching would likely alter their calculations. Second, their treatment asked only in which direction filaments would grow the fastest. They did not explicitly deal with population kinetics. Finally, calculation of the optimal angle is sensitive to assumptions of the load force, filament-bending stiffness, and free filament end length, and with different parameters, a different angle would be calculated.
An evolutionary self-organization process of supramolecular ensembles carries genetic and behavioral implications. Such a process is economical in terms of the information required to specify the final structure. Thus, one physiological role of natural selection of actin filaments may be to minimize the genomic costs of construction of the protruding network, which contributes to the fitness of the higher-level evolving entity, the cell, and ultimately the organism. An evolutionary self-organization process is also intrinsically adaptive. Cells can respond to chemotactic stimuli and to substratum cues by altering their direction of movement. In terms of the dendritic nucleation/array treadmilling model, a turning response means preferential assembly of the actin network in one direction. Our evolutionary model provides a conceptual framework for understanding how this might occur. The constitutive existence of a spectrum of filament orientations combined with variation of orientation provides the raw materials from which favored orientations will be naturally selected. Our study demonstrates that the natural selection of supramolecular complexes is among the mechanisms that, working on results of expression of genetic information and self-assembly, facilitate the self-organization of the motility machinery.
Acknowledgments
We thank Drs. Tatyana Svitkina, Edwin Taylor, Alex Mogilner, Guenter Albrecht-Buehler, and Viktor Maly for critical reading of the manuscript. This work was supported by National Institutes of Health Grant GM 62431.
Appendix
In general, the abundance of a type is given by the numbers ni of filaments of the orientations φi, i = 1, 2, or 3, that belong to the type. Let us arrange these numbers ni in the order of increase of φi to form a vector n and introduce χ, which will be the largest of φi. Then for large ni and φ ≥ 0,
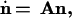 |
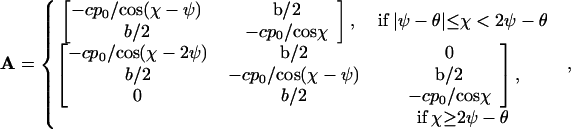 |
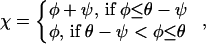 |
and the fitness f(φ) of the type to which filaments with orientation φ belong is given by the largest eigenvalue of A. For φ < 0, f(φ) = f(−φ).
Appendix
Electron micrographs of the actin network were provided by T. M. Svitkina, University of Northwestern Medical School. The methods used in preparation of cells and microscopy were as described previously (9). In brief, keratocytes and fibroblasts were obtained by trypsin digestion of tissue fragments from anesthetized Xenopus tadpoles or black tetras. The cells were plated onto coverslips and incubated at 27°C in L-15 medium (Sigma) diluted to 70% and supplemented with 20% fetal bovine serum (HyClone) for 1 h. The cells were extracted for 3 min at room temperature with 1% Triton X-100 in 100 mM Pipes, pH 6.9/1 mM MgCl2/1 mM EGTA containing 2 μM phalloidin (Sigma). Extracted cells were fixed with 2% glutaraldehyde, and platinum–carbon replicas of the cytoskeleton were prepared for electron microscopy.
Analysis of images of the actin network was performed in matlab software (MathWorks, Natick, MA). Electron micrographs were digitized so that 1 pixel in the digital file corresponded to 1 nm in the original image. Circular regions 0.6 μm in diameter, adjacent to the margin of the lamellipodium, were selected in the electron microscopic images. Edges of the filaments in each area were detected by use of the Canny algorithm (26), and the images were binarized and then subjected to the Radon transform (27, 28). Noise in the Radon transform was removed by leaving only the signal above the mean plus two standard deviations. Such filtered Radon transforms were integrated over the linear coordinate to obtain the density function g(α) of the angle α between filaments and the coordinate axis X of the image. If the margin of the lamellipodium formed an angle ω with the coordinate axis X of the image, the distribution of the angle φ between the filaments and the normal to the margin is r(φ) = g(φ + ω). To suppress noise, r(φ) was averaged for 20 overlapping regions within each lamellipodium that together covered a continuous area of 2 μm2. A total of 12 lamellipodia were analyzed. This method measures, in effect, total length rather than number of filaments in a given orientation. In the model, however, the mean length of filaments after capping, that is, of filaments inside lamellipodia, is independent of their orientation, because it is determined by competition of elongation and capping that takes place when the tip of a filament is open. Therefore, the prediction of the model for the distribution of the total length in a given direction is the same as its prediction for the distribution of the number of filaments, or simply distribution of angle in the population of filaments. The imaging method is therefore suited to test the model. In tests, the method identified angles of individual lines in artificial images containing many lines.
References
- 1.Pollard T D, Blanchoin L, Mullins R D. Annu Rev Biophys Biomol Struct. 2000;29:545–576. doi: 10.1146/annurev.biophys.29.1.545. [DOI] [PubMed] [Google Scholar]
- 2.Small J V, Herzog M, Anderson K. J Cell Biol. 1995;129:1275–1286. doi: 10.1083/jcb.129.5.1275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Michod R E. Darwinian Dynamics: Evolutionary Transitions in Fitness and Individuality. Princeton, NJ: Princeton Univ. Press; 1999. [Google Scholar]
- 4.Grant V. The Evolutionary Process: A Critical Review of Evolutionary Theory. New York: Columbia Univ. Press; 1985. [Google Scholar]
- 5.Rowe G W. Theoretical Models in Biology: The Origin of Life, the Immune System, and the Brain. New York: Oxford Univ. Press; 1994. [Google Scholar]
- 6.Nowak M A, Plotkin J B, Jansen V A A. Nature (London) 2000;404:495–498. doi: 10.1038/35006635. [DOI] [PubMed] [Google Scholar]
- 7.Nowak M A, Komarova N L, Niyogi P. Science. 2001;291:114–118. doi: 10.1126/science.291.5501.114. [DOI] [PubMed] [Google Scholar]
- 8.Mullins R D, Heuser J A, Pollard T D. Proc Natl Acad Sci USA. 1998;95:6181–6186. doi: 10.1073/pnas.95.11.6181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Svitkina T M, Borisy G G. J Cell Biol. 1999;145:1009–1026. doi: 10.1083/jcb.145.5.1009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Borisy G G, Svitkina T M. Curr Opin Cell Biol. 2000;12:104–112. doi: 10.1016/s0955-0674(99)00063-0. [DOI] [PubMed] [Google Scholar]
- 11.Blanchoin L, Amann K J, Higgs H N, Marchand J-B, Kaiser D A, Pollard T D. Nature (London) 2000;404:1007–1010. doi: 10.1038/35010008. [DOI] [PubMed] [Google Scholar]
- 12.Mogilner A, Oster G. Biophys J. 1996;71:3030–3045. doi: 10.1016/S0006-3495(96)79496-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Machesky L M, Insall R H. Curr Biol. 1998;8:1347–1356. doi: 10.1016/s0960-9822(98)00015-3. [DOI] [PubMed] [Google Scholar]
- 14.Rohatgi R, Ma L, Miki H, Lopez M, Kirchhausen T, Takenawa T, Kirschner M W. Cell. 1999;97:221–231. doi: 10.1016/s0092-8674(00)80732-1. [DOI] [PubMed] [Google Scholar]
- 15.Yarar D, To W, Abo A, Welch M D. Curr Biol. 1999;9:555–558. doi: 10.1016/s0960-9822(99)80243-7. [DOI] [PubMed] [Google Scholar]
- 16.Fisher R A. The Genetical Theory of Natural Selection. Oxford, U.K.: Oxford Univ. Press; 1999. [Google Scholar]
- 17.Crow J F, Kimura M. An Introduction to Population Genetics Theory. New York: Harper & Row; 1970. [Google Scholar]
- 18.Reif E. Fundamentals of Statistical and Thermal Physics. New York: McGraw–Hill; 1965. [Google Scholar]
- 19.Baker C T H. The Numerical Treatment of Integral Equations. Oxford, U.K.: Clarendon Press; 1977. [Google Scholar]
- 20.Small J V, Celis J E. Eur J Cell Biol. 1978;16:308–325. [Google Scholar]
- 21.Abraham V C, Krishnamurthi V, Taylor D L, Lanni F. Biophys J. 1999;77:1721–1732. doi: 10.1016/S0006-3495(99)77018-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Helgason S. The Radon Transform. Boston: Birkhauser; 1999. [Google Scholar]
- 23.Leavers V F. Shape Detection in Computer Vision Using the Hough Transform. New York: Springer; 1992. [Google Scholar]
- 24.Canny J. IEEE Trans PAMI. 1986;8:679–698. [PubMed] [Google Scholar]
- 25.Schafer D A, Jennings P B, Cooper J A. J Cell Biol. 1996;135:169–179. doi: 10.1083/jcb.135.1.169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Marchand J-B, Moreau P, Paoletti A, Cossart P, Carlier M-F, Pantaloni D. J Cell Biol. 1995;130:331–343. doi: 10.1083/jcb.130.2.331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pollard T D. J Cell Biol. 1986;103:2747–2754. doi: 10.1083/jcb.103.6.2747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Holmes K C, Popp D, Gebhard W, Kabsch W. Nature (London) 1990;347:44–49. doi: 10.1038/347044a0. [DOI] [PubMed] [Google Scholar]
- 29.Lee J, Ishihara A, Theriot J A, Jacobson K. Nature (London) 1993;362:167–171. doi: 10.1038/362167a0. [DOI] [PubMed] [Google Scholar]