Significance
Talin is an adaptor protein that transduces mechanical signals into biochemical cues by recruiting a network of protein ligands in a force-dependent way. These force cues have a complex nature, oscillate in time with different frequency components, and are often embedded in noise. However, most assays to explore the mechanics of force-sensing proteins rely on simple perturbations, such as constant or ramped forces. Here, we use our magnetic tweezers design to subject single talin domains to oscillatory forces and external mechanical noise. We show that talin ignores random external fluctuations but synchronizes its folding dynamics with force oscillations in a frequency-dependent way. We hypothesize that this finely tuned response could underpin talin force-sensing properties.
Keywords: talin, stochastic resonance, magnetic tweezers, protein folding
Abstract
Cells continually sample their mechanical environment using exquisite force sensors such as talin, whose folding status triggers mechanotransduction pathways by recruiting binding partners. Mechanical signals in biology change quickly over time and are often embedded in noise; however, the mechanics of force-sensing proteins have only been tested using simple force protocols, such as constant or ramped forces. Here, using our magnetic tape head tweezers design, we measure the folding dynamics of single talin proteins in response to external mechanical noise and cyclic force perturbations. Our experiments demonstrate that talin filters out external mechanical noise but detects periodic force signals over a finely tuned frequency range. Hence, talin operates as a mechanical band-pass filter, able to read and interpret frequency-dependent mechanical information through its folding dynamics. We describe our observations in the context of stochastic resonance, which we propose as a mechanism by which mechanosensing proteins could respond accurately to force signals in the naturally noisy biological environment.
The precise interpretation of complex mechanical signals underpins a vast range of biological processes (1–3). These force signals are accurately detected by cellular force sensors and transduced into electrical or biochemical signals to trigger a physiological response—mechanotransduction (4, 5). For instance, the human auditory system converts complex vibration patterns into electrophysiological signals with astonishing speed and accuracy, detecting frequencies from 20 Hz to 20,000 Hz with a sensitivity finer than the music interval and a dynamic range greater than 120 dB (6, 7). Akin to sound waves, mechanical signals in biology oscillate at frequencies that span over several timescales and, yet, are effectively decomposed and interpreted by cells. Furthermore, in addition to the intrinsic thermal noise that drives Brownian motion, athermal noise is a protagonist at the molecular and cellular level (8). Every mechanical communication is thus challenged by a background of noninformative fluctuations that, still, do not interfere with a robust cellular response. However, how molecular force sensors interpret complex mechanical signals in a finely tuned way remains mostly unknown.
Cells continuously receive and transmit mechanical signals between neighbor cells and the extracellular matrix, which guides diverse processes such as embryonic development (9), cell traction (10), or tumor proliferation (11). These force stimuli are transduced into biochemical signals, generally by inducing conformational changes in force-bearing proteins that modulate the affinity of binding partners or induce posttranslational modifications (4, 12, 13). For instance, cells migrate following the stiffness gradient of their substrate, which is sampled by periodic forces applied by focal adhesions—durotaxis (14, 15). Talin is a mechanosensing hub protein in focal adhesions, which cross-links transmembrane integrins with the active F-actin filaments and recruits several binding proteins to control the function and fate of this organelle (12, 15–17). For example, vinculin binds to cryptic helices in mechanically unfolded talin domains, subsequently recruiting actin filaments that reinforce the cellular junction (13, 18–20). Hence, talin transduces mechanical forces through its folding dynamics.
The mechanics of talin have been studied using force spectroscopy techniques, which typically apply ramped or constant forces to monitor folding or unfolding reactions (21, 22). These studies have shown that force drives talin response by unfolding each of the 13-rod bundle domains hierarchically; increasing forces result in a gradual unfolding of the talin rod (23, 24). This response establishes a simple mechanotransduction pathway; the force load on talin determines the number of unfolded talin domains and, hence, how many vinculin molecules can be recruited. However, the response of talin under complex mechanical signals has never been studied, so it remains unknown how talin folding dynamics couple to forces that change in time or if its response is affected when the mechanical perturbation is buried in external noise fluctuations.
Here, we measure the folding dynamics of the talin R3 domain under complex force signals, which include external mechanical noise and sinusoidal perturbations. Using our magnetic tape head tweezers design (Fig. 1A), we demonstrate that talin rejects external mechanical noise but exhibits phase-locked folding dynamics when subject to oscillating forces. Talin response is finely tuned, and it only detects signals over a narrow frequency range, which is defined by its mechanical stability; the R3 wild-type (R3 WT) domain responds to signals around 7 Hz, while the more stable R3 IVVI mutant (mutation T809I/T833V/T867V/T901I) detects slower signals at 1 Hz. We ascribe our results to the physical phenomenon of stochastic resonance, which we propose as a mechanism by which force-sensing proteins could interpret complex mechanical signals through their folding dynamics, by operating as a “biochemical Fourier transform.”
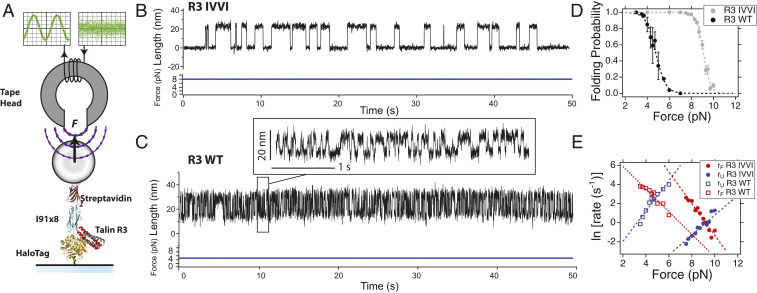
Fig. 1.
Mechanical characterization of the talin R3 domain. (A) Schematics of our magnetic tweezers assay for applying complex force signals to single proteins. Our construct contains the talin R3 domain followed by eight repeats of the titin I91 domain, flanked by a HaloTag for covalent anchoring to the glass surface and biotin for tethering with streptavidin-coated M-270 magnetic beads. Forces with a bandwidth greater than 10 kHz are generated using a magnetic tape head. (B) Typical single-molecule recording of talin R3 IVVI at 9 pN. (C) Typical recording of talin R3 WT at 5 pN. (Inset) Detail of the trajectory, highlighting the faster dynamics of R3 WT compared to the mutant R3 IVVI. Traces acquired at a frame rate between 1 kHz and 1.5 kHz and smoothed with a Savitzky–Golay fourth-order filter, with a 101-points box (R3 IVVI) and a 31-points box (R3 WT). (D) Folding probability of the R3 IVVI and R3 WT talin domains. The R3 IVVI mutant has a higher mechanical stability, and its folding probability is shifted to higher forces by 4 pN. (E) Folding (red) and unfolding (blue) rates for R3 IVVI (solid) and R3 WT (empty) talin domains. At the coexistence force, the rates of the WT are 12 , compared to the slower ones of R3 IVVI (1.5 ). Data are fitted with the Bell–Evans model (dotted lines), yielding nm, and nm, for R3 WT, and nm, and nm, for R3 IVVI.
Results
Mechanical Characterization of the Talin R3 Domain.
The talin R3 domain is the weakest of all 13-rod domains, thought to be the precursor of talin-based adhesions, given its low unfolding force and the presence of two vinculin-binding sites (16, 20, 23, 24). This low mechanical stability is due to the four-residue threonine belt on its hydrophobic core; the substitution of these residues in the mutant R3 IVVI increases its stability significantly (16, 20). Due to these different mechanical properties, we explore both the R3 WT and R3 IVVI domains perturbed by complex mechanical signals, which will allow us to compare and relate their responses with their mechanics. First, in order to establish the benchmarks for the study under complex force signals, we characterize the folding mechanics of both domains at constant force (Fig. 1).
Fig. 1 B and C shows representative recordings measured at the coexistence force (; same occupation of the folded and unfolded states), which is 9 pN for R3 IVVI and 5 pN for R3 WT. Their folding dynamics are characterized by reversible transitions between the folded and unfolded states with an extension change of 20 nm, but the kinetics of R3 WT is nearly 10 times faster, compared to those of R3 IVVI (Fig. 1 C, Inset). From equilibrium trajectories such as these, we measure the relative occupation of the folded state (folding probability; Fig. 1D), and the folding (rF) and unfolding (rU) rates (Fig. 1E). The folding probability spans less than 2 pN, illustrating the exquisite force sensitivity of both domains. Due to this steep force dependency, the folding and unfolding rates have an exponential Bell-like dependency (; ref. 25), with similar distances to transition state from the folded and unfolded states. Overall, both domains exhibit two-state–like dynamics, occurring at different force ranges—between 4 pN and 6 pN (R3 WT), and 8 pN to 10 pN (R3 IVVI)—and kinetic rates on a very different timescale—at , 12 (R3 WT), and 1.5 (R3 IVVI).
Talin Discerns between External Mechanical Noise and Oscillatory Forces.
Motivated by the naturally noisy cellular environment, we first asked whether talin maintains a robust response when subject to a randomly fluctuating perturbation instead of a constant force. Applying forces that change rapidly is challenging, as force spectrometers typically change the force by displacing large mechanical probes. To this aim, we take advantage of our magnetic tape head tweezers design, able to change the force with a bandwidth greater than 10 kHz while maintaining intrinsic force-clamp conditions (Fig. 1A and ref. 26). We generate external mechanical noise as a broadband uncorrelated force signal, with an average of 9 pN and a peak-to-peak amplitude greater than 7 pN (SI Appendix, Fig. S1 and Supplementary Methods), and apply it to the talin R3 IVVI domain. This signal fluctuates around over a force range that significantly exceeds the folding regime of R3 IVVI. Importantly, this external mechanical noise is different from the intrinsic thermal noise provided by the heat bath, which we do not control in our experiment and that induces the stochastic folding and unfolding transitions we observe at constant force.
Fig. 2 A, Left shows the dynamics of R3 IVVI perturbed by external mechanical noise. Strikingly, despite the fine force sensitivity of talin and the broad force range over which the external mechanical noise fluctuates, we do not observe any effect on talin dynamics, which are statistically indistinguishable from those measured at the average force of 9 pN. The dwell-time histograms—obtained using a maximum-likelihood procedure (SI Appendix, Fig. S2)—are both exponential distributions with approximately the same time constant— s (noise) versus s (no noise) (Fig. 2 A, Right). This apparent insensitivity to external mechanical fluctuations is maintained at any other folding force. We observe no statistically significant differences (within a 95% CI) between the folding probabilities measured in the presence or absence of external mechanical noise, and the coexistence forces () obtained under both conditions overlap within error bars (SI Appendix, Fig. S3). This evidence suggests that talin has a robust mechanical response, filtering out the randomly fluctuating components, and responding only to the average force.
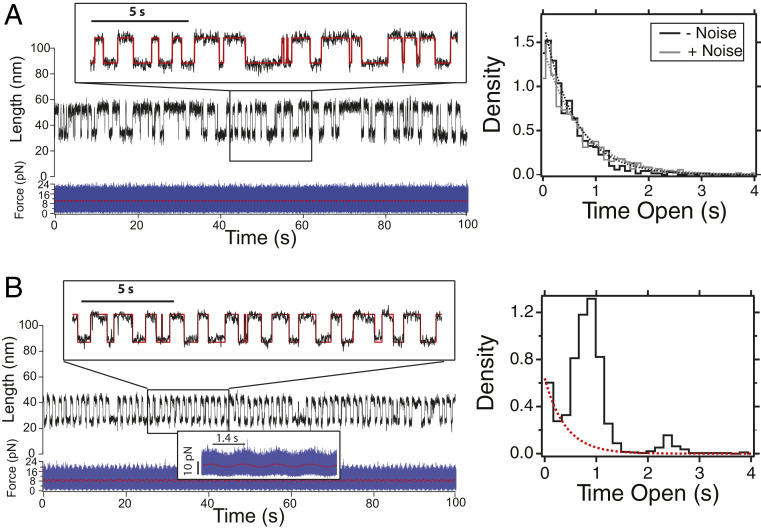
Fig. 2.
Talin detects oscillatory signals among mechanical noise. (A) (Left) Dynamics of the talin R3 IVVI domain under mechanical white noise with an average of 9 pN and an SD of 2.8 pN. (Inset) Detail of the trajectory with the idealized trace (red). (Right) Comparison of the dwell-time histograms in the unfolded state perturbed by a constant force of 9 pN (black) and external mechanical noise (gray). Both distributions are comparable, as talin remains insensitive to randomly fluctuating forces and responds only to the average perturbation. Histograms are built from 1,063 (no noise) and 704 transitions (noise). (B) (Left) Dynamics of the talin R3 IVVI domain perturbed by a force signal oscillating at 0.7 Hz, with an amplitude of 1 pN, and submerged in mechanical white noise with an SD of 2.8 pN. (Inset, Upper) Detailed of the idealized trace (red. (Inset, Lower) Detail of the force perturbation (red). (Right) Dwell-time histogram measured under such signal. The folding transitions are synchronized with the oscillating force, while the mechanical noise is ignored. These dynamics shift the shape of the dwell-time distribution, which shows resonance peaks at odd multiples of half of the period of the signal. The remnant stochastic behavior is appreciated as an underlying exponential distribution (red dotted line). Histogram is built with 2,295 transitions. Traces are acquired at a frame rate of 1–1.5 kHz, and smoothed with a Savitzky–Golay fourth-order algorithm with a 101-points box size.
Given the ability of talin to remain indifferent to the external mechanical noise, we explore its response under a force signal that oscillates at a specific frequency and is submerged in external mechanical noise. We build this signal by adding a sinusoidal force (with pN, pN, and Hz) to external mechanical noise with the same properties employed before. Hence, the amplitude of the correlated component is small compared to the background fluctuations (Fig. 2 B, Inset). By contrast, talin dynamics are now dramatically altered, and most transitions occur at regular intervals of 0.7 s, while the mechanical noise is ignored (Fig. 2 B, Left). These entrained folding dynamics shift the shape of the dwell-time histogram from an exponential to a peaked distribution (Fig. 2 B, Right). The first peak is centered at 0.7 s, which coincides with the half-period of , while the second peak appears at 3 times that value, 2.1 s. Despite the dominant entrained dynamics, we observe an underlying exponential distribution, which reflects a minority of remnant stochastic transitions, occurring at a time constant compatible to a force of 9 pN (Fig. 2 B, Right, red dotted line). Hence, unlike random force fluctuations, talin detects force oscillations through its folding dynamics, which shift from stochastic—characterized by exponentially distributed dwell times—to a phase-locked response, reflected in peaked dwell-time distributions.
Mechanical Signal Detection by Talin is Frequency Dependent.
The talin R3 domain detects minimal force changes through its folding dynamics; differences in force of only 0.3 pN shift the folding probability by up to 30% (Fig. 1D). Since our data demonstrate that talin detects oscillatory forces, we seek to test whether such a response is also frequency sensitive. To this aim, we subject R3 IVVI to purely oscillating forces at different frequencies, , 1, and 10 Hz, with a mean value of pN, and amplitude of pN.
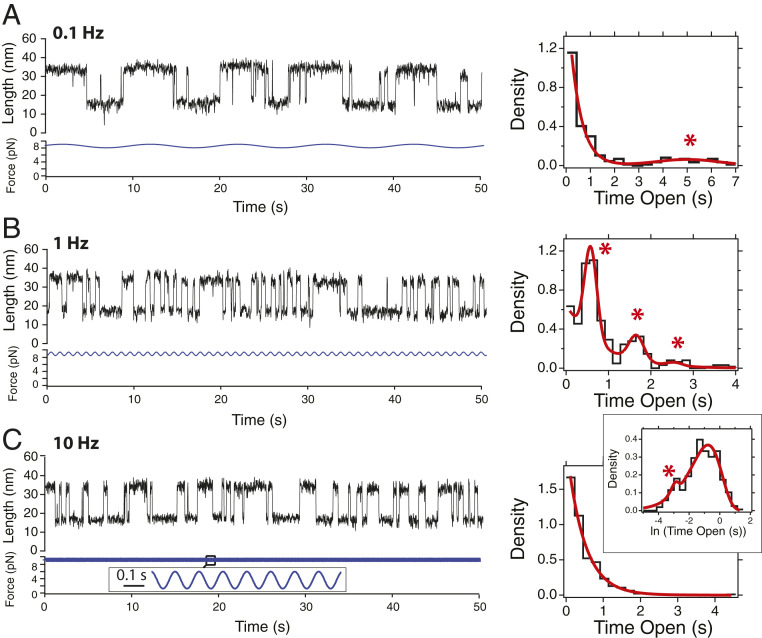
Fig. 3 shows R3 IVVI folding dynamics under these three oscillatory force signals (Fig. 3, Left), with the associated dwell-time histograms (Fig. 3, Right). Under the slowest perturbation ( Hz; Fig. 3A), we observe that, while the extension of the protein follows the oscillation, most transitions are stochastic, as the force changes much more slowly than the natural folding kinetics—0.1 Hz versus 1.5 Hz. The dwell-time histogram is an exponential distribution with a time constant compatible to a constant force of 9 pN (), and a marginal contribution of entrained transitions as a small peak at 5 s (red asterisk). At Hz (Fig. 2B), most folding transitions are synchronized with the perturbation and occur at regularly spaced time intervals. The dwell-time histogram has three peaks of diminishing amplitude and a small underlying exponential distribution. These peaks are centered at odd multiples of half of the driving period—0.5, 1.5, and 2.5 s—and represent harmonics of talin phase-locked response. Finally, at a driving frequency of 10 Hz (Fig. 3C), the stochastic behavior is recovered with the same dynamics as those measured at 9 pN. The dwell-time histogram is an exponential distribution with a time constant of , which indicates that talin filters this fast oscillation. Only when calculating the dwell-time distribution with logarithmic binning, we observe a small contribution at 0.05 s corresponding to a minority of entrained transitions (Fig. 3 C, Inset). Hence, these data indicate a frequency-selective response of talin upon oscillating forces. Interestingly, talin folding dynamics segregate into phase-locked dynamics that respond to the oscillation with a frequency-dependent intensity, and a stochastic behavior that filters the signal and detects only the average of the perturbation.
Fig. 3.
Dynamics of the talin R3 IVVI domain under signals of different frequencies. (Left) The 50-s-long fragments of magnetic tweezers recordings showing R3 IVVI under a periodic signal with an amplitude of 0.7 pN, and frequencies of 0.1 (A), 1 (B), and 10 Hz (C). (Right) Dwell-time histograms on the unfolded state calculated for each of these signals. The interplay between the stochastic and resonant dynamics is manifested as a combination of exponential and Gaussian distributions, with relative weights that indicate the level of response (red fits). At 0.1 Hz (A), most transitions are stochastic, and only a small peak at 5 s appears (red asterisk). At 1 Hz (B), the response is optimal, and the majority of the histogram is built by Gaussian peaks, located at odd multiples of the half-period of the driving signal (red asterisk). At a high frequency of 10 Hz (C), the distribution is exponential, and only a logarithmic binning reveals a small proportion of resonant transitions at 0.05 s (Inset, red asterisk). Histograms are built with 223 (A), 337 (B), and 363 (C) transitions. Traces are acquired at a frame rate between 1 kHz and 1.5 kHz, and smoothed with a Savitzky–Golay fourth-order filter, with a 101-points box.
Talin Response is Governed by the Mechanical Stability of the Domain.
The response of the R3 IVVI domain suggests that the entrained dynamics manifest optimally at frequencies of the order of the natural folding rates, which, at 9 pN, are 1.5 (Fig. 1E). Hence, it can be expected that proteins with faster kinetic rates will respond to higher frequencies and vice versa, providing a tuning mechanism based on the mechanical stability of the protein domain. In order to test this hypothesis, we measure the folding dynamics of the R3 WT domain subject to oscillatory forces given that, at the coexistence force pN, its kinetic rates are nearly 10 times faster (12 ; Fig. 1E).
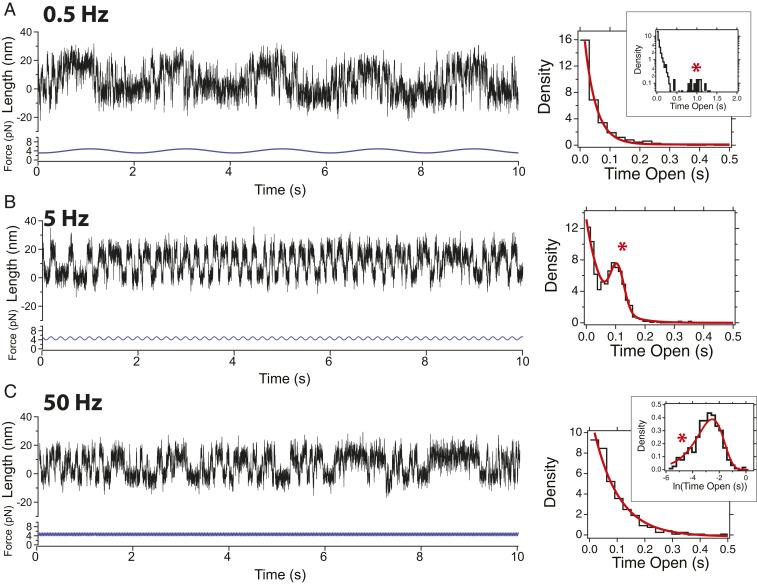
Fig. 4 shows single-molecule recordings of R3 WT perturbed with sinusoidal signals of 0.5 (Fig. 4A), 5 (Fig. 4B), and 50 Hz (Fig. 4C), an average of pN, and amplitude of pN. These data show an analogous response to that measured for R3 IVVI but shifted to higher frequencies. At 0.5 Hz, the dynamics are exponentially distributed, with a minor entrained contribution appreciable in log scale (Fig. 4 A, Inset). At 5 Hz, the transitions are entrained with the force signal, showing a peak at 0.1 s and an underlying exponential distribution with a time constant compatible to that measured at 5 pN (). At 50 Hz, the dynamics are stochastic, with a rate of and a minimal contribution at 0.01 s appreciable with logarithmic binning (Fig. 4 C, Inset). These results suggest the generality of the frequency-dependent signal detection by talin folding dynamics, where the mechanical stability of the protein domain selects the responsive frequency regime. Additionally, we measured the folding probability of R3 WT in the presence and absence of external mechanical noise, observing no statistically significant difference (SI Appendix, Fig. S3). These data suggest that, similar to the mutant R3 IVVI, R3 WT filters out random mechanical fluctuations but responds to coherent force oscillations.
Fig. 4.
Response of the R3 WT domain under signals of different frequencies. (Left) The 10-s-long fragments of magnetic tweezers recordings showing R3 WT under a sinusoidal force signal with an amplitude of 0.7 pN, and frequencies of 0.5 (A), 5 (B), and 50 Hz (C), respectively. (Right) Dwell-time histograms on the unfolded state, for each of these signals. At 0.5 Hz (A) most transitions are stochastic, with a small entrained contribution appreciable in log-scale (Inset, red asterisk). At 5 Hz (B), the response is optimal and the dwell-time histogram has a major peaked contribution (red asterisk). At 50 Hz (C), the distribution is exponential, and only a minor entrained contribution is observed with logarithmic binning (Inset, red asterisk). Histograms are built with 715 (A), 2,736 (B), and 1,945 (C) transitions. Raw traces are shown, acquired at rates of 1 kHz to 1.5 kHz.
Stochastic Resonance in Talin Folding Dynamics.
Our observations show a phase-locked response of talin folding dynamics as a mechanism of mechanical signal detection. This behavior resembles the physical phenomenon of stochastic resonance, by which nonlinear systems exhibit an amplified response upon a weak input signal due to the presence of stochastic noise (27, 28). Stochastic resonance has been demonstrated in very diverse contexts, such as climate dynamics (29), optical systems (30), DNA hairpin dynamics (31), and quantum systems (32), since it only requires three fundamental ingredients: a bistable system, a weak periodic input, and an intrinsic source of noise. All three of these conditions are fulfilled by our system; the free energy landscape of the R3 domain is well approximated by a symmetric double-well potential (SI Appendix, Fig. S4), and the thermal bath provides the intrinsic noise. Importantly, this intrinsic thermal noise is different from the external mechanical noise we used in Fig. 2, which was applied as an external random force on talin.
Signal detection by stochastic resonance typically refers to an increase in the signal-to-noise ratio (SNR) of the system output, which is the metric usually employed to characterize this physical phenomenon (27). Indeed, the power spectrum of talin folding response under a periodic force perturbation (calculated on the idealized trace to remove the elastic contribution) exhibits a resonant peak at the driving frequency (SI Appendix, Fig. S5). However, we can also characterize stochastic resonance by the shape of the dwell-time distributions, which, as discussed before, include a combination of stochastic and resonant transitions. Hence, these distributions can be modeled as the combination of an exponential distribution (stochastic), and a series of Gaussian peaks (resonant),
| [1] |
where is the stochastic folding rate of talin (exponential contribution), is the period of the driving force, and and are the amplitudes of the stochastic and resonant contributions, respectively. When the frequency is in the responsive regime, we observe several peaks at odd multiples of half of the driving frequency (; Fig. 3B). These contributions correspond to resonant transitions where one or more periods are missed but the transition occurs coherently with the driving signal at a future cycle. Hence, we can quantify statistically the fraction of resonant transitions as the relative weight between the Gaussian distributions and the underlying exponential one. If the distribution is normalized (), .
To demonstrate the response of talin over a broad range of frequencies, we carry out experiments on both the R3 IVVI and R3 WT domains under signals with pN and frequencies ranging from 0.05 Hz to 100 Hz. Fig. 5A shows as a function of the driving frequency . At frequencies above , the resonant peak can be buried in the shape of the exponential distribution, and it is not possible to directly determine its contribution. In such cases, we calculate the dwell-time histogram with logarithmic binning to separate fast timescales and estimate the relative weight from a logarithmic transform of Eq. 1 (SI Appendix, Figs. S6 and S7). Similarly, we use the SNR to characterize stochastic resonance, measured from the power spectrum of the folding/unfolding time series (SI Appendix, Fig. S5). For both R3 IVVI and R3 WT, we observe the same dependence of the SNR on the driving frequency as that obtained using the fraction of resonant transitions, which illustrates the equivalence of both quantities to characterize stochastic resonance (SI Appendix, Fig. S5).
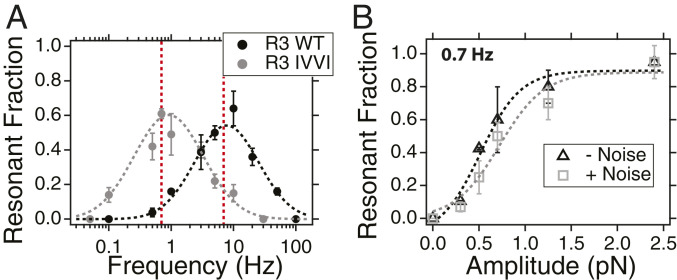
Fig. 5.
Quantitative characterization of the stochastic resonant dynamics by talin. (A) Fraction of resonant transitions for the R3 WT (black) and R3 IVVI (gray) domains. We characterize the level of resonant dynamics as the relative weight of the Gaussian-distributed transitions as measured from fits to the dwell-time distributions. Both domains show an optimal frequency range for signal detection around 10 Hz for R3 WT and 1 Hz for R3 IVVI. Higher frequencies are filtered, while lower ones show a majority of stochastic transitions due to the slow oscillation. Red dotted lines show the theoretical resonance frequency, based on the natural folding rates at the coexistence force. The histograms and fits used to determine are shown in SI Appendix, Figs. S6 and S7. (B) Fraction of resonant transitions as a function of the signal amplitude for a purely sinusoidal perturbation (black) and a sinusoid plus external mechanical noise (SD = 2.8 pN; gray), measured for R3 IVVI at f = 0.7 Hz. Dotted lines are sigmoidal fits to the data. Within statistical significance, there is no difference in talin response under either perturbation, which indicates that stochastic resonance is not affected by the addition of external mechanical noise to the coherent signal.
Fig. 5A shows that talin operates as a mechanical band-pass filter, responding only over a narrow frequency range defined by the mechanical stability of the protein domain. For a bistable system, the optimal resonance frequency can be estimated as (27) (red dotted line), which agrees with the experimental data. This resonance frequency is associated with the height of the intrinsic free energy barrier that separates the folded and unfolded states. Oscillating forces tilt the protein landscape toward the folded and unfolded states cyclically, increasing and decreasing the barrier periodically. If this periodic forcing occurs on a timescale compatible with the thermal-activated transitions, the state switching synchronizes with the perturbation. If the driving frequency is much faster than the intrinsic rates, the system responds only to the average barrier, filtering the oscillation; if the oscillation is too slow, the transitions are much more frequent than the timescale imposed by the external forcing.
Molecular kinetic processes measured with single-molecule techniques can be altered by the tethering system, which occasionally leads to artifactual effects arising from the interplay between the molecule and the dynamics of the pulling apparatus (33). Hence, in order to test whether our observations are an intrinsic property of the talin protein or are influenced by the magnetic probe, we conduct control experiments on R3 IVVI using magnetic beads of a larger size (M-450 with 4.5-m diameter, compared to the standard M-270 with 2.8-m diameter). These beads require a different chemical strategy to anchor our molecular constructs (SI Appendix, Supplementary Methods and Fig. S8). The experiments with the larger M-450 beads show no appreciable difference than those measured with the smaller M-270, despite its significant difference in size; R3 IVVI filters external mechanical noise of large bandwidth and gets optimally entrained under signals with a frequency of 1 Hz (SI Appendix, Figs. S9–S11). Hence, these data suggest that our observations are not altered by the tethering used in our experiments, likely because the diffusion coefficient of the magnetic beads is much higher than that of the elastic and folding response of talin, which, hence, become rate limiting.
All of the experiments in Fig. 5A were done using signals of constant amplitude, pN, which is a moderate perturbation compared with the folding probability. In order to test the limit of signal detection, we measure the response of R3 IVVI at the resonance frequency Hz and under different amplitudes (Fig. 5B). When the force signal spans the whole folding probability range (A 1 pN), the resonant response is saturated, and nearly all transitions are entrained with the periodic forcing. Under signals as small as 0.3 pN, we still observe an effect of resonant transitions of nearly 15%. This amplitude-dependent response is unaffected when the signal is buried in external mechanical noise (gray squares), which indicates that these random mechanical fluctuations do not influence the resonant properties exhibited by talin. This behavior is also reproduced with the R3 WT domain (SI Appendix, Fig. S12), which suggests that both protein domains respond similarly to force signals that combine coherent oscillations and randomly fluctuating components. Although the amplitude of the periodic forcing enhances the level of signal detection, stochastic resonance does not arise simply from the magnitude of the oscillating forcing applied to the system. At an amplitude of pN, where the response at the resonance frequency is saturated, we obtain the same frequency response dependence as that at half that amplitude, indicating that the high selectivity of talin toward the driving force is amplitude independent (SI Appendix, Fig. S13).
Discussion
Our data demonstrate that talin detects force oscillations by undergoing stochastic resonance. While stochastic resonance has been observed in biomolecules with very simple structures, such as RNA or DNA hairpins (31, 34), it is intriguing whether this phenomenon is of generality among any protein under mechanical force, or whether the talin R3 domain has some particularities due to its force-sensing function. Interestingly, the free energy landscape of both R3 IVVI and R3 WT at has a symmetric bistable shape (SI Appendix, Fig. S4), which makes them canonical models for stochastic resonance to occur (27). By contrast, other proteins that have been characterized under force, such as protein L or the titin I91 domain, have very shallow force dependencies of their unfolding rates, which leads to short distances to transition state from the folded state and very asymmetric folding landscapes (35, 36). Hence, it is unclear whether proteins with these characteristics would exhibit entrained folding dynamics, given that their folding landscapes do not fulfill the ideal conditions to undergo stochastic resonance.
Our most surprising result is the absence of a measurable effect of broadband external mechanical noise on the folding dynamics of talin. This is astonishing given that the mechanical noise amplitude of nearly 20 pN peak-to-peak used here dwarfs the 2 pN folding range of talin vastly. The physical basis of the external mechanical noise rejection mechanism is intriguing and contrasts sharply with the exquisite sensitivity shown by talin folding to periodic signals as low as 0.6 pN peak-to-peak. A possible interpretation of the effect of the external mechanical noise would be an effective increase of the temperature along the protein pulling axis; however, protein folding is very sensitive to temperature, and we do not observe any measurable effect on talin folding dynamics (37). Although there is clearly much about the physics of proteins folding under force that remains poorly understood, our experiments are strongly suggestive that stochastic resonance could play an essential role in the biological function of talin as a mechanosensor.
Although initially formulated in the context of nonlinear physics, stochastic resonance has been demonstrated in a broad range of biological systems, with particular emphasis as a sensory mechanism in mechanoreceptors, like the crayfish hair cells (38), the cricket cercal system (39), or the vestibular and auditory system (6, 40). Interestingly, in all of these examples, signal transduction involves the activation of gated ion channels, which convert mechanical perturbations into electrophysiological signals. However, mechanotransduction also involves biochemical signaling, where force stimuli trigger downstream signaling pathways through a complex network of interacting proteins (3–5). In this sense, it remains to be explored whether stochastic resonance could also play a role in mechanotransduction pathways that involve ligand binding to force-bearing proteins instead of gating of mechanosensitive channels.
Mechanical signal transduction relies on the robust and finely tuned response of molecular force sensors. Mechanical information is encoded in both the amplitude of the signal and its time-dependent evolution. Hence, both components must be accurately deciphered and interpreted by cellular force sensors. The auditory system is the paradigm of a mechanotransduction organ (7, 41, 42). The hair cells are responsible for sound detection and transduction into electrical signals. Sound waves travel through the cochlea and induce vibrations on the basilar and tectorial membranes, which have a gradient of thickness and stiffness between the base and the apex. Hence, each frequency resonates at different positions along the membranes, which effectively decomposes the sound wave into its basic components that excite hair cells at different locations along the cochlea. The deflection of the hair bundles triggers the fast opening and closing of gated channels, ultimately converting the complex sound wave into nerve impulses that are interpreted by the brain. This process is highly nonlinear and has an excellent performance in the presence of noise, which, indeed, can induce deflections of the stereocilia over a hundred times larger than those caused by threshold stimuli (28). Hence, stochastic resonance has often been discussed to operate as an adaptive mechanism for enhanced sensitivity in the naturally noisy hearing process (6, 40, 43, 44).
In a similar sense, cells constantly receive and transmit complex force stimuli between cells and their environment, which are converted into biochemical signals that ultimately modulate gene expression. For example, durotaxis is directed by maintained fluctuating forces oscillating at frequencies of 0.1 Hz to 0.5 Hz that cell junctions apply to the extracellular matrix to sample its stiffness (15). Additionally, protrusive podosomes generate oscillating forces that underpin their mechanosensing activity (45, 46). At the protein level, single-cell measurements have demonstrated that talin experiences cyclic fluctuations with an amplitude that necessarily involves folding and unfolding transitions (47). All of this recent evidence suggests the physiological relevance of force oscillations in mechanosensing; however, how cellular force sensors decompose these complex signals in a finely tuned way remains mostly unknown.
Our results show that individual talin R3 domains detect force oscillations in a finely tuned way by shifting their natural stochastic dynamics to a phase-locked folding response over a frequency range that is defined by the mechanical stability of the protein domain. The 13 talin rod domains have a graded mechanical stability and respond to the amplitude of the force signal by unfolding hierarchically upon increasing loads (23, 24). In the context of our findings, this could suggest that each talin bundle responds to complex force signals by undergoing stochastic resonance at different frequencies correlated with its unfolding force; weak domains would respond to fast frequencies while more stable ones would detect slow oscillations. Altogether, the talin rod would resonate at different segments over its extension, providing a mechanism for signal decomposition, analogous to that in the cochlear membranes.
Ultimately, the force on talin is transduced into a biochemical signal by the recruitment of binding proteins, which is regulated by the folding status of talin domains. There are at least 11 vinculin-binding sites buried in the hydrophobic core of the 13 talin bundle domains (16, 18). Hence, vinculin binding is force dependent, and maximal vinculin recruitment requires sufficient load on talin to unfold all of the rod domains. By contrast, other ligands such as RIAM or DLC1 bind to folded talin bundles, and are inhibited by the amplitude of the force borne by talin, often competing antagonistically with vinculin for the same substrate (16, 48). Therefore, the transduction of force stimuli into biochemical signaling by talin is controlled by force-dependent binding constants. Our data demonstrate that the emergence of resonant dynamics shifts the distribution of folding/unfolding transitions from stochastic to deterministic dynamics, which are characterized by regularly spaced transitions. We propose that the change from random to deterministic folding kinetics in entrained talin domains plays a vital role in the binding kinetics of its ligands. If this proves to be correct, entrained folding dynamics may provide for a mechanism to convert complex mechanical signals into Fourier-decomposed biochemical signals along the talin mechanosensor.
Materials and Methods
Single-Molecule Experiments.
All of our experiments were carried out in our custom-made magnetic tape head tweezers setup, detailed in ref. 26. The fluid chambers were built and functionalized as described before (26, 49). Experiments are carried out in Hepes buffer with 10 mM ascorbic acid (pH 7.3). The data are acquired at rates between 1 kHz and 1.6 kHz with our custom-made software, written onto a binary file, and visualized in real time with Igor Pro 8 (Wavemetrics). Single-molecule recordings are smoothed with a Savitzki–Golay algorithm with a 101-point box size (R3 IVVI) or a 31-point box size (R3 WT). Recordings are idealized for analysis with a double-threshold algorithm to detect the occupations on the folded and unfolded states automatically. Further details on experimental analysis are described in SI Appendix.
Protein Expression and Purification.
Polyprotein constructs are engineered using BamHI, BglII, and KpnI restriction sites in pFN18a restriction vector, as described previously (25). Our protein construct contains the R3 IVVI or R3 WT mouse talin domain, followed by eight titin I91 domains, and flanked by an N-terminal HaloTag enzyme and a C-terminal AviTag for biotinylation.
Supplementary Material
Acknowledgments
We thank Dr. Igor Barsukov from University of Liverpool for sharing the R3 IVVI plasmid with us. We thank all of the members of the J.M.F. laboratory for the valuable discussions and comments on the manuscript. This work was supported by NIH Grant R35129962. R.T-R. and A.A-C. acknowledge Fundacion Ramon Areces for financial support.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2004091117/-/DCSupplemental.
Data Availability.
All necessary data are available in the manuscript and SI Appendix
References
- 1.Eyckmans J., Boudou T., Yu X., Chen C. S., A hitchhiker’s guide to mechanobiology. Dev. Cell 21, 35–47 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Roca-Cusachs P., Conte V., Trepat X., Quantifying forces in cell biology. Nat. Cell Biol. 19, 742–751 (2017). [DOI] [PubMed] [Google Scholar]
- 3.Yusko E. C., Asbury C. L., Force is a signal that cells cannot ignore. Mol. Biol. Cell 25, 3717–3725 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Orr A. W., Helmke B. P., Blackman B. R., Schwartz M. A., Mechanisms of mechanotransduction. Dev. Cell 10, 11–20 (2006). [DOI] [PubMed] [Google Scholar]
- 5.Martino F., Perestrelo A. R., Vinarský V., Pagliari S., Forte G., Cellular mechanotransduction: From tension to function. Front. Physiol. 9, 824 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hudspeth A., Making an effort to listen: Mechanical amplification in the ear. Neuron 59, 530–545 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Vollrath M. A., Kwan K. Y., Corey D. P., The micromachinery of mechanotransduction in hair cells. Annu. Rev. Neurosci. 30, 339–365 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tsimring L. S., Noise in biology. Rep. Prog. Phys. 77, 026601 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Engler A. J., Sen S., Sweeney H. L., Discher D. E., Matrix elasticity directs stem cell lineage specification. Cell 126, 677–689 (2006). [DOI] [PubMed] [Google Scholar]
- 10.Chan C. E., Odde D. J., Traction dynamics of filopodia on compliant substrates. Science 322, 1687–1691 (2008). [DOI] [PubMed] [Google Scholar]
- 11.Paszek M. J., et al. , Tensional homeostasis and the malignant phenotype. Canc. Cell 8, 241–254 (2005). [DOI] [PubMed] [Google Scholar]
- 12.Case L. B., Waterman C. M., Integration of actin dynamics and cell adhesion by a three-dimensional, mechanosensitive molecular clutch. Nat. Cell Biol. 17, 955–963 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.del Rio A., et al. , Stretching single talin rod molecules activates vinculin binding. Science 323, 638–641 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sunyer R., et al. , Collective cell durotaxis emerges from long-range intercellular force transmission. Science 353, 1157–1161 (2016). [DOI] [PubMed] [Google Scholar]
- 15.Plotnikov S. V., Pasapera A. M., Sabass B., Waterman C. M., Force fluctuations within focal adhesions mediate ecm-rigidity sensing to guide directed cell migration. Cell 151, 1513–1527 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Goult B. T., et al. , Riam and vinculin binding to talin are mutually exclusive and regulate adhesion assembly and turnover. J. Biol. Chem. 288, 8238–8249 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Burridge K., Chrzanowska-Wodnicka M., Focal adhesions, contractility, and signaling. Annu. Rev. Cell Dev. Biol. 12, 463–519 (1996). [DOI] [PubMed] [Google Scholar]
- 18.Bass M. D., et al. , Further characterization of the interaction between the cytoskeletal proteins talin and vinculin. Biochem. J. 362, 761–768 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yao M., et al. , Mechanical activation of vinculin binding to talin locks talin in an unfolded conformation. Sci. Rep. 4, 4610 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tapia-Rojo R., Alonso-Caballero A., Fernandez J. M., Direct observation of a coil-to-helix contraction triggered by vinculin binding to talin. Sci. Adv. 6, eaaz4707 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fernandez J. M., Li H., Force-clamp spectroscopy monitors the folding trajectory of a single protein. Science 303, 1674–1678 (2004). [DOI] [PubMed] [Google Scholar]
- 22.Rief M., Gautel M., Oesterhelt F., Fernandez J. M., Gaub H. E., Reversible unfolding of individual titin immunoglobulin domains by afm. Science 276, 1109–1112 (1997). [DOI] [PubMed] [Google Scholar]
- 23.Haining A. W. M., von Essen M., Attwood S. J., Hytönen V. P., del Río Hernández A., All subdomains of the talin rod are mechanically vulnerable and may contribute to cellular mechanosensing. ACS Nano 10, 6648–6658 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yao M., et al. , The mechanical response of talin. Nat. Commun. 7, 11966 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bell G., Models for the specific adhesion of cells to cells. Science 200, 618–627 (1978). [DOI] [PubMed] [Google Scholar]
- 26.Tapia-Rojo R., Eckels E. C., Fernández J. M., Ephemeral states in protein folding under force captured with a magnetic tweezers design. Proc. Natl. Acad. Sci. U.S.A. 116, 7873–7878 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gammaitoni L., Hänggi P., Jung P., Marchesoni F., Stochastic resonance. Rev. Mod. Phys. 70, 223–287 (1998). [Google Scholar]
- 28.Wiesenfeld K., Jaramillo F., Minireview of stochastic resonance. Chaos Interdiscip. J. Nonlinear Sci. 8, 539–548 (1998). [DOI] [PubMed] [Google Scholar]
- 29.Benzi R., Parisi G., Sutera A., Vulpiani A., Stochastic resonance in climatic change. Tellus 34, 10–15 (1982). [Google Scholar]
- 30.Jost B. M., Saleh B. E. A., Signal-to-noise ratio improvement by stochastic resonance in a unidirectional photorefractive ring resonator. Opt. Lett. 21, 287–289 (1996). [DOI] [PubMed] [Google Scholar]
- 31.Hayashi K., de Lorenzo S., Manosas M., Huguet J. M., Ritort F., Single-molecule stochastic resonance. Phys. Rev. X 2, 031012 (2012). [Google Scholar]
- 32.Grifoni M., Hänggi P., Coherent and incoherent quantum stochastic resonance. Phys. Rev. Lett. 76, 1611–1614 (1996). [DOI] [PubMed] [Google Scholar]
- 33.Cossio P., Hummer G., Szabo A., On artifacts in single-molecule force spectroscopy. Proc. Natl. Acad. Sci. U.S.A. 112, 14248–14253 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kim W. K., Hyeon C., Sung W., Weak temporal signals can synchronize and accelerate the transition dynamics of biopolymers under tension. Proc. Natl. Acad. Sci. U.S.A. 109, 14410–14415 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Valle-Orero J., et al. , Proteins breaking bad: A free energy perspective. J. Phys. Chem. Lett. 8, 3642–3647 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Yuan G., et al. , Elasticity of the transition state leading to an unexpected mechanical stabilization of titin immunoglobulin domains. Angew. Chem. Int. Ed. 56, 5490–5493 (2017). [DOI] [PubMed] [Google Scholar]
- 37.Popa I., Fernández J. M., Garcia-Manyes S., Direct quantification of the attempt frequency determining the mechanical unfolding of ubiquitin protein. J. Biol. Chem. 286, 31072–31079 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Douglass J. K., Wilkens L., Pantazelou E., Moss F., Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance. Nature 365, 337–340 (1993). [DOI] [PubMed] [Google Scholar]
- 39.Levin J. E., Miller J. P., Broadband neural encoding in the cricket cereal sensory system enhanced by stochastic resonance. Nature 380, 165–168 (1996). [DOI] [PubMed] [Google Scholar]
- 40.Wiesenfeld K., Jaramillo F., Mechanoelectrical transduction assisted by Brownian motion: A role for noise in the auditory system. Nat. Neurosci. 1, 384–388 (1998). [DOI] [PubMed] [Google Scholar]
- 41.Gillespie P. G., Müller U., Mechanotransduction by hair cells: Models, molecules, and mechanisms. Cell 139, 33–44 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hudspeth A. J., Integrating the active process of hair cells with cochlear function. Nat. Rev. Neurosci. 15, 600–614 (2014). [DOI] [PubMed] [Google Scholar]
- 43.Roongthumskul Y., Shlomovitz R., Bruinsma R., Bozovic D., Phase slips in oscillatory hair bundles. Phys. Rev. Lett. 110, 148103 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Nadrowski B., Martin P., Jülicher F., Active hair-bundle motility harnesses noise to operate near an optimum of mechanosensitivity. Proc. Natl. Acad. Sci. U.S.A. 101, 12195–12200 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Labernadie A., et al. , Protrusion force microscopy reveals oscillatory force generation and mechanosensing activity of human macrophage podosomes. Nat. Commun. 5, 5343 (2014). [DOI] [PubMed] [Google Scholar]
- 46.Kronenberg N. M., et al. , Long-term imaging of cellular forces with high precision by elastic resonator interference stress microscopy. Nat. Cell Biol. 19, 864–872 (2017). [DOI] [PubMed] [Google Scholar]
- 47.Margadant F., et al. , Mechanotransduction in vivo by repeated talin stretch-relaxation events depends upon vinculin. PLoS Biol. 9, e1001223 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Haining A. W. M., et al. , Mechanotransduction in talin through the interaction of the R8 domain with DLC1. PLoS Biol. 16, e2005599 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Popa I., et al. , A halotag anchored ruler for week-long studies of protein dynamics. J. Am. Chem. Soc. 138, 10546–10553 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All necessary data are available in the manuscript and SI Appendix