Abstract
We present a systematic evaluation of state-of-the-art algorithms for inferring gene regulatory networks (GRNs) from single-cell transcriptional data. As the ground truth for assessing accuracy, we use synthetic networks with predictable trajectories, literature-curated Boolean models, and diverse transcriptional regulatory networks. We develop a strategy to simulate single-cell transcriptional data from synthetic and Boolean networks that avoids pitfalls of previously-used methods. Furthermore, we collect networks from multiple experimental single-cell RNA-seq datasets. We develop an evaluation framework called BEELINE. We find that the AUPRC and early precision of the algorithms are moderate. The methods are better in recovering interactions in synthetic networks than Boolean models. The algorithms with the best early precision values for Boolean models also perform well on experimental datasets. Techniques that do not require pseudotime-ordered cells are generally more accurate. Based on these results, we present recommendations to end users. BEELINE will aid the development of GRN inference algorithms.
Single-cell RNA-sequencing technology has made it possible to trace cellular lineages during differentiation and to identify new cell types1,2. A central question that arises now is whether we can discover the gene regulatory networks (GRNs) that control cellular differentiation and drive transitions from one cell type to another. In such a GRN, each edge connects a transcription factor (TF) to a gene it regulates. Ideally, the edge is directed from the TF to the target gene, represents direct rather than indirect regulation, and corresponds to activation or inhibition.
Single-cell expression data are especially promising for computing GRNs because, unlike bulk transcriptomic data, they do not obscure biological signals by averaging over all the cells in a sample. However, these data have features that pose significant difficulties, e.g., substantial cellular heterogeneity3, cell-to-cell variation in sequencing depth, the high sparsity caused by dropouts4, and cell-cycle-related effects5. Despite these challenges, over a dozen methods have been developed or used to infer GRNs from single-cell data6–19. An experimentalist seeking to analyze a new dataset faces a daunting task in selecting an appropriate inference method since there are no widely-accepted ground truth datasets for assessing algorithm accuracy and the criteria for evaluation and comparison of methods are varied.
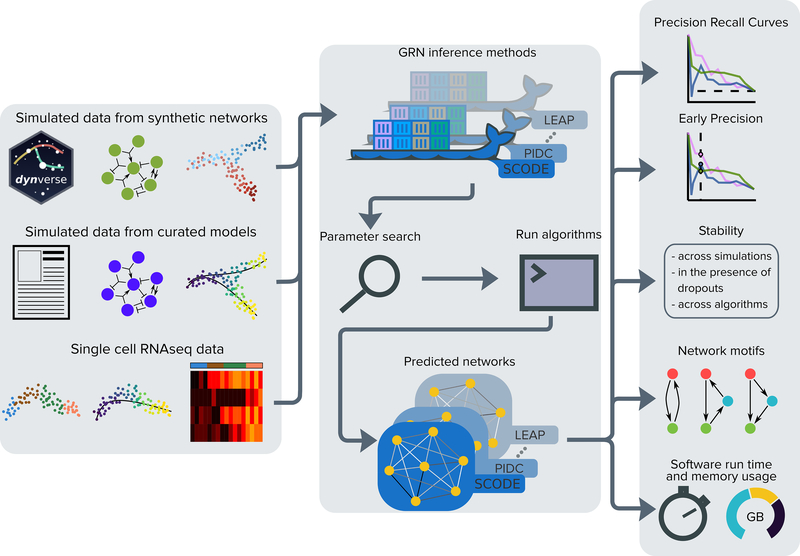
We have developed BEELINE, a comprehensive evaluation framework to assess the accuracy, robustness, and efficiency of GRN inference techniques for single-cell gene expression data based on well-defined benchmark datasets (Figure 1). BEELINE incorporates 12 diverse GRN inference algorithms. It provides an easy-to-use and uniform interface to each method in the form of a Docker image. BEELINE implements several measures for estimating and comparing the accuracy, stability, and efficiency of these algorithms. Thus, BEELINE facilitates reproducible, rigorous, and extensible evaluations of GRN inference methods for single-cell gene expression data.
Figure 1:
An overview of the BEELINE evaluation framework. We apply GRN inference algorithms to three types of data: datasets from synthetic networks, datasets from curated Boolean models from the literature, and experimental single-cell transcriptional measurements. We process each dataset through a uniform pipeline: pre-processing, Docker containers for 12 GRN inference algorithms, parameter estimation, post-processing, and evaluation. We compare algorithms based on accuracy (AUPRC and early precision), stability of results (across simulations, in the presence of dropouts, and across algorithms), analysis of network motifs, and scalability.
Results
Overview of Algorithms
We surveyed the literature and bioRxiv for papers that either published a new GRN inference algorithm or used an existing approach. We ignored methods that did not assign weights or ranks to the interactions, required additional datasets or supervision, or sought to discover cell-type specific networks. We selected 12 algorithms using these criteria (Online Methods).
We used BEELINE to evaluate these approaches on over 400 simulated datasets (across six synthetic networks and four curated Boolean models) and five experimental human or mouse single-cell RNA-Seq datasets. Since eight algorithms require pseudotime-ordered cells, we used datasets (both simulated and real) that focus on cell differentiation and development, processes in which there is a meaningful temporal progression of cell states. We did not study GRNs relevant to other biological processes, e.g., changes in disease states or differences among cell types.
Datasets from Synthetic Networks
Our motivations for using synthetic networks were two-fold. First, we wanted to use a known GRN that could serve as the ground truth. Second, we desired to create in silico single-cell gene expression datasets that were isolated from any limitations of pseudotime inference algorithms. Therefore, we started with six synthetic networks (Supplementary Figure 1(a), Supplementary Table 1). Simulating these networks should produce a variety of different trajectories seen in differentiating and developing cells20. Several recent studies on GRN inference14,16,17,21,22 have used GeneNetWeaver23 to create in silico single-cell gene expression datasets. However, when we simulated the six synthetic networks using GeneNetWeaver (Online Methods), we observed no discernible trajectories in the two-dimensional projections of these data (Supplementary Figure 1(d)).
We therefore used our BoolODE approach (Online Methods) to simulate these networks. For each gene in a GRN, BoolODE requires a Boolean function that specifies how that gene’s regulators combine to control its state. We represent each Boolean function as a truth table, which we convert into a non-linear ordinary differential equation (ODE). This approach provides a reliable method to capture the logical relationships among the regulators precisely in the components of the ODE. We add noise terms to make the equation stochastic20,24.
For each network, we applied BoolODE by sampling ODE parameters ten times and generating 5,000 simulations per parameter set (Online Methods). We created five datasets per parameter set, one each with 100, 200, 500, 2,000, and 5,000 cells by sampling one cell per simulation, to obtain 50 different expression datasets. Analyzing the two-dimensional projections of these simulations reassured us that BoolODE was successful in correctly simulating the network models (Supplementary Figures 1(b) and 1(c), Supplementary Note 1.1).
Setting each network as the ground truth, we executed the 12 algorithms on every one of the 50 simulated datasets. For those GRN inference methods that required time information, we provided the simulation time at which we sampled each cell. For the Bifurcating, Bifurcating Converging, and Trifurcating networks, we ran the algorithms that need time information on each trajectory individually and combined the outputs (Online Methods). Six algorithms required one or more parameters to be specified. We performed a parameter sweep to determine the values which gave the highest median AUPRC (Supplementary Note 1.2).
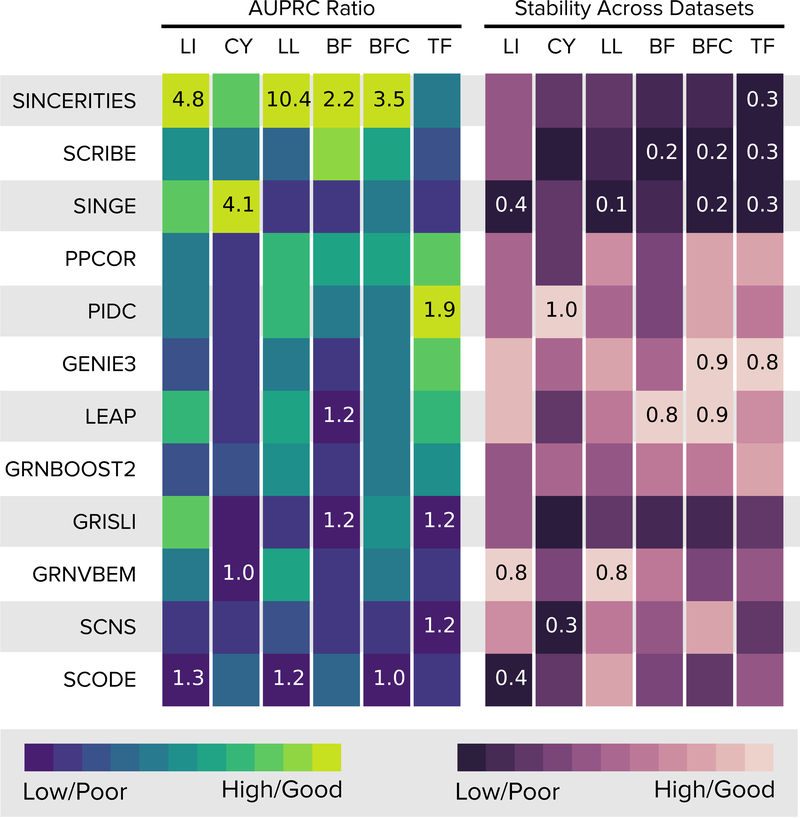
For each network-algorithm pair, Figure 2 displays the median AUPRC ratio (the AUPRC divided by that of a random predictor). Supplementary Figures 2 and 3 show the box plots of AUPRC and AUROC values. The methods performed best for the Linear network: 10 out of 12 algorithms had a median AUPRC ratio greater than 2.0. Seven methods had a median AUPRC ratio greater than 5.0 for the Linear Long Network. The Cycle, Bifurcating Converging, Bifurcating, and Trifurcating networks were progressively harder to infer, with no algorithm achieving an AUPRC ratio of two or more on the last network. SINCERITIES obtained the highest median AUPRC ratio for four out of the six networks. SINGE had the highest median AUPRC ratio for Cycle and PIDC for Trifurcating.
Figure 2:
Summary of results for datasets from synthetic networks. The first six columns display the median AUPRC ratios for the 20 datasets with 2,000 and 5,000 cells, with algorithms (rows) ordered in decreasing order of the median of the median per-network AUPRC ratios. The next set of six columns display the median stability scores across multiple datasets (Online Methods). For each network, the color in each cell is proportional to the corresponding value (scaled between 0 and 1). We display the highest and lowest values for each network inside the corresponding cells. Abbreviations: LI: Linear, CY: Cycle, LL: Linear Long, BF: Bifurcating, BFC: Bifurcating Converging, TF: Trifurcating.
We examined the effect of the number of cells on AUPRC by comparing the values for 100, 200, 500, and 2000 cells to those for 5000 cells (Supplementary Note 1.3). As the number of cells increased from 100 to 500, the number of algorithms with significantly lower AUPRC values in comparison to 5,000 cells decreased from seven to four. The number of cells had no significant effect on five algorithms (GENIE3, GRNVBEM, LEAP, SCNS, and SCODE).
To examine the stability of the results, we considered the GRNs formed by the k edges with the highest ranks, with k set to the number of edges in each synthetic network, computed the Jaccard indices of all pairs of GRNs, and recorded the medians of these values (Figure 2, Online Methods). While SINCERITIES, SINGE, and SCRIBE had the three highest median-of-median AUPRC ratios, the networks they predicted were relatively less stable (median Jaccard index between 0.28 and 0.35). PPCOR and PIDC, the other two methods in the top five, had higher median Jaccard indices of 0.62 each.
We simulated the inferred GRNs to see if they had the same number of steady states as the ground truth networks. Apart from the linear network, we found that more than 60% of the GRNs yielded more steady states than in the ground truth (Supplementary Note 1.4). For networks with multiple steady states, there was no clear benefit to computing a single GRN after combining all trajectories over merging the GRNs inferred for each trajectory (Supplementary Note 1.5).
Datasets from Curated Models
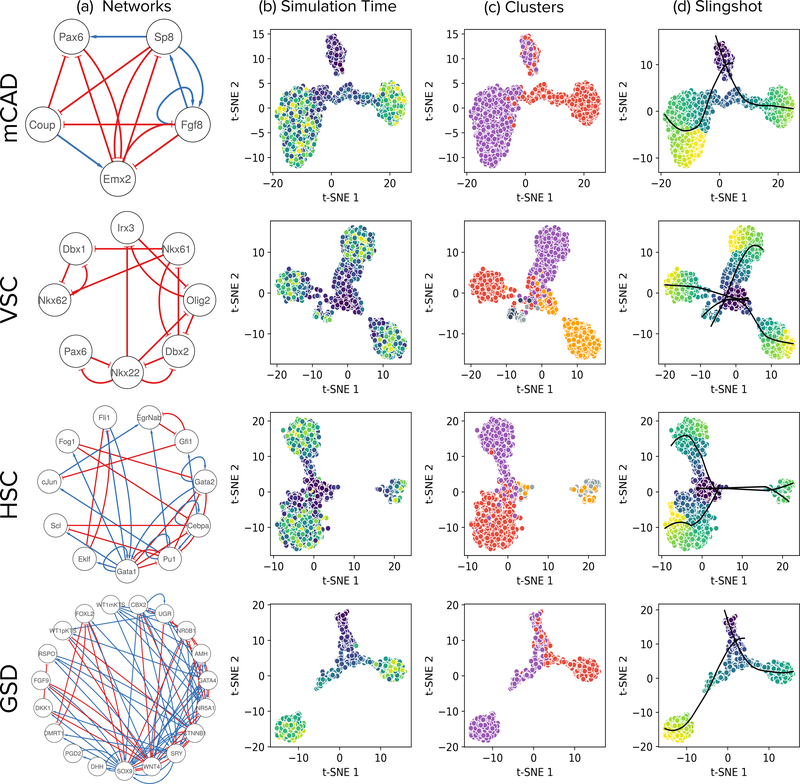
Dense sub-networks of large-scale gene regulatory networks that have been used to generate simulated datasets of single-cell gene expression14,16,17,21,22 may not capture the complex regulation in any specific developmental process. To avoid this pitfall, we selected four published Boolean models: Mammalian Cortical Area Development (mCAD)25, Ventral Spinal Cord Development (VSC)26, Hematopoietic Stem Cell Differentiation (HSC) 27, and Gonadal Sex Determination (GSD)28 (Figure 3, Supplementary Table 2).
Figure 3:
Visualization of t-SNE projections of simulations reveals trajectories leading to steady states that correspond to those of the curated models. Each row in the figure corresponds to a model, indicated on the left: Mammalian Cortical Area Development (mCAD), Ventral Spinal Cord Development (VSC), Hematopoietic Stem Cell Differentiation (HSC), and Gonadal Sex Determination (GSD). (a) Network diagrams of the models. (b) t-SNE visualizations of 2,000 cells sampled from BoolODE output. The color of each point indicates the corresponding simulation time. (c) Each color corresponds to a different subset of cells obtained by using k-means clustering of simulations, with k set to the number of steady states reported in the relevant publication (two for mCAD, five for VSC, four for HSC, and two for GSD). (d) Pseudotimes and principal curves (black) computed by Slingshot showing correspondence with simulation times in (b) and clusters in (c), respectively. Colors of simulation time and pseudotime: blue for early, green for intermediate, and yellow for later.
We confirmed that the BoolODE-simulated datasets for each Boolean model (a) captured the same number of steady states as in the model (Figure 3(b)) and (b) matched the unique gene expression pattern that characterized each steady state of that model, as reported in the corresponding publication (Supplementary Note 2.1). Encouraged by these results, we used BoolODE to create 10 different datasets with 2,000 cells for each model. For each dataset, we generated one version with a dropout rate of q = 50 and another with a rate of q = 70 (Online Methods)14. We computed pseudotimes using Slingshot29 for each dataset and provided these values to the algorithms, to mimic a real analysis pipeline. We performed a parameter sweep and selected the values which gave the highest median AUPRC for each model (Supplementary Note 2.2). We then ran each of the 12 algorithms on each of the 120 datasets (30 per model).
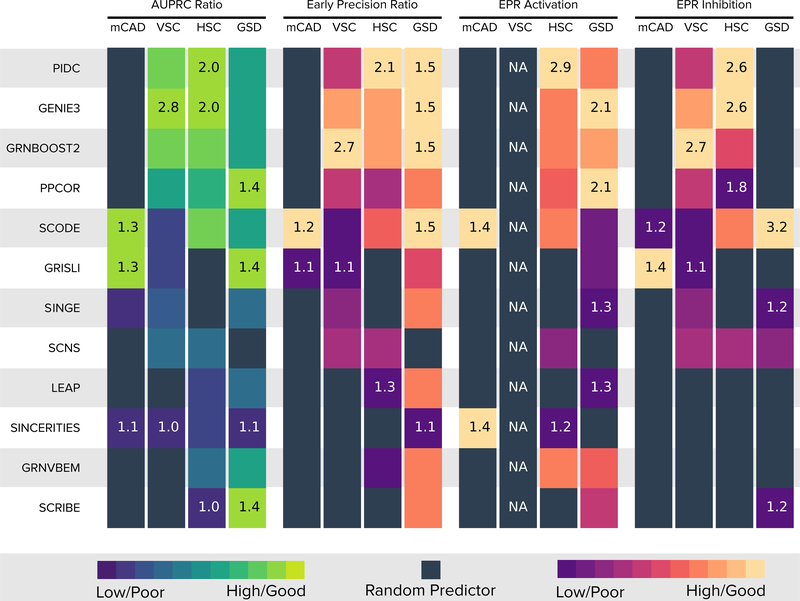
Figure 4 summarizes our findings for the datasets without dropouts. Only four methods (GRISLI, SCODE, SINGE and SINCERITIES) had a median AUPRC ratio greater than 1 for the mCAD model. The reason may be the high density of the underlying network (Supplementary Table 2). For the VSC model, which only has inhibitory edges, three methods (PIDC, GRNBoost2, and GENIE3) had an AUPRC ratio greater than 2.5. These three methods also had an AUPRC ratio close to 2.0 for the HSC model. PPCOR, GRISLI, and SCRIBE tied for the highest median AUPRC ratio of 1.4 for the GSD model. Overall, GENIE3, GRNBoost2, and PIDC had among the highest median AUPRC ratios for two out of the four models. Surprisingly, SINCERITIES, SCRIBE, and SINGE, which were the best algorithms according to the AUPRC ratios for the datasets from synthetic networks, had a close to random median AUPRC ratio for all four curated models. We address this trend in “Discussion.”.
Figure 4:
Summary of results for 10 datasets without dropouts from curated models. Rows corresponds to algorithms ordered by decreasing median of the per-model median AUPRC ratios. The four sets of four columns each display the median AUPRC ratios, median early precision ratio (EPR), median EPR for activating edges, and median EPR for inhibitory edges. For each model, the color in each cell is proportional to the corresponding value (scaled between 0 and 1, ignoring values that are less than that of a random predictor, shown as black squares). We display the highest and lowest values for each model inside the corresponding cells.
Supplementary Figures 4 and 5 show distributions of the AUPRC and AUROC values for all dropout rates. To study the effect of dropouts, for each algorithm, we compared the distributions of AUPRC scores across all Boolean models between q = 0 and q = 50 and between q = 0 and q = 70. Four and seven GRN inference methods had a statistically significant difference in AUPRC values for the 0–50 and the 0–70 comparison, respectively (Supplementary Note 2.3). The four algorithms that were unaffected by dropout rates (GRNVBEM, LEAP, SCRIBE, SINCERITIES) had worse-than-random AUPRC values on the mCAD and VSC datasets.
Next, we studied the early precision and early precision ratio (EPR) values of the top-k predictions (Online Methods) for each of the four models. In at least one of the four models, 11 algorithms had a median EPR less than or close to one, i.e., similar to a random predictor (black squares in Figure 4). In the 29 cases when the median EPR was at least one, it was 1.5 or larger only 16 times. The mCAD model had the smallest number of algorithms (two, GRISLI and SCODE) with median EPR larger than one. For datasets with dropouts, we did not see any clear trends in terms of smaller or larger early precision values compared to the dropout-free results (Supplementary Figure 6).
We also investigated if the GRN inference methods were better at recovering activating edges or inhibitory edges. The mCAD model was again an outlier for EPR for activating and inhibitory edges, with only SCODE having slightly better-than-random scores for both. Overall, the GRN inference algorithms performed poorly when it comes to recovering the true edges within the top-k predictions.
We examined which algorithms produced similar reconstructions. For every model, the three best performing methods (PIDC, GENIE3, and GRNBoost2) had similar outputs (Supplementary Note 2.4). In addition, LEAP and PPCOR were similar to the first three methods for the mCAD and GSD models. Pairwise similarities were poor for the other algorithms.
The GRNs formed by the top-k edges contained a higher than expected number of feed-forward loops and lower than expected feedback loops and mutual interactions (Supplementary Note 2.5). Further, a very large fraction of false positives in the top-k edges corresponded to paths of length two in the ground truth networks (Supplementary Note 2.6). This tendency to predict “indirect” interactions could be the reason for the low EPR values.
Experimental Single-Cell RNA-Seq Datasets
We selected five experimental single-cell RNA-Seq datasets, two in human and three in mouse cells, comprising seven cell types (Online Methods and Supplementary Table 3). We collected three different types of ground truth networks: cell-type-specific ChIP-Seq, non-specific ChIP-Seq, and functional interaction networks (Online Methods and Supplementary Table 4).
To measure the running time of the algorithms, we selected three cell types, namely, hHEP, hESC and mHSC-E, which contained different numbers of cells. We executed the algorithms on multiple subsets of highly-varying genes in each dataset. For 5,000 genes, the running times ranged from minutes (PPCOR, LEAP, SINCERITIES, SCODE) to hours (GRNBOOST2) to nearly a day (GENIE3, PIDC). GRNVBEM, SCRIBE, and SINGE were the slowest methods taking a few hours to nearly a day for 1,000 genes (Supplementary Figure 7). There was little to no variation in the running times of any method with increasing number of cells. Since the implementations of GENIE3, GRNBoost2, and SINGE are multithreaded, their wall-clock times can be lowered by a factor proportional to the number of threads available. Most of the algorithms did not require more than 4GB of RAM for up to 2,000 genes.
For further analysis, we selected the five algorithms with the highest median AUPRC in each of the earlier two datasets: SINCERITIES, SCRIBE, SINGE, PPCOR, and PIDC for synthetic networks and PIDC, GENIE3, GRNBoost2, PPCOR, and SCODE for Boolean models; PIDC and PPCOR were in both sets. We did not retain SINGE and SCRIBE because of the time taken for parameter search.
For each RNA-Seq dataset, we created four subsets of genes containing all the significantly-varying TFs and either (a) the 500 or (b) 1,000 most varying genes and only the (c) 500 or (d) 1,000 most varying genes. We intersected each ground truth network with each set of genes.
We compared the algorithms based on the EPR, reasoning that predicted interactions of higher confidence will be more interesting to experimentalists. We used the top-k networks, setting k equal to the number of edges in the corresponding reduced ground truth dataset. We performed parameter search to optimize the EPR (Supplementary Note 3.1).
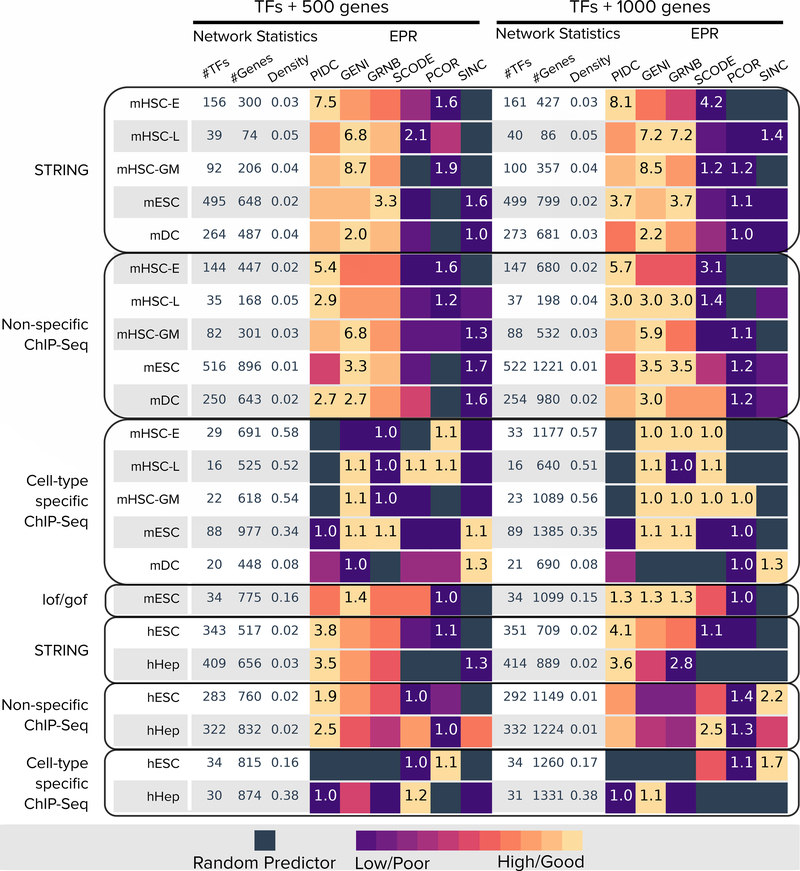
In general, the algorithms achieved lower EPR values in networks with higher densities, i.e., the cell-type specific ChIP-Seq networks (Figure 5 and Supplementary Figure 8). While the STRING and non-cell-type specific ChIP-Seq networks had similar densities, the GRN methods typically achieved a higher EPR for the former. STRING networks contain both physical and functional (indirect) interactions. The higher EPR ratios obtained for STRING networks compared to ChIP-Seq networks of similar density suggested that a substantial fraction of the edges in the inferred GRNs were indirect, reinforcing our findings for Boolean models. The densities of the cell-type specific ChIP-Seq networks varied considerably (from 0.08 to 0.58). The EPR of most of the methods on these networks was close to 1, i.e., similar to a random predictor, with no EPR value exceeding 1.5.
Figure 5:
Summary of EPR results for experimental single-cell RNA-seq datasets. The left half of the figure (TFs+500 genes) shows results for datasets composed of all significantly-varying TFs and the 500 most-varying genes. Each row corresponds to one scRNA-seq dataset. The first three columns report network statistics. The next six columns report EPR values. The right half (TFs+1000 genes) shows results for all significantly-varying TFs and the 1000 most-varying genes. In both sections, algorithms are sorted by median EPR across the datasets (rows) for the TFs+500 gene set. For each dataset, the color in each cell is proportional to the corresponding value scaled between 0 and 1 (ignoring values that are less than that of a random predictor, which are shown as black squares). We display the highest and lowest values for each dataset inside the corresponding cells. Abbreviations: GENI: GENIE3, GRNB: GRNBoost2, PCOR: PPCOR, SINC: SINCERIETIES.
GENIE3, PIDC, and GRNBoost2 were the three methods with the highest EPR values for experimental datasets (Figure 5 and Supplementary Figure 8), just as they were for curated models (Figure 4). These methods also performed equally well for AUPRC ratios (Supplementary Figures 9 and 10). When we computed modules in the GRNs output by these methods, we found that they had a good concordance with clusters determined directly from the gene expression data (Supplementary Note 3.2). PPCOR, which was consistently in the top-four methods for both synthetic networks and curated models, had only a slightly better than random EPR across all experimental datasets. PPCOR’s AUPRC decreased moderately as we increased dropouts in datasets from curated models (Supplementary Figure 4). We speculate that dropouts in experimental single-cell RNA-Seq datasets had a severe effect on PPCOR.
To examine the effect of the number of genes, as well as including all significantly varying TFs, we evaluated the three top performing methods, PIDC, GENIE3, and GRNBoost2, on the non-specific ChIP-Seq and STRING networks. We found that the median EPR had a statistically-significant improvement when we included all significantly varying TFs in the analysis (Supplementary Note 3.3). However, the addition of highly varying genes (500 vs. 1,000) did not lead to a significant improvement in EPR values. The AUPRC ratio did not vary with the number of genes.
Almost every algorithm produced nearly identical outputs when we ran it on the same dataset multiple times (Supplementary Note 3.4). However, for the same dataset, the results varied substantially from one algorithm to another (Supplementary Note 3.5), in contrast to curated models where the top performing methods yielded similar results (Supplementary Note 2.4). Moreover, ensembles of the algorithm outputs did not perform systematically better than the best method for each dataset (Supplementary Note 3.5). This result stands in contrast to the success of ensembles in inferring GRNs from bulk transcriptional data30.
Discussion
We have presented BEELINE, a framework for benchmarking algorithms that infer GRNs from single-cell gene expression data. Figure 6 summarizes the properties of the algorithms and the insights from this study. Despite considerable variation in algorithm performance across the different types of datasets, we noted a few trends. The synthetic networks were easier to recover than the curated models. The reason may be that the synthetic networks have simple and well-defined trajectories. For curated models, each of which has multiple trajectories, we found that methods that do not require pseudotime information (GENIE3, GRNBoost2, and PIDC) performed the best. Methods that performed well for Boolean models also inferred GRNs of good accuracy for experimental datasets. Nevertheless, the overall performance of these approaches was less than ideal.
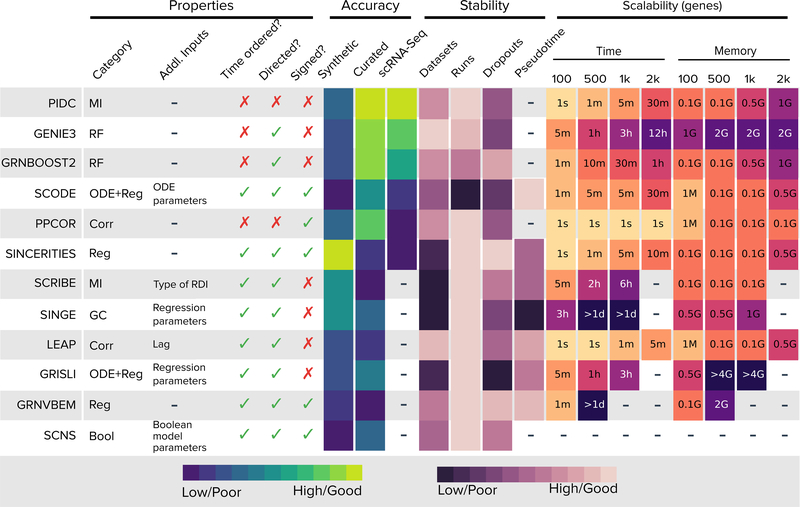
Figure 6:
Summary of properties of GRN inference algorithms and results obtained from BEELINE. Each row corresponds to one of the algorithms included in our evaluation. The first six columns display algorithm methodology, required additional inputs, whether the method needs cells to be time-ordered, and whether the inferred edges are directed and signed. The next three columns summarize the results in Figures 2, 4, and 5. The next four columns present results for different types of stability. The final set of columns contain the running time and memory usage. For the “Pseudotime” column, we only considered the seven methods that required these values, ignoring SCNS due to its long execution time. See “Methods” for details on how we generated this figure. Abbreviations: MI: Mutual Information, RF: Random Forest, Corr: Correlation, Reg: Regression, GC: Granger Causality, Bool: Boolean Model.
A surprising trend was that the best performing algorithms for datasets from synthetic networks (SINCERITIES, SCRIBE, and SINGE, Figure 2) had poor results on datasets from curated models (Figure 4); SINCERITIES had close to or worse-than-random EPRs on experimental datasets as well (Figure 5). When we inferred GRNs for synthetic networks using shuffled pseudotimes (Online Methods), we observed a general decrease in performance with an increase in the size of the window over which we shuffled the pseudotime values, with the effect being most pronounced for SINCERITIES, SCRIBE, and SINGE (“Pseudotime” in Figure 6 and Supplementary Figure 11). This analysis suggests that these algorithms may be sensitive to accurate pseudotime imputation.
Based on these observations, we make specific recommendations for users seeking to apply these methods.
PIDC, GENIE3, and GRNBoost2 are the methods of choice, since they were leading and consistent performers for curated models and experimental datasets in terms of accuracy.
GENIE3 and PIDC also had better stability across multiple runs whereas GRNBoost2 was less sensitive to the presence of dropouts. Since these methods do not require pseudotime-ordered cells, they are immune to any errors in pseudotime computation. As the quality of pseudotime inference improves, SINCERITIES may become a good choice, especially since it is quite stable across multiple runs and in the presence of dropouts.
Since GRNBoost2 and GENIE3 have multithreaded implementations8, they are as efficient as PIDC for 2,000 genes or less.
Our results suggest that adding more highly-varying genes (1,000 rather than 500) and/or considering all significantly-varying TFs contribute to significant improvements in the EPR of the best-performing algorithms. However, there is no effect on AUPRC. A recent best-practice guide31 has suggested using 1,000–5,000 highly-variable genes for single-cell RNA-Seq analyses such as clustering and differential expression. However, GRN algorithms may require significant computation time beyond 1,000 genes. Hence, the strategy for selection of genes merits further analysis.
Inference of GRNs has been an active area of research for more than 20 years. Our evaluation shows that GRN inference remains a challenging problem. One possible reason is that single-cell RNA-Seq techniques may not still provide sufficient resolution and variation in expression for the reliable inference of GRNs despite rapid advances both in the number of cells that can be measured and the depth of coverage32. There may also be inherent shortcomings to the assumption that statistical relationships between expression patterns correspond to regulatory interactions. In this context, we observed that false positive edges form feedforward loops when added to ground truth networks (Supplementary Note 2.5). To avoid such indirect interactions, it may be important to integrate additional types of data such as known transcription factor binding sites or ChIP-Seq measurements15. Finally, a target gene’s expression level may change even if the regulating TF does not vary in abundance. Recent approaches that interrogate single cells along multiple modalities33,34 may be important for the next generation of GRN inference algorithms.
BoolODE was a critical component of our analysis. We developed BoolODE after noting that reported AUROC or precision at early recall values for GRN algorithms were often close to that of a random predictor6,10,11,13,15, as we also observed. Therefore, we reasoned that it would be valuable to the community to benchmark GRN algorithms by applying them to accurate simulations of Boolean models with predictable trajectories. BoolODE is successful at this task and promises to be useful as an independent tool.
As single-cell experiments become more complex, cellular trajectories will also be more intricate, perhaps involving multiple stages of bifurcation and/or cycling. A key challenge that lies ahead is accurately computing the underlying GRNs. We hope that scientists will use BEELINE in conjunction with BoolODE as they develop new approaches for GRN inference.
Online Methods
Regulatory Network Inference Algorithms
We briefly describe each algorithm we have included in this evaluation. We have ordered the methods chronologically by year and month of publication. Every software package had an open source license, other than GRNVBEM and GRISLI, which did not have any license.
GENIE3 (GEne Network Inference with Ensemble of trees)35 Developed originally for bulk transcriptional data, GENIE3 computes the regulatory network for each gene independently. It uses tree-based ensemble methods such as Random Forests to predict the expression profile of each target gene from profiles of all the other genes. The weight of an interaction comes from the importance of an input gene in the predictor for a target gene’s expression pattern. Aggregating these weighted interactions over all the genes yields the regulatory network. This method was the top performer in the DREAM4 In Silico network challenge (multifactorial subchallenge).
PPCOR7 This R package computes the partial and semi-partial correlation coefficients for every pair of variables (genes, in our case) with respect to all the other variables. It also computes a p-value for each correlation. We use this package to compute the partial correlation coefficients. Since these values are symmetric, this method yields an undirected regulatory network. We use the sign of the correlation, which is bounded between −1 and 1, to signify whether an interaction is inhibitory (negative) or activating (positive).
LEAP (Lag-based Expression Association for Pseudotime-series)12 Starting with pseudotime-ordered data, LEAP calculates the Pearson’s correlation of normalized mapped-read counts over temporal windows of a fixed size with different lags. The score recorded for a pair of genes is the maximum Pearson’s correlation over all the values of lag that the method considers. The software includes a permutation test to estimate false discovery rates. Since the correlation computed is not symmetric, this method can output directed networks.
SCODE13 This method uses linear Ordinary Differential Equations (ODEs) to represent how a regulatory network results in observed gene expression dynamics. SCODE relies on a specific relational expression that can be estimated efficiently using linear regression. In combination with dimension reduction, this approach leads to a considerable reduction in the time complexity of the algorithm.
PIDC (Partial Information Decomposition and Context)14 This method uses concepts from information theory. For every pair of genes x and y, given a third gene z, the method partitions the pairwise mutual information between x and y into a redundant and a unique component. It computes the ratio between the unique component and the mutual information. The sum of this ratio over all other genes z is the proportional unique contribution (PUC) between x and y. The method then uses per-gene thresholds to identify the most important interactions for each gene. The resulting network is undirected since the PUC is symmetric.
SINCERITIES (SINgle CEll Regularized Inference using TIme-stamped Expression profileS)16 Given time-stamped transcriptional data, this method computes temporal changes in each gene’s expression through the distance of the marginal distributions between two consecutive time points using the Kolmogorov–Smirnov (KS) statistic. To infer regulatory connections between TFs and target genes, the approach uses Granger causality, i.e., it uses the changes in the gene expression of TFs in one time window to predict how the expression distributions of target genes shift in the next time window. The authors formulate inference as a ridge regression problem. They infer the signs of the edges using partial correlation analyses.
SCNS (Single Cell Network Synthesis)18 This method takes single-cell gene expression data taken over a time course as input and computes logical rules (Boolean formulae) that drive the progression and transformation from initial cell states to later cell states. By design, the resulting logical model facilitates the prediction of the effect of gene perturbations (e.g., knockout or overexpression) on specific lineages.
GRNVBEM (GRN Variational Bayesian Expectation-Maximization)17 This approach infers a Bayesian network representing the gene regulatory interactions. It uses a first-order autoregressive model to estimate the fold change of a gene at a specific time as a linear combination of the expression of the gene’s regulators in the Bayesian network at the previous time point. It infers the gene regulatory network within a variational Bayesian framework. This method can associate signs with its directed edges.
SCRIBE19 Similar to PIDC, this approach uses ideas from information theory. The relevant concept here is conditioned Restricted Directed Information (cRDI), which measures the mutual information between the past state (expression values) of a regulator and the current state of a target gene conditioned on the state of the target at the previous time point. To obtain efficiency for large datasets, the authors use an unconditioned version called RDI, followed by the Context Likelihood of Relatedness (CLR) algorithm36 to remove edges that correspond to indirect effects. We used this strategy for experimental single-cell RNA-seq datasets.
GRNBoost28 GRNBoost2 is a fast alternative for GENIE3, especially suited for datasets with tens of thousands of observations. Like GENIE3, GRNBoost2 trains a regression model to select the most important regulators for each gene in the dataset. GRNBoost2 achieves its efficiency by using stochastic Gradient Boosting Machine regression with early-stopping regularization to infer the network.
GRISLI (Gene Regulation Inference for Single-cell with LInear differential equations and velocity inference)9 Like SCODE, this approach uses a linear ODE-based formalism. GRISLI estimates the parameters of the model using different ideas. Taking either the experimental time of the cells or estimated pseudotime as input, it first estimates the velocity of each cell, i.e., how each gene’s expression value changes as each cell undergoes a dynamical process37. It then computes the structure of the underlying gene regulatory network by solving a sparse regression problem that relates the gene expression and velocity profiles of each cell.
SINGE (Single-cell Inference of Networks using Granger Ensembles)10 The authors observe that while many gene inference algorithms start by computing a pseudotime value for each cell, the distribution of cells along the underlying dynamical process may not be uniform. To address this limitation, SINGE uses kernel-based Granger Causality regression to alleviate irregularities in pseudotime values. SINGE performs multiple regressions, one for each set of input parameters, and aggregates the resulting predictions using a modified Borda method.
In summary, most algorithms developed explicitly for single-cell transcriptomic data required the cells to be ordered by pseudotime in the input, with PIDC14 being an exception. These methods ideally require datasets corresponding to linear trajectories; some techniques recommend that data with branched trajectories be split into multiple linear ones before input10,19. In contrast, methods that had originally been developed for bulk transcriptional data did not impose this requirement7,35. Almost all the methods we included output directed networks with exceptions being PPCOR and PIDC7,14. Only five methods output signed networks, i.e., they indicated whether each interaction was activating or inhibitory7,13,16–18. A number of methods inferred each pairwise interaction independently of the others, sometimes conditioned on the other genes7,12,14,19. Several other methods computed all the regulators of a gene simultaneously but solved the problem independently for each gene8–10,13,16,18,35.
Other methods
We now discuss other papers on this topic and our rationale for not including them in the comparison. We did not consider a method if it was supervised38 or used additional information, e.g., a database of transcription factors and their targets15 or a lineage tree39. We did not include methods that output a single GRN without any edge weights21,24, since any such approach would yield just a single point on a precision-recall curve. Other than SCNS, we did not consider methods that output Boolean networks21,39,40.
BoolODE: Converting Boolean Models to Ordinary Differential Equations
GeneNetWeaver23,41,42 is a widely used method to simulate bulk transcriptomic data from GRNs. GeneNetWeaver has also been applied in single-cell analysis14,16,17,21,22 but has limitations, as we have demonstrated (Supplementary Figure 1). To deal with this challenge, we develop a method called BoolODE that systematically and accurately converts a Boolean model into a system of stochastic differential equations.
We start this section by giving an overview of GeneNetWeaver. Next, we describe our BoolODE framework that we have developed and highlight its differences with GeneNetWeaver. We end this section by summarizing BoolODE and the reasons we prefer it over GeneNetWeaver.
GeneNetWeaver
This method starts with a network of regulatory interactions among transcription factors (TFs) and their targets. It computes a connected, dense subnetwork around a randomly selected seed node and converts this network into a system of differential equations. To express this network in the form of Ordinary Differential Equations (ODEs), it assigns each node i in the network a ‘gene’ variable (xi) representing the level of mRNA expression and a ‘protein’ variable (pi) representing the amount of transcription factor produced by protein translation as follows:
where m is the mRNA transcription rate, lx is the mRNA degradation rate, r is the protein translation rate, and lp is the protein degradation rate. In the first equation, Ri denotes the set of regulators of node i. The non-linear input function f(Ri) captures all the regulatory interactions controlling the expression of node i42; we specify it below.
If there are N regulators for a given gene, there are 2N possible configurations of how the regulators can bind to the gene’s promoter. Considering cooperative effects of regulator binding, the probability of each configuration , the powerset of Ri, is given by the following equation43:
where k and n are the Hill threshold and Hill coefficient respectively. Here, we use q to denote a single regulator in the configuration S and the product in the numerator ranges over all regulators that are present (bound) in S. In the summation in the denominator of this equation, the set T ranges over all members of the powerset other than the empty set. GeneNetWeaver further introduces a randomly-sampled parameter αS ∈ [0,1] to specify the efficiency of transcription activation by a specific configuration S of bound regulators. Thus, the function f(Ri) thus takes the following form:
Next, GeneNetWeaver adds a noise term to each equation to mimic stochastic effects in gene expression23. In addition, in order to create variations among individual experimental samples, GeneNetWeaver recommends adopting a multifactorial perturbation23 that increases or decreases the basal activation of each gene in the GRN simultaneously by a small, randomly-selected value. GeneNetWeaver removes this perturbation after the first half of the simulation. Simulating this system of SDEs generates the requisite gene expression data.
BoolODE uses Boolean models to create simulated datasets
In order to generate simulated time course data for our analysis, we used the GeneNetWeaver framework with one critical difference and one minor variation. The form of the equations used by BoolODE is identical to that of GeneNetWeaver. The critical difference is that we do not sample the αS parameters in Equation 2 randomly, i.e., we do not combine the regulators of each gene using a random logic function. Instead, we use the fact that in both the artificial networks and the literature-curated models, we know the Boolean function that specifies how the states of the regulators control the state of the target genes. Moreover, we can express any arbitrary Boolean function in the form of a truth table relating the input states (i.e., activities of transcription factors) to the output state (the activity of target gene). For a gene with N regulators in its Boolean function, we explore all 2N combinations of transcription factor states and evaluate the transcriptional activity of each specific regulator configuration. Since the value of the Boolean function is the logical disjunction (‘or’) of all these values, we set the α value to one (respectively, zero) for every configuration that evaluates to ‘on’ (respectively, ‘off’). The following example illustrates our approach. Consider a gene X with two activators (P and Q) and one inhibitor (R), represented by the following rule:
The truth table corresponding to this rule along with the α parameters is shown in Supplementary Table 5. Therefore, the ODE governing the time dynamics of gene X is
since only αP, αQ, and αPQ have the value one and every other parameter has the value zero.
Next, we discuss the minor variation of BoolODE from GeneNetWeaver, which is in how we sample kinetic parameters. The GeneNetWeaver equations use four kinetic parameters: one each for mRNA transcription, protein translation, and mRNA and protein degradation rates. Saelens et al.20 sample them uniformly from parameter specific intervals. Independently for every dataset, we sample each parameter from a normal distribution using the value shown in Supplementary Table 6 as the mean and a standard deviation of up to 10% of this mean value. Within a single dataset and for all simulations for that dataset, we fix each parameter (e.g., mRNA degradation rate) for all genes. We choose the values in Supplementary Table 6 so as to achieve the following characteristics: The maximal steady state achievable by the mRNAs is two (the value of m/lx), of the proteins is 10 (the value of r/lp), and the timescale of protein production is ten times that of the mRNAs (since the characteristic time scale of production is inversely proportional to the degradation rate).
In order to create stochastic simulations, we use the formulation proposed by Saelens et al.20 to modify the ODE expressions as follows:
where s is the noise strength. We use s = 10 in our simulations. We use the Euler-Maruyama scheme for numerical integration of the SDEs with time step of h = 0.01.
Defining a single cell
We define the vector of gene expression values corresponding to a particular time point in a model simulation as a single cell. For every analysis, we sample one time point, i.e. one cell from a single simulation. Using this procedure, for a dataset generated from 5,000 simulations, we can obtain up to 5,000 cells.
Creating GeneNetWeaver simulations for comparison with BoolODE
In order to simulate a synthetic network using GeneNetWeaver, we used its edge list as the input network to GeneNetWeaver. To create the simulations, we used the default options of the noise parameter (0.05) and multifactorial perturbations. We only performed wildtype simulations and used the DREAM4 time series output format for comparison with the BoolODE output.
Summary
We developed the BoolODE approach to convert Boolean functions specifying a GRN directly to ODE equations. Our proposed BoolODE pipeline accepts a file describing a Boolean model as input, creates an equivalent ODE model, adds noise terms, and numerically simulates a stochastic time course. Different model topologies can produce different numbers of steady states. Since we carry out stochastic simulations, we perform a large number of simulations in an attempt to ensure that we can reach every steady state. Our analysis of the trajectories computed by BoolODE on datasets from curated models demonstrates the success of our approach in this regard (Supplementary Note 2.1). We prefer BoolODE over a direct application of GeneNetWeaver to create datasets from synthetic networks and datasets from curated models for three reasons: (a) A dense regulatory subnetwork computed around a randomly-selected node, as used by GeneNetWeaver, may not correspond to a real biological process. (b) GeneNetWeaver introduces a random, initial, multifactorial perturbation and removes it halfway in order to create variations in the expression profiles of genes across samples. This stimulation may not correspond to how single-cell gene expression data is collected. (c) GeneNetWeaver’s SDEs do not appear to capture single-cell expression trajectories, as we have shown in Supplementary Figure 1(d).
Datasets
A major challenge that arises when we evaluate GRN inference algorithms for single-cell RNA-seq data is that the “ground truth”, i.e. the network of regulatory interactions governing the dynamics of genes of interest, is usually unknown. Consequently, it is a common practice to create artificial graphs or extract subnetworks from large-scale transcriptional networks.
To address this challenge, we used three sets of networks that serve as the ground truth for GRN inference. The first group included six “toy” networks with specific topologies that give rise to different cellular trajectories with predictable qualitative properties20. For the second set of networks, we curated four published Boolean models that explore gene regulatory interactions underlying various developmental and tissue differentiation processes. Mutual inhibition between a pair of genes is a key characteristic of each of these models; this type of relationship is important in creating branching gene expression trajectories. The regulatory networks underlying the Boolean models serve as the ground truth during evaluation. We used the third group of networks for experimental scRNA-Seq datasets. We matched each scRNA-Seq dataset with an appropriate ChIP-Seq-derived network connecting TFs to their targets; we ensure that the ChIP-Seq data was collected in the same or similar cell type as the scRNA-Seq measurements. In addition, we used non-cell-type-specific transcriptional regulatory networks44–46 as well as the functional interactions in the STRING47 database as the ground truth.
Creating Datasets from Synthetic Networks
We now describe how we selected synthetic networks, converted these networks into systems of stochastic differential equations (SDEs), simulated these systems, and pre-processed the resulting datasets for input to GRN inference algorithms.
Selecting networks
In order to create synthetic datasets exhibiting diverse temporal trajectories, we use six “toy” networks created in Dynverse, a comparison of pseudotime inference algorithms20 (Supplementary Figure 1 and Supplementary Table 1). When simulated as SDEs, we expect the models produce to trajectories with the following qualitative properties:
Linear: a gene activation cascade that results in a single temporal trajectory with distinct final and initial states.
Linear long: similar to Linear but with a larger number of intermediate genes.
Cycle: an oscillatory circuit that produces a linear trajectory where the final state overlaps with the initial state.
Bifurcating: a network that contains a mutual inhibition motif between two genes resulting in two distinct branches starting from a common trajectory.
Trifurcating: mutual inhibition motifs involving three genes in this network result in three distinct steady states.
Bifurcating Converging: an initial bifurcation creates two branches, which ultimately converge to a single steady state.
We then used the following approach to simulate the above networks.
Converting networks into SDE models and simulating them
We manually convert each of these networks to a Boolean model: we set a node to be ‘on’ if and only if at least one activator is ‘on’ and every inhibitor is ‘off’. We simulate these networks using BoolODE. We use the initial conditions specified in the Dynverse software20 (Supplementary Table 6). In order to sample cells from the simulations that capture various locations along a trajectory, we limit the duration of each simulation according to the characteristics of the model (Supplementary Table 7). For example, we simulated the Linear Long network for 15 time units but the Linear network, which has fewer nodes, for 5 time units.
Comparing simulated datasets with the expected trajectories from synthetic networks
It is common to visualize simulated time courses from ODE/SDE models as time course plots or phase plane diagrams with two or three dimensions. The latter are useful to qualitatively explore the state-space of a model at hand. The recent popularity of t-SNE as a tool to visualize and cluster high dimensional scRNA-Seq data motivated us to consider this technique to visualize simulated single-cell data. Supplementary Figure 1(b) shows two-dimensional t-SNE visualizations of each of the toy models.
Pre-processing datasets from synthetic networks for GRN algorithms
Pseudotime inference methods perform well for linear and bifurcating trajectories20. However, even the best performing pseudotime algorithm fails to accurately identify more complex trajectories such as Cycle and Bifurcating Converging. Therefore, we sought to develop an approach for pre-processing synthetic datasets that mimicked a real single cell gene expression pipeline while isolating the GRN inference algorithms from the limitations of pseudotime techniques. Accordingly, we used the following four-step approach to generate single-cell gene expression data from each of the six synthetic networks:
Using the values in Supplementary Table 6 as the means, and 10% of these values as the standard deviations, we sampled a parameter set. We then used BoolODE to perform 5,000 simulations using this parameter set.
We represented each simulation as a |G| × |C| matrix, where G is the set of genes in the model and C is the set of cells in the simulation. We converted each of the 5,000 matrices into a 1-D vector of length |G| × |C| and clustered the vectors using k-means clustering with k set to the number of expected trajectories for each network. For example, the Bifurcating network in Supplementary Figure 1(b) has two distinct trajectories, so we used k = 2. We use the cluster information in Step 4.
We then randomly sampled one set each of 100, 200, 500, 2000, and 5000 cells from the 5,000 simulations.
Finally, we set as input to each algorithm the |G| × |D| matrix, where G is the set of genes in the model and D is the set of randomly sampled cells. For those methods that require time information, we specified the simulation time at which the cell was sampled along with the trajectory (cluster) to which each cell belonged.
We repeated this procedure on 10 different sampled parameter sets to obtain 50 datasets. We ran each algorithm on these 50 datasets.
Note that we used the same set of sampled parameters for all simulations in a dataset and that we varied parameters only across datasets. As an alternative, we considered sampling a different set of parameters per simulation since they may vary from cell to cell. However, this approach caused so much variation that we could not recapitulate the steady states of the Boolean models in the BoolODE-created data.
Note that we clustered simulations themselves (with each simulation represented by the complete time courses of all genes) before we sampled cells. The reason we adopted this ordering is that the goal of the clustering was to partition the cells such that each group would (a) correspond to a distinct steady state of the network and (b) contain cells sampled from the entire time course of the simulations. Clustering the simulations helped us to compute these types of clusters. Subsequently sampling one cell from each simulation permitted us to assign each cell to the cluster to which its simulation belonged and satisfy both properties we desired.
In contrast, if we had sampled cells and then clustered them, we were concerned that some cells would have belonged to a cluster corresponding only to early timepoints and some only to intermediate, resulting in the possibility that some steady states would not have any clusters. Alternatively, we would have had to increase the number of clusters we sought to compute, which may also have resulted in clusters corresponding only to early or only to intermediate timepoints.
Creating Datasets from Curated Models
While the synthetic models presented above are useful for generating simulated data with a variety of specific trajectories, these networks do not correspond to any real cellular process. In order to create simulated datasets that better reflect the characteristics of single-cell transcriptomic datasets, we turned to published Boolean models of gene regulatory networks, as these models are reflective of the real “ground truth” control systems in biology.
Since tissue differentiation and development are active areas of investigation by single cell methods, we examined the literature from the past 10 years to look for published Boolean models of gene regulatory networks involved in these processes. We selected four published models for analysis. Supplementary Table 2 lists the size of the regulatory networks and the number of steady states. Below, we discuss the biological background, the interpretation of model steady states, and the expected type of trajectories for each of these Boolean models.
Mammalian Cortical Area Development
Giacomantonio et al. explored mammalian Cortical Area Development (mCAD) as a consequence of the expression of regulatory transcription factors along an anterior-posterior gradient25. The model contains five transcription factors connected by 14 interactions, captures the expected gene expression patterns in the anterior and posterior compartments respectively, and results in two steady states. Figure 3 displays the regulatory network underlying the model along with a t-SNE visualization of the trajectories simulated using BoolODE. In Supplementary Note 2.1, we show that the two clusters observed in the t-SNE visualization correspond to the two biological states captured by the Boolean model.
Ventral Spinal Cord Development
Lovrics et al. investigated the regulatory basis of ventral spinal cord development26. The model consisting of 8 transcription factors involved in ventralization contains 15 interactions, all of which are inhibitory. It succeeds in accounting for five distinct neural progenitor cell types. We expect to see five steady states from this model. Figure 3 shows the regulatory network underlying the model along with the t-SNE visualization of the trajectories simulated using BoolODE. In Supplementary Note 2.1, we show that the five steady state clusters observed in the t-SNE visualization correspond to the five biological states captured by the model.
Hematopoietic Stem Cell Differentiation
Krumsiek et al. investigated the gene regulatory network underlying myeloid differentiation27. The proposed model has 11 transcription factors and captures the differentiation of multipotent Myeloid Progenitor (CMP cells) into erythrocytes, megakaryocytes, monocytes and granulocytes. The Boolean model exhibits four steady states, each corresponding to one of the four cell types mentioned above. Figure 3 shows the regulatory network of the HSC model along with the t-SNE visualization of the trajectories simulated using BoolODE. In Supplementary Note 2.1, we show that the four steady-state clusters observed in the t-SNE visualization correspond to the four biological states captured by the Boolean model.
Gonadal Sex Determination
Rios et al. modeled the gonadal differentiation circuit that regulates the maturation of the Bipotential Gonadal Primordium (BGP) into either male (testes) or female (ovary) gonads28. The model consists of 18 genes and a node representing the Urogenital Ridge (UGR), which serves as the input to the model. For the wildtype simulations, the Boolean model predominantly exhibits two steady states corresponding to the Sertoli cells (male gonad precursors) or the Granulosa cells (female gonad precursor), and one rare state corresponding to a dysfunctional pathway. Figure 3 shows the regulatory network of the GSD model along with the t-SNE visualization of the trajectories simulated using BoolODE. In Supplementary Note 2.1, we show that the two steady state clusters observed in the t-SNE visualization correspond to the two predominant biological states capture by the Boolean model.
Pre-processing datasets from curated models for GRN algorithms
As with the datasets from synthetic networks, we used the following approach to generate simulated datasets for each of the four curated models. Using the values in Supplementary Table 6 as means and 5% of these values as the standard deviations we sampled a parameter set. We used BoolODE to perform 2,000 simulations and randomly sampled one cell from each simulation. We repeated this procedure on 10 different sampled parameter sets to obtain 10 datasets. In order to closely mimic the preprocessing steps performed for real single-cell gene expression data, we use the following steps for each dataset:
-
Pseudotime inference using Slingshot. In the case of datasets from synthetic networks, we used the simulation time directly for those GRN inference methods that required cells to be time-ordered. In contrast, for datasets from curated models, we ordered cells by pseudotime, which we computed using Slingshot29. We selected Slingshot for pseduotime inference due to its proven success in correctly identifying cellular trajectories in a recent comprehensive evaluation of this type of algorithm20. Slingshot needs a lower dimensional representation of the gene expression data as input. In addition, if the cells belong to multiple trajectories, Slingshot needs a vector of cluster labels for the cells, as well as the cluster labels for cells in the start and end states in the trajectories. To obtain these additional input data for Slingshot, we used the following procedure:
- We use t-SNE on the |G| × |C| matrix representing the data to obtain a two-dimensional representation of the cells.
- We performed k-means clustering on this lower dimensional representation of the cells with k set to one more than the expected number of trajectories. For example, since we knew that the GSD model had a bifurcating trajectory, we used k = 3.
- We computed the average simulation time of the cells belonging to each of the k clusters. We set the cluster label corresponding to the smallest average time as the starting state and the rest of clusters as ending states.
- We then ran Slingshot with the t-SNE-projected data and starting and ending clusters as input. We obtained the trajectories to which each cell belonged and its pseudotime as output from Slingshot.
Figure 3(d) displays the results for one dataset of 2,000 cells for each of the four models. We observed that Slingshot does a very good job of correctly identifying cells belonging to various trajectories. Further, the pseudotime computed for each cell by Slingshot is highly correlated with the simulation time at which we sampled the cell (Supplementary Table 8).
Note that the k-means clustering whose results we display in Figure 3(c) is different from the k-means clustering described above. To obtain the results in Figure 3(c), we followed the procedure described for synthetic models: we clustered the simulations (complete time-courses) themselves, with k set to the number of steady states. Our goal was to confirm visually that each cluster contained cells spanning the entire length of the simulation. In contrast, before applying Slingshot, we clustered the (lower dimensional representation of the samples) cells; we set k as described above so that we could input to Slingshot one starting cluster and as many ending clusters as the number of steady states.
Inducing dropouts in datasets from curated models. We used the same procedure as Chan et al.14 in order to induce dropouts, which are commonly seen in single cell RNA-Seq datasets, especially for transcripts with low abundance48. We created a dataset with a dropout rate of q as follows: for every gene, we sorted the cells in increasing order of that gene’s expression value. We set the expression of that gene in each of the lowest qth percentile of cells in this order to zero with a q% chance. For example, choosing q = 50 resulted in a 50% chance of setting a gene’s expression values below the 50th percentile to 0, which affected about 25% of the dataset. Note that we used the same parameter twice simply for convenience; we do not expect the trends we find to deviate considerably if we had used two different parameters for percentile and for probability. We applied two different dropout rates: q = 50 and q = 70. We used Slingshot to recompute pseudotime for each dataset with dropouts. We did note a considerable decrease in this correlation when we added dropouts to the simulated datasets, for all but the GSD network (Supplementary Table 8).
At the end of this step, we had 30 datasets with 2,000 cells for each of the four models: 10 datasets without dropouts, 10 with a dropout rate of q = 50, and 10 with a rate of q = 70.
Collecting Experimental Single-Cell RNA-seq Datasets and Ground Truth Networks
Experimental Single-Cell RNA-seq Datasets
We obtained five different single cell RNA-seq datasets, three in mouse and two in human (Supplementary Table 3). There were a total of seven cell types across these datasets. We pre-processed each dataset using the procedure described in the corresponding paper. In general, if the publication did not provide normalized expression values, we log-transformed the TPM or FPKM counts using a pseudocount of 1 and used the results as the expression values. We additionally filtered out any genes that were expressed in fewer than 10% of the cells. We describe the details of the datasets and the pseudotime computation below:
Mouse Hematopoietic Stem and Progenitor Cells (mHSC)49: We obtained the normalized expression data for 1,656 HSPCs across 4,773 genes from the supplementary data provided by the authors. We used the first three dimensions from DiffusionMap in order to compute pseudotime values. We used the E-SLAM population as the starting cell type and computed pseudotime using Slingshot along three lineages, namely, erythroid (E), granulocyte-monocyte (GM), and lymphoid (L). We inferred GRNs for each lineage independently.
Mouse Embryonic Stem Cells (mESC)50: This dataset contains scRNA-seq expression measurements for 421 primitive endoderm (PrE) cells differentiated from mESCs, collected at five different time points (0h, 12h, 24h, 48h, until 72 hours). SCODE,13 SINGE,10 and GRISLI9 used this dataset to evaluate their performance. We computed pseudotime using Slingshot with cells measured at 0h as the starting cluster and the cells measured at 72h as the ending cluster.
Mouse Dendritic Cells (mDC)51: This dataset corresponds to over 1,700 bone-marrow derived dendritic cells under various conditions. Following SCRIBE19, we used the LPS stimulated wild-type cells measured at 1h, 2h, 4h, and 6h. We then computed the pseudotime using Slingshot with cells measured at 1h as the starting cluster and the cells measured at 6h as the ending cluster.
Human Mature Hepatocytes (hHep)52: This dataset is from an scRNA-seq experiment on induced pluripotent stem cells (iPSCs) in 2D culture differentiating to hepatocyte-like cells. The dataset contains 425 scRNA-seq measurements from multiple time points: days 0 (iPS cells), 6, 8, 14, and 21 (mature hepatocyte-like (MH)). We computed the pseudotime using Slingshot with cells measured on day 0 (iPSCs) as the starting cluster and the cells measured on 21 (MHs) as the ending cluster.
Human Embryonic Stem Cells (hESC)53: This dataset is from a time course scRNA-seq experiment derived from 758 cells along the differentiation protocol to produce definitive endoderm (DE) cells from human embryonic stem cells, measured at 0h, 12h, 24h, 36h, 72h and 96h. We computed the pseudotime with cells measured at 0h as the starting cluster and the cells measured at 96h as the ending cluster. SCODE13 used this dataset to evaluate its performance.
Once we obtained the pseduotime values for the cells in each dataset, we computed which genes had varying expression values across pseudotime. We used the general additive model (GAM) implemented in the ‘gam’ R package to compute the variance and the p-value of this variance. We used the Bonferroni method to correct for testing multiple hypotheses. Supplementary Table 3 provides the statistics on the number of significantly-varying genes and TFs in each dataset after using a corrected p-value cutoff of 0.01. We selected genes for GRN inference in two different ways.
We considered all genes with p-value less than a threshold. We selected thresholds so that we obtained 500 and 1,000 genes. We recorded the number of TFs in these sets.
We started by including all TFs whose variance had p-value at most 0.01. Then, we added 500 and 1,000 additional genes as in the previous option. This approach enabled the GRN methods to consider TFs that may have a modest variation in gene expression but still regulate their targets.
After applying a GRN inference algorithm to a dataset, we only considered interactions outgoing from a TF in further evaluation.
Ground truth networks collection and processing
In the GRN inference literature, a common practice is to evaluate the accuracy of a resulting network by comparing its edges to an appropriate database of TFs and their targets. For example, SCODE used the RikenTFdb and animalTFDB resources to define ground truth networks for mouse and human gene expression data, respectively13. We used three types of ground truth datasets (Supplementary Table 4).
Cell-type specific: For each experimental scRNA-seq dataset, we searched the ENCODE, ChIP-Atlas, and ESCAPE databases for ChIP-Seq data from the same or similar cell type. We also included the loss-of-function/gain-of-function dataset from the ESCAPE database.
- Non-specific: Here, we used the following resources:
- DoRothEA46 integrates ChIP-Seq and transcriptional regulatory information from multiple sources. We considered two levels of evidence in this database: A (curated/high confidence) and B (likely confidence).
- RegNetwork44 incorporates genome-wide TF-TF, TF-gene, TF-miRNA regulatory relationships in human and mouse collected from various sources. We used the TF-TF and TF-gene interactions for our analysis.
- TRRUST45 contains TF-target interactions collected based on text-mining followed by manual curation for human and mouse.
Functional: Finally, we used the human and mouse STRING47 networks. An interaction here is functional and need not correspond to transcriptional regulation. We selected this type of ground truth network due to our observation that many GRN methods predict indirect interactions for Boolean models.
Evaluation Pipeline
One of the major challenges we faced was that the GRN inference methods we included in this evaluation were implemented in a variety of languages such as R, MATLAB, Python, Julia and F#. In order to obtain an efficient and reproducible pipeline, we Dockerized the implementation of each algorithm. Supplementary Table 9 contains details on the specific software or GitHub commit versions we downloaded and used in our pipeline. For methods implemented in MATLAB, we created MATLAB executable files (.mex files) that we could execute within a Docker container using the MATLAB Runtime. We further studied the publications and the documentation of the software (and the source code, on occasion) to determine how the authors recommended that their methods be used. We implemented these suggestions as well as we could. We provide more details in Supplementary Note 4.
Inputs
For datasets from synthetic networks and for datasets from curated models, we provided the gene expression values obtained from the simulations directly after optionally inducing dropouts in the second type of data. Eight out of the 12 methods also required some form of time information for every cell in the dataset (Figure 6). Of these, two methods (GRNVBEM and LEAP) only required cells to be ordered according to their pseudotime and did not require the pseudotime values themselves.
Parameter estimation
Six of the methods also required one or more parameters to be specified. To this end, we performed parameter estimation for each of these methods separately for datasets from synthetic networks, datasets from curated models, and real datasets and provided them with the parameters that resulted in the best AUPRC values. See Supplementary Note 1.2 for details.
Output processing
Ten of the GRN inference methods output a confidence score for every possible edge in the network, either as an edge list or as an adjacency matrix, which we converted to a ranked edge list. We gave the same rank to edges with the same confidence scores.
Performance evaluation
We used a common evaluation pipeline across all the datasets considered in this paper. We evaluated the result of each algorithm using the following criteria:
AUPRC, AUROC: We computed areas under the Precision-Recall (PR) and Receiver Operating Characteristic (ROC) curves using the edges in the relevant network as ground truth and ranked edges from each method as the predictions. We ignored self-loops for this analysis since some methods such as PPCOR always assigned the highest rank to such edges and some other methods such as SINGE always ignored them. Most of the networks we considered have a density of 0.3 or less, i.e., the positive-to-negative ratio is worse than 1:3. Since the GRN inference problem for these networks is moderately imbalanced, we focus on AUPRC scores in the main text54,55. For readers who are interested in AUROC plots, we provide them as supplementary figures (only for the synthetic networks and curated models).
Stability across multiple runs: We executed each algorithm 10 times on a dataset to ask if the inferred networks changed from one run to another. We represented every result by the corresponding ranked list of edges. For every pair of results, we computed the Spearman’s correlation of the ranked lists. We performed this analysis for curated models and for experimental datasets.
Identifying top-k edges: We first identified top-k edges for each method, where k equaled the number of edges in the ground truth network (excluding self-loops). In multiple edges were tied for a rank of k, we considered all of them. If a method provided a confidence score for fewer than k edges, we used only those edges. For experimental single-cell RNA-seq datasets, this number varied from one ground truth dataset to another.
Stability across multiple datasets: For each method, once we obtained the set of top-k edges for each each dataset, we then computed the Jaccard index of every pair of these sets. We used the median of the values as an indication of the robustness of a method’s output to variations in the simulated datasets from a given synthetic network or curated model.
Early precision (EP) and Early precision ratio (EPR): We defined early precision as the fraction of true positives in the top-k edges. We also computed the early precision ratio, which represents the ratio of early precision value and the early precision for a random predictor for that model. A random predictor’s precision is the edge density of the ground truth network.
Early precision of signed edges: We desired to check whether there were any differences in how accurately a GRN inference algorithm identified activating edges in comparison to inhibitory edges. To this end, we computed the top-ka edges from the ranked list of edges output by each method, where ka is the number of activating edges in the ground-truth network. In this step, we ignored any inhibitory edges in the ground truth network. We defined the early precision of activating edges as the fraction of true edges of this type in the top ka edges. We used an analogous approach to compute early precision of inhibitory edges. We also computed the early precision ratio for these values. We performed this analysis only for curated models.
Datasets with multiple trajectories
Seven methods we evaluated require pseudotime-ordered cells (Figure 6), but cannot directly handle data with branched trajectories. In these cases, as suggested by many of these methods, we separated the cells into multiple linear trajectories using Slingshot and applied the algorithm to the set of cells in each trajectory individually. To combine the GRNs, for each interaction, we recorded the largest score for it across all the networks and ranked the interactions by these values. In the case of GRISLI, which outputs ranked edges, for each interaction, we took the best (smallest) rank for it across all the networks.
As an alternative, we merged all the trajectories into one set of cells and executed each algorithm on this dataset. We performed this analysis for the three synthetic networks with multiple trajectories (Bifurcating, Bifurcating converging, and Trifurcating).
Shuffling simulation times
We investigated the effect of shuffling the pseudotime values on the performance of methods that require this information. We used three window sizes, namely, 15%, 30% and 45%, which defined the range of indices to sample from as a fraction of the total number of cells in a dataset. Thus, for a dataset with 2,000 cells, using a window size of 30% resulted in a range of 2000×0.3 = 600. Therefore, after sorting the cells in increasing order of pseudotime, for every index i, we sampled a new index from the interval [max(0,i−300),min(i+300,2000)] and swapped the cells at these two indices. We performed this analysis for the three synthetic networks with a single trajectory (Linear, Cycle, and Linear Long). Here each original (unshuffled) pseudotime was equal to the simulation time.
Procedure for creating Figure 6
We chose the following measures presented in earlier sections for summarize our key findings:
Accuracy: We computed the median of the per-network median AUPRC value obtained for datasets containing 2,000 and 5,000 cells for the six synthetic networks (Figure 2). For datasets from curated models, we used the median of the per-model median AUPRC value obtained for 10 datasets without dropouts for each the four datasets from curated models (Figure 4). For experimental single-cell RNA-Seq datasets, we used the median EPR obtained for each dataset-evaluation network combination (all significantly-varying TFs and the 500 most-varying genes) (Figure 5). We have ordered the algorithms by their median EPR score across experimental single-cell RNA-Seq datasets followed by median AURPCs in datasets from synthetic networks.
Stability: We present four such measures: (a) across datasets: the median score of the Jaccard index obtained for all six datasets from synthetic networks (Figure 2); (b) across runs: median Spearman’s correlation of outputs for each of the four datasets from curated models (one dataset each, Supplementary Note 3.4); (c) across dropouts: median percentage decrease in AUPRC for the q = 50 dropout rate compared to no dropouts (Supplementary Figure 4); (d) across pseudotime: median percentage decrease in AUPRC after shuffling time values within a 30% window compared to the original simulation time for datasets from synthetic networks (Supplementary Figure 11).
Scalability: Median running times and memory consumption for three different scRNA-Seq datasets, namely hHEP, hESC and mHSC-E, which contain 400, 750 and 1000 cells, respectively (Supplementary Figure 7). Missing values indicate that either the method did not complete even after running for over a day or it gave a run-time error.
Data availability
The datasets simulated from the synthetic networks and curated models and the processed experimental single-cell gene expression datasets are available on Zenodo at https://doi.org/10.5281/zenodo.3378975. The gene experimental scRNA-Seq datasets we downloaded from GEO had accession numbers: GSE81252 (hHEP), GSE75748 (hESC), GSE98664 (mESC), GSE48968 (mDC), and GSE81682 (mHSC).
Reporting Summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Code availability
A Python implementation of the BEELINE framework is available under the GNU General Public License v3 at https://github.com/murali-group/BEELINE
Supplementary Material
Acknowledgements
Grants from the National Science Foundation (CCF-1617678, DBI-1759858) and the National Cancer Institute (UH2CA203768) supported this work. The research is also based upon work supported by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), via the Army Research Office (ARO) under cooperative Agreement Number [W911NF-17-2-0105]. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of the ODNI, IARPA, ARO, or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright annotation thereon. The funding bodies played no role in the design of the study, the collection, analysis, and interpretation of data, or in writing the manuscript.
Footnotes
Competing Interests
The authors declare no competing interests.
References
- 1.Villani AC et al. Single-cell RNA-seq reveals new types of human blood dendritic cells, monocytes, and progenitors. Science (80-. ). 356, (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Rozenblatt-Rosen O, Stubbington MJT, Regev A & Teichmann SA The Human Cell Atlas: from vision to reality. Nature 550, 451–453 (2017). [DOI] [PubMed] [Google Scholar]
- 3.Wagner A, Regev A & Yosef N Revealing the vectors of cellular identity with single-cell genomics. Nat. Biotechnol. 34, 1145–1160 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kharchenko PV, Silberstein L & Scadden DT Bayesian approach to single-cell differential expression analysis. Nat. Methods 11, 740–742 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Buettner F et al. Computational analysis of cell-to-cell heterogeneity in single-cell RNA-sequencing data reveals hidden subpopulations of cells. Nat. Biotechnol. (2015). doi: 10.1038/nbt.3102 [DOI] [PubMed] [Google Scholar]
- 6.Huynh-Thu VA, Irrthum A, Wehenkel L & Geurts P Inferring Regulatory Networks from Expression Data Using Tree-Based Methods. PLoS One 5, e12776+ (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kim S ppcor: An R Package for a Fast Calculation to Semi-partial Correlation Coefficients. Commun. Stat. Appl. Methods 22, 665–674 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Moerman T et al. GRNBoost2 and Arboreto: efficient and scalable inference of gene regulatory networks. Bioinformatics (2018). doi: 10.1093/bioinformatics/bty916 [DOI] [PubMed] [Google Scholar]
- 9.Aubin-Frankowski P-C & Vert J-P Gene regulation inference from single-cell RNA-seq data with linear differential equations and velocity inference. bioRxiv 464479 (2018). doi: 10.1101/464479 [DOI] [PubMed] [Google Scholar]
- 10.Deshpande A, Chu L-F, Stewart R & Gitter A Network Inference with Granger Causality Ensembles on Single-Cell Transcriptomic Data. bioRxiv 534834 (2019). doi: 10.1101/534834 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Huynh-Thu VA & Sanguinetti G Combining tree-based and dynamical systems for the inference of gene regulatory networks. Bioinformatics 31, 1614–1622 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Specht AT & Li J LEAP: Constructing gene co-expression networks for single-cell RNA-sequencing data using pseudotime ordering. Bioinformatics 33, 764–766 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Matsumoto H et al. SCODE: An efficient regulatory network inference algorithm from single-cell RNA-Seq during differentiation. Bioinformatics 33, 2314–2321 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chan TE, Stumpf MPH & Babtie AC Gene Regulatory Network Inference from Single-Cell Data Using Multivariate Information Measures. Cell Syst. (2017). doi: 10.1016/j.cels.2017.08.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Aibar S et al. SCENIC: single-cell regulatory network inference and clustering. Nat. Methods 14, 1083–1086 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Papili Gao N, Ud-Dean SMM, Gandrillon O & Gunawan R SINCERITIES: Inferring gene regulatory networks from time-stamped single cell transcriptional expression profiles. Bioinformatics 34, 258–266 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sanchez-Castillo M, Blanco D, Tienda-Luna IM, Carrion MC & Huang Y A Bayesian framework for the inference of gene regulatory networks from time and pseudo-time series data. Bioinformatics 34, 964–970 (2018). [DOI] [PubMed] [Google Scholar]
- 18.Woodhouse S, Piterman N, Wintersteiger CM, Göttgens B & Fisher J SCNS: A graphical tool for reconstructing executable regulatory networks from single-cell genomic data. BMC Syst. Biol. 12, 59 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Qiu X et al. Towards inferring causal gene regulatory networks from single cell expression measurements. bioRxiv 0–45 (2018). doi: 10.1101/426981 [DOI] [Google Scholar]
- 20.Saelens W, Cannoodt R, Todorov H & Saeys Y A comparison of single-cell trajectory inference methods. Nat. Biotechnol. 37, 547–554 (2019). [DOI] [PubMed] [Google Scholar]
- 21.Lim CY et al. BTR: training asynchronous Boolean models using single-cell expression data. BMC Bioinformatics 17, 355 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chen S & Mar JC Evaluating methods of inferring gene regulatory networks highlights their lack of performance for single cell gene expression data. BMC Bioinformatics 19, 232 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Schaffter T, Marbach D & Floreano D GeneNetWeaver: in silico benchmark generation and performance profiling of network inference methods. Bioinformatics (2011). doi: 10.1093/bioinformatics/btr373 [DOI] [PubMed] [Google Scholar]
- 24.Ocone A, Haghverdi L, Mueller NS & Theis FJ Reconstructing gene regulatory dynamics from high-dimensional single-cell snapshot data. Bioinformatics 31, 89–96 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Giacomantonio CE & Goodhill GJ A boolean model of the gene regulatory network underlying mammalian cortical area development. PLoS Comput. Biol. 6, e1000936 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lovrics A et al. Boolean Modelling reveals new regulatory connections between transcription factors orchestrating the development of the ventral spinal cord. PLoS One 9, e111430 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Krumsiek J, Marr C, Schroeder T & Theis FJ Hierarchical Differentiation of Myeloid Progenitors Is Encoded in the Transcription Tactor Network. PLoS One 6, e22649 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ríos O et al. A Boolean network model of human gonadal sex determination. Theor. Biol. Med. Model. 12, 26 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Street K et al. Slingshot: cell lineage and pseudotime inference for single-cell transcriptomics. BMC Genomics 19, 477 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Marbach D et al. Wisdom of crowds for robust gene network inference. Nat. Methods 9, 796–804 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Luecken MD & Theis FJ Current best practices in single‐cell RNA‐seq analysis: a tutorial. Mol. Syst. Biol. (2019). doi: 10.15252/msb.20188746 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Svensson V, Vento-Tormo R & Teichmann SA Exponential scaling of single-cell RNA-seq in the past decade. Nat. Protoc. 13, 599–604 (2018). [DOI] [PubMed] [Google Scholar]
- 33.Stuart T et al. Comprehensive Integration of Single-Cell Data. Cell 177, 1888–1902.e21 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mimitou EP et al. Multiplexed detection of proteins, transcriptomes, clonotypes and CRISPR perturbations in single cells. Nat. Methods 16, 409–412 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
References
- 35.Huynh-Thu VA, Irrthum A, Wehenkel L & Geurts P Inferring regulatory networks from expression data using tree-based methods. PLoS One 5, (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Faith JJ et al. Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles. PLoS Biol. 5, 0054–0066 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.La Manno G et al. RNA velocity of single cells. Nature 560, 494–498 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Yuan Y & Bar-Joseph Z Deep learning for inferring gene relationships from single-cell expression data. bioRxiv (2019). doi: 10.1101/365007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Chen H et al. Single-cell transcriptional analysis to uncover regulatory circuits driving cell fate decisions in early mouse development. Bioinformatics 31, 1060–1066 (2015). [DOI] [PubMed] [Google Scholar]
- 40.Hamey FK et al. Reconstructing blood stem cell regulatory network models from single-cell molecular profiles. Proc. Natl. Acad. Sci. U.S.A. 114, 5822–5829 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Marbach D, Schaffter T, Mattiussi C & Floreano D Generating realistic in silico gene networks for performance assessment of reverse engineering methods. J. Comput. Biol. 16, 229–239 (2009). [DOI] [PubMed] [Google Scholar]
- 42.Marbach D et al. Revealing strengths and weaknesses of methods for gene network inference. Proc. Natl. Acad. Sci. U. S. A. 107, 6286–6291 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ackers GK, Johnson AD & Shea MA Quantitative model for gene regulation by lambda phage repressor. Proc. Natl. Acad. Sci. 79, 1129–1133 (1982). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Liu ZP, Wu C, Miao H & Wu H RegNetwork: an integrated database of transcriptional and post-transcriptional regulatory networks in human and mouse. Database (Oxford) 2015, (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Han H et al. TRRUST v2: an expanded reference database of human and mouse transcriptional regulatory interactions. Nucleic Acids Res. 46, D380–D386 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Garcia-Alonso L, Holland CH, Ibrahim MM, Turei D & Saez-Rodriguez J Benchmark and integration of resources for the estimation of human transcription factor activities. Genome Res. (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Szklarczyk D et al. STRING v11: protein–protein association networks with increased coverage, supporting functional discovery in genome-wide experimental datasets. Nucleic Acids Res. (2018). doi: 10.1093/nar/gky1131 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Brennecke P et al. Accounting for technical noise in single-cell RNA-seq experiments. Nat. Methods 10, 1093–1095 (2013). [DOI] [PubMed] [Google Scholar]
- 49.Nestorowa S et al. A single-cell resolution map of mouse hematopoietic stem and progenitor cell differentiation. Blood 128, 20–31 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Hayashi T et al. Single-cell full-length total RNA sequencing uncovers dynamics of recursive splicing and enhancer RNAs. Nat. Commun. 9, 619 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Shalek AK et al. Single-cell RNA-seq reveals dynamic paracrine control of cellular variation. Nature 510, 363–369 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Camp JG et al. Multilineage communication regulates human liver bud development from pluripotency. Nature 546, 533–538 (2017). [DOI] [PubMed] [Google Scholar]
- 53.Chu LF et al. Single-cell RNA-seq reveals novel regulators of human embryonic stem cell differentiation to definitive endoderm. Genome Biol. 17, 173 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Saito T & Rehmsmeier M The precision-recall plot is more informative than the ROC plot when evaluating binary classifiers on imbalanced datasets. PLoS One 10, e0118432 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Saito T & Rehmsmeier M Precrec: Fast and accurate precision-recall and ROC curve calculations in R. Bioinformatics 33, 145–147 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets simulated from the synthetic networks and curated models and the processed experimental single-cell gene expression datasets are available on Zenodo at https://doi.org/10.5281/zenodo.3378975. The gene experimental scRNA-Seq datasets we downloaded from GEO had accession numbers: GSE81252 (hHEP), GSE75748 (hESC), GSE98664 (mESC), GSE48968 (mDC), and GSE81682 (mHSC).