Abstract
Advances in molecular biology, optics, genetics and bioinformatics have opened the door to mapping, in molecular detail, processes inside living cells. With the ability to observe the individual moving parts of cellular machinery, concepts formerly confined to physics are entering mainstream biology. This article discusses a few ideas of this sort related to chromosome biology, to illustrate what kinds of insights physics might yet bring to our understanding of living systems.
Graphical Abstract
Introduction
I teach a course for first-year biology graduate students entitled “Quantitative Biology”, created to address a 2005-era impetus from a number of bodies including the NRC [1] for biology students to receive quantitative training*. My course is focused on thinking mechanistically about molecules and cells. Picking papers to look at has been easy, since very year there has been further development of this kind of thought in the biology research literature: terms like “physical biology”, “Brownian machines”, “phase separation”, “semi-dilute solution”, “random walk”, “Ostwald ripening” and the like increasingly appear in biological papers. Cell biology is being pollinated by 1990s-style condensed matter physics!
This paper will discuss a few concepts which could be useful for the practicing biologist trying to sort out their nanometers from their piconewtons, with a bias towards topics from chromosome biology. I distinguish “biophysics” which tends to worry about in vitro things (biophysics and the more physical end of “biochemistry” are often hard to separate from one another), “biological physics”, which is often used by physicists to talk about stuff that might be related to living things, and “physical biology” which aims to understand what is going on inside living cells quantitatively, using physical law. Recognition and use of the laws of nature – mechanics, electromagnetism, statistical mechanics, and quantum mechanics – is what separates physics from applied mathematics. The power of physics is the universality of physical law: exactly the same laws that govern atoms and molecules in inert materials apply to living matter.
MKS
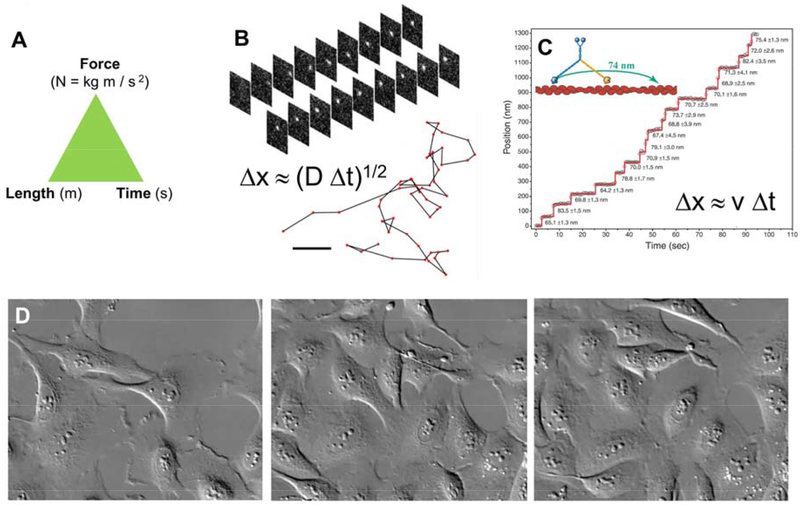
The emergence of an array of powerful techniques for super-resolution imaging, DNA deep sequencing, use of antibody libraries, and now gene editing has provided us with unprecedented maps, in space and to some degree in time, of where molecules are and how they are juxtaposed or organized inside the cell. Powerful bioinformatics tools (e.g., ENCODE [2] and HiGlass [3]) allow one to play with and combine these maps, which often give striking new insights into biology (e.g., the “topologically associated domains” seen in eukaryote genomes [4]) by just looking. However, given these marvelous mapping methods we should remember that for a truly mechanistic view of cellular machinery, a kinematic description, solely in terms of space and time, is incomplete. The characterization of any machine (simple or otherwise) requires us to examine its dynamics – a fact emphasized by the name “MKS” for the SI subset of units relevant to elementary mechanics, the K standing for kilogram (kg; M and S stand for meters and seconds) [5] *. Without the kg there is no way to make a force (the MKS unit being the Newton = N = kg m / s2, as in F = ma). Just recording how things are moving is merely kinematics: you need measurements of the forces responsible to complete a story of dynamics – to answer why things are moving (Fig. 1A).
Figure 1.
A. The triad of quantities with different units that characterize a simple machine: length, time and force. B. Thermal fluctuations drive random-walk diffusive motions of molecules, the basis of all molecular motion inside cells: a diffusive trajectory of a Dendra2 molecule in a cell is shown (bar 500 nm, time between data points 10 ms) [12]. C. Molecular motors use chemical energy (e.g., ATP) to make molecules move processively in one direction: observations of the motion of an individual myosin V molecule are shown [13]. D. Images of human U2OS cells crawling in a culture dish [14], field of view approximately 60 μm, time between frames approximately 30 minutes.
The elementary physics dictum “work equals force times displacement” reminds us that energy has the SI unit of N m = Joule = J = kg m2 / s2, and so to get energy we again need the kg. The basic energy scale that biological molecules must contend with is the energy kBT = 4 × 10−21 J (for T = 300 Kelvin) associated with thermal motion, which deforms every molecular spring so as to be excited an average of about kBT above its minimum energy state (thermal fluctuations also drive diffusion, Fig. 1B).
A nice way to think about kBT is that it is the energy scale at which entropy (thermal fluctuations) can compete with interaction energy: interactions much larger than kBT are only rarely disrupted by thermal fluctuations. As an example, the primary structure of biomolecules is defined by covalent bonds, which have barriers to their rupture of tens of kBT, making them suitably unbreakable by thermal motion (recall the Boltzmann distribution which tells us that the probability of an excited state of energy E occurring by thermal fluctuation is proportional to exp(−E/kBT)). Plugging E = 1 eV = 40 kBT into indicates us that our biomolecules are stable against thermal fluctuation alone (here T is absolute temperature, i.e., the strength of thermal fluctuations in biology is essentially a constant corresponding to T ≈ 300 Kelvin).
At the next scale up we can think about secondary structure or biomolecule recognition and binding via non-covalent interactions. Such interactions establish structure at the nanometer (1 nm = 10−9 m) scale, about the size of an amino acid or nucleic acid residue and the basic information storage scale of biology. Establishing structure with nm precision requires interactions that generate confining forces of about 1 kBT/nm = 4 × 10−12 N = 4 piconewtons = 4 pN. This force scale is indeed roughly that needed to unfold proteins [6], pull apart protein-DNA complexes [7], unzip DNA (as occurs in the cell – DNA is of course never thermally melted in vivo, that only happens in the PCR machine) [8], and stall molecular motors (Fig. 1C) [9]. The pN is the basic force scale of molecular biology. Molecular motors can work together to generate larger forces: the mitotic apparatus of animal cells, using dozens of microtubules and associated motors can generate tens or even hundreds of pN [10]; crawling human cells can generate thousands (1000 pN = 1 nanonewton = 10−9 N) [11] (Fig. 1D).
Einstein’s Diffusive Work was a Drag
Einstein was one of the first people to understand the relation between diffusion and friction for any particle diffusing in a liquid, and arrived at the strikingly simple formula for the diffusion constant
Here ζ is the drag coefficient of the diffusing particle, essentially the product of the particle radius and liquid viscosity [15]. The drag coefficient tells us what force is needed to drag a particle through water at constant velocity, via f = ζν. For a sphere of radius R ζ= 6πηR, where the biologically relevant viscosity (e.g., that of the fluid component of cytoplasm) is usually not far from that of water, η ≈ 10−3 kg / (m · s). It is a good exercise to multiply the units together to check that the diffusion constant D indeed has dimensions of length2/time. Another good exercise is to figure out what order of magnitude of force is needed to propel an E. coli cell at ν ≈ 10 μm/sec (Can you guess the order of magnitude before doing the computation? You may consider the cell to be a sphere of 1 μm radius.).
This inverse relationship between friction (drag) and diffusion constant is central to understanding molecular motion inside living cells. In fact, active transport often can be thought of as diffusion as well, just constrained by use of stored energy to be biased to occur in a particular direction (molecular motors and transmembrane pumps are excellent examples).
Phase Separation – Friend or Foe?
The recognition of weak, relatively nonspecific, attractive biomolecule interactions as being a driver for formation of membraneless organelles in vivo [16] is an example of a simple physical idea – the same mechanism driving separation of extra virgin olive oil from balsamic vinegar – that has been recognized as important to subcellular self-organization. The key is that only about a kBT of interaction (sticking energy) between two molecules is enough to make them tend to stay together, and if those interactions are multivalent (as nonspecific interactions between unstructured proteins can easily be) – bulk phase separation may well occur. Notably, this is independent of molecular size (the loss of positional entropy due to phase separation is crudely speaking kB per molecule) so that a solution of polymers of N units will phase separate when the stickiness is only about kBT/N per monomer (when the energy per monomer-monomer contact overwhelms the entropy cost of forming separated phases of about one kBT per polymer molecule) [17]. So, if you want to drive phase separation of monomer units by very weak interactions, just join them together into polymers.
Once true phase separation starts it won’t stop until the concentrated phase becomes one large droplet, either by droplet fusion or by diffusion of molecules from small droplets to large ones. The reason for this is that phase separation is characterized by an energy cost per unit area of surface at which the concentrated and dilute phases touch. This quantity is called surface tension σ and has units of J/m2 = N/m. The (surface) energy per volume for a droplet of radius R is E = σR2 / R3 = σ/R, and goes down as R increases, indefinitely (Fig. 2A [18]).
Figure 2.
A. Optical observation of phase separation of synthetic polymer liquids in two dimensions: as in all bulk phase separation processes the domains or “bubbles” of the separating phases grown indefinitely in size [18] (all bars 100 μm). B. If two polymers with the tendency to separate are chemically bonded together (sketch) to make a diblock copolymer, they can undergo microphase formation to form layers (left) [21], or other more exotic structures such as the bicontinuous network (right) where regions shaped locally like the “tetrapod” sketched to right self-organize [22]. C. Nucleoli in Xenopus oocytes take the form of many small droplets (bar 100 μm) which can be observed to undergo fusion and flow (lower panels, smaller droplets approximately 20 μm diameter) similar to coalescence during phase separation [23]. D. Nucleoli in human cells (red in upper panels, bar 5 μm) have been observed to undergo shape changes in time similar to that of small liquid droplets (upper right panels: the fluctuations are small, refer to the original paper for details); fusion events also have been observed (lower panels, bar 2 μm) [24].
How big can we expect σ to be? When we are in the vicinity of the onset of phase separation, this will be on the order of σ=kBT/r2 where r is the size of the molecules involved. For polymers, we can expect r to grow with N (r = N1/2b for random walk polymers, or r = N1/3b for collapsed polymers, e.g., folded proteins, where b is the monomer size) so this surface tension becomes lower as N increases. For molecules of r = 3 nm size (a typical size for a folded protein) we can estimate σ = 4×10−4 N/m for concentrated solution. A droplet of micron size (R = 10−6 m) can therefore apply a force f = σR = 4×10−10 N = 400 pN (!) as it seeks equilibrium via droplet fusions, or as it moves to a location where it enjoys favorable contact energy. Put another way, a bubble of size R is able to exert a stress or pressure of p = σ/R (sometimes called Laplace pressure, note the reappearance of this formula), which for this example is p = 400 Pa, large enough to severely deform the cytoskeleton or chromosomes. For lower protein concentrations or for larger molecules or complexes a correspondingly larger length scale (say r = 30 nm) might reduce the surface tension to σ ≈ 10−6 N/m, but this still provides a force in the few-pN range. Even this level of force is enough to influence cellular machinery, e.g., individual molecular interactions or motors [19, 20].
Taming the Savage Bubble – Microphase Separation
In a cell, one often observes apparent regulation of the size of organelles, and uncontrolled phase separation will work against such a goal. One might want to think about how to achieve formation of droplets of controlled size. If we think about two species of polymers A and B, they will tend to separate into an A-rich and a B-rich phase, assuming that there is some tendency of A and B to separate. However, if we simply chemically link the A chains to the B chains to make an A-B diblock copolymer the result will be the impossibility of formation of indefinitely large A- or B-rich droplets. Instead, one will form microdomains of about the size of the A and B blocks, with the precise morphology (alternating A-B layering, droplets of A immersed in B…) dependent on the molecular details and relative size of the A and B blocks (Fig. 2B) [21, 22]. Importantly, the size of the domains thus formed can be controlled by the molecular architecture of the molecules involved, opening the door to biological regulation.
A chromosome-oriented example that highlights the differences between bulk and micro- phase separation appears to be the behavior of nucleoli, which in Xenopus oocytes appear as many droplets floating around in the nucleus, organized around the many (amplified) rDNA fragments which provide massive production of rRNAs. These many pieces of DNA carry sequences which act as templates to organize the individual nucleoli droplets, and smaller nucleoli are observed to fuse together and slowly increase in size with time, under conditions where they are able to move around. In the frog egg case, actin network disruption allows the nucleoli to combine into one large nucleolus (Fig. 2C) [23, 25].
Conversely, in human somatic cells the rDNAs are present on five acrocentric chromosomes, and must crowd together to form a nucleolus. Although fusion events have been observed (Fig. 2D) [24], the fact that one often sees more than one nucleolus might reflect the fact that the 200 or so copies of the ribosomal genes have difficulty packing together, and tend instead to have a crowding-limited size. This could be a case of a domain size set by “short-ranged attraction” (the sticking together of rDNA regions) and “long-ranged repulsion” (the limit on nucleolar size set by crowding of the peri-rDNA regions). Interestingly, the surface tension of nucleoli in human cells has recently been measured to have the very small value of σ ≈ 10−6 N/m [24], suggestive of the basic objects which are driving aggregation being roughly r = (kBT/σ)1/2 > 50 nm in size – and therefore more likely large complexes of RNA, DNA and protein rather than individual smaller (e.g., protein) molecules. Recent work suggests that active (energy-consuming) rearrangements of chromatin play a role in nucleolar fusion [26], which might prove to be inconsistent with a simple “passive” surface tension-driven-viscous-flow model of the fusion dynamics.
A rather clear example of phase/microphase separation in the nucleus is the organization of alternation of euchromatic “A” and heterochromatic “B” regions along eukaryote chromosomes [27]. As a result of B-B attractions (mediated by, for example, HP1α- or polycomb- methylated-histone interactions) combined with the constraint of attachment of B regions to the nuclear envelope, the nucleus is organized into A- and B-rich “microdomains” [28]. When released from the nuclear envelope, there is apparently enough conformational flexibility of the B regions to allow formation of a large, central heterochromatic domain in the middle of an “inverted nucleus” [29]. In all these cases, when looking at membraneless organelles, two questions immediately arise: What is the surface tension?, and Is there something limiting or regulating the size of the droplet-organelles?
Liquid Versus Solid Versus Something In Between
Looking at the heterochromatic regions near the eukaryote nuclear envelope [30] raises the question of whether they are more of a liquid or a solid. Mechanical experiments on the nucleus suggest that the B regions are actually solid, at least on few-minute timescales [31]. Increased amounts of heterochromatin lead to increased elastic stiffness [32]: if the heterochromatic B regions were liquid, there would be no change in elasticity. Experiments demonstrating that the nuclear envelope is stabilized (destabilized) against spontaneous rupture by increased (decreased) heterochromatinization further support this conclusion [33].
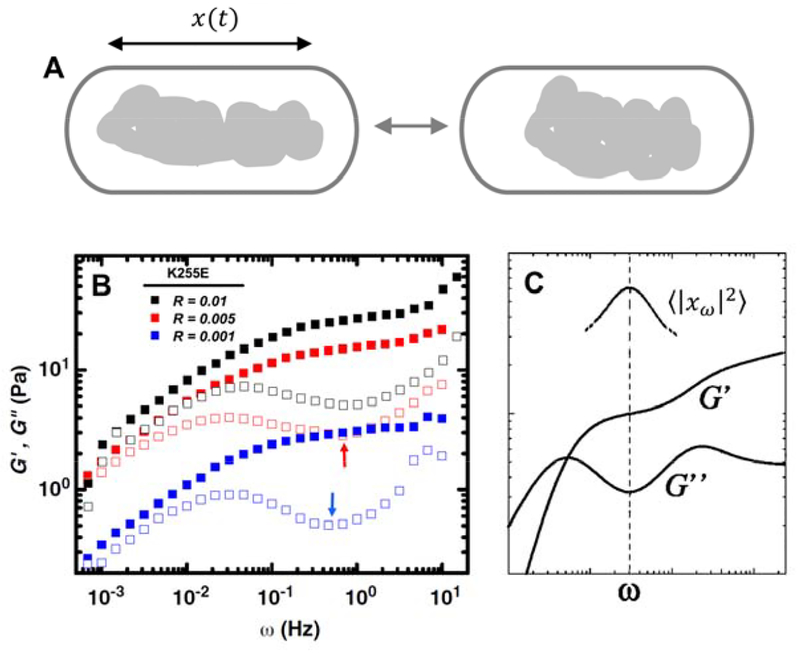
One can have an intermediate behavior between solid and liquid, namely viscoelastic behavior. Suppose we are looking at an object – say part of the cytoskeleton, or a chromosome - in a cell, and we can see it undergoing fluctuations either due to either thermal or nonthermal forces (Fig. 3A). Any force acting to deform the chromosome must balance the sum of spring-like elasticity and viscous drag forces
The distinction between liquid and solid is whether the “spring constant” k is zero or nonzero (x and dx/dt are the position and velocity of some measure of the deformation of the chromosome, say its overall length). The force balance equation can be written in terms of the frequency components of x (xω, related to x(t) via the Fourier transform x(t) = Σω xω eiωt):
This is the same equation, but now in terms of frequency ω has the simple solution (the Fourier transform eliminates the time derivative) xω = fω / (k + i ω ζ), showing that more elasticity (k) or more friction (viscous drag ζ) lowers the amplitude of response xω to a force jiggling at frequency ω.
Figure 3.
A. Viscoelastic object in cell (e.g., cytoskeleton, chromosome) jiggling, undergoing length and width changes in time which can be analyzed to obtain frequency-dependent storage G′ and loss G″ moduli. B. Moduli for cytoskeletal material (actin non-covalently crosslinked by an actin-crosslinking protein) studied in vitro. Filled squares indicate G′ while open squares indicate G″; note dips in G″ (arrows) [34]. C. Sketch of moduli of “soft glassy” materials similar to those of B [36], which under white-noise drive can show a viscoelastic peak, due to the dip in G″ (reminiscent in shape to a resonance but of entirely different physical origin; figure adapted from Ref. [36]).
Moderately complicated soft materials (e.g., gels with finite-lifetime crosslinks) often have slow and frequency-dependent energy dissipation (friction) [34]. This can be modeled simply by making ζ frequency-dependent (the general case): we suddenly have xω = fω / (k + i ω ζω) (we keep the k to permit a zero-frequency static spring constant). The frequency-dependence of drag coefficient is viscoelastic behavior, typical of polymer and other soft materials which are somewhere between solids and liquids, with stiffness and friction that depend on the temporal frequency that we stress them at (Sec. 7.3 of [35]). It is conventional to refer to the combination iωζω = gω as the viscoelastic modulus (or in this simple spring model, more properly the viscoelastic spring constant), so that the solution has the simple form xω = fω / (k +gω). Here gω is complex-valued, with its real part Re gω referred to as the “storage modulus” (springiness, called G′ for bulk viscoelastic materials) and its imaginary part Im gω referred to as the “loss modulus” (drag or friction, G″).
For random fluctuations generated by the action of many largely independent molecular motors it is reasonable to use a white-noise model where the mean-squared noise amplitude is constant with frequency, 〈∣fω∣2〉 = ε (〈〉 indicates “average” here). Now, the mean squared fluctuation amplitude is
It is worth noting that we can now set k=0 and this formula still makes sense – in that case we have a viscoelastic liquid which can store energy like a spring on relatively short time scales, but which will flow on longer time scales.
Given that for many complex biomaterials one finds local minima in Im gω as a function of ω (Fig. 3B) it is possible to have peaks in 〈∣xω∣2〉 (often called the “power spectrum”) as a function of frequency (Fig. 3C) [34, 36]. Analysis of the case of purely thermal fluctuations requires us to use a specific type of “colored” noise [37] in which case the question of whether or not there are peaks in the power spectrum is more complicated, but peaks do require minima in Im gω. While reminiscent of resonance (e.g., the ringing of a bell after it is struck), such peaks arising from dips in ζω are of entirely nonresonant origin (there is no inertia: ζω is pure friction), and instead correspond to a timescale over which there is “memory” of past deformations, e.g., the lifetime of non-covalent cross-linkers or other transient structural elements that move slowly compared to the filaments that they interconnect. Evidence for this kind of “strain memory” viscoelastic behavior has been observed for bacterial and eukaryote chromosomes [38, 39].
The Case of the Exploding Bacterial Chromosome
When we lysozyme away a bacterial cell wall, it is not long until that cell bursts, particularly when in low-osmolality solution. Bacterial chromosomologists know that once outside the cell the bacterial chromosome expands in radius by a factor from 3 to 10 – meaning a gigantic volume increase [40–42] – Why does that happen?
One often hears that it is the DNA concentration driving this (and molecular crowding compressing the nucleoid in vivo) – but in fact the DNA concentration is in some sense not terribly high: about 107 base pairs (bp) in a cubic micron (DNA volume fraction roughly 2%). For confined DNA, each persistence length (region along double helix that one bend occurs along) of 150 bp acts as an independent particle, so the (osmotic) pressure due to the DNA comes from a persistence length density of around c = 6×104 / 10−18 m3 = 1023 m−3. Shoving these persistence lengths into the nucleoid requires a pressure p = kBT c = 200 Pascals (Pa). This is a pretty small pressure (standard atmospheric pressure is 101 kPa), and indeed this is the scale of the elastic modulus inferred for chromosomes inside cells. Ribosomes and proteins that are unable to penetrate the chromosome can compress it (“crowd” it) via their own osmotic pressure (similar concentrations and resulting pressures to the DNA segment pressure estimated above).
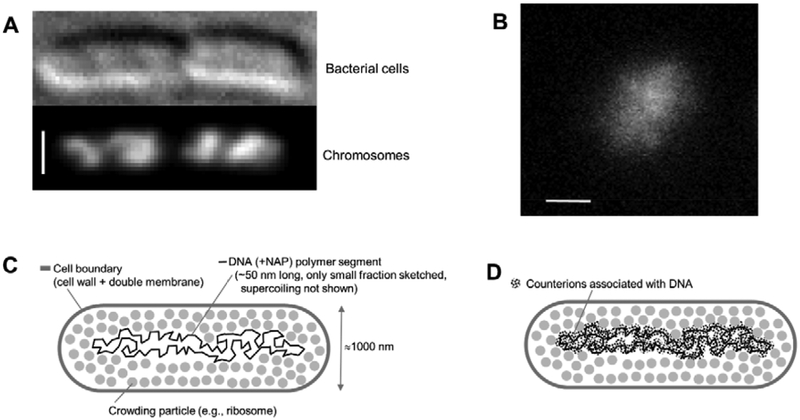
Now, confining DNA also means confining counterions for all those phosphates. There are 300 (univalent) ions per persistence length (150 bp), and therefore 300 times the pressure, or more than 50,000 Pa = 50 kPa – about half an atmosphere! This is what swells polyelectrolyte gels, and this is an additional pressure that one must work against to confine the bacterial chromosome in vivo. In fact, the density of counterions in the nucleoid is around c = 2×107 / 10−18 = 2 × 1025 m−3: using the conversion 1 M = 0.6 × 1027 m−3 (or the more useful 1 nM = 0.6 molecules per μm3) we see that there is around 50 mM excess cation concentration in the nucleoid. Of course, DNA-binding proteins and polyvalent cations can be expected to reduce the counterion pressure somewhat below what we have estimated above (perhaps down to 10 kPa). But this counterion pressure dominates osmotic pressure of the DNA segments. In eukaryotes, a higher fraction of DNA phosphates is neutralized by histones and polyamines, plus there is nuclear confinement and a denser internal crosslinking infrastructure, leading to a lower degree of polyelectrolyte swelling when nuclei and chromosomes are released from eukaryote cells. One must keep in mind that the net pressures and stresses inside and outside the chromosome must be in balance: if not, the chromosome and crowders would rearrange until hydrostatic/osmotic/mechanical equilibrium was reached. So, there must be a large net pressure in the 10 kPa range in the region outside the chromosome (Fig. 4D, gray balls) as well as inside it, ultimately balanced by stress in the solid cell wall.
Figure 4.
Bacterial chromosome inside [43](A, bar 2 μm), and outside (B, bar 2 μm) [42] a cell. Tightly confining DNA, as inside these two bacterial cells, means confining not just the polymer segments (C) but the many counterions per segment (D), with a resulting large counterion pressure.
Getting the Tangles Out – Conditioning the Chromosome
The bacterial nucleoid is sometimes thought of as a little drop of polymer (DNA) solution confined inside the cell – but such an organization would be a kind of bad idea since one expects about one entanglement per every few hundred persistence lengths, or something like 1000 entanglements within each chromosome. It has been pointed out that the elongated shape of many bacterial cells helps to reduce entanglements by forcing DNA molecules to be organized in an elongated fashion [44], rather like train cars in a tunnel (the train cars being the “blobs” associated with one-dimensional confinement, see Sec. I.4.2 of [17]). Additionally, it does appear in many studies as if the bacterial chromosome is “folded” into a supra-molecular noodle or filament inside the cell. In any case, bacteria must be careful about how their chromosomes are folded: simple condensation of the nucleoid – sticking of protein-DNA segments together willy-nilly – will increase entanglement, due to the larger number of close contacts, as occurs in a polymer melt (Sec. VIII of [17]). Lurking in the background are type-II topoisomerases which allow DNA segment to pass through DNA segment, permitting DNA topology change to occur, but under close confinement, those topoisomerases will happily increase the level of DNA entanglement.
The scaling behavior of the linking number of separate polymers confined together like the chromosomes in a bacterium or cell nucleus has been studied, and the basic result is that for n polymers each N segments long (crudely, persistence lengths), the mean-squared linking number (linking number of separate DNA duplexes is often called “catenation number” or Ca) scales up as [45]
Here the mean-squared form reflects the fact that individual links are signed + or − (left- or right-handed crossings), and so the total catenation number “diffuses”, like a random walk. If we suppose that left- and right- handed catenations are equally likely, the average Ca will be zero; however, the width of the Ca distribution 〈Ca2〉 grows with N, meaning that the typical entanglement of chromosomes will increase with N (the typical value of Ca will have magnitude of the square root of 〈Ca2〉). The number q is the probability that any particular segment is the point at which an entanglement is present (think of two “hooked” polymer chains). One can think about 1/q as the entanglement length, or number of segments along a polymer involved in each entanglement. For a polymer melt, q ≈ 1/100 (this is a kind of universal number), meaning that the entanglement length is around 100 segments. For “naked” bacterial chromosomes with N ≈105, we obtain 〈Ca2〉 ≈103. This represents the steady-state entanglement that would arise from letting type-II topos run wild on confined, naked bacterial chromosome DNAs.
This formula indicates that there are two ways for type-II topos to be “told” how to disentangle chromosomes. One is to increase n and decrease N, i.e., chop the genome up into many tiny bits. Budding yeast may employ this strategy, having a rather prodigious number of rather short chromosomes that appear to move as via “Rouse dynamics” characteristic of disentangled polymers [47]. But, this approach is untenable for large genomes and in any case is not how most bacteria and eukaryotes have evolved. The alternative is to keep n relatively small, but decrease N. This means – reduce the number of effective polymer segments along each chromosome. This can be done by lengthwise compaction, or locally “bunching up” DNA along the length of the chromosome with nearby cis contacts, while avoiding distant and trans contacts [45] – appropriately “dressing” the naked DNAs.
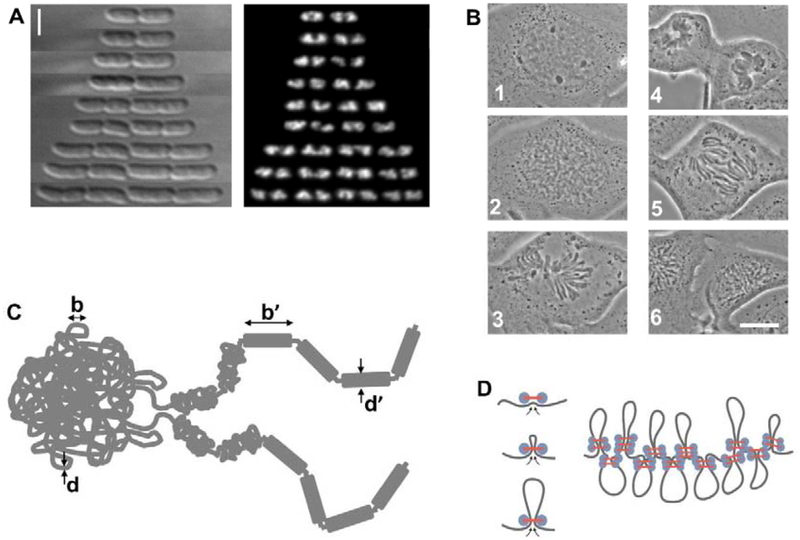
A bit of polymer physics indicates that less than a 100-fold or so reduction in length - along with a concomitant increase in thickness - is sufficient to reach the point where 〈Ca2〉 < 1, even for very large or tightly confined chromosomes [45]. In the bacterial case, a 50-fold compaction in length from 1500 μm to 30 μm will make the chromosome roughly 7-fold thicker, generating up to a 74 ≈ 2000-fold increase in persistence length (the 4th power can be argued to apply for dense crosslinking; we can expect less for less tightly linked DNA in a chromosome). For a more modest 200-fold persistence length increase to about 1 μm we arrive at a segment length for the lengthwise-compacted N ≈ 30 μm / 1 μm = 30, a short enough chromosome to be usually fully disentangled from its sister chromatid in its topological steady state. There are a number of studies which have concluded this kind of “thick filament” picture of bacterial chromosomes [43, 48]: the same lengthwise compaction is precisely how the large eukaryote chromosomes of vertebrates are observed to self-organize during prophase.
How could lengthwise compaction occur? Largely on the basis of electron-microscope observations, many researchers have hypothesized that this is achieved by self-organization of the chromosome into a tandem array of loops [49–55], perhaps further compacted by proteins that stabilize DNA-DNA “crosslinking” interactions. The loops themselves may be established by SMC complexes which are thought to be capable of actively driving “loop extrusion” and chromosome individualization [51, 54, 56, 57]. In vitro such dynamics have been observed for single SMCs [58], albeit along isolated naked DNAs. If future experiments continue to support this “lengthwise-compaction by SMC-complex driven loop extrusion” hypothesis, we will see a remarkable unification of chromosome dynamics spanning all the kingdoms of life, in which statistical physics will have played a central explanatory and predictive role.
Figure 5.
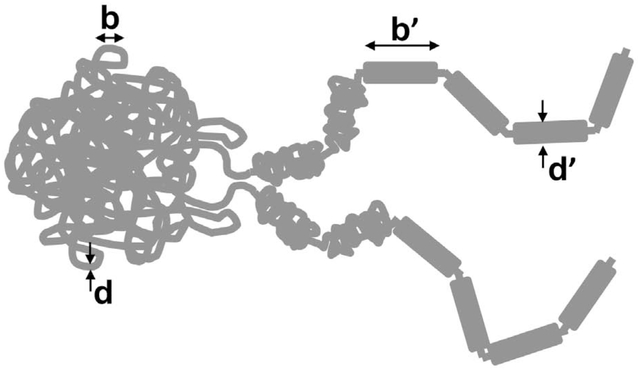
A. Images of chromosomes in rapidly growing and dividing E. coli bacterial cells where replicated chromosomes are thought to separate themselves from one another without the aid of cytoskeletal structures. Bar is 2 μm. B. Eukaryote cell cycle metaphase chromosome compaction process. (images are of newt N. viridescens cells, bar is 20 μm [46]). C. Lengthwise compaction. As polymers (chromosomes) are lengthwise compacted (made shorter and thicker by local folding), under conditions where topology can change (if topoisomerases are present and active), entanglements will be progressively removed at larger and larger length scales. D. Loop extrusion hypothesis for lengthwise compaction. Loop-extruding machines (LEMs) bind and actively generate loops (left); if they dissociate slowly, they will self-organize a long polymer into an array of loops robustly anchored by multiple LEMs.
Acknowledgements
I thank the CNRS and Drs. J.-M. Victor and M. Barbi for supporting my stay at SU, and Dr. H. Brandao, Prof. C. Brangwynne, and Prof. A. Zidovska for their thoughtful comments. This work was supported by NIH grants GM105847, CA193419 (NU-PS-OC), and by subcontract to DK107980 (4DN).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
This has gradually become somewhat official: the 2017 NIGMS T32 RFA mentions training in “quantitative approaches” as a desirable outcome, https://grants.nih.gov/grants/guide/pa-files/par-17-341.html.
According to the US government, only three countries have not officially adopted the SI system of units: Myanmar, Liberia, and the US, https://www.cia.gov/library/publications/the-world-factbook/appendix/appendix-g.html
References Cited
- [1].National Research Council. BIO2010: Transforming Undergraduate Education for Future Research Biologists. Washington, DC: The National Academies Press; 2003. [PubMed] [Google Scholar]
- [2].Davis CA, Hitz BC, Sloan CA, Chan ET, Davidson JM, Gabdank I, et al. The Encyclopedia of DNA elements (ENCODE): data portal update. Nucleic acids research. 2018;46:D794–D801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Kerpedjiev P, Abdennur N, Lekschas F, McCallum C, Dinkla K, Strobelt H, et al. HiGlass: web-based visual exploration and analysis of genome interaction maps. Genome Biol. 2018;19:125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Eagen KP. Principles of Chromosome Architecture Revealed by Hi-C. Trends Biochem Sci. 2018;43:469–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Clouter WG, Powell LS. The M.K.S. system. The Vocational Aspect of Secondary and Further Education. 1952;4:71–81. [Google Scholar]
- [6].Yao M, Goult BT, Klapholz B, Hu X, Toseland CP, Guo Y, et al. The mechanical response of talin. Nature communications. 2016;7:11966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Skoko D, Yoo D, Bai H, Schnurr B, Yan J, McLeod SM, et al. Mechanism of chromosome compaction and looping by the Escherichia coli nucleoid protein Fis. Journal of molecular biology. 2006;364:777–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Essevaz-Roulet B, Bockelmann U, Heslot F. Mechanical separation of the complementary strands of DNA. Proceedings of the National Academy of Sciences of the United States of America. 1997;94:11935–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Visscher K, Schnitzer MJ, Block SM. Single kinesin molecules studied with a molecular force clamp. Nature. 1999;400:184–9. [DOI] [PubMed] [Google Scholar]
- [10].Civelekoglu-Scholey G, Scholey JM. Mitotic force generators and chromosome segregation. Cellular and molecular life sciences: CMLS. 2010;67:2231–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Prass M, Jacobson K, Mogilner A, Radmacher M. Direct measurement of the lamellipodial protrusive force in a migrating cell. The Journal of cell biology. 2006;174:767–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Izeddin I, Recamier V, Bosanac L, Cisse II, Boudarene L, Dugast-Darzacq C, et al. Single-molecule tracking in live cells reveals distinct target-search strategies of transcription factors in the nucleus. eLife. 2014;3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Yildiz A, Forkey JN, McKinney SA, Ha T, Goldman YE, Selvin PR. Myosin V Walks Hand-Over-Hand: Single Fluorophore Imaging with 1.5-nm Localization. Science. 2003;300:2061–5. [DOI] [PubMed] [Google Scholar]
- [14].Nikon. Cell Motility, https://www.microscopyu.com/galleries/cell-motility. 2019. p. U2OS cells, Movie 1.
- [15].Berg HC. Random Walks in Biology: New and Expanded Edition: Princeton University Press; 1993. [Google Scholar]
- [16].Wheeler RJ, Hyman AA. Controlling compartmentalization by non-membrane-bound organelles. Philosophical transactions of the Royal Society of London Series B, Biological sciences. 2018;373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].de Gennes PG. Scaling concepts in polymer physics: Cornell University Press; 1979. [Google Scholar]
- [18].Katzen D, Reich S. Image-Analysis of Phase-Separation in Polymers Blends. Europhys Lett. 1993;21:55–60. [Google Scholar]
- [19].Bergeron-Sandoval L-P, Heris HK, Chang C, Cornell CE, Keller SL, Francois P, et al. Endocytosis caused by liquid-liquid phase separation of proteins. bioRxiv. 2018:145664. [Google Scholar]
- [20].Shin Y, Chang YC, Lee DSW, Berry J, Sanders DW, Ronceray P, et al. Liquid Nuclear Condensates Mechanically Sense and Restructure the Genome. Cell. 2018;175:1481–91 e13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Hashimoto T, Nagatoshi K, Todo A, Hasegawa H, Kawai H. Domain-Boundary Structure of Styrene-Isoprene Block Copolymer Films Cast from Toluene Solutions. Macromolecules. 1974;7:364–73. [Google Scholar]
- [22].Hasegawa H, Tanaka H, Yamasaki K, Hashimoto T. Bicontinuous microdomain morphology of block copolymers. 1. Tetrapod-network structure of polystyrene-polyisoprene diblock polymers. Macromolecules. 1987;20:1651–62. [Google Scholar]
- [23].Brangwynne CP, Mitchison TJ, Hyman AA. Active liquid-like behavior of nucleoli determines their size and shape in Xenopus laevis oocytes. Proceedings of the National Academy of Sciences of the United States of America. 2011;108:4334–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Caragine CM, Haley SC, Zidovska A. Surface Fluctuations and Coalescence of Nucleolar Droplets in the Human Cell Nucleus. Physical review letters. 2018;121:148101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Feric M, Brangwynne CP. A nuclear F-actin scaffold stabilizes ribonucleoprotein droplets against gravity in large cells. Nat Cell Biol. 2013;15:1253–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Caragine CM, Haley SC, Zidovska A. Nucleolar dynamics and interactions with nucleoplasm in living cells. eLife. 2019;8:e47533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Lieberman-Aiden E, van Berkum NL, Williams L, Imakaev M, Ragoczy T, Telling A, et al. Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science. 2009;326:289–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Belaghzal H, Borrman T, Stephens AD, Lafontaine DL, Venev SV, Weng Z, et al. Compartment-dependent chromatin interaction dynamics revealed by liquid chromatin Hi-C. bioRxiv. 2019:704957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Falk M, Feodorova Y, Naumova N, Imakaev M, Lajoie BR, Leonhardt H, et al. Heterochromatin drives compartmentalization of inverted and conventional nuclei. Nature. 2019;570:395–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Ou HD, Phan S, Deerinck TJ, Thor A, Ellisman MH, O’Shea CC. ChromEMT: Visualizing 3D chromatin structure and compaction in interphase and mitotic cells. Science. 2017;357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Stephens AD, Banigan EJ, Adam SA, Goldman RD, Marko JF. Chromatin and lamin A determine two different mechanical response regimes of the cell nucleus. Molecular biology of the cell. 2017;28:1984–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Stephens AD, Liu PZ, Banigan EJ, Almassalha LM, Backman V, Adam SA, et al. Chromatin histone modifications and rigidity affect nuclear morphology independent of lamins. Molecular biology of the cell. 2018;29:220–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Stephens AD, Liu PZ, Kandula V, Chen H, Almassalha LM, Herman C, et al. Physicochemical mechanotransduction alters nuclear shape and mechanics via heterochromatin formation. Molecular biology of the cell. 2019;30:2320–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Yao NY, Becker DJ, Broedersz CP, Depken M, Mackintosh FC, Pollak MR, et al. Nonlinear viscoelasticity of actin transiently cross-linked with mutant alpha-actinin-4. Journal of molecular biology. 2011;411:1062–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Doi M, Edwards SF. The Theory of Polymer Dynamics: Oxford University Press; 1986. [Google Scholar]
- [36].Sollich P. Rheological constitutive equation for a model of soft glassy materials. Phys Rev E. 1998;58:738–59. [Google Scholar]
- [37].Kubo R. The Fluctuation-Dissipation Theorem. Rep Prog Phys. 1966;29:255–84. [Google Scholar]
- [38].Weber SC, Spakowitz AJ, Theriot JA. Bacterial chromosomal loci move subdiffusively through a viscoelastic cytoplasm. Physical review letters. 2010;104:238102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Lucas Joseph S, Zhang Y, Dudko Olga K, Murre C. 3D Trajectories Adopted by Coding and Regulatory DNA Elements: First-Passage Times for Genomic Interactions. Cell. 2014;158:339–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Pelletier J, Halvorsen K, Ha BY, Paparcone R, Sandler SJ, Woldringh CL, et al. Physical manipulation of the Escherichia coli chromosome reveals its soft nature. Proceedings of the National Academy of Sciences of the United States of America. 2012;109:E2649–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Cunha S, Woldringh CL, Odijk T. Polymer-mediated compaction and internal dynamics of isolated Escherichia coli nucleoids. Journal of structural biology. 2001;136:53–66. [DOI] [PubMed] [Google Scholar]
- [42].Hadizadeh N, Johnson RC, Marko JF. Facilitated Dissociation of a Nucleoid Protein from the Bacterial Chromosome. Journal of bacteriology. 2016;198:1735–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Hadizadeh Yazdi N, Guet CC, Johnson RC, Marko JF. Variation of the folding and dynamics of the Escherichia coli chromosome with growth conditions. Molecular microbiology. 2012;86:1318–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Jun S, Mulder B. Entropy-driven spatial organization of highly confined polymers: lessons for the bacterial chromosome. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:12388–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Marko JF. Scaling of Linking and Writhing Numbers for Spherically Confined and Topologically Equilibrated Flexible Polymers. Journal of statistical physics. 2011;142:1353–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Marko JF. Micromechanical studies of mitotic chromosomes. Chromosome research: an international journal on the molecular, supramolecular and evolutionary aspects of chromosome biology. 2008;16:469–97. [DOI] [PubMed] [Google Scholar]
- [47].Hajjoul H, Mathon J, Ranchon H, Goiffon I, Mozziconacci J, Albert B, et al. High-throughput chromatin motion tracking in living yeast reveals the flexibility of the fiber throughout the genome. Genome research. 2013;23:1829–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Fisher JK, Bourniquel A, Witz G, Weiner B, Prentiss M, Kleckner N. Four-dimensional imaging of E. coli nucleoid organization and dynamics in living cells. Cell. 2013;153:882–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Alipour E, Marko JF. Self-organization of domain structures by DNA-loop-extruding enzymes. Nucleic acids research. 2012;40:11202–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Goloborodko A, Marko JF, Mirny LA. Chromosome Compaction by Active Loop Extrusion. Biophysical journal. 2016;110:2162–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Goloborodko A, Imakaev MV, Marko JF, Mirny L. Compaction and segregation of sister chromatids via active loop extrusion. eLife. 2016;5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Maeshima K, Laemmli UK. A two-step scaffolding model for mitotic chromosome assembly. Developmental cell. 2003;4:467–80. [DOI] [PubMed] [Google Scholar]
- [53].Naumova N, Imakaev M, Fudenberg G, Zhan Y, Lajoie BR, Mirny LA, et al. Organization of the mitotic chromosome. Science. 2013;342:948–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Gibcus JH, Samejima K, Goloborodko A, Samejima I, Naumova N, Nuebler J, et al. A pathway for mitotic chromosome formation. Science. 2018;359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Brahmachari S, Marko JF. Chromosome disentanglement driven via optimal compaction of loop-extruded brush structures. Proceedings of the National Academy of Sciences of the United States of America. 2019;in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Marko JF, De Los Rios P, Barducci A, Gruber S. DNA-segment-capture model for loop extrusion by structural maintenance of chromosome (SMC) protein complexes. Nucleic acids research. 2019;47:6956–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Sun M, Biggs R, Hornick J, Marko JF. Condensin controls mitotic chromosome stiffness and stability without forming a structurally contiguous scaffold. Chromosome research: an international journal on the molecular, supramolecular and evolutionary aspects of chromosome biology. 2018;26:277–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Ganji M, Shaltiel IA, Bisht S, Kim E, Kalichava A, Haering CH, et al. Real-time imaging of DNA loop extrusion by condensin. Science. 2018;360:102–5. [DOI] [PMC free article] [PubMed] [Google Scholar]