Abstract
Background
No prior study to our knowledge has examined the joint contribution of a polygenic risk score (PRS), mammographic density (MD), and postmenopausal endogenous hormone levels—all well-confirmed risk factors for invasive breast cancer—to existing breast cancer risk prediction models.
Methods and findings
We conducted a nested case–control study within the prospective Nurses’ Health Study and Nurses’ Health Study II including 4,006 cases and 7,874 controls ages 34–70 years up to 1 June 2010. We added a breast cancer PRS using 67 single nucleotide polymorphisms, MD, and circulating testosterone, estrone sulfate, and prolactin levels to existing risk models. We calculated area under the curve (AUC), controlling for age and stratified by menopausal status, for the 5-year absolute risk of invasive breast cancer. We estimated the population distribution of 5-year predicted risks for models with and without biomarkers. For the Gail model, the AUC improved (p-values < 0.001) from 55.9 to 64.1 (8.2 units) in premenopausal women (Gail + PRS + MD), from 55.5 to 66.0 (10.5 units) in postmenopausal women not using hormone therapy (HT) (Gail + PRS + MD + all hormones), and from 58.0 to 64.9 (6.9 units) in postmenopausal women using HT (Gail + PRS + MD + prolactin). For the Rosner–Colditz model, the corresponding AUCs improved (p-values < 0.001) by 5.7, 6.2, and 6.5 units. For estrogen-receptor-positive tumors, among postmenopausal women not using HT, the AUCs improved (p-values < 0.001) by 14.3 units for the Gail model and 7.3 units for the Rosner–Colditz model. Additionally, the percentage of 50-year-old women predicted to be at more than twice 5-year average risk (≥2.27%) was 0.2% for the Gail model alone and 6.6% for the Gail + PRS + MD + all hormones model. Limitations of our study included the limited racial/ethnic diversity of our cohort, and that general population exposure distributions were unavailable for some risk factors.
Conclusions
In this study, the addition of PRS, MD, and endogenous hormones substantially improved existing breast cancer risk prediction models. Further studies will be needed to confirm these findings and to determine whether improved risk prediction models have practical value in identifying women at higher risk who would most benefit from chemoprevention, screening, and other risk-reducing strategies.
In a case-control study, Xuehong Zhang and colleagues study incorporation of genetic and other information into breast cancer risk models.
Author summary
Why was this study done?
A polygenic risk score (PRS), mammographic density (MD), and postmenopausal endogenous hormone levels are all well-confirmed breast cancer risk factors.
No prior study to our knowledge has comprehensively examined the joint contribution of these biological factors to improving existing breast cancer risk prediction models (i.e., the Gail model and the Rosner–Colditz model).
What did the researchers do and find?
We conducted a nested case–control study within the prospective Nurses’ Health Study and Nurses’ Health Study II that included 4,006 cases and 7,874 controls ages 34–70 years.
We calculated the area under the curve (AUC), controlling for age and stratified by menopausal status, for the 5-year absolute risk of invasive breast cancer.
We found that for both the Gail and Rosner–Colditz models, the AUC was significantly improved for both invasive and estrogen-receptor-positive breast cancers in postmenopausal women not using hormone therapy.
Additionally, the percentage of 50-year-old women predicted to be at more than twice 5-year average risk (≥2.27%) was 0.2% for the Gail model alone and 6.6% for the Gail + PRS + MD + all hormones model.
What do these findings mean?
In this study, the addition of PRS, MD, and endogenous hormones substantially improved existing breast cancer risk prediction models.
If confirmed, these findings may help identify women at higher risk who would most benefit from chemoprevention or other risk-reducing strategies.
Introduction
Breast cancer is the most commonly diagnosed cancer in women. Risk prediction models have been developed to estimate an individual woman’s breast cancer risk, and have been used to both set clinical trial entry criteria [1] and provide tailored recommendations for screening, chemoprevention, and other risk-reducing strategies. Among such models, the Gail and Rosner–Colditz models have been well validated and have been used to identify high-risk women [2–4]. The original Gail model includes 5 confirmed risk factors (e.g., family history of breast cancer and reproductive factors) [3]; the Rosner–Colditz model includes the same factors plus additional established breast cancer risk factors such as BMI, alcohol intake, and postmenopausal hormone therapy (HT) use [5]. Both models are well calibrated in white populations, although their discriminatory ability is relatively modest [6,7]. Neither model includes biological markers of risk.
Multiple common genetic risk variants [8] and breast density [9], as measured on a mammogram, are additional well-confirmed breast cancer risk factors. Recent studies, though limited, have shown that including genetic risk variants (either individually or as a polygenic risk score [PRS]) and/or mammographic density (MD) significantly improves both the Gail model [10–17] and the Rosner–Colditz model [18]. In addition, considerable evidence supports an association of circulating estrogens, androgens, and prolactin with postmenopausal breast cancer risk [19–23]. These circulating hormones are only modestly correlated with either breast cancer genetic risk variants or MD [9]. We [24] and others [25] have recently found that incorporating hormones can improve breast cancer risk prediction. However, except for 1 small study on estrogen-receptor-positive (ER+) breast cancer [26], no other study to our knowledge has examined the degree to which incorporating all of these biological markers of risk improves risk prediction. Hence, we conducted an evaluation of the independent and joint contribution of PRS, MD, and endogenous hormone levels to the Gail and Rosner–Colditz models in the Nurses’ Health Study (NHS; follow-up 1976–2010) [27] and the Nurses’ Health Study II (NHSII; 1997–2009) [21].
Methods
Study population
The NHS was established in 1976 and included 121,700 female registered nurses aged 30–55 years [27], and the NHSII was established in 1989 and included 116,429 female registered nurses aged 25–42 years [21]. Questionnaires were mailed to women biennially to collect information on breast cancer risk factors, including age at menarche, age at first birth, parity, family history of breast cancer, height, weight, physical activity, menopausal status, age at menopause, and HT use. Alcohol consumption was assessed using a validated semi-quantitative food frequency questionnaire. This study was approved by the ethical review committees at Brigham and Women’s Hospital and the Harvard T.H. Chan School of Public Health. The completion and mailed return of the self-administered questionnaire was considered to imply informed consent of the participants.
Outcome
We identified incident breast cancer cases up to 1 June 2010 through biennial questionnaires, confirmed the diagnoses with the participants (or next of kin), and obtained permission to collect relevant medical or pathology reports. We restricted this analysis to invasive breast cancer. We used tumor tissue microarrays (TMAs) [28,29] as the primary source to determine estrogen receptor (ER) status; when TMA data were not available (62%), we used medical/pathology reports to determine ER status. We observed high concordance (92%) of ER status between TMAs and medical/pathology reports [29,30].
Gail and Rosner–Colditz models
In each cohort, we assessed 5-year breast cancer risk using the Gail and Rosner–Colditz risk scores. The Gail score includes number of first-degree relatives with a history of breast cancer, age at menarche, age at first birth, number of previous breast biopsies by age, and information on atypical hyperplasia at biopsy [2,3]. We used a modified Gail score [7] with family history (yes/no) and excluded data on atypical hyperplasia because it was not available. Because of its low prevalence, exclusion of atypical hyperplasia does not substantially alter the calibration in our cohorts [7].
The original factors included in the Rosner–Colditz model were age at menarche, age at first birth, birth index (a combination of number of children and birth spacing), family history of breast cancer, history of benign breast disease, premenopausal duration, type of menopause, postmenopausal duration, duration of postmenopausal HT use by type and timing, BMI, height, and alcohol intake [5]. Recently, we updated the Rosner–Colditz model by further including early life somatotype [18,31,32].
Nested case–control study
The biospecimen collections for each cohort have been described in detail elsewhere [27,33–36]. Briefly, in the NHS, 32,826 participants provided blood samples in 1989–1990 and 18,743 women provided a second blood sample in 2000–2002. Among women who had not provided a blood sample, 29,684 provided a buccal cell sample in 2000–2006. In the NHSII, 29,611 participants provided blood samples in 1996–1999 and an additional 29,859 women provided cheek cells in 2004–2006. We conducted a nested case–control study among women who provided blood or buccal cell samples. We used risk set sampling and chose controls who were free from breast cancer at the same time point as the index case was diagnosed. In each cohort, we matched 1–2 control individuals by age (±1 year) and by month (±1) of biospecimen collection, and, for blood samples, by time of day (±2 hours), fasting status (≥10 hours since a meal versus <10 hours or unknown), menopausal status, and HT use at blood collection. Of note, we matched 2 controls for each postmenopausal case not using HT at blood collection and 1 control otherwise. For this study, we included invasive cases and matched controls and further included controls previously matched to in situ cases (n = 1,309) to improve statistical power. No women were identified more than once in this study. Sixty-one women initially identified as controls who subsequently became breast cancer cases were excluded from the analysis.
PRS, MD, and laboratory assays
As previously reported [37], we used the TaqMan OpenArray SNP genotyping platform (Biotrove, Woburn, MA) to genotype 67 breast-cancer-associated variants identified from a large meta-analysis of 9 genome-wide association studies [8]. We created a PRS assuming a multiplicative joint effects model, and weighted SNPs by the logarithm of the odds ratio observed in the meta-analysis (S1 Table) [8]. Among women who provided blood samples in each cohort, we collected mammograms (pre-diagnostic for cases) and measured MD (i.e., percentage dense area, the dense area divided by the total area) in the NHS for breast cancer cases diagnosed through 2004 and matched controls, and in the NHSII through 2009 [9,38]. We previously measured testosterone (T), estrone sulfate (E1S), and prolactin (PRL) in pre-diagnostic plasma samples [19,39].
Statistical analyses
We used unconditional logistic regression models to assess the relative risks (95% CIs) of invasive breast cancer with both continuous measures and quartile categories (based on control distributions) of PRS, MD, and circulating hormone levels, adjusting for matching factors. To evaluate improvement in risk prediction, we calculated the age-adjusted area under the curve (AUC) [40] as a measure of discrimination. Specifically, we compared the model including only a term for either the Gail or Rosner–Colditz risk score with a model with the risk score plus continuous measures of PRS, MD, and/or circulating hormones (each of the coefficients was obtained from age-adjusted logistic regression models). We computed separate age-specific AUCs and conducted a meta-analysis of these [40] to remove the effect of age. The population used in the analysis is shown in S2 Table. We have multiplied the AUC values by 100 for ease of presentation.
Since endogenous hormone–breast cancer associations differ by menopausal status and HT use [36], we evaluated the addition of plasma hormones only in the relevant subgroups. Specifically, for postmenopausal women not using HT at blood draw, we assessed the added value of T, E1S, and PRL. For postmenopausal women using HT at blood draw, we assessed the added value of PRL. We did not consider the addition of plasma hormones among premenopausal women because we observed weak or null associations in prior analyses [21,36]. MD and hormone levels were only available in a subset of women with genetic and questionnaire data (S2 Table). Thus, we imputed missing values to maintain the largest sample size possible. As previously described [41], we used linear regression to impute the values based on the beta coefficients obtained from a regression model, and added error to the predicted values; we used log transformed measured values as the outcome, and covariate predictors (including case status) selected based on previously published data and associations observed in our datasets. Details on imputing missing values are provided in S1 Methods.
Besides primary analyses stratified by menopausal status and HT use, we further evaluated the overall contribution of adding PRS, MD, and hormones among all invasive cases. Because the PRS and hormones are particularly strongly associated with ER+ breast cancer [8,39], we also repeated our analyses for ER+ tumors in postmenopausal women not using HT. For all models, we conducted sensitivity analyses excluding women with imputed values.
For the Gail model among postmenopausal women not using HT (the subset for which all the hormones, PRS, and MD were added), we also calculated the population distribution of predicted 5-year risks. To do this, we used the following data: (1) the relative risks from the nested case–control study [42,43], (2) the distribution of risk factors observed in our controls, and (3) age-specific incidence rates. The age-specific incidence rates were based on SEER (Surveillance, Epidemiology, and End Results; http://seer.cancer.gov/) data in white women for the years 2000–2008 (SEER17). We decided a priori to not conduct a similar analysis for the Rosner–Colditz model. Because we used the exposure distribution in our controls to estimate the population distribution, the greater the number of risk factors involved (e.g., BMI), the greater the chance our controls would not provide a sufficiently accurate reflection of the population distribution.
To assess potential model over-fitting, we used 10-fold cross-validation [24]. Lastly, we calculated the net reclassification index (NRI) to summarize the difference in proportion of individuals moving up in risk category minus the proportion moving down for those with breast cancer, and the proportion of individuals moving down minus the proportion moving up for those without breast cancer. NRI [44] is another measurement to evaluate the comparative discrimination ability of risk prediction models, and positive values of NRI indicate models’ improvement. For these analyses, we used twice the 5-year average risk (2.27%) in the general population to define the moving up or down groups (i.e., ≥2.27% versus <2.27%). We conducted all analyses using SAS version 9.2 (SAS Institute, Cary, NC). All statistical tests were 2-sided with a p-value < 0.05 indicating statistical significance. The analyses employed were all planned a priori. Additional study methods are provided in S1 Methods.
Results
Compared with controls, cases were more likely to have benign breast disease, have breast cancer family history, and consume alcohol. Also, the PRS, MD, and circulating hormone levels were higher among cases than controls (Tables 1 and S3 for individuals included in the Gail and Rosner–Colditz models, respectively).
Table 1. Baseline characteristics of cases and controls in the Nurses’ Health Study (NHS; 1990) and Nurses’ Health Study II (NHSII; 1997) for the Gail model.
| Characteristic | Cases | Controls |
|---|---|---|
| Number of cases/controls* | 4,006 | 7,874 |
| NHS | 3,048 | 4,809 |
| NHSII | 958 | 3,065 |
| Demographic/lifestyle factors | ||
| Age at blood draw, years, mean (SD) | 53.7 (8.0) | 52.1 (8.3) |
| Age at blood draw, years, n (%) | ||
| <40 | 139 (3%) | 434 (6%) |
| 40–44 | 415 (10%) | 1,168 (15%) |
| 45–49 | 928 (23%) | 2,056 (26%) |
| 50–54 | 769 (19%) | 1,395 (18%) |
| 55–59 | 711 (18%) | 1,106 (14%) |
| 60–64 | 635 (16%) | 1,016 (13%) |
| 65+ | 409 (10%) | 699 (9%) |
| BMI at blood draw, kg/m2, mean (SD) | 25.4 (4.0) | 25.5 (4.5) |
| Age at menarche, years, mean (SD) | 12.5 (1.4) | 12.5 (1.4) |
| Age at first birth, years, mean (SD) | 25.7 (3.7) | 25.5 (3.7) |
| Age at menopause, years, mean (SD) | 51.4 (4.3) | 51.1 (5.2) |
| Physical activity, MET-h/wk, mean (SD) | 16.3 (19.0) | 17.0 (19.8) |
| Alcohol consumption, g/d, mean (SD) | 4.8 (9.1) | 4.2 (8.0) |
| Parous, percent | 92% | 94% |
| Previous history of benign breast disease, percent | 50% | 42% |
| Family history of breast cancer, percent | 17% | 11% |
| Postmenopausal, percent | 61% | 55% |
| Postmenopausal women not using HT, percent | 25% | 26% |
| Postmenopausal women using HT, percent | 36% | 29% |
| Polygenic risk score†, mean | 0.19 | −0.15 |
| Percent mammographic density, mean | 33.3 | 28.7 |
| 5-year breast cancer risk score, mean | ||
| Gail score, mean | 0.017 | 0.014 |
| Hormones, median (10–90th percentile) | ||
| Estrone sulfate (pmol/l)‡ | 723 (298, 1,772) | 562 (240, 1,316) |
| Testosterone (nmol/l)‡ | 0.73 (0.40, 1.42) | 0.66 (0.34, 1.26) |
| Prolactin (μg/l)§ | 10.6 (5.8, 19.3) | 9.7 (5.5, 18.3) |
*Cheek cell data were used for 3,411 women (1,369 cases/2,042 controls) in the NHS and 2,269 women (519 cases/1,750 controls) in the NHS II. Although age and menopausal status were matching factors, the addition of unmatched controls from the excluded in situ cases resulted in imbalance on age and menopausal status.
†The polygenic risk score was created using 67 independent SNPs previously identified in genome-wide association studies; the SNPs were weighted by the natural logarithm of their respective effect sizes and standardized (converted to mean = 0 and SD = 1) among all participants. A negative value indicates that a woman is less likely to develop breast cancer than the average-risk women, based on genetic data from these SNPs. Results presented in this table were among women who contributed to Gail model analyses.
‡Among postmenopausal women not using postmenopausal HT (1,005 cases/2,070 controls).
§Among postmenopausal women (2,435 cases/4,349 controls).
HT, hormone therapy; MET, metabolic equivalent task.
Each of the PRS, MD, and plasma hormones were significantly associated with invasive breast cancer risk. Similar results were observed when including imputed hormone and MD data (S4 and S5 Tables).
The AUC was statistically significantly improved with the combination of the PRS, MD, and hormones. For example, in postmenopausal women not using HT, where we included all these markers, the AUC improved from 55.5 (Gail) to 66.0 (Gail + PRS + MD + all hormones) for the Gail model (p-value < 0.001; Table 2). The AUC improved from 61.1 (Rosner–Colditz) to 67.4 (Rosner–Colditz + PRS + MD + all hormones) for the Rosner–Colditz model (p-value < 0.001; Table 3). The NRI values were 0.080 (95% CI 0.052–0.107) for the Gail model and 0.095 (95% CI 0.051–0.139) for the Rosner–Colditz model, indicating a significant improvement in the models’ discrimination ability. Significant, but more modest, improvements were observed for premenopausal women and for postmenopausal women using HT.
Table 2. Change in age-adjusted AUC of Gail model for invasive breast cancer by including PRS, percent MD, and circulating hormones.
| Population and model | Number of cases/controls | AUC (95% CI) | Change in AUC (95% CI) |
|---|---|---|---|
| Premenopausal women | 1,571/3,525 | 55.9 (54.1–57.7)* | |
| + PRS | 60.8 (59.0–62.6) | 4.8 (2.8–6.8) | |
| + MD | 61.1 (59.3–62.9) | 5.2 (3.2–7.2) | |
| + PRS + MD | 64.1 (62.5–65.7) | 8.2 (6.0–10.4) | |
| Postmenopausal women not using HT | 1,005/2,070 | 55.5 (53.3–57.7)* | |
| + PRS | 61.1 (58.9–63.3) | 5.8 (3.3–8.3) | |
| + MD | 58.2 (56.0–60.4) | 2.8 (0.6–5.0) | |
| + T + E1S + PRL | 62.5 (60.3–64.7) | 6.8 (4.3–9.3) | |
| + PRS + MD | 62.4 (60.2–64.6) | 7.0 (4.5–9.5) | |
| + PRS + T + E1S + PRL | 64.8 (62.8–66.8) | 9.4 (6.9–11.9) | |
| + MD + T + E1S + PRL | 63.7 (61.5–65.9) | 8.2 (5.7–10.7) | |
| + PRS + MD + T + E1S + PRL | 66.0 (64.0–68.0) | 10.5 (8.0–13.0) | |
| Postmenopausal women using HT | 1,430/2,279 | 58.0 (56.0–60.0)* | |
| + PRS | 61.9 (60.1–63.7) | 3.9 (1.7–6.1) | |
| + MD | 60.9 (58.9–62.9) | 3.0 (0.8–5.2) | |
| + PRL | 59.3 (57.3–61.3) | 1.2 (-0.2–2.6) | |
| + PRS + MD | 64.3 (62.5–66.1) | 6.3 (4.1–8.5) | |
| + PRS + PRL | 62.8 (61.0–64.6) | 4.8 (2.6–7.0) | |
| + MD + PRL | 62.0 (60.2–63.8) | 3.9 (1.7–6.1) | |
| + PRS + MD + PRL | 64.9 (63.1–66.7) | 6.9 (4.7–9.1) | |
| All women | 4,006/7,874 | 56.3 (55.1–57.5)* | |
| + PRS + MD + T + E1S + PRL | 65.0 (64.0–66.0) | 8.8 (7.4–10.2) |
PRS, MD, and circulating hormones were modeled as continuous variables. Some of the changes in AUC did not match exactly to the difference in AUC shown in the table due to rounding.
*These are “baseline” AUC of the Gail model without any of the biomarkers included.
AUC, area under the curve; E1S, estrone sulfate; HT, hormone therapy; MD, mammographic density; PRL, prolactin; PRS, polygenic risk score; T, testosterone.
Table 3. Change in age-adjusted AUC of Rosner–Colditz model for invasive breast cancer by including PRS, percent MD, and circulating hormones.
| Population and model | Number of cases/controls | AUC (95% CI) | Change in AUC (95% CI) |
|---|---|---|---|
| Premenopausal women | 1,164/2,741 | 60.5 (58.5–62.5)* | |
| + PRS | 64.1 (62.1–66.1) | 3.6 (2.0–5.2) | |
| + MD | 63.3 (61.3–65.3) | 2.7 (1.1–4.3) | |
| + PRS + MD | 66.3 (64.5–68.1) | 5.7 (3.9–7.5) | |
| Postmenopausal women not using HT | 653/1,336 | 61.1 (58.6–63.6)* | |
| + PRS | 64.9 (62.4–67.4) | 3.8 (1.8–5.8) | |
| + MD | 61.9 (59.4–64.4) | 1.0 (-0.4–2.4) | |
| + T + E1S + PRL | 64.3 (61.8–66.8) | 3.1 (1.1–5.1) | |
| + PRS + MD | 65.4 (62.9–67.9) | 4.4 (2.2–6.6) | |
| + PRS + T + E1S + PRL | 66.5 (64.0–69.0) | 5.3 (2.9–7.7) | |
| + MD + T + E1S + PRL | 65.2 (62.7–67.7) | 4.0 (1.8–6.2) | |
| + PRS + MD + T + E1S + PRL | 67.4 (64.9–69.9) | 6.2 (3.8–8.6) | |
| Postmenopausal women using HT | 859/1,407 | 63.3 (60.9–65.7)* | |
| + PRS | 67.1 (64.7–69.5) | 3.9 (1.9–5.9) | |
| + MD | 65.9 (63.5–68.3) | 2.4 (1.0–3.8) | |
| + PRL | 64.6 (62.2–67.0) | 1.1 (0.1–2.1) | |
| + PRS + MD | 69.5 (67.3–71.7) | 6.1 (3.9–8.3) | |
| + PRS + PRL | 67.8 (65.4–70.2) | 4.5 (2.3–6.7) | |
| + MD + PRL | 66.7 (64.3–69.1) | 3.1 (1.5–4.7) | |
| + PRS + MD + PRL | 69.9 (67.7–72.1) | 6.5 (4.3–8.7) | |
| All women | 2,676/5,484 | 61.8 (60.4–63.2)* | |
| + PRS + MD + T + E1S + PRL | 67.8 (66.6–69.0) | 6.1 (4.9–7.3) |
PRS, MD, and circulating hormones were modeled as continuous variables. Some of the changes in AUC did not match exactly to the difference in AUC shown in the table due to rounding.
*These are “baseline” AUC for the Rosner–Colditz model without any of the biomarkers included.
AUC, area under the curve; E1S, estrone sulfate; HT, hormone therapy; MD, mammographic density; PRL, prolactin; PRS, polygenic risk score; T, testosterone.
In sensitivity analyses, results were essentially the same when we excluded controls that were matched to in situ cases. Age-stratified results are shown in S6 and S7 Tables. We observed similar significant, albeit slightly stronger, improvements in risk prediction if we restricted our analyses to those women with measured MD and plasma hormone data (S8 and S9 Tables). In addition, for the Gail model, the average changes in age-adjusted AUC for 10-fold cross-validation among postmenopausal women not using HT were 10.4 for the 90% training dataset and 9.4 for the 10% validation dataset. The corresponding values were 6.2 and 5.9 for the Rosner–Colditz model. For ER+ tumors, the AUCs improved by 14.3 units for the Gail model and by 7.3 units for the Rosner–Colditz model (all p-values < 0.001) when including PRS, MD, and all hormones for postmenopausal women not using HT (S10 Table). We further provide the coefficients for each of the input parameters for our model (S11 Table).
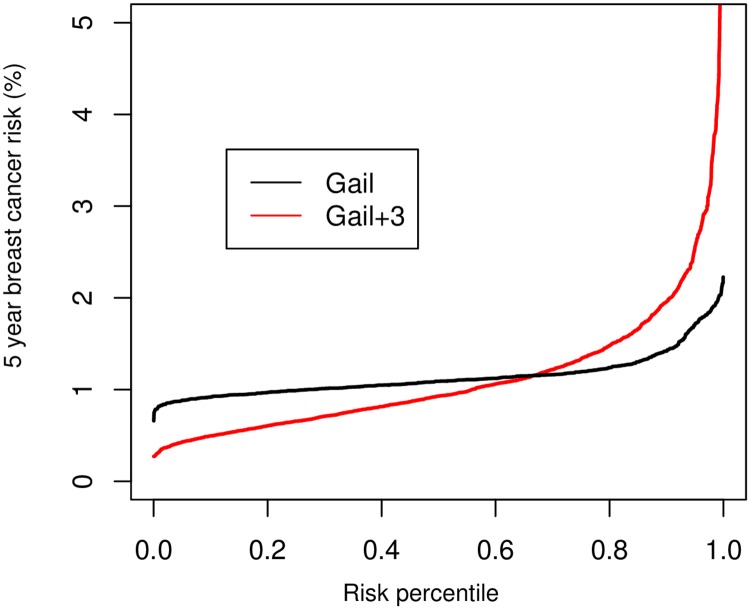
For the Gail model among postmenopausal women not using HT, we calculated the distribution of 5-year absolute risk for 50-year-old women and found that including PRS, MD, and hormones better identified low- versus high-risk women (Fig 1). Specifically, the 5-year absolute risk (10th–90th percentile) ranged from 0.93% to 1.41% for Gail, and from 0.48% to 1.95% for Gail + PRS + MD + all hormones. Additionally, the Gail model alone predicted risk at or above 2.27% (i.e., twice average risk) for 0.2% of 50-year-old women, while the Gail + PRS + MD + all hormones model predicted risk at or above 2.27% for 6.6% of 50-year-old women.
Fig 1. Predicted 5-year risk of breast cancer by risk score percentile comparing the Gail model to the Gail model plus 3 biological markers among postmenopausal women not using hormone therapy.
In the figure, the y-axis was truncated at 5% because very few (0.69%) 50-year-old women were at 5-year risk at or greater than 5% to 12% (the maximum risk observed in our population) using the Gail + polygenic risk score + mammographic density + hormones (Gail + 3) model. The x-axis represents the risk percentile, ranging from >0 to 1 (i.e., a rank ordering of risk from >0% to 100% for the population).
Discussion
To our knowledge, this is the first study to examine the added value of incorporating multiple biomarkers, including PRS, MD, and endogenous hormones, into the Gail and Rosner–Colditz models. Although these factors individually and together improved risk prediction for both invasive and ER+ breast cancer, the model improved the most among postmenopausal women not using HT, where each of the biomarkers significantly predicted risk.
Although only 1 prior study [26] has considered PRS, MD, and endogenous hormones together, our observed associations for including individual biomarkers were consistent with previous findings [9,45,46]. For example, in our study the observed added value of the PRS (improved AUC by 3.9–5.8 units) and MD (improved AUC by 2.8–5.2) to the Gail model was comparable to that in previous studies, with AUC increases of 3–7 units after adding 9 to 77 SNPs versus the Gail model alone [10,11,45,47–49] and of 2–5 units when including Breast Imaging Reporting and Data System (BI-RADS) categories or continuous MD [15,50,51]. Given their largely independent nature, we further found that any combination of the biomarkers improved prediction beyond the addition of a single biomarker.
Furthermore, among postmenopausal women not using HT, we were able to include 3 endogenous hormones—representing 3 hormone axes only modestly correlated—which improved the model by a similar magnitude as that observed for PRS and MD. Including all these factors together improved the model the most (i.e., by 10.5 units versus the Gail model alone). We selected a minimal set of hormones that have been shown to provide the largest prediction improvement for invasive breast cancer [24]. Circulating levels of these hormones are, at most, modestly correlated with either the individual breast cancer SNPs or MD [9,46]. The overall increase in AUC when adding all biomarkers was less for the Rosner–Colditz than the Gail model, likely because estrogens and MD are strongly associated with BMI, which is included in the former model. Our results are consistent with prior studies (including our own) that have suggested independent, potentially additive associations for PRS, MD, and hormones with breast cancer risk [9,46]. For example, compared with postmenopausal women in the lowest tertile of both MD and T, women at the highest tertile of both were at 5- to 6-fold greater risk of breast cancer.
Notably, in our study population, only approximately 45% of postmenopausal women were not using HT, as the blood collections occurred during a period of time when HT was used more frequently than in the US today. In contrast, based on 1999–2010 data from the US National Health and Nutrition Examination Survey (NHANES), about 95% of postmenopausal women are not current HT users [52]. This suggests that the predictive improvement provided by adding PRS, MD, and hormones in the US population as a whole will be larger than what we observed in this study. Furthermore, we found greater improvements in the AUC among ER+ tumors than among all invasive breast cancers, suggesting that development of a risk prediction model specifically for ER+ disease might lead to better discrimination ability and more targeted chemoprevention [53,54].
Multiple issues important to the potential clinical use of these biomarkers for risk prediction still need to be addressed. Our prior work found that circulating hormone levels may only need to be measured every 10 years [39], although confirmation is needed. Further, an assessment of the cost of including endogenous hormones and risk SNPs relative to the added predictive value needs to be considered. Currently, MD is clinically reported using the BI-RADS classification system; future study should evaluate whether using the computer-assisted thresholding method (used here) or other newly developed automated methods would add significantly more information for risk prediction. In addition, the Endocrine Society and the Centers for Disease Control and Prevention have recently developed a national standardization program for the measurement of T and estradiol [55,56], thus facilitating accurate measurement of these hormones on a routine basis, but E1S and PRL measurements still need to be addressed. Importantly, further assessments of clinical usefulness, including relative benefits and harms (both objective and subjective) of actions taken after receiving a risk score (e.g., chemoprevention) also are needed in future work.
Limitations of this study deserve comment. Although this study represents one of the largest to date to evaluate the contribution of measured MD or hormone levels to risk prediction, we did not have such data on all women. However, the baseline AUCs were similar among women with measured and imputed data, and results were similar when using measured data. Because of our nested case–control design with age matching, we were not able to assess the contribution of age to the AUC, and our absolute AUC values are as a result lower than those including age would be. Also, we only included 67 SNPs, although a larger set of SNPs (at least 94) has been identified [57], which may further improve discrimination. In calculating Gail model absolute risks (with and without biomarkers), we used the risk factor distribution in our controls to estimate the distribution in the general non-Hispanic white population, in part because population distributions were not available for the biomarkers. This may have caused either an over- or underestimation of our risk estimates. To minimize assumptions made about comparability between our controls and the general population (e.g., in BMI), we only evaluated absolute risk using the simpler Gail model. In addition, it is critical to assess model calibration, and to validate these models in independent populations, which was beyond the scope of the current work. However, there are several reasons to believe our findings will hold up. We utilized 2 well-validated statistical models as the base model, the exposures added to these models were each very well confirmed and quite well quantified breast cancer risk factors, and our cross-validation analyses suggested little to no over-fitting. Lastly, our study population was predominantly white: It will be important to identify the best subset of biomarkers for breast cancer, as well as evaluate their added value, in additional racial/ethnic populations [58,59].
In summary, our findings indicate that the incorporation of multiple biomarkers improves the current Gail and Rosner–Colditz models for both total invasive breast cancer and ER+ breast cancer. If validated in independent populations, our findings could help identify women at higher risk who would most benefit from chemoprevention, screening, and other risk-reducing strategies.
Supporting information
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
Acknowledgments
We appreciate the assistance from Dr. Oana Zeleznik for the figure generation. We would like to thank the participants and staff of the NHS and NHSII for their valuable contributions as well as the state cancer registries of the following states for their help: AL, AZ, AR, CA, CO, CT, DE, FL, GA, ID, IL, IN, IA, KY, LA, ME, MD, MA, MI, NE, NH, NJ, NY, NC, ND, OH, OK, OR, PA, RI, SC, TN, TX, VA, WA, and WY. The authors assume full responsibility for analyses and interpretation of these data.
The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Abbreviations
- AUC
area under the curve
- BI-RADS
Breast Imaging Reporting and Data System
- E1S
estrone sulfate
- ER
estrogen receptor
- ER+
estrogen-receptor-positive
- HT
hormone therapy
- MD
mammographic density
- NHS
Nurses’ Health Study
- NHSII
Nurses’ Health Study II
- NRI
net reclassification index
- PRL
prolactin
- PRS
polygenic risk score
- T
testosterone
Data Availability
Investigators who wish to use data collected in the Nurses’ Health Studies are encouraged to visit http://www.nurseshealthstudy.org/researchers and contact nhsaccess@channing.harvard.edu for the Nurses’ Health Study. Access to statistical codes and datasets will be facilitated following the existing data sharing guidelines provided, which can be found on the study websites.
Funding Statement
This work was supported by the Breast Cancer Research Foundation and the National Institutes of Health (NIH) grants, UM1CA186107, R01CA49449 (to SEH), R01CA207369 (to SEH), R01CA138580 (to SST), UM1CA176726 (to WCW), R01CA131332 and R01CA175080 (to RMT). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Fisher B, Costantino JP, Wickerham DL, Redmond CK, Kavanah M, Cronin WM, et al. Tamoxifen for prevention of breast cancer: report of the National Surgical Adjuvant Breast and Bowel Project P-1 Study. J Natl Cancer Inst. 1998;90(18):1371–88. [DOI] [PubMed] [Google Scholar]
- 2.Costantino JP, Gail MH, Pee D, Anderson S, Redmond CK, Benichou J, et al. Validation studies for models projecting the risk of invasive and total breast cancer incidence. J Natl Cancer Inst. 1999;91(18):1541–8. [DOI] [PubMed] [Google Scholar]
- 3.Gail MH, Brinton LA, Byar DP, Corle DK, Green SB, Schairer C, et al. Projecting individualized probabilities of developing breast cancer for white females who are being examined annually. J Natl Cancer Inst. 1989;81(24):1879–86. [DOI] [PubMed] [Google Scholar]
- 4.Rosner BA, Colditz GA, Hankinson SE, Sullivan-Halley J, Lacey JV Jr, Bernstein L. Validation of Rosner-Colditz breast cancer incidence model using an independent data set, the California Teachers Study. Breast Cancer Res Treat. 2013;142(1):187–202. 10.1007/s10549-013-2719-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Colditz GA, Rosner B. Cumulative risk of breast cancer to age 70 years according to risk factor status: data from the Nurses’ Health Study. Am J Epidemiol. 2000;152(10):950–64. [DOI] [PubMed] [Google Scholar]
- 6.Rockhill B, Byrne C, Rosner B, Louie MM, Colditz G. Breast cancer risk prediction with a log-incidence model: evaluation of accuracy. J Clin Epidemiol. 2003;56(9):856–61. [DOI] [PubMed] [Google Scholar]
- 7.Rockhill B, Spiegelman D, Byrne C, Hunter DJ, Colditz GA. Validation of the Gail et al. model of breast cancer risk prediction and implications for chemoprevention. J Natl Cancer Inst. 2001;93(5):358–66. [DOI] [PubMed] [Google Scholar]
- 8.Michailidou K, Hall P, Gonzalez-Neira A, Ghoussaini M, Dennis J, Milne RL, et al. Large-scale genotyping identifies 41 new loci associated with breast cancer risk. Nat Genet. 2013;45(4):353–61, 61e1–2. 10.1038/ng.2563 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tamimi RM, Byrne C, Colditz GA, Hankinson SE. Endogenous hormone levels, mammographic density, and subsequent risk of breast cancer in postmenopausal women. J Natl Cancer Inst. 2007;99(15):1178–87. 10.1093/jnci/djm062 [DOI] [PubMed] [Google Scholar]
- 10.Wacholder S, Hartge P, Prentice R, Garcia-Closas M, Feigelson HS, Diver WR, et al. Performance of common genetic variants in breast-cancer risk models. N Engl J Med. 2010;362(11):986–93. 10.1056/NEJMoa0907727 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gail MH. Value of adding single-nucleotide polymorphism genotypes to a breast cancer risk model. J Natl Cancer Inst. 2009;101(13):959–63. 10.1093/jnci/djp130 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chen J, Pee D, Ayyagari R, Graubard B, Schairer C, Byrne C, et al. Projecting absolute invasive breast cancer risk in white women with a model that includes mammographic density. J Natl Cancer Inst. 2006;98(17):1215–26. 10.1093/jnci/djj332 [DOI] [PubMed] [Google Scholar]
- 13.Cook NR, Paynter NP. Genetics and breast cancer risk prediction—are we there yet? J Natl Cancer Inst. 2010;102(21):1605–6. 10.1093/jnci/djq413 [DOI] [PubMed] [Google Scholar]
- 14.Cheddad A, Czene K, Shepherd JA, Li J, Hall P, Humphreys K. Enhancement of mammographic density measures in breast cancer risk prediction. Cancer Epidemiol Biomarkers Prev. 2014;23(7):1314–23. 10.1158/1055-9965.EPI-13-1240 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Vachon CM, van Gils CH, Sellers TA, Ghosh K, Pruthi S, Brandt KR, et al. Mammographic density, breast cancer risk and risk prediction. Breast Cancer Res. 2007;9(6):217 10.1186/bcr1829 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Maas P, Barrdahl M, Joshi AD, Auer PL, Gaudet MM, Milne RL, et al. Breast cancer risk from modifiable and nonmodifiable risk factors among white women in the United States. JAMA Oncol. 2016;2(10):1295–302. 10.1001/jamaoncol.2016.1025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Garcia-Closas M, Gunsoy NB, Chatterjee N. Combined associations of genetic and environmental risk factors: implications for prevention of breast cancer. J Natl Cancer Inst. 2014;106(11):dju305. 10.1093/jnci/dju305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rice MS, Tworoger SS, Hankinson SE, Tamimi RM, Eliassen AH, Willett WC, et al. Breast cancer risk prediction: an update to the Rosner–Colditz breast cancer incidence model. Breast Cancer Res Treat. 2017;166(1):227–40. 10.1007/s10549-017-4391-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tworoger SS, Eliassen AH, Zhang X, Qian J, Sluss PM, Rosner BA, et al. A 20-year prospective study of plasma prolactin as a risk marker of breast cancer development. Cancer Res. 2013;73(15):4810–9. 10.1158/0008-5472.CAN-13-0665 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Endogenous Hormones and Breast Cancer Collaborative Group, Key TJ, Appleby PN, Reeves GK, Travis RC, Alberg AJ, et al. Sex hormones and risk of breast cancer in premenopausal women: a collaborative reanalysis of individual participant data from seven prospective studies. Lancet Oncol. 2013;14(10):1009–19. 10.1016/S1470-2045(13)70301-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fortner RT, Eliassen AH, Spiegelman D, Willett WC, Barbieri RL, Hankinson SE. Premenopausal endogenous steroid hormones and breast cancer risk: results from the Nurses’ Health Study II. Breast Cancer Res. 2013;15(2):R19 10.1186/bcr3394 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tikk K, Sookthai D, Johnson T, Rinaldi S, Romieu I, Tjonneland A, et al. Circulating prolactin and breast cancer risk among pre- and postmenopausal women in the EPIC cohort. Ann Oncol. 2014;25(7):1422–8. 10.1093/annonc/mdu150 [DOI] [PubMed] [Google Scholar]
- 23.Key TJ, Appleby PN, Reeves GK, Travis RC, Brinton LA, Helzlsouer KJ, et al. Steroid hormone measurements from different types of assays in relation to body mass index and breast cancer risk in postmenopausal women: reanalysis of eighteen prospective studies. Steroids. 2015;99(Pt A):49–55. 10.1016/j.steroids.2014.09.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tworoger SS, Zhang X, Eliassen AH, Qian J, Colditz GA, Willett WC, et al. Inclusion of endogenous hormone levels in risk prediction models of postmenopausal breast cancer. J Clin Oncol. 2014;32(28):3111–7. 10.1200/JCO.2014.56.1068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Husing A, Fortner RT, Kuhn T, Overvad K, Tjonneland A, Olsen A, et al. Added value of serum hormone measurements in risk prediction models for breast cancer for women not using exogenous hormones: results from the EPIC cohort. Clin Cancer Res. 2017;23(15):4181–9. 10.1158/1078-0432.CCR-16-3011 [DOI] [PubMed] [Google Scholar]
- 26.Shieh Y, Hu D, Ma L, Huntsman S, Gard CC, Leung JWT, et al. Joint relative risks for estrogen receptor-positive breast cancer from a clinical model, polygenic risk score, and sex hormones. Breast Cancer Res Treat. 2017;166(2):603–12. 10.1007/s10549-017-4430-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Colditz GA, Hankinson SE. The Nurses’ Health Study: lifestyle and health among women. Nat Rev Cancer. 2005;5(5):388–96. 10.1038/nrc1608 [DOI] [PubMed] [Google Scholar]
- 28.Tamimi RM, Baer HJ, Marotti J, Galan M, Galaburda L, Fu Y, et al. Comparison of molecular phenotypes of ductal carcinoma in situ and invasive breast cancer. Breast Cancer Res. 2008;10(4):R67 10.1186/bcr2128 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Collins LC, Marotti JD, Baer HJ, Tamimi RM. Comparison of estrogen receptor results from pathology reports with results from central laboratory testing. J Natl Cancer Inst. 2008;100(3):218–21. 10.1093/jnci/djm270 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Poole EM, Schernhammer E, Mills L, Hankinson SE, Tworoger SS. Urinary melatonin and risk of ovarian cancer. Cancer Causes Control. 2015;26(10):1501–6. 10.1007/s10552-015-0640-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Baer HJ, Colditz GA, Rosner B, Michels KB, Rich-Edwards JW, Hunter DJ, et al. Body fatness during childhood and adolescence and incidence of breast cancer in premenopausal women: a prospective cohort study. Breast Cancer Res. 2005;7(3):R314–25. 10.1186/bcr998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sexton KR, Franzini L, Day RS, Brewster A, Vernon SW, Bondy ML. A review of body size and breast cancer risk in Hispanic and African American women. Cancer. 2011;117(23):5271–81. 10.1002/cncr.26217 [DOI] [PubMed] [Google Scholar]
- 33.Belanger CF, Hennekens CH, Rosner B, Speizer FE. The Nurses’ Health Study. Am J Nurs. 1978;78(6):1039–40. [PubMed] [Google Scholar]
- 34.Hankinson SE, Willett WC, Manson JE, Hunter DJ, Colditz GA, Stampfer MJ, et al. Alcohol, height, and adiposity in relation to estrogen and prolactin levels in postmenopausal women. J Natl Cancer Inst. 1995;87(17):1297–302. [DOI] [PubMed] [Google Scholar]
- 35.Missmer SA, Eliassen AH, Barbieri RL, Hankinson SE. Endogenous estrogen, androgen, and progesterone concentrations and breast cancer risk among postmenopausal women. J Natl Cancer Inst. 2004;96(24):1856–65. 10.1093/jnci/djh336 [DOI] [PubMed] [Google Scholar]
- 36.Hankinson SE, Willett WC, Manson JE, Colditz GA, Hunter DJ, Spiegelman D, et al. Plasma sex steroid hormone levels and risk of breast cancer in postmenopausal women. J Natl Cancer Inst. 1998;90(17):1292–9. 10.1093/jnci/90.17.1292 [DOI] [PubMed] [Google Scholar]
- 37.Hiraki LT, Joshi AD, Ng K, Fuchs CS, Ma J, Hazra A, et al. Joint effects of colorectal cancer susceptibility loci, circulating 25-hydroxyvitamin D and risk of colorectal cancer. PLoS ONE. 2014;9(3):e92212 10.1371/journal.pone.0092212 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Pettersson A, Hankinson SE, Willett WC, Lagiou P, Trichopoulos D, Tamimi RM. Nondense mammographic area and risk of breast cancer. Breast Cancer Res. 2011;13(5):R100 10.1186/bcr3041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zhang X, Tworoger SS, Eliassen AH, Hankinson SE. Postmenopausal plasma sex hormone levels and breast cancer risk over 20 years of follow-up. Breast Cancer Res Treat. 2013;137(3):883–92. 10.1007/s10549-012-2391-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Rosner B, Glynn RJ. Power and sample size estimation for the Wilcoxon rank sum test with application to comparisons of C statistics from alternative prediction models. Biometrics. 2009;65(1):188–97. 10.1111/j.1541-0420.2008.01062.x [DOI] [PubMed] [Google Scholar]
- 41.Rosner B, Colditz GA, Iglehart JD, Hankinson SE. Risk prediction models with incomplete data with application to prediction of estrogen receptor-positive breast cancer: prospective data from the Nurses’ Health Study. Breast Cancer Res. 2008;10(4):R55 10.1186/bcr2110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Klein AP, Lindstrom S, Mendelsohn JB, Steplowski E, Arslan AA, Bueno-de-Mesquita HB, et al. An absolute risk model to identify individuals at elevated risk for pancreatic cancer in the general population. PLoS ONE. 2013;8(9):e72311 10.1371/journal.pone.0072311 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dupont WD. Converting relative risks to absolute risks: a graphical approach. Stat Med. 1989;8(6):641–51. [DOI] [PubMed] [Google Scholar]
- 44.Vickers AJ, Van Calster B, Steyerberg EW. Net benefit approaches to the evaluation of prediction models, molecular markers, and diagnostic tests. BMJ. 2016;352:i6 10.1136/bmj.i6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mavaddat N, Pharoah PD, Michailidou K, Tyrer J, Brook MN, Bolla MK, et al. Prediction of breast cancer risk based on profiling with common genetic variants. J Natl Cancer Inst. 2015;107(5):djv036. 10.1093/jnci/djv036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Schoemaker MJ, Folkerd EJ, Jones ME, Rae M, Allen S, Ashworth A, et al. Combined effects of endogenous sex hormone levels and mammographic density on postmenopausal breast cancer risk: results from the Breakthrough Generations Study. Br J Cancer. 2014;110(7):1898–907. 10.1038/bjc.2014.64 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Husing A, Canzian F, Beckmann L, Garcia-Closas M, Diver WR, Thun MJ, et al. Prediction of breast cancer risk by genetic risk factors, overall and by hormone receptor status. J Med Genet. 2012;49(9):601–8. 10.1136/jmedgenet-2011-100716 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Mealiffe ME, Stokowski RP, Rhees BK, Prentice RL, Pettinger M, Hinds DA. Assessment of clinical validity of a breast cancer risk model combining genetic and clinical information. J Natl Cancer Inst. 2010;102(21):1618–27. 10.1093/jnci/djq388 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Vachon CM, Pankratz VS, Scott CG, Haeberle L, Ziv E, Jensen MR, et al. The contributions of breast density and common genetic variation to breast cancer risk. J Natl Cancer Inst. 2015;107(5):dju397. 10.1093/jnci/dju397 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Tice JA, Cummings SR, Smith-Bindman R, Ichikawa L, Barlow WE, Kerlikowske K. Using clinical factors and mammographic breast density to estimate breast cancer risk: development and validation of a new predictive model. Ann Intern Med. 2008;148(5):337–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Darabi H, Czene K, Zhao W, Liu J, Hall P, Humphreys K. Breast cancer risk prediction and individualised screening based on common genetic variation and breast density measurement. Breast Cancer Res. 2012;14(1):R25 10.1186/bcr3110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Sprague BL, Trentham-Dietz A, Cronin KA. A sustained decline in postmenopausal hormone use: results from the National Health and Nutrition Examination Survey, 1999–2010. Obstet Gynecol. 2012;120(3):595–603. 10.1097/AOG.0b013e318265df42 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Cuzick J, Powles T, Veronesi U, Forbes J, Edwards R, Ashley S, et al. Overview of the main outcomes in breast-cancer prevention trials. Lancet. 2003;361(9354):296–300. 10.1016/S0140-6736(03)12342-2 [DOI] [PubMed] [Google Scholar]
- 54.Cummings SR, Eckert S, Krueger KA, Grady D, Powles TJ, Cauley JA, et al. The effect of raloxifene on risk of breast cancer in postmenopausal women: results from the MORE randomized trial. Multiple Outcomes of Raloxifene Evaluation. JAMA. 1999;281(23):2189–97. [DOI] [PubMed] [Google Scholar]
- 55.Rosner W, Hankinson SE, Sluss PM, Vesper HW, Wierman ME. Challenges to the measurement of estradiol: an endocrine society position statement. J Clin Endocrinol Metab. 2013;98(4):1376–87. 10.1210/jc.2012-3780 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Rosner W, Vesper H. Toward excellence in testosterone testing: a consensus statement. J Clin Endocrinol Metab. 2010;95(10):4542–8. 10.1210/jc.2010-1314 [DOI] [PubMed] [Google Scholar]
- 57.Michailidou K, Beesley J, Lindstrom S, Canisius S, Dennis J, Lush MJ, et al. Genome-wide association analysis of more than 120,000 individuals identifies 15 new susceptibility loci for breast cancer. Nat Genet. 2015;47(4):373–80. 10.1038/ng.3242 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Boggs DA, Rosenberg L, Adams-Campbell LL, Palmer JR. Prospective approach to breast cancer risk prediction in African American women: the black women’s health study model. J Clin Oncol. 2015;33(9):1038–44. 10.1200/JCO.2014.57.2750 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Allman R, Dite GS, Hopper JL, Gordon O, Starlard-Davenport A, Chlebowski R, et al. SNPs and breast cancer risk prediction for African American and Hispanic women. Breast Cancer Res Treat. 2015;154(3):583–9. 10.1007/s10549-015-3641-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
Data Availability Statement
Investigators who wish to use data collected in the Nurses’ Health Studies are encouraged to visit http://www.nurseshealthstudy.org/researchers and contact nhsaccess@channing.harvard.edu for the Nurses’ Health Study. Access to statistical codes and datasets will be facilitated following the existing data sharing guidelines provided, which can be found on the study websites.