Abstract
The ability to measure mechanics and forces in biological nanostructures, such as DNA, proteins and cells, is of great importance as a means to analyze biomolecular systems. However, current force detection methods often require specialized instrumentation. Here, we present a novel and versatile method to quantify tension in molecular systems locally and in real time, using intercalated DNA fluorescence. This approach can report forces over a range of at least ∼0.5–65 pN with a resolution of 1–3 pN, using commercially available intercalating dyes and a general-purpose fluorescence microscope. We demonstrate that the method can be easily implemented to report double-stranded (ds)DNA tension in any single-molecule assay that is compatible with fluorescence microscopy. This is particularly useful for multiplexed techniques, where measuring applied force in parallel is technically challenging. Moreover, tension measurements based on local dye binding offer the unique opportunity to determine how an applied force is distributed locally within biomolecular structures. Exploiting this, we apply our method to quantify the position-dependent force profile along the length of flow-stretched DNA and reveal that stretched and entwined DNA molecules—mimicking catenated DNA structures in vivo—display transient DNA–DNA interactions. The method reported here has obvious and broad applications for the study of DNA and DNA–protein interactions. Additionally, we propose that it could be employed to measure forces in any system to which dsDNA can be tethered, for applications including protein unfolding, chromosome mechanics, cell motility, and DNA nanomachines.
Keywords: force sensor, molecular tension, DNA, intercalators, fluorescence microscopy
Mechanical force plays a crucial role in many cellular functions. Processes such as cell adhesion, migration, and division all rely on forces generated within the cell.1−5 DNA is also frequently subjected to mechanical strain, resulting in the structural deformations that facilitate replication, transcription, and repair of the genome.6−8 Additionally, a range of force-sensing proteins has been discovered, in which mechanical unfolding can induce enzymatic activity.9,10 The growth of single-molecule manipulation techniques, including optical and magnetic tweezers,7,8,11−13 atomic force microscopy (AFM),6,13 acoustic force spectroscopy14 and flow-stretching,15−19 has revolutionized our ability to study such processes in vitro. Furthermore, the recent development of molecular tension sensors has provided a means to report inter- and intra-cellular forces without applying an external perturbation.20−25 Inspired by these achievements, there is now a growing desire to design improved biomolecular force sensors, with enhanced sensitivity and greater applicability. Here, we present a versatile fluorescence-based method to sensitively report DNA tension using cyanine intercalator dyes.
Intercalators are small planar molecules that bind reversibly between adjacent base-pairs of double-stranded (ds)DNA.26 Cyanine intercalator dyes, such as YO-PRO and SYTOX Orange, exhibit drastically enhanced fluorescence when intercalated.27,28 For this reason, these dyes are commonly used to study the structure and conformation of dsDNA,8,16 as well as probe the action of DNA-binding proteins.15,17,18,29−31 Today, a wide range of intercalator dyes is commercially available, and their DNA-binding properties have been characterized extensively.28,32,33 From these studies, it has been revealed that their DNA-binding affinity is strongly dependent on the force applied to the DNA.28,32 In the case of cyanine dyes, for instance, the DNA-binding affinity typically varies by 2–4 orders of magnitude over a force range of 0–60 pN.28
While the force-dependent DNA affinity of intercalator dyes under equilibrium binding conditions is well-established, it has never been realized, let alone exploited, that this makes intercalated DNA a powerful force sensor. Here, we present a novel fluorescence-based method to quantify tension in molecular systems locally and in real time using intercalated DNA. The approach can be employed on any general-purpose fluorescence microscope using commercially available (bio)chemicals. This method has broad applications for the study of DNA and DNA–protein interactions and could be employed more widely for applications as diverse as protein unfolding, chromosome mechanics and cell motility, as well as DNA nanomachines and other nanomechanical systems.
Intercalated DNA Fluorescence as a Means to Report Tension
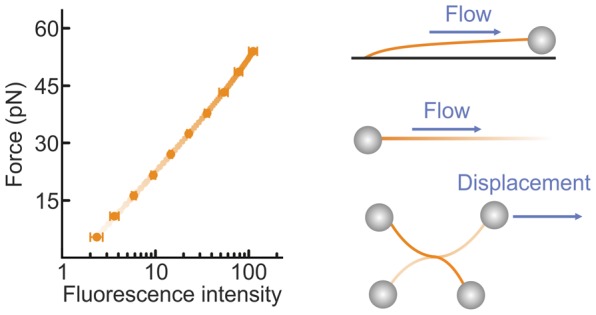
To demonstrate that intercalated DNA fluorescence can be used as an independent force sensor, we first employed combined dual-trap optical tweezers and fluorescence microscopy to correlate the fluorescence intensity from cyanine intercalating dyes with the independently measured force on a dsDNA molecule (see Supporting Methods). Figure 1a presents snapshots of fluorescence images recorded for a dsDNA molecule (λ phage, ∼48.5 kb) under increasing tension in the presence of the cyanine dye YO-PRO (YO) (10 nM). A clear increase in fluorescence intensity is observed as the applied force is raised. This trend is quantified in Figure 1b for two different cyanine dyes: YO and SYTOX Orange (SxO). Using the known equilibrium binding properties of intercalating dyes, we derive here that the total (background-corrected) intercalator fluorescence intensity (IF) is related to the applied force (F) on dsDNA by the following expression:
| 1 |
where Imax (the background-corrected fluorescence intensity at saturated coverage) and B are parameters defined by eqs S6 and S7, respectively (see SI). ϕ is the characteristic force equal to kBT/Δxeq, where Δxeq represents the equilibrium average elongation per bound dye molecule.32 Fitting the data in Figure 1b to eq 1 (solid lines) provides an excellent match over the wide range of forces considered (see also Figure S1). In the Methods, we describe how to determine Imax, B, and ϕ using a straightforward protocol. The above approach can be simplified when the dye coverage is far from saturation (i.e., at lower force ranges or lower dye concentrations). In this case, the fractional dye coverage ϑ scales linearly with both the intercalator concentration and the binding affinity, and thus (using eq S1) the fluorescence signal will increase monoexponentially with dsDNA tension. On the basis of this, any change in applied force (ΔF = F2 – F1) can be determined simply by using the following relation:
| 2 |
where IFi is the background-corrected fluorescence intensity at Fi. The absolute value of an unknown force (say F2) can then be calculated by comparing the fluorescence intensity at this force with that at a known reference force (F1). A useful reference force here could be ∼0.5 pN (Methods). The dashed lines in Figure 1b confirm that, indeed, a monoexponential fit describes the measured data well under low-coverage conditions (e.g., up to ∼45 pN in the case of 6 nM SxO). In the SI, we describe how to identify when the DNA is far from saturated, and therefore when eq 2 can be employed. Thus, using optical tweezers as a benchmark, we establish that cyanine intercalator fluorescence can be employed as an independent and sensitive dsDNA tension sensor. Note that, since the method relies on the equilibrium binding properties of intercalators, the fluorescence signal is completely reversible upon decreasing the applied force (see Movies S1–S3). The temporal resolution of this method is mainly governed by the equilibration time of the employed dye (see Supplementary Note 1) and in our case is at least 5 s (SxO) to 1 s (YO) (Figure S2). The force resolution depends on the signal-to-noise ratio associated with the fluorescence images. Under the imaging conditions commonly employed in our assays, we achieve a local force resolution in the range of 1–3 pN (Figure S3).
Figure 1.
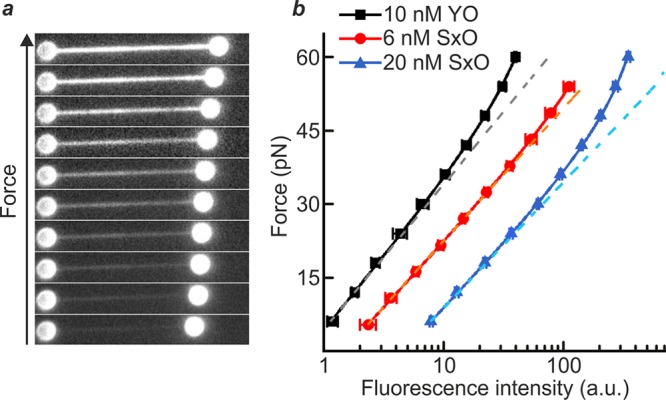
Intercalated DNA fluorescence as an independent force sensor. (a) Sample fluorescence images of a λ-DNA molecule, held between two optically trapped microspheres (1.84 μm), in the presence of YO (10 nM) as the applied force is increased progressively from 6 pN to 60 pN through displacement of one of the microspheres. (b) Plot of the dsDNA tension as a function of the total fluorescence intensity for YO (10 nM, black) and SxO (6 nM, red; 20 nM, blue). The tension applied to the DNA was determined independently by standard back focal plane detection of the scattered optical trapping light from the stationary bead. Fits of these data to eq 1 (solid lines, with fit parameters detailed in Table S1) and a monoexponential function (dashed lines) are also displayed. Data were obtained in a buffer containing 20 mM HEPES pH 7.5, 100/150 mM NaCl, 2/10 mM MgCl2, 0.02% casein, and 0.05% Pluronics F127 for YO/SxO studies, respectively. All errors are SEM.
Fluorescence-Based Force Detection of Flow-Stretched DNA
On the basis of the above results, we propose that cyanine intercalator fluorescence can be employed to measure changes in dsDNA tension in any single-molecule assay that is compatible with fluorescence imaging. One particularly relevant example is the application of intercalator staining to report the force applied to DNA in commonly used flow-based assays, where the DNA is manipulated with hydrodynamic flow. In such assays, the DNA is typically tethered on one end to a surface, while the other end is either free in solution,16,17,30,34 connected to a microsphere,15,29,31 or tethered to another region of the surface.18,19 Through visualizing DNA-binding dyes or fluorescently labeled proteins, these approaches have been employed with great effect to measure the biophysical properties of DNA,16,30,34 as well as probe the action of DNA-binding proteins.15,17−19,31 When the DNA is tethered to a microsphere, the drag force can be determined using the equipartition theorem, based on the Brownian motion of the microsphere.15,29 Often, however, it is either undesirable or impractical to tether a bead to the DNA.18,19,35 In such cases, the force applied to the DNA can only be estimated based on the apparent molecular extension.
We propose that intercalator staining provides a straightforward and sensitive means to determine dsDNA tension in any flow-based assay. To demonstrate this, we employed a standard surface-based setup,15,29,31,34 in which dsDNA molecules were each tethered on one end to the surface of a glass flow-cell and on the other end to a polystyrene bead (diameter 1.76 μm), as illustrated schematically in Figure 2a. We then used hydrodynamic flow to stretch the surface-tethered DNA (via a drag force applied to the bead) in the presence of SxO (20 nM), while measuring the fluorescence intensity associated with dye intercalation. Figure 2b presents sample fluorescence images (left panel) and the corresponding kymograph (right panel) obtained as the flow is increased. Visual inspection of Figure 2b (as well as Figure S4 and Movie S2) reveals a significant change in fluorescence intensity as the fluid flow (and thus drag force) is increased. Figure 2c quantifies the force associated with the dsDNA molecule in each image of Figure 2b, calculated using eq 1. We note that the average force deduced from the fluorescence signal compares well with the hydrodynamic bead drag that can be estimated from the volume turnover through the flow-cell (see Supplementary Note 2).
Figure 2.
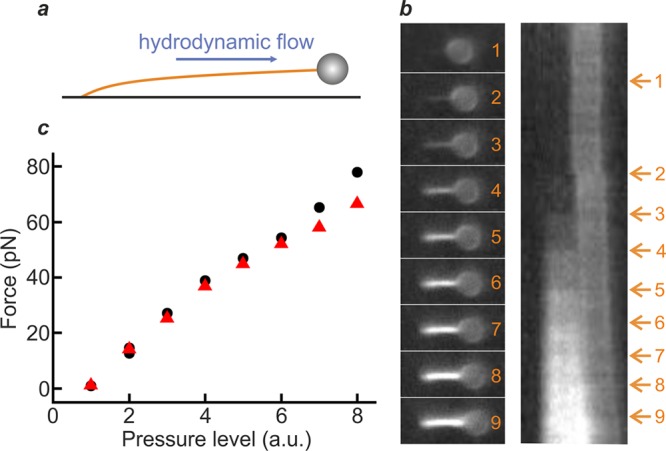
Hydrodynamic drag force on dsDNA can be determined from intercalator fluorescence intensity. (a) Experimental scheme, showing a dsDNA molecule (∼8.6 kb) tethered between the surface of a flow-cell and a bead of 1.76 μm diameter. The DNA molecule is stretched by using hydrodynamic flow to impart a drag force on the bead. (b) Left: Sample fluorescence images of a flow-stretched dsDNA molecule in the presence of SxO (20 nM) as the flow is increased (stepwise, frames 1–9). Right: Corresponding kymograph from which the snapshots were extracted. Arrows indicate the force jumps induced by increasing the flow. (c) Average DNA tension as a function of pressure level (which governs the hydrodynamic flow). The force was calculated using eq 1, while the flow was tuned through the pressure applied to the reservoir containing the intercalator solution. Note that black data points correspond to the snapshots in panel (b), while red data points are derived from fluorescence images of a second surface-tethered DNA molecule (Figure S4 and Movie S2). Data were obtained in a buffer containing 20 mM HEPES pH 7.5, 150 mM NaCl, 10 mM MgCl2, 0.05% casein, and 0.1% Pluronics F127.
We thus demonstrate that intercalator fluorescence provides real time, reliable, and robust force detection in a commonly used DNA flow-stretch configuration. A similar approach could be readily implemented in more complex flow-based techniques, where force detection can be more challenging. This includes DNA curtains18 and hydrodynamic trapping.35 Since many intercalated DNA molecules can be imaged and analyzed simultaneously in the field of view, force detection based on intercalator fluorescence also lends itself excellently to multiplexed methods. These include the above-mentioned DNA curtain and flow-stretch assays, as well as holographic optical tweezers36 and nanophotonic optical trapping.37
Quantifying Force Gradients in DNA Due to Hydrodynamic Flow
The fact that intercalator-based DNA force detection relies on the molecular equilibrium binding means that this approach can also provide unrivalled insight into the local partitioning of tension within regions of dsDNA. One application where such information is insightful is the quantification of local DNA tension due to hydrodynamic flow. Using fluorescent markers to track changes in DNA extension, it has been shown previously that the elastic response of dsDNA to uniform hydrodynamic flow can be inhomogeneous along the length of the molecule.34 In order to apply flow-stretch assays to study DNA–protein interactions, for example, it can therefore be highly advantageous to quantify how tension varies along the length of a DNA substrate.
Here, we demonstrate that the force-dependent fluorescence signal from intercalating cyanine dyes can be used to map, in detail, the heterogeneous tension profile along a dsDNA molecule, arising as a result of hydrodynamic flow. To achieve this, we applied a constant fluid flow to a dsDNA molecule that was tethered on one end to an optically trapped microsphere in the presence of SxO (20 nM), as illustrated schematically in Figure 3a (inset). Figure 3a (left) compares snapshots of fluorescence images obtained as the flow velocity is reduced from 8.8 mm s–1 to 2.1 mm s–1 (see also Movie S3). Note that the flow velocity was calculated using Stokes’ law, based on the force acting on the microsphere as measured with the optical trap (see Supplementary Note 2). The corresponding kymograph (Figure 3a, right) shows the fluorescence intensity along the length of the DNA molecule as a function of flow velocity. At the higher flow rates investigated, we observe a nonuniform fluorescence signal (corresponding to a heterogeneous force) along the DNA contour. This heterogeneity is expected due to the cumulative effect of the flow drag as a function of DNA length, with the local tension greatest near the anchor point. Figure 3b quantifies this trend, using eq 1 to calculate the force profile along the length of the DNA for different flow velocities. Figure S5 displays similar results obtained using both a different dye (YO) and a different concentration of SxO (6 nM). Figure 3c summarizes these latter data, plotting the maximum DNA tension detected from fluorescence measurements as a function of flow velocity for these different dyes and concentrations. This is insightful, as it highlights that the observed trends are independent of the choice of intercalator dye and its concentration, thus showcasing the power of intercalator fluorescence to reveal localized changes in DNA tension. Note that the DNA drag force determined with our method is in excellent agreement with that deduced independently using optical tweezers, based on the force measured on the bead (Figure S6).
Figure 3.
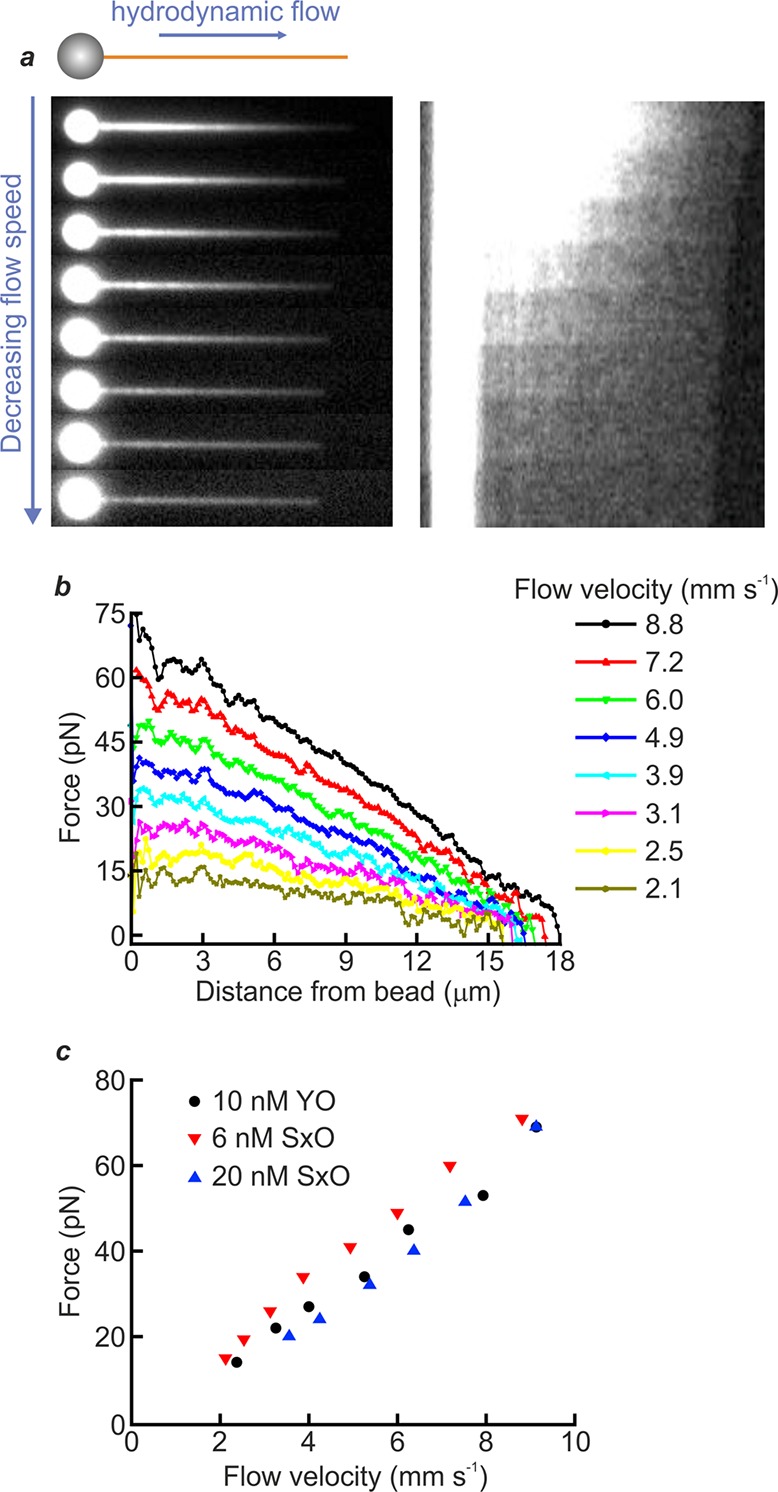
Quantifying heterogeneous tension along a flow-stretched dsDNA molecule. (a) Inset presents a schematic illustration of the experimental scheme: a λ-DNA molecule, tethered on one end to an optically trapped bead (1.84 μm diameter), is stretched by hydrodynamic flow (blue arrow) in the presence of intercalator dye. The left main panel displays sample fluorescence images obtained as the DNA is stretched using different flow velocities in the presence of SxO (20 nM). The corresponding kymograph is shown on the right, with the contrast enhanced to enable visualization of the free end of the dsDNA. (b) Tension along the length of the DNA molecule shown in panel (a) (left, main) for different flow velocities. The tension over the different segments of the DNA was derived using eq 1. The flow velocity was calculated using Stokes’ law (see Supplementary Note 2). (c) Comparison of the maximum force, near the tethered end of the dsDNA molecule (calculated from the fluorescence profile), as a function of flow velocity for two different dyes: YO (10 nM) and SxO (6 nM, 20 nM). Data were obtained in a buffer containing 20 mM HEPES pH 7.5, 100/150 mM NaCl, 2/10 mM MgCl2, 0.02% casein, and 0.05% Pluronics F127 for YO/SxO studies, respectively.
Using Intercalator Fluorescence to Measure DNA–DNA Interactions
More complex tension patterns can arise in two-dimensional or three-dimensional molecular architectures, as commonly encountered in living systems. One such example involves the entanglement of multiple DNA molecules. The study of entwined DNA is of considerable interest from both a physical and biological perspective. It has recently been discovered, for instance, that stretched and entwined dsDNA tracts are generated regularly in vivo during chromosome segregation through the formation of so-called ultrafine DNA bridges.38 It is insightful, therefore, to understand how forces can be partitioned within multicomponent DNA complexes. We propose that the local force detection provided by cyanine intercalator fluorescence is ideally placed to answer this question.
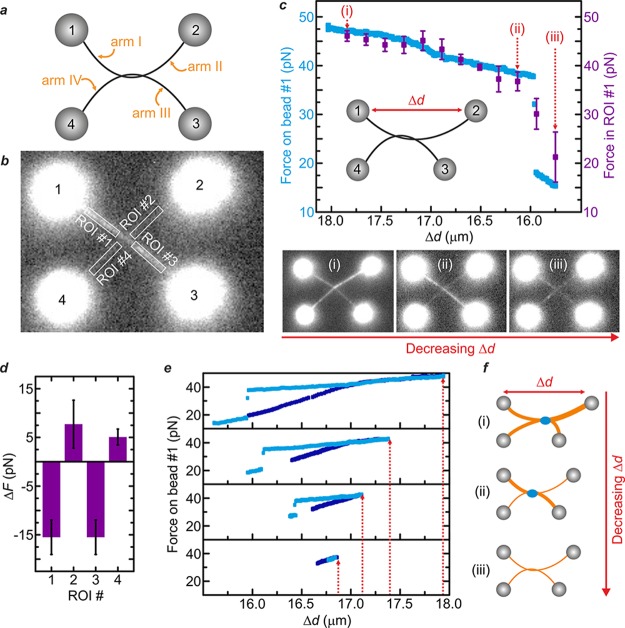
Highlighting this, we apply our method to demonstrate that transient DNA–DNA interactions can be generated within stretched and entwined DNA structures that mimic ultrafine DNA bridges in vivo. To this end, we used a quadruple optical tweezers instrument to manipulate two dsDNA molecules, each one held between a pair of optically trapped beads.39,40 By wrapping one dsDNA molecule once around the other, we created an entwined dual-dsDNA structure that can be considered as consisting of four different arms (labeled I–IV), each tethered to a different bead (numbered 1–4). This is illustrated schematically in Figure 4a. We then incubated the entwined DNA assembly in SxO (20 nM) and imaged the fluorescence along each arm of the DNA structure (e.g., Figure 4b and Movie S4). Following this, tension within the entwined DNA structure was generated and then released, by increasing and subsequently decreasing the distance between bead #1 and bead #2 (Δd), as shown schematically in Figure 4c (inset). Using eq 2, we measured the reduction in tension within arm I as Δd is decreased (following its initial extension), based on the changes in fluorescence intensity associated with arm I. During this experiment, an abrupt, discontinuous drop in force is observed as Δd is decreased (∼16 μm, Figure 4c upper panel, purple data). This is consistent with a sudden conformational rearrangement within the dual-DNA structure.
Figure 4.
Quantifying DNA–DNA interactions within stretched and entwined dsDNA molecules. (a) An entwined dsDNA architecture is created by wrapping one λ-DNA molecule (tethered between optically trapped beads #1 and #2) around another (held between beads #3 and #4). (b) Sample fluorescence image of the entwined DNA structure in the presence of SxO (20 nM). Four regions of interest (ROI) are established, one on each “arm” of the construct. (c) Inset: Tension is applied, and then released, by increasing and decreasing the distance between bead #1 and bead #2 (Δd), respectively, via displacement of bead #2. Upper panel: Measured tension within arm I as Δd is decreased (after its initial extension). Data in purple are based on the changes in SxO fluorescence intensity within ROI #1 (calculated using eq 2); data in blue are derived using back focal plane detection of the scattered optical trapping light from bead #1. Lower panel: Fluorescence images (of SxO) recorded at maximum Δd (i), directly before (ii) and after (iii) the sudden drop in force identified in the upper panel. (d) Rearrangements in local force between frames (ii) and (iii), determined using the change in fluorescence intensity within ROI #1, ROI #2, ROI #3, and ROI #4, respectively. (e) Force measured on bead #1 directly (via back focal plane detection of the scattered optical trapping light) upon increasing (dark blue) and then decreasing (light blue) Δd. From bottom to top, panels show the effect of increasing the maximum value of Δd (highlighted by the red arrows). (f) Schematic illustration of the change in fluorescence intensity (i.e., local DNA tension) as Δd is decreased, corresponding to the images shown in (i)–(iii) in panel (c). At a critical force, a DNA–DNA interaction is induced that locks the DNA molecules together at the point of intersection (blue circle). Consequently, upon moving bead #2 back to its initial location, the tension in the orthogonal arms (I/III) cannot be released to the same extent as in arms II/IV (which are near-parallel to the translational axis of bead #2). Once the inter–DNA interaction is broken (signified by the jump in force in Figure 4 panel c), the remaining tension is redistributed within the four arms. In this scheme, the local DNA tension in the different arms is indicated by the line thickness (orange). All data were obtained in a buffer of 20 mΜ Tris-HCl pH 7.6 and 50 mM NaCl. Errors are SEM.
The above force jump can also be determined by measuring the force response of bead #1 in the optical trap (Figure 4c upper panel, blue data). However, in quadruple optical tweezers, there is currently no means to measure the force applied to all four optically trapped beads; this hinders a full understanding of the conformational rearrangement of the entwined DNA assembly. To overcome this, we rely on intercalator fluorescence alone to extract the local force distribution throughout the two-dimensional DNA structure as Δd is decreased. The lower panel of Figure 4c compares the fluorescence images recorded at maximum Δd (i), as well as directly before (ii) and after (iii) the abrupt change in force identified above. Figure 4d quantifies the change in tension within each arm of the entwined DNA complex between frames (ii) and (iii), using eq 2. This analysis reveals that a sudden reduction in force of ∼15 pN occurs along both arm I and arm III, while a simultaneous increase in force of ∼5–10 pN is detected along both arm II and arm IV.
The above behavior occurs after an initial force of at least ∼40 pN has been applied to the system (Figure 4e) and is almost only observed when the DNA molecules are entwined in a right-handed configuration. This suggests a structural interaction between local regions of denatured DNA at the point of entanglement, perhaps forming a localized region of triple-stranded DNA, or even a g-quadruplex between the two juxtaposed strands. The observation of inter-DNA interactions induced within entwined DNA assemblies is highly repeatable (N > 30). Thus, we argue that the effect is distinct from the collapse of nicked and braided duplex DNA reported previously.41 We therefore explain the results in Figure 4 as follows. By displacing bead #2 to the right (Figure 4c, inset), tension is applied to the entire entwined DNA assembly (arms I–IV). At a critical force, a DNA–DNA interaction (see above) is induced that locks the DNA molecules together at the point of intersection. Consequently, upon moving bead #2 back to its initial location, the tension in the orthogonal arms (I/III) cannot be released to the same extent as in arms II/IV (which are near-parallel to the translational axis of bead #2). Once the inter-DNA interaction is broken (signified by the jump in force in Figure 4c), the remaining tension is redistributed within the four arms (Figure 4f).
Using the configuration introduced in Figure 4a, we also consider the case of displacing beads #3 and #4 simultaneously, either in a rightwards or leftwards direction, relative to the stationary beads (#1 and #2). If the entwined DNA molecules are held taut, it is anticipated that steric restraint will generate mechanical resistance at the point of entwinement. If, on the other hand, the interlocked molecules have some tensile slack during this process, they might be expected to slide past one another, at least until there is no slack left in the system. In support of the latter behavior, we note that it has previously been shown that the friction between two DNA molecules is less than 1 pN.42Figure 5 displays fluorescence images (from Movie S5) as beads #3 and #4 are displaced simultaneously rightwards then leftwards, relative to the stationary positions of beads #1 and #2, in the presence of SxO (20 nM). From these images, a semiregular buildup and release of fluorescence intensity is observed, primarily along arms I and III for rightwards displacement and along arms II and IV for leftwards displacement. To quantify these force fluctuations, we consider the change in total fluorescence intensity in a fixed region of interest that always spans the intersection point of the two entwined DNA molecules (Figure 5b). Figure 5c presents the measured change in force at the intersection point as beads #3 and #4 are displaced, as well as the corresponding change in the position of this intersection point (Δd). Interestingly, the largest ruptures in force correspond to discrete changes in Δd, as highlighted by the gray-colored domains in Figure 5c. Taken together, these data indicate that, for the DNA configuration highlighted in Figure 5a, one DNA molecule is able to “slip” past the other once a critical resistance force has built up. The above examples serve to highlight how intercalator fluorescence can be exploited to quantify, in remarkable detail, the redistribution of local forces within complex DNA architectures. Extrapolating this, we raise the intriguing prospect that intercalator fluorescence could even be used to probe local changes in DNA tension in vivo, such as during chromosome segregation.38
Figure 5.

Stick–slip sliding dynamics observed within entwined dual-DNA architectures. (a) Upper panel shows a schematic representation of the experimental assay: using the four-bead geometry described in Figure 4a, beads #3 and #4 are displaced simultaneously (rightwards or leftwards) with respect to beads #1 and #2. Lower panel shows sample fluorescence images of the entwined DNA structure in the presence of SxO (20 nM) as beads #3 and #4 are displaced. (b) Kymograph showing the point of intersection as beads #3 and #4 are displaced. (c) Plot showing the force measured from the kymograph in panel (b) (determined using eq 2), as well as the change in position of the intersection point of the two dsDNA molecules (Δd) as beads #3 and #4 are displaced. The largest ruptures in force correspond to discrete changes in Δd, as highlighted by the gray-colored domains in panel (c). All data were obtained in a buffer of 20 mM Tris-HCl pH 7.6 and 50 mM NaCl.
Wider Applications of Intercalated DNA Fluorescence as a Tension Sensor
We have established here that fluorescence from commercially available intercalator dyes represents a robust, versatile, and powerful tool to report DNA tension over a range of <0.5 to ∼65 pN in any assay that can be combined with fluorescence microscopy. Higher forces could also be measured by using DNA constructs that divide externally applied tension over multiple parallel strands. In addition to its wide applicability, intercalator fluorescence is also advantageous in that it provides a direct read-out of the local force profile along the length of a DNA molecule, which is difficult or near impossible to achieve using other methods. Although our method is most straightforwardly applied to DNA that is torsionally unconstrained, there are possibilities to extend it to torsionally constrained DNA (see Supplementary Note 3). It is important to note that intercalators can induce unwanted modifications to the mechanical properties of DNA, as well as alter the binding and processivity of certain enzymes.28 For example, intercalation will lengthen the DNA; this, however, does not impact correct force measurement, and in many systems, the absolute DNA extension is of no particular importance (e.g., see Figures 2–5). Furthermore, potential negative effects of intercalation can be significantly minimized in several ways, depending on the requirements of an experiment. First, in some assays, force detection is only strictly required before or after a biophysical measurement. In such cases, the dye does not even need to be present during the experiment. If, on the other hand, real time force detection is required, users should employ the lowest possible dye concentration required to detect fluorescence (see Supplementary Note 4). It is also noteworthy that perturbations to dynamic processes, such as enzymes processing along DNA, are determined primarily by the off-rate of the intercalator.28 Thus, by maximizing its off-rate (through the choice of dye and ionic strength) the deleterious effects of intercalators on DNA processes can be further minimized (see Supplementary Note 1).28 Indeed, many single-molecule assays already use cyanine dyes to image dsDNA, with negligible perturbations to DNA–protein interactions.17,18,29,31
Extending our findings, we propose that cyanine dye fluorescence can also be employed more generally to report forces in any system that can be mechanically coupled to dsDNA linker molecules. For instance, Ha and co-workers recently devised the tension gauge tether (TGT) approach, whereby small linker dsDNA molecules, which rupture at discrete forces, are used to measure cell–cell and cell–matrix interaction forces.21,25 TGTs can determine an applied biomechanical force within a range determined by the tension tolerance of the dsDNA linker. We suggest that cyanine dye fluorescence could be used to extend the scope of the TGT approach, by allowing continuous changes in biomechanical force to be detected across a wide (∼0.5–65 pN) range and in real time. Intercalator-based force detection could further be employed to measure protein unfolding rupture events due to mechanical strain. Often, such studies are performed using optical tweezers or AFM, in which the protein is tethered between dsDNA handles.43 Addition of cyanine dye would allow the applied force to be monitored simply by imaging the dsDNA handles. This would, in turn, enable protein unfolding experiments to be conducted using alternative (and arguably simpler) single-molecule methods, such as flow-stretch assays. Finally, we note the potential of intercalator-based force detection to the burgeoning field of DNA origami nanomachines. In recent years, a host of DNA–protein and protein–protein interactions have been probed using advanced DNA origami platforms.44,45 We suggest that such interaction forces could be measured using cyanine dye fluorescence from dsDNA linker arms embedded within these nanomachines. For these reasons, intercalated DNA fluorescence represents a powerful means to report molecular tension in a wide range of assays.
Methods
In order to use eq 1 to calculate the absolute force applied to dsDNA, three parameters must be determined: Imax, B, and ϕ. ϕ has been determined previously for a range of commonly used cyanine dyes at both low (0.1 M NaCl) and high (1 M NaCl) ionic strength.28 ϕ can also be calculated independently, if required, by plotting the dsDNA elongation due to the binding of intercalators against the number of intercalated molecules. A linear fit to this plot yields Δxeq, from which ϕ can then be calculated.28 In order to extract Imax and B, we outline below two alternative approaches. In the first case, we assert that (using eqs S6–S8) Imax and B can be expressed via the following two equations:
| 3 |
| 4 |
Assuming we know two reference force values, denoted here as F1 and F2 (with corresponding fluorescence intensity values IF1 and IF2), we can derive the following:
| 5 |
By inserting the known reference forces (along with their measured fluorescence intensities) into eq 5, Imax can be calculated. The magnitude of B can then be determined by inserting this value of Imax into eq 4. To this end, we recommend using the following reference forces: (i) ∼0.5 pN, which can be established by minimizing the applied tension on the dsDNA; and (ii) the onset of dsDNA overstretching in the presence of intercalators, which typically occurs at 70 ± 5 pN (depending on the solution conditions).28 Note that the onset of overstretching can be identified by the emergence of dark regions in the DNA molecule that are no longer bound by intercalators. In a related, but slightly different approach, Imax and B can be determined from a fit of eq 1 using either (i) two reference force values (along with their corresponding fluorescence intensities) at a constant intercalator concentration or (ii) two reference intercalator concentrations (along with the associated fluorescence intensities) at a constant known force.
Acknowledgments
Douwe Kamsma and Onno Broekmans (Vrije Universiteit Amsterdam) as well as Alexei Kornyshev, Dominic Lee, and Roberto Cortini (Imperial College London) are acknowledged for advice and helpful discussions. This work was part of a research program of the Foundation for Fundamental Research on Matter (FOM) (E.J.G.P. and G.J.L.W.), which is associated with The Netherlands Organization for Scientific Research (NWO). The work was further supported by a Human Frontier Science Program grant (E.J.G.P and G.J.L.W.). The authors also acknowledge support from NWO VICI grants (G.J.L.W. and E.J.G.P.), a Starting Independent Investigator grant from the European Research Council (G.J.L.W.), an NWO VIDI grant (I.H.), and a long-term postdoctoral fellowship from the European Molecular Biology Organization (G.A.K.).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.7b04842.
Supporting methods describing the experimental designs as well as the derivation of the relationship between applied force and intercalator fluorescence intensity (PDF)
Movie S1: Fluorescence movie of a single λ-DNA molecule tethered between two 1.84 μm beads held by optical tweezers in the presence of 20 nM SxO (AVI)
Movie S2: Fluorescence movie from which the snapshots and kymographs in Figure 2 and Figure S4 were extracted (AVI)
Movie S3: Fluorescence movie showing a λ-DNA molecule tethered to an optically trapped 1.84 μm bead and extended by hydrodynamic flow applied from the left side in the presence of 20 nM SxO (AVI)
Movie S4: Fluorescence movie from which the images in Figure 4 were extracted (AVI)
Movie S5: Fluorescence movie from which the images in Figure 5 were extracted (AVI)
Author Contributions
# G. A. King, A. S. Biebricher and I. Heller contributed equally. E. J. G. Peterman and G. J. L. Wuite jointly supervised this work.
The authors declare the following competing financial interest(s): The combined optical tweezers and fluorescence technologies and methods used in this article are patented and licensed to LUMICKS B.V., in which I.H., E.J.G.P., and G.J.L.W. have a financial interest.
Supplementary Material
References
- Eyckmans J.; Boudou T.; Yu X.; Chen C. S. Dev. Cell 2011, 21, 35–47. 10.1016/j.devcel.2011.06.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheetz M. P.; Felsenfeld D. P.; Galbraith C. G. Trends Cell Biol. 1998, 8, 51–54. 10.1016/S0962-8924(98)80005-6. [DOI] [PubMed] [Google Scholar]
- Vicente-Manzanares M.; Ma X.; Adelstein R. S. Nat. Rev. Mol. Cell Biol. 2009, 10, 778–790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp D. J.; Rogers G. C.; Scholey J. M. Nature 2000, 7, 41–47. 10.1038/35024000. [DOI] [PubMed] [Google Scholar]
- Dogterom M.; Kerssemakers J. W. J.; Romet-Lemonne G.; Janson M. E. Curr. Opin. Cell Biol. 2005, 17, 67–74. 10.1016/j.ceb.2004.12.011. [DOI] [PubMed] [Google Scholar]
- Bustamante C.; Cheng W.; Mejia Y. X. Cell 2011, 144, 480–497. 10.1016/j.cell.2011.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forth S.; Sheinin M. Y.; Inman J.; Wang W. D. Annu. Rev. Biophys. 2013, 42, 583–604. 10.1146/annurev-biophys-083012-130412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heller I.; Hoekstra T. P.; King G. A.; Peterman E. J. G.; Wuite G. J. L. Chem. Rev. 2014, 114, 3087–3119. 10.1021/cr4003006. [DOI] [PubMed] [Google Scholar]
- Gebhardt J. C. M.; Rief M. Science 2009, 324, 1278–1280. 10.1126/science.1175874. [DOI] [PubMed] [Google Scholar]
- Puchner E. M.; Alexandrovich A.; Kho A. L.; Hensen U.; Schäfer L. V.; Brandmeier B.; Gräter F.; Grubmüller H.; Gaub H. E.; Gautel M. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 13385–13390. 10.1073/pnas.0805034105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moffitt J. R.; Chemla Y. R.; Smith S. B.; Bustamante C. Annu. Rev. Biochem. 2008, 77, 205–228. 10.1146/annurev.biochem.77.043007.090225. [DOI] [PubMed] [Google Scholar]
- de Vlaminck I.; Dekker C. Annu. Rev. Biophys. 2012, 41, 453–472. 10.1146/annurev-biophys-122311-100544. [DOI] [PubMed] [Google Scholar]
- Neuman K. C.; Nagy A. Nat. Methods 2008, 5, 491–505. 10.1038/nmeth.1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sitters G.; Kamsma D.; Thalhammer G.; Ritsch-Marte M.; Peterman E. J. G.; Wuite G. J. L. Nat. Methods 2015, 12, 47–50. 10.1038/nmeth.3183. [DOI] [PubMed] [Google Scholar]
- van Oijen A. M.; Blainey P. C.; Crampton D. J.; Richardson C. C.; Ellenberger T.; Xie X. S. Science 2003, 301, 1235–1238. 10.1126/science.1084387. [DOI] [PubMed] [Google Scholar]
- Perkins T. T.; Smith D. E.; Larson R. G. Science 1995, 268, 83–87. 10.1126/science.7701345. [DOI] [PubMed] [Google Scholar]
- Bianco P. R.; Brewer L. R.; Corzett M.; Balhorn R.; Yeh Y.; Kowalczykowski S. C.; Baskin R. J. Nature 2001, 409, 374–378. 10.1038/35053131. [DOI] [PubMed] [Google Scholar]
- Finkelstein I. J.; Visnapuu M. L.; Greene E. C. Nature 2010, 468, 983–987. 10.1038/nature09561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuculis L.; Abil Z.; Zhao H.; Schroeder C. M. Nat. Chem. Biol. 2016, 12, 831–837. 10.1038/nchembio.2152. [DOI] [PubMed] [Google Scholar]
- Grashoff C.; Hoffman B. D.; Brenner M. D.; Zhou R.; Parsons M.; Yang M. T.; McLean M. A.; Sligar S. G.; Chen C. S.; Ha T.; Schwartz M. A. Nature 2010, 466, 263–267. 10.1038/nature09198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X.; Ha T. Science 2013, 340, 991–994. 10.1126/science.1231041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y.; Yehl K.; Narui Y.; Salaita K. J. Am. Chem. Soc. 2013, 135, 5320–5323. 10.1021/ja401494e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morimatsu M.; Mekhdjian A. H.; Adhikari A. S.; Dunn A. R. Nano Lett. 2013, 13, 3985–3989. 10.1021/nl4005145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cingil H. E.; Storm I. M.; Yorulmaz Y.; te Brake D. W.; de Vries R.; Cohen Stuart M. A.; Sprakel J. J. Am. Chem. Soc. 2015, 137, 9800–9803. 10.1021/jacs.5b05914. [DOI] [PubMed] [Google Scholar]
- Chowdhury F.; Li I. T. S.; Ngo T. T. M.; Leslie B. J.; Kim B. C. K.; Sokoloski J. E.; Weiland E.; Wang X.; Chemla Y. R.; Lohman T. M.; Ha T. Nano Lett. 2016, 16, 3892–3897. 10.1021/acs.nanolett.6b01403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lerman L. S. J. Mol. Biol. 1961, 3, 18–30. 10.1016/S0022-2836(61)80004-1. [DOI] [PubMed] [Google Scholar]
- Glazer A. N.; Rye H. S. Nature 1992, 359, 859–861. 10.1038/359859a0. [DOI] [PubMed] [Google Scholar]
- Biebricher A. S.; Heller I.; Roijmans R. F. H.; Hoekstra T. P.; Peterman E. J. G.; Wuite G. J. L. Nat. Commun. 2015, 6, 7304–7315. 10.1038/ncomms8304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S.; Blainey P. C.; Schroder C. M.; Xie X. S. Nat. Methods 2007, 4, 397–399. 10.1038/nmeth1037. [DOI] [PubMed] [Google Scholar]
- Kim H.; Loparo J. J. Nat. Commun. 2016, 7, 10200–10212. 10.1038/ncomms10200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamdan S. M.; Loparo J. J.; Takahashi M.; Richardson C. C.; van Oijen A. M. Nature 2009, 457, 336–339. 10.1038/nature07512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vladescu I. D.; McCauley M. J.; Nuñez M. E.; Rouzina I.; Williams M. C. Nat. Methods 2007, 4, 517–522. 10.1038/nmeth1044. [DOI] [PubMed] [Google Scholar]
- Almaqwashi A. A.; Paramanathan T.; Rouzina I.; Williams M. C. Nucleic Acids Res. 2016, 44, 3971–3988. 10.1093/nar/gkw237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price A. C.; Pilkiewicz K. R.; Graham T. G. W.; Song D.; Eaves J. D.; Loparo J. J. Biophys. J. 2015, 108, 2532–2540. 10.1016/j.bpj.2015.04.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y.; Hsiao K. W.; Brockman C. A.; Yates D. Y.; Robertson-Anderson R. M.; Kornfield J. A.; San Francisco M. J.; Schroeder C. M.; McKenna G. B. Macromolecules 2015, 48, 5997–6001. 10.1021/acs.macromol.5b01374. [DOI] [Google Scholar]
- Curtis J. E.; Koss B. A.; Grier D. G. Opt. Commun. 2002, 207, 169–175. 10.1016/S0030-4018(02)01524-9. [DOI] [Google Scholar]
- Soltani M.; Lin J.; Forties R. A.; Inman J. T.; Saraf S. N.; Fulbright R. M.; Lipson M.; Wang M. D. Nat. Nanotechnol. 2014, 9, 448–452. 10.1038/nnano.2014.79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y.; Nielsen C. F.; Yao Q.; Hickson I. D. Curr. Opin. Genet. Dev. 2002, 26, 1–5. 10.1016/j.gde.2014.03.003. [DOI] [PubMed] [Google Scholar]
- Dame R. T.; Noom M. C.; Wuite G. J. L. Nature 2006, 444, 387–390. 10.1038/nature05283. [DOI] [PubMed] [Google Scholar]
- Brouwer I.; Sitters G.; Candelli A.; Heerema S. J.; Heller I.; de Melo A. J.; Zhang H.; Normanno D.; Modesti M.; Peterman E. J. G.; Wuite G. J. L. Nature 2016, 535, 566–569. 10.1038/nature18643. [DOI] [PubMed] [Google Scholar]
- Charvin G.; Vologodskii A.; Bensimon D.; Croquette V. Biophys. J. 2005, 88, 4124–4136. 10.1529/biophysj.104.056945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noom M. C.; van den Broek B.; van Mameren J.; Wuite G. J. L. Nat. Methods 2007, 4, 1031–1036. 10.1038/nmeth1126. [DOI] [PubMed] [Google Scholar]
- Mashaghi A.; Bezrukavnikov S.; Minde D. P.; Wentink A. S.; Kityk R.; Zachmann-Brand B.; Mayer M. P.; Kramer G.; Bukau B.; Tans S. J. Nature 2016, 539, 448–451. 10.1038/nature20137. [DOI] [PubMed] [Google Scholar]
- Yamamoto S.; De D.; Hidaka K.; Kim K. K.; Endo M.; Sugiyama H. S. Nano Lett. 2014, 14, 2286–2292. 10.1021/nl4044949. [DOI] [PubMed] [Google Scholar]
- Funke J. J.; Ketterer P.; Lieleg C.; Schunter S.; Korber P.; Dietz H. Sci. Adv. 2016, 2, e1600974. 10.1126/sciadv.1600974. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.