Abstract
Motivation
Recent advances in microarray technologies have made it feasible to interrogate whole genomes with tiling arrays and this technique is rapidly becoming one of the most important high-throughput functional genomics assays. For large mammalian genomes, analyzing oligonucleotide tiling array data is complicated by the presence of non-unique sequences on the array, which increases the overall noise in the data and may lead to false positive results due to cross-hybridization. The ability to create custom microarrays using maskless array synthesis has led us to consider ways to optimize array design characteristics for improving data quality and analysis. We have identified a number of design parameters to be optimized including uniqueness of the probe sequences within the whole genome, melting temperature and self-hybridization potential.
Results
We introduce the uniqueness score, U, a novel quality measure for oligonucleotide probes and present a method to quickly compute it. We show that U is equivalent to the number of shortest unique substrings in the probe and describe an efficient greedy algorithm to design mammalian whole genome tiling arrays using probes that maximize U. Using the mouse genome, we demonstrate how several optimizations influence the tiling array design characteristics. With a sensible set of parameters, our designs cover 78% of the mouse genome including many regions previously considered ‘untilable’ due to the presence of repetitive sequence. Finally, we compare our whole genome tiling array designs with commercially available designs.
Availability
Source code is available under an open source license from http://www.ebi.ac.uk/~graef/arraydesign/
1. Introduction
1.1. Background
Genome sequences are providing an important template on which we seek to understand biological function. This template has been exploited in a number of ways to guide biological investigation at unprecedented resolution. A number of recent results have demonstrated the utility of tiled microarrays for unbiased biological discovery. In contrast to gene expression microarrays, which seek to measure the relative abundance of a specifically targeted set of sequences (e.g. expressed mRNAs in a specific cell type or experimental condition), tiling microarrays are composed of a large number of probes from a contiguous region of the genome selected so that they are immediately adjacent to (or overlap) one another. In this way, analysis with a tiling microarray can, for example discover transcribed regions of the genome outside of any known annotation (Bertone et al., 2004; Kapranov et al., 2002).
Tiling arrays have also been extensively used to localize DNA–protein interactions identified with chromatin immunoprecipitation (ChIP). In this technique (known as ChIP-chip), DNA fragments isolated in the ChIP step are labeled and hybridized to tiling microarrays (Buck and Lieb, 2004). ChIP-chip has been used to create a genome-wide map of active human promoters (Kim et al., 2005b), and is one of the major experimental techniques adopted by the ENCODE project in its attempt to determine all of the functional elements in the genome (ENCODE Project Consortium, 2004). Moreover, combining tiling array data with other genome-wide data sources has the potential to dramatically increase our understanding of genome function (Guezennec et al., 2005).
1.2. Tiling array platforms
A number of unique tiling array platforms using both PCR products and short oligonucleotide probes have been created for a variety of applications in mammalian genomes, including unbiased regional or whole-genome arrays and specifically targeted arrays encompassing certain classes of genomic regions such as known promoters or other genomic features.
Tiling arrays based on PCR fragments have successfully mapped DNA–protein interactions for selected regions of the human genome (Kim et al., 2005a; Rada-Iglesias et al., 2005). PCR arrays have also been successful at mapping interactions that are more widespread in their genomic extent, such as histone modifications (Koch et al., 2007). However, whole genome oligonucleotide tiling arrays, which are commercially available from a number of companies, outperform PCR fragment based tiling arrays, at least for transcriptional mapping (Emanuelsson et al., 2006). This result may apply to transcription factor binding experiments as well since transcription factor binding sites are generally short sequence motifs. Ultimately, the effort and expense required to create PCR product tiling arrays will likely limit the extent of their coverage to relatively small regions of the genome.
Previous whole genome tiling array designs have generally excluded or made little use of the repetitive portions of large vertebrate genomes (Bertone et al., 2006). However, with this strategy DNA–protein interactions will be invisible if they occur in regions identified by programs such as RepeatMasker (Smit et al., 2004). Indeed, DNA–protein interactions within repeats have been especially important in epigenetic studies (Martens et al., 2005) and direct measurement and localization of these interactions by ChIP-chip analysis could be important to understanding the function of genomic repeats. Some tiling array design methods allow for tiling through repeat features for exactly this purpose (Ryder et al., 2006).
1.3. Problem definition
Whole genome tiling array designs must balance competing interests. The ability to discover new biology in an unbiased fashion with the highest possible resolution requires maximal coverage of the genome at the highest possible density. In large mammalian genomes, data quality is significantly impacted by the presence of repetitive sequence because of the potential for cross-hybridization. Thus, most previous whole genome tiling array designs have concentrated only on the non-repetitive portion of the genome to ensure uniqueness. Another significant consideration is the cost of the experiment including both the array manufacturing cost and the expense of reagents for multiple slide hybridization experiments. Moreover, current array manufacturing techniques prevent some specific sequences from being synthesized. Finally, any array design should aim at facilitating optimal analysis of the resulting data.
1.3.1. Probe uniqueness
Methods for determining unique oligonucleotides are critical for accurate results from microarray experiments since non-unique sequences are likely to cross-hybridize. Enrichment from unexpected portions of the genome, especially when this enrichment is distributed across probes in an unknown way, will give rise to significant experimental noise, which may compromise analysis and limit conclusions that can be drawn from the experiment.
As noted above, the simplest possible approach to the problem of repetitive sequences in large genomes is to ignore those sequences that are annotated as repetitive. This naive approach ignores both those ancient repeats that have significantly diverged over evolutionary time and those ‘non-repetitive’ sequences that, in fact, occur many times in the genome due to their presence in gene families or other multicopy, but not repetitive sequence as traditionally defined. A more direct approach used by previous oligonucleotide design methods addresses the problem of probe uniqueness using an alignment-based approach in which prospective probes are tested for uniqueness using a procedure based on elongation of exact matches (with BLAST or a similar algorithm) against a sequence database representing the possible sequences that a probe on the array will encounter (Bertone et al., 2006; Wang and Seed, 2003).
1.3.2. Biochemical properties
Tiling array design must take into account a number of biochemical and biophysical properties of oligonucleotide sequences that have the potential to interfere with hybridization. These properties fall into two distinct groups: first, several properties affect the performance of the probes during the hybridization experiment including probe melting temperature and probe self-hybridization potential (Bloomfield et al., 2000). Second, the manufacturing of the arrays requires specific chemistry which may damage longer probes and renders certain nucleotide sequences difficult to accurately manufacture (Lockhart et al., 1996).
1.3.3. Analysis considerations
The analysis to be performed is largely determined by the experimental use of the tiling array. Transcriptional mapping is most successful with overlapping probes or tiling arrays with high probe density (Emanuelsson et al., 2006; Huber et al., 2006), while array-based approaches for copy number variation commonly use comparably sparse tiling arrays (Graubert et al., 2007). ChIP-chip applications, in which we are most interested, require relatively dense arrays. Additionally, for ChIP-chip approximately uniform spacing of probe enrichment data has been shown to be effective in localizing DNA–protein interactions (Qi et al., 2006).
2. Models and Algorithms
2.1. Defining the uniqueness score
We are interested in unique substrings for a hypothetical genome sequence G of ~3 · 109 nucleotide which contains significant repetitive sequences (e.g. a mammalian genome). Uniqueness always refers to the complete genome sequence including both the forward and reverse strand of the assembled chromosomes and additional, but not yet assembled, sequence. Thus, we assume that this complete genome sequence set is on the order of 6·109 characters and is referred to as GS in the following. Of course, if we make a substring of G only large enough, it will become unique. So as a representation of unique substrings, we are interested only in the minimum unique substrings. A substring x of G is a minimum unique substring if x occurs exactly once in GS and each proper substring of x occurs more than once in GS.
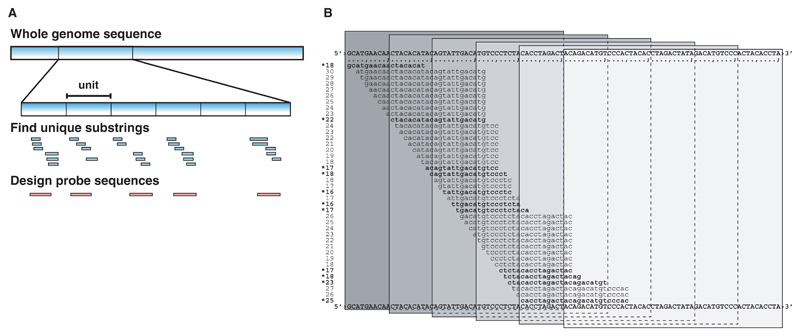
As shown in Figure 1A, we divide G into non-overlapping substrings s of length ℓ (which we refer to as a unit). For a given probe length h, we shift a window of size h over s and determine the uniqueness score U(s, r) at all possible offsets r, 1 ≤ r ≤ ℓ − h + 1. U(s, r) is defined as the number of minimum unique substrings of length ≤K ending in some position j, r ≤ j ≤ r + h − 1. To efficiently determine U(s, r), we compute minimum unique prefixes at all possible positions in s:
Fig. 1.
Design strategy. (A) The genomic sequence is subdivided in unit-sized windows. Within each window, all minimum unique substrings with length ≤K are determined. These are the basis for the uniqueness scoring to design optimized probes. (B) Uniqueness scoring function (exemplified by Mus musculus, chr17:3028401-3028500). The shown sequences represent all the minimum unique prefixes for a unit window. In each window of seed length h, the uniqueness score is calculated by counting the number of minimum unique substrings. For the windows shown, the uniqueness scores are 7, 9, 7, 4, 1, 0. The minimum unique substrings that add to the score are indicated by stars.
For each i ∈ [1, ℓ], mup(s, i) is defined by the following two statements:
If s[i..ℓ] occurs more than once as a substring in GS, then mup(s, i) is undefined, denoted by mup(s, i) = ⊥.
If s[i..ℓ] does not occur more than once in GS, then mup(s, i) = m, where m is the smallest positive integer such that i + m − 1 ≤ ℓ and s[i..i + m − 1] occurs exactly once as a substring in GS. Here, s[i..i + m − 1] denotes the substring of s from position i to position i + m − 1.
The substring s[i..i + mup(s, i) − 1] is denoted minimum unique prefix at position i. To explain the relationship between minimum unique prefixes and minimum unique substrings, we consider the set φ(j) of start positions of minimum unique prefixes ending at j, i.e. φ(j) = {i | i ≥ 1, i + mup(s, i) − 1 = j}. The following lemmata show the relationships:
Lemma Let φ(j) ≠ ∅ and i = max φ(j). Then s[i..j] is a minimum unique substring.
Proof: By definition j = i + mup(s, i) − 1, i.e. s[i..j] is the minimum unique prefix at position i. It occurs once in GS. By definition, s[i..j − 1] occurs more than once in GS. Since i = max φ(j), we conclude i + ∉ φ(j). Hence, i + 1+ mup(s, i + 1) − 1 ≠ j. Now suppose i + 1 + mup(s, i + 1) − <j. This implies that s[i + 1..i + 1 + mup(s, i + 1) − 1] is a proper prefix of s[i + 1..j]. Hence, s[i..i + 1 + mup(s, i + 1) − 1] is a proper prefix of s[i..j] and so s[i..i + 1 + mup(s, i + 1) − 1] occurs more than once in GS. Hence, s[i + 1..i + 1 + mup(s, i + 1) − 1] occurs more than once in GS. This is a contradiction. Thus the assumption i + 1 + mup(s, i + 1) − 1<j was wrong, and we conclude i + 1 + mup(s, i + 1) − 1>j. Hence, s[i + 1..j] occurs more than once in GS. Now consider a proper substring p of s[i..j]. p must be a substring of s[i + 1..j] or s[i..j − 1]. Since these occur more than once in GS, so does p. Hence, all proper substrings of s[i..j] occur more than once in GS, which means that s[i..j] is a minimum unique substring.
Lemma Let s[i..j] be a minimum unique substring. Then φ(j) ≠ ∅, i = max φ(j) and j = i + mup(s, i) − 1.
Proof: By definition, s[i..j] occurs once in GS. Suppose that mup(s, i) is undefined. Then s[i..ℓ] occurs more than once in GS. Since j ≤ ℓ, s[i..j] occurs more than once in GS. This is a contradiction. Hence mup(s, i) is defined. Suppose j<i + mup(s, i) − 1. Then s[i..j] occurs more than once in GS, a contradiction. Suppose j + mup(s, i) − 1. Then s[i..i + mup(s, i) − 1] is a proper prefix of s[i..j] which occurs once in GS. This contradicts the fact that any proper substring of s[i..j] occurs more than once in GS. Thus we conclude j = i + mup(s, i) − i which also implies φ(j) ≠ ∅. Obviously i ∈ φ(j). Suppose i<i′ where i′ = max φ(j). Then j = i′ + mup(s, i′) − 1. By definition, s[i′..j] only occurs once in GS. But since s[i′..j] is a proper suffix of s[i..j], it occurs more than once in GS. This is a contradiction. Hence i = max φ(i).
As a consequence, there is a one-to-one correspondence between the minimum unique substrings and the distinct end positions of minimum unique prefixes (Fig. 1B). In other words, counting the distinct end positions of minimum unique prefixes is equivalent to counting the number of minimum unique substrings. This holds for each unit s as well as for the entire genome under consideration. We can thus compute
Given the mup(s, i)-values for a unit s, we can compute all values U(s, r) in time proportional to ℓ.
2.2. Computing minimum unique prefixes
Our uniqueness problem involves the comparison of 3 · 109/ℓ units (each with ℓ positions) against a sequence of 2 × 3 · 109 characters. The huge number of uniqueness queries against the same data set requires us to preprocess GS into a string index.
The most well known string index structures are suffix trees (Gusfield, 1997; Weiner, 1973) and suffix arrays (Manber and Myers, 1993). The standard suffix-tree/suffix-array-based algorithms for string searching can easily be adopted to determine the sought minimum unique prefix lengths for a given unit. While suffix trees deliver the minimum unique prefixes in optimal time (i.e. time proportional to the length of a unit), a suffix array (in its simplest form) requires time proportional to log n, where s is the given unit and n is the total length of all sequences in GS. However, the reduced running time for a suffix-tree-based solution is at the cost of a larger space consumption. While the simplest form of suffix arrays for GS can be implemented in bytes, the most space efficient implementations for suffix trees (Giegerich et al., 2003; Kurtz, 1999) require about three times more space. This led us to the conclusion that we are not able to solve our uniqueness problem with suffix trees.
A suffix array for GS requires n⌈log2 n⌉ = 4.125n = 24.75 · 109 bytes, which conveniently fits into the 48 GB RAM of the machine we had available for this task. However, our first program to solve the uniqueness problem was based on the suffix arrays implemented in the software package Vmatch (http://www.vmatch.de). This program uses 64-bit integers for representing numbers larger than 232 − 1, resulting in a space requirement of 8n = 48 · 109 GB. Given that we additionally have to represent the sequence set GS, we are not able to store all required information in the given amount of memory. Note that it is also not obvious how to solve the uniqueness problem by a divide and conquer approach, i.e. solving it for disjoint subsets of GS and combining the results.
For these reasons, we have developed a solution based on a compressed index structure, namely the FMindex, originally proposed by Ferragina and Manzini (2000). The FMindex is based on the Burrows–Wheeler transform (Burrows and Wheeler, 1994), which is known from data compression. The simplest way of explaining the concept of the FMindex is via suffix arrays. So let us first define these.
Suppose that we have reversed all sequences from GS and concatenated them into one very long string S with a unique separator symbol between adjacent sequences and a final unique sentinel symbol following the last sequence. Let n be the length of S. By Si = S[i..n], we denote the suffix of S beginning at position i. Now let Si1, Si2, . . . , Sin−1, Sin be the sequence of all suffixes of S sorted in lexicographic order, i.e. ij ≠ ik for j ≠ k and Sij is lexicographically smaller than Sij+1 for each j, 1 ≤ j ≤ n − 1. Obviously, we can represent the sequence of ordered suffixes by the array [i1, i2, . . . , in−1, in] of start positions. This array is termed suffix array. The Burrows–Wheeler transform T is a sequence of length n storing the character to the left of each suffix in the order, the suffixes are sorted. That is, for each j, 1 ≤ j ≤ n, T[j] = S[ij − 1] if ij>1 and T[j] is undefined if ij = 1. T is a permutation of S allowing us to search all substrings occurring in S. The search requires to implement a table C and a function Occ defined as follows:
C is an array of length 4 where C[a] is the total number of occurrences of characters in T which are alphabetically smaller than a.
Occ(a, q) is a function delivering the number of occurrences of character a in the prefix T[1..q].
The substrings of S can be searched in reverse order, from right to left. Thus, the reversed strings in S (i.e. the original strings from GS) can be searched from left to right, which allows to conveniently compute the mup-values. Here is a simple algorithm to compute mup(s, i) for a given unit s of length ℓ and all i in the range [1, ℓ] is shown by Algorithm 1:
Algorithm 1 Compute mup(s, i) for a given unit s of length l.
1: for i = 1 to ℓ do
2: first = 1;
3: last = n;
4: j = i
5: while j≤ℓ && first < last do
6: a = s[j];
7: first = C[a] + Occ(a, first − 1) + 1;
8: last = C[a] + Occ(a, last);
9: j = j + 1;
10: end while
11: if first == last then
12: printf (“mup %d=%d\n”,i,j − i);
13: end if
14: end for
Recent advances show that the FMindex can be implemented such that Occ(a, q) can be computed in constant time (Ferragina et al., 2006). As a consequence, Algorithm 1 runs where ℓ = 100. This is faster by a factor log n compared to the suffix-array-based solution. Our implementation is based on a simpler technique similar to Navarro (2004), but tailored for processing DNA sequences. It also has some features in common with the technique described in Healy et al. (2003), but we use less space.
The Burrows–Wheeler transform T is stored uncompressed in (2 + δ)n bits where δ ≤ 1 depends on the number of positions in S not containing a base a, c, g or t. Besides T we need bytes to implement function Occ, where b is some user defined constant smaller than 256. Occ(a, q) is computed in O(b) time.
Since the Burrows–Wheeler transform is based on the suffix array for S, we first construct this. As described above, we cannot construct the entire suffix array in memory. Therefore, we choose the following approach: we divide the original sequences used to create GS into a small number A of disjoint subsets (e.g. one for each chromosome), each only containing the original sequence (no reverse complemented sequences). The subsets are small enough such that we can compute the suffix arrays in main memory. Then, for each of the A subsets, we construct two suffix arrays using the program mkvtree from the Vmatch software package: one suffix array for the reverse of the input sequences, and one for the complement of the input sequences. Note that the complement of the input sequences is the same as the reverse of the reverse complement of the input sequences. In this way, we obtain 2 × A suffix arrays, which are all stored in different files. In a second step, we use a multiway merging procedure which simultaneously reads all suffix arrays from left to right. With each merging step, we obtain the next suffix in the sorted order of all suffixes of S and obtain the corresponding character of the Burrows–Wheeler transform plus the remaining information comprising the FMindex. Note that the merging step does not require us to have the suffix arrays in main memory, because they are not randomly accessed. However, the sequences, for which the suffix arrays are constructed must be stored in the RAM. Once we have the FMindex stored on file, we can solve our uniqueness problem.
2.3. Validating the uniqueness score
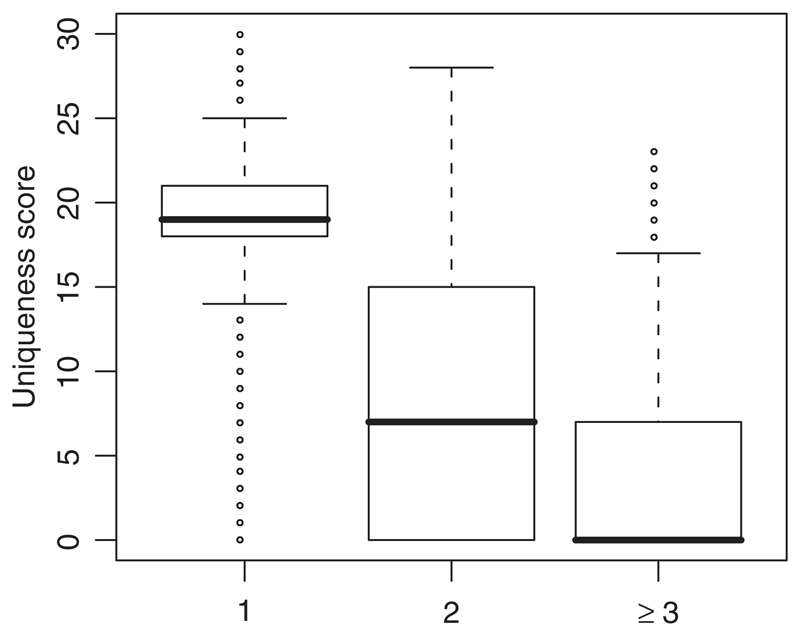
To validate the uniqueness score, we used a collection of nearly 670 000 50mer probes from the NimbleGen whole genome tiling array specifically designed for human chromosomes 22 and X. For each of these probes, we determined both U as defined above and the number of hybridization-quality alignments (see Methods Section) for each probe to the genome using BLAT (Kent, 2002). More than 91% of the probes we tested aligned only once and 97.5% aligned no more than twice. Figure 2 is a box and whiskers plot clearly showing that probes with a single BLAT alignment to the genome have significantly higher values for U than probes that align to the genome more than once. In fact, only one quartile of probes with exactly two BLAT alignments in the genome have U>15 and the median value of U for probes that align three or more times is zero.
Fig. 2.
The distribution of U with respect to the number of genome-wide hybridization-quality BLAT alignments for a large set of 50mer probes. The box-and-whiskers plot represents the median value of U by a bold line and the first and third quartiles of the U distribution are represented by the outline of the box. Whiskers represent the largest and smallest values of U within 1.5 × IQR (inter quartile range).
2.4. Probe selection algorithm
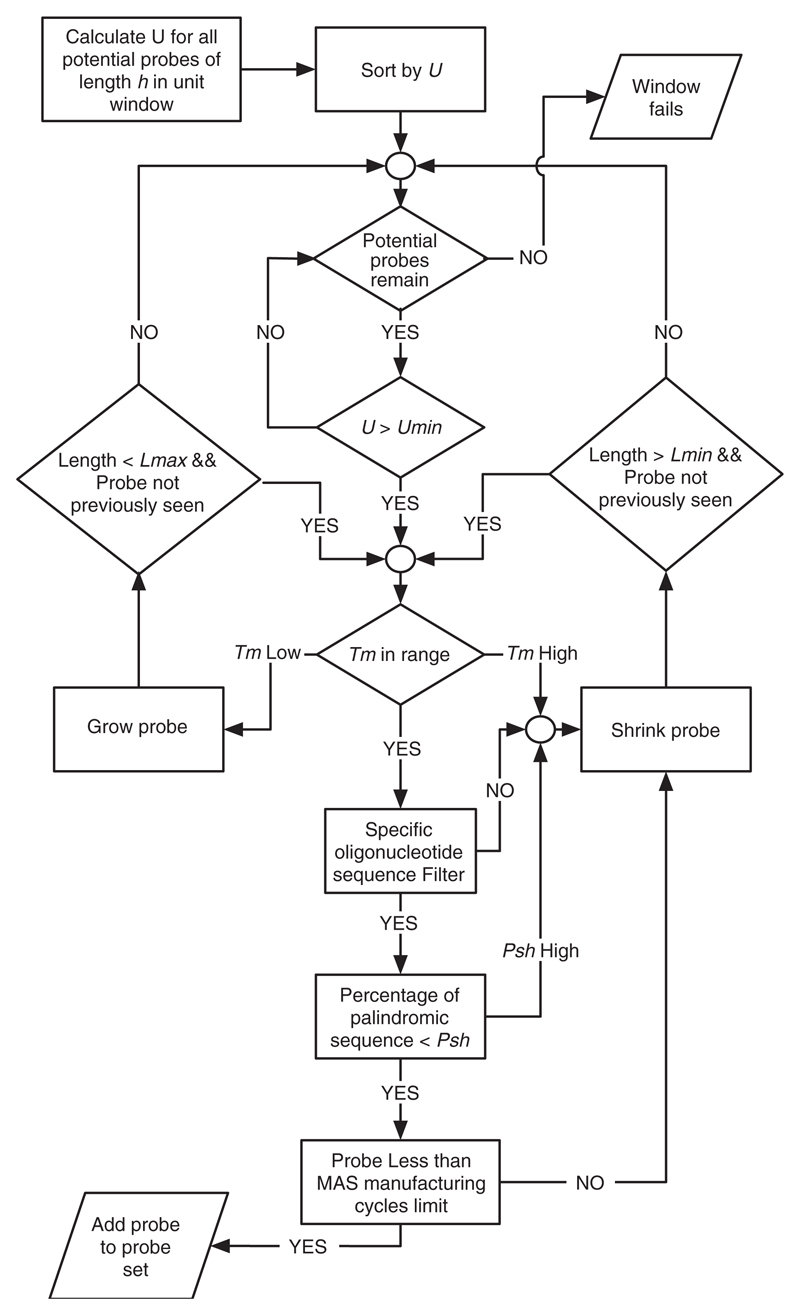
As shown in Figure 1, for a given probe length h we determine U(s, r) for all r, 1 ≤ r ≤ ℓ − h + 1, and sort the values by decreasing uniqueness scores. We say that probe p = s[r..r + h − 1] has uniqueness score U(s, r). From the sorted uniqueness scores, we determine the optimal probe in the unit using a greedy selection strategy, which addresses the biochemical properties of oligonucleotide probe design by considering a number of additional constraints on our probes. These are described below and shown graphically in Figure 3.
Fig. 3.
Probe selection algorithm.
Starting with the probe p that has the highest uniqueness score U, we ensure that the uniqueness score is higher than a given U threshold. If this is not the case, we will not place a probe in this unit-sized window. Otherwise, we will calculate the melting temperature using the following salt-adjusted approximation (Sambrook et al., 1989):
where c(Na+) is the salt concentration, fGC the frequency of Gs and Cs and N the overall number of nucleotides in the sequence.
If the melting temperature is within our defined range, we test the sequence for specific composition filters. In particular, we make sure that it does not contain any specific runs of oligonucleotides that are known to be difficult to manufacture (e.g. more than 6 consecutive Gs). Finally, we check that the sequence does not contain more than a given percentage of palindromic sequence to exclude probes with significant self-hybridization potential. In a final test, we may reject a probe that exceeds a given maskless array synthesis (MAS) manufacturing cycle limit. If one of these tests fails, we adjust the sequence either by growing or shrinking by a given step size within a given length range. This changes the sequence characteristics which are subsequently reassessed with the tests described above to find an alternative solution. If we are unable to find a probe with a uniqueness score greater than some threshold U, and satisfying all of the additional requirements, we will not place a probe in that unit-sized window. Figure 3 shows a flowchart of the probe selection algorithm.
3. Methods
The algorithm was implemented in a combination of C (FMindex creation and Algorithm 1) and Perl (probe selection algorithm). We have constructed our whole genome tiling array designs based on NCBI Build 36 of the mouse genome sequence downloaded from release 42 of Ensembl (ftp://ftp.ensembl.org).
To test the relationship between U and the number of BLAT alignments, the default settings were used to match the probe sequences from a non-isothermal, repeatmasked, 50mer NimbleGen whole genome tiling array design against build NCBI35 of the human genome. Alignments that met the following criteria were deemed unlikely to hybridize well to the probes and were ignored: (a) matches with more than one gap; (b) matches of length <30 (i.e. matching <60% of the probe); (c) matches with gap length >3 and (d) matches with more than three mismatched bases. The number of remaining matches was defined as the number of hybridization quality alignments for the probe.
4. Results and Assessment
We have used our algorithm to create whole genome tiling array designs for the 2.6 gigabase-pair mouse genome as a typical example of a repeat-rich mammalian genome. The mouse was the second mammalian genome sequenced (Mouse Genome Sequencing Consortium, 2002) and is a rich resource for biomedical research. Additionally, mouse whole genome tiling arrays are available from a number of commercial providers.
4.1. Computational requirements
The time required for completion of indexing steps is dependent on the number of repetitive sequences in the input sequence length. For the case of the mouse genome, and considering both strands simultaneously, the input sequence length is ~5.2 · 109 characters.
Approximately 1.7 h on a single 2.2 GHz AMD Opteron processor are required to create suffix arrays for all of the chromosome sequences (and the additional sequences that have not yet been confidently placed on the mouse genome assembly as of NCBI build 36). The multi-way merging procedure requires a further 6 h using the same configuration. This is a considerable improvement in construction time over Healy et al. (2003). The entire FMindex is computed in 5 GB of memory. After building the index, creation of one complete tiling array design from a typical parameter set, which sets ℓ = 100 and K = 30, takes ~22 h on a single processor.
4.2. Tiling array designs
To test the performance of the design algorithm, we have chosen a number of specific parameters for consideration. Specifically, we considered designs limited by two values of uniqueness score, U>0 and U>15; two values of initial seed length, h = 50 and h = 80; two ranges for probe hybridization temperature, 73 ≤ Tm ≤ 76 and 77 ≤ Tm ≤ 80; and two values for probe self-hybridization potential (i.e. palindromic content), Psh ≤ 30% and Psh ≤ 50%. For all designs, we limited the length range of the final probes to h ± 15. Two additional filters on the array design based on considerations of hybridization potential and manufacturing efficiency. These additional filters prohibit any probe with six or more consecutive guanine bases and limit the number of synthesis cycles that would be needed to manufacture the design using the maskless array synthesis. Cycle limits of 148 and 186 were tested.
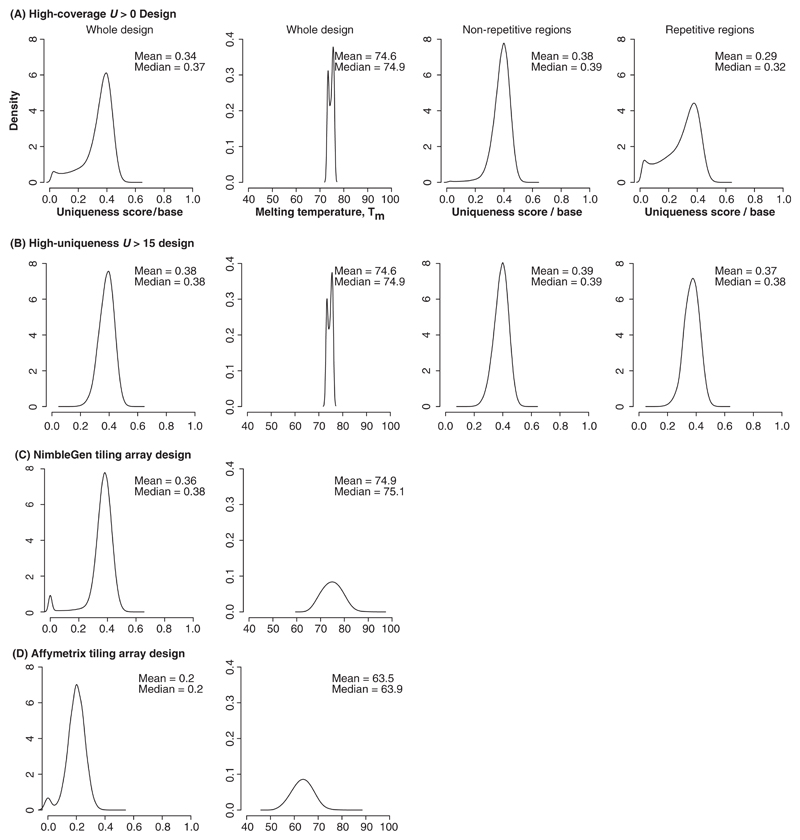
Figure 4A and B shows the effect of the two uniqueness score parameter settings on the final design of the tiling array.
Fig. 4.
Density plots of optimized characteristics for our high-coverage and high-uniqueness tiling array designs and comparison to commercial whole-genome tiling arrays. (A) The full design uniqueness score per base, Tm distribution and the uniqueness score per base for the disjoint subsets represented by the non-repetitive and repetitive portions of the mouse genome for our high-coverage U>0 design containing 19 343 498 probes in the entire design of which 10 565 728 probes are in regions not identified as repetitive and 8 777 770 probes are in repetitive regions; (B) The full design uniqueness score per base, Tm distribution and the uniqueness score per base for the disjoint subsets represented by the non-repetitive and repetitive portions of the mouse genome for our high-uniqueness U>15 design containing 15 658 735 probes in the entire design of which 10 213 493 probes are in regions not identified as repetitive and 5 445 242 probes are in repetitive regions; (C) The full design uniqueness score per base and the Tm distribution for the NimbleGen 50mers in 100 bp windows whole-genome design containing 14 579 139 probes designed to the non-repetitive portion of the genome and (D) The full design uniqueness score per base and the Tm distribution for the Affymetrix 25mers in 35 bp windows whole-genome design containing 38 346 501 probes designed to the non-repetitive portion of the genome. See Table 1 for additional design information.
4.2.1. Effect of algorithm parameters on design characteristics
As shown in Figure 3, each probe is chosen to maximize U while respecting the other parameters of the design. This leads to a direct trade-off between the coverage of the genome (the fraction of unit-sized windows in which probes are successfully placed) and minimum allowed uniqueness score. In Figure 4B, we show the effect of removing probes from the design which have U ≤ 15. For probes with an initial seed length of 50 and regardless of the allowable Tm range, setting U>15 results in preservation of ~80% of the probes with a uniqueness score U> 0, while removing those most likely to participate in cross-hybridization reactions.
Increasing the initial seed length to 80, while retaining all of the other parameters constant results in a larger fraction of windows retaining probes after the filter for uniqueness score. However, as expected, the number of synthesis cycles must be increased to achieve comparable genome coverage with the longer probes (data not shown).
Because standard oligonucleotide tiling arrays do not include the repetitive regions of the genome, we were interested in the uniqueness score of probes that are placed in regions annotated as repeats. To address this, we divided the probe sets into those that were placed in repetitive and non-repetitive regions based on a standard set of comprehensive repeat identification procedures designed to facilitate genome annotation (Curwen et al., 2004). Figure 4A and B shows that a much lower fraction of the probes with U>15 are placed in repetitive regions than probes limited only to U>0. In fact, the uniqueness score per base (described below) for probes in the non-repetitive regions with U>0 is the same as the mean uniqueness score per base for the probes in the full design with U>15.
Compared to U, filters for palindromic content have a relatively minor effect on the number of probes potentially removed from the design. Surprisingly, the palindromic filter removes a greater fraction of probes with U>15, than with U ≤ 15 showing that palindromic sequences are more unique in the genome.
4.2.2. Design coverage
A primary goal of our work is to create a tiling array with the highest possible coverage of the genome while maintaining the maximum possible uniqueness. To adequately assess the coverage of our tiling array designs, we consider multiple measures of coverage. The first, and most simple, measure is the number of genomic base pairs actually present on the tiling arrays. This value can theoretically be larger than 100% for the case of overlapping probes. We have also measured the number of base pairs in unit-sized windows for which a probe was successfully placed. Finally, we measure the extent of regions in which probes are placed in continuous unit-sized windows (we require four or five consecutive windows to have probes for a region to be called continuous). This measure is based on the common analysis technique of using sliding window analysis to determine the positive regions on the tiling arrays (e.g. Bertone et al., 2004; Buck et al., 2005). Coverage values for our array designs are shown in Table 1
Table 1.
Coverage of the mouse genome, expressed as a percentage of the length of the genome assembly, for the base pair, window and region measures for various tiling array designs
| Design parameters | Base pair | Window | Region |
|---|---|---|---|
| U > 0; 73 ≤ Tm ≤ 76; Psh ≤ 0.3 | 35.1 | 73.2 | 78.1 |
| U > 15; 73 ≤ Tm ≤ 76; Psh ≤ 0.3 | 28.4 | 59.2 | 60.7 |
| NimbleGen* | 27.6 | 55.1 | 52.7 |
| Affymetrix† | 36.5 | 50.8 | 50.5 |
Design number C4527-SET-01.
GeneChip© Mouse Tiling 2.0R Array Set.
With a goal of increasing coverage, we tested ℓ values of 75, 100, 150 and 200 bp. As expected the fraction of windows in which we are able to place a probe increases with window size, while the total number of probes placed falls. Base-pair coverage does increase marginally with smaller ℓ values. For example, using the U > 15 design described in Table 1, base-pair coverage increased from 28.4% for ℓ = 100 to 30.9% for ℓ = 75. However, this increase does not effect array resolution which is based on probe density (Emanuelsson et al., 2006). As described above, our interest in ChIP-chip applications demands relatively dense tiling arrays which explains our choice of ℓ = 100 to match the resolution of the NimbleGen designs that have been used successfully for this technique.
4.3. Array design comparison
We sought to compare our tiling array design with standard catalog tiling array designs available from Affymetrix and NimbleGen. Each of these designs has characteristics that make exact comparison difficult. For example, both the Affymetrix and NimbleGen designs used fixed-length oligonucleotide probes (25 and 50 bases, respectively) and both designs seek to have a uniform distribution of the probes within tiled regions. Neither explicitly considers the hybridization temperature. Consideration of these differences allows us to assess the effect of Tm optimization in our algorithm and led us to generalize the uniqueness score metric as described below.
In general, uniqueness score is proportional to probe length. Thus to compare tilling array designs with differing probe lengths we compute the normalized uniqueness score for each probe, which is defined as the uniqueness score divided by the probe length. For these comparisons listed below, we only consider our designs with an MAS synthesis cycle limit of 148 to be comparable with the NimbleGen catalog tiling array design. Although we use the same cycle number limitation as the NimbleGen design, our probes are shorter, on average, due principally to the effect of the Tm optimization. Probes in the U > 15 high-uniqueness design have a mean length of 48.0 bp and SD of 5.85 bp. For the U > 0 high-coverage design these values are fractionally smaller.
Figure 4C and D shows the uniqueness score per base, and the Tm distribution for the NimbleGen and Affymetrix whole genome tiling array designs. When we compare these to the designs produced by our algorithm, we see that our high-uniqueness design contains nearly the same number of probes as the NimbleGen design, but with higher coverage and less Tm variability. As expected, Affymetrix’s shorter probes are less unique and have a lower average Tm that the other designs.
5. Discussion
In this article, we have described an algorithm for the efficient design of whole genome tiling arrays created from large mammalian genomes. A key feature of this design is the definition of a new measure of probe quality that we have termed the uniqueness score. We have demonstrated that U can be efficiently calculated using an FMindex data structure and that probes with high uniqueness scores can be found in regions of the genome annotated as repetitive by programs such as RepeatMasker and therefore missing from standard whole genome tiling array designs. The approach differs fundamentally from the Bertone et al. (2006) approach which presents an optimal solution for placing tiles larger than 300 bp in a RepeatMasked genome. Bertone et al. (2006) also discuss the effect of parameters such as probe uniqueness and Tm for oligonucleotide tiling arrays similar to the ones considered in Section 4.3, but do not present an algorithm for this case.
Our algorithm was designed to support and improve data analysis techniques. For example, by creating high-quality and consistent probes within unit-sized windows, we anticipate that the experimental results from each probe will serve as a proxy for the response of the entire window. By selecting only probes with maximal uniqueness scores and, perhaps more importantly, knowing the uniqueness of each probe on the array, we are better able to estimate the potential for experimental noise caused by cross-hybridization.
Our approach to scoring uniqueness is considerably different from existing approaches which either are based on aligning the probes to the genome or counting short sequence frequencies, e.g. summing the genome-wide frequency of kmers occurring in an probe sequence. One example of the latter technique used an algorithm for counting genome-wide occurrence of 15mers developed by Healy et al. (2003) to find the best 70 bp probe in each of collection 200–1200 bp fragments created by restriction digest. Lucito et al. (2003) used these probes on an array designed to find genome copy number variation. In this case, the variable window lengths are much larger than the windows that we use and, although appropriate in their CNV study, do not provide the needed resolution for ChIP-chip.
Aligning probes and counting short sequence frequencies are actually estimates of similarity rather than of uniqueness. Put another way, both alignment and frequency counting approaches estimate the potential for a probe to cross-hybridize by determining the extent of the rest of the genome that is very similar to the probe. Our uniqueness score, on the other hand, is an estimation of how unlike the probe is from everything else in the genome. Our assumption is that the more unique the probe, the lower the probability that it will be able to hybridize to any other sequence in the genome.
We believe there are several significant advantages to our approach over methods that use alignments to estimate the cross-hybridization potential: first, the alignment approach depends heavily on the alignment method used and the parameter settings for acceptable alignments. Additionally, the resulting alignments do not have a one-to-one correspondence with possible hybridizations. The uniqueness score, on the other hand, can be considered a well-defined property of any subsequence of the genome, independent of the choice of implementation. Second, our method is significantly faster than any similar alignment-based approach, since the score is pre-calculated over the entire genome sequence and defined for any subsequence of the genome. We can, therefore, optimize our choice of probes to the positions with maximum uniqueness score. A similar optimization with an alignment-based approach would require a new genome-wide alignment for each potential probe sequence. For our design with h = 50 and final probe lengths limited to h ± 15 this corresponds to calculating more than 8 · 1010 genome-wide alignments in the worst case.
Our designs, created with a sensible set of parameters, are more unique than the Affymetrix or NimbleGen designs (as measured by the uniqueness score), and have a more consistent Tm distribution while notably increasing coverage. We have not compared our designs to iso-thermal tiling designs available from any manufacturer as these are currently limited to select regions of the genome, such as promoter arrays.
Finally, we observe probes placed in windows for which no probe can be placed in the window to either side of the placed probe. These ‘singleton’ probes are more common in repeat regions. This is a potentially important feature for the analysis of DNA–protein interactions in repetitive regions with techniques such as ChIP-chip, although fairly sophisticated data analysis methods will be required for these cases. Properly constructed tiling arrays including singleton probes in repetitive regions are potentially useful for assessing copy number variation and certain repeat polymorphisms.
6. Conclusion
We propose uniqueness score as a general measure of probe quality for tiling array designs. The uniqueness score is based on the content of shortest unique substrings in the probes and measures how unlike the probe is from anything else in the genome. We use U at the heart of an algorithm to efficiently design whole-genome tiling arrays with relatively modest computational requirements. Our code implementing this algorithm is provided under an open source license.
In collaboration with NimbleGen, we are in the process of testing these designs with ChIP-chip experiments across a significant portion of mouse chromosome 17. We expect the results of these tests to guide further improvements to tiling array design.
Acknowledgements
The authors would like to thank Paul Bertone, Kyle Munn, Todd Richmond, Xinmin Zhang, Srinka Ghosh, Chris Davies, Vera van Noort and Lene M. Favrholdt for helpful discussions at several points during the project. This work is partially supported by the EU FP6 HEROIC project.
Footnotes
Conflict of Interest: none declared.
References
- Bertone P, et al. Global identification of human transcribed sequences with genome tiling arrays. Science. 2004;306:2242–2246. doi: 10.1126/science.1103388. [DOI] [PubMed] [Google Scholar]
- Bertone P, et al. Design optimization methods for genomic DNA tiling arrays. Genome Res. 2006;16:271–281. doi: 10.1101/gr.4452906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloomfield VA, et al. Nucleic Acids: Structures, Properties, and Functions. University Science Books; Herndon, VA, USA: 2000. [Google Scholar]
- Buck MJ, Lieb JD. ChIP-chip: considerations for the design, analysis, and application of genome-wide chromatin immunoprecipitation experiments. Genomics. 2004;83:349–360. doi: 10.1016/j.ygeno.2003.11.004. [DOI] [PubMed] [Google Scholar]
- Buck MJ, et al. ChIPOTle: a user-friendly tool for the analysis of ChIP-chip data. Genome Biol. 2005;6:R97. doi: 10.1186/gb-2005-6-11-r97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burrows M, Wheeler D. Research Report 124. Digital Systems Research Center; 1994. A Block-Sorting Lossless Data Compression Algorithm. [Google Scholar]
- Curwen V, et al. The Ensembl automatic gene annotation system. Genome Res. 2004;14:942–950. doi: 10.1101/gr.1858004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emanuelsson O, et al. Assessing the performance of different high-density tiling microarray strategies for mapping transcribed regions of the human genome. Genome Res. 2006 Nov 21; doi: 10.1101/gr.5014606. Advance online publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ENCODE Project Consortium. The ENCODE (ENCyclopedia Of DNA Elements) Project. Science. 2004;306:636–640. doi: 10.1126/science.1105136. [DOI] [PubMed] [Google Scholar]
- Ferragina P, Manzini G. Opportunistic data structures with applications. IEEE Symposium on Foundations of Computer Science; 2000. pp. 390–398. [Google Scholar]
- Ferragina P, et al. Compressed Representations of Sequences and Full-Text Indexes. ACM Trans Algorithms. 2006 to appear. [Google Scholar]
- Giegerich R, et al. Efficient implementation of lazy suffix trees. Softw Pract Exper. 2003;33:1035–1049. [Google Scholar]
- Graubert TA, et al. A high-resolution map of segmental DNA copy number variation in the mouse genome. PLoS Genet. 2007;3:e3. doi: 10.1371/journal.pgen.0030003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guezennec XL, et al. Targeted discovery tools: proteomics and chromatin immunoprecipitation-on-chip. BJU Int. 2005;96(Suppl. 2):16–22. doi: 10.1111/j.1464-410X.2005.05942.x. [DOI] [PubMed] [Google Scholar]
- Gusfield D. Algorithms on Strings, Trees, and Sequences. Cambridge University Press; New York: 1997. [Google Scholar]
- Healy J, et al. Annotating large genomes with exact word matches. Genome Res. 2003;13:2306–2315. doi: 10.1101/gr.1350803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huber W, et al. Transcript mapping with highdensity oligonucleotide tiling arrays. Bioinformatics. 2006;22:1963–1970. doi: 10.1093/bioinformatics/btl289. [DOI] [PubMed] [Google Scholar]
- Kapranov P, et al. Large-scale transcriptional activity in chromosomes 21 and 22. Science. 2002;296:916–919. doi: 10.1126/science.1068597. [DOI] [PubMed] [Google Scholar]
- Kent WJ. BLAT – The BLAST-Like Alignment Tool. Genome Res. 2002;12:656–664. doi: 10.1101/gr.229202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim TH, et al. Direct isolation and identification of promoters in the human genome. Genome Res. 2005a;15:830–839. doi: 10.1101/gr.3430605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim TH, et al. A high-resolution map of active promoters in the human genome. Nature. 2005b;436:876–880. doi: 10.1038/nature03877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koch CM, et al. The landscape of histone modifications across 1% of the human genome in five human cell lines. Genome Res. 2007;17:691–70. doi: 10.1101/gr.5704207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurtz S. Reducing the space requirement of suffix trees. Softw Pract Exper. 1999;29:1149–1171. [Google Scholar]
- Lockhart DJ, et al. Expression monitoring by hybridization to high-density oligonucleotide arrays. Nat Biotechnol. 1996;14:1675–1680. doi: 10.1038/nbt1296-1675. [DOI] [PubMed] [Google Scholar]
- Lucito R, et al. Representational oligonucleotide microarray analysis: a high-resolution method to detect genome copy number variation. Genome Res. 2003;13:2291–2305. doi: 10.1101/gr.1349003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manber U, Myers E. Suffix arrays: a new method for on-line string searches. SIAM J Comput. 1993;22:935–948. [Google Scholar]
- Martens J, et al. The profile of repeat-associated histone lysine methylation states in the mouse genome. EMBO J. 2005;24:800–812. doi: 10.1038/sj.emboj.7600545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mouse Genome Sequencing Consortium. Initial sequencing and comparative analysis of the mouse genome. Nature. 2002;420:520–562. doi: 10.1038/nature01262. [DOI] [PubMed] [Google Scholar]
- Navarro G. The LZ-index: a text index based on the Ziv Lempel trie. J Discrete Algorithms. 2004;2:87–114. [Google Scholar]
- Qi Y, et al. High-resolution computational models of genome binding events. Nat Biotechnol. 2006;24:963–970. doi: 10.1038/nbt1233. [DOI] [PubMed] [Google Scholar]
- Rada-Iglesias A, et al. Binding sites for metabolic disease related transcription factors inferred at base pair resolution by chromatin immuno-precipitation and genomic microarrays. Hum Mol Genet. 2005;14:3435–3447. doi: 10.1093/hmg/ddi378. [DOI] [PubMed] [Google Scholar]
- Ryder E, et al. MAMMOT – a set of tools for the design, management and visualization of genomic tiling arrays. Bioinformatics. 2006;22:883–884. doi: 10.1093/bioinformatics/btl031. [DOI] [PubMed] [Google Scholar]
- Sambrook J, et al. Molecular Cloning: A Laboratory Manual. 2nd edn. Cold Spring Harbor Laboratory Press; 1989. [Google Scholar]
- Smit A, et al. RepeatMasker Open-3.0. 1996–2004 http://www.repeatmasker.org.
- Wang X, Seed B. Selection of oligonucleotide probes for protein coding sequences. Bioinformatics. 2003;19:796–802. doi: 10.1093/bioinformatics/btg086. [DOI] [PubMed] [Google Scholar]
- Weiner P. Linear Pattern Matching Algorithms. Proceedings of the 14th IEEE Annual Symposium on Switching and Automata Theory; Northridge, CA USA. The University of Iowa, Iowa City, IEEE Computer Society, Publications Office; 1973. pp. 1–11. [Google Scholar]