Abstract
Although often conflated, determining the best treatment for an individual (the task of a doctor) is fundamentally different from determining the average effect of treatment in a population (the purpose of a trial). In this paper, we review concepts of heterogeneity of treatment effects (HTE) essential in providing the evidence base for precision medicine and patient-centred care, and explore some inherent limitations of using group data (e.g. from a randomized trial) to guide treatment decisions for individuals. We distinguish between person-level HTE (i.e. that individuals experience different effects from a treatment) and group-level HTE (i.e. that subgroups have different average treatment effects), and discuss the reference class problem, engendered by the large number of potentially informative subgroupings of a study population (each of which may lead to applying a different estimated effect to the same patient), and the scale dependence of group-level HTE. We also review the limitations of conventional ‘one-variable-at-a-time’ subgroup analyses and discuss the potential benefits of using more comprehensive subgrouping schemes that incorporate information on multiple variables, such as those based on predicted outcome risk. Understanding the conceptual underpinnings of HTE is critical for understanding how studies can be designed, analysed, and interpreted to better inform individualized clinical decisions.
Keywords: Heterogeneity of treatment effects, effect measure modification, statistical interaction, subgroup analysis
The emerging areas of comparative effectiveness research1 and precision medicine2 share the same core mission: determining which treatment works best, for whom and under what circumstances. Thus, the concept of heterogeneity of treatment effects (HTE) - the idea that treatment effects can vary across patients - is at the centre of both comparative effectiveness research and precision medicine.1,3
There has been increased attention to HTE, and the term seems to be used differently by various stakeholders. Clinicians, for example, intuitively understand that no two patients are identical, and perceive pervasive HTE in their practice. In contrast, statistical analyses of clinical trials even when based on very large studies rarely identify factors that reliably predict differential treatment effectiveness. This leaves clinicians with an evidence base composed principally of average trial results, which is incongruent with their intuition derived from treating patients who vary both in their apparent responses to treatment and in clinical characteristics that determine the probability of good and bad outcomes, with and without a particular treatment.
Precision medicine holds the promise that a fuller understanding of inter-individual molecular variation can account for the variation in individual treatment effects, but herein we discuss conceptual and methodological challenges that have so far limited our ability to leverage even readily available clinical information to provide more patient centred evidence, and which will not be resolved, and are likely to be amplified, by the addition of new molecular data. Many of the concepts presented here are not new, but they are not widely appreciated and are often overlooked in the broad discussion of ‘-omics’, in clinical trial reporting and in guideline development. We hope that the synthesis of ideas from various sources can facilitate the interpretation of HTE analyses, aid clinical decision-making and guide future research.
Person-level HTE is ubiquitous but unobservable
The choice among multiple treatments should ideally be guided by comparing an individual’s potential outcomes under each treatment. When comparing a new treatment versus usual care to prevent a binary adverse outcome, at most four types of individuals can exist in a given population (Box 1): those who would not experience the outcome regardless of treatment (‘immune’), those who would experience the outcome regardless of treatment (‘doomed’), and those who would experience the outcome only under treatment or only in its absence (‘harmed’ or ‘saved’, respectively).4,5 Perfect decision making would be possible if the category to which each patient belongs was known upfront. In fact, in general it is impossible to know who belongs in which category even after treatment has been administered and outcomes observed. For example, in the treatment group patients may be either ‘harmed’ or ‘doomed’ if they experience the outcome, and either ‘immune’ or ‘saved’ if they do not. This is a consequence of the fundamental problem of causal inference: only one of the potential outcomes can be observed for a given patient whereas outcomes under other treatments remain counterfactual.6 Thus, person-level treatment effects cannot be identified, even in large well-conducted randomized trials (with the potential exception of N-of-1 trials).
Nevertheless, we can use randomized trials to estimate average treatment effects.7–9 Box 1 shows how person-level treatment effects, although unidentifiable, are aggregated to yield average treatment effects using three common measures: the risk difference (RD), relative risk (RR) and odds ratio (OR).10–12 Randomization makes treatment groups comparable on average (more precisely, ‘exchangeable’), but it does not affect the degree of heterogeneity among patients in each treatment group. Indeed, each group will usually include patients from several of the categories shown in Box 1. We refer to this variation at the individual level as person-level HTE. Clinicians believe that it is important and ubiquitous, and logic demonstrates that it is unknowable.
It is easy to forget individual patients when interpreting estimates of overall effects from clinical trials. For example, if each of the four categories in Box 1 was equally represented in the population, the ‘true’ average treatment effect would be exactly zero, and we might falsely conclude that the treatment was totally ineffective and innocuous. Yet, in this fictitious example, 25% of patients experience benefit and another 25% experience harm from treatment. Thus, by examining estimates of the average treatment effect, we learn something about the whole population, not about each individual. Trial findings are often used to support uniform treatment recommendations for all patients, even when ideally optimized care would result from targeting just one of the four patient types (i.e. the ‘saved’). Fortunately, some targeting of treatment is possible by judicious consideration of treatment effects within subgroups.
Group-level HTE: examining treatment effects in subgroups
A comparison of treatment effects across subgroups of RCT participants quantifies HTE over levels of a subgrouping variable (e.g. sex, age, disease severity). When treatment effects vary across levels, we say that the variable is an effect modifier; this form of group-level HTE corresponds to the epidemiological concept of effect measure modification.13–15 The purpose of examining group-level HTE is to individualize treatment decision making. For example, we can obtain sex-specific treatment effects that apply to men or women. Yet, dividing the population into subgroups reveals the reference class problem,16,17 a key problem in using group results to select treatments for individuals:18,19 that each patient has innumerable characteristics, and therefore can belong to an indefinite number of different subgroups. It follows too that there is an indefinite number of ways to disaggregate a trial population into subgroups. This makes obtaining individualized treatment effect estimates problematic, because for any individual patient each alternative disaggregation can produce a different result for each of the reference classes to which that patient belongs. Selection of the best subgrouping scheme is a critical, but largely ignored, issue in HTE analysis, to which we return later.
Another important issue in group-level HTE analysis is scale dependence: the way we measure the treatment effect within each subgroup has implications on whether HTE across subgroups is present or not.20,21 In our hypothetical randomized trial, the treatment effect can be estimated using the event proportion in the new treatment () and the usual care group () (Box 1). Because commonly used effect measures (RD, RR, OR) are different combinations of these two proportions, lack of HTE on one measure will indicate the presence of HTE on the others (when the overall effect is not null and baseline risk varies across subgroups). The relationships among alternative measures of effect in the presence of HTE can be complex and often counteri-ntuitive.22
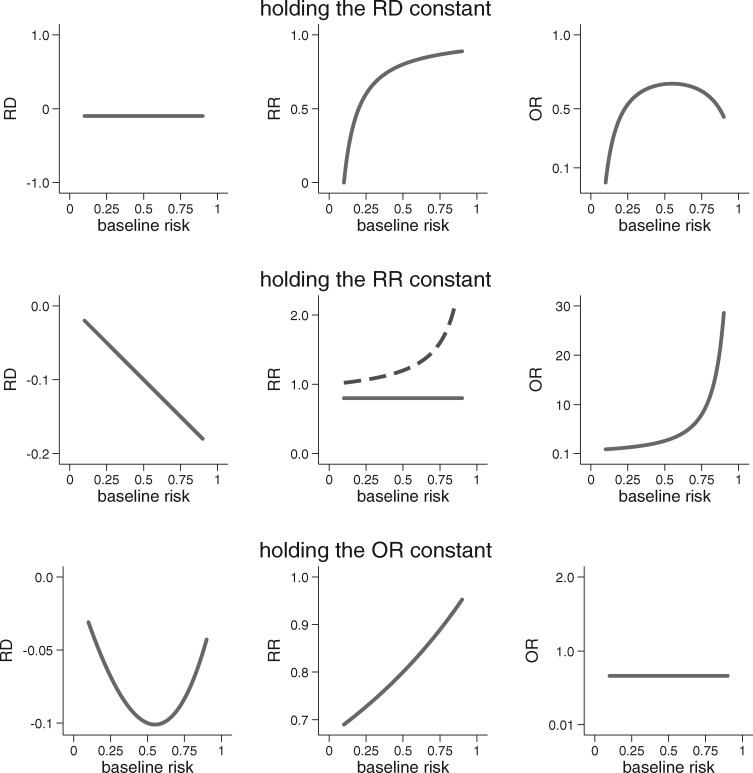
The scale-dependence of group-level HTE is easily seen when we examine effect heterogeneity across subgroups that vary with respect to baseline risk. Figure 1 shows how the RD, RR and OR behave when one of them is fixed (i.e. homogeneous) over the range of baseline risk. For any non-zero treatment effect, there will always be HTE on some measure whenever there is variation in baseline risk. For example, when the treatment has a homogeneous effect on the RR scale, absolute benefit (on the RD scale) will increase linearly as baseline risk increases. The central panel of the figure demonstrates another, less appreciated, issue: as baseline risk varies, homogeneity of treatment on the RR scale cannot be present for each of two complementary outcomes (e.g. both death and non-death), when baseline risk varies.23
Figure 1.
An illustration of the scale dependence of HTE. When treatment effect is non-null and baseline risk varies, HTE is inevitable on at least two out of three of the most commonly used scales for treatment effect. The graphs above show that when one measure of treatment effect is held constant, the other two must vary substantially as the baseline risk changes. The centre panel also demonstrates that when the treatment effect is non-null and baseline risk varies, when the RR is held constant for ‘event occurrence’, then there will exist HTE for the complementary outcome (i.e. ‘no event occurrence’, shown by the dotted line). When held constant, the RD = −0.1, the RR = 0.8 and the OR = 0.66. Results are shown over baseline outcome risks ranging from 0.1 to 0.9.
Identifying and interpreting HTE
Most often HTE detection in clinical trial analyses relies on the assessment of statistical interactions.24–28 These analyses compare treatment effects across strata of a covariate and produce P-values for a test of the null hypothesis of no effect heterogeneity.25,29 In interpreting these statistical interactions, it is important to keep in mind the narrowness of the hypothesis being assessed: whether the treatment effect is constant across levels of a specific subgrouping variable on a given scale. Clinical interpretation of HTE is typically complicated by the fact that interactions are usually examined analytically on relative scales (primarily for computational convenience), but it is generally agreed that the absolute risk difference (RD) or its inverse, the number needed to treat, is the most relevant effect metric for clinical decision making. 11,30–32 Thus, regardless of whether a subgroup analysis yields statistically significant HTE, what determines whether HTE is of clinical consequence is whether or not variation in the RD across different subgroups of patients spans a decisionally important threshold- a threshold that will depend on the potential harms of therapy, patient values and (in some cases) economic considerations. This condition might be fulfilled even in the absence of statistically significant HTE on a relative scale (e.g. when baseline risk varies substantially), and not fulfilled even in its presence (e.g. when treatment is clearly beneficial for all subgroups despite relative risk variation).
As an aside, we stress that the presence of statistical interaction does not imply that manipulating the subgrouping variable will affect the outcome. Even in a randomized study, differences in the treatment effect over a subgrouping variable may be due to uncontrolled relationships between the variable, factors for which it operates as a proxy, and the outcome.30,33,34 For example, if acute stroke patients with extreme hypertension are shown to benefit less from thrombolytics, it does not imply that acute blood pressure lowering will improve effectiveness.35 Although important for understanding disease and treatment mechanisms, establishing the presence of causal interactions is not a requirement for using HTE analyses to guide clinical decisions.
Challenges in the detection of clinically-relevant HTE
In the context of precision medicine and comparative effectiveness research, the goal of HTE analysis is to inform clinical decisions by providing estimates of treatment effect that are more specific to individuals. Disaggregating trial results to provide reliable patient-centred estimates of treatment effectiveness in practical data analyses is challenging. Many of these challenges relate to the fundamental conceptual issues discussed, and also the complexity of the phenomena under study, not the choice of a particular statistical approach. That said, reliance on conventional ‘one-variable-at-a-time’ subgroup analysis—where each potentially influential variable is serially considered in isolation—are particularly problematic and can lead to avoidable erroneous inferences. Below we review these issues and suggest an approach based on risk modelling, which at least partially addresses many of these challenges.
Problems related to one-variable-at-a-time approaches
Under-representation of explainable heterogeneity
The conventional approach to exploring group-level HTE is to serially test for interactions between treatment and each potential effect modifier for example, comparing men with women, old with young, smokers with non-smokers and so forth. Whereas patients have multiple characteristics that vary simultaneously, one-variable-at-a-time analyses look for differences between groups that differ systematically only on a single variable. Because most variables are expected to account for small differences in treatment effects, the magnitude of HTE over any single variable may be small and not reliably detectable.
Inadequacy for supporting patient-centred care
Each patient belongs to multiple subgroups, some of which may be associated with increased benefit from treatment whereas others may not. Thus, it can be difficult to apply the results of one-variable-at-time subgroup analyses to individuals. For example, if treatment is more beneficial for female (compared with male) and younger (compared with older) patients, the optimal treatment for a young male patient is not immediately obvious. Ideally, all factors that potentially modify the treatment effect should be examined jointly.
Problems related to hypothesis testing
Multiplicity of comparisons and spurious findings
Because patients have a nearly limitless number of characteristics, only a subset of which are likely to influence treatment effects, when one-variable-a-time analyses are combined with P-value-based criteria for identifying effect modifiers, the risk of false-positive findings (due to multiple comparisons) is increased. Solutions that control the false-positive error rate have been proposed, but generally require even larger datasets.
Statistical power for HTE detection
Randomized clinical trials are typically powered to reliably detect the main effects of treatment (e.g. at 80% or 90%). In general, HTE analyses require a much larger sample size compared with analyses of the overall effect, to have reasonable power.25,36,37 The problem of low power is exacerbated when variables that have small influence on the treatment effect individually are evaluated one at a time; underpowered subgroup analyses can appear to support ‘consistency of effects’ across each subgrouping variable, while providing little information about whether clinically relevant HTE would be detectable when considering multiple variables jointly. Thus, claims of ‘consistency of effect’ should generally be viewed as reflecting data and analytical limitations, rather than as an accurate or complete description of HTE.
Less widely appreciated is that the low power of subgroup analyses not only decreases the likelihood of finding interactions, but also decreases the credibility of any ‘positive’ results. In many research settings, particularly when performing multiple exploratory analyses (i.e. testing of multiple variables when true effect modifiers are rare), most statistically significant between-subgroup differences are expected to be false-positives (Figure 2).
Figure 2.
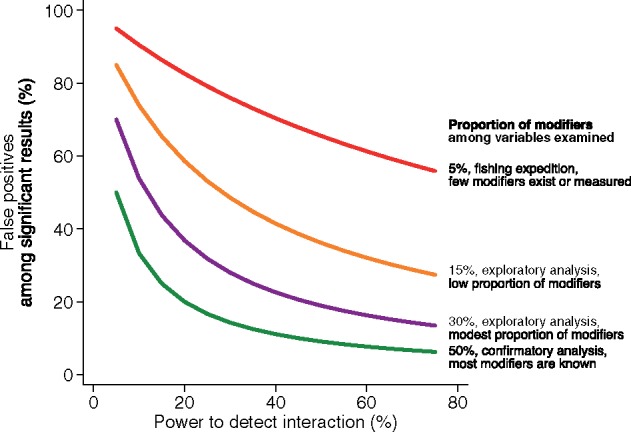
Impact of statistical power and the proportion of ‘true’ modifiers among the variables examined on the credibility of statistically significant results in HTE analyses. Plot of the percentage of false-positive findings among all statistically significant findings as a function of power to detect an interaction. Coloured lines represent results for varying percentages of ‘true’ effect modifiers among those assessed (i.e. differences in ‘previous probabilities’). For reference, simulations have shown that when a study has 80% power to detect the average treatment effect, a subgroup analysis for a balanced binary variable (e.g. males versus females) has only 29% power when the magnitude of the effect is the same as the main effect.25 Note that positive results of exploratory analyses performed at this power are likely to represent false-positives.
Towards more informative HTE analyses
Because the problem of spurious subgroup results from multiple comparisons is well appreciated, guidance for analysing, reporting and interpreting HTE has generally focused on improving the credibility of subgroup analyses.38–40 There is broad agreement across published recommendations that subgroups be fully defined a priori (to prevent data dredging), that they be limited in number, that formal tests for interaction be performed (using an appropriate test procedure and possibly corrected for multiple comparisons) and that results should be interpreted with caution.25,41,42 The main problem with these solutions is that they generally address only one aspect of the central dilemma of HTE: minimizing the risk of a false-positive finding (i.e. finding a statistically significant interaction when the null hypothesis is true). Although the importance of the second aspect potentially over-generalizing the summary results to all patients meeting inclusion criteria is increasingly recognized,43–49 guidance to address this has been less satisfactory.
One proposed framework50 attempts to address the limitations of the usual approach to subgroup analysis by: (i) limiting the use of hypothesis-testing subgroup analysis (to just those few attributes, if any, with previous evidence for effect modification), while still permitting exploratory subgroup analyses explicitly labelled as hypothesis-generating to inform future research; and (ii) prioritizing analyses of HTE over the predicted risk of the primary outcome, where risk is predicted using a multivariable outcome model. The first proposal is based on the understanding that the credibility of a statistically significant subgroup-by-treatment interaction greatly depends the prevalence of true effect modifiers. (Figure 2). The second proposal for privileging subgroup analyses based on predicted risk is based on the understanding that outcome risk is a mathematical determinant of the treatment effect (as illustrated in Figure 1). Because baseline risk usually varies substantially within enrolled populations, HTE must be present on some scale (RD, RR or OR) unless the treatment effect is null. In particular, when outcome risk varies considerably across the trial population, it is almost inevitable that the RD, the most clinically relevant effect measure, will also vary across risk groups. Thus, these analyses avoid many of the issues of ‘one-variable-at-a-time’ analyses and of hypothesis testing, since they can reveal important differences in treatment effect across subgroups, whether there is statistical evidence of HTE on the relative scale or not. Of note, whereas the previous framework primarily discussed the use of predicted outcome risk as a subgrouping variable (e.g. to stratify patients into subgroups of increasing outcome risk), it may be more advantageous to flexibly model the relationship between predicted risk and the treatment effect (see, for example,51,52 for related methods).
The intuition behind risk stratification is not new53 and is evident in many common clinical scenarios. For example, when considering the use of a new and expensive antibiotic (e.g. fidoxamicin) versus vancomycin to treat C. difficile colitis, the risk of recurrence determines in part the potential for treatment benefit and is determined, in turn, by a combination of factors (older age, severity of diarrhoea and presence of renal insufficiency or previous episodes of C. difficile).54 Similarly, when considering primary percutaneous intervention versus medical therapy, a 45-year-old without comorbidities who presents with stable vital signs and a small inferior wall ST-elevation myocardial infarction (STEMI) (30-day mortality risk ∼ 1%) does not have the same potential benefit from treatment as a 78-year-old man with diabetes who presents with haemodynamic instability and a large anterior wall STEMI (30-day mortality risk ∼ 25%).55,56 In both these examples, the pivotal clinical trials included patients with varying predicted outcome risk, reported a single summary result and suggested that effects were similar for all patients meeting enrolment criteria based on one-variable-at a time subgroup analyses. Only in subsequent, post hoc risk-stratified analyses did heterogeneity of treatment effects become apparent.54,56
Whereas we have focused our exposition on trials examining treatments, the concepts discussed in this paper apply also to trials comparing alternative test-and-treatment strategies (e.g. the risk-stratified analysis of the National Lung Screening Trial57 which found screening to be substantially more beneficial among patients at high risk for cancer mortality compared with those at lower risk). Because design and analysis issues related to trials of test-and-treatment strategies are fairly complex,58 we do not address them in this overview.
As in these examples, the distribution of predicted risk is usually highly skewed on the probability scale, particularly when outcomes are rare and the prediction model discriminates well; most patients are thus at lower than average predicted risk (i.e. median predicted risk is lower than mean predicted risk).59 Importantly, observed outcome risk typically varies substantially (sometimes 5–20-fold) when comparing individuals with high predicted outcome risk versus those with low predicted risk.60 Because of this, examining treatment effects over predicted outcome risk often reveals clinically informative patterns;61–66 estimates of overall effectiveness are often driven by a small group of influential (typically high-risk) patients and the average benefit reflected in the summary result is often larger than the predicted benefit (especially on the RD scale) for most patients. These issues are under-appreciated because trial results are rarely risk-stratified potentially leading to preventable over- and under-treatment.
Although the risk of the primary outcome without treatment does not determine which of the four categories in Box 1 an individual belongs to, excellent outcome prediction can identify individuals with very little potential for benefit (those at very low baseline risk are most likely to belong to the ‘immune’ or ‘harmed’ categories), because only patients destined to experience the outcome if not treated can potentially benefit. Models predicting risk of the primary outcome can be developed using external sources of data (e.g. cohort studies based in large registries or administrative databases). These models can then be used across multiple clinical trials of similar patient populations to estimate risk-specific treatment effects. Where multiple trials examine the same intervention, evidence synthesis can be facilitated by harmonization of the scheme for determining subgroups and by access to individual patient data.
Box 1 Potential outcomes for a binary exposure and outcome in a hypothetical trial of a new treatment versus usual care
| Group description | Outcome with new treatment | Outcome with usual care | Treatment effect |
|---|---|---|---|
| Doomed | 1 | 1 | 0 (no effect) |
| Saved | 0 | 1 | −1 (benefit) |
| Harmed | 1 | 0 | 1 (harm) |
| Immune | 0 | 0 | 0 (no effect) |
|
| |||
Each row represents a response type, defined on the basis of potential outcomes under a new therapy (Ynew) or usual care (Yusual). Occurrence of an adverse outcome is denoted by ‘1’ and non-occurrence is denoted by ‘0’. The fourth column shows (unobservable) person-level treatment effects.
When more is known about the determinants of treatment benefit and harm, models combining variables that capture other important effect modifiers may provide additional information. For example, predicted risk of treatment-related harm may be a treatment effect modifier, as is the case for the risk of perioperative stroke (captured by a risk model) or the risk of thrombolytic-related intracranial haemorrhage (captured by a separate model), for carotid endarterectomy or thrombolysis in acute ischaemic stroke, respectively.67,68 The general approach is to use combinations of variables to describe the risk profiles of those most likely to benefit, by integrating clinical reasoning and previous empirical findings with statistical modelling.
Whereas risk modelling can become complex when more than one ‘risk dimension’ is combined,64,68 simple risk stratification (based on risk of the primary outcome) is usually feasible and can often uncover clinically important information. We have previously argued that reporting just the summary result, without clearly presenting the absolute and proportional effects across different risk strata, is tantamount to under-reporting trial results.50,69 When a well-validated risk model is not available, approaches for risk stratification using the trial data can be used to assess HTE and serve as an impetus for developing reliable risk models for clinical use.70,71
To be sure, the predicted outcome risk under no treatment is in theory unlikely to be the ‘best’ subgrouping scheme for disaggregating patients. Ideally, one would like to group patients based on determinants of the treatment effect predicted outcome risk under one treatment versus outcome risk under the alternative. However, naïve methods that attempt to predict person-level effects (i.e. methods that include treatment assignment in the model) may lead to biased estimates of the treatment effect within subgroups, due to model mis-specification and over-fitting. Statistical methods that address these issues and rigorous approaches for model evaluation have been proposed51,72–74 but practical experience with their application is limited. Outcome risk models, on the other hand, can be created using data independent of the clinical trial or by using trial data ‘blinded’ to the treatment status, protecting them from this type of bias.70,71,75 Note also that in some circumstances trial stratification (or the conduct of totally independent trials) may be more appropriate than the modelling approaches we discuss, particularly when there is prior information that a particular characteristic can define patient subgroups that are fundamentally distinct in their response to therapy.
Future Directions
Evidence is derived from groups, yet decisions are made for individuals. This fundamental mismatch means that we can never fully escape the problems inherent in cross-level inference. We summarize some conceptual issues and specific methodological approaches relevant to HTE analysis (Box 2), but we acknowledge that major challenges remain in using trial results to guide patient care.76 Generating patient-centred evidence will ultimately require changes in the clinical research infrastructure to support much larger trials, designed with a view to HTE detection, undergirded by a more rigorous understanding of determinants of the outcome based on large and information-rich observational databases (e.g. the million-person cohort envisioned under the Precision Medicine Initiative). Applying this evidence will require a clinical informatics infrastructure supporting clinical decision aids and ‘individualized’ practice guidelines. Recognizing the substantial obstacles on the path towards patient-centred care should not be an excuse for settling on using overall average trial results, when we can do much better. Addressing the difficulties of HTE analysis—by fully applying our current set of methods and by developing new ones—remains one of the most important challenges facing clinical research.
Box 2 Assessing heterogeneity of treatment effects (HTE) in clinical trials and interpreting the results of statistical analyses
Person-level HTE is ubiquitous but impossible to detect, even when data from well-designed large randomized trials are available.
Group-level HTE refers to variation of treatment effects (on some scale) across levels of a covariate. It corresponds to the epidemiological concept of effect measure modification.
In clinical trials, we can identify HTE by comparing treatment effects (on a chosen scale) between subgroups (statistical interaction). HTE and statistical interaction are ‘scale-dependent’.
When baseline risk varies across subgroups in a trial population and the treatment effect is not null, there will always be HTE on some scale.
Statistical interactions should not be confused with causal interactions. Additionally, the presence (or absence) of statistical interaction should not be equated with the presence (or absence) of clinically-relevant HTE.
The purpose of statistical analyses for HTE is to identify groups of patients who are as dissimilar as possible between them with respect to their response to treatment.
Conventional subgroup analyses which serially examine ‘one-variable-at-a-time’ subgroups under-represent heterogeneity, do not provide ‘patient-centred’ effect estimates, are typically grossly under-powered and are prone to both false-positive and false-negative results.
Because baseline outcome risk is a mathematical determinant of treatment effect, multivariable risk models can be employed to evaluate treatment effect across strata defined by baseline outcome risk. For clinical decision making, it is important to consider treatment effects on the risk difference scale across strata.
Improved methods for HTE detection are needed to allow flexible modelling of multiple potential modifiers while avoiding bias. New methods will require very large datasets.
Funding
This work was supported by: the Patient-Centered Outcomes Research Institute (PCORI) [grant numbers: 1IP2PI000722 to D.M.K. and ME-1306‐03758 and ME-1502‐27794 to I.J.D.]; the National Institutes of Health (NIH) [grant numbers: U01 NS086294, UL1 TR001064 to D.M.K.]; the Veterans Administration (VA) Quality Enhancement Research Initiative [grant number: QUERI DIB 98‐001 to R.A.H.]; and the Methods Core of the Michigan Center for Diabetes Translational Research [grant number: NIH P60 DK-20572 to R.A.H.]. All statements in this paper are solely those of the authors and do not necessarily represent the views of the PCORI, its Board of Governors and Methodology Committee, the NI or the VA.
Key Messages
Person-level treatment effects cannot be identified in randomized clinical trials and population average treatment effects may not apply to all patients.
One-variable-at-a-time subgroup analyses are highly prone to false-positive results due to multiple comparisons and false-negative results due to inadequate power, and have limited ability to inform decisions for individuals, because individuals vary from one another in multiple ways simultaneously.
Subgroup analyses that incorporate information on multiple variables, such as those based on predicted outcome risk, may yield more patient-centred results.
Acknowledgements
The authors thank Drs Frank Davidoff, Thomas Trikalinos and Benjamin Wessler for helpful comments on an earlier version of the manuscript. Drs Dahabreh and Kent co-drafted the initial version of this manuscript, which was subsequently revised for content by all authors.
Conflict of interest: None declared.
References
- 1. Abraham I. More research is needed - but what type? BMJ 2010;342:c4662. [Google Scholar]
- 2. Collins FS, Varmus H. A new initiative on precision medicine. N Engl J Med 2015;372:793–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Pauker SG, Kassirer JP. Decision analysis. N Engl J Med 1987;316:250–58. [DOI] [PubMed] [Google Scholar]
- 4. Robins JM. Confidence intervals for causal parameters. Stat Med 1988;7:773–85. [DOI] [PubMed] [Google Scholar]
- 5. Copas JB. Randomization models for the Matched and Unmatched 2 × 2 Tables. Biometrika 1973;60:467–76. [Google Scholar]
- 6. Holland PW. Statistics and causal inference. J Am Stat Assoc 1986;81:945–60. [Google Scholar]
- 7. Greenland S. Randomization, statistics, and causal inference. Epidemiology 1990;1:421–29. [DOI] [PubMed] [Google Scholar]
- 8. Rubin D. Estimating causal effects of treatments in randomized and nonrandomized studies. J Educ Psychol 1974;66:688–701. [Google Scholar]
- 9. Rubin DB. Bayesian inference for causal effects:The role of randomization. Ann Stat 1978;6:34–58. [Google Scholar]
- 10. Greenland S. Choosing effect measures for epidemiologic data. J Clin Epidemiol 2002;55:423–24. [DOI] [PubMed] [Google Scholar]
- 11. Greenland S. Interpretation and choice of effect measures in epidemiologic analyses. Am J Epidemiol 1987;125:761–68. [DOI] [PubMed] [Google Scholar]
- 12. Greenland S. Model-based estimation of relative risks and other epidemiologic measures in studies of common outcomes and in case-control studies. Am J Epidemiol 2004;160:301–05. [DOI] [PubMed] [Google Scholar]
- 13. VanderWeele TY. Confounding and effect modification:distribution and measure. Epidemiol Methods 2012;1:55–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Maldonado G, Greenland S. Estimating causal effects. Int J Epidemiol 2002;31:422–29. [PubMed] [Google Scholar]
- 15. Suzuki E, Mitsuhashi T, Tsuda T, Yamamoto E. A counterfactual approach to bias and effect modification in terms of response types. BMC Med Res Methodol 2013;13:101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Venn J. The Logic of Chance. 2nd edn London: Macmillan, 1876. [Google Scholar]
- 17. Reichenbach H. The Theory of Probability. Berkeley, CA: University of California Press, 1949. [Google Scholar]
- 18. Stern RH. Individual risk. J Clin Hypertens (Greenwich) 2012;14:261–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Kent DM, Shah ND. Risk models and patient-centred evidence: should physicians expect one right answer? JAMA 2012;307:1585–86. [DOI] [PubMed] [Google Scholar]
- 20. White IR, Elbourne D. Assessing subgroup effects with binary data: can the use of different effect measures lead to different conclusions? BMC Med Res Methodol 2005;5:15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Venekamp RP, Rovers MM, Hoes AW, Knol MJ. Subgroup analysis in randomized controlled trials appeared to be dependent on whether relative or absolute effect measures were used. J Clin Epidemiol 2014;67:410–15. [DOI] [PubMed] [Google Scholar]
- 22. Brumback B, Berg A. On effect-measure modification: Relationships among changes in the relative risk, odds ratio, and risk difference. Stat Med 2008;27:3453–65. [DOI] [PubMed] [Google Scholar]
- 23. Scanlan JP. Assumption of constant relative risk reductions across different baseline rates is unsound (responding to Barratt A, Wyer PC, McGinn T, et al.). Tips for learners of evidence-based medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ 2004;171:353–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Cui L, Hung HM, Wang SJ, Tsong Y. Issues related to subgroup analysis in clinical trials. J Biopharm Stat 2002;12:347–58. [DOI] [PubMed] [Google Scholar]
- 25. Brookes ST, Whitley E, Peters TJ, Mulheran PA, Egger M, Davey Smith G. Subgroup analyses in randomised controlled trials: quantifying the risks of false-positives and false-negatives. Health Technol Assess 2001;5:1–56. [DOI] [PubMed] [Google Scholar]
- 26. Cox DR. Interaction. Int Rev Stat 1984;52:1–24. [Google Scholar]
- 27. Varadhan R, Segal JB, Boyd CM, Wu AW, Weiss CO. A framework for the analysis of heterogeneity of treatment effect in patient-centred outcomes research. J Clin Epidemiol 2013;66:818–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. van Klaveren D, Vergouwe Y, Farooq V, Serruys PW, Steyerberg EW. Estimates of absolute treatment benefit for individual patients required careful modeling of statistical interactions. J Clin Epidemiol 2015;68:1366–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Altman DG, Bland JM. Interaction revisited: the difference between two estimates. BMJ 2003;326:219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Rothman KJ, Greenland S, Walker AM. Concepts of interaction. Am J Epidemiol 1980;112:467–70. [DOI] [PubMed] [Google Scholar]
- 31. Saracci R. Interaction and synergism. Am J Epidemiol 1980;112:465–66. [DOI] [PubMed] [Google Scholar]
- 32. Greenland S. Basic problems in interaction assessment. Environ Health Perspect 1993;101(Suppl 4):59–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. VanderWeele TJ, Robins JM. Four types of effect modification: a classification based on directed acyclic graphs. Epidemiology 2007;18:561–68. [DOI] [PubMed] [Google Scholar]
- 34. VanderWeele TJ. On the distinction between interaction and effect modification. Epidemiology 2009;20:863–71. [DOI] [PubMed] [Google Scholar]
- 35. Kent DM, Selker HP, Ruthazer R, Bluhmki E, Hacke W. The stroke-thrombolytic predictive instrument: a predictive instrument for intravenous thrombolysis in acute ischaemic stroke. Stroke 2006;37:2957–62. [DOI] [PubMed] [Google Scholar]
- 36. Brookes ST, Whitely E, Egger M, Davey Smith G, Mulheran PA, Peters TJ. Subgroup analyses in randomized trials: risks of subgroup-specific analyses; power and sample size for the interaction test. J Clin Epidemiol 2004;57:229–36. [DOI] [PubMed] [Google Scholar]
- 37. Schmidt AF, Groenwold RH, Knol MJ et al. Exploring interaction effects in small samples increases rates of false-positive and false-negative findings: results from a systematic review and simulation study. J Clin Epidemiol 2014;67:821–29. [DOI] [PubMed] [Google Scholar]
- 38. Sun X, Briel M, Busse JW et al. Credibility of claims of subgroup effects in randomised controlled trials:systematic review. BMJ 2012;344:e1553. [DOI] [PubMed] [Google Scholar]
- 39. Wang R, Lagakos SW, Ware JH, Hunter DJ, Drazen JM. Statistics in medicine – reporting of subgroup analyses in clinical trials. N Engl J Med 2007;357:2189–94. [DOI] [PubMed] [Google Scholar]
- 40. PCORI (Patient-Centred Outcomes Research Institute) Methodology Committee. The PCORI Methodology Report. 2013. http://www.pcori.org/assets/2013/11/PCORI-Methodology-Report.pdf (22 March 2016, date last accessed).
- 41. Oxman AD, Guyatt GH. A consumer's guide to subgroup analyses. Ann Intern Med 1992;116:78–84. [DOI] [PubMed] [Google Scholar]
- 42. Sun X, Briel M, Walter SD, Guyatt GH. Is a subgroup effect believable? Updating criteria to evaluate the credibility of subgroup analyses. BMJ 2010;340:c117. [DOI] [PubMed] [Google Scholar]
- 43. Rothwell PM, Mehta Z, Howard SC, Gutnikov SA, Warlow CP. Treating individuals 3: from subgroups to individuals: general principles and the example of carotid endarterectomy. Lancet 2005;365:256–65. [DOI] [PubMed] [Google Scholar]
- 44. Kravitz RL, Duan N, Braslow J. Evidence-based medicine, heterogeneity of treatment effects, and the trouble with averages. Milbank Q 2004;82:661–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Kraemer HC, Frank E, Kupfer DJ. Moderators of treatment outcomes: clinical, research, and policy importance. JAMA 2006;296:1286–89. [DOI] [PubMed] [Google Scholar]
- 46. Davidoff F. Heterogeneity is not always noise:lessons from improvement. JAMA 2009;302:2580–86. [DOI] [PubMed] [Google Scholar]
- 47. Rothwell PM. Can overall results of clinical trials be applied to all patients? Lancet 1995;345:1616–19. [DOI] [PubMed] [Google Scholar]
- 48. Rothwell PM. Treating individuals 2. Subgroup analysis in randomised controlled trials: importance, indications, and interpretation. Lancet 2005;365:176–86. [DOI] [PubMed] [Google Scholar]
- 49. Greenfield S, Kravitz R, Duan N, Kaplan SH. Heterogeneity of treatment effects: implications for guidelines, payment, and quality assessment. Am J Med 2007;120:S3–9. [DOI] [PubMed] [Google Scholar]
- 50. Kent DM, Rothwell PM, Ioannidis JP, Altman DG, Hayward RA. Assessing and reporting heterogeneity in treatment effects in clinical trials: a proposal. Trials 2010;11:85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Cai T, Tian L, Wong PH, Wei LJ. Analysis of randomized comparative clinical trial data for personalized treatment selections. Biostatistics 2011;12:270–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Lu T, Zhao X. Statistical methods for personalized medicine. Advanced Medical Statistics. 2nd edn Singapore: World Scientific Publishing, 2015. [Google Scholar]
- 53. Davey Smith G, Egger M. Who benefits from medical interventions? BMJ 1994;308:72–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. D'Agostino RB Sr, Collins SH, Pencina KM, Kean Y, Gorbach S. Risk estimation for recurrent Clostridium difficile infection based on clinical factors. Clin Infect Dis 2014;58:1386–93. [DOI] [PubMed] [Google Scholar]
- 55. Selker HP, Griffith JL, Beshansky JR et al. Patient-specific predictions of outcomes in myocardial infarction for real-time emergency use: a thrombolytic predictive instrument. Ann Intern Med 1997;127:538–56. [DOI] [PubMed] [Google Scholar]
- 56. Thune JJ, Hoefsten DE, Lindholm MG et al. Simple risk stratification at admission to identify patients with reduced mortality from primary angioplasty. Circulation 2005;112:2017–21. [DOI] [PubMed] [Google Scholar]
- 57. Kovalchik SA, Tammemagi M, Berg CD et al. Targeting of low-dose CT screening according to the risk of lung-cancer death. N Engl J Med 2013;369:245–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Robins JM. Discussion of a paper by Professor Miettinen. Epidemiol Methods 2015;4:33–36. [Google Scholar]
- 59. Vickers AJ, Kent DM. The Lake Wobegon effect:Why most patients are at below-average risk. Ann Intern Med 2015;162:886–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Kent DM, Nelson J, Dahabreh IJ, Rothwell PM, Altman DG, Hayward RA. Risk and treatment effect heterogeneity: re-analysis of individual participant data from 32 large clinical trials. Int J Epidemiol 2016;45:2075–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Ioannidis JP, Lau J. Heterogeneity of the baseline risk within patient populations of clinical trials: a proposed evaluation algorithm. Am J Epidemiol 1998;148:1117–26. [DOI] [PubMed] [Google Scholar]
- 62. Ioannidis JP, Lau J. The impact of high-risk patients on the results of clinical trials. J Clin Epidemiol 1997;50:1089–98. [DOI] [PubMed] [Google Scholar]
- 63. Kent DM, Schmid CH, Lau J, Selker HP. Is primary angioplasty for some as good as primary angioplasty for all? J Gen Intern Med 2002;17:887–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Kent DM, Hayward RA, Griffith JL et al. An independently derived and validated predictive model for selecting patients with myocardial infarction who are likely to benefit from tissue plasminogen activator compared with streptokinase. Am J Med 2002;113:104–11. [DOI] [PubMed] [Google Scholar]
- 65. Kent DM, Hayward RA. Limitations of applying summary results of clinical trials to individual patients: the need for risk stratification. JAMA 2007;298:1209–12. [DOI] [PubMed] [Google Scholar]
- 66. Dorresteijn JA, Visseren FL, Ridker PM et al. Estimating treatment effects for individual patients based on the results of randomised clinical trials. BMJ 2011;343:d5888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Kent DM, Ruthazer R, Selker HP. Are some patients likely to benefit from recombinant tissue-type plasminogen activator for acute ischemic stroke even beyond 3 hours from symptom onset? Stroke 2003;34:464–67. [DOI] [PubMed] [Google Scholar]
- 68. Rothwell PM, Warlow CP. Prediction of benefit from carotid endarterectomy in individual patients: a risk-modelling study. European Carotid Surgery Trialists' Collaborative Group. Lancet 1999;353:2105–10. [DOI] [PubMed] [Google Scholar]
- 69. Hayward RA, Kent DM, Vijan S, Hofer TP. Reporting clinical trial results to inform providers, payers, and consumers. Health Aff (Millwood) 2005;24:1571–81. [DOI] [PubMed] [Google Scholar]
- 70. Follmann DA, Proschan MA. A multivariate test of interaction for use in clinical trials. Biometrics 1999;55:1151–55. [DOI] [PubMed] [Google Scholar]
- 71. Burke JF, Hayward RA, Nelson JP, Kent DM. Using internally developed risk models to assess heterogeneity in treatment effects in clinical trials. Circ Cardiovasc Qual Outcomes 2014;7:163–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Kovalchik SA, De MS, Landi MT et al. A regression model for risk difference estimation in population-based case-control studies clarifies gender differences in lung cancer risk of smokers and never smokers. BMC Med Res Methodol 2013;13:143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Clagget B, Zhao L, Tian L, Castagno D, Wei LJ. Estimating subject-specific treatment differences for risk-benefit assessment with competing risk event-time data. Harvard University, Biostatistics Working Paper Series 2011. [Google Scholar]
- 74. Claggett B, Tian L, Castagno D, Wei LJ. Treatment selections using risk-benefit profiles based on data from comparative randomized clinical trials with multiple endpoints. Harvard University, Biostatistics Working Paper Series 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Pocock SJ, Lubsen J. More on subgroup analyses in clinical trials. N Engl J Med 2008;358:2076–77. [DOI] [PubMed] [Google Scholar]
- 76. Davey Smith G, Egger M. Incommunicable knowledge? Interpreting and applying the results of clinical trials and meta-analyses. J Clin Epidemiol 1998;51:289–95. [DOI] [PubMed] [Google Scholar]