Abstract
To achieve sample sizes necessary for effectively conducting genome‐wide association studies (GWASs), researchers often combine data from samples possessing multiple potential sources of heterogeneity. This is particularly relevant for psychiatric disorders, where symptom self‐report, differing assessment instruments, and diagnostic comorbidity complicates the phenotypes and contribute to difficulties with detecting and replicating genetic association signals. We investigated sources of heterogeneity of anxiety disorders (ADs) across five large cohorts used in a GWAS meta‐analysis project using a dimensional structural modeling approach including confirmatory factor analyses (CFAs) and measurement invariance (MI) testing. CFA indicated a single‐factor model provided the best fit in each sample with the same pattern of factor loadings. MI testing indicated degrees of failure of metric and scalar invariance which depended on the inclusion of the effects of sex and age in the model. This is the first study to examine the phenotypic structure of psychiatric disorder phenotypes simultaneously across multiple, large cohorts used for GWAS. The analyses provide evidence for higher order invariance but possible break‐down at more detailed levels that can be subtly influenced by included covariates, suggesting caution when combining such data. These methods have significance for large‐scale collaborative studies that draw on multiple, potentially heterogeneous datasets. Copyright © 2016 John Wiley & Sons, Ltd.
Keywords: anxiety disorder, factor analysis, measurement invariance
Introduction
Over the past decade, genome‐wide association studies (GWASs) have become the standard approach for investigating and identifying common variants underlying individual differences in complex genetic phenotypes. Due to the strong polygenicity and related small effect sizes of individual variants, enormous sample sizes are required to obtain adequate statistical power to detect their association signals with the phenotypes (Visscher et al., 2012). This, together with the effort and expense associated with subject recruitment and assessment, makes the required sample size often unattainable within a single study designed for this purpose. This situation often leads to the compromise of having to combine data from multiple studies that used disparate designs. Modern approaches that make use of large‐scale imputation to standard human reference genotypic datasets such as the 1000 Genomes project (Auton et al., 2015) can largely overcome previous limitations imposed by differences in genotyping platforms. However, analogous issues arising with phenotypes are not as readily addressed. There are non‐trivial differences between combining data across studies of more straightforwardly assessed phenotypes such as height and those of the more complex and often heterogeneous phenotypes encountered in medical and psychiatric disorder research. Phenotypic heterogeneity is often cited as a potential contribution to loss of power for genetic studies of complex disease (Manchia et al., 2013) but rarely investigated empirically. One exception is a recent large meta‐analysis of personality that applied item response theory in an attempt to place items that served as indicators of the latent personality constructs from different surveys on the same liability scale (van den Berg et al., 2014) before including them in GWASs (de Moor et al., 2015).
In the Anxiety Neurogenetics Study (ANGST) consortium, we seek to collate and combine data from multiple, large datasets that are phenotypically and genetically informative for studying the five primary anxiety disorders (ADs) as recognized in the Diagnostic and Statistical Manual of Mental Disorders, fifth edition (DSM‐5; American Psychiatric Association, 2013): generalized anxiety disorder (GAD), panic disorder (PD), agoraphobia (AG), social phobia (SOC), and specific phobia (SP). This strategy of studying clinically related disorders in concert rather than one‐by‐one draws on the findings from genetic epidemiologic literature that suggest that, although complex, a common phenotypic liability structure including both shared and disorder‐specific risk factors can account for the high lifetime comorbidity across ADs (Hettema et al., 2005). In prior genetic association studies, we applied phenotypic and twin biometric factor analyses to individual datasets to identify a single latent liability factor and used it as the dependent outcome for association analysis (Hettema et al., 2008). For ANGST, we applied similar factor analyses within each individual dataset prior to GWASs and meta‐analysis (Otowa et al., 2016). However, this makes the assumption that the same dimensional structure accounts for the covariation among these five clinical disorder phenotypes equally well in each of the samples (homogeneity). If not, it is possible that tests of genetic variants may produce inconsistent association signals, in part, due to differences in how the phenotype is defined across samples, which in turn may contribute to misleading conclusions about association findings in the meta‐analysis. We note that this becomes an even greater issue for mega‐analyses that directly combine phenotypic data prior to GWASs.
In the present study, we investigated the consistency and equivalence of the covariance structure of lifetime ADs across multiple, independently collected and characterized cohorts of European background. These samples come from different countries, have different age ranges, and use different instruments for psychiatric assessment. This serves as an example study for applying extant statistical approaches in a novel manner in order to address issues of heterogeneity for large genetic studies that require the combination of such diverse data. We sought to answer the following questions:
Does the same phenotypic pattern and structure exist across the ADs in each study?
If not, what are the sources of heterogeneity, and how can they be characterized statistically?
How do the effects of other phenotypic predictors such as age and sex vary between studies and impact these findings?
Material and methods
Samples and phenotypes
For the ANGST GWAS meta‐analysis, seven independent cohort samples of Caucasian subjects of European background were included, each containing the five AD phenotypes and genotypic information. Two cohort samples were excluded from the current analysis due to major differences in their ascertainment designs compared to the others: QIMR (Jardine et al., 1984), an Australian twin‐family sample which required the selection of one member from each family for the GWAS and also did not assess each of the five ADs in each ascertainment wave; NESDA/NTR, a hybrid case/control sample combined from two independent Dutch studies initially to investigate the genetics of major depressive disorder (Boomsma et al., 2008). The five samples examined herein are described in Table 1 with details in the references cited there. Data from human subjects in each study was obtained in accordance with the Declaration of Helsinki after informed consent in a manner approved by the respective local institutional review board.
Table 1.
Sample characteristics and prevalence of anxiety disorders in each sample
| Sample | ||||||
|---|---|---|---|---|---|---|
| MGS | PsyCoLaus | RS | SHIP | TRAILS | ||
| Sample size (N) | 3775 | 3575 | 9718 | 2291 | 1584 | |
| Country | USA | Switzerland | Netherlands | Germany | Netherlands | |
| Female (%) | 54.5 | 53.3 | 58.3 | 52.3 | 50.8 | |
| Age (years) | ||||||
| Mean age (SD) | 49.5 (16.3) | 51.0 (8.8) | 66.5 (10.8) | 55.4 (14.0) | 18.7 (0.6) | |
| Age group (%) | <20 | 1.6 | — | — | — | 89.7 |
| 20–29 | 12.2 | — | — | — | 10.3 | |
| 30–39 | 15.3 | 10.1 | — | 16.0 | — | |
| 40–49 | 22.4 | 37.2 | 5.1 | 21.7 | — | |
| 50–59 | 19.6 | 30.4 | 22.2 | 21.7 | — | |
| ≥60 | 28.9 | 22.3 | 72.8 | 40.6 | — | |
| Diagnostic Instrument | ||||||
|---|---|---|---|---|---|---|
| Frequencya (%) | Score | CIDI‐SF | DIGS, SADS‐LA | M‐CIDI | M‐CIDI | CIDI |
| GAD | 0 | 2783 (0.74) | 3442 (0.96) | 9201 (0.96) | 2078 (0.92) | 1480 (0.94) |
| 1 | 270 (0.07) | 75 (0.02) | 146 (0.02) | 137 (0.06) | 35 (0.02) | |
| 2 | 690 (0.18) | 58 (0.02) | 242 (0.03) | 54 (0.02) | 62 (0.04) | |
| SP | 0 | 2264 (0.60) | 2806 (0.79) | 6805 (0.71) | 1423 (0.63) | 792 (0.50) |
| 1 | 1066 (0.28) | 203 (0.06) | 2626 (0.27) | 447 (0.20) | 602 (0.38) | |
| 2 | 442 (0.12) | 566 (0.16) | 160 (0.02) | 398 (0.18) | 183 (0.12) | |
| SOC | 0 | 2362 (0.63) | 3027 (0.85) | 9148 (0.96) | 1908 (0.84) | 1029 (0.65) |
| 1 | 874 (0.23) | 110 (0.03) | 289 (0.03) | 217 (0.10) | 352 (0.22) | |
| 2 | 538 (0.14) | 438 (0.12) | 120 (0.01) | 153 (0.07) | 196 (0.12) | |
| AG | 0 | 3224 (0.85) | 3337 (0.93) | 8789 (0.92) | 2049 (0.90) | 1423 (0.90) |
| 1 | 303 (0.08) | 89 (0.03) | 361 (0.04) | 93 (0.04) | 107 (0.07) | |
| 2 | 246 (0.07) | 149 (0.04) | 433 (0.05) | 136 (0.06) | 47 (0.03) | |
| PD | 0 | 3648 (0.97) | 3254 (0.91) | 9046 (0.94) | 2110 (0.93) | 1312 (0.83) |
| 1 | 41 (0.01) | 164 (0.05) | 125 (0.01) | 56 (0.03) | 240 (0.15) | |
| 2 | 78 (0.02) | 157 (0.04) | 450 (0.05) | 111 (0.05) | 25 (0.02) |
Abbreviations: CIDI‐SF, Composite International Diagnostic Interview, Short Form; DIGS, Diagnostic Interview for Genetic Studies; SADS‐LA, Schedule for Affective Disorders and Schizophrenia – Lifetime and Anxiety disorder version (French version); M‐CIDI, Munich version of the Composite International Diagnostic Interview; MGS, Molecular Genetics of Schizophrenia; RS, Rotterdam Study; SHIP, Study of Health in Pomerania; TRAILS, Tracking Adolescents’ Individual Lives Survey; GAD, generalized anxiety disorder; SP, specific phobia; SOC, social phobia; AG, agoraphobia; PD, panic disorder.
Not including missing values.
Each cohort contained symptom criteria level information on the five primary AD phenotypes (GAD, PD, AG, SOC, and SP). These were assessed using standardized DSM‐based instruments from which we developed a scheme for each sample to assign a classification score for each individual based on the extent of symptomatic criteria endorsed for each disorder. Scores were assigned as follows: for each of the ADs, subjects meeting full symptomatic criteria were denoted as “full cases” (score = 2); subjects who were highly symptomatic but did not meet full criteria were labeled as “sub‐syndromal” (score = 1); and finally those with few or no prior symptoms were classified as “unaffected/controls” (score = 0). A score of one was operationalized by either (i) keeping the full symptomatic criteria and removing the diagnostic requirements of distress/impairment or (ii) reducing the symptomatic severity or duration. This scoring strategy resulted in an ordered categorical (ordinal) variable for each of the ADs rather than the more typical minimal information binary “unaffected” versus “affected” variable. These five ordinal AD variables were input to the dimensional latent factor analyses to be described later. These factor analyses were used to estimate quantitative factor scores for each subject as input to the GWAS (Otowa et al., 2016). This coding strategy was also used to identify more extreme comparison groups used in a separate case‐control GWAS, since diagnostic thresholds are defined for clinical purposes and may not sufficiently differentiate subjects by the risk alleles they carry. Demographic characteristics and the prevalence of these ADs in each sample are presented in Table 1.
Within‐sample factor analysis
Exploratory factor analysis (EFA) was used to determine the number of continuous latent factors required to explain the covariance structure across the five ADs. Confirmatory factor analysis (CFA) was conducted using the robust weighted least squares mean and variance adjusted estimator (WLSMV) to verify the factor structure. EFA and CFA were performed separately for each sample in Mplus 7.1 (Muthen & Muthen, 2012). In each study, (i) unidimensionality of the five AD indicators was tested, and (ii) the effects of exogenous covariates sex and age on the latent factor were also investigated. Identification was achieved by fixing one of the disorder indicator variables to 1.0 and freely estimating the factor variance. Age was rescaled to centuries by dividing age in years by 100 to establish a common metric across all samples. Model fit was assessed following the recommended cutoffs for several fit indexes: the comparative fit index (CFI), the Tucker–Lewis Index (TLI), and the root mean square error of approximation (RMSEA). Current recommendations suggest TLI and CFI values ≥ 0.95 indicate good fit whereas values > 0.90 indicate acceptable model fit. RMSEA values ≤ 0.05 are considered good approximating model fits whereas values of 0.08 are considered acceptable (Hu and Bentler, 1999).
Assessing measurement invariance
Measurement invariance (MI) across the samples was investigated using a multi‐group CFA framework. Different forms of invariance can be tested by comparing nested models with increasing levels of restrictions on the measurement parameters across groups. Nested models were organized in a hierarchical fashion starting from a baseline model (Meredith, 1993;Vandenberg and Lance, 2000; Cheung and Rensvold, 2002). Since the AD indicators were constructed as ordered categorical variables, the model specification and fitting strategy for MI testing with categorical variables was as described in Millsap and Yun‐Tein (2004) and implemented in the Mplus software. The initial step to evaluating factorial invariance is to test for configural invariance. In this model, factor loadings and thresholds are freely estimated in each of the samples (except for the fixed parameters necessary for model identification). Configural invariance examines whether the overall factor structure as defined by the patterning of factor loadings is invariant across samples. For example, is a single common factor model adequate to account for the associations among the ordinal disorder variables in all samples? Next, metric invariance is imposed by adding constraints forcing all factor loadings to be equal across samples except for a referent indicator fixed to one for identification and thus equal across samples. Thresholds are allowed to vary across samples except for those indicator thresholds constrained for model identification purposes. More specifically, the first threshold of each indicator is constrained to be equal across samples and the second threshold of the reference indicator is also held equal across samples. Also referred to as “weak” invariance, this model tests whether the expected change in the inferred unobserved liability for each AD indicator variable per unit change on the latent common factor (i.e. the slope) is the same across samples. The most stringent level of the invariance tested here, scalar invariance, evaluates the impact of constraining both factor loadings and thresholds to be equal across all samples. This restriction on the measurement parameters implies that individuals who have the same score on the latent factor should have the same expected observed score on the disorder indicator variable in each sample (Mellenbergh, 1989). Scalar invariance is required for meaningfully interpreting comparisons of latent construct means across samples.
This series of measurement invariance testing was further extended by examining models with and without the covariate effects of sex and age on the latent factor within each sample. In MI tests with covariates, age effects were allowed to vary across samples, while the sex effect was constrained to be equal in order for a metric invariance model to be identified (sex and age invariance across samples is tested later). The chi‐square difference test was utilized to evaluate the statistical significance of nested model fit comparisons. However, since the chi‐square difference is known to be sensitive to increasing sample size, we also examined changes in omnibus model fit indices based on recommendations proposed by Chen (2007). Change in CFI ≥ 0.01 or RMSEA ≥ 0.015 are evidence for the presence of significant non‐invariance.
For the exogenous covariate analyses, the invariant effects of sex and age on the latent anxiety liability factor across samples were investigated under the configural and scalar invariance models, respectively. We note that we could not test the effect of the binary sex variable on the latent AD factor under the metric invariance condition due to convergence problems possibly due to issues related to model identification.
Results
Before reviewing the analytical results, it is informative to compare the characteristics of each sample (Table 1). These come from four different countries, with sample sizes ranging from around 1500 in TRAILS (Tracking Adolescents’ Individual Lives Survey) to almost 10,000 in RS (Rotterdam Study). Age at assessment also varied appreciably, with the youngest participants within a narrow range in TRAILS (late teens to early twenties) and the oldest in RS (primarily an elderly sample, with 72% above the age of 60). The proportions of males to females were more consistent. Some version of the Composite International Diagnostic Interview (CIDI) was used for psychiatric assessment in all studies except for PsyCoLaus. The prevalence of each AD ordinal category varied somewhat, with particular differences seen for GAD = 2 (18%) in MGS (Molecular Genetics of Schizophrenia) study, SP = 1 in PsyCoLaus (6%) and TRAILS (38%), SP = 2 (2%) and SOC = 2 (1%) in RS, PD = 1 (15%) in TRAILS, and overall greater variation in SOC = 1 across all the cohorts.
Factor structure within samples
Results from the EFA and CFA for each sample supported the hypothesis that a single‐common factor model adequately accounted for the association among the five ordinal AD indicator variables (see Figure 1). Table 2 presents the estimated factor loadings and model fit indices for each single‐group, single‐factor model. Allowing separate covariate effects of sex and age on the common factor in each sample, the mean effect of sex was positive (i.e. higher for females) and statistically significant in each sample. This reflects the expected sex differences between males and females on the common latent anxiety factor while taking into account sampling variation and controlling for age. Significant linear age effects on the latent factor were detected in all samples except for PsyCoLaus and TRAILS. Overall, the inclusion of these exogenous covariates did not alter the estimated pattern of factor loadings.
Figure 1.
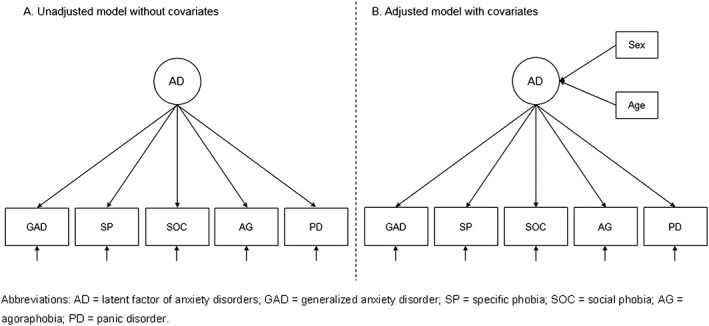
Diagram of factor structure in each sample for measurement invariance testing based on the single‐factor model.
Table 2.
Within sample standardized factor loadings, model fit indices, and covariate effects for one‐factor confirmatory factor analysis (CFA), by sample
| Factor loading | Fit indices | Covariate effects | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Sample | GAD | SP | SOC | AG | PD | CFI | RMSEA | Agea | Sexa |
| Unadjusted b | |||||||||
| MGS | 0.674 | 0.589 | 0.730 | 0.880 | 0.600 | 0.997 | 0.023 | ||
| PsyCoLaus | 0.397 | 0.395 | 0.379 | 0.774 | 0.787 | 0.970 | 0.034 | ||
| RS | 0.515 | 0.476 | 0.636 | 0.809 | 0.548 | 0.989 | 0.020 | NA | |
| SHIP | 0.601 | 0.529 | 0.636 | 0.820 | 0.743 | 0.978 | 0.047 | ||
| TRAILS | 0.604 | 0.514 | 0.544 | 0.726 | 0.598 | 0.983 | 0.035 | ||
| Adjusted b | |||||||||
| MGS | 0.682 | 0.594 | 0.728 | 0.877 | 0.600 | 0.985 | 0.033 | − 0.092 | 0.223 |
| PsyCoLaus | 0.394 | 0.431 | 0.381 | 0.775 | 0.773 | 0.937 | 0.033 | −0.050 | 0.291 |
| RS | 0.520 | 0.525 | 0.620 | 0.775 | 0.588 | 0.904 | 0.041 | −0.110 | 0.340 |
| SHIP | 0.603 | 0.553 | 0.633 | 0.813 | 0.743 | 0.969 | 0.035 | −0.137 | 0.303 |
| TRAILS | 0.612 | 0.528 | 0.530 | 0.721 | 0.599 | 0.979 | 0.025 | 0.021 | 0.284 |
Abbreviations: MGS, Molecular Genetics of Schizophrenia; RS, Rotterdam Study; SHIP, Study of Health in Pomerania; TRAILS, Tracking Adolescents’ Individual Lives Survey; GAD, generalized anxiety disorder; SP, specific phobia; SOC, social phobia; AG, agoraphobia; PD, panic disorder; CFI, comparative fit index; RMSEA, root mean square error of approximation; CI, confidence interval; NA, not applicable.
Age was rescaled by dividing by 100; sex was coded one for female and zero for male.
Indicating whether or not the covariate effects (sex and age) on the latent factor were included in the models; Unadjusted = the models not including covariates; Adjusted = the models including covariates.
Note: All factor loadings were statistically significant, and the covariate effects in italic typeface were significant. Each separate common factor model was identified by fixing the same anxiety disorder (AD) variable (GAD) to one. Standardized loadings were obtained for each sample separately making these factor loading estimates more difficult to compare across samples but more interpretable within samples.
Measurement invariance testing across samples
Model fitting results for MI testing are shown in Table 3. Configural invariance testing supported the hypothesis that a single‐factor structure adequately accounted for the associations among the five ADs in each of the samples (CFI = 0.989, TLI = 0.978, RMSEA = 0.029). Imposing the additional restrictive constraint of metric invariance (equal factor loadings) across samples resulted in poorer goodness‐of‐fit indices (CFI = 0.887, TLI = 0.862, RMSEA = 0.072). The metric invariance chi‐square difference test was significant when compared with the fit of the configural invariance model (Δχ 2 = 726.7, df = 16, ΔCFI = 0.102, ΔRMSEA = 0.043). The test of scalar invariance, in which all remaining free within‐sample thresholds are forced to be equal across samples, also produced significantly poorer model goodness‐of‐fit indexes (CFI = 0.837, TLI = 0.857, RMSEA = 0.074) as well as an increase in misfit based on the chi‐square difference test when compared to the configural (Δχ 2 = 1154.2, df = 32, ΔCFI = 0.152, ΔRMSEA = 0.045) and metric invariance (Δχ 2 = 452.8, df = 16, ΔCFI = 0.05, ΔRMSEA = 0.002) models. Given the large sample sizes, all of these tests were significant at p < 0.0001.
Table 3.
Results of measurement invariance testing across samples
| Model fit indices | Model comparison | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Measurement Invariance | χ 2 | df | CFI | TLI | RMSEA | RMSEA 90% CI | Comparisona | ∆χ 2 | ∆df | P | ∆CFI | ∆RMSEA |
| Unadjusted b | ||||||||||||
| 1. Configural | 110.4 | 25 | 0.989 | 0.978 | 0.029 | 0.023–0.034 | 2 versus 1 | 726.7 | 16 | 0.000 | 0.102 | 0.043 |
| 2. Metric | 936.6 | 41 | 0.887 | 0.862 | 0.072 | 0.068–0.076 | 3 versus 2 | 452.8 | 16 | 0.000 | 0.050 | 0.002 |
| 3. Scalar | 1346.6 | 57 | 0.837 | 0.857 | 0.074 | 0.070–0.077 | 3 versus 1 | 1154.2 | 32 | 0.000 | 0.152 | 0.045 |
| Adjusted b | ||||||||||||
| 1. Configural | 432.4 | 69 | 0.958 | 0.939 | 0.036 | 0.032–0.039 | 2 versus 1 | 295.6 | 16 | 0.000 | 0.020 | 0.003 |
| 2. Metric | 624.9 | 85 | 0.938 | 0.927 | 0.039 | 0.036–0.042 | 3 versus 2 | 256.8 | 16 | 0.000 | 0.013 | 0.000 |
| 3. Scalar | 749.4 | 101 | 0.925 | 0.926 | 0.039 | 0.037–0.042 | 3 versus 1 | 420.0 | 32 | 0.000 | 0.033 | 0.003 |
Abbreviations: CFI, comparative fit index; TLI, Tucker–Lewis index; RMSEA, root mean square error of approximation; CI, confidence interval; df, degrees of freedom.
First number indexes the more restricted nested model number, and second number is that of the less restricted comparison model.
Indicating whether or not the covariate effects (sex and age) on the latent factor were included in the models; Unadjusted = the models not including covariates; Adjusted = the models including covariates (age effect was freely estimated, but sex effect was fixed to be equal across samples for identification purposes).
Note: Model comparisons are based on the fit index difference (∆) between nested models: ∆CFI = CFA reference – CFA nested, ∆RMSEA = RMSEA nested – RMSEA reference (negative values in ∆CFI and ∆RMSEA indicate better fit compared to the reference model, otherwise worse fit was obtained).
The sequence of invariance testing was repeated, but this time taking into account the effects of sex and age on the latent common AD factor (bottom half of Table 3). Due to convergence issues in metric invariance, models were fit allowing age effects to vary across samples, but sex effects were constrained to be equal in all samples. The metric and scalar invariance model tests, when including covariate effects on the latent anxiety factor, showed improvement in fit compared to the MI model fitting results without covariates (CFI > 0.9, TLI > 0.9, RMSEA < 0.05). The chi‐square difference misfit test statistics were noticeably reduced, now with ΔCFI but not ΔRMSEA above their suggested cutoffs, respectively, for MI.
Sex and age invariance
Having established the baseline invariance models (configural and scalar invariance) in which the covariate effects are freely estimated in each of the samples, the effects of sex and age on the common factor were constrained to be equal across samples. The configural and scalar measurement invariance model fits served as reference comparisons for assessing the fit of the invariance model including the sex and age covariates. Table 4 gives the results of the invariance testing for the covariates. It shows that both the configural and scalar invariance models including sex and age effects on the common AD factor had better fits than the baseline models (non‐significant chi‐square differences, decrease in CFI, and increase in RMSEA).
Table 4.
Results of testing sex and age invariance effects on the common factor across samples
| Model fit indices | Model comparison | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Covariate invariance | χ 2 | df | CFI | TLI | RMSEA | RMSEA 90% CI | Comparisona | ∆χ 2 | ∆df | P | ∆CFI | ∆RMSEA |
| Based on configural invariance | ||||||||||||
| 1. All covariates free | 448.4 | 65 | 0.956 | 0.932 | 0.038 | 0.034–0.041 | ||||||
| 2. Sex invariance | 432.4 | 69 | 0.958 | 0.939 | 0.036 | 0.032–0.039 | 2 versus 1 | 8.9 | 4 | 0.065 | −0.002 | −0.002 |
| 3. Age invariance | 424.5 | 69 | 0.959 | 0.941 | 0.035 | 0.032–0.038 | 3 versus 1 | 6.0 | 4 | 0.202 | −0.003 | −0.003 |
| 4. Sex & Age invariance | 410.6 | 73 | 0.961 | 0.947 | 0.033 | 0.030–0.036 | 4 versus 1 | 12.0 | 8 | 0.151 | −0.005 | −0.005 |
| Based on scalar invariance | ||||||||||||
| 1. All covariates free | 731.5 | 97 | 0.927 | 0.925 | 0.040 | 0.037–0.042 | ||||||
| 2. Sex invariance | 749.3 | 101 | 0.925 | 0.926 | 0.039 | 0.037–0.042 | 2 versus 1 | 49.1 | 4 | 0.000 | 0.002 | −0.001 |
| 3. Age invariance | 722.0 | 101 | 0.929 | 0.929 | 0.038 | 0.036–0.041 | 3 versus 1 | 14.9 | 4 | 0.005 | −0.002 | −0.002 |
| 4. Sex & Age invariance | 729.7 | 105 | 0.928 | 0.932 | 0.038 | 0.035–0.040 | 4 versus 1 | 36.5 | 8 | 0.000 | −0.001 | −0.002 |
Abbreviations: CFI, comparative fit index; TLI, Tucker–Lewis index; RMSEA, root mean square error of approximation; CI, confidence interval; df, degrees of freedom.
First number is the nested model number of interest and second number is the reference model number for model comparison.
Note: Model comparisons are based on the fit index difference (∆) between nested models: ∆CFI = CFA reference – CFA nested, ∆RMSEA = RMSEA nested – RMSEA reference (negative values in ∆CFI and ∆RMSEA indicate better fit compared to the reference model, otherwise worse fit was obtained).
Discussion
In this study, we investigated the question of phenotypic heterogeneity among five clinically distinct lifetime ADs across five independently collected and characterized cohorts of European background. We will address our findings in turn for the three questions we posed for the study.
(1) Does the same phenotypic pattern and structure exist across the ADs in each study?
We examined this question via MI testing within a dimensional structural modeling approach for the five ADs. We treated the ordinal coded AD variables as indicators of a single latent AD liability across the five cohorts, fitting common factor models separately in each sample. Consistent results across each of the samples indicated that the five AD variables adequately functioned as indicators of a single anxiety factor (Table 2). This added support that a single common factor structure, as applied to our recent GWAS meta‐analysis (Otowa et al., 2016), was an appropriate representation of the covariation among the five AD indicators in each of the samples. In general, AG tended to have the highest loading on the AD common factor across samples, indicating that this indicator discriminated most strongly in the calibration of individual differences on the common factor.
(2) If not, what are the sources of heterogeneity, and how can they be characterized statistically?
We investigated more subtle sources of heterogeneity by applying increasing levels of restrictions on the AD item factor loadings and thresholds across the samples. Models specifying configural invariance fit the data well. However, metric and scalar MI testing results called into question the assumption that the AD indicator factor loadings and thresholds are invariant (i.e. function equivalently) in the different cohort samples (Table 3). This is evidence suggesting that individual differences on the unidimensional common liability underlying the AD variables may not be calibrated in exactly the same way due to some form of differential item functioning among the five AD variables across the different cohorts. These findings statistically quantify the various differences seen in the disorder category frequencies (Table 1) and sample loadings (Table 2).
(3) How do the effects of other phenotypic predictors such as age and sex vary between studies and impact these findings?
Similar sex effects were seen across the samples during the common factor analyses, showing that, on average, females had higher AD liability scores compared to males across the samples. Higher female AD risk is consistent with extant research findings. Age effects were more variable, with the TRAILS sample and its younger, narrower age range as a non‐significant outlier. A noteworthy finding is that accounting for relevant demographic covariates such as sex and age at the level of the common AD liability factor can impact the item level MI testing results. Although the covariate effects in the present study were limited to the latent factor, it appears that some of the non‐invariance operative at the individual AD item factor loading and threshold levels can be accounted for by simply allowing linear sex and age effects on the common AD factor. Importantly, this resulted in more nominal and mixed evidence for the failure of MI based on the global item model testing misfit levels. Sex and age were included as regressors in the genetic association analyses conducted in each sample rather than at the level of the latent factor, as the former is a more standard practice in GWASs.
Several benefits of the MI testing procedure described and applied here can be highlighted in situations where often diverse samples gathered under different sampling and data collection protocols are to be combined to increase power for GWAS analysis. First, if symptoms are simply “counted up” to create aggregate sum scores or algorithmically collapsed to form an affected versus unaffected diagnosis, it is not possible to evaluate whether the “same” phenotype is defined in different samples by the items. These strategies tacitly assume this to be true. However, without empirically evaluating whether phenotypes are equivalent across samples, it leaves open questions about whether differences in how the phenotype is defined in different samples contribute to discrepancies or inconsistencies that emerge in GWAS findings when samples are analyzed separately and compared. Meta‐analysis would not be of much help in that case.
Second, detecting the presence of measurement non‐invariance across samples opens the possibility of identifying the sources of the failure of MI. For the data examined herein, MI was partially recovered after allowing for effects of sex and age on the common factor. If that were not the case, one may employ more detailed strategies that can identify which item characteristics are the major sources contributing to the non‐invariance across samples. If a subset of items can be found that are invariant in their measuring properties, it may be possible to impose partial measurement invariance (Byrne et al., 1989) in an attempt to establish equivalent phenotypes across samples. Future research into establishing equivalent phenotypes and the degree to which attention to measurement issues raised here can impact the outcome of GWAS analyses, especially in the context of applications using multiple data sources, seems worthwhile.
Limitations
There are several potential limiting aspects of the current research that should be considered when interpreting these findings. MI testing is typically applied to the most basic level of data information — the individual items. Although we had access to symptom level data, this finer grain information was not necessary for identifying a latent AD common liability phenotype that closely paralleled the DSM diagnostic classification system for the purpose of genetic association testing. Also, because the constraints for the metric invariance testing specification are not satisfied in the case of binary variables, the ordered three‐category classification coding was necessary for examining this aspect of MI. However, given these heuristic justifications for the strategy used, it should be pointed out that a full item level MI analysis may produce a different perspective on the nature of invariance/equivalence of the common AD phenotype across the five cohorts.
A second more technical point to note is that extending multiple group CFA MI model testing to include demographic covariate effects on the common AD liability factor is not conventionally done. However, the results we obtained using this approach suggest potential advantages. As noted previously, allowing binary sex effects to vary across cohort samples resulted in convergence problems when testing for metric (i.e. factor loading) invariance across cohorts, preventing us from testing these effects.
Third, we note that we used an atypical three‐level ordinal scoring system for each AD due to the aforementioned advantages for a genetics study over the usual case‐control design. For comparison, we reanalyzed these invariance models using standard case‐control assignments (in our scheme, full cases = subjects scored as two and controls = subjects scored as zero or one). However, only the configural invariance model is identified for binary indicators, preventing us from testing for metric and scalar invariance. Configural invariance fit the data well (CFI/TLI > 0.98 and RMSEA = 0.02), providing reassurance that these results are generally applicable to both coding schemes.
This is the first study to examine the phenotypic structure of psychiatric disorder phenotypes simultaneously across multiple, large cohorts used for GWASs. The analyses provide evidence for higher‐level invariance for the ADs but possible break‐down at more detailed levels that can be subtly influenced by included covariates, suggesting caution when combining such data. Thus, formal invariance testing has practical value for identifying and characterizing phenotypic heterogeneity with significance for large‐scale collaborative efforts such as genetic association studies that draw on multiple, potentially heterogeneous sources of data. In particular, these results have specific utility for studies that combine multi‐factor phenotypes across different cohorts. This could apply to (a) single disorders for which symptom item‐level data might be analyzed to assess cryptic heterogeneity across samples (e.g. major depression [Kendler et al., 2013]); (b) disorders considered to consist of multiple inherent factors (e.g. post‐traumatic stress disorder (Friedman et al., 2011), obsessive‐compulsive disorder (Bloch et al., 2008)); or (c) multiple disorders jointly analyzed due to their a priori genetic covariance (e.g. polysubstance abuse [Kendler et al., 2003]) similar to what we have done for ADs.
Declaration of interest statement
The authors have no competing interests.
Acknowledgements
This overall project was supported by the National Institutes of Health (NIH) grant R01MH87646 to JMH. The authors are grateful to everyone who participated in this research or worked on this project to make it possible.
Molecular Genetics of Schizophrenia (MGS)
Samples and associated phenotype data for the Molecular Genetics of Schizophrenia (MGS) study were collected under the following grants: National Institute of Mental Health (NIMH) Schizophrenia Genetics Initiative U01s: MH046276 (CR Cloninger), MH46289 (C Kaufmann), and MH46318 (MT Tsuang); and MGS Part 1 (MGS1) and Part 2 (MGS2) R01s: MH67257 (NG Buccola), MH59588 (BJ Mowry), MH59571 (PV Gejman), MH59565(Robert Freedman), MH59587 (F Amin), MH60870 (WF Byerley), MH59566 (DW Black), MH59586 (JM Silverman), MH61675 (DF Levinson), and MH60879 (CR Cloninger).
Rotterdam Study (RS)
The Rotterdam Study (RS) is supported by the Research Institute for Diseases in the Elderly (014‐93‐015; RIDE2), the Netherlands Genomics Initiative (NGI)/Netherlands Consortium for Healthy Ageing (NCHA) project No. 050‐060‐810. The work of Henning Tiemeier is supported by Vidi (grant 017.106.370). The RS is funded by Erasmus Medical Center, Rotterdam, the Netherlands Organization for the Health Research and Development (ZonMw), the Ministry of Education, Culture and Science, and the Ministry for Health, Welfare and Sports.
Study of Health in Pomerania (SHIP)
Study of Health in Pomerania (SHIP) is part of the Community Medicine Research net of the University of Greifswald, Germany, which is funded by the Federal Ministry of Education and Research (grants no. 01ZZ9603, 01ZZ0103, and 01ZZ0403), the Ministry of Cultural Affairs and the Social Ministry of the Federal State of Mecklenburg‐West Pomerania. This work was also funded by the German Research Foundation (DFG: GR 1912/5‐1).
PsyCoLaus
The CoLaus|PsyCoLaus study was and is supported by research grants from GlaxoSmithKline, the Faculty of Biology and Medicine of Lausanne, and the Swiss National Science Foundation (grants 3200B0–105993, 3200B0‐118308, 33CSCO‐122661, 33CS30‐139468 and 33CS30‐148401).
Tracking Adolescents’ Individual Lives Survey (TRAILS)
Tracking Adolescents’ Individual Lives Survey (TRAILS) has been financially supported by grants from the Netherlands Organization for Scientific Research NWO (Medical Research Council program grant GB‐MW 940‐38‐011; ZonMW Brainpower grant 100‐001‐004; ZonMw Risk Behavior and Dependence grants 60‐60600‐97‐118; ZonMw Culture and Health grant 261‐98‐710; Social Sciences Council medium‐sized investment grants GB‐MaGW 480‐01‐006 and GB‐MaGW 480‐07‐001; Social Sciences Council project grants GB‐MaGW 452‐04‐314 and GB‐MaGW 452‐06‐004; NWO large‐sized investment grant 175.010.2003.005; NWO Longitudinal Survey and Panel Funding 481‐08‐013 and 481‐11‐001), the Dutch Ministry of Justice (WODC), the European Science Foundation (EuroSTRESS project FP‐006), Biobanking and Biomolecular Resources Research Infrastructure BBMRI‐NL (CP 32), and the participating centers (University Medical Center and University of Groningen, Erasmus University Medical Center Rotterdam, University of Utrecht, Radboud Medical Center Nijmegen, and Parnassia Bavo group).
Lee, M. , Aggen, S. H. , Otowa, T. , Castelao, E. , Preisig, M. , Grabe, H. J. , Hartman, C. A. , Oldehinkel, A. J. , Middeldorp, C. M. , Tiemeier, H. , and Hettema, J. M. (2016) Assessment and characterization of phenotypic heterogeneity of anxiety disorders across five large cohorts. Int J Methods Psychiatr Res, 25: 255–266. doi: 10.1002/mpr.1519.
Footnotes
Strict invariance, which places the additional restriction that indicator residual variances be equal across samples, is the most stringent form of invariance that can be tested. However, this level of invariance is deemed beyond the requirements necessary to adequately establish a basis for determining equivalence across samples in the present context and, therefore, was not examined.
More specifically, such an item level MI analysis would include a higher order factor model where the different sets of AD symptom criteria define first‐order liability factors for each of the five ADs and a second‐order factor accounts for the inter‐factor correlations among the first‐order factors. Such a model that takes into account the patterning of the symptom criteria data would substantially increase the complexity of model fitting by including many more parameters that could be examined and tested for invariance across the cohorts.
References
- American Psychiatric Association (2013) Diagnostic and Statistical Manual of Mental Disorders: DSM‐5, Washington, DC: American Psychiatric Association. [Google Scholar]
- Auton A., Brooks L.D., Durbin R.M., Garrison E.P., Kang H.M., Korbel J.O., Marchini J.L., McCarthy S., McVean G.A., Abecasis G.R. (2015) A global reference for human genetic variation. Nature, 526(7571), 68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloch M.H., Landeros‐Weisenberger A., Rosario M.C., Pittenger C., Leckman J.F. (2008) Meta‐analysis of the symptom structure of obsessive‐compulsive disorder. American Journal of Psychiatry, 165(12), 1532–1542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boomsma D.I., Willemsen G., Sullivan P.F., Heutink P., Meijer P., Sondervan D., Kluft C., Smit G., Nolen W.A., Zitman F.G., Smit J.H., Hoogendijk W.J., van D.R. , De Geus E.J., Penninx B.W. (2008) Genome‐wide association of major depression: description of samples for the GAIN Major Depressive Disorder Study: NTR and NESDA biobank projects. European Journal of Human Genetics, 16(3), 335–342. [DOI] [PubMed] [Google Scholar]
- Byrne B.M., Shavelson R.J., Muthén B. (1989) Testing for equivalence of factor covariance and mean structures: the issue of partial measurement invariance. Psychological Bulletin, 105(3), 456–466. [Google Scholar]
- Chen F.F. (2007) Sensitivity of goodness of fit indexes to lack of measurement invariance. Structural Equation Modeling, 14(3), 464–504. [Google Scholar]
- Cheung G.W., Rensvold R.B. (2002) Evaluating goodness‐of‐fit indexes for testing measurement invariance. Structural Equation Modeling, 9(2), 233–255. [Google Scholar]
- de Moor M.H., van den Berg S.M., Verweij K.J., Krueger R.F., Luciano M., Arias V.A., Matteson L.K., Derringer J., Esko T., Amin N., Gordon S.D., Hansell N.K., Hart A.B., Seppala I., Huffman J.E., Konte B., Lahti J., Lee M., Miller M., Nutile T., Tanaka T., Teumer A., Viktorin A., Wedenoja J., Abecasis G.R., Adkins D.E., Agrawal A., Allik J., Appel K., Bigdeli T.B., Busonero F., Campbell H., Costa P.T., Davey Smith G., Davies G., de Wit H., Ding J., Engelhardt B.E., Eriksson J.G., Fedko I.O., Ferrucci L., Franke B., Giegling I., Grucza R., Hartmann A.M., Heath A.C., Heinonen K., Henders A.K., Homuth G., Hottenga J.J., Iacono W.G., Janzing J., Jokela M., Karlsson R., Kemp J.P., Kirkpatrick M.G., Latvala A., Lehtimaki T., Liewald D.C., Madden P.A., Magri C., Magnusson P.K., Marten J., Maschio A., Medland S.E., Mihailov E., Milaneschi Y., Montgomery G.W., Nauck M., Ouwens K.G., Palotie A., Pettersson E., Polasek O., Qian Y., Pulkki‐Raback L., Raitakari O.T., Realo A., Rose R.J., Ruggiero D., Schmidt C.O., Slutske W.S., Sorice R., Starr J.M., St Pourcain B., Sutin A.R., Timpson N.J., Trochet H., Vermeulen S., Vuoksimaa E., Widen E., Wouda J., Wright M.J., Zgaga L., Porteous D., Minelli A., Palmer A.A., Rujescu D., Ciullo M., Hayward C., Rudan I., Metspalu A., Kaprio J., Deary I.J., Raikkonen K., Wilson J.F., Keltikangas‐Jarvinen L., Bierut L.J., Hettema J.M., Grabe H.J., van Duijn C.M., Evans D.M., Schlessinger D., Pedersen N.L., Terracciano A., McGue M., Penninx B.W., Martin N.G., Boomsma D.I. (2015) Meta‐analysis of genome‐wide association studies for neuroticism, and the polygenic association with major depressive disorder. JAMA Psychiatry, 72(7), 642–650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman M.J., Resick P.A., Bryant R.A., Brewin C.R. (2011) Considering PTSD for DSM‐5. Depression and Anxiety, 28(9), 750–769. [DOI] [PubMed] [Google Scholar]
- Hettema J.M., An S.S., Bukszar J., van den Oord E.J., Neale M.C., Kendler K.S., Chen X. (2008) Catechol‐O‐methyltransferase contributes to genetic susceptibility shared among anxiety spectrum phenotypes. Biological Psychiatry, 64(4), 302–310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hettema J.M., Prescott C.A., Myers J.M., Neale M.C., Kendler K.S. (2005) The structure of genetic and environmental risk factors for anxiety disorders in men and women. Archives of General Psychiatry, 62(2), 182–189. [DOI] [PubMed] [Google Scholar]
- Hu L., Bentler P.M. (1999) Cutoff criteria for fit indexes in covariance structure analysis: conventional criteria versus new alternatives. Structural Equation Modeling, 6(1), 1–55. [Google Scholar]
- Jardine R., Martin N.G., Henderson A.S. (1984) Genetic covariation between neuroticism and the symptoms of anxiety and depression. Genetic Epidemiology, 1(2), 89–107. [DOI] [PubMed] [Google Scholar]
- Kendler K.S., Aggen S.H., Neale M.C. (2013) Evidence for multiple genetic factors underlying DSM‐IV criteria for major depression. JAMA Psychiatry, 70(6), 599–607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kendler K.S., Jacobson K.C., Prescott C.A., Neale M.C. (2003) Specificity of genetic and environmental risk factors for use and abuse/dependence of cannabis, cocaine, hallucinogens, sedatives, stimulants, and opiates in male twins. American Journal of Psychiatry, 160(4), 687–695. [DOI] [PubMed] [Google Scholar]
- Manchia M., Cullis J., Turecki G., Rouleau G.A., Uher R., Alda M. (2013) The impact of phenotypic and genetic heterogeneity on results of genome wide association studies of complex diseases. PloS One, 8(10), e76295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mellenbergh G.J. (1989) Item bias and item response theory. International Journal of Educational Research, 13(2), 127–143. [Google Scholar]
- Meredith W. (1993) Measurement invariance, factor analysis and factorial invariance. Psychometrika, 58(4), 525–543. [Google Scholar]
- Millsap R.E., Yun‐Tein J. (2004) Assessing factorial invariance in ordered‐categorical measures. Multivariate Behavioral Research, 39(3), 479–515. [Google Scholar]
- Muthen L.K., Muthen B.O. (2012) Mplus User's Guide, Los Angeles, CA: Muthen & Muthen. [Google Scholar]
- Otowa T., Hek K., Lee M., Byrne E.M., Mirza S.S., Nivard M.G., Bigdeli T., Aggen S.H., Adkins D., Wolen A., Fanous A., Keller M.C., Castelao E., Kutalik Z., der Auwera S.V., Homuth G., Nauck M., Teumer A., Milaneschi Y., Hottenga J.J., Direk N., Hofman A., Uitterlinden A., Mulder C.L., Henders A.K., Medland S.E., Gordon S., Heath A.C., Madden P.A., Pergadia M.L., van der Most P.J., Nolte I.M., van Oort F.V., Hartman C.A., Oldehinkel A.J., Preisig M., Grabe H.J., Middeldorp C.M., Penninx B.W., Boomsma D., Martin N.G., Montgomery G., Maher B.S., van den Oord E.J., Wray N.R., Tiemeier H., Hettema J.M. (2016) Meta‐analysis of genome‐wide association studies of anxiety disorders. Molecular Psychiatry. DOI: 10.1038/mp.2015.197. [DOI] [PubMed] [Google Scholar]
- van den Berg S.M., de Moor M.H., McGue M., Pettersson E., Terracciano A., Verweij K.J., Amin N., Derringer J., Esko T., van Grootheest G., Hansell N.K., Huffman J., Konte B., Lahti J., Luciano M., Matteson L.K., Viktorin A., Wouda J., Agrawal A., Allik J., Bierut L., Broms U., Campbell H., Smith G.D., Eriksson J.G., Ferrucci L., Franke B., Fox J.P., De Geus E.J., Giegling I., Gow A.J., Grucza R., Hartmann A.M., Heath A.C., Heikkila K., Iacono W.G., Janzing J., Jokela M., Kiemeney L., Lehtimaki T., Madden P.A., Magnusson P.K., Northstone K., Nutile T., Ouwens K.G., Palotie A., Pattie A., Pesonen A.K., Polasek O., Pulkkinen L., Pulkki‐Raback L., Raitakari O.T., Realo A., Rose R.J., Ruggiero D., Seppala I., Slutske W.S., Smyth D.C., Sorice R., Starr J.M., Sutin A.R., Tanaka T., Verhagen J., Vermeulen S., Vuoksimaa E., Widen E., Willemsen G., Wright M.J., Zgaga L., Rujescu D., Metspalu A., Wilson J.F., Ciullo M., Hayward C., Rudan I., Deary I.J., Raikkonen K., Arias V.A., Costa P.T., Keltikangas‐Jarvinen L., van Duijn C.M., Penninx B.W., Krueger R.F., Evans D.M., Kaprio J., Pedersen N.L., Martin N.G., Boomsma D.I. (2014) Harmonization of neuroticism and extraversion phenotypes across inventories and cohorts in the Genetics of Personality Consortium: an application of item response theory. Behavior Genetics, 44(4), 295–313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandenberg R.J., Lance C.E. (2000) A review and synthesis of the measurement invariance literature: suggestions, practices, and recommendations for organizational research. Organizational Research Methods, 3(1), 4–70. [Google Scholar]
- Visscher P.M., Brown M.A., McCarthy M.I., Yang J. (2012) Five years of GWAS discovery. American Journal of Human Genetics, 90(1), 7–24. [DOI] [PMC free article] [PubMed] [Google Scholar]


