Significance
Sensorimotor integration is important for the acquisition and performance of motor skills. Here, we show the emergence of neuroplastic changes in the interactions between the motor and somatosensory areas of the primate cortex during learning. Interareal coherence is frequency- and network-specific and exhibits a spatiotemporal organization. Time-sensitive sensorimotor integration and plasticity may rely on coherence of local and large-scale sensorimotor networks in order for cortical processes to operate at multiple temporal and spatial scales. Understanding cortico-cortical interactions may be important for developing therapies for sensorimotor disorders, such as those affecting feeding and speech that are commonly found in stroke and Parkinson’s disease.
Keywords: motor cortex, somatosensory cortex, coherence, learning, orofacial cortex
Abstract
Skilled movements rely on sensory information to shape optimal motor responses, for which the sensory and motor cortical areas are critical. How these areas interact to mediate sensorimotor integration is largely unknown. Here, we measure intercortical coherence between the orofacial motor (MIo) and somatosensory (SIo) areas of cortex as monkeys learn to generate tongue-protrusive force. We report that coherence between MIo and SIo is reciprocal and that neuroplastic changes in coherence gradually emerge over a few days. These functional networks of coherent spiking and local field potentials exhibit frequency-specific spatiotemporal properties. During force generation, theta coherence (2–6 Hz) is prominent and exhibited by numerous paired signals; before or after force generation, coherence is evident in alpha (6–13 Hz), beta (15–30 Hz), and gamma (30–50 Hz) bands, but the functional networks are smaller and weaker. Unlike coherence in the higher frequency bands, the distribution of the phase at peak theta coherence is bimodal with peaks near 0° and ±180°, suggesting that communication between somatosensory and motor areas is coordinated temporally by the phase of theta coherence. Time-sensitive sensorimotor integration and plasticity may rely on coherence of local and large-scale functional networks for cortical processes to operate at multiple temporal and spatial scales.
Synchrony between cortical areas has been implicated in neuronal communication and plasticity (1–4). Sensorimotor integration and formation of motor memories during learning are examples wherein effective communication between sensory and motor areas of the cerebral cortex is critical. However, very few studies have investigated coherence between the somatosensory and motor pathways in primates (5–7). These past studies have been confined to upper limb tasks, and none of them looked at changes in coherence during learning. Here, we investigated the synchronous activity between the orofacial primary motor (MIo) and somatosensory (SIo) cortical areas that play important roles in the control of orofacial behaviors (8–10). Sensorimotor control of oral behaviors is complex, involving the integration of afferent information for moving the tongue and facial muscles. Anatomical connections between MIo and SIo are dense and both areas have bilateral orofacial representations and project to brainstem cranial nerve motor nuclei containing the motoneurons projecting to jaw, facial, and tongue muscles (11, 12). These connections provide a substrate for interareal communication between MIo and SIo for the control and learning of orofacial behaviors. To investigate cortico-cortical interactions between these areas, we measured coherence of spiking and local field potentials (LFPs) recorded simultaneously from MIo and SIo of the left hemisphere as monkeys learned a simple and controlled tongue protrusion task. Several studies using this behavioral paradigm have reported neuroplasticity and modulation of neuronal activity related to tongue protrusion separately in MIo and SIo (13–17). Here, we show that interactions between MIo and SIo involve coherent networks at multiple frequencies. Cortical processes may make use of the dynamics of oscillatory rhythms and coherence phase to coordinate the activation of sensorimotor networks at multiple spatial and temporal scales.
Results
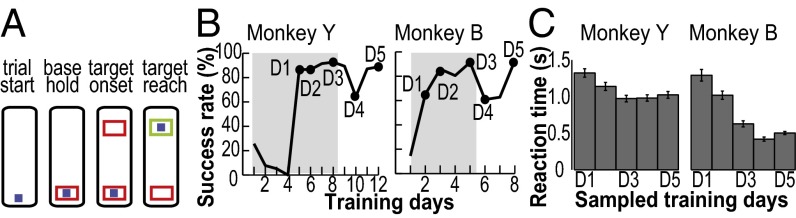
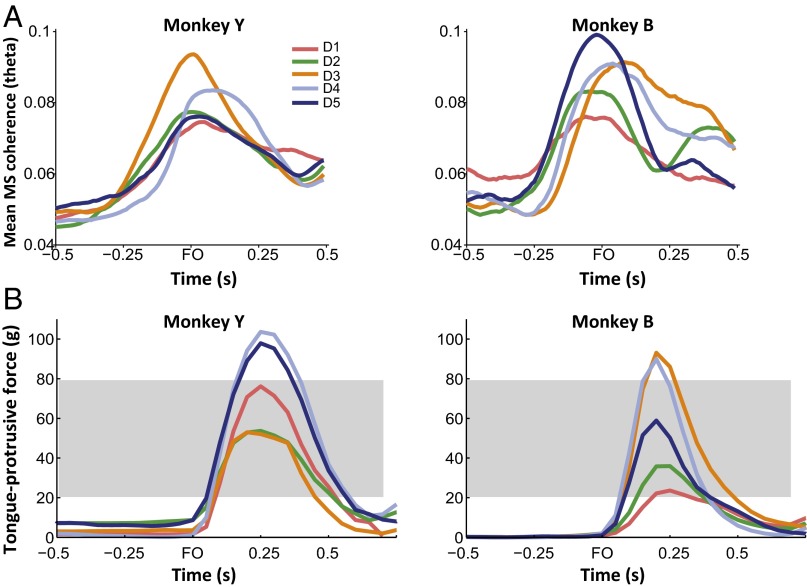
We trained two naïve monkeys to protrude the tongue onto a force transducer and apply isometric force at the level cued by target positions shown on a video screen (Fig. 1A). The monkeys learned to associate the target position with the required tongue-protrusive force after a few hundred trials, but proficient task performance was achieved after 8–12 training days (Fig. 1 B and C). To investigate the emergence of interactions between MIo and SIo as monkeys learned to associate sensory information with motor response, we evaluated the coherence between the spiking of neurons recorded in MIo and SIo (MS in Fig. 2A) and the coherence between the spiking of MIo or SIo neurons with LFPs in SIo or MIo, respectively (MSf and SMf in Fig. 2A) These measures of coherence are presumed to represent the correlation of the outputs from both areas (MS) and the correlation of the outputs from one area with the inputs in the other (MSf and SMf). For each of the 5 sampled training days, D1–D5, we estimated coherence by using a 0.5-s sliding window with 0.01-s steps to show a time-resolved coherence profile in the theta (2–6 Hz), alpha (6–13 Hz), beta (15–30 Hz), and gamma (30–50 Hz) bands. Coherence in these frequency bands is believed to play a role in attention, memory, motor control, and plasticity (16, 18–20). As the results for alpha/beta were similar to gamma, we only discuss the results in the gamma band here and show the results for alpha and beta bands in Supporting Information.
Fig. 1.
Behavioral task and performance. (A) Diagram of the sequence of events in a trial of the tongue protrusion task. The blue square represents the force cursor, whereas the red and green boxes represent the base and force targets. (B) Success rates shown separately for each monkey. Dots mark the 5 d that were analyzed (i.e., sampled training days D1 to D5). Shaded area corresponds to training days when the required force level was 50 g. Required force level was increased to 80 g when success rates reached >75% for at least 3 consecutive days. (C) Reaction time shown as mean (±1 SEM error bars) across all trials for D1 to D5. B and C adapted from ref. 16.
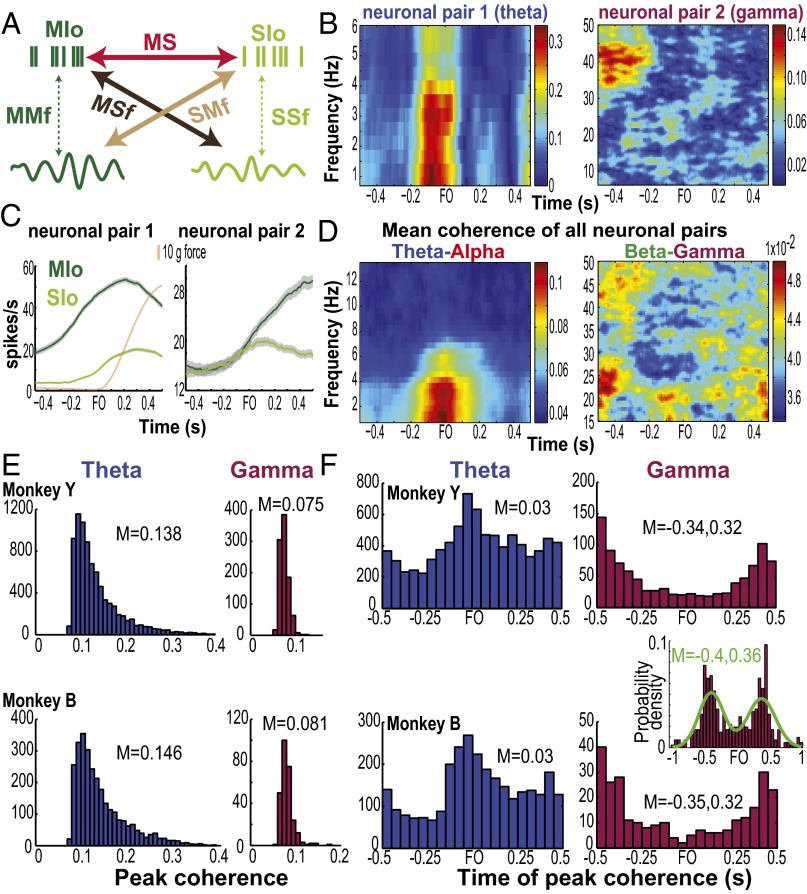
Fig. 2.
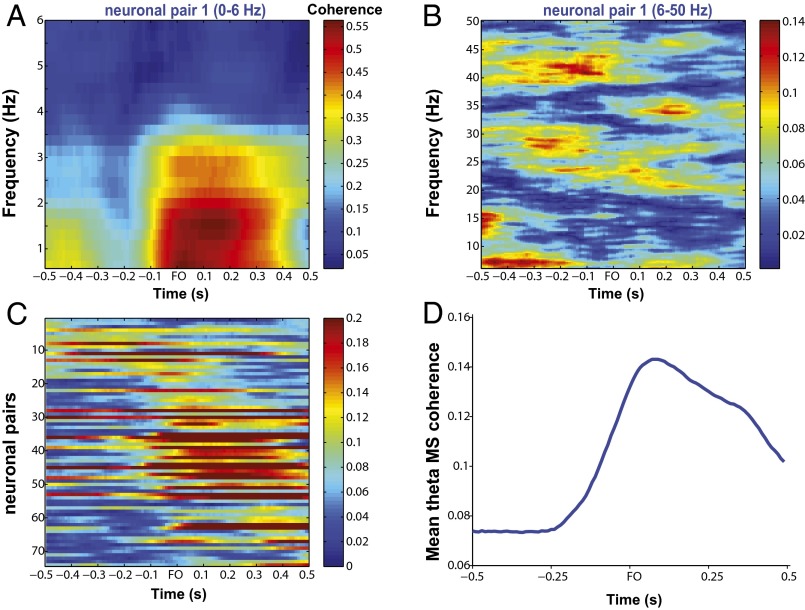
Frequency-specific modulation of MS coherence between MIo and SIo neurons. (A) Schema of paired signals used in interareal coherence: paired spikes from MIo and SIo (MS), paired MIo spikes and SIo LFPs (MSf), and paired SIo spikes and MIo LFPs (SMf). We also analyzed intraareal coherence, i.e., paired spikes and LFPs within each area (MMf and SSf). (B) Coherogram of two pairs of neurons with significant MS coherence (color scale). Coherence is aligned to the right edge of the 0.5-s window, e.g., coherence at force onset (FO) corresponds to a 0.5-s window ending at FO. (C) Mean firing rates of MIo and SIo neurons whose coherent activity is shown in B. Rates were calculated using a 0.5-s sliding window with 0.01-s steps per trial then averaged across trials. Gray shades denote 1 SEM. Orange line denotes mean tongue-protrusive force of the first 100 trials of a training day. The force profile is averaged over a 0.5-s window. Timescales for rates and force are plotted to the right edge of 0.5-s window over which they were computed. (D) Mean coherence across all unique pairs of neurons (SI Methods) with significant coherence in one dataset, shown for the theta–alpha bands (n = 75 pairs) and beta–gamma bands (n = 67), respectively. (E) Histograms of peak coherence of all pairs with significant coherence in the theta and gamma bands. Shown for monkeys Y (ntheta = 8,148, ngamma = 967) and B (ntheta = 2,874, ngamma = 271) separately. Data pooled across D1 to D5. M, mean. (F) As in E, for time of peak coherence. (Inset) Histogram of time of peak gamma coherence ranging from –1.5 and 1 s relative to FO. Green line indicates Gaussian mixture model fit using two components. Data include only unique neuronal pairs with significant modulation of coherence, pooled across days and monkeys.
Frequency-Specific Modulation of Spike–Spike Coherence (MS) During Task Performance.
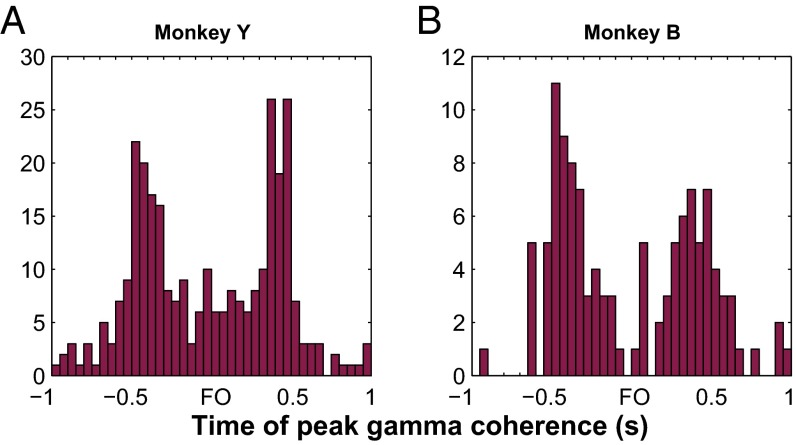
Coherence between the spiking of MIo and SIo neurons (MS) at multiple frequencies was dynamically modulated; single neuronal pairs exhibited increases and decreases in coherence as well as firing-rate modulations relative to the onset of tongue-protrusive force (Fig. 2 B and C, and Fig. S1). Similar patterns were observed for the mean MS coherence across neuronal pairs with significant modulation of coherence (Fig. 2D, shuffle test, P < 0.01), consistent with the task modulation of theta coherence previously found within MIo and within SIo (16). Out of all of the possible combinations of paired signals (n = 44,152) from 10 datasets, the proportion of neuronal pairs that showed significant task modulation of MS coherence (i.e., “functional network”) was highest in theta and was significantly lower in the higher frequency bands (Fig. S1E, McNemar test, P < 0.01). The larger theta network (i.e., highest proportion of paired neurons with significant coherence) exhibited the strongest coherence (i.e., highest mean peak coherence), whereas the sparser networks in the alpha/beta/gamma bands exhibited weaker coherence. This was observed for each monkey (Fig. 2E) and for data pooled across monkeys [Kruskal–Wallis peak by frequency, , P = 0, post hoc, P < 0.001]. Differences in spectral power across frequencies cannot explain this result as the cross-spectrum is normalized by the autospectra. We also found frequency-specific differences in the time of peak MS coherence; pairs of MIo and SIo neurons exhibited a unimodal distribution of time of peak coherence in theta and a bimodal distribution in all other frequency bands [Fig. 2F, Kruskal–Wallis peak times by frequency, , P = 3e-26]. The mean time to peak theta coherence (0.03 s, SD = 0.07) occurred before and at force onset (note that coherence values were aligned to the right edge of the 0.5-s window). This suggests that theta coherence may play a role in generating the tongue-protrusive force. In contrast, the distribution of the times of peak gamma coherence was bimodal based on a two-component Gaussian mixture model having the lowest Akaike information criterion compared with models with one, three, or four components. The bimodal distribution of the peak times of gamma coherence was further confirmed by extending the time windows analyzed relative to force onset (Fig. 2F, Inset, and Fig. S2), indicating a suppression of gamma coherence at force onset. Peaks in gamma coherence [mean (M) = –0.35 s, 0.33 s (SD = 0.02) relative to force onset] occurred when monkeys were getting ready to apply the tongue-protrusive force or when monkeys were decreasing force production after being rewarded. On average, monkeys reached the force target at 0.15 s (SEM = 0.02) after force onset. Force offset typically occurred 0.5 s after force onset. The results of the coherence analyses in the theta band using a 0.5-s window were similar to the coherence results using a 1-s window (Fig. S3), and in the gamma band, the results using a 0.5-s window were similar to the results using a 0.3-s window.
Fig. S1.
Modulation of spike–spike coherence (MS) in the alpha and beta bands. (A) Spike–spike coherence (MS) of a pair of neurons in the alpha and beta bands. (B) MS coherence of neuronal pairs (rows) that showed significant task modulation of coherence in the alpha (Left) and beta (Right) bands. Color represents the magnitude of coherence, and the neuronal pairs were sorted according to the time of peak coherence relative to FO. Shown for one dataset (D3) from each monkey (rows). (C and D) Histograms of peak MS coherence and time of peak MS coherence, respectively, in the alpha and beta bands. Shown for monkeys Y and B separately. (E) Proportion of neuronal pairs with significant modulation of MS coherence in each frequency band. Data pooled across all training days and monkeys (ntheta = 11,022, nalpha = 5,632, nbeta = 2,444, ngamma = 1,238).
Fig. S2.
Suppression of MS gamma coherence around force onset. (A and B) Distributions of time of peak MS coherence in the gamma band shown for monkeys Y and B, respectively. By extending the time windows analyzed relative to FO, each distribution shows peaks around ±0.5 s relative to FO. Data pooled across training days but include only unique neuronal pairs (SI Methods) for each training day.
Fig. S3.
Coherence using 1-s time window. (A and B) Coherograms show the MS coherence of a neuronal pair as a function of time (x axis, using a 1-s time window) and frequency (y axis) in the 0- to 6-Hz and 6- to 50-Hz ranges, respectively. (C) MS theta coherence of nonoverlapping (unique) neuronal pairs recorded from D3. (D) Mean MS theta coherence across the neuronal pairs shown in C. Note that the time of peak coherence in the 1-s window was comparable to a 0.5-s window.
In sum, task-modulated MS coherence differed between low- and high-frequency bands in terms of network size (i.e., the number of paired neurons with significant coherence in a specific band), peak time, and peak magnitude. Such dynamic modulation cannot be attributed to common task-related modulation nor to common inputs received by the neuronal pair because the shuffling procedure effectively estimates these coincident effects. A cross-validation approach (SI Results and Figs. S4 and S5) and performing the same analyses using only unique neuronal pairs further confirmed the dynamic modulation of coherence.
Fig. S4.
Cross-validation of time of peak MS coherence in the theta band. Proportion of neuronal pairs in the test subset with significant MS coherence at the mean time of peak MS coherence determined by the training subset of neuronal pairs. Shown for each sampled training day D1 to D5 for monkeys Y and B.
Fig. S5.
Cross-validation of time of peak MS coherence in the gamma band. (A and B) Proportion of neuronal pairs in the test subset with significant MS coherence at the mean time of peak MS coherence determined by the training subset of neuronal pairs shown for monkeys Y and B, respectively. Cross-validation test was performed on two peak times corresponding to the means based on a two-component Gaussian mixture model fit.
Changes in Spike–Spike Coherence (MS) with Learning.
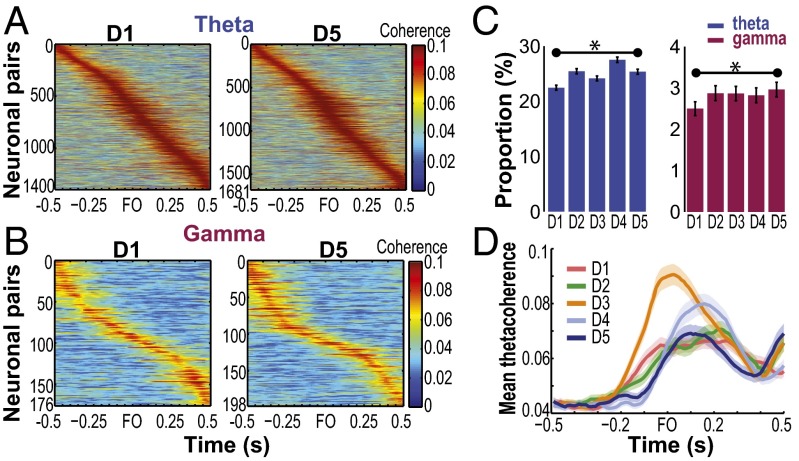
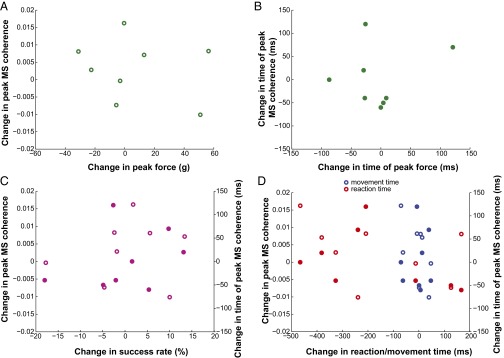
Fig. 3 A and B illustrates the coherent activity of the population of paired MIo–SIo neurons for D1 and D5 of monkey Y. Proportions of neuronal pairs with significant modulation of MS coherence changed during training from day to day. We tested statistical significance between D1 and D5 for each band and found P < 0.05 (Fig. 3C, binomial test). We also found day-to-day changes in peak and time of peak coherence in the theta band [Fig. 3D and Fig. S6, Kruskal–Wallis, peak by days: , P = 7e-11; peak time by days: , P = 2e-6] but not in the other frequency bands (Kruskal–Wallis, P > 0.10, peak/time of peak coherence by days separately for alpha/beta/gamma). We did not find any systematic changes in peak and time of peak coherence in relation to changes in tongue protrusion force, success rates, and reaction and movement times (Fig. S7, Pearson’s correlation, P > 0.10). Furthermore, changes in firing rates cannot account for changes in MS coherence; no significant correlation was found between mean firing rates and mean MS coherence (Fig. S8, Pearson’s correlation, P > 0.10). These indicate that coherence does not directly relate to the encoding of specific behavioral parameters and suggests a role of coherence in the spatiotemporal coordination of different functional networks that emerge or are reshaped during learning.
Fig. 3.
Modulation of MS coherence by learning. (A and B) MS coherence of neuronal pairs with significant coherence in the theta and gamma bands, respectively, for D1 and D5 of monkey Y. Each plot shows changes in coherence of a neuronal pair (corresponding to a row in the y axis) relative to FO. Neuronal pairs are sorted according to the time of peak coherence relative to FO. (C) Day-to-day changes in the proportion of neuronal pairs with significant modulation of MS coherence. Data pooled across monkeys: in both theta and gamma bands, proportion increased from D1 (ntheta = 1,971/8,770, ngamma = 219/8,770) to D5 (ntheta = 2,306/9,089, ngamma = 269/9,089). *P < 0.05. Error bars indicate ±1 SEM (based on a binomial distribution assumption). (D) Day-to-day changes in MS theta coherence. Shown as mean (±1 SEM) coherence across pairs of stable neurons in monkey Y.
Fig. S6.
Day-to-day changes in MS coherence cannot be explained by changes in tongue-protrusive force. (A) Mean MS coherence across neuronal pairs that showed significant coherence in the theta band. Shown for each training day of monkeys Y and B. The change of peak MS coherence relative to D1 [e.g., delta = (D2 peak – D1 peak)/D1 peak] ranged from 2% to 26% in monkey Y and 9% to 30% in monkey B. (B) Mean tongue-protrusive force across the first 100 successful trials for the corresponding days in A. Shaded gray area corresponds to the force target window for the 50-g target set for D1–D3. On D1, monkey B was learning to gauge how much force was needed. On D2, success rates increased indicating that the monkey was applying more force than he did on D1. Monkey used the same strategy on D3, suggesting that the monkey might have associated increased success rates with increased force. In principle, the monkey could have used a strategy in which he applied maximal force because he was not required to hold the force at the target. However, in practice, that was not observed. In monkey Y, the peak tongue force on D1–D3 never exceeded the upper boundary of the gray area. This was also true for D1–D2 in monkey B. Both monkeys did not exceed the upper force boundary (110 g) for D4–D5.
Fig. S7.
Changes in MS theta coherence were not correlated with changes in behavior. (A) Correlation between day-to-day changes in peak force and changes in peak MS theta coherence. Day-to-day change was calculated as the difference between the mean values of two consecutive days (n = 8, 4 data points per monkey). (B) As in A, for correlation between time of peak force and time of peak MS theta coherence. (C) Correlations of changes in success rate and changes in peak MS theta coherence (empty circles) and time of peak MS theta coherence (filled circles) were not significant (Pearson’s correlation, P > 0.10). (D) As in C, for reaction and movement times (Pearson’s correlation, P > 0.10).
Fig. S8.
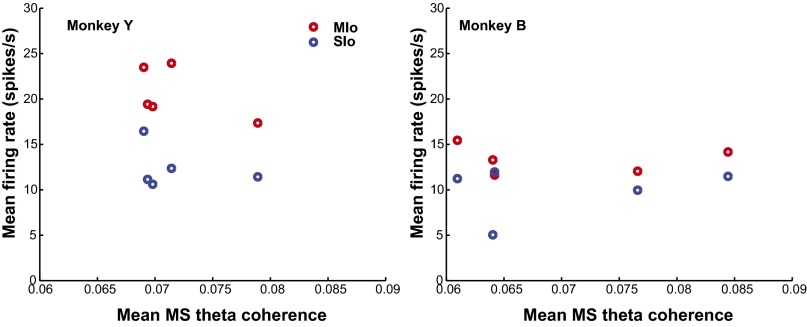
Changes in MS theta coherence across training sessions do not follow mean firing rates of MIo and SIo neurons. Scatterplot of mean firing rates (across all MIo or SIo neurons) of each sampled training day (D1–D5) and the mean MS theta coherence across all pairs for the time window –0.3–0.2 s relative to FO, shown for each monkey. No significant correlation was found between mean firing rates and mean MS theta coherence (Pearson’s correlation, P > 0.10 for each monkey and for each cortical area). Similar results were found with other time windows (from 0.5 s before FO until FO, from FO to 0.5 s after FO).
Network-Specific Modulation of Spike–Field Coherence.
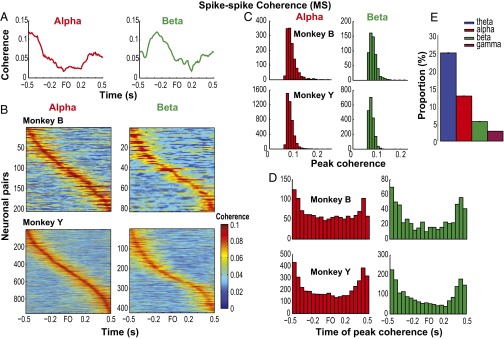
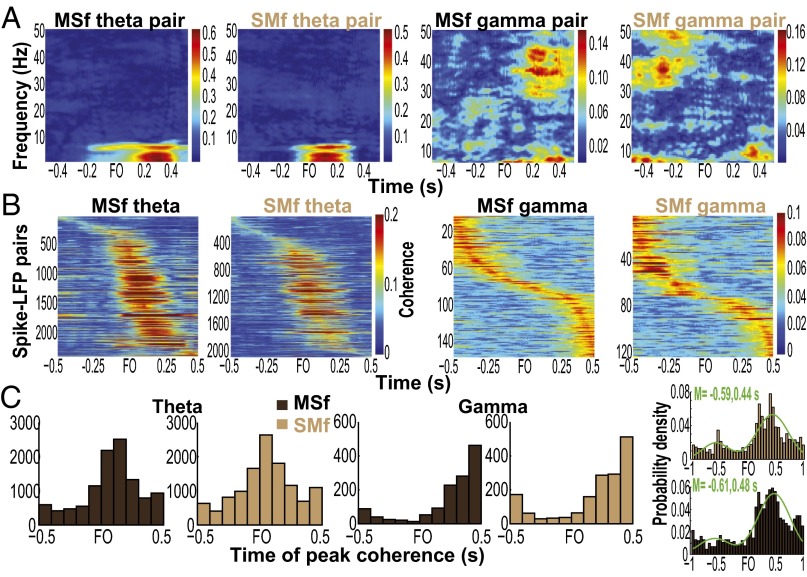
LFPs are considered to represent the aggregate subthreshold activity of neurons in a localized area near the recording electrode (21, 22), thereby providing information about the inputs to an area. A brief description of LFP properties in the orofacial sensorimotor cortex relevant to our analyses is presented in the SI Results and Figs. S9 and S10. Interareal spike–field coherence (MSf and SMf) also exhibited task modulation across multiple frequencies as illustrated for single pairs and for the population of paired signals (Fig. 4 A and B, and Fig. S11). The task modulation of MSf and SMf coherence was distinct from the modulation of LFP spectral power in MIo and SIo (Fig. S10). As was found in MS coherence, the spike–field coherent networks were large and strong in theta and were sparse and weak in alpha/beta/gamma [Fig. S12; McNemar test, P < 0.01; Kruskal–Wallis, peak by frequency, MSf: , P = 0; SMf: , P = 0, post hoc, P < 0.01]. Spike–field networks also exhibited preferred frequency bands; MSf coherence was stronger than SMf in theta, whereas SMf coherence was stronger than MSf in gamma [Kruskal–Wallis, peak by networks, theta: , P = 0; gamma: , P = 5e-15; post hoc, P < 0.001]. Theoretic work has suggested that higher firing rates are correlated with stronger spike–field coherence (23). However, differences in firing rates of neurons cannot account for these results as no linear relations were found between firing rates of MIo or SIo neurons and the MSf/SMf coherence in either theta or gamma bands (Fig. S13). Temporal differences between theta and gamma also support the notion of frequency-specific roles of coherence in MIo and SIo. In theta MSf and SMf, the distributions of time of peak coherence were unimodal with peaks around force onset but the distributions were bimodal in gamma with peaks around ±0.35 s relative to force onset (Fig. 4C and Table S1).
Fig. S9.
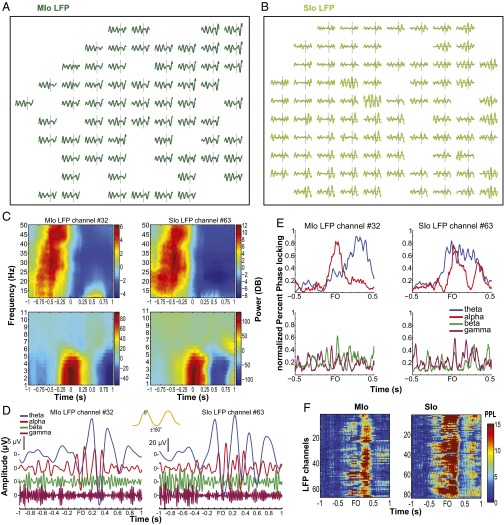
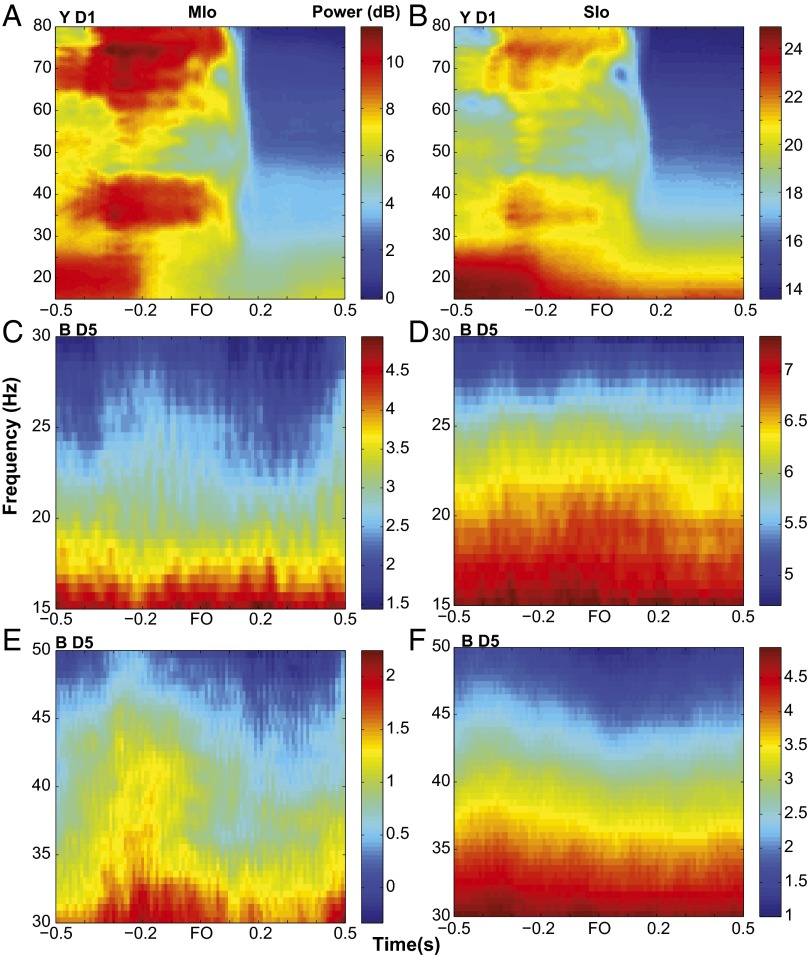
Rhythmic oscillations in the primate orofacial sensorimotor cortex. (A) Single-trial LFPs from MIo or SIo. Each subplot illustrates bandpass-filtered (2–6 Hz), single-trial LFPs recorded from one electrode of the microelectrode array implanted in MIo. Horizontal gray lines in each subplot denote 0 μV and time window from 1 s before force onset to 0.5 s after force onset (FO). Vertical gray lines in each subplot denote ±50-μV LFP amplitude and force onset. Data from training day 3 of monkey Y. (B) As in A, for SIo LFPs, except that vertical gray lines denote ±225-μV LFP amplitude. (C) Trial-averaged spectrograms of LFPs from a single channel in MIo and in SIo. We used a 0.5-s sliding window with 0.01-s steps to calculate the power spectrum. We then subtracted the mean power (per frequency for ±1 s relative to FO) from the power at each time point and frequency. Different scales for spectral power were used for 1–11 Hz and 11–50 Hz to show the modulation of power in the low versus high frequencies. (D) Bandpass-filtered trial-averaged LFPs from the same channels shown in C, aligned to FO, and plotted relative to 0 μV. Inset waveform shows peak and trough of the oscillation corresponds to 0° and ±180°, respectively. (E) Normalized percent phase locking (PPL) as a function of time for MIo and SIo channels shown in C. Shown for each frequency band. (F) Theta band’s PPL relative to FO (represented by color scale). Shown for all LFP channels in MIo (Top) and in SIo (Bottom). Each row of a subplot corresponds to one LFP channel.
Fig. S10.
Modulation of spectral power in MIo and SIo do not follow the modulation of coherence. (A and B) Spectrograms of mean power across all LFPs in MIo and SIo from D1 of monkey Y. Spectral power of beta (15–30 Hz) in MIo and SIo was high before FO. Attenuation of beta power occurred around 0.2 s before FO and was sustained until 0.5 after FO. The modulation of gamma power (30–50 Hz) in MIo and SIo was different from that of gamma coherence; gamma power was high before FO until 0.1 s after FO when it decreased and remained low until 0.5 s after force onset. (C–F) As in A and B, for D5 of monkey B. Different power scales were used for beta (C and D) and gamma (E and F). No attenuation of beta power was found in MIo nor SIo. Modulation of gamma power was evident in MIo but not in SIo.
Fig. 4.
Network-specific modulation of spike–field coherence. (A) Each coherogram shows spike–field coherence (MSf or SMf) of a single pair of signals as a function of frequency. (B) Theta and gamma spike–field coherence (MSf or SMf) of a population of pairs (y axis) from one dataset. Each row is a coherogram from a pair of signals and is the average over the theta (2–6 Hz) or gamma (30–50 Hz) band. Paired signals are sorted according to the time of peak coherence relative to FO. (C) Histograms of time of peak coherence for theta and gamma bands in MSf and SMf. Data pooled across training days and monkeys. (Inset) Histograms of time of peak gamma coherence (SMf and MSf) ranging from –1.5 and 1 s relative to FO. Green line indicates Gaussian mixture best model fit using two components. M, mean.
Fig. S11.
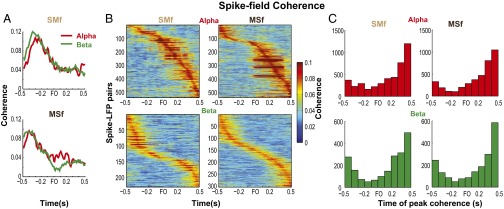
Modulation of spike–field coherence in the alpha and beta bands. (A) Spike–field coherence of a paired signal in SMf and another in MSf in the alpha and beta bands. (B) Spike–field coherence of neuronal pairs (rows) that showed significant task modulation of coherence in the alpha (Top) and beta (Bottom) bands. Color represents the magnitude of coherence, and the spike–LFP pairs were sorted according to the time of peak coherence relative to FO. Shown for SMf (left column) and MSf (right column). Data from D5 of monkey Y. (C) Histograms of time of peak coherence for alpha and beta bands in SMf and MSf. Data pooled across sampled training days and monkeys.
Fig. S12.
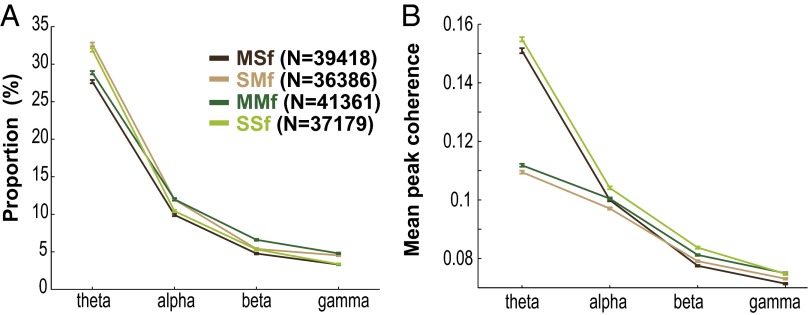
Properties of spike–field coherence. (A) Proportion of paired signals with significant modulation of spike–field coherence (mean, 1 SEM). Shown for each frequency band and network (SMf, SIo spikes with MIo LFPs; MSf, MIo spikes with SIo LFPs; MMf, MIo spikes with MIo LFPs; and SSf, SIo spikes with SIo LFPs). N corresponds to the total number of paired signals evaluated for significant modulation of coherence. (B) Mean peak coherence. Error bars indicate ±1 SEM (based on a binomial distribution assumption). Note that the proportion and the peak coherence were comparable between intraareal (MMf and SSf) and interareal (MSf and SMf) networks.
Fig. S13.
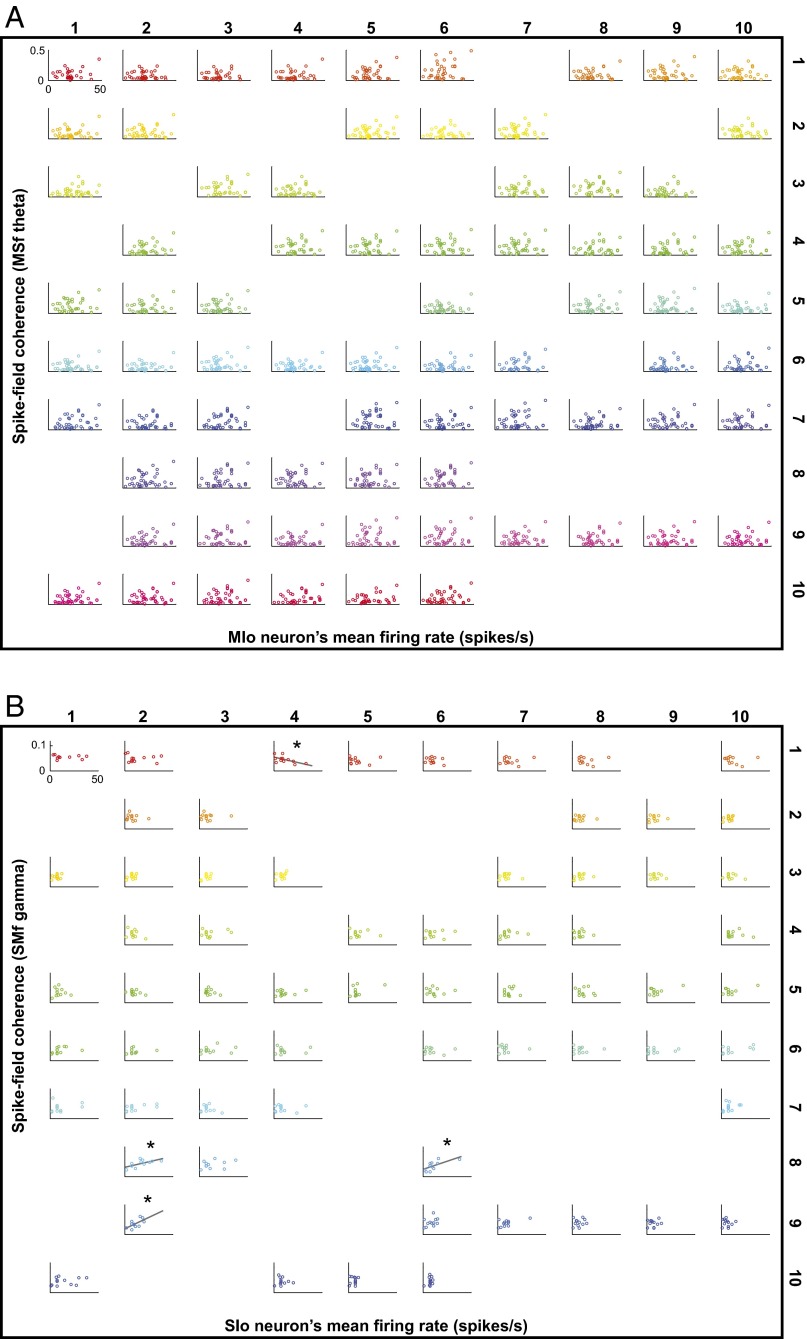
Relation between firing rates and spike–field coherence. (A) Map of the theta spike–field coherence in MSf recorded from the 10 × 10 Utah array. Each subplot illustrates the relationship of the firing rates of many different MIo neurons to the coherence between these neurons and a single SIo LFP. The position of the subplot corresponds to the electrode from which SIo LFPs were recorded (i.e., 74 subplots correspond to 74 electrodes). A dot in each subplot represents the mean firing rate of one MIo neuron plotted against the magnitude of its coherence with a single SIo LFP. Shown only for paired signals that showed significant coherence. For all subplots, mean firing rates and coherence were calculated for –0.3 to 0.2 s relative to FO, and same x and y axes were used. The linear fit of rates to coherence was not significant for any LFP channels (P > 0.10). Data from D5 of monkey Y. Similar results were obtained from other time windows, other days, for SIo neurons in SMf, and for monkey B. (B) As in A, but for gamma spike–field coherence in SMf. Firing rates correspond to SIo neurons. Data from D3 of monkey Y. For this dataset, there were 4 out of 65 electrodes that showed significant linear fit (*P < 0.05, gray line). Similar results were obtained from other time windows, other days, for MIo neurons in MSf, and for monkey B.
Table S1.
Properties of a two-component Gaussian mixture model fit to the distributions of time-of-peak gamma coherence
| Paired signals | Mixing proportions* | Means, s | SD | ||
| MSf | 0.14 | 0.86 | −0.36 | 0.34 | 0.015 |
| SMf | 0.19 | 0.81 | −0.37 | 0.32 | 0.017 |
| MMf | 0.17 | 0.83 | −0.37 | 0.35 | 0.013 |
| SSf | 0.24 | 0.76 | −0.35 | 0.32 | 0.02 |
The columns of the mixing proportions correspond to the columns of the mean time-to-peak coherence (in seconds). SD, SD of the shared covariance.
Bimodal Distribution of Phase at Peak Coherence Reveals Subnetworks.
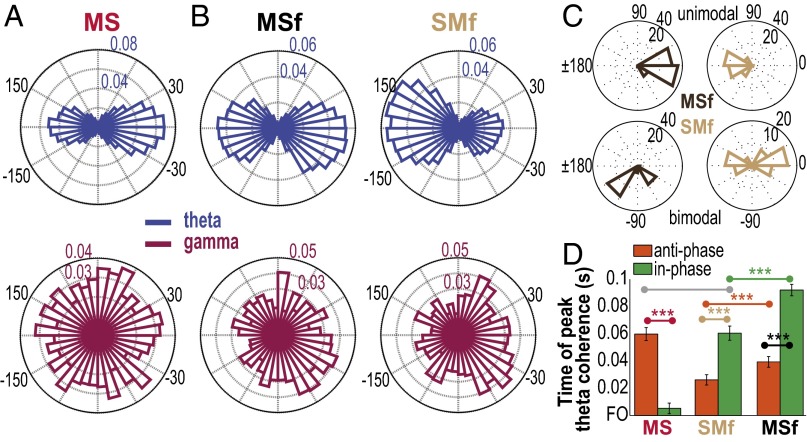
The coherence analyses also measure the phase difference, ϕxy(t), between two signals x and y. Two signals are in-phase when ϕxy(t) = 0°, or antiphase when ϕxy(t) = ±180°. The phase at peak coherence (Cϕ) may provide important information on the temporal organization of the coherent signals. For MS coherence, the distribution of Cϕ was bimodal in theta (Fig. 5A, blue, Rayleigh test for bimodal distribution, P < 0.00001; circular mean: –2° and 178°) but uniform in gamma (Fig. 5A, fuchsia, Rayleigh test, P > 0.10). The bimodal distribution of theta Cϕ could not be explained by paired neurons that modulated their firing rates in phase (i.e., both neurons increased or decreased their firing rate concurrently) or out of phase (i.e., one increased its firing rate while the other decreased its firing rate) with each other relative to force generation (SI Results, Fig. S14). A similar bimodal distribution of theta Cϕ was observed in MSf and SMf (Fig. 5B, blue; Rayleigh test for bimodal distribution, P < 0.00001; circular mean: MSf: –4° and 176°; SMf: –6° and 174° at 6 Hz), but the gamma Cϕ distribution in MSf and SMf was unimodal (Fig. 5B, fuchsia, Rayleigh test for unimodal distribution, P < 0.00001; circular mean: MSf: –31°; SMf: –26° at 40 Hz). The bimodal distribution of theta Cϕ was also found in the intraareal coherence MMf and SSf (Rayleigh test for bimodal distribution, P < 0.00001). These results suggest two subnetworks of coherent signals, i.e., in-phase and antiphase. Thus, we examined the theta Cϕ distribution of each neuron with all other neurons in MS to see whether there were distinct subpopulations of neurons. We found that, in MS, a larger number of neurons exhibited a significant bimodal theta Cϕ distribution (Rayleigh test for bimodal distribution, P < 0.05; mean and SEM across D1–D5; Y: 61 ± 13%; B: 40 ± 9%) than unimodal distribution (Rayleigh test for unimodal distribution, P < 0.05; Y: 7 ± 2%; B: 4 ± 1%). We found the reverse for MSf and SMf; over 50% of single neurons in MIo and SIo exhibited a single preferred Cϕ relation with all theta oscillations in MSf and SMf, respectively (Fig. 5C, top plots; Rayleigh test for unimodal distribution, P < 0.05), whereas a smaller number of single neurons showed two preferred Cϕ (Fig. 5C, bottom plots; Y: MSf, 17 ± 5%, SMf, 13 ± 3%; B: MSf, 21 ± 6%, SMf, 19 ± 5%). We verified that phase lags did not depend on specific LFP channels because Cϕ distributions of each LFP channel with all single units were also bimodal (0° and ± 180°). Last, we examined the temporal organization based on the Cϕ by comparing the time of peak coherence of paired signals whose Cϕ fell between –30° to 30° (i.e., the in-phase subnetwork) and between –150° to 150° (i.e., the antiphase subnetwork). In MS, time of peak coherence of the in-phase neurons was significantly earlier than that of the antiphase neurons (Fig. 5D, red; Mann–Whitney, P < 0.001). However, in both SMf and MSf, the antiphase subnetwork had significantly earlier time of peak coherence than the in-phase subnetwork (Fig. 5D, brown and black; P < 0.001). Time of peak coherence of both in-phase and antiphase subnetworks in SMf were significantly earlier than in MSf (Fig. 5D, green and orange; P < 0.001). These results indicate temporal differences based on Cϕ and the network: in-phase MS (n = 4,046) → antiphase SMf (n = 3,842) → antiphase MSf (n = 2,873) → antiphase MS (n = 2,895) and in-phase SMf (n = 2,229) → in-phase MSf (n = 3,217).
Fig. 5.
Bimodal distribution of phase at peak coherence reveals subnetworks in theta. (A) Distributions of phase at peak coherence at 6 Hz (theta) and 40 Hz (gamma) for MS coherence. Data pooled across D1 to D5 of both monkeys and normalized by the total count in each frequency. (B) As in A, for MSf and SMf. (C) Four examples of theta Cϕ distribution of a single neuron with all LFP channels. MIo or SIo neurons in MSf or SMf, respectively, exhibited either a unimodal (top plots) or bimodal (bottom plots) Cϕ distribution in theta. (D) Mean (±1 SEM error bars) time of peak theta coherence relative to FO of in-phase and antiphase subnetworks of MS, SMf, and MSf. Paired comparisons denoted by connected dots whose colors correspond to specific networks. ***P < 0.001.
Fig. S14.
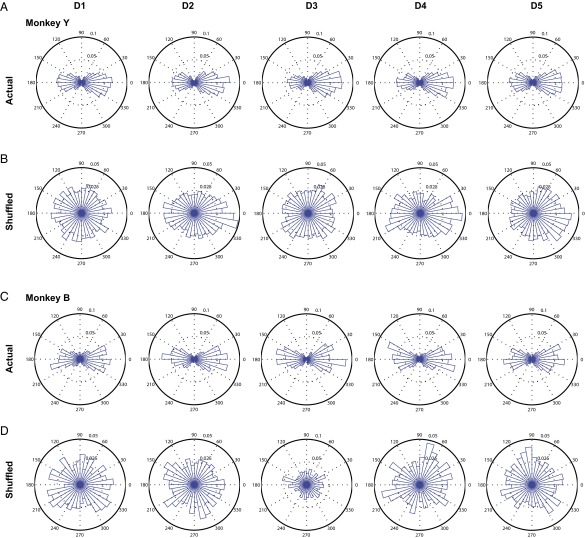
Bimodal distribution of phase at peak MS theta coherence cannot be explained by firing-rate patterns during movement. (A and B) Comparison between the distributions of phase at peak MS theta coherence from actual data versus shuffled data, respectively. Shown for monkey Y. (C and D) As in A and B, for monkey B.
Coherent Activity Follows a Spatiotemporal Pattern.
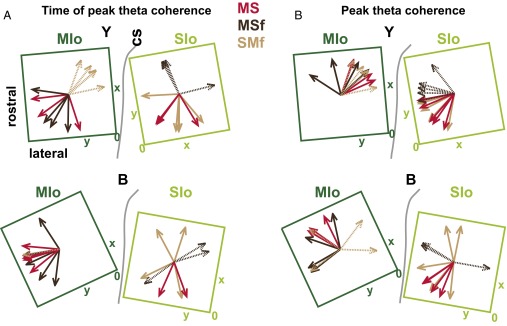
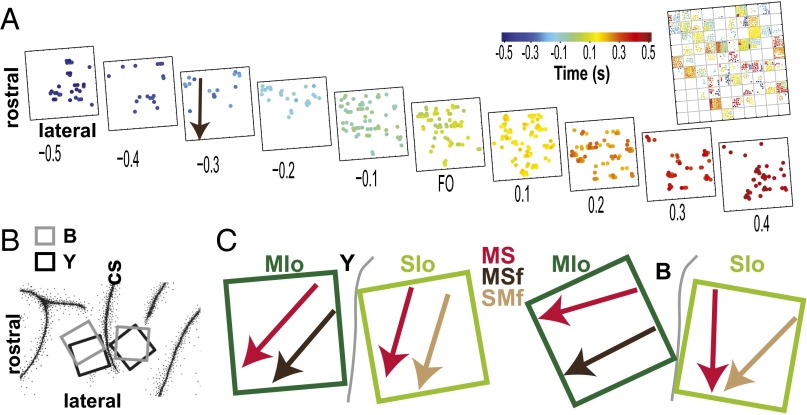
Fig. 3 A and B shows that coherent neuronal pairs do not reach their peak activity all at the same time. Does the spatial location of coherent neurons influence the timing and the magnitude of their peak coherence? We tested this in MS, MSf, and SMf for both theta and gamma coherence but only found significant results in theta (SI Results, Table S2, and Fig. S15). Fig. 6A maps the mediolateral progression of the time of peak theta MSf coherence on the MIo array from D3 of monkey Y; the spatial gradient was apparent from 0.3 s before force onset when MIo neurons located medially exhibited the earliest peak MSf coherence. At 0.4 s after force onset, MIo neurons that exhibited peak coherence were mostly at the lateral border. The mean (across training days) spatial gradient for time of peak theta coherence for MIo neurons in MS and MSf was initiated close to the central sulcus and progressed in the rostrolateral direction (Fig. 6 B and C, MIo array). This may be related to our previous finding that MIo neurons whose spiking activity led the tongue-protrusive force were located closer to the central sulcus than neurons whose spiking activity lagged the force (16). For SIo neurons in MS and SMf, the mean spatial gradient for time of peak theta coherence was from medial to lateral (Fig. 6C, SIo array). Because opening of the lips preceded tongue protrusion, the spatial gradient of the time of peak coherence may relate to the order in which sensory information was received from the lips and the tongue. Indeed, mechanoreceptive fields (RFs) of the lips are located at the medial border of SIo and RFs of the tongue at the lateral border of SIo (24). For the LFP component of MSf and SMf, time of peak coherence progressed medially and toward the central sulcus for MSf and medially for SMf (Fig. S14A, dashed arrows). The results suggest a spatiotemporal organization of coherence based on the temporal relation of MIo neurons’ spiking to tongue force and on the spatial features of MIo and SIo neurons’ RFs.
Table S2.
Summary of the results of linear regression of the time-of-peak or peak coherence by the location of neurons or LFPs in MIo or SIo
| Paired signals | Time-of-peak coherence | Peak coherence | ||||||
| Monkey Y | Monkey B | Monkey Y | Monkey B | |||||
| MS | ||||||||
| MIo neurons | ||||||||
| D1 | >0.1 | — | >0.1 | — | 3.2 × 10−11 | −25.1 | 0.078 | 34.6 |
| D2 | 9 × 10−3 | 121.0 | 1 × 10−3 | 82.3 | 5.7 × 10−8 | 8.8 | >0.1 | — |
| D3 | 0.016 | −166.9 | 6 × 10−4 | 103.6 | 4.2 × 10−24 | −59.5 | 0.02 | 30.1 |
| D4 | >0.1 | — | 4 × 10−5 | 60.4 | 3.2 × 10−30 | −71.0 | >0.1 | — |
| D5 | 3 × 10−5 | 92.0 | 1 × 10−5 | 78.8 | 2.4 × 10−11 | −24.1 | 0.02 | 1.2 |
| SIo neurons | ||||||||
| D1 | >0.1 | — | >0.1 | — | 1 × 10−6 | −178.9 | >0.1 | — |
| D2 | 0.055 | −138.2 | 0.004 | 165.9 | 8 × 10−9 | −140.6 | 4 × 10−10 | 134.6 |
| D3 | 0.084 | −136.2 | 0.017 | −149.7 | 9 × 10−10 | −166.8 | 6 × 10−8 | 153.1 |
| D4 | 0.062 | −68.9 | >0.1 | — | 3 × 10−6 | −115.5 | 0.004 | 167.8 |
| D5 | >0.1 | — | >0.1 | — | 1 × 10−6 | −134.7 | 0.023 | 134.0 |
| MSf | ||||||||
| MIo neurons | ||||||||
| D1 | >0.1 | — | >0.1 | — | 1 × 10−6 | −178.9 | >0.1 | — |
| D2 | 0.055 | −138.2 | 0.004 | 165.9 | 8 × 10−9 | −140.6 | 4 × 10−10 | 134.6 |
| D3 | 0.084 | −136.2 | 0.017 | −149.7 | 9 × 10−10 | −166.8 | 6 × 10−8 | 153.1 |
| D4 | 0.062 | −68.9 | >0.1 | — | 3 × 10−6 | −115.5 | 0.004 | 167.8 |
| D5 | >0.1 | — | >0.1 | — | 1 × 10−6 | −134.7 | 0.023 | 134.0 |
| SIo LFPs | ||||||||
| D1 | 8 × 10−6 | 106.39 | >0.1 | — | 6 × 10−22 | 118.0 | >0.1 | — |
| D2 | 1 × 10−7 | 107.66 | 6 × 10−10 | −49.1 | 2 × 10−18 | 154.5 | 4 × 10−19 | 67.5 |
| D3 | 0.090 | 4.47 | >0.1 | — | 3 × 10−15 | 169.0 | 6 × 10−5 | 71.9 |
| D4 | >0.1 | — | 0.001 | 136.1 | 2 × 10−9 | 161.2 | 3 × 10−4 | −90.3 |
| D5 | 0.052 | 101.67 | 0.012 | −62.9 | 1 × 10−7 | −177.7 | >0.1 | — |
| SMf | ||||||||
| MIo LFPs | ||||||||
| D1 | 0.003 | −83.1 | >0.1 | — | 3 × 10−25 | −41.8 | >0.1 | — |
| D2 | 0.048 | −54.3 | >0.1 | — | 1 × 10−54 | −58.4 | 10 × 10−4 | 31.6 |
| D3 | 1 × 10−11 | −24.8 | >0.1 | — | 4 × 10−75 | −53.1 | 7 × 10−5 | −62.1 |
| D4 | 1 × 10−9 | −43.46 | 0.003 | 74.4 | 8 × 10−31 | −53.3 | 7 × 10−8 | −116.7 |
| D5 | 8 × 10−6 | −53.1 | >0.1 | — | 4 × 10−45 | −44.5 | 0.087 | 101.4 |
| SIo neurons | ||||||||
| D1 | 2 × 10−7 | 173.2 | 0.006 | 37.97 | 10 × 10−11 | −175.7 | 2 × 10−6 | −176.1 |
| D2 | 2 × 10−21 | −100.1 | 4 × 10−30 | −150.4 | 2 × 10−18 | −143.3 | 6 × 10−6 | 21.6 |
| D3 | 1 × 10−16 | −60.5 | 1 × 10−9 | −8.1 | 2 × 10−27 | −173.9 | 1 × 10−8 | 109.3 |
| D4 | 1 × 10−18 | −104.9 | 1 × 10−14 | 125.9 | 3 × 10−26 | −110.4 | 5 × 10−9 | 150.2 |
| D5 | 3 × 10−32 | −100.99 | 1 × 10−8 | −157.8 | 9 × 10−23 | −161.9 | 3 × 10−15 | −1.3 |
P value and angular direction (in degrees) of the linear relation shown for each training day (D1–D5) of each monkey. Zero-degree reference for the angular values is found in Fig. S15. Shown for MIo and SIo neurons in MS, for MIo neurons and SIo LFPs in MSf, and for SIo neurons and MIo LFPs in SMf.
Fig. S15.
Spatial organization of interareal coherence. (A) Direction of the linear relations for time of peak theta coherence (P < 0.1), respectively, for each training day of monkeys Y and B. Arrow colors, network; solid lines, neuron; dashed lines, LFPs; 0, zero degree reference for the angular values (Table S1) computed as the inverse tangent of the two linear coefficients, y and x. (B) As in A, for peak theta coherence.
Fig. 6.
Coherent activity follows a spatiotemporal pattern. (A) Square panels represent a map of the time of peak theta MSf coherence per position of each MIo neuron on the microelectrode array per 0.1-s block (monkey Y, D3). The orientation of the panel is matched to the array location on the cortex. The color of each dot represents the time of peak coherence relative to FO, and the positions of the dots have been jittered to show all individual MSf coherence values at each electrode. Arrow represents the direction of the linear relation between the time of peak coherence and the location of neurons on the microelectrode array. [Inset (Top Right)] All of the times of peak coherence on the 10 panels are plotted together in one panel to show the varied times of peak coherence (colored squares) for each electrode (area delineated by gray lines). (B) Location of the microelectrode arrays in MIo and SIo of monkeys Y and B. cs, central sulcus. (C) Summary of the mean direction of the progression of the time of peak coherence of the neurons in MIo and SIo for MS, MSf, and SMf. Shown for monkeys B and Y.
Discussion
To our knowledge, this study provides the first documentation of the emergence of neuroplastic changes in the coherence between motor and somatosensory areas of the primate cortex during sensorimotor learning. Interareal coherence was frequency- and network-specific and exhibited a spatiotemporal organization. Such interactions may imply communication between sensory and motor cortical areas for integrating new sensory and motor events and for forming and retrieving memories during learning.
Coherent Networks Involve Multiple Frequencies.
The simultaneous presence of cortical rhythms in multiple frequencies in the arm sensorimotor cortex has been reported (25, 26), but (to our knowledge) this is the first documentation of frequency-specific coherent activity in the orofacial sensorimotor cortex. Larger and stronger sensorimotor networks occurred in theta, whereas sparser and weaker networks occurred in alpha/beta/gamma, consistent with the general feature of cortical rhythms that slow oscillations engage larger networks whereas fast oscillations engage more localized networks (27). Synchronous activity of local- and large-scale networks may be organized through multiple frequency bands for different cortical processes to operate at multiple temporal and spatial scales. Specifically, different functional demands at different phases of the task may require interareal coherence at different frequencies. Previous studies in the arm sensorimotor cortex suggest that theta synchrony is organized according to movement phases (28, 29). Thus, the high theta coherence at force onset may relate to the generation of tongue-protrusive force. In contrast, the high gamma coherence before and after force onset may relate to other processes such as sensory gating (30, 31), attention (18), and memory encoding/retrieval in association with theta coherence (32).
Reciprocal Interaction Between MIo and SIo.
The observed interactions between MIo and SIo may be explained by a common source of modulatory activity, such as from the thalamus and not due to direct cortico-cortical communication. There are abundant projections from thalamus to MIo and SIo (11, 33), and thalamic neurons have been found to oscillate at 6, 10, and 40 Hz and thus have the potential to generate an oscillatory drive to the cortex in these frequencies (32, 34, 35). However, oscillations may be initiated in the cortex and propagated to the thalamus, which then sends oscillations back to the cortex, thus increasing the cortico-thalamo-cortical resonance (36). This is in agreement with findings in rats, which have spike-and-wave discharges originating from SIo, and then propagating to the thalamus (37). Alternatively, our results may instead represent a direct interaction between MIo and SIo. The dense anatomical connections between MIo and SIo provide a substrate for coherent firing of neurons that may underlie the formation of neuronal assemblies (2, 38, 39). Thus, the increased proportion of coherent neurons may represent the new coupling of a motor output to specific sensory inputs as learning unfolds. Our results also suggest that this process involves reciprocal interactions; MIo modulates sensory processing in SIo (40, 41) and SIo transmits afferent information to MIo critical for successful task performance (5, 6, 42, 43). Because both MIo and SIo have bilateral orofacial representations, cross-hemisphere interactions in the orofacial sensorimotor area may share some properties of the intercortical coherence observed here.
Coherence Phase Reveals Temporal Organization of Subnetworks.
To our knowledge, this study is the first to report a bimodal distribution of phase at peak theta coherence in the sensorimotor cortex, i.e., in-phase (zero lag) and antiphase (near 180° lag). Zero-lag coherence has been suggested to result from either common input, reciprocal interaction, or a combination of both (44), whereas non–zero-lag coherence in gamma has been suggested to reflect interareal conduction delays in unidirectional interactions (45–47). Antiphase synchronization (15–30 Hz) between spikes in the parietal reach region and LFPs in the dorsal premotor cortex has been implicated in down-modulation of communication to selectively prevent transmission of movement-related information (48). Likewise, bimodal distributions of relative phases (0° and 180°) between LFPs (8–25 Hz) in the prefrontal and posterior parietal cortical areas has been suggested to represent specific patterns of coupling among neurons in these areas (49). Given that conduction delays within an area and even across areas are much smaller than the half period of a theta cycle, the antiphase relations in theta coherence found here are likely not due to conduction delays but may represent different populations of MIo neurons whose activity either leads or lags the force generation (16, 49) or a down-modulation of communication between MIo and SIo to prevent transmission of irrelevant sensory or movement-related information (48). The results further refine the understanding of the temporal sequence of coherent activity between MIo and SIo and suggest that cortico-cortical coherence may use phase to organize the activity of neuronal assemblies at different timescales or for segregating feedforward and feedback influences so that orofacial sensorimotor behaviors using different muscles and motor patterns are appropriately coordinated during learning.
Methods
Subjects.
All experiments were performed in two adult male rhesus macaques (Macaca mulatta), B (10 kg) and Y (12 kg). All protocols were approved by the University of Chicago Animal Care and Use Committee and complied with the National Institutes of Health Guide for the Care and Use of Laboratory Animals (50).
Behavioral Task.
We used a long-term learning paradigm wherein the subjects were exposed to the same behavioral task parameters over days until subjects achieve a success rate >75% consistently for 3 d (16). Monkeys were trained to protrude the tongue onto a force transducer and apply isometric force at the level cued by target positions. Fig. 1A illustrates the sequence of events in a trial. Detailed description of the task can be found in SI Methods. The behavioral program was written using Spike2 software (Cambridge Electronic Design). Force transducer (Revere Transducers; mode 462-D3-2-10P1R) signals and the behavioral event logs and time stamps were recorded at 2 kHz and stored using a Power 1401 data acquisition system (Cambridge Electronic Design). User-designed pulse signals were generated to mark behavioral events and were sent to the neural data acquisition systems for off-line synchronization of time stamps across the different data acquisition systems.
Further details are available in SI Methods.
SI Methods
Description of the Behavioral Task.
The trial started with the appearance of a cursor that represented the amplitude of the tongue-protrusive force applied on the transducer. After a random period between 0.75 and 1.25 s from trial start, the base target window appeared to cue the monkey to keep the cursor within the base target window by generating force between 1 and 15 g for a random hold period between 0.5 and 1 s. Upon successful hold at the base target, the force target window appeared to signal the monkey to move the cursor into the force target window. The force target was set at 50 g (D1–D3) or 80 g (D4 to D5), and the size of the force target window corresponded to a range of ±30 g from the required force level. To achieve success, monkey had to generate a force of at least 20 g (for 50-g target) or 50 g (for 80-g target) within the allotted time (5 s). Because there was no requirement to hold the force within the force target range, a trial was still successful even when the force exceeded the range. To indicate success, the force target window changed color and the monkey immediately received a juice reward. We set an intertrial interval of 3 s.
Electrophysiology.
Under general anesthesia, each monkey was chronically implanted with two silicon-based arrays of 100 microelectrodes (BlackRock Microsystems), one in MIo and one in SIo of the left hemisphere. The microelectrodes on the array were separated from their immediate neighbors by 400 μm and their length was 1.0 mm for all implanted arrays except for one array that was 1.5 mm in length (MIo of monkey Y). Implantation sites were verified based on surface landmarks and exhibited evoked responses from the tongue and fingers following monopolar surface stimulation of MIo (50 Hz, 200-µs pulse duration, 2–5 mA) during the surgical procedure. Signals from both arrays were amplified with a gain of 5,000, simultaneously recorded digitally (14 bit) with a sampling rate of 30 kHz, and hardware-filtered between 0.3 and 7.5 kHz (Cerebus acquisition systems; BlackRock Microsystems). This was followed by digital bandpass filtering for spikes (0.25–7.5 kHz) and for LFPs (0.3–250 Hz). LFPs were then resampled at 1 kHz. Spike waveforms were stored and sorted off-line using Off-line Sorter (Plexon). Data from array channels with no signal or with large amounts of 60-Hz line noise were excluded.
Data Analysis.
We performed all of the analyses for each dataset as described below. Results were pooled across all datasets (five datasets per monkey) whenever appropriate. Only successful trials were used in the analyses. We included only task-modulated neurons and LFP channels with task-modulated neurons, i.e., neurons whose mean firing rate during the movement epoch (force onset to 0.5 s after) differed significantly from the mean firing rate during a hold period of 0.5 s before target onset until target onset (paired t test, P < 0.01). Of the total number of neurons recorded from both monkeys (MIo: n = 989; SIo: n = 906), 80% (n = 793) of MIo neurons and 72% (n = 650) of SIo neurons were task modulated. LFP channels included in the analyses were 576 for MIo and 528 for SIo (pooled across monkeys and sampled training days). Coherence was analyzed by using the multitapers method of the Chronux Toolbox (51, 52). Coherence, , is a frequency-domain representation of the cross-correlation between two signals, i.e., the raw (unsmoothed) spike trains of neurons x and y for spike–spike coherence, and the raw (unsmoothed) spike trains of neurons x and the LFPs of channel y for spike–field coherence. It is calculated as the cross-spectrum, , normalized by the geometric mean of their autospectra, , respectively, , where is a complex number whose modulus corresponds to the degree of coherence (0–1) and the phase as the relative phase difference between the two spike trains. We used a 0.5-s sliding window with 0.01-s steps and applied a time-bandwidth product of 3 and 5 orthogonal Slepian tapers to the first 100 trials. To determine the statistical significance of the coherence, we calculated the coherence between paired signals by shuffling the trials on one of the signals for the time window of the peak coherence. Trial shuffling was tested with 1,000 and 10,000 repetitions which yielded similar results. Since trial shuffling with 1,000 and 10,000 repetitions yielded similar results, we reported the results for trial shuffling with 1,000 repetitions. Paired signals with peak coherence that exceeded the highest 49th coherence amplitude obtained from shuffling were deemed significant (P < 0.05). To address the concern that coherence between pairs of neurons is not independent, we also performed the same analyses on unique pairs (i.e., no two neuronal pairs have a common neuron) from each dataset and found similar results. The unique pairs (i.e., no two neuronal pairs have a common neuron) were determined once by arranging MIo/SIo neurons in ascending order of the electrode number they were recorded from. We first paired, for example, unit MIo-1 to unit SIo-1. Then, we paired the next unit MIo-2 with another SIo neuron that had not been paired previously with a MIo neuron. To evaluate spatial patterns of coherence, we performed a multivariate linear regression with x and y coordinates of the electrode on which a MIo or SIo neuron was recorded as the predictors and the time of peak coherence (or peak coherence magnitude) as the response variable. Note that a single neuron contributes multiple values to the regression because it is coherent with many other neurons. Regression of the time of peak coherence was weighted by the peak coherence. We then derived the orientation of the significant linear gradient by computing the inverse tangent of the coefficients. Circular statistics was performed with CircStat (53). We used the nonparametric Kruskal–Wallis one-way analysis of variance and the Tukey–Kramer test for post hoc multiple paired comparison with significance level set at P < 0.05, unless otherwise noted. All other analyses were performed using built-in and user-defined functions in Matlab (Mathworks). The data will be made available upon request.
SI Results
Cross-Validation of the Time of Peak Coherence.
We applied a cross-validation approach to verify the results of the shuffling test that determined the paired signals with significant modulation of coherence. The cross-validation involved determining the time of peak coherence on a training subset and then testing the significance of the peak value at that time on a test subset. Specifically, we took a subset (50%) of the paired signals that showed significant coherence and determined their mean time of peak coherence. We then tested the remaining dataset for significance of the coherence at this time of peak coherence using the shuffling method. This method addresses the issue of bias because the time of peak coherence to test for significance was predetermined on the training set. We found significant proportions of paired neurons from a test subset exhibited coherence above chance level at the time of peak coherence determined from a training subset (Figs. S4 and S5).
Local Field Potentials in MIo and SIo.
Fig. S9 A and B illustrates single-trial local field potentials (LFPs) (2–6 Hz) recorded simultaneously from electrodes in MIo and SIo. Spectral analysis of LFPs revealed dominant power in the theta (2–6 Hz) band, but weak power in the alpha (6–13 Hz), beta (15–30 Hz), and gamma (30–50 Hz) (Fig. S9C). Fig. S9D plots within-trial changes in the amplitude of the bandpass-filtered (zero-phase forward and reverse fourth-order Butterworth filter) and trial-averaged LFP signals recorded from a single channel in MIo and another in SIo.
For each LFP channel y and time point j over all trials, we quantified percent phase locking (PPL) of bandpass-filtered LFPs to the force onset (54, 55) as , where is the instantaneous phase and a(y,j) is the instantaneous amplitude of the Hilbert transform of the LFP signal. H is the Shannon entropy , where N is the number of bins (n = 4) and pk is the fraction of values of of the kth bin. . PPL is a measure of the trial-by-trial consistency of phase at a given time and is 0 when phases are randomly distributed and 100 if they are identical. The troughs (±180°) of the LFPs were found to be aligned to the force onset, suggesting phase locking of LFPs to behavioral events (55). Indeed, many single LFP channels in MIo and SIo exhibited phase locking across multiple frequencies (Fig. S9E). Typically in the theta band, SIo showed phase locking closer to force onset than MIo, but LFPs in most channels in MIo and SIo showed maximal phase locking after force onset (Fig. S9F). Such modulation of the amplitude and phase of the ongoing oscillations signifies evoked responses in the LFPs during the performance of the tongue protrusion task.
Bimodal Distribution of Phase at Peak Coherence (Cϕ).
One could argue that the bimodal distribution of MS Cϕ in the theta band might be due to some neuron pairs concurrently increasing or decreasing their firing (in-phase modulation) while other pairs modulate their firing rate out of phase (e.g., one neuron increases its firing rate while the other decreases its firing rate) . To test this, we examined the distribution of theta MS Cϕ obtained from shuffled trials. Shuffling the trials will break any coherence that is beyond the inherent rate modulation of neurons. Assuming that a neuron’s firing pattern (increasing or decreasing) was consistent across trials (because the movements are approximately repeated from trial to trial), the distribution of Cϕ from shuffled data would be bimodal if the coherence were to be explained by in-phase or out-of-phase firing-rate modulation. We found that this was not the case, i.e., the distribution of theta MS Cϕ in shuffled trials were not bimodal (Fig. S14).
Spatial Gradients of Peak Theta Coherence.
We also found significant spatial gradients with peak coherence (Table S2 and Fig. S15B); peak coherence of SIo neurons (SMf) and LFPs (MSf) progressed in the rostral direction and were highest near the central sulcus where SIo neuronal mechanoreceptive fields were smaller and less complex (56). Significant spatial gradients were observed for MIo neurons (MSf) and LFPs (SMf); however, the directions were not consistent across monkeys (Fig. S15B).
Acknowledgments
We thank Dr. Jason Lee, Kevin Brown, and Dr. Kate Murray for assistance with the experiments; Prof. Yali Amit for help with the statistical analyses; Dr. Aaron Suminski and Matt Best for helpful discussions; and the veterinary staff of the University of Chicago for animal care. This work was supported by CIHR Grant MOP-4918, NIH Grant R01 DE023816, and the University of Chicago Research Computing Center.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1600788113/-/DCSupplemental.
References
- 1.Singer W, Gray CM. Visual feature integration and the temporal correlation hypothesis. Annu Rev Neurosci. 1995;18:555–586. doi: 10.1146/annurev.ne.18.030195.003011. [DOI] [PubMed] [Google Scholar]
- 2.Fries P. A mechanism for cognitive dynamics: Neuronal communication through neuronal coherence. Trends Cogn Sci. 2005;9(10):474–480. doi: 10.1016/j.tics.2005.08.011. [DOI] [PubMed] [Google Scholar]
- 3.DeCoteau WE, et al. Learning-related coordination of striatal and hippocampal theta rhythms during acquisition of a procedural maze task. Proc Natl Acad Sci USA. 2007;104(13):5644–5649. doi: 10.1073/pnas.0700818104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Thorn CA, Graybiel AM. Differential entrainment and learning-related dynamics of spike and local field potential activity in the sensorimotor and associative striatum. J Neurosci. 2014;34(8):2845–2859. doi: 10.1523/JNEUROSCI.1782-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Brovelli A, et al. Beta oscillations in a large-scale sensorimotor cortical network: Directional influences revealed by Granger causality. Proc Natl Acad Sci USA. 2004;101(26):9849–9854. doi: 10.1073/pnas.0308538101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Witham CL, Wang M, Baker SN. Corticomuscular coherence between motor cortex, somatosensory areas and forearm muscles in the monkey. Front Syst Neurosci. 2010;4:38. doi: 10.3389/fnsys.2010.00038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Murthy VN, Fetz EE. Coherent 25- to 35-Hz oscillations in the sensorimotor cortex of awake behaving monkeys. Proc Natl Acad Sci USA. 1992;89(12):5670–5674. doi: 10.1073/pnas.89.12.5670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sessle BJ. Mechanisms of oral somatosensory and motor functions and their clinical correlates. J Oral Rehabil. 2006;33(4):243–261. doi: 10.1111/j.1365-2842.2006.01623.x. [DOI] [PubMed] [Google Scholar]
- 9.Avivi-Arber L, Martin R, Lee JC, Sessle BJ. Face sensorimotor cortex and its neuroplasticity related to orofacial sensorimotor functions. Arch Oral Biol. 2011;56(12):1440–1465. doi: 10.1016/j.archoralbio.2011.04.005. [DOI] [PubMed] [Google Scholar]
- 10.Huang CS, Hiraba H, Sessle BJ. Input-output relationships of the primary face motor cortex in the monkey (Macaca fascicularis) J Neurophysiol. 1989;61(2):350–362. doi: 10.1152/jn.1989.61.2.350. [DOI] [PubMed] [Google Scholar]
- 11.Hatanaka N, Tokuno H, Nambu A, Inoue T, Takada M. Input-output organization of jaw movement-related areas in monkey frontal cortex. J Comp Neurol. 2005;492(4):401–425. doi: 10.1002/cne.20730. [DOI] [PubMed] [Google Scholar]
- 12.Kuypers HG. Some projections from the peri-central cortex to the pons and lower brain stem in monkey and chimpanzee. J Comp Neurol. 1958;110(2):221–255. doi: 10.1002/cne.901100205. [DOI] [PubMed] [Google Scholar]
- 13.Lin LD, Sessle BJ. Functional properties of single neurons in the primate face primary somatosensory cortex. III. Modulation of responses to peripheral stimuli during trained orofacial motor behaviors. J Neurophysiol. 1994;71(6):2401–2413. doi: 10.1152/jn.1994.71.6.2401. [DOI] [PubMed] [Google Scholar]
- 14.Murray GM, Sessle BJ. Functional properties of single neurons in the face primary motor cortex of the primate. I. Input and output features of tongue motor cortex. J Neurophysiol. 1992;67(3):747–758. doi: 10.1152/jn.1992.67.3.747. [DOI] [PubMed] [Google Scholar]
- 15.Arce FI, Lee JC, Ross CF, Sessle BJ, Hatsopoulos NG. Directional information from neuronal ensembles in the primate orofacial sensorimotor cortex. J Neurophysiol. 2013;110(6):1357–1369. doi: 10.1152/jn.00144.2013. [DOI] [PubMed] [Google Scholar]
- 16.Arce-McShane FI, Hatsopoulos NG, Lee J-C, Ross CF, Sessle BJ. Modulation dynamics in the orofacial sensorimotor cortex during motor skill acquisition. J Neurosci. 2014;34(17):5985–5997. doi: 10.1523/JNEUROSCI.4367-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Boudreau SA, et al. Features of cortical neuroplasticity associated with multidirectional novel motor skill training: A TMS mapping study. Exp Brain Res. 2013;225(4):513–526. doi: 10.1007/s00221-012-3391-2. [DOI] [PubMed] [Google Scholar]
- 18.Fell J, Axmacher N. The role of phase synchronization in memory processes. Nat Rev Neurosci. 2011;12(2):105–118. doi: 10.1038/nrn2979. [DOI] [PubMed] [Google Scholar]
- 19.Siegel M, Donner TH, Engel AK. Spectral fingerprints of large-scale neuronal interactions. Nat Rev Neurosci. 2012;13(2):121–134. doi: 10.1038/nrn3137. [DOI] [PubMed] [Google Scholar]
- 20.Menzer DL, Rao NG, Bondy A, Truccolo W, Donoghue JP. Population interactions between parietal and primary motor cortices during reach. J Neurophysiol. 2014;112(11):2959–2984. doi: 10.1152/jn.00851.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mitzdorf U. Current source-density method and application in cat cerebral cortex: Investigation of evoked potentials and EEG phenomena. Physiol Rev. 1985;65(1):37–100. doi: 10.1152/physrev.1985.65.1.37. [DOI] [PubMed] [Google Scholar]
- 22.Katzner S, et al. Local origin of field potentials in visual cortex. Neuron. 2009;61(1):35–41. doi: 10.1016/j.neuron.2008.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lepage KQ, Kramer MA, Eden UT. The dependence of spike field coherence on expected intensity. Neural Comput. 2011;23(9):2209–2241. doi: 10.1162/NECO_a_00169. [DOI] [PubMed] [Google Scholar]
- 24.Huang CS, Hiraba H, Murray GM, Sessle BJ. Topographical distribution and functional properties of cortically induced rhythmical jaw movements in the monkey (Macaca fascicularis) J Neurophysiol. 1989;61(3):635–650. doi: 10.1152/jn.1989.61.3.635. [DOI] [PubMed] [Google Scholar]
- 25.Popivanov D, Mineva A, Krekule I. EEG patterns in theta and gamma frequency range and their probable relation to human voluntary movement organization. Neurosci Lett. 1999;267(1):5–8. doi: 10.1016/s0304-3940(99)00271-2. [DOI] [PubMed] [Google Scholar]
- 26.Jackson A, Spinks RL, Freeman TCB, Wolpert DM, Lemon RN. Rhythm generation in monkey motor cortex explored using pyramidal tract stimulation. J Physiol. 2002;541(Pt 3):685–699. doi: 10.1113/jphysiol.2001.015099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Buzsáki G, Draguhn A. Neuronal oscillations in cortical networks. Science. 2004;304(5679):1926–1929. doi: 10.1126/science.1099745. [DOI] [PubMed] [Google Scholar]
- 28.Feige B, Aertsen A, Kristeva-Feige R. Dynamic synchronization between multiple cortical motor areas and muscle activity in phasic voluntary movements. J Neurophysiol. 2000;84(5):2622–2629. doi: 10.1152/jn.2000.84.5.2622. [DOI] [PubMed] [Google Scholar]
- 29.Ohara S, et al. Increased synchronization of cortical oscillatory activities between human supplementary motor and primary sensorimotor areas during voluntary movements. J Neurosci. 2001;21(23):9377–9386. doi: 10.1523/JNEUROSCI.21-23-09377.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Cardin JA, et al. Driving fast-spiking cells induces gamma rhythm and controls sensory responses. Nature. 2009;459(7247):663–667. doi: 10.1038/nature08002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Engel AK, Fries P, König P, Brecht M, Singer W. Temporal binding, binocular rivalry, and consciousness. Conscious Cogn. 1999;8(2):128–151. doi: 10.1006/ccog.1999.0389. [DOI] [PubMed] [Google Scholar]
- 32.Ketz NA, Jensen O, O’Reilly RC. Thalamic pathways underlying prefrontal cortex-medial temporal lobe oscillatory interactions. Trends Neurosci. 2015;38(1):3–12. doi: 10.1016/j.tins.2014.09.007. [DOI] [PubMed] [Google Scholar]
- 33.Cerkevich CM, Qi H-X, Kaas JH. Thalamic input to representations of the teeth, tongue, and face in somatosensory area 3b of macaque monkeys. J Comp Neurol. 2013;521(17):3954–3971. doi: 10.1002/cne.23386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Steriade M, Gloor P, Llinás RR, Lopes de Silva FH, Mesulam MM. Report of IFCN Committee on Basic Mechanisms. Basic mechanisms of cerebral rhythmic activities. Electroencephalogr Clin Neurophysiol. 1990;76(6):481–508. doi: 10.1016/0013-4694(90)90001-z. [DOI] [PubMed] [Google Scholar]
- 35.Poulet JFA, Fernandez LMJ, Crochet S, Petersen CCH. Thalamic control of cortical states. Nat Neurosci. 2012;15(3):370–372. doi: 10.1038/nn.3035. [DOI] [PubMed] [Google Scholar]
- 36.Llinás RR. Intrinsic electrical properties of mammalian neurons and CNS function: A historical perspective. Front Cell Neurosci. 2014;8(November):320. doi: 10.3389/fncel.2014.00320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Polack P-O, Mahon S, Chavez M, Charpier S. Inactivation of the somatosensory cortex prevents paroxysmal oscillations in cortical and related thalamic neurons in a genetic model of absence epilepsy. Cereb Cortex. 2009;19(9):2078–2091. doi: 10.1093/cercor/bhn237. [DOI] [PubMed] [Google Scholar]
- 38.Gerstein GL, Bedenbaugh P, Aertsen MH. Neuronal assemblies. IEEE Trans Biomed Eng. 1989;36(1):4–14. doi: 10.1109/10.16444. [DOI] [PubMed] [Google Scholar]
- 39.Hayashi-Takagi A, et al. Labelling and optical erasure of synaptic memory traces in the motor cortex. Nature. 2015;525(7569):333–338. doi: 10.1038/nature15257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zagha E, Casale AE, Sachdev RNS, McGinley MJ, McCormick DA. Motor cortex feedback influences sensory processing by modulating network state. Neuron. 2013;79(3):567–578. doi: 10.1016/j.neuron.2013.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Petreanu L, et al. Activity in motor-sensory projections reveals distributed coding in somatosensation. Nature. 2012;489(7415):299–303. doi: 10.1038/nature11321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lee J-C, Sood M, Sessle BJ. The effects of orofacial sensory loss on tongue-protrusion task performance in monkeys. Soc Neurosci Abstr. 2011;37:809.13. [Google Scholar]
- 43.Lin LD, Murray GM, Sessle BJ. The effect of bilateral cold block of the primate face primary somatosensory cortex on the performance of trained tongue-protrusion task and biting tasks. J Neurophysiol. 1993;70(3):985–996. doi: 10.1152/jn.1993.70.3.985. [DOI] [PubMed] [Google Scholar]
- 44.Rajagovindan R, Ding M. Decomposing neural synchrony: Toward an explanation for near-zero phase-lag in cortical oscillatory networks. PLoS One. 2008;3(11):e3649. doi: 10.1371/journal.pone.0003649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bastos AM, Vezoli J, Fries P. Communication through coherence with inter-areal delays. Curr Opin Neurobiol. 2015;31:173–180. doi: 10.1016/j.conb.2014.11.001. [DOI] [PubMed] [Google Scholar]
- 46.Bosman CA, et al. Attentional stimulus selection through selective synchronization between monkey visual areas. Neuron. 2012;75(5):875–888. doi: 10.1016/j.neuron.2012.06.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Grothe I, Neitzel SD, Mandon S, Kreiter AK. Switching neuronal inputs by differential modulations of gamma-band phase-coherence. J Neurosci. 2012;32(46):16172–16180. doi: 10.1523/JNEUROSCI.0890-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Stetson C, Andersen RA. The parietal reach region selectively anti-synchronizes with dorsal premotor cortex during planning. J Neurosci. 2014;34(36):11948–11958. doi: 10.1523/JNEUROSCI.0097-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Dotson NM, Salazar RF, Gray CM. Frontoparietal correlation dynamics reveal interplay between integration and segregation during visual working memory. J Neurosci. 2014;34(41):13600–13613. doi: 10.1523/JNEUROSCI.1961-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. National Research Council (2011) Guide for the Care and Use of Laboratory Animals (National Academies Press, Washington, DC), 8th Ed.
- 51.Mitra PP, Pesaran B. Analysis of dynamic brain imaging data. Biophys J. 1999;76(2):691–708. doi: 10.1016/S0006-3495(99)77236-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Bokil HS, Pesaran B, Andersen RA, Mitra PP. A method for detection and classification of events in neural activity. IEEE Trans Biomed Eng. 2006;53(8):1678–1687. doi: 10.1109/TBME.2006.877802. [DOI] [PubMed] [Google Scholar]
- 53.Berens P. CircStat: A MATLAB toolbox for circular statistics. J Stat Softw. 2009;31(10):1–21. [Google Scholar]
- 54.Le Van Quyen M, et al. Comparison of Hilbert transform and wavelet methods for the analysis of neuronal synchrony. J Neurosci Methods. 2001;111(2):83–98. doi: 10.1016/s0165-0270(01)00372-7. [DOI] [PubMed] [Google Scholar]
- 55.Rubino D, Robbins KA, Hatsopoulos NG. Propagating waves mediate information transfer in the motor cortex. Nat Neurosci. 2006;9(12):1549–1557. doi: 10.1038/nn1802. [DOI] [PubMed] [Google Scholar]
- 56.Toda T, Taoka M. Hierarchical somesthetic processing of tongue inputs in the postcentral somatosensory cortex of conscious macaque monkeys. Exp Brain Res. 2002;147(2):243–251. doi: 10.1007/s00221-002-1239-x. [DOI] [PubMed] [Google Scholar]