Significance
Improved regimens for treatment of tuberculosis are needed to shorten the duration of treatment and combat the emergence of drug resistance. Selection of optimized regimens requires assessment of numerous combinations of existing drugs at multiple dose levels. This requirement presents a challenge because of the exponentially large number of combinations—NM for N doses of M drugs. We show here using a high-throughput macrophage model of Mycobacterium tuberculosis infection that a feedback system control technique can determine optimal drug treatment regimens by testing a relatively small number of drug–dose combinations. In an independent assay measuring intramacrophage killing of M. tuberculosis, the optimized regimens are superior to the current standard regimen.
Keywords: feedback system control, tuberculosis, drug combination optimization, Mycobacterium tuberculosis
Abstract
Tuberculosis (TB) remains a major global public health problem, and improved treatments are needed to shorten duration of therapy, decrease disease burden, improve compliance, and combat emergence of drug resistance. Ideally, the most effective regimen would be identified by a systematic and comprehensive combinatorial search of large numbers of TB drugs. However, optimization of regimens by standard methods is challenging, especially as the number of drugs increases, because of the extremely large number of drug–dose combinations requiring testing. Herein, we used an optimization platform, feedback system control (FSC) methodology, to identify improved drug–dose combinations for TB treatment using a fluorescence-based human macrophage cell culture model of TB, in which macrophages are infected with isopropyl β-D-1-thiogalactopyranoside (IPTG)-inducible green fluorescent protein (GFP)-expressing Mycobacterium tuberculosis (Mtb). On the basis of only a single screening test and three iterations, we identified highly efficacious three- and four-drug combinations. To verify the efficacy of these combinations, we further evaluated them using a methodologically independent assay for intramacrophage killing of Mtb; the optimized combinations showed greater efficacy than the current standard TB drug regimen. Surprisingly, all top three- and four-drug optimized regimens included the third-line drug clofazimine, and none included the first-line drugs isoniazid and rifampin, which had insignificant or antagonistic impacts on efficacy. Because top regimens also did not include a fluoroquinolone or aminoglycoside, they are potentially of use for treating many cases of multidrug- and extensively drug-resistant TB. Our study shows the power of an FSC platform to identify promising previously unidentified drug–dose combinations for treatment of TB.
The bacterium Mycobacterium tuberculosis (Mtb), the etiologic agent of tuberculosis (TB), is a global health problem that infects one-third of the world’s population (1). In 2014, 9.6 million people fell ill with TB, and 1.5 million died. Worldwide, TB ranks with HIV/AIDS as one of the greatest killers caused by a single infectious agent, and it is a major cause of mortality in HIV-positive people, accounting for one-quarter of all HIV-related deaths (1). The current standard of care for TB recommended by the World Health Organization is a multidrug regimen lasting 6–8 mo. This lengthy treatment is complicated by toxicities and poor compliance, which in turn, leads to drug resistance and disease relapse. The rise of multidrug-resistant TB further complicates treatment, requiring even longer regimens with second- and third-line drugs that are often more expensive, less effective, and/or more toxic (2, 3). More effective regimens that allow a shorter course of treatment would greatly facilitate monitoring and compliance and counter the emergence of drug resistance (4).
The current standard regimen for treatment of TB has evolved through a gradual stepwise process over several decades rather than by a systematic combinatorial analysis of a wide range of potential drug combinations. The first effective TB drug, streptomycin (STR), was introduced in 1944, but used as monotherapy, resistance to it developed readily. Combination therapy with additional drugs, such as isoniazid (INH), para-aminosalicylic acid (PAS), and ethambutol (EMB), reduced the problem of drug resistance, but lengthy treatments of 18–24 mo were required. In the 1970s, the addition of rifampicin (RIF) to the regimen of STR, INH, and EMB allowed a shortening of treatment to 9–12 mo. In the 1980s, it was found that replacing STR with pyrazinamide (PZA) yielded more rapid sterilization, allowing a shortening of treatment to 6–8 mo (5). Although a significant focus of current TB treatment research is the development of new TB drugs (4, 6), major hurdles are the identification and optimization of drug combinations and dosing regimens using the arsenal of known TB drugs. Such optimization holds promise for additional reductions in duration of treatment.
A major challenge to identifying optimal drug–dosage combinations is the exponentially large number of possible combinations: M drugs at N dose levels generates NM possible combinations; thus, for example, studying 14 TB drugs evaluated in this study at just five dose levels would require >6 billion tests. Identifying optimal combinations in such a large parametric space by a brute force approach is prohibitively laborious, expensive, and time-consuming. To solve these issues, we developed a first generation feedback system control (FSC.I) technique as a rational and systematic approach to identifying optimal drug–dose combinations from among millions of possible combinations. The FSC.I approach involves an iterative feedback search process, in which a stochastic search algorithm uses the experimental data obtained from each iteration to determine the drug–dose combinations to be tested on the subsequent iteration. Multiple FSC.I studies have supported three key findings. First, likely because of synergies in mechanisms of action, the concentration needed for each drug in a combination is significantly lower than when the drug is used alone. Second, only 10–20 iterative tests are needed to identify an optimal combination among millions of possibilities, and third, a smooth quadratic surface represents the system response (efficacy and/or toxicity) plotted against drug doses (7–10). Consequently, a very small number of tested drug–dose combinations is sufficient to describe the system response and thus, converge to an optimum drug combination. Based on the key discovery of the quadratic response surface, we subsequently developed the second generation feedback system control (FSC.II) technology, a parallel search approach that can locate the best drug–dose combinations from billions of choices, dramatically reducing the number of iterations required for drug–dose optimization and the time, effort, and cost for doing so compared with both FSC.I and conventional approaches (11). The power of the FSC.II platform is its capability of simultaneously identifying the optimal drug ratios for each drug in a combination and rank ordering all such optimized drug combinations by efficacy; whereas FSC.I was practicable for evaluation of a small number of drugs (≤5 in practice), FSC.II was readily amenable to evaluation of large numbers of drugs (≥10). Key advantages of the FSC approach are that it is output-driven and thus, does not require any knowledge or assumptions about the biology of the system and that it greatly reduces the number of experimental drug combinations that must be tested (11). The previously developed FSC.I platform has been used to identify optimal drug regimens in several other biological systems, including antiretroviral therapy for HSV (12), and the FSC.II platform has been applied to identifying drug combinations for cancer chemotherapy (13). However, neither the FSC.I platform nor the FSC.II platform has been used previously for evaluation of antibacterial drug combination therapy. We do so herein for the first time, to our knowledge, and because we are using the more powerful FSC.II platform, we are able to model an exceptionally large collection of drugs.
In this study, we have applied the FSC.II platform to a high-throughput macrophage cell culture model of TB using M. tuberculosis that expresses isopropyl β-D-1-thiogalactopyranoside-inducible green fluorescent protein (Mtb-iGFP). Using this model, in only a screening test and three iterations, we identified the most efficacious 3- and 4-drug combinations for TB treatment as well as the optimal drug ratios for each drug within each of these combinations from among 1,365 possible 3- and 4-drug combinations of 14 different TB drugs. We then tested the most efficacious optimized combinations in a macrophage cell culture system using a cfu-based assay to verify Mtb killing.
Materials and Methods
TB Drugs.
Anti-TB drugs amoxicillin/clavulanate (AMC), clofazimine (CLZ), cycloserine (CYS), EMB, INH, linezolid (LZD), moxifloxacin (MXF), PAS, prothionamide (PRO), PZA, RIF, and STR were purchased from Sigma-Aldrich. PA-824 (PA824) and TMC-207 (TMC) were provided by the Global Alliance for TB Drug Development, and SQ-109 (SQ109) was provided by Sequella, Inc. The various FSC.II experimental regimens, the 1970s standard regimen (INH, RIF, EMB, and STR), and the 1980s standard regimen (INH, RIF, EMB, and PZA) were mixed in 96-well deep-well plates using the Microlab STAR Line Liquid Handling Workstation (Hamilton) operated by Venus One software. A list of all TB drugs tested in this study and their abbreviations are shown in Table 1.
Table 1.
Abbreviations of TB drugs tested in this study
| Abbreviation | Drug |
| AMC | Amoxicillin/clavulanate |
| CLZ | Clofazimine |
| CYS | Cycloserine |
| EMB | Ethambutol |
| INH | Isoniazid |
| LZD | Linezolid |
| MXF | Moxifloxacin |
| PA824 | PA-824 |
| PAS | Para-aminosalicylic acid |
| PRO | Prothionamide |
| PZA | Pyrazinamide |
| RIF | Rifampicin |
| SQ109 | SQ-109 |
| TMC | TMC-207 |
| STR | Streptomycin |
| SR70 | Standard regimen 1970s (INH, RIF, EMB, and STR) |
| SR80 | Standard regimen 1980s (INH, RIF, EMB, and PZA) |
Preparation of Mtb Bacteria.
Mtb Erdman strain (ATCC#35801; ATCC) and Mtb-iGFP (14) were used in the in vitro cfu-based killing assay and the fluorescence-based inhibition assay, respectively. The infecting inoculum was prepared by culturing a glycerol stock of the strain on 7H11 agar plates without antibiotic (Mtb) or with hygromycin (50 μg/mL)/kanamycin (15 μg/mL) (Mtb-iGFP). After incubation at 37 °C with 5% CO2 and 95% air for 10 d, bacterial lawns were scraped from the agar plates into RPMI-1640 supplemented with 20 mM Hepes. Bacterial aggregates were dispersed by sonication of the bacterial suspension in a water bath sonicator (Astrason) for eight periods of 15 s each, with cooling of the suspension in an ice bath in between sonications. Residual aggregates were removed by centrifugation at 200 × g for 10 min at 4 °C, and then, the remaining bacterial suspension in the supernatant was centrifuged again under the same conditions; this process was repeated for a total of five times. OD of the final suspension was measured with a GENESYS 10S UV-Vis Spectrophotometer (Thermo Scientific) at 540 nm. Bacterial numbers in the final suspension were determined according to the equation OD at 540 nm of 0.1 = 2 × 108 bacteria/mL; 4 × 108 bacteria/mL were opsonized in RPMI with 10% (vol/vol) human serum type AB at 37 °C for 10 min, diluted 20-fold, and used to infect macrophages.
Preparation of Human Macrophages.
The human monocytic cell line THP-1 (TIB-202; ATCC) was grown in RPMI-1640 supplemented with 2 mM glutamine, 10% (vol/vol) heat-inactivated FBS, penicillin [100 International Units (IU)], and STR (100 μg/mL). Before use in infection experiments, the THP-1 cells were pelleted by centrifugation at 200 × g for 10 min at room temperature; resuspended in RPMI-1640 supplemented with 2 mM glutamine, 10% (vol/vol) heat-inactivated FBS, and 100 nM phorbol 12-myristate 13-acetate (PMA) without antibiotics; and seeded in 96-well glass-bottom microplates (Matrical) at a density of 1 × 105 cells per 200 μL per well for 3 d at 37 °C in a 5% CO2 and 95% air atmosphere.
Efficacy of TB Drug Combinations in Inhibiting Intramacrophage Mtb-iGFP Using Fluorescence-Based Assay with High-Throughput Imaging Analysis.
Monolayers of PMA-differentiated THP-1 cells were infected for 3 h with Mtb-iGFP at a ratio of 20:1 before incubating in medium with 1 mM IPTG and experimental TB drug combinations. Included in each 96-well plate were wells not infected with Mtb-iGFP (no infection control), wells to which the inducer IPTG was not added (no IPTG control), and wells to which TB drugs were not added (no drug control). All conditions were in triplicate with randomized well positions. The cultures were incubated for 4 d before fixing for 1 h in 4% paraformaldehyde in Dulbecco’s PBS (PBS). Cell nuclei were stained for 10 min with 1 μg/mL Hoechst 33342 in PBS containing 0.1% Tween 20. Monolayers were washed twice with PBS and imaged with an ImageXpress High-Throughput Epifluorescence Microscope (Molecular Devices) using a 10× objective lens. Three GFP and Hoechst epifluorescence images were acquired from nonoverlapping regions of each well using FITC and DAPI filter cubes, respectively. Automated image analysis was done using the granularity and count nuclei modules of MetaXpress (Molecular Devices) software to quantitate the integrated GFP fluorescence intensity and the number of macrophage nuclei, respectively, for each area imaged. Inhibition is defined by the following equation:
| [1] |
Efficacy of TB Drug Combinations in Killing Intramacrophage Mtb Using cfu-Based Assay.
Monolayers of PMA-differentiated THP-1 cells were infected for 90 min with Mtb at a ratio of 10:1, washed with RPMI, and incubated in medium with no drug (no drug control), the 1980s standard regimen (INH, RIF, EMB, and PZA), or experimental TB drug regimens at 37 °C in a 5% CO2 and 95% air atmosphere. The 1980s standard regimen and experimental TB drugs were administered at dosages of 1×, 4×, and 16×, where the 1× drug concentration was the 25% inhibition dose in the fluorescence assay (SI Appendix, Table S1). The cfu in the no drug control well were assayed at 90 min, 1 d, and 3 d to establish the amount of bacterial growth over the course of the assay, and cfu were assayed from all drug-treated wells at 1 and 3 d to assess drug efficacy. The cfu were assayed by lysing the infected macrophages with 0.1% SDS for 10 s, serially diluting the lysate, plating the dilutions on 7H11 0.4% charcoal agar, incubating the plates at 37 °C in a 5% CO2 and 95% air atmosphere for 4 wk, and counting the number of cfu of Mtb on each plate. Killing is defined by the following equation:
| [2] |
FSC.II Methodology.
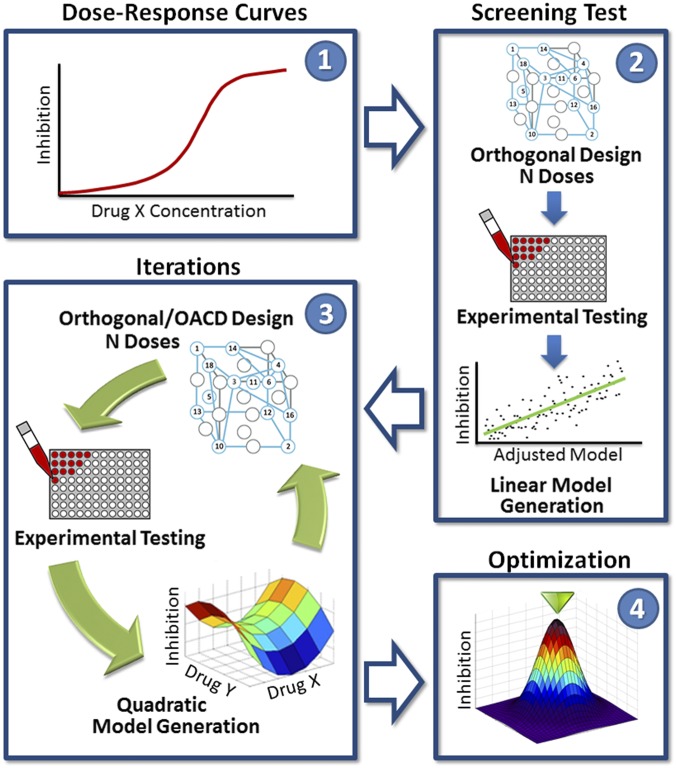
The protocol of the FSC.II methodology is shown in Fig. 1. In this study, drugs are the variables of interest, and the objective of FSC.II is to find the proper drug–dose combinations to optimize an output: Mtb inhibition in a fluorescence-based assay. During the first phase, a drug–dose response for each of the individual drugs is obtained to determine the concentration range of interest for each drug. The second phase, the screening test, uses a two-level orthogonal array experimental design to construct a first-order linear model that expresses the relationship between drug–dose combinations and Mtb inhibition. From the first-order linear model, the drugs with the greatest impact are identified for additional testing. In the third phase, a different experimental design tests the selected drugs from the screening test and constructs a quadratic model to describe the relationship between drug–dose combinations and Mtb inhibition. The quadratic model is used to identify synergistic and antagonistic drug–drug interactions, which helps determine the optimal drug combinations and their drug ratios; this third phase can be repeated in an iterative process, where a subset of drugs is selected to continue into the next iteration. The second and third phases depend on experimental designs, such as a two-level orthogonal array and a three-level orthogonal array central composite design that determine and narrow the pool of drugs to be examined (15). Lastly, during the fourth phase, in-depth analysis of the finalized second-order quadratic model from the third phase is used to construct a model surface describing the relationship between drug–dose combinations and Mtb inhibition. From this surface, the optimal drug combinations and their drug ratios are identified.
Fig. 1.
FSC.II schematic. The diagram depicts the FSC.II technique loop used for drug optimization with the fluorescence-based assay. The FSC.II methodology has four phases: (i) dose–response curve established for each drug (1), (ii) screening test with two-level orthogonal array design (results used to construct a first-order linear model; 2), (iii) iterations testing drug combinations based on orthogonal or orthogonal array central composite design (OACD) design (results used to construct a second-order quadratic model and surface model; 3); and (iv) optimization of the drug combinations and drug ratios from the final surface model constructed in phase 3 (4).
In the screening test, we used the experimental results obtained to derive a first-order linear model expressed as
| [3] |
where is the efficacy of combinatorial drugs or in this case, the percentage of inhibition; is the intercept term; is the th drug dosage; is the single-drug coefficient of the th drug; and is the interaction coefficient between the th and th drugs.
After the general equation was fitted, we performed a stepwise regression process, where terms from a generalized quadratic model were systematically added or removed in steps and the criteria to do so were the statistical significances of each term in explaining the response variable.
The stepwise regression was initialized with the first-order drug terms ( is the th drug dosage) and their estimated coefficients ( is the single-drug coefficient of the th drug). Interaction terms between drugs and their corresponding coefficients ( is the interaction coefficient between the th and th drugs) were sequentially added into the original initialized equation. The sequential order in which the interaction terms were added was based on the lowest P values (statistically significant) in F test variance comparisons between the original initialized equation (reference equation) and the subsequent equation with the added interaction term. Statistical significance was set to be P ≤ 0.05. After a synergistic term was added, the newly calibrated equation served as the reference equation to be used for the F-test comparisons with new interaction terms. The reference equation was updated stepwise after each F test with the added interaction term(s). This process was continued until all possible interaction terms were exhausted and all interaction terms were added that were found to be statistically significant in affecting the variances of the equations.
After the statistically significant interaction terms were added into the reference equation, first-order drug terms and their corresponding coefficients were removed sequentially from the reference equation. The reference equation was updated stepwise after each F test with the removed term(s). Similar F-test comparisons were made between the reference equation and equations with first-order drug terms removed. Two conditions had to be satisfied before removing the first-order drug term: (i) the drug was not in any of the added interaction terms, and (ii) the first-order drug term was statistically insignificant.
To evaluate the predictive power of the generated models, we calculated the adjusted R2 and correlation coefficients to assess how well the model predicted the observation while taking into account the number of drug and drug–drug interaction terms. Correlation coefficients (measures of the strength of the linear association between two variables ranging in value between zero and one) were then derived from the experimental inhibition values and projected inhibition values for the corresponding drug combinations; the closer the correlation coefficient was to one, the better the reference equation closely modeled the experimental inhibition values.
In phase 3, results from each iteration were fitted to a second-order quadratic model expressed as
| [4] |
where represents the percentage of inhibition, is the th drug dosage, is the intercept term, is the single-drug coefficient of the th drug, is the interaction coefficient between the th and th drugs, and is the quadratic coefficient for the th drug.
For phase 3, the stepwise regression is initialized with the first-order drug terms, interaction terms between drugs, and second-order drug terms, with their corresponding estimated coefficients. Interaction terms and second-order drug terms were removed sequentially based on highest P values in F-test variance comparisons between the reference equation and the subsequent equation with the removed interaction or second-order drug term.
Data Analysis.
The data collected for each FSC.II phase were analyzed and used for generating the regression models with MATLAB.
Results
Optimization of TB Drug Combinations by FSC.II Technique.
The FSC.II was carried out in four phases as summarized in Fig. 1 and as discussed below.
Phase 1: Establishment of Dose–Response Curve for Each Drug.
We developed a high-throughput assay suitable for testing the efficacy of TB drug combinations in inhibiting Mtb-iGFP in human macrophages in cell culture that is compatible with the FSC.II technique. This assay used automated microscopy for image acquisition and analysis, allowing quantitation of the inhibitory effect on Mtb of single and combinatorial anti-TB drugs. The assay relies on the capacity of IPTG to induce expression of GFP in live (but not dead) Mtb-iGFP, and the integrated green fluorescence intensity per THP-1 cell (enumerated by DAPI staining of macrophage nuclei) is quantified. Although there is a relatively minor 6–13% decrease in the number of DAPI-stained nuclei over the 4-d period of infection, the evaluation of bacterial green fluorescence intensity per nucleus corrects for this decrease. We selected and acquired 14 TB drugs for testing by the FSC.II technique, including first-line drugs (INH, RIF, PZA, EMB), second-line drugs (MXF, PAS, PRO, CYS, and TMC), third-line drugs (AMC, CLZ, and LZD), and experimental drugs in clinical trials (PA824 and SQ109). In addition, we studied STR as part of the control 1970s regimen (INH, RIF, EMB, and STR), and we studied the combination comprising the 1980s standard regimen (INH, RIF, EMB, and PZA) (5). During the first phase of the FSC.II methodology, a dose–response curve for each individual drug was established by serially diluting single drugs in culture medium containing the inducer IPTG and adding the solution to the monolayer of THP-1 macrophages infected with Mtb-iGFP. After 4 d of incubation, the extent of bacterial inhibition was quantitated by automated image acquisition and analysis of the infected monolayers. A direct relationship between the inhibition level and drug concentration was observed for all 14 drugs included in this study (SI Appendix, Fig. S1).
Phase 2: Screening Test.
The second phase of the FSC.II methodology, the screening test, used drug combinations identified by a two-level orthogonal array experimental design, which allowed for the generation of a first-order linear model that could be used to reduce the pool of 14 drugs for subsequent experiments. The initial pool of drugs consisted of AMC, CLZ, CYS, EMB, INH, LZD, MXF, PA824, PAS, PRO, PZA, RIF, SQ109, and TMC. The screening test, which consisted of 128 drug–dose combinations, evaluated 14 drugs in combinations at two different concentrations—no drug or the dose that resulted in 10% inhibition of Mtb-iGFP as defined in Eq. 1 (SI Appendix, Tables S1 and S3).
The stepwise regression terms and their coefficients, indicating the impact of each drug as an individual element as well as any potential drug–drug interactions, derived from the screening test were found to be as shown in SI Appendix, Table S2. Our ultimate goal was to identify drug combinations with the highest percentage of inhibition expressed as in Eq. 3 (Materials and Methods), and for each drug or drug–drug interaction, a positive coefficient reflected a higher percentage of inhibition, whereas a negative coefficient reflected a lower percentage of inhibition. However, during the screening test, the drug selection was not based on the coefficient values but was based on the significance of each term coefficient, which was indicated by each coefficient’s P value. From these results, the stepwise regression analysis eliminated the drugs CYS and INH, because there were no interaction terms involving them and their first-order terms were statistically insignificant; thus, no estimated coefficients are reported for these drugs. From the single-drug terms that were included in the model, it was noted that AMC, EMB, LZD, and MXF have P values greater than 0.05; thus, these drugs are candidates for being excluded from subsequent experiments based on the relatively low significance of their coefficient. Of these four drugs, AMC, LZD, and MXF have negative coefficients (i.e., they all had a negative impact on the desired outcome, decreasing the expected percentage inhibition). In contrast, EMB still had a positive coefficient (i.e., a positive impact on the desired outcome). Thus, EMB was retained for the following iteration. In addition, there were some synergistic interactions noted as positive coefficients, such as AMC–EMB, AMC–LZD, and LZD–MXF. However, these synergistic effects were not enough to overcome the negative impact generated by these individual drugs to the overall model; hence, AMC, LZD, and MXF were eliminated. There were also some antagonistic interactions noted as negative coefficients, such as CLZ–RIF, PA824–RIF, and PZA–RIF. However, RIF had a very high positive impact on the model, and thus, it was kept to further corroborate its negative interactions and investigate its contribution to the upcoming models.
In summary, five drugs (CYS, INH, AMC, LZD, and MXF,) of the original 14 drugs were eliminated. The remaining nine drugs (CLZ, EMB, PA824, PAS, PRO, PZA, RIF, SQ109, and TMC) proceeded to phase 3 (iteration 1).
Phase 3: Iteration 1.
Iteration 1 marks the beginning of phase 3 in the FSC.II methodology. The first iteration’s experimental design was based on a three-level orthogonal array central composite design array (16). It consisted of 155 drug–dose combinations evaluating nine drugs preselected by the screening test, with each drug being tested at 0×, 0.5×, or 1× dose, where the 1× dose represented the concentration of the drug that achieved 15% inhibition in the screening test (SI Appendix, Table S1). Results from this iteration, shown in SI Appendix, Table S4, were fitted to a second-order quadratic model (Eq. 4). The coefficients that were obtained to fit this equation based on the tested experimental design are shown in SI Appendix, Table S2.
Many four-drug combinations emerged from the fitted model to have a projected inhibition higher than the standard regimens from the 1970s and 1980s, which for comparison, were also subjected to the fluorescence-based assay (Tables 2 and 3). The top six four-drug combinations with projected inhibitions greater than 90% all included CLZ. In contrast, none of the top combinations included PAS.
Table 2.
Iteration 1: FSC.II-projected inhibitions for the top four-drug combinations
| No. | CLZ | EMB | PA824 | PRO | PZA | RIF | SQ109 | TMC | Inhibition* (%) |
| 1 | H | 0 | 0 | 0 | H | 0 | H | H | 98 |
| 2 | H | H | 0 | H | 0 | 0 | 0 | H | 96 |
| 3 | L | 0 | 0 | H | H | 0 | H | 0 | 94 |
| 4 | H | 0 | H | 0 | H | 0 | H | 0 | 94 |
| 5 | H | H | H | 0 | 0 | 0 | 0 | H | 93 |
| 6 | L | H | 0 | H | 0 | H | 0 | 0 | 93 |
H, 15% drug level; L, 7.5% drug level; 0, 0% drug level.
Projected.
Table 3.
Iteration 1: Experimental inhibitions of the standardregimens
| Regimen | INH | RIF | EMB | STR | PZA | Inhibition* (%) |
| SR70 | H | H | H | H | 0 | 88 |
| SR80 | H | H | H | 0 | H | 85 |
H, 15% drug level; 0, 0% drug level; SR70, standard regimen 1970s; SR80, standard regimen 1980s.
Experimental.
The selection of drugs to participate in the subsequent iteration was based on (i) the effect of each drug on the overall projected inhibition, which is based on the product of each drug’s concentration and its corresponding estimated coefficient as explained above, and (ii) the status of a drug for approval for use clinically in the United States and China. Consistent with its absence from the top four-drug combinations, PAS had a small effect on the model and was, thus, eliminated. PA824 had a positive impact over the model, but the experimental drug status of PA824 nominated it for removal from this first set of studies along with SQ109. It was also confirmed that RIF continued showing several negative interactions denoted as negative coefficients for the CLZ–RIF, PZA–RIF, RIF–SQ109, and RIF–TMC terms, but it was still considered valuable enough to be kept for the next iteration. Interestingly, plots of the different drug–drug interactions revealed that EMB and SQ109 seem to have very similar effects on the remaining drugs (SI Appendix, Fig. S2). This observation implied that the drugs have a similar mechanism of action and are, thus, interchangeable; indeed, SQ109 is an analog of EMB.
In summary, PAS was eliminated on account of its poor impact on efficacy, and PA824 and SQ109 were eliminated from this set of studies on account of their as yet unapproved status; CLZ, EMB, PRO, PZA, RIF, and TMC continued to iteration 2.
Phase 3: Iteration 2.
During the second iteration, six remaining drugs were tested in 50 drug–dose combinations at three different concentrations. Each drug was tested at 0×, 0.5×, or 1× dose, where the 1× dose represented the concentration of the drug that achieved 20% Mtb inhibition (SI Appendix, Tables S1 and S5). Individual drug performance and estimated drug–drug interactions are summarized in SI Appendix, Table S2. This iteration showed that RIF continued to have negative interactions with the remaining drugs (i.e., CLZ and TMC); thus, it was eliminated from the next iteration. The top six four-drug combinations obtained from modeling of the experimental dataset are listed in Tables 4 and 5. As in iteration 1, CLZ was present in all of the top six four-drug combinations.
Table 4.
Iteration 2: FSC.II-projected inhibitions for the top four-drug combinations
| No. | CLZ | EMB | PRO | PZA | RIF | TMC | Inhibition* (%) |
| 1 | H | 0 | H | H | 0 | H | 81 |
| 2 | H | M | 0 | H | 0 | H | 76 |
| 3 | H | 0 | H | L | 0 | H | 73 |
| 4 | H | 0 | H | H | H | 0 | 73 |
| 5 | H | 0 | 0 | H | L | H | 73 |
| 6 | H | M | H | 0 | 0 | H | 72 |
H, 20% drug level; M, 15% drug level; L, 10% drug level; 0, 0% drug level.
Projected.
Table 5.
Iteration 2: Experimental inhibitions of the standardregimens
| Regimen | INH | RIF | EMB | STR | PZA | Inhibition* (%) |
| SR70 | H | H | H | H | 0 | 71 |
| SR80 | H | H | H | 0 | H | 62 |
H, 20% drug level; 0, 0% drug level; SR70, standard regimen 1970s; SR80, standard regimen 1980s.
Experimental.
Phase 3: Iteration 3.
This iteration was the last iteration performed to identify optimal drug combinations. A pool of five drugs at five different concentrations was evaluated using a five-level orthogonal array experimental design (SI Appendix, Tables S1 and S6), resulting in 100 drug–dose combinations. Each drug was tested at 0×, 0.25×, 0.5×, 0.75×, or 1× dose, where the 1× dose represented the concentration of the drug that achieved 20% Mtb inhibition. Results from this experiment were fitted to a second-order quadratic model and are summarized in SI Appendix, Table S2.
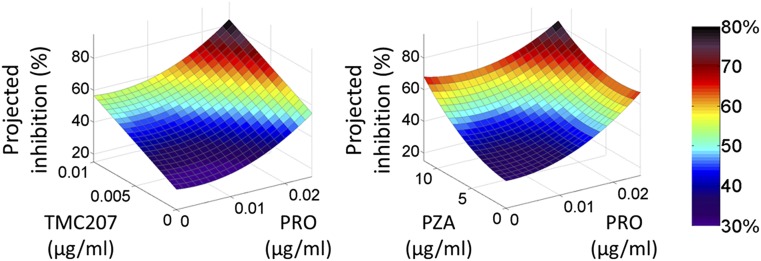
This iteration revealed two major drug–drug interactions—CLZ–TMC and PRO–PZA (both antagonistic). Phase 4 of the FSC.II methodology fully evaluates these drug–drug interactions as shown in Fig. 2. When Mtb inhibition is plotted against drug doses, it can be appreciated that, despite both drug–drug interactions being antagonistic, increasing the drug concentrations still yields a better projected inhibition because of the individual effect of each drug.
Fig. 2.
3D surface modeling of drug–drug interactions. Surface representations of drug–drug interactions obtained during phase 4 of the FSC.II methodology. Although the drug–drug interactions between both (Left) TMC and PRO and (Right) PZA and PRO are antagonistic, increasing the drug concentrations yields higher projected inhibitions because of the individual effect of each drug.
A summary of the best three- and four-drug combinations identified in iteration 3 are shown in Table 6. Although the highest inhibition achieved experimentally by a four-drug combination was 73% (SI Appendix, Table S6), the modeling indicated, with a slight increase in drug concentration for CLZ, EMB, PZA, and TMC, that it is possible to achieve 100% inhibition with any of the four-drug combinations out of the pool of five drugs in iteration 3.
Table 6.
Iteration 3: FSC.II-projected inhibition of the top three- and four-drug combinations
| Combination | CLZ | EMB | PRO | PZA | TMC | Projected inhibition (%) |
| 1 | 0.1 | 0.125 | 0.025 | 11.875 | 0 | ≥100 |
| 2 | 0.1 | 0.125 | 0.025 | 0 | 0.01 | ≥100 |
| 3 | 0.1 | 0.125 | 0 | 11.875 | 0.01 | ≥100 |
| 4 | 0.1 | 0 | 0.025 | 11.875 | 0.01 | ≥100 |
| 5 | 0 | 0.125 | 0.025 | 11.875 | 0.01 | ≥100 |
| 6 | 0 | 0.125 | 0.025 | 0 | 0.01 | 90 |
| 7 | 0.1 | 0 | 0.025 | 0 | 0.01 | 89 |
| 8 | 0.1 | 0.125 | 0.025 | 0 | 0 | 86 |
| 9 | 0.1 | 0 | 0.025 | 11.875 | 0 | 86 |
Concentration for each drug is expressed in micrograms per milliliter.
FSC.II-Projected Efficacy as a Function of Drug Ratio.
An important finding revealed by our analysis of the projected inhibitions calculated from the derived models was the importance of drug ratio. We were particularly interested in studying the ratios of drugs in the top combinations found in our FSC.II analysis. Tables 7–9 present analyses of three different drug combinations for which there are several possible ratios of the drugs.
Table 7.
Iteration 3: Drug ratio analysis for drug combination 1
| Drug ratio | CLZ | PRO | TMC | Projected inhibition (%) |
| 1 | 0.1 | 0.025 | 0.01 | 89 |
| 2 | 0.05* | 0.025 | 0.01 | 82 |
| 3 | 0.1 | 0.0125* | 0.01 | 62 |
| 4 | 0.05* | 0.025 | 0.005* | 68 |
Concentration for each drug is expressed in micrograms per milliliter.
Drug concentration is reduced by half.
Table 9.
Iteration 3: Drug ratio analysis for drug combination 3
| Drug ratio | CLZ | EMB | PZA | TMC | Projected inhibition (%) |
| 1 | 0.1 | 0.125 | 11.875 | 0.01 | 100 |
| 2 | 0.05* | 0.125 | 11.875 | 0.01 | 98 |
| 3 | 0.1 | 0.125 | 5.9375* | 0.01 | 80 |
| 4 | 0.05* | 0.0625* | 11.875 | 0.01 | 90 |
Concentration for each drug is expressed in micrograms per milliliter.
Drug concentration is reduced by half.
Table 8.
Iteration 3: Drug ratio analysis for drug combination 2
| Drug ratio | CLZ | EMB | PRO | TMC | Projected inhibition (%) |
| 1 | 0.1 | 0.125 | 0.025 | 0.01 | 100 |
| 2 | 0.05* | 0.125 | 0.025 | 0.01 | 98 |
| 3 | 0.1 | 0.125 | 0.0125* | 0.01 | 78 |
| 4 | 0.05* | 0.0625* | 0.025 | 0.01 | 90 |
Concentration for each drug is expressed in micrograms per milliliter.
Drug concentration is reduced by half.
In each drug combination shown in Tables 7–9, drug ratio 1 was comprised of the maximum drug concentrations used. Drug ratios 2 and 3 reduced the concentration of a single drug in drug ratio 1 by 50% as indicated. Drug ratio 4 reduced the concentrations of two drugs in drug ratio 1 by 50% as indicated. As expected, for each of three drug combinations, drug ratio 1 achieved the highest projected inhibition. Surprisingly, the reduction of one drug by 50% (drug ratio 2) lowered the projected inhibition only slightly—7%, 2%, and 2% in Tables 7–9, respectively, whereas the reduction of a different drug by 50% (drug ratio 3) lowered the projected inhibition markedly—27%, 22%, and 20% in Tables 7–9, respectively. Interestingly, concurrently reducing both of these drugs by 50% in drug ratio 4 achieved a better projected inhibition than reducing only one drug in drug ratio 3 in each of three drug combinations. These results highlight the importance of not just the drugs in the combinations but also, the ratios of their dosages to each other.
Experimental TB Drug Regimens Are More Efficacious than the Standard Regimen in Killing Mtb in Macrophages.
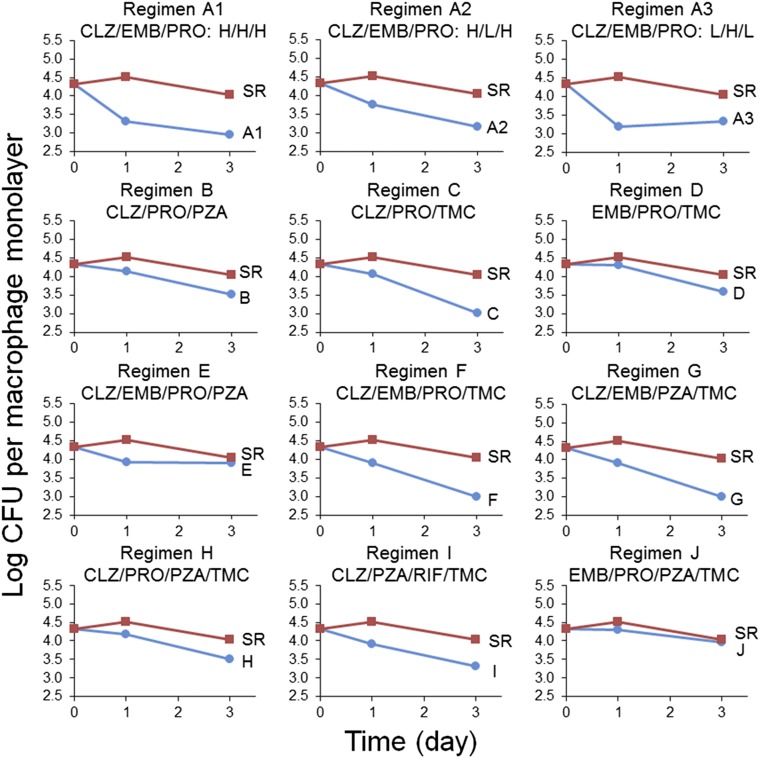
The results obtained using the FSC.II platform were based on a GFP fluorescence assay that assessed inhibition of Mtb growth. To determine if the drug combinations identified by this approach as being especially efficacious also resulted in significant killing of Mtb, we tested these drug combinations in a methodologically independent THP-1 macrophage infection assay based on cfu. The dose of each drug that achieved 25% inhibition in the fluorescence-based inhibition assay was used as the 1× concentration for that drug in a three- or four-drug combination in the cfu-based killing assay (SI Appendix, Table S1). Keeping these ratios constant, the experimental regimens and the 1980s standard regimen were also tested at 4× and 16× the drug concentrations (SI Appendix, Fig. S3). The viability of Mtb was assayed at 0, 1, and 3 d after drug exposure. Additionally, one combination was tested at different ratios (treatments A1–A3).
Except for regimen J, which was nearly indistinguishable from the 1980s standard regimen, treatment with any of the drug regimens (three- or four-drug combinations) resulted in greater killing of Mtb in macrophages than the 1980s standard regimen at the 16× concentration (Fig. 3 and SI Appendix, Table S7). At this concentration, drug regimens surpassed the 1980s standard regimen by 1 d of treatment. At 4× concentration, treatment with the drug regimens E–I killed more Mtb than the 1980s standard regimen by 3 d after treatment initiation (SI Appendix, Table S7). These results show that, with the exception of regimen J, the regimens are superior to the 1980s standard regimen. Moreover, killing is dose-dependent (SI Appendix, Table S7). Among the four three-drug regimens assayed, PRO paired with any two of three drugs CLZ, EMB, and TMC outperformed the four-drug 1980s standard regimen (Fig. 3). As for the top four-drug regimens, CLZ and TMC were consistently present in the most potent combinations (regimens F–I) (Fig. 3). We obtained similar results for human monocyte-derived macrophages, with all of the FSC-identified regimens showing antimicrobial efficacy superior to that of the 1980s standard regimen (SI Appendix, Fig. S4).
Fig. 3.
Efficacy of the top three- and four-drug combinations in killing Mtb in macrophages. The three-drug regimens A1–A3 and B–D and the four-drug regimens E–J are plotted against the 1980s standard regimen (SR) at 16× concentrations. Regimens A2 and A3 are also plotted against the SR at 16× concentrations; however, with regimen A2, the dose of EMB was halved, and with regimen A3, the doses of CLZ and PRO were halved (L indicates one-half of the regular dose, and H is the regular dose). The drug dose for the 1× concentration is shown in SI Appendix, Table S1.
As shown in the analyses of the fluorescence-based assay, drug ratio may have a major influence on the efficacy of a drug combination. We tested this concept in the killing assay using a three-drug combination of CLZ, EMB, and PRO (regimen A1) as an example. Our results showed that reducing the concentration of two of three drugs by 50% (regimen A3) yielded a faster killing rate (comparing values at day 1) than reducing the concentration of only the third drug (regimen A2), confirming the importance of drug ratio (Fig. 3).
Our methodologically independent cfu-based macrophage cell culture model assay corroborated our findings from the fluorescence-based assay in indicating that several regimens were superior to the 1980s standard regimen (INH, EMB, PZA, and RIF), including CLZ, EMB, and PRO (with or without TMC) and CLZ, EMB, and PRO (with or without PZA).
Discussion
In this study, we used an experimental parallel search process, the FSC.II platform, to optimize drug–dose combinations for TB treatment in a fluorescence-based macrophage cell culture model of TB. A brute force approach to identifying the best combinations and doses of 14 different drugs would require assays of billions of different combinations. In contrast, the FSC.II approach identified optimized drug–dose combinations with only a single screening test and three iterations, each involving an assay of only 86–155 drug–dose combinations. It is noteworthy that the FSC.II approach identified several optimal three- and four-drug combinations on the basis of efficacy in our fluorescence-based macrophage cell culture model of TB and that these combinations were subsequently shown to be superior to the 1970s and current 1980s standard regimens in a cfu-based macrophage cell culture model of TB.
The use of the FSC approach to antibacterial combinations represents a major advance, because previously used approaches, such as a checkerboard approach, are able to combine only limited numbers of drugs (typically 2–3) at a time, whereas the FSC.II approach used herein used a quadratic polynomial equation that is able to model the response surface of numerous drugs: 14 in this study. Thus, with a small number of experiments, we were able to identify the most efficacious regimens among 1,365 possible three- or four-drug combinations after optimizing the drug ratios for each drug within each regimen. Conventional approaches would have required billions of tests to achieve this outcome.
We used an IPTG-inducible expression system to evaluate the antimicrobial efficacy of the drug combinations in an in vitro human macrophage culture system. This fluorescence-based assay relies on inhibition of Mtb metabolic activity by antimicrobials and has the advantage of facilitating high-throughput screening. It is possible that this assay might underestimate killing if the bacteria respond to IPTG before they are killed by the antibiotic and that it might overestimate killing if the absence of GFP expression is related to metabolic inactivity of the bacterium rather than killing (e.g., as a result of being in an unfavorable compartment within the macrophage) (14). However, we believe that these over- and underestimations are relatively minor, because our cfu-based measurements validated our fluorescence-based measurements. Moreover, it takes 2 d of induction with IPTG for Mtb-iGFP to produce a level of fluorescence intensity suitable for high-throughput imaging (exposure time in milliseconds). Although some bacteria may express GFP stably and then, be killed, their fluorescence intensity level would be very low, and thus, the overestimate would also be very low unless the drug combination was extremely slow-acting, which would render it undesirable in any case. Likewise, where bacteria reside in unfavorable cellular compartments, such that they are metabolically inactive and do not multiply, the readout of low GFP-inducible fluorescence would provide an accurate assessment that there has been very little growth of bacteria in the monolayer.
Our Mtb-iGFP macrophage cell culture model, as with any model, has both advantages and limitations. It has an advantage over liquid culture assays of assaying the activity of the drugs in human host cells that reflect the host cells for Mtb replication in vivo. Our macrophage assay system has the potential to detect both synergistic and antagonistic drug interactions in the cellular environment in which Mtb are replicating. In this regard, it is noteworthy that PZA was consistently selected as one of the drugs in our optimized regimens, but the antimycobacterial activity of PZA activity is only detected in cell-free assays that use acidified media (pH 6). It is also intriguing that CLZ was consistently selected in our optimized drug regimens and has been noted to perform favorably in combination with both first- and second-line drug regimens in a mouse model of pulmonary TB (17, 18). Our model and FSC analyses yielded surprising results, in that both INH and RIF were eliminated from the optimized regimens because of an insignificant effect on efficacy (INH) or antagonistic interactions with other drugs (RIF). Antagonistic interactions of INH and RIF with other first-line TB drugs have been observed in liquid culture (19) and a mouse model of TB (20).
In the final iteration studied herein, we eliminated two promising drugs from consideration—PA824 and SQ109—only because they were not approved for human use. In future studies, we intend to evaluate these drugs as well as OPC-67683 (delamanid)—now approved for treatment of drug-resistant TB—in combination with the other drugs evaluated in iteration 3 to determine if the FSC.II approach places them in optimized combinations that are superior to the 1980s standard regimen.
The results of any model must be verified in other systems and if warranted, ultimately, a clinical trial. Neither liquid culture models nor our macrophage cell culture model takes into account drug metabolism and clearance factors, area under the curve/minimum inhibitory concentration ratios, drug–drug cytochrome P450 interactions, and organ toxicities, which play a critical role when drug combinations are given to animals or humans. In this regard, we are currently evaluating our optimized regimens in vivo in a mouse model of pulmonary TB. In ongoing studies using this model, two of our optimized combinations, including one comprised exclusively of generic antibiotics, have already shown marked superiority compared with the current (1980s) standard regimen in mice, allowing relapse-free cure in as little as 3–4 wk vs. 3–4 mo for the standard regimen. On this basis, one of these regimens has entered clinical trials. Because none of our optimized regimens contain either INH or RIF, they are potentially of value in treating both drug-sensitive and -resistant TB. Moreover, because none of our optimized regimens contain fluoroquinolones or injectable aminoglycosides, they also are potentially of value in treating extensively drug-resistant TB.
Supplementary Material
Acknowledgments
We thank Barbara Jane Dillon, Saša Masleša-Galić, and Susana Nava for excellent technical assistance and Maryellie Ramler and Michael Dinh for substantial editorial contributions. We also thank Robert Damoiseaux and the University of California, Los Angeles (UCLA) Molecular Screening Shared Resource Facility for assistance with high-throughput screening. We also appreciate many discussions with Prof. Hongquan Xu (Department of Statistics, UCLA). This work was supported by a subgrant from Shanghai Jiao Tong University and Global Health Grant OPP1070754 from the Bill and Melinda Gates Foundation.
Footnotes
Conflict of interest statement: The authors have filed patent applications covering the findings described in this paper.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1600812113/-/DCSupplemental.
References
- 1.WHO 2014 Global Tuberculosis Report 2014. Available at apps.who.int/iris/bitstream/10665/137094/1/9789241564809_eng.pdf?ua=1. Accessed June 5, 2015.
- 2.Institute of Medicine (US) Forum on Drug Discovery D and Translation . Developing and Strengthening the Global Supply Chain for Second-Line Drugs for Multidrug-Resistant Tuberculosis: Workshop Summary. National Academies Press; Washington, DC: 2013. [PubMed] [Google Scholar]
- 3.Spigelman MK. New tuberculosis therapeutics: A growing pipeline. J Infect Dis. 2007;196(Suppl 1):S28–S34. doi: 10.1086/518663. [DOI] [PubMed] [Google Scholar]
- 4.Zumla A, et al. Tuberculosis treatment and management—an update on treatment regimens, trials, new drugs, and adjunct therapies. Lancet Respir Med. 2015;3(3):220–234. doi: 10.1016/S2213-2600(15)00063-6. [DOI] [PubMed] [Google Scholar]
- 5.Ma Z, Lienhardt C, McIlleron H, Nunn AJ, Wang X. Global tuberculosis drug development pipeline: The need and the reality. Lancet. 2010;375(9731):2100–2109. doi: 10.1016/S0140-6736(10)60359-9. [DOI] [PubMed] [Google Scholar]
- 6.Nuermberger EL, Spigelman MK, Yew WW. Current development and future prospects in chemotherapy of tuberculosis. Respirology. 2010;15(5):764–778. doi: 10.1111/j.1440-1843.2010.01775.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ding X, et al. Discovery of a low order drug-cell response surface for applications in personalized medicine. Phys Biol. 2014;11(6):065003. doi: 10.1088/1478-3975/11/6/065003. [DOI] [PubMed] [Google Scholar]
- 8.Wong PK, et al. Closed-loop control of cellular functions using combinatory drugs guided by a stochastic search algorithm. Proc Natl Acad Sci USA. 2008;105(13):5105–5110. doi: 10.1073/pnas.0800823105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Valamehr B, Tsutsui H, Ho CM, Wu H. Developing defined culture systems for human pluripotent stem cells. Regen Med. 2011;6(5):623–634. doi: 10.2217/rme.11.54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Al-Shyoukh I, et al. Systematic quantitative characterization of cellular responses induced by multiple signals. BMC Syst Biol. 2011;5:88. doi: 10.1186/1752-0509-5-88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wang H, et al. Mechanism-independent optimization of combinatorial nanodiamond and unmodified drug delivery using a phenotypically driven platform technology. ACS Nano. 2015;9(3):3332–3344. doi: 10.1021/acsnano.5b00638. [DOI] [PubMed] [Google Scholar]
- 12.Ding X, et al. Cascade search for HSV-1 combinatorial drugs with high antiviral efficacy and low toxicity. Int J Nanomedicine. 2012;7:2281–2292. doi: 10.2147/IJN.S27540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Weiss A, et al. A streamlined search technology for identification of synergistic drug combinations. Sci Rep. 2015;5:14508. doi: 10.1038/srep14508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lee BY, Clemens DL, Horwitz MA. The metabolic activity of Mycobacterium tuberculosis, assessed by use of a novel inducible GFP expression system, correlates with its capacity to inhibit phagosomal maturation and acidification in human macrophages. Mol Microbiol. 2008;68(4):1047–1060. doi: 10.1111/j.1365-2958.2008.06214.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jaynes J, Ding X, Xu H, Wong WK, Ho CM. Application of fractional factorial designs to study drug combinations. Stat Med. 2013;32(2):307–318. doi: 10.1002/sim.5526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Xu H, Jaynes J, Ding X. Combining two-level and three-level orthogonal arrays for factor screening and response surface exploration. Stat Sin. 2014;24(1):269–289. [Google Scholar]
- 17.Tyagi S, et al. Clofazimine shortens the duration of the first-line treatment regimen for experimental chemotherapy of tuberculosis. Proc Natl Acad Sci USA. 2015;112(3):869–874. doi: 10.1073/pnas.1416951112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Grosset JH, et al. Assessment of clofazimine activity in a second-line regimen for tuberculosis in mice. Am J Respir Crit Care Med. 2013;188(5):608–612. doi: 10.1164/rccm.201304-0753OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dickinson JM, Aber VR, Mitchison DA. Bactericidal activity of streptomycin, isoniazid, rifampin, ethambutol, and pyrazinamide alone and in combination against Mycobacterium tuberculosis. Am Rev Respir Dis. 1977;116(4):627–635. doi: 10.1164/arrd.1977.116.4.627. [DOI] [PubMed] [Google Scholar]
- 20.Almeida D, et al. Paradoxical effect of isoniazid on the activity of rifampin-pyrazinamide combination in a mouse model of tuberculosis. Antimicrob Agents Chemother. 2009;53(10):4178–4184. doi: 10.1128/AAC.00830-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.