Abstract
Type II topoisomerases are essential enzymes that regulate DNA topology through a strand-passage mechanism. Some type II topoisomerases relax supercoils, unknot and decatenate DNA to below thermodynamic equilibrium. Several models of this non-equilibrium topology simplification phenomenon have been proposed. The kinetic proofreading (KPR) model postulates that strand passage requires a DNA-bound topoisomerase to collide twice in rapid succession with a second DNA segment, implying a quadratic relationship between DNA collision frequency and relaxation rate. To test this model, we used a single-molecule assay to measure the unlinking rate as a function of DNA collision frequency for Escherichia coli topoisomerase IV (topo IV) that displays efficient non-equilibrium topology simplification activity, and for E. coli topoisomerase III (topo III), a type IA topoisomerase that unlinks and unknots DNA to equilibrium levels. Contrary to the predictions of the KPR model, topo IV and topo III unlinking rates were linearly related to the DNA collision frequency. Furthermore, topo III exhibited decatenation activity comparable with that of topo IV, supporting proposed roles for topo III in DNA segregation. This study enables us to rule out the KPR model for non-equilibrium topology simplification. More generally, we establish an experimental approach to systematically control DNA collision frequency.
INTRODUCTION
DNA topoisomerases are ubiquitous enzymes with essential roles in regulating DNA topology in all domains of life (1–5). They are categorized into two classes, type I and II, based on the number of DNA strands cleaved and dependence on adenosine triphosphate (ATP) hydrolysis (1). Type I topoisomerases introduce a transient nick in one strand of duplex DNA and either pass the intact single-stranded segment of DNA through the nick (type IA) or allow controlled rotation around the phosphate bond in the intact single strand (type IB). Type I topoisomerases relax supercoiled DNA towards thermodynamic equilibrium, as they do not use ATP. Type II topoisomerases (topo II), which are further subdivided into type IIA (eukaryotic, prokaryotic and viral) and IIB (archaeal, some higher plants and a few bacteria) based on structural, biochemical and evolutionary differences, introduce a transient double-strand break in one segment of duplex DNA (the gate or G-segment) through which a second segment of duplex DNA (the transfer or T-segment) is passed (6,7). Through this ATP-dependent reaction, type II topoisomerases can relax DNA supercoils, as well as generate and remove links and knots in or between closed DNA molecules. Among the type IIA topoisomerases, DNA gyrase displays the unique ability to negatively supercoil DNA and is the only type IIA topoisomerase that uses the energy of ATP hydrolysis to perform work on the DNA (1,4,8–10). The remainder of the type IIA enzymes catalyse, on average, energetically favourable topological reactions, i.e. relaxing supercoiled DNA. However, Rybenkov et al. (11) demonstrated that type IIA topoisomerases, with the exception of gyrase, simplify DNA topology to steady-state concentrations of unlinked and unknotted molecules that are lower than those found at thermodynamic equilibrium and generate topoisomer distributions of relaxed DNA that have smaller variances than the equilibrium distribution. As topo IIA enzymatic activity is coupled to the energy release of ATP hydrolysis, no thermodynamic principles are violated; however, the mechanism by which topo IIA acting at the local scale can sense the global topology of the DNA substrate remains speculative. Proposed models of non-equilibrium topology simplification posit different mechanisms of topological discrimination, i.e. how the topoisomerase distinguishes DNA crossings in linked, knotted and supercoiled DNA from those occurring randomly in or between DNA molecules (8,12). Two of the models currently under debate, the G-segment DNA-bending model and the hooked-juxtaposition model, assume that local geometry sensing by the topo IIA enzyme influences T-segment capture and transfer (12–18). In the G-segment–bending model, the degree of G-segment bending imposed by topo IIA dictates the degree of non-equilibrium topology simplification (12,16,19,20). However, a recent study found that the degree of G-segment bending by several topo IIAs was similar and uncorrelated with their non-equilibrium unlinking activity. This finding is inconsistent with predictions of the G-segment–bending model and suggests that DNA bending alone is insufficient to account for non-equilibrium topology simplification (21). The hooked-juxtaposition model posits that topo IIA preferentially unlinks juxtaposed DNA segments that are sharply bent towards one another (13,14,22–24). Simulations suggest that the specific unlinking of hooked juxtapositions can account for much, but not all, of the observed degree of topological simplification (22); however, the model has not yet been experimentally tested. In contrast to these geometric selection models, the kinetic proofreading (KPR) model, based on KPR mechanisms proposed by Hopfield and Ninio (25,26), posits that topo IIA uses ‘kinetic selection’ of the T-segment (17–19). In this model, G-segment–bound topo IIA undergoes a transition to an ‘activated’ state on the first collision with a T-segment (Figure 1B). Coupling this activated state transition with the energy of ATP binding makes it irreversible. Strand passage occurs only if a second T-segment collision occurs before decay of the activated state. Non-equilibrium topology simplification results because strand passage depends on the product of the initial, activating strand collision frequency and the second, productive strand collision frequency (Figure 1B). Under the assumption that these frequencies are comparable, the unlinking rate would scale with the square of the collision frequency. This non-linear relationship between unlinking rate and strand collision frequency results in non-equilibrium simplification, as the equilibrium simplification reaction would depend linearly on the collision frequency. As a concrete example, consider the steady-state inter-conversion of linked and unlinked circular DNA molecules. At equilibrium, the concentrations of linked and unlinked DNA would be proportional to the ratio of strand collision frequencies of unlinked and linked circles. Under the KPR model, the concentrations of the two species would be proportional to the square of the DNA collision frequencies for the unlinked and linked molecules. The quadratic dependence on the collision frequency arises because, in order for strand passage to take place, two collisions must occur in rapid succession, the probability of which scales as the square of the collision rate. Thus, the central tenet of the KPR model is that the strand transfer rate scales quadratically with the DNA strand-collision frequency.
Figure 1.
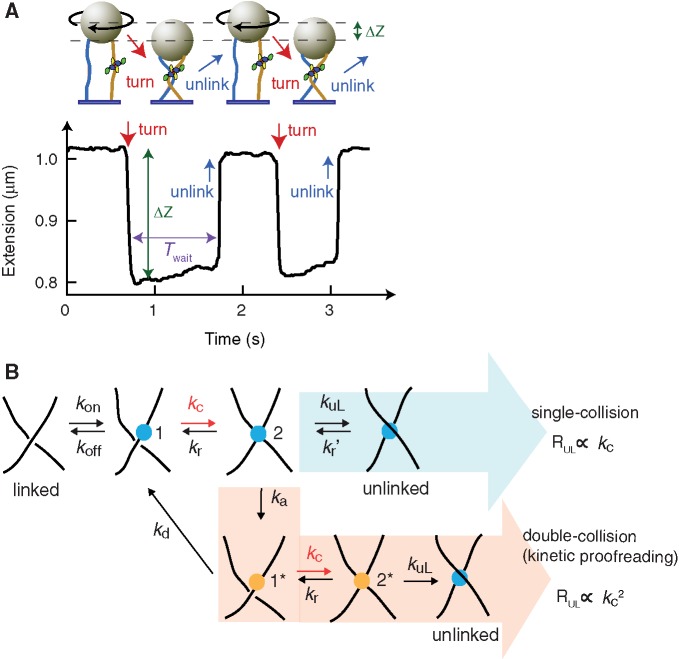
Topoisomerase unlinking assay and KPR model. (A) Cartoon of experiment (not to scale). A 1-µm magnetic bead (beige) is tethered to the surface of the flow chamber by two 5 kb torsionally unconstrained dsDNA molecules (blue and gold). A link between the DNA molecules is generated by rotating the bead (black arrow) using a magnet assembly (not shown), which decreases the DNA extension by ΔZ (red arrow). Strand passage mediated by a topoisomerase (shown bound to DNA), unlinks the DNA (blue arrow), leading to an increase in DNA extension. After a brief re-equilibration time, the process is automatically repeated. Extension of the double tether as a function of time shows the decrease in extension associated with introducing the link, and the subsequent increase in extension when the link is resolved by the strand-passage reaction of the topoisomerase. The time between these events is defined as the waiting time (Twait). DNA extension was measured by video tracking the bead in real time at 100 Hz with ∼2-nm spatial resolution. (B) DNA strand-passage mechanisms. DNA unlinking can occur via a single- or double-collision mechanism. Topoisomerase binds the G-segment (blue dot 1) and collides with a potential T-segment with rate constant kc (blue dot 2). In the single-collision mechanism (blue shaded arrow), strand passage occurs from this state with rate constant kuL. In the double-collision mechanism, i.e. the KPR model (pink shaded arrow), the initial T-segment collision activates the topoisomerase (yellow dot 1*). The activated topoisomerase will effectuate strand passage if it collides with a second potential T-segment (yellow dot 2*) before it decays back to the inactive state (blue dot 1) with rate constant kd. The single-collision strand-passage rate (RUL) is proportional to the collision frequency kc, whereas the double-collision RUL, posited by the KPR model, is proportional to the square of the collision frequency. Here, kon and koff are on and off rate constants of topoisomerase binding to G-segment DNA. kr and kr′ are release rate constants of a potential T-segment by the topoisomerase.
Simulations of the KPR model suggest that the kinetic amplification may not be sufficient to achieve experimentally observed levels of non-equilibrium topology simplification for DNA knots unless combined with aspects of the DNA G-segment–bending model or some other complementary non-equilibrium simplification mechanism (16,27). Furthermore, the KPR model seems difficult to rationalize with accepted models of strand passage in which ATP binding triggers N-gate closure that traps the T-segment and favours its passage through the cleaved G-segment (7,28–31). This model, based on a combination of structural and biochemical evidence, seems to be at odds with the central tenet of the KPR model that postulates T-segment release and recapture after the binding of at least one ATP (8,10). Despite this apparent contradiction, there is sufficient uncertainty in the kinetics of binding two ATP molecules and the subsequent kinetics of N-clamp closure that the KPR model, which is a kinetic model, cannot be entirely ruled out based on existing data. Therefore, the hypothesis that topo IIA requires a double collision between the G-segment–bound topoisomerase and a T-segment for strand passage remains a potential, but unverified, mechanism that would result in non-equilibrium topology simplification. Although ensemble approaches allow geometric features of DNA-topoisomerases complexes to be indirectly measured and, therefore, used to test the validity of models based on DNA bending, testing the KPR model experimentally is challenging, as it requires a means of assessing and varying the collision frequency between DNA strands, referred to hereafter as collision frequency.
Here, we tested the KPR model by investigating the relationship between DNA collision frequency and DNA unlinking rate using a novel strategy based on the micromanipulation of a single-DNA crossing. We measured the unlinking rates of Escherichia coli topo IV, a type IIA topoisomerase that displays efficient non-equilibrium topology simplification, using a single-molecule DNA unlinking assay in which the relative collision frequency could be controlled (Figure 1A). Combining these measurements with collision frequencies obtained from Monte Carlo (MC) simulations permitted a sensitive measure of the relationship between collision frequency and unlinking rate. Because this comparison relies on the assumption that the collision frequency obtained from MC simulations is proportional to the actual collision frequency, we measured the unlinking rate as a function of computed collision frequency for E. coli topo III, a type IA topoisomerase that unlinks and unknots DNA to equilibrium levels (11). Topo III is an efficient decatenase that is thought to play important roles in chromosome segregation and the resolution of linked DNA intermediates without using ATP (32–35). Topo III uses a strand-passage mechanism common to all type IA topos (1,4,36,37), but it can uniquely pass duplex DNA through a single-stranded nick or gap (1), thereby permitting reversible linking and knotting reactions with gapped DNA substrates. In the context of the KPR model, topo III is expected to display a linear relationship between unlinking rate and collision frequency because it uses an ATP-independent mechanism based on a single collision of two DNA segments (Figure 1B).
Contrary to the predictions of the KPR model, we found that the unlinking rates of both topo IV and topo III were linearly related to the collision frequency. Moreover, the unlinking rates of the two enzymes measured with comparable double tether geometries were linearly related over the range of DNA collision frequencies investigated. We conclude from these results that non-equilibrium topology simplification activity does not arise in whole or in part from a KPR mechanism, thus ruling out the KPR model. However, our results reveal that topo III, unlike E. coli topoisomerase IA (topo I), is an efficient DNA decatenase, on par with topo IV, lending support to its putative roles in chromosome segregation and unlinking in vivo (33).
MATERIALS AND METHODS
Topoisomerase IV unlinking substrate
Linear 5-kb dsDNA labelled with a single biotin or digoxigenin at each 5′-end was prepared by polymerase chain reaction (PCR) using pET28b (EMD Science) as a template with a biotin-labelled forward primer and digoxigenin-labelled reverse primer (Eurofins MWG Operon). The PCR product was purified with a QIAquick PCR purification kit (Qiagen).
Topoisomerase I and III unlinking substrate
Linear 5-kb dsDNA with a 37-nt gap (2258–2294) with a single biotin or digoxigenin at each 5′-end was prepared similarly to the topo IV DNA substrate except that the PCR template was pKZ1. pKZ1 was made by ligating a 44-bp dsDNA segment containing two BbvCI sites separated by 37 nt into pET28b at the BamHI site. The 5-kb PCR product was digested with Nt.BbvCI (New England Biolabs) to create two nicks at positions 2258 and 2294, near the middle of the DNA template. After digestion, the 37-nt oligomer was removed by heating the DNA to 80°C for 20 min and cooling down gradually to 4°C in the presence of excess complementary 37-nt oligomer. The 4-kb multi-nicked DNA molecules were prepared by PCR of pFC94 (38) from position 5422–9520 with a biotin-labelled forward primer and digoxigenin-labelled reverse primer (Eurofins MWG Operon) and were nicked with four nicking enzymes: Nb.BsmI, Nt.AIwI, Nb.BtsI and Nt.BtsNBI (New England Biolabs), generating 14 nicks located over the middle third of the DNA.
Protein preparations
E. coli topoisomerase I
E. coli topoisomerase I was purchased from New England Biolabs.
E. coli topoisomerase III
The pET-15btopB plasmid encoding K12 E. coli topoisomerase III was provided by J. Keck (University of Wisconsin Madison). A tobacco etch virus (TEV) protease cleavage site with an additional two glycine residue spacer was inserted upstream of the topB gene using the QuikChange II XL mutagenesis kit (Stratagene), and the sequence of the resulting plasmid (pET-15btopB+TEV) was verified. Rosetta (DE3) pLysS Competent Cells (EMD4Bioscience) transformed with pET-15btopB+TEV were grown at 37°C in Luria-Bertani broth containing 50 μg/ml of carbenicillin and 34 μg/ml of chloramphenicol. The expressed protein was induced with 1 mM isopropyl β-d-thiogalactopyranoside. After induction at 37°C for 20 h, cells were harvested by centrifugation. The collected cells were suspended in buffer A [50 mM Tris–HCl, pH 7.5, 300 mM NaCl and 10% (v/v) glycerol] and emulsified using a high pressure cell homogenizer (Avestin). The cell lysate was then centrifuged at 40 krpm at 4°C for 1 h in a Ti45 rotor (Beckman). The supernatant was loaded onto a HisTrap-FF 5 ml Ni-Nitrilotriacetic acid (NTA) column (GE). His-tagged protein was eluted with buffer B [50 mM Tris–HCl, pH 7.5, 0.5 M imidazole, 0.3 M NaCl, 10 mM β-mercaptoethanol and 10% (v/v) glycerol]. The eluted proteins were concentrated and buffer-exchanged with buffer A using an Amicon Ultra-15 centrifugal filter unit with Ultracel-30 membrane (Millipore). The his tag was removed from the protein by digestion with 0.5 U/μg of Pro-TEV (Promega) for 6 h. The protein digestion mixture was run twice through an Ni-NTA column (Qiagen) to remove Pro-TEV and uncleaved protein. The size and purity of cleaved topo III were evaluated by sodium dodecyl sulphate–polyacrylamide gel electrophoresis (Invitrogen).
E. coli topoisomerase IV
ParC and ParE subunits of topo IV were purified to a final concentration of 1.5 μM as previously described (21,39). Equimolar amounts of ParC and ParE were mixed to make 0.75 μM of topo IV heterotetramer.
Experimental procedure
To prepare double-DNA tethers for DNA unlinking experiments, 1 µl of 0.15 nM singly biotin- and digoxigenin-labelled 5-kb dsDNA was incubated with 1 µl of magnetic beads [1% (w/v), MyOne, Invitrogen] in 200 µl of wash buffer [WB: 1× phosphate-buffered saline, 0.3% (w/v) bovine serum albumin (BSA) and 0.04% Tween-20) at room temperature (22°C) overnight at a 3:1 DNA to bead ratio. The sample cell was incubated with 30 µl of 10 µg/ml of anti-digoxigenin in 1× phosphate-buffered saline for 1 h at room temperature followed by a wash with 200 µl of WB. The DNA-bead mixture was incubated in the anti–digoxigenin-coated sample cell for 30 min before washing with 400 µl of WB. The magnetic tweezers instrumentation has been previously described (40–42). During the experiment, double-DNA tethered beads were identified by rotating the magnet assembly. In contrast to a bead tethered by a single DNA, the DNA extension of a double-DNA tethered bead decreases symmetrically for negative and positive turns (Figure 2A) independent of the tension on the DNA (43). Topo IV activity buffer [25 mM Tris–HCl, pH 7.5, 100 mM potassium glutamate, 10 mM magnesium chloride, 1 mM dithiothreitol, 0.3% (w/v) BSA and 0.04% (v/v) Tween-20] containing 2 nM topo IV and 1 mM ATP was introduced once 20 double-tethered beads were found, and their tethering geometries (spacing between DNA molecules and verification of parallel tether geometry—see later in the text) were characterized. Topo IV DNA unlinking rates were measured for bead rotations of −0.6 to −1 turn (Figure 3A), which imposes left-handed DNA crossings as found in positive writhe. Topo III unlinking measurements were similar except that 5-kb DNA molecules containing a 37-nt gap near their centres were used as substrates, as topo III requires a single-stranded region for strand passage. Unlinking measurements were performed with 5 nM topo III in topo III activity buffer [40 mM HEPES, pH 8.0 adjusted with KOH, 1 mM magnesium acetate, pH 7, 0.3% (w/v) BSA and 0.04% (v/v) Tween-20]. Data traces were analysed using a custom step-finding algorithm to identify the waiting time, Twait (the time interval between rotating the bead to generate the DNA link and it being unlinked by topoisomerase). The Twait values (100–200 events for each rotation) were binned, and the histogram was fitted with a single exponential to obtain the strand-passage rate. Topo I (New England Biolabs) unlinking measurements were performed using the same substrate used for topo III experiments with ∼130 or 325 nM of topo I in topo I activity buffer [50 mM potassium acetate, pH 7.9, 10 mM magnesium acetate, 1 mM dithiothreitol, 0.3% (w/v) BSA and 0.04% (v/v) Tween-20].
Figure 2.
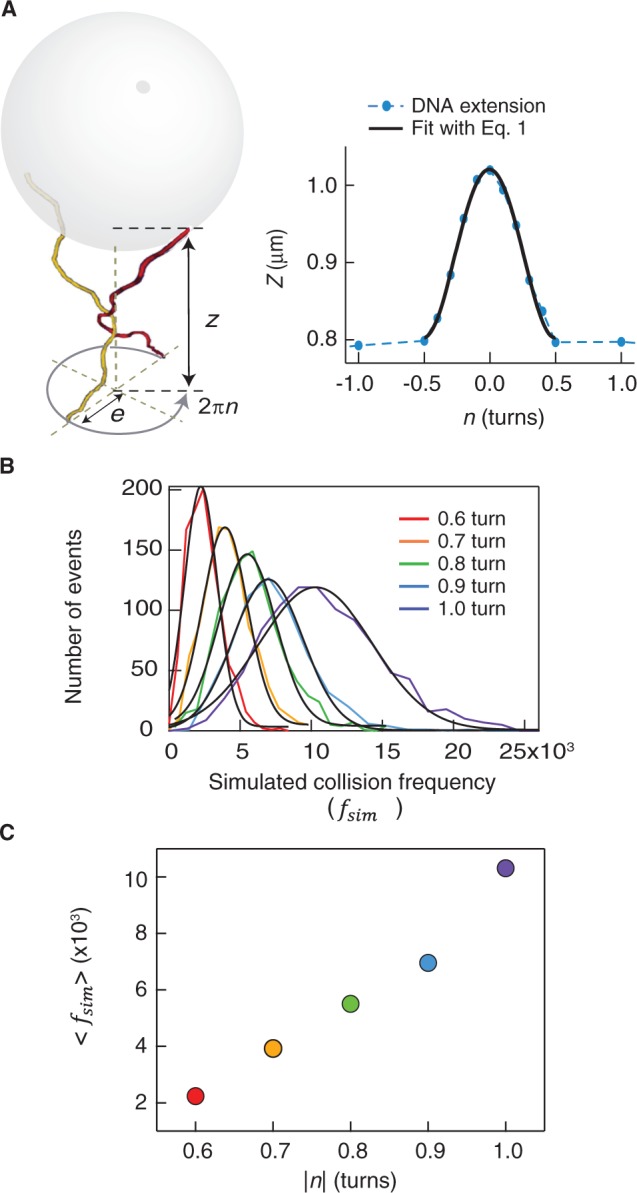
Characterization of DNA tether geometry and rotation-dependent collision frequency obtained from MC simulations. (A) In situ measurement of DNA tether geometry (not to scale). The double tether consists of two 5-kb DNA molecules attached between the surface and a streptavidin-coated magnetic bead (grey). To obtain the tether geometry, the DNA extension was measured as the bead was rotated from −0.5 to 0.5 rotations in increments of 0.1 turns (blue dots and dashed line). The DNA extension over the range −0.5–0.5 rotations was fit with Equation (1) (black solid line) to obtain the spacing between the DNA molecules, 2e, and the DNA extension at zero rotation, Z0. (B) Example collision frequency distributions for different imposed turns, n, from MC simulations of one double tether. Distributions of collision frequencies (number per 103 simulation steps) are fit with Gaussians (black solid lines) to obtain the mean collision frequency, <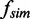 >, for each turn. (C) Mean collision frequency, <
>, for each turn. (C) Mean collision frequency, <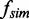 >, as a function of imposed turns, n. Values are colour-coded based on the corresponding number of imposed turns shown in B.
>, as a function of imposed turns, n. Values are colour-coded based on the corresponding number of imposed turns shown in B.
Figure 3.
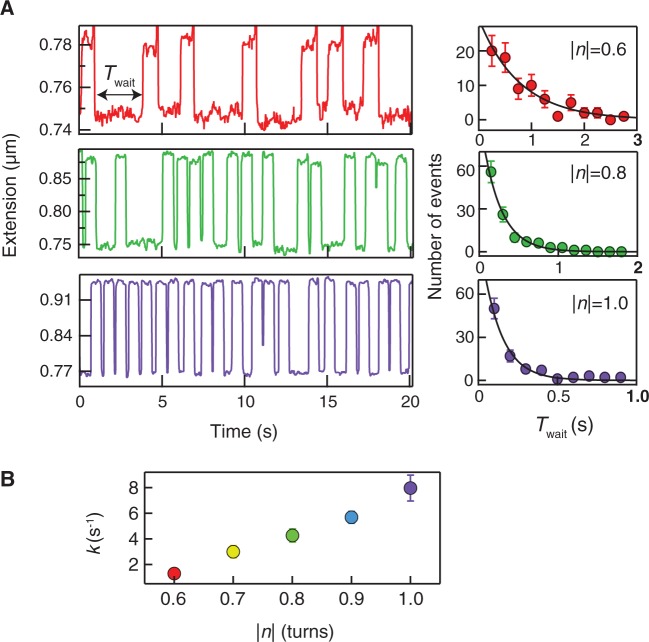
DNA extension traces of unlinking and mean rates of unlinking as a function of bead rotation. (A) DNA extension traces show unlinking activity of topo IV at three different imposed bead rotations (0.6, 0.8 and 1) for one double tether. The distributions of waiting times (Twait) (right panels) are well fit by single exponentials (black solid lines) to obtain the unlinking rates, k(n). (B) The unlinking rates are plotted as a function of bead rotation, n. Error bars correspond to the SD of the fit parameter.
DNA crossing geometry calculation
The geometry of the two DNA strands tethering the bead to the surface was determined by measuring the extension, Z(n), as a function of the number of turns (n). The region from −0.5 to 0.5 turns was fit with Equation (1) to obtain the distance between two DNA molecules (2e) and the DNA extension at n = 0 (Z0) (Figure 2A):
| (1) |
where Rb is the bead radius (0.5 μm) (44). Tethered beads were selected for unlinking measurements if the DNA extension at zero rotation (Z0) was within 10% of the predicted extension at the applied force. This selection criterion eliminated tether geometries that were not parallel, as trapezoidal tether geometry would result in a decreased DNA extension at zero rotation, and eliminated beads tethered by more than two DNA molecules.
DNA collision frequency calculation from Monte Carlo simulations
The experimentally determined tether geometry (2e, n, DNA length and applied force, F) was used to calculate the number of collisions between two DNA segments using a custom-written MC simulation routine for double-tethered beads, as previously described (44,45). Briefly, the simulation program models the two DNA molecules as discrete worm-like chains consisting of 10-nm rigid segments of fixed length. For each braid geometry, 106 simulation steps were calculated and were sampled once every 103 steps to obtain uncorrelated configurations. At each sample step, the collision frequency, 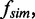 was calculated from the total number of collisions over the previous 103 MC steps. Collisions were considered to have occurred when two segments on the two DNA molecules were closer than a cut-off distance of 12 nm. Thus, for 106 steps, 103 collision frequencies were generated for each tether geometry. The
was calculated from the total number of collisions over the previous 103 MC steps. Collisions were considered to have occurred when two segments on the two DNA molecules were closer than a cut-off distance of 12 nm. Thus, for 106 steps, 103 collision frequencies were generated for each tether geometry. The 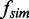 values for each condition were binned, plotted as a histogram and fitted with a Gaussian distribution to obtain the mean
values for each condition were binned, plotted as a histogram and fitted with a Gaussian distribution to obtain the mean 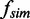 as shown in Figure 2B.
as shown in Figure 2B.
RESULTS
Single-DNA crossing assay measures unlinking rate as a function of DNA strand collision frequency
To test the KPR model of non-equilibrium topology simplification, we developed a single-molecule DNA unlinking assay (Figure 2A) that permitted measurement of the unlinking rate as a function of strand collision frequency. The KPR model predicts a quadratic relationship between unlinking rate and collision frequency. The unlinking assay is a variation on similar unlinking assays (44–46) in which a magnetic bead is tethered by two rotationally unconstrained 5-kb DNA molecules. Rotating the bead wraps the two DNA strands around one another, which reduces the height of the bead. The action of a single topoisomerase on this substrate resulted in a sudden increase in the height, indicating the unlinking of the DNA strands. After a brief delay, the bead was automatically rotated to create a new substrate for the enzyme (Figure 1). The experiment consists of imposing a series of partial rotations (−1 ≤ n ≤ −0.6, corresponding to positive writhe) on the bead and measuring the rate at which the corresponding crossings are unlinked by topo IV. The frequency of DNA strand collisions is expected to increase in proportion to the degree of linking, i.e. the magnitude of the bead rotation, which has been verified by MC simulations (Figure 2B and C). Therefore, by measuring the unlinking rate as a function of imposed bead rotation and estimating the strand collision frequency from MC simulations of the experimental configuration, the relationship between strand collision frequency and unlinking rate can be determined.
In practice, once a double-tethered magnetic bead was identified, the DNA crossing geometry was characterized to obtain the spacing between the DNA tethers, 2e (Figure 2A). Based on the tether geometry and the applied force, the inter-strand collision frequency as a function of bead rotation was obtained from MC simulations (Figure 2B and C). The unlinking rate was measured as a function of bead rotation from −0.6 to −1 turn in the presence of 2 nM topo IV (above the Kd of ∼0.2 nM measured under similar conditions) (47) and saturating (1 mM) ATP. Under these conditions, T-segment capture is expected to be rate limiting for strand passage; thus, the unlinking rate will be determined by the DNA collision frequency. The observed increase in unlinking rate with rotation (Figure 3B) is consistent with this assumption. The time interval between rotating the bead and the unlinking reaction was obtained from the extension traces (Figure 1), and the distributions of unlinking times were fit with single-exponential functions to obtain the mean unlinking rate for each rotation (Figure 3). To compare unlinking rates as a function of bead rotation measured with different double-tether geometries and to account for other possible differences among nominally identical measurement conditions, unlinking rates for each tether were normalized to the unlinking rate at n = 1 turn (Figure 4A).
Figure 4.
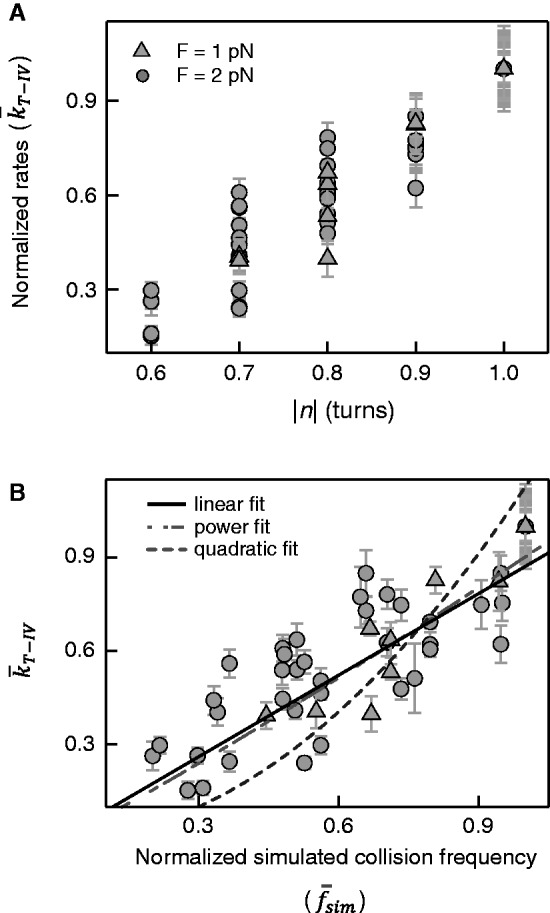
Normalized unlinking rates of topo IV as a function of bead rotation and normalized collision frequency. (A) Normalized unlinking rates of topo IV measured with 12 different double tethers, 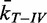 , are plotted as a function of bead rotation (n) for applied forces of 1 pN (triangles) and 2 pN (circles). Error bars are calculated through propagation of uncertainties (SD) in the initial fit parameters. (B)
, are plotted as a function of bead rotation (n) for applied forces of 1 pN (triangles) and 2 pN (circles). Error bars are calculated through propagation of uncertainties (SD) in the initial fit parameters. (B) 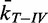 as a function of the normalized simulated collision frequency,
as a function of the normalized simulated collision frequency, 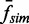 , fit with linear (solid line), quadratic (dashed line) and power (short-long dashed line) functions. The power fit,
, fit with linear (solid line), quadratic (dashed line) and power (short-long dashed line) functions. The power fit, 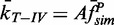 returned a power close to 1 (A = 0.90 ± 0.01 and P = 1.10 ± 0.03,
returned a power close to 1 (A = 0.90 ± 0.01 and P = 1.10 ± 0.03, 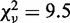 ). The data are poorly fit by a quadratic relation (
). The data are poorly fit by a quadratic relation (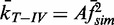 ) as evidenced by the 2-fold increase in reduced chi-square,
) as evidenced by the 2-fold increase in reduced chi-square, 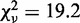 . Fitting to a line returned a slope of 0.87 ± 0.01 and a linear correlation coefficient of 0.75 with
. Fitting to a line returned a slope of 0.87 ± 0.01 and a linear correlation coefficient of 0.75 with 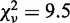 .
.
The unlinking rate of topo IV is linearly related to the collision frequency
The normalized unlinking rates, 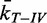 , increased as a function of bead rotation at both 1 and 2 pN of applied force on the bead (Figure 4A). To investigate the relationship between the unlinking rates and collision frequencies, we plotted
, increased as a function of bead rotation at both 1 and 2 pN of applied force on the bead (Figure 4A). To investigate the relationship between the unlinking rates and collision frequencies, we plotted 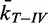 (n) as a function of the normalized collision frequencies at the same bead rotation,
(n) as a function of the normalized collision frequencies at the same bead rotation, 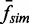 (n) (Figure 4B). The
(n) (Figure 4B). The 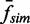 values were calculated in a similar manner to that used to obtain
values were calculated in a similar manner to that used to obtain 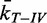 : the collision frequency at each rotation was normalized by the collision frequency at n = 1 turn for each double-tether geometry. The normalized unlinking rates seemed to be linearly related to the normalized collision frequencies (Figure 4B). Fitting
: the collision frequency at each rotation was normalized by the collision frequency at n = 1 turn for each double-tether geometry. The normalized unlinking rates seemed to be linearly related to the normalized collision frequencies (Figure 4B). Fitting 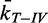 versus
versus 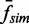 with a power function,
with a power function, 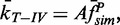 returned a power close to 1: P = 1.10 ± 0.03 (±SD) with a reduced chi-square,
returned a power close to 1: P = 1.10 ± 0.03 (±SD) with a reduced chi-square, 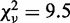 . Fitting with P = 2 resulted in a 2-fold increase in reduced chi-square,
. Fitting with P = 2 resulted in a 2-fold increase in reduced chi-square, 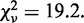 Fitting to a line (P = 1) returned a slope of 0.87 ± 0.01 (±SD) and a linear correlation coefficient of 0.75. Overall, the fits suggest a linear relationship between the normalized rates and collision frequencies in contrast to the quadratic relationship predicted by the KPR model.
Fitting to a line (P = 1) returned a slope of 0.87 ± 0.01 (±SD) and a linear correlation coefficient of 0.75. Overall, the fits suggest a linear relationship between the normalized rates and collision frequencies in contrast to the quadratic relationship predicted by the KPR model.
Topo III but not topo I efficiently decatenates linked DNA molecules containing a single-stranded gapped region
Although we found a linear relationship between the normalized unlinking rates of topo IV and the predicted collision frequencies, it is possible that the collision frequencies obtained from MC simulations were not good estimates of the relative collision frequencies. To verify the MC simulation results, we measured the unlinking rates of topo III as a function of bead rotation and compared the normalized rates with the normalized computed collision frequencies.
The unlinking rates of topo III (10 nM) as a function of bead rotation were measured using the same protocol and conditions used for topo IV except that the 5-kb DNA tethers contained a 37-nt single-stranded gapped region near the middle of each DNA molecule, as intact 5-kb DNA molecules and multi-nicked 4-kb DNA molecules were not decatenated by topo III. These observations confirmed that a single-stranded region of DNA is essential for topo III decatenation in addition to relaxation, similar to topo I (35,36). However, we found that E. coli topo IA was incapable of decatenation. Despite rapidly relaxing negative supercoils, topo IA did not unlink crossings of a double-DNA tether at a ∼30-fold higher concentration (325 nM) than that of topo III, for which efficient unlinking of the same tether was observed (Supplementary Figures S2 and S3). The average unlinking rate at one turn for topo III (5.9 ± 0.7 s−1 mean ± standard error) was comparable with that for topo IV (5.1 ± 0.5 s−1), indicating that topo III is an efficient decatenase on par with topo IV. The normalized rates for topo III (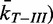 were plotted as a function of
were plotted as a function of 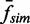 , calculated in the same manner as for topo IV (Figure 5A) and fitted with a linear function. As expected, the topo III unlinking rate was linearly related to, and strongly correlated with, the collision frequency. The fit returned a slope = 1.00 ± 0.01 (±SD),
, calculated in the same manner as for topo IV (Figure 5A) and fitted with a linear function. As expected, the topo III unlinking rate was linearly related to, and strongly correlated with, the collision frequency. The fit returned a slope = 1.00 ± 0.01 (±SD), 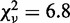 , and a linear correlation coefficient = 0.76.
, and a linear correlation coefficient = 0.76.
Figure 5.
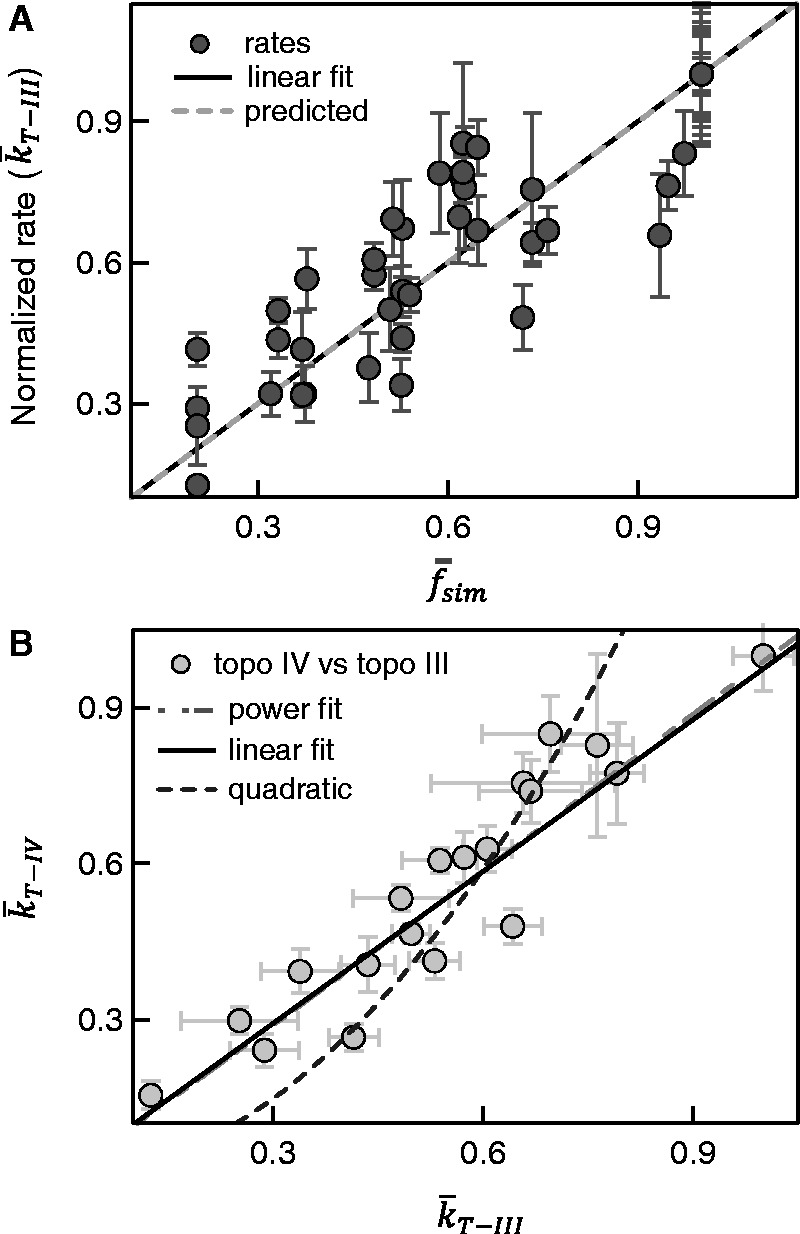
Normalized unlinking rates of topo III versus normalized collision frequency and comparison with topo IV. (A) Normalized unlinking rates of topo III, 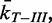 are plotted as a function of the normalized collision frequency from MC simulations,
are plotted as a function of the normalized collision frequency from MC simulations, 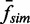 , and fit to a line, with slope = 1.00 ± 0.01,
, and fit to a line, with slope = 1.00 ± 0.01, 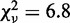 , and a linear correlation coefficient = 0.76. Error bars are calculated through propagation of uncertainties (SD) in the initial fit parameters. (B) Normalized rates of topo IV are directly compared with the normalized rates of topo III in a scatter plot, in which each point corresponds to the two normalized unlinking rates (topo III -x, and topo IV -y) measured with double tethers of comparable geometry at the same imposed rotation. Fitting the scatter plot with a linear function gave a slope S = 0.97 ± 0.02 with linear correlation coefficient 0.78 and
, and a linear correlation coefficient = 0.76. Error bars are calculated through propagation of uncertainties (SD) in the initial fit parameters. (B) Normalized rates of topo IV are directly compared with the normalized rates of topo III in a scatter plot, in which each point corresponds to the two normalized unlinking rates (topo III -x, and topo IV -y) measured with double tethers of comparable geometry at the same imposed rotation. Fitting the scatter plot with a linear function gave a slope S = 0.97 ± 0.02 with linear correlation coefficient 0.78 and 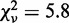 . Fitting to power function (y = AxP) returned A = 0.99 ± 0.04 and P = 1.02 ± 0.05 with
. Fitting to power function (y = AxP) returned A = 0.99 ± 0.04 and P = 1.02 ± 0.05 with 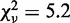 . Fitting to a quadratic function (y = Ax2) resulted in a significantly increased reduced chi-squared value,
. Fitting to a quadratic function (y = Ax2) resulted in a significantly increased reduced chi-squared value, 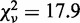 .
.
Topo III and topo IV display similar rotation-dependent unlinking rates
Comparing the unlinking rates of topo III and topo IV as a function of bead rotation, i.e. DNA collision frequency for similar bead geometries, provides an independent test of the KPR model that does not depend on the results of the MC simulations. As the unlinking rate of topo III is reasonably expected to be linearly related to the strand collision frequency, the normalized topo III unlinking rate reflects the relative strand collision frequency. Therefore, plotting the normalized relaxation rates of topo IV as a function of the normalized relaxation rates of topo III at the same bead rotation for comparable tether geometries (difference in 2e ≤ 0.2 µm) and applied force provides a simulation-independent comparison between unlinking rate and strand collision frequency (Figure 5B). Fitting 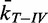 versus
versus 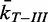 to a line returned a slope of 0.97 ± 0.02 with
to a line returned a slope of 0.97 ± 0.02 with 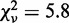 and a linear correlation coefficient of 0.78. Fitting the data with a power function,
and a linear correlation coefficient of 0.78. Fitting the data with a power function, 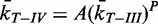 , returned A = 0.99 ± 0.04 and P = 1.02 ± 0.05 with
, returned A = 0.99 ± 0.04 and P = 1.02 ± 0.05 with 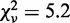 . Fixing P = 2, i.e. a quadratic fit, increased
. Fixing P = 2, i.e. a quadratic fit, increased 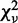 to 17.9. This direct comparison confirmed that the strand-passage reaction of topo IV and topo III depends linearly on the DNA collision frequency.
to 17.9. This direct comparison confirmed that the strand-passage reaction of topo IV and topo III depends linearly on the DNA collision frequency.
CONCLUSION AND DISCUSSION
In this study, we showed that the unlinking rate of topo IV increases linearly rather than quadratically with increasing collision frequencies between two DNA segments. The linear relationship between the topo III unlinking rate and collision frequency confirmed the validity of the combined experimental and computational approach while providing a simulation-independent test of the KPR model. Overall, our study indicates that a single collision with T-segment DNA is likely sufficient for strand passage by topo IV, suggesting that non-equilibrium topology simplification cannot be explained within the framework of the KPR model (17,18). This conclusion is further supported by the fact that Drosophila topo II (48) showed a similar linear relationship when compared with topo III under similar geometric conditions (Supplementary Figure S1). Although theoretical and computational studies have shown that the KPR model could not fully explain the measured non-equilibrium topology simplification (12), our work experimentally demonstrates that topo IV does not require a double collision with a T-segment DNA for strand passage. This result likely applies to other topo IIA enzymes, as they share a common two-gate mechanism for a strand passage through well-conserved core domains (4,49,50), and topo IV exhibits the most dramatic non-equilibrium topology simplification activity among the type IIA topoisomerases for which this activity has been characterized (11).
Since the remarkable discovery by Rybenkov et al. (11) that type IIA topoisomerases can simplify DNA topology to below equilibrium levels, several mechanisms of non-equilibrium topology simplification have been proposed, and their merits have been debated, largely through simulations. Recently, experimental tests of some non-equilibrium models have been performed. For example, direct measurements of the bend angles imposed on G-segment DNA by three type IIA topoisomerases suggest that the bend-angle model can account for some but not all of the non-equilibrium simplification activity (21). Stuchinskaya et al. (27) made a number of measurements of non-equilibrium topology simplification activity, some of which ruled out a ‘translocation’ model originally proposed by Rybenkov et al. to explain the non-equilibrium activity. In this model, type II topos use the energy of ATP hydrolysis to translocate along the DNA, thereby localizing links to smaller loops that are more readily removed. Contrary to the premise of this model, the presence of high affinity DNA-binding proteins acting as translocation ‘roadblocks’ did not alter the degree of non-equilibrium topology simplification. A ‘three-segment’ binding model that postulates the binding of two separate potential T-segments, one of which is passed through the G-segment, provides a mechanism of non-equilibrium simplification, but it is also associated with a shift of the centre of the steady-state topoisomer distribution that has not been observed in multiple independent studies (21,27). The remaining models that have not been directly tested are the KPR model and the hooked-juxtaposition model. The hooked-juxtaposition model shares elements of the bend-angle model, but rather than the enzyme imposing a bend on the G-segment, the model postulates that the enzyme preferentially unlinks T- and G-segments that are bent towards each other. We focused our attention on the KPR model, in which the strand-passage rate scales non-linearly, likely quadratically, with the strand collision frequency.
The experimental challenge was to devise a method of reproducibly controlling the strand collision frequency and measuring the unlinking rate. To address this challenge, we modified a single-molecule DNA ‘braiding’ assay, in which two strands of DNA attached to a magnetic bead can be wrapped around one another by rotating the bead in a magnetic tweezers instrument. We reasoned that rotating the bead by less than one full turn would impose on average a partial link between the two DNA strands, and that the relative frequency of strand collisions that a topoisomerase could act on would increase with increasing bead rotation. MC simulations of the DNA configurations based on the geometry of the double tether measured in situ confirm that the relative probability of strand collisions, which is proportional to the frequency of strand collisions under reasonable equilibrium assumptions, increases linearly with increasing bead rotation (Figure 3). Unlinking measurements with topo III confirm the increase in collision frequency with increasing bead rotation and provide a test of the assumptions implicit in comparing the results of MC simulations that provide the probability of strand collision with experimental measurement of unlinking rate. As the conclusions of the current study rely heavily on this reasonable but untested hypothesis, the topo III results were an important verification of the approach and serve as a validation of the method, which may be generally useful to probe protein-mediated DNA synapse formation. In addition, the unlinking measurements of topo III provide explicit experimental evidence, indicating that topo III is an efficient decatenase, comparable with topo IV, provided the linked DNA includes a single-stranded gapped region, lending support to its putative roles in chromosome segregation and unlinking in vivo (33). In comparison with topo III, we found that topo I failed to unlink crossed DNA molecules when tested with the same substrate, confirming that topo I and topo III likely play different roles in in vivo (Supplementary Figure S3).
The combination of the partial linking assay and MC simulations of DNA conformations permitted a sensitive test of the non-linear relationship between strand collision frequency and unlinking rate that is the central feature of the KPR model. Ruling out the kinetic selection embodied in this model raises the question as to how topo IIA enzymes achieve non-equilibrium topology simplification. As has been pointed out by Vologodskii and others, local DNA conformations and the corresponding probability of topological conversions by a topoisomerase likely result in different degrees of non-equilibrium topology simplification by different topo IIA enzymes (11,13–17,19). As proposed models have been experimentally tested and shown to be either inconsistent or insufficient to fully account for the degree of topological simplification, we posit that either local DNA bending coupled with an as yet undetermined mechanism or a selection based on an existing local conformation such as ‘hookedness’ hold the greatest promise to explain this phenomenon (13,14). MC simulations of the DNA tethers used in this study suggest that local DNA bending and hookedness did not vary significantly under our experimental conditions; thus, we were unable to test the effects of local geometry with the current measurements. We anticipate that similar approaches may be applicable to evaluate the effect of local bending and hookedness on DNA unlinking activity, and that these approaches will help elucidate the mechanistic basis for non-equilibrium topology simplification and, more generally, the process of strand capture and passage that is central to the activity of type II topoisomerases.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online: Supplementary Figures 1–3 and Supplementary References [48,51].
FUNDING
Intramural Research Program of the National Heart, Lung, and Blood Institute, National Institutes of Health (in part); Young Investigator Award from the Human Frontiers Science Program (to K.C.N.) (in part). Funding for open access charge: The Intramural Research Program of the National Heart, Lung, and Blood Institute, National Institutes of Health.
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
The authors thank James Keck for providing the topo III expression construct, Richard Neuman and Tamara Litwin for editing the manuscript, Krishan Zaveri for assistance with the gapped template construction, Alfonso Mondragón for useful discussions and David Bensimon and Vincent Croquette for supporting and encouraging this work in its initial phase.
REFERENCES
- 1.Champoux JJ. DNA topoisomerases: structure, function, and mechanism. Annu. Rev. Biochem. 2001;70:369–413. doi: 10.1146/annurev.biochem.70.1.369. [DOI] [PubMed] [Google Scholar]
- 2.Corbett KD, Berger JM. Structure, molecular mechanisms, and evolutionary relationships in DNA topoisomerases. Annu. Rev. Biophys. Biomol. Struct. 2004;33:95–118. doi: 10.1146/annurev.biophys.33.110502.140357. [DOI] [PubMed] [Google Scholar]
- 3.Forterre P, Gribaldo S, Gadelle D, Serre MC. Origin and evolution of DNA topoisomerases. Biochimie. 2007;89:427–446. doi: 10.1016/j.biochi.2006.12.009. [DOI] [PubMed] [Google Scholar]
- 4.Schoeffler AJ, Berger JM. DNA topoisomerases: harnessing and constraining energy to govern chromosome topology. Q. Rev. Biophys. 2008;41:41–101. doi: 10.1017/S003358350800468X. [DOI] [PubMed] [Google Scholar]
- 5.Wang JC. Cellular roles of DNA topoisomerases: a molecular perspective. Nat. Rev. Mol. Cell Biol. 2002;3:430–440. doi: 10.1038/nrm831. [DOI] [PubMed] [Google Scholar]
- 6.Gadelle D, Filee J, Buhler C, Forterre P. Phylogenomics of type II DNA topoisomerases. Bioessays. 2003;25:232–242. doi: 10.1002/bies.10245. [DOI] [PubMed] [Google Scholar]
- 7.Wang JC. Moving one DNA double helix through another by a type II DNA topoisomerase: the story of a simple molecular machine. Q. Rev. Biophys. 1998;31:107–144. doi: 10.1017/s0033583598003424. [DOI] [PubMed] [Google Scholar]
- 8.Bates AD, Maxwell A. Energy coupling in type II topoisomerases: why do they hydrolyze ATP? Biochemistry. 2007;46:7929–7941. doi: 10.1021/bi700789g. [DOI] [PubMed] [Google Scholar]
- 9.Wang JC. DNA topoisomerases. Annu. Rev. Biochem. 1996;65:635–692. doi: 10.1146/annurev.bi.65.070196.003223. [DOI] [PubMed] [Google Scholar]
- 10.Bates AD, Berger JM, Maxwell A. The ancestral role of ATP hydrolysis in type II topoisomerases: prevention of DNA double-strand breaks. Nucleic Acids Res. 2011;39:6327–6339. doi: 10.1093/nar/gkr258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rybenkov VV, Ullsperger C, Vologodskii AV, Cozzarelli NR. Simplification of DNA topology below equilibrium values by type II topoisomerases. Science. 1997;277:690–693. doi: 10.1126/science.277.5326.690. [DOI] [PubMed] [Google Scholar]
- 12.Vologodskii A. Theoretical models of DNA topology simplification by type IIA DNA topoisomerases. Nucleic Acids Res. 2009;37:3125–3133. doi: 10.1093/nar/gkp250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Buck GR, Lynn Zechiedrich E. DNA disentangling by type-2 topoisomerases. J. Mol. Biol. 2004;340:933–939. doi: 10.1016/j.jmb.2004.05.034. [DOI] [PubMed] [Google Scholar]
- 14.Liu Z, Zechiedrich EL, Chan HS. Inferring global topology from local juxtaposition geometry: interlinking polymer rings and ramifications for topoisomerase action. Biophys. J. 2006;90:2344–2355. doi: 10.1529/biophysj.105.076778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Trigueros S, Salceda J, Bermúdez I, Fernández X, Roca J. Asymmetric removal of supercoils suggests how topoisomerase II simplifies DNA topology. J. Mol. Biol. 2004;335:723–731. doi: 10.1016/j.jmb.2003.11.011. [DOI] [PubMed] [Google Scholar]
- 16.Vologodskii AV, Zhang W, Rybenkov VV, Podtelezhnikov AA, Subramanian D, Griffith JD, Cozzarelli NR. Mechanism of topology simplification by type II DNA topoisomerases. Proc. Natl Acad. Sci. 2001;98:3045–3049. doi: 10.1073/pnas.061029098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Yan J, Magnasco MO, Marko JF. A kinetic proofreading mechanism for disentanglement of DNA by topoisomerases. Nature. 1999;401:932–935. doi: 10.1038/44872. [DOI] [PubMed] [Google Scholar]
- 18.Yan J, Magnasco MO, Marko JF. Kinetic proofreading can explain the supression of supercoiling of circular DNA molecules by type-II topoisomerases. Phys. Rev. E Stat. Nonlin. Soft. Matter Phys. 2001;63(3 Pt 1):031909. doi: 10.1103/PhysRevE.63.031909. [DOI] [PubMed] [Google Scholar]
- 19.Timsit Y. Local sensing of global DNA topology: from crossover geometry to type II topoisomerase processivity. Nucleic Acids Res. 2011;39:8665–8676. doi: 10.1093/nar/gkr556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Klenin K, Langowski J, Vologodskii A. Computational analysis of the chiral action of type II DNA topoisomerases. J. Mol. Biol. 2002;320:359–367. doi: 10.1016/S0022-2836(02)00447-3. [DOI] [PubMed] [Google Scholar]
- 21.Hardin AH, Sarkar SK, Seol Y, Liou GF, Osheroff N, Neuman KC. Direct measurement of DNA bending by type IIA topoisomerases: implications for non-equilibrium topology simplification. Nucleic Acids Res. 2011;39:5729–5743. doi: 10.1093/nar/gkr109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liu ZR, Zechiedrich L, Chan HS. Local site preference rationalizes disentangling by DNA topoisomerases. Phys. Rev. E Stat. Nonlin. Soft. Matter Phys. 2010;81(3 Pt 1):031902. doi: 10.1103/PhysRevE.81.031902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Liu ZR, Zechiedrich L, Chan HS. Action at hooked or twisted-hooked DNA juxtapositions rationalizes unlinking preference of type-2 topoisomerases. J. Mol. Biol. 2010;400:963–982. doi: 10.1016/j.jmb.2010.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Liu ZR, Mann JK, Zechiedrich EL, Chan HS. Topological information embodied in local juxtaposition geometry provides a statistical mechanical basis for unknotting by type-2 DNA topoisomerases. J. Mol. Biol. 2006;361:268–285. doi: 10.1016/j.jmb.2006.06.005. [DOI] [PubMed] [Google Scholar]
- 25.Hopfield JJ. Kinetic proofreading: a new mechanism for reducing errors in biosynthetic processes requiring high specificity. Proc. Natl Acad. Sci. USA. 1974;71:4135–4139. doi: 10.1073/pnas.71.10.4135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ninio J. Kinetic amplification of enzyme discrimination. Biochimie. 1975;57:587–595. doi: 10.1016/s0300-9084(75)80139-8. [DOI] [PubMed] [Google Scholar]
- 27.Stuchinskaya T, Mitchenall LA, Schoeffler AJ, Corbett KD, Berger JM, Bates AD, Maxwell A. How do type II topoisomerases use ATP hydrolysis to simplify DNA topology beyond equilibrium? Investigating the relaxation reaction of nonsupercoiling type II topoisomerases. J. Mol. Biol. 2009;385:1397–1408. doi: 10.1016/j.jmb.2008.11.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schoeffler AJ, Berger JM. DNA topoisomerases: harnessing and constraining energy to govern chromosome topology. Q. Rev. Biophys. 2008;41:41–101. doi: 10.1017/S003358350800468X. [DOI] [PubMed] [Google Scholar]
- 29.Corbett KD, Berger JM. Structure, molecular mechanisms, and evolutionary relationships in DNA topoisomerases. Annu. Rev. Biophys. Biomol. Struct. 2004;33:95–118. doi: 10.1146/annurev.biophys.33.110502.140357. [DOI] [PubMed] [Google Scholar]
- 30.Roca J, Wang JC. The probabilities of supercoil removal and decatenation by yeast DNA topoisomerase II. Genes Cells. 1996;1:17–27. doi: 10.1046/j.1365-2443.1996.01001.x. [DOI] [PubMed] [Google Scholar]
- 31.Roca J, Wang JC. DNA transport by a type II DNA topoisomerase: evidence in favor of a two-gate mechanism. Cell. 1994;77:609–616. doi: 10.1016/0092-8674(94)90222-4. [DOI] [PubMed] [Google Scholar]
- 32.Hiasa H, Marians KJ. Topoisomerase III, but not topoisomerase I, can support nascent chain elongation during theta-type DNA replication. J. Biol. Chem. 1994;269:32655–32659. [PubMed] [Google Scholar]
- 33.Perez-Cheeks BA, Lee C, Hayama R, Marians KJ. A role for topoisomerase III in Escherichia coli chromosome segregation. Mol. Microbiol. 2012;86:1007–1022. doi: 10.1111/mmi.12039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hiasa H, DiGate RJ, Marians KJ. Decatenating activity of Escherichia coli DNA gyrase and topoisomerases I and III during oriC and pBR322 DNA replication in vitro. J. Biol. Chem. 1994;269:2093–2099. [PubMed] [Google Scholar]
- 35.Terekhova K, Gunn KH, Marko JF, Mondragón A. Bacterial topoisomerase I and topoisomerase III relax supercoiled DNA via distinct pathways. Nucleic Acids Res. 2012;40:10432–10440. doi: 10.1093/nar/gks780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Dekker NH, Rybenkov VV, Duguet M, Crisona NJ, Cozzarelli NR, Bensimon D, Croquette V. The mechanism of type IA topoisomerases. Proc. Natl Acad. Sci. USA. 2002;99:12126–12131. doi: 10.1073/pnas.132378799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lima CD, Wang JC, Mondragon A. Three-dimensional structure of the 67K N-terminal fragment of E. coli DNA topoisomerase I. Nature. 1994;367:138–146. doi: 10.1038/367138a0. [DOI] [PubMed] [Google Scholar]
- 38.Cornet F, Louarn J, Patte J, Louarn JM. Restriction of the activity of the recombination site dif to a small zone of the Escherichia coli chromosome. Genes Dev. 1996;10:1152–1161. doi: 10.1101/gad.10.9.1152. [DOI] [PubMed] [Google Scholar]
- 39.Corbett KD, Schoeffler AJ, Thomsen ND, Berger JM. The structural basis for substrate specificity in DNA topoisomerase IV. J. Mol. Biol. 2005;351:545–561. doi: 10.1016/j.jmb.2005.06.029. [DOI] [PubMed] [Google Scholar]
- 40.Seol Y, Neuman KC. Magnetic tweezers for single-molecule manipulation. Methods Mol. Biol. 2011;783:265–293. doi: 10.1007/978-1-61779-282-3_15. [DOI] [PubMed] [Google Scholar]
- 41.Seol Y, Neuman KC. Single-molecule measurements of topoisomerase activity with magnetic tweezers. Methods Mol. Biol. 2011;778:229–241. doi: 10.1007/978-1-61779-261-8_15. [DOI] [PubMed] [Google Scholar]
- 42.Seol Y, Zhang H, Pommier Y, Neuman KC. A kinetic clutch governs religation by type IB topoisomerases and determines camptothecin sensitivity. Proc. Natl Acad. Sci. USA. 2012;109:16125–16130. doi: 10.1073/pnas.1206480109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Neuman KC. Single-molecule measurements of DNA topology and topoisomerases. J. Biol. Chem. 2010;285:18967–18971. doi: 10.1074/jbc.R109.092437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Neuman KC, Charvin G, Bensimon D, Croquette V. Mechanisms of chiral discrimination by topoisomerase IV. Proc. Natl Acad. Sci. USA. 2009;106:6986–6991. doi: 10.1073/pnas.0900574106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Charvin G, Vologodskii A, Bensimon D, Croquette V. Braiding DNA: experiments, simulations, and models. Biophys. J. 2005;88:4124–4136. doi: 10.1529/biophysj.104.056945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Charvin G, Bensimon D, Croquette V. Single-molecule study of DNA unlinking by eukaryotic and prokaryotic type-II topoisomerases. Proc. Natl Acad. Sci. USA. 2003;100:9820–9825. doi: 10.1073/pnas.1631550100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Charvin G, Strick TR, Bensimon D, Croquette V. Topoisomerase IV bends and overtwists DNA upon binding. Biophys. J. 2005;89:384–392. doi: 10.1529/biophysj.105.060202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Charvin,G. (2004) Etudes des topoisomérases de type II par micromanipulation d'ADN. Ph.D. Thesis. Université De Paris 7, Paris, France.
- 49.Mizuuchi K, Fisher LM, O'Dea MH, Gellert M. DNA gyrase action involves the introduction of transient double-strand breaks into DNA. Proc. Natl Acad. Sci. USA. 1980;77:1847–1851. doi: 10.1073/pnas.77.4.1847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wang JC, Kirkegaard K. DNA topoisomerases. Gene Amplif. Anal. 1981;2:455–473. [PubMed] [Google Scholar]
- 51.Strick TR, Croquette V, Bensimon D. Single-molecule analysis of DNA uncoiling by a type II topoisomerase. Nature. 2000;404:901–904. doi: 10.1038/35009144. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.