Abstract
Structural models of macromolecular assemblies are instrumental for gaining a mechanistic understanding of cellular processes. Determining these structures is a major challenge for experimental techniques, such as X-ray crystallography, NMR spectroscopy and electron microscopy. Thus, computational modeling techniques, including molecular docking, are required. The development of most molecular docking methods has so far been focused on modeling of binary complexes. We have recently introduced the MultiFit method for modeling the structure of a multi-subunit complex by simultaneously optimizing the fit of the model into an electron microscopy density map of the entire complex and the shape complementarity between interacting subunits. Here, we report algorithmic advances of the MultiFit method that result in an efficient and accurate assembly of the input subunits into their density map. The successful predictions and the increasing number of complexes being characterized by electron microscopy suggests that the CAPRI challenge could be extended to include docking-based modeling of macromolecular assemblies guided by electron microscopy.
Keywords: symmetry, macromolecules, integrative modeling, electron microscopy, Gaussian mixture model, point alignment, inference
Introduction
Protein complexes are vital molecular machines of the cell1; structural characterization of these complexes provides insight into their function2. Given the number of undetermined protein complexes3 and inherent difficulties in experimentally determining the structures of these complexes at atomic resolution4, there is an acute need to develop computational methods for structural modeling of macromolecular assemblies.
Molecular docking techniques have traditionally been used to predict binary complexes given their unbound component structures. These methods rely on a global search of a large set of possible binary configurations, maximizing geometrical and physicochemical complementarities between a pair of constituent subunits5–9. The CAPRI challenge provides a critical assessment of such docking methods10. Analysis of CAPRI results shows that in some cases docking methods suffer from relatively low accuracy, especially when the individual protein subunits are modeled or when their bound and unbound conformations significantly differ9,11–13. This limitation has led to the emergence of restrained docking procedures that guide sampling and/or filter docking solutions based on additional sources of information9,14,15. Notably, the HADDOCK webserver can incorporate multiple sources of information into its docking procedure16.
While most docking methods are designed to deal with two molecules, the majority of functional macromolecular assemblies in the cell consist of more than two components. Inspired by targets in previous CAPRI rounds12, several groups have proposed docking-based modeling methods for symmetric complexes17–21. Fewer docking methods have been developed for the significantly more challenging case of asymmetric assembly modeling14,22. A major obstacle for macromolecular docking algorithms is the ability to select near-native models from an ensemble of possible solutions. Knowledge of the overall shape of a complex, even at low resolution, can significantly reduce ambiguity inherent in such an ensemble when it is used to filter the set of candidate models. Such overall shape information can be obtained by Electron microscopy (EM) 23–25 or small angle X-ray scattering 26,27 techniques.
EM is becoming a method of choice for structural visualization of large protein complexes. EM reconstruction techniques provide a density map of a complex at resolutions typically ranging from 5 Å to 25 Å28. Following generation of a density map, atomic structures of complex components are often fitted into the map to construct a “quasiatomic” model of the complex 29–31. Thus, EM data can be used not only to filter docking solutions but also to fit assembly subunits into their density. Rigid fitting techniques rely on a global search for the placement (position and orientation) of a single subunit inside the density map that maximizes the overlap between the model and the map32. However, the majority of these techniques are designed to work independently on single subunits, without taking into account protein-protein interaction interfaces.
To combine the strengths of molecular docking and molecular fitting approaches, and to overcome their limitations, we have developed the MultiFit method. MultiFit simultaneously positions protein subunits into a density map of a protein assembly by combining geometric principles commonly used in molecular fitting and molecular docking33. Here, we describe new algorithms for two of the stages of the MultiFit algorithm that significantly improve the accuracy of the method. In addition, we describe an extension of the MultiFit method for cyclic symmetric assemblies, resulting in a highly efficient algorithm that accurately treats such cases.
Below, we outline the MultiFit algorithm and describe the recent algorithmic advances. We then illustrate the method by modeling the structure of the methane monooxygenase enzyme (asymmetric complex) and the GroEL chaperone (cyclic symmetric complex), followed by results on a 10 complex benchmark. Finally, we discuss the advantages of incorporating EM data in macromolecular docking algorithms.
Methods
MultiFit is a computational method for simultaneous fitting of atomic protein structures into a protein assembly density map at resolutions as low as 25 Å. The input to the method is a set of atomic structures of subunits and an EM density map of their assembly. The MultiFit algorithm simultaneously fits the subunits into their assembly density map and optimizes the interfaces between neighboring subunits. The method’s output is a ranked list of assembly models. An assembly model of n subunits is defined as a set of n rigid three-dimensional (3D) transformations, each applied on a corresponding assembly subunit.
Scoring function
Assembly models are ranked by a geometric scoring function composed of a linear combination of three terms: (i) the quality-of-fit term scores how well a model fits into the assembly density map, (ii) the protrusion term scores how well each subunit is placed inside the density envelope and (iii) the interaction term scores the pairwise shape complementarity between pairs of interacting subunits and also accounts for their excluded volume. We use a combination of these three terms, as each alone is insufficient for an unambiguous identification of the native configuration. A detailed mathematical description of these terms is provided elsewhere33.
Optimization procedure
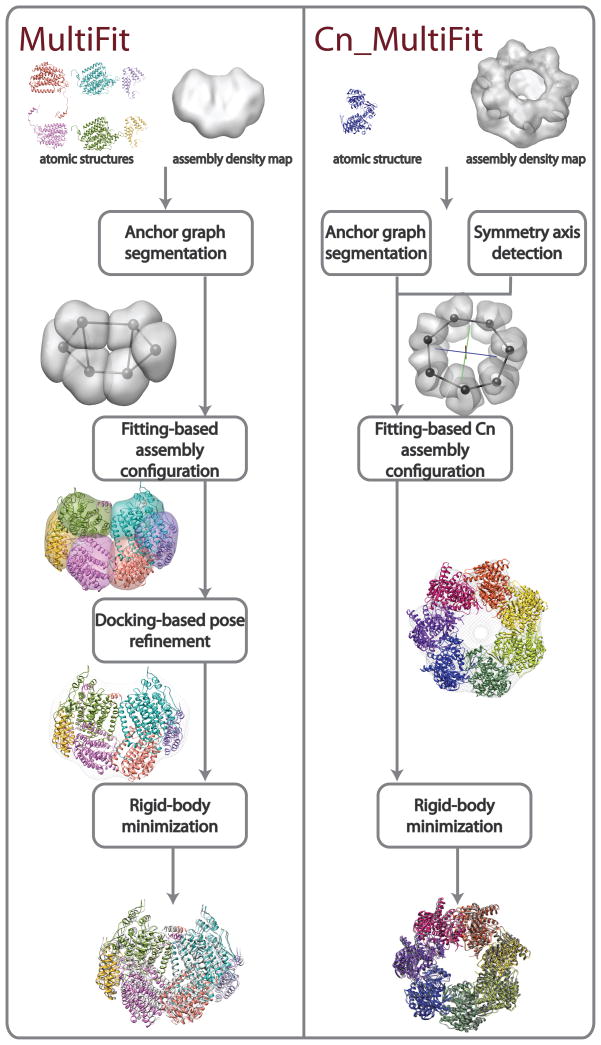
The optimization algorithm is composed of four stages, each sampling assembly models at increasingly higher resolution and accuracy, further restricting the search space to be sampled in the following stage (Figure 1): (i) anchor graph segmentation, (ii) fitting-based assembly configuration, (iii) docking-based pose refinement, and (iv) rigid-body minimization. In “anchor graph segmentation”, an unlabeled segmentation of the density map into n regions is calculated using a Gaussian mixture model clustering procedure; the segmented n regions correspond approximately to the regions allocated by the n subunits in the complex. In “fitting-based assembly configuration”, a set of coarse assembly models is found by an enumeration over possible assignments of subunits to regions, followed by simultaneous local fitting of the subunits in the corresponding regions. In “docking-based pose refinement”, each of the models found in the “configuration” stage is refined by simultaneous local optimization of the interfaces between pairs of interacting subunits. In “rigid body minimization”, each of the models found in the “refinement” stage is further refined using a local Monte Carlo/conjugate gradients minimization procedure34. Detailed description of the original optimization procedure is provided in a previous publication33. The recently developed algorithms for the “anchor graph segmentation” and “fitting-based assembly configuration” stages are described in Supplementary Materials.
Figure 1. Outline of the MultiFit protocol for simultaneous fitting.
The stages of the MultiFit (left) and the Cn_MultiFit (right) algorithms are illustrated from top to bottom. (left) The input is a density map of the MMO hydroxylase complex simulated to 20 Å resolution (gray) and atomic models of the α, β and γ subunits (colors). Segmentation of the density map into 6 regions (light gray) and the corresponding anchor graph (black) as calculated in the “anchor graph segmentation stage”. An assignment of subunits into regions and an atomic model as sampled in the “fitting-based assembly configuration” stage (colors). A refinement of the model (colors) as sampled in the “docking-based pose refinement” stage fitted to the density map (light gray). The final model (colors) superposed on the native complex (gray). (right) The input is an experimentally determined density map of the GroEL complex at 23.5 Å resolution and an atomic structure of the monomeric subunit. The predicted symmetry axis (red) as calculated in the “symmetry axis detection” stage. Segmentation of the density map into 7 regions (light gray) and the corresponding anchor graph (black). A models sampled in the “fitting-based Cn assembly configuration” stage (colors) fitting to the density map (light gray). The final model (colors) superposed on the native complex (gray).
Optimization of cyclic symmetric complexes
Many of the protein complexes determined by EM techniques are symmetric; reconstruction algorithms exploit the symmetry constraint to enhance the resolution of the generated density map28,35–37. Symmetry can also be exploited for the purpose of fitting multiple subunits into a density map of their symmetric assembly. Inspired by the success of symmetric docking algorithms20,21, we have extended MultiFit to exploit cyclic symmetry (Cn) in the optimization algorithm (Cn_MultiFit). The optimization procedure of Cn_MultiFit is composed of the following stages: (i) symmetry axis detection, (ii) anchor graph segmentation, (iii) fitting-based Cn assembly configuration, and (iv) rigid-body minimization (Figure 1). The main differences between the optimization procedures of MultiFit and Cn_MultiFit are in the “symmetry axis detection” and the “fitting-based Cn assembly configuration” stages, as described below.
Symmetry axis detection
A principal component analysis38 (PCA) based procedure is applied to determine the symmetry axis of a Cn symmetric complex. Specifically, the procedure first calculates three principal axes for the set of 3D coordinates of density map voxels that have density values within the top 20% of those for voxels in the density map. It can be shown that the assembly symmetry axis is one of its density map’s principal axes39. A statistical consistency score is then applied to identify the symmetry axis among the three principal axes39.
Fitting-based Cn assembly configuration
First, a single asymmetric subunit is fitted to a segmented region of the density map. Then, for each of the top ten fitting hypotheses, possible ring models of n copies around the complex symmetry axis are sampled. Specifically, the ring models are constructed by applying n-1 symmetry operations to the fitted asymmetric subunit. The symmetry operation that minimizes the MultiFit scoring function is selected among transformations with rotations of 360/n ± 5° around the symmetry axis and translations of ±3Å.
Results and Discussion
Modeling of the methane monooxygenase enzyme using MultiFit
To illustrate the MultiFit algorithm, we describe in detail an application to the methane monooxygenase (MMO) enzyme. The MMO enzyme plays a critical role in the metabolic pathway of Methanotrophic bacteria. It is composed of 6 subunits arranged as a dimer of hetro-trimers. We demonstrate that the structure of the MMO enzyme can be determined by simultaneously fitting its subunits into the assembly density. A density map was simulated from the MMO hydroxylase crystal structure (PDB entry 1MTY40) using the pdb2vol command of Situs41. The structures of the α, β and γ subunits were modeled using templates with sequence identities ranging from 21 to 99 using the MODELLER software42 (PDB entries 1xmgD43, 2indA44 and 1xveF45). The Cα-RMSDs between the models of the α, β and γ subunits and their bound conformations were 2.26 Å, 9.36 Å and 0.82 Å, correspondingly. MultiFit solutions were validated against a reference structure constructed by superposing the α, β and γ subunits models on the assembly crystal structure.
In the “anchor graph segmentation” stage, the assembly density map was segmented into six regions that correspond approximately to locations of the six subunits in their assembly. The segmentation procedure separated the density into such regions well, even though the shapes of the subunits were not part of the input of the procedure (Figure 1). The segmented density map was represented as an anchor graph that provides an unlabeled representation of the assembly topology. The nodes of the anchor graph correspond to the centroids of the segmented regions while edges are defined between pairs of neighboring regions. In the “fitting-based assembly configuration” stage, coarse assembly models were determined for possible assignments of subunits to anchor graph nodes. In detail, for each possible labeling of subunits to the anchor graph nodes (i.e., positioning of the assembly subunits centroids at the centroids of the segmented regions), a discrete sampling space was generated by locally fitting each subunit into its assigned region. The DOMINO optimizer33 was applied to search for the best scoring combination of fitting solutions. The Cα RMSD of the top 20 scored models to the reference complex ranges from 5.7 Å to 15.2 Å to the reference complex. Each such solution provides relatively accurate positioning of the subunits in the assembly; however, the interfaces were inaccurate as the sampling was performed independently on each subunit.
These solutions were then refined in the “docking-based pose refinement” stage. Each model found in the previous stage suggests a pairwise interaction map of the complex and approximate interfaces. A new discrete sampling space was generated by running the restrained pairwise docking program PatchDock46 on predicted interacting subunits. The PatchDock procedure was preformed with updated parameters that allowed for nonnegligible steric clashes. The DOMINO optimizer was again applied to search for the best scoring combinations of the resulting docking solutions. The result of this optimization stage was a set of 20 models, with Cα RMSD ranging from 3.9 Å to 10.5 Å to the reference complex. Finally, a rigid-body minimization procedure was applied to each of these models resulting in a best scoring model with 3.2 Å Cα RMSD to the reference complex.
For comparison, we modeled the MMO enzyme complex given its bound subunits as input. The Cα RMSD of the final model to the native complex was 1.8 Å. In the bound case, the performance of the pairwise docking algorithm could have been sufficient to model the assembly by combinatorial docking22. However, in the unbound case, due to the differences between the modeled subunits and their corresponding bound conformations, pairwise docking alone was not sufficient to supply useful intermediate results. In this example, the EM density map-based fitting procedure was crucial for detecting a near-native model.
Modeling of the GroEL chaperone using Cn_MultiFit
To illustrate the Cn_MultiFit algorithm, we describe in detail modeling of the GroEL chaperone complex. GroEL is a bacterial chaperonin that assists in the proper folding of proteins. It is composed of two back-to-back 7-mer rings. The structure of the GroEL complex has been studied extensively by EM (the EM data base47 contains 30 density maps of the GroEL complex). The input to Cn_MultiFit was a 7-mer ring of the GroEL protein extracted from an experimental density map at 23.5 Å resolution (EMD entry 104648) and a monomeric GroEL structure, which was obtained from the corresponding atomic structure (PDB entry 1GRU48). In the “symmetry axis detection” stage, the symmetry axis was correctly identified (Figure 1). In the “anchor graph segmentation” stage, the density map was segmented into 7 regions. The centroids of the segmented regions accurately correlate to the centroids of the subunits in complex, further validating our symmetry axis prediction. In the “fitting-based Cn assembly configuration” stage, we fitted a single copy of the GroEL structure to the density and used the symmetry to build possible models. The result of this stage was a set of 20 models, with Cα RMSD ranging from 4.2 Å to 9.5 Å to the native complex. Finally, a rigid body minimization procedure was applied and a model with Cα RMSD of 3.4 Å was the top-ranked result.
Benchmark
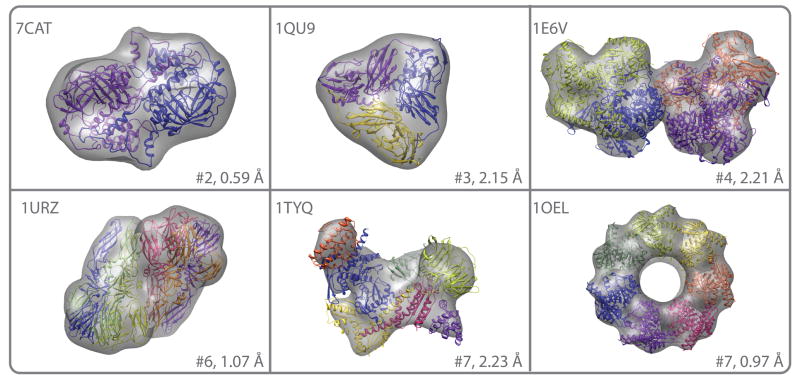
We tested the MultiFit and Cn_MultiFit algorithms on a benchmark of additional 10 complexes, six of which are asymmetric and four of which are Cn symmetric (Table I, Figure 2). The complexes were obtained from the Protein Data Bank (PDB49) and were composed of two to seven subunits. The input to each test case was an assembly density map at 20 Å resolution and structures of the assembly subunits, in the bound state, at atomic resolution. The assembly density maps were simulated using the pdb2vol command in SITUS41. The accuracy of the final set of models was assessed by the assembly placement score33, and Cα-RMSD between each model and its corresponding native structure. In all 10 cases, a model with Cα-RMSD lower than 5.05 Å was found among the top 10 ranked models.
Table I.
Benchmark results
| Assembly name | Assembly Characteristics | Best model among top ten ranked models | |||
|---|---|---|---|---|---|
| #subunits, size (mean, variance) | Cn symmetry | Difficulty level | Assembly score (°, Å) | Cα-RMSD | |
| 7CAT | 2, (498, 0) | N | Easy | (0.72, 0.01) | 0.59 |
| 1Z5S | 4, (113.7, 42.5) | N | Difficult | (33.48, 0.30) | 5.05 |
| 1GTE | 4, (1005, 0) | N | Easy | (2.22, 0.02) | 1.6 |
| 1E6V | 6, (409.6, 122.6) | N | Difficult | (10.29, 0.08) | 2.21 |
| 1URZ | 6, (385.0, 2.3) | N | Easy | (1.13, 0.013) | 1.07 |
| 1TYQ | 7, (241.7, 92.2) | N | Difficult | (5.28, 0.09) | 2.23 |
| 1NIC | 3, (333, 0) | Y | Easy | (7.63, 0.09) | 2.43 |
| 1QU9 | 3, (127, 0) | Y | Easy | (9.03, 0.16) | 2.15 |
| 2REC | 6, (303, 0) | Y | Easy | (0.87, 0.02) | 0.61 |
| 1OEL | 7, (524, 0) | Y | Easy | (1.77, 0.03) | 0.97 |
Figure 2. Benchmark results.
Final models (colors) for 6 of the benchmark cases. For each test case the PDB entry code, the number of subunits and the final Cα-RMSD to the native structure are listed.
Our results demonstrate the relative robustness of MultiFit to inaccuracies in fitting and/or docking techniques. Benchmarking revealed that fitting into an assembly of subunits with different shapes (“mixed complexes”) was less reliable than fitting a subunit into an assembly of subunits with similar shapes (“uniform complexes”), such as Cn symmetric complexes. Reasons for the relatively ambiguous intermediate results of the “fitting-based assembly configuration” stage for the “mixed complexes” versus the “uniform complexes” include: (i) the nature of the cross-correlation measure, which is biased towards high-density regions of the map31, (ii) the reduction in the number of degrees of freedom derived from the imposed Cn symmetry for some of the “uniform complexes” and (iii) errors in the segmentation used in the “anchor graph segmentation” stage, resulting in segmented regions that do not completely correspond to subunits of mixed sizes and shapes. Despite ambiguous intermediate solutions obtained in fitting some of the subunits into their assembly densities in difficult cases, a near-native model (2.21 Å to 5.05 Å Cα RMSD) was found among the top 10 models. For example, for the 1TYQ assembly of 7 subunits (Table I, Figure 2), the positions of 4 out of the 7 subunits of the complex (chains D-F) were difficult to detect by fitting techniques. However, docking between pairs of interacting subunits, as detected in the “docking based pose refinement” stage, improved the placements of these subunits; most notable is the improvement from 14.6 Å to 2.3 Å Cα-RMSD for subunit G.
In addition, ranking of docking-based models by pairwise docking methods may be inaccurate10. The strength of using EM data as an additional source of information is again demonstrated by the 1TYQ example. The correct docking pose between subunits B and F was ranked only number 943 by the PatchDock procedure, but was the top ranked result by the MultiFit combined geometric score.
Conclusions
With the growing number of macromolecular assemblies characterized by EM47, data-guided modeling techniques are becoming increasingly useful for a mechanistic understanding of these assemblies. We have recently addressed the problem of modeling architectures of macromolecular complexes by simultaneously optimizing the fit of the individual subunits into their assembly density maps and optimizing the interfaces between interacting subunits33. Here, we report algorithmic advances in the density map segmentation and subunit fitting algorithms of the MultiFit method as well as a new algorithm for the modeling of cyclic symmetric complexes. We show that even low-resolution density maps are helpful for modeling assembly architectures and can resolve ambiguous intermediate docking or fitting results. As EM techniques continue to improve, an increasing number of macromolecular complexes will be visualized at sub-nanometer resolution. Integration of intermediate-to-high resolution density map data into computational docking techniques may be extremely useful in resolving ambiguities in docking of unbound subunits and in the refinement of docking solutions. Extending the CAPRI challenge to include docking-based modeling of macromolecular assemblies guided by EM would help to advance these methods and their applicability. The MultiFit software, benchmark, and a tutorial are available as part of the IMP package under the open source lesser-GPL license at http://www.salilab.org/MultiFit/. Remaining challenges include, among others, treating protein flexibility and incorporation of data from additional sources, such as those from proteomics50.
Supplementary Material
Acknowledgments
We thank Ben Webb and Daniel Russel for continuous help and support with the IMP framework, Jeremy Phillips for useful discussions about integrative modeling and careful reading of the manuscript, Dina Schneidman for help with the PatchDock program and the reviewers for constructive suggestions. KL has been supported by the Clore Foundation PhD Scholars program, and carried out her research in partial fulfillment of the requirements for the Ph.D. degree at TAU. AS has been supported by the Sandler Family Supporting Foundation, National Institutes of Health (R01 GM54762, U54 RR022220, PN2 EY016525, and R01 GM083960). We are also grateful to Ron Conway, Mike Homer, Hewlett-Packard, NetApp, IBM, and Intel for computer hardware gifts. HJW acknowledges support from the Israel Science Foundation (grant no. 1403/09) and from the Hermann Minkowski Minerva Center for Geometry at TAU.
References
- 1.Alberts B. The cell as a collection of protein machines: preparing the next generation of molecular biologists. Cell. 1998;92(3):291–294. doi: 10.1016/s0092-8674(00)80922-8. [DOI] [PubMed] [Google Scholar]
- 2.Robinson CV, Sali A, Baumeister W. Molecular sociology of the cell. Nature. 2007;450:973–982. doi: 10.1038/nature06523. [DOI] [PubMed] [Google Scholar]
- 3.Sali A, Glaeser R, Earnest T, Baumeister W. From words to literature in structural proteomics. Nature. 2003;422(6928):216–225. doi: 10.1038/nature01513. [DOI] [PubMed] [Google Scholar]
- 4.Alber F, Forster F, Korkin D, Topf M, Sali A. Integrating diverse data for structure determination of macromolecular assemblies. Annu Rev Biochem. 2008;77:443–477. doi: 10.1146/annurev.biochem.77.060407.135530. [DOI] [PubMed] [Google Scholar]
- 5.Pons C, Grosdidier S, Solernou A, Perez-Cano L, Fernandez-Recio J. Present and future challenges and limitations in protein-protein docking. Proteins. 78(1):95–108. doi: 10.1002/prot.22564. [DOI] [PubMed] [Google Scholar]
- 6.Halperin I, Ma B, Wolfson H, Nussinov R. Principles of docking: An overview of search algorithms and a guide to scoring functions. Proteins. 2002;47(4):409–443. doi: 10.1002/prot.10115. [DOI] [PubMed] [Google Scholar]
- 7.Vajda S, Kozakov D. Convergence and combination of methods in protein-protein docking. Curr Opin Struct Biol. 2009;19(2):164–170. doi: 10.1016/j.sbi.2009.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ben-Zeev E, Kowalsman N, Ben-Shimon A, Segal D, Atarot T, Noivirt O, Shay T, Eisenstein M. Docking to single-domain and multiple-domain proteins: old and new challenges. Proteins. 2005;60(2):195–201. doi: 10.1002/prot.20557. [DOI] [PubMed] [Google Scholar]
- 9.Ritchie DW. Recent progress and future directions in protein-protein docking. Curr Protein Pept Sci. 2008;9(1):1–15. doi: 10.2174/138920308783565741. [DOI] [PubMed] [Google Scholar]
- 10.Janin J, Henrick K, Moult J, Eyck LT, Sternberg MJ, Vajda S, Vakser I, Wodak SJ. CAPRI: a Critical Assessment of PRedicted Interactions. Proteins. 2003;52(1):2–9. doi: 10.1002/prot.10381. [DOI] [PubMed] [Google Scholar]
- 11.Lensink MF, Mendez R, Wodak SJ. Docking and scoring protein complexes: CAPRI 3rd Edition. Proteins. 2007;69(4):704–718. doi: 10.1002/prot.21804. [DOI] [PubMed] [Google Scholar]
- 12.Janin J. The targets of CAPRI rounds 3–5. Proteins. 2005;60(2):170–175. doi: 10.1002/prot.20553. [DOI] [PubMed] [Google Scholar]
- 13.Janin J. Assessing predictions of protein-protein interaction: the CAPRI experiment. Protein Sci. 2005;14(2):278–283. doi: 10.1110/ps.041081905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Karaca E, Melquiond AS, de Vries SJ, Kastritis PL, Bonvin AM. Building macromolecular assemblies by information-driven docking: introducing the HADDOCK multi-body docking server. Mol Cell Proteomics. doi: 10.1074/mcp.M000051-MCP201. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Miled N, Yan Y, Hon WC, Perisic O, Zvelebil M, Inbar Y, Schneidman-Duhovny D, Wolfson HJ, Backer JM, Williams RL. Mechanism of two classes of cancer mutations in the phosphoinositide 3-kinase catalytic subunit. Science. 2007;317(5835):239–242. doi: 10.1126/science.1135394. [DOI] [PubMed] [Google Scholar]
- 16.de Vries SJ, van Dijk M, Bonvin AM. The HADDOCK web server for data-driven biomolecular docking. Nat Protoc. 2010;5(5):883–897. doi: 10.1038/nprot.2010.32. [DOI] [PubMed] [Google Scholar]
- 17.Berchanski A, Segal D, Eisenstein M. Modeling oligomers with Cn or Dn symmetry: application to CAPRI target 10. Proteins. 2005;60(2):202–206. doi: 10.1002/prot.20558. [DOI] [PubMed] [Google Scholar]
- 18.Comeau SR, Camacho CJ. Predicting oligomeric assemblies: N-mers a primer. J Struct Biol. 2005;150(3):233–244. doi: 10.1016/j.jsb.2005.03.006. [DOI] [PubMed] [Google Scholar]
- 19.Pierce B, Tong W, Weng Z. M-ZDOCK: a grid-based approach for Cn symmetric multimer docking. Bioinformatics. 2005;21(8):1472–1478. doi: 10.1093/bioinformatics/bti229. [DOI] [PubMed] [Google Scholar]
- 20.Schneidman-Duhovny D, Inbar Y, Nussinov R, Wolfson HJ. Geometry-based flexible and symmetric protein docking. Proteins. 2005;60(2):224–231. doi: 10.1002/prot.20562. [DOI] [PubMed] [Google Scholar]
- 21.Andre I, Bradley P, Wang C, Baker D. Prediction of the structure of symmetrical protein assemblies. Proc Natl Acad Sci U S A. 2007;104(45):17656–17661. doi: 10.1073/pnas.0702626104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Inbar Y, Benyamini H, Nussinov R, Wolfson HJ. Prediction of multimolecular assemblies by multiple docking. J Mol Biol. 2005;349(2):435–447. doi: 10.1016/j.jmb.2005.03.039. [DOI] [PubMed] [Google Scholar]
- 23.Stahlberg H, Walz T. Molecular electron microscopy: state of the art and current challenges. ACS Chem Biol. 2008;3(5):268–281. doi: 10.1021/cb800037d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chiu W, Baker ML, Jiang W, Dougherty M, Schmid MF. Electron cryomicroscopy of biological machines at subnanometer resolution. Structure. 2005;13(3):363–372. doi: 10.1016/j.str.2004.12.016. [DOI] [PubMed] [Google Scholar]
- 25.Lucic V, Leis A, Baumeister W. Cryo-electron tomography of cells: connecting structure and function. Histochem Cell Biol. 2008;130(2):185–196. doi: 10.1007/s00418-008-0459-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mertens HD, Svergun DI. Structural characterization of proteins and complexes using small-angle X-ray solution scattering. J Struct Biol. 2010 doi: 10.1016/j.jsb.2010.06.012. [DOI] [PubMed] [Google Scholar]
- 27.Hura GL, Menon AL, Hammel M, Rambo RP, Poole FL, 2nd, Tsutakawa SE, Jenney FE, Jr, Classen S, Frankel KA, Hopkins RC, Yang SJ, Scott JW, Dillard BD, Adams MW, Tainer JA. Robust, high-throughput solution structural analyses by small angle X-ray scattering (SAXS) Nat Methods. 2009;6(8):606–612. doi: 10.1038/nmeth.1353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Frank J. Three-Dimensional Electron Microscopy of Macromolecular Assemblies: Visualization of Biological Molecules in Their Native State. New York: Oxford University Press; 2006. [Google Scholar]
- 29.Topf M, Sali A. Combining electron microscopy and comparative protein structure modeling. Curr Opin Struct Biol. 2005;15(5):578–585. doi: 10.1016/j.sbi.2005.08.001. [DOI] [PubMed] [Google Scholar]
- 30.Lindert S, Stewart PL, Meiler J. Hybrid approaches: applying computational methods in cryo-electron microscopy. Curr Opin Struct Biol. 2009;19(2):218–225. doi: 10.1016/j.sbi.2009.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Fabiola F, Chapman MS. Fitting of high-resolution structures into electron microscopy reconstruction images. Structure. 2005;13(3):389–400. doi: 10.1016/j.str.2005.01.007. [DOI] [PubMed] [Google Scholar]
- 32.Rossmann MG, Morais MC, Leiman PG, Zhang W. Combining X-ray crystallography and electron microscopy. Structure. 2005;13(3):355–362. doi: 10.1016/j.str.2005.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lasker K, Topf M, Sali A, Wolfson H. Inferential optimization for simultaneous fitting of multiple components into a cryoEM map of their assembly. J Mol Biol. 2009;388(1):180–194. doi: 10.1016/j.jmb.2009.02.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Topf M, Lasker K, Webb B, Wolfson H, Chiu W, Sali A. Protein structure fitting and refinement guided by cryo-EM density. Structure. 2008;16(2):295–307. doi: 10.1016/j.str.2007.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zhang J, Baker ML, Schroder GF, Douglas NR, Reissmann S, Jakana J, Dougherty M, Fu CJ, Levitt M, Ludtke SJ, Frydman J, Chiu W. Mechanism of folding chamber closure in a group II chaperonin. Nature. 2010;463(7279):379–383. doi: 10.1038/nature08701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhang X, Jin L, Fang Q, Hui WH, Zhou ZH. 3.3 A cryo-EM structure of a nonenveloped virus reveals a priming mechanism for cell entry. Cell. 2010;141(3):472–482. doi: 10.1016/j.cell.2010.03.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wolf M, Garcea RL, Grigorieff N, Harrison SC. Subunit interactions in bovine papillomavirus. Proc Natl Acad Sci U S A. 2010;107(14):6298–6303. doi: 10.1073/pnas.0914604107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bishop CM. Pattern Recognition and Machine Learning (Information Science and Statistics) New York: Springer; 2007. [Google Scholar]
- 39.Lasker K, Dror O, Shatsky M, Nussinov R, Wolfson HJ. EMatch: discovery of high resolution structural homologues of protein domains in intermediate resolution cryo-EM maps. IEEE/ACM Trans Comput Biol Bioinform. 2007;4(1):28–39. doi: 10.1109/TCBB.2007.1003. [DOI] [PubMed] [Google Scholar]
- 40.Rosenzweig AC, Brandstetter H, Whittington DA, Nordlund P, Lippard SJ, Frederick CA. Crystal structures of the methane monooxygenase hydroxylase from Methylococcus capsulatus (Bath): implications for substrate gating and component interactions. Proteins. 1997;29(2):141–152. [PubMed] [Google Scholar]
- 41.Wriggers W, Milligan RA, McCammon JA. Situs: A Package for Docking Crystal Structures into Low-Resolution Maps from Electron Microscopy. J Struct Biol. 1999;125:185–195. doi: 10.1006/jsbi.1998.4080. [DOI] [PubMed] [Google Scholar]
- 42.Sali A, Blundell TL. Comparative protein modelling by satisfaction of spatial restraints. J Mol Biol. 1993;234(3):779–815. doi: 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]
- 43.Sazinsky MH, Merkx M, Cadieux E, Tang S, Lippard SJ. Preparation and X-ray structures of metal-free, dicobalt and dimanganese forms of soluble methane monooxygenase hydroxylase from Methylococcus capsulatus (Bath) Biochemistry. 2004;43(51):16263–16276. doi: 10.1021/bi048140z. [DOI] [PubMed] [Google Scholar]
- 44.McCormick MS, Sazinsky MH, Condon KL, Lippard SJ. X-ray crystal structures of manganese(II)-reconstituted and native toluene/o-xylene monooxygenase hydroxylase reveal rotamer shifts in conserved residues and an enhanced view of the protein interior. J Am Chem Soc. 2006;128(47):15108–15110. doi: 10.1021/ja064837r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Sazinsky MH, Lippard SJ. Product bound structures of the soluble methane monooxygenase hydroxylase from Methylococcus capsulatus (Bath): protein motion in the alpha-subunit. J Am Chem Soc. 2005;127(16):5814–5825. doi: 10.1021/ja044099b. [DOI] [PubMed] [Google Scholar]
- 46.Duhovny D, Nussinov R, Wolfson HJ. Efficient Unbound Docking of Rigid Molecules. In: Guido R, Gusfield D, editors. Lecture Notes in Computer Science London; Second International Workshop on Algorithms in Bioinformatics; Springer-Verlag: 2002. pp. 185–200. [Google Scholar]
- 47.Henrick K, Newman R, Tagari M, Chagoyen M. EMDep: a web-based system for the deposition and validation of high-resolution electron microscopy macromolecular structural information. J Struct Biol. 2003;144(1–2):228–237. doi: 10.1016/j.jsb.2003.09.009. [DOI] [PubMed] [Google Scholar]
- 48.Ranson NA, Farr GW, Roseman AM, Gowen B, Fenton WA, Horwich AL, Saibil HR. ATP-bound states of GroEL captured by cryo-electron microscopy. Cell. 2001;107(7):869–879. doi: 10.1016/s0092-8674(01)00617-1. [DOI] [PubMed] [Google Scholar]
- 49.Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The protein data bank. Nucleic Acids Res. 2000;28(1):235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lasker K, Phillips JL, Russel D, Velazquez-Muriel J, Schneidman-Duhovny D, Webb B, Schlessinger A, Sali A. Integrative Structure Modeling of Macromolecular Assemblies from Proteomics Data. Mol Cell Proteomics. 2010 doi: 10.1074/mcp.R110.000067. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.