Abstract
Electrodermal activity is characterized by the superposition of what appear to be single distinct skin conductance responses (SCRs). Classic trough-to-peak analysis of these responses is impeded by their apparent superposition. A deconvolution approach is proposed, which separates SC data into continuous signals of tonic and phasic activity. The resulting phasic activity shows a zero baseline, and overlapping SCRs are represented by predominantly distinct, compact impulses showing an average duration of less than 2 s. A time integration of the continuous measure of phasic activity is proposed as a straightforward indicator of event-related sympathetic activity. The quality and benefit of the proposed measure is demonstrated in an experiment with short interstimulus intervals as well as by means of a simulation study. The advances compared to previous decomposition methods are discussed.
Keywords: EDA, SC, GSR, Deconvolution, Decomposition, Phasic, Tonic, Integration, Sudomotor activity
1. Introduction
Electrodermal activity (EDA) refers to the variation of the electrical properties of the skin in response to sweat secretion. By applying a low constant voltage, the change in skin conductance (SC) can be measured non-invasively (Fowles et al., 1981). This easy acquisition and the exclusive innervation of the sweat glands by the sympathetic nervous system contribute to the wide application of SC measures in basic as well as clinical research (Dawson et al., 2007). Sudomotor activity plays a major role in thermoregulation (Wenger, 2003) and in keeping the skin flexible for sensory discrimination (Jänig, 2006), but it is also a concomitant of the orienting response and more general of emotional arousal (Boucsein, 1992). Clinical application encompasses a variety of fields, such as the assessment of pain (e.g., Ledowski et al., 2007; Storm, 2008), schizophrenia (e.g., Raine et al., 1999; Yamamoto and Hornykiewicz, 2004) or peripheral neuropathy (e.g., Polo et al., 2000; Torigoe et al., 1999).
The activity of sweat glands is triggered by postganglionic sudomotor fibers. Each sweat gland is innervated by many different sudomotor fibers (Kennedy et al., 1994; Riedl et al., 1998) and each sudomotor fiber innervates a skin area of about 1.28 cm2 (Schmelz et al., 1998). The average firing rate of sudomotor fibers was assessed as 0.62 Hz (Macefield and Wallin, 1996). The temporal concurrence in the firing of multiple fibers is identified as a nerve burst in the integrated nerve record; however, single fibers usually contribute only one single spike to each nerve burst (Macefield and Wallin, 1996). A sudomotor nerve burst corresponds to an observable skin conductance response (SCR). The spike density (as reflected by the amplitude of the nerve burst in the integrated nerve record) is linearly related to the number of recruited sweat glands (Freedman et al., 1994; Nishiyama et al., 2001) and to the amplitude of the corresponding SCR (Bini et al., 1980; Lidberg and Wallin, 1981). The SCR amplitude can therefore be considered as an index of sympathetic activity.
The time series of SC can be characterized by a slowly varying tonic activity (i.e., skin conductance level; SCL) and a fast varying phasic activity (i.e., SCRs). SCRs may reflect stimulus-specific responses or non-specific responses. An SCR shows a steep incline to the peak and a slow decline to the baseline. The succession of SCRs usually results in a superposition of subsequent SCRs, as one SCR arises on top of the declining trail of the preceding one. In empirical research, it is a common procedure to assess the event-related activity to a given stimulus or intervention by gauging the amplitude of the elicited SCRs. The standard peak detection method (trough-to-peak) defines the SCR amplitude as the difference of the SC values at its peak and at the preceding trough (Boucsein, 1992; Edelberg, 1967). SCRs which occur in a predefined response window (typically 1–3 s or 1–5 s after the stimulus) are attributed to the stimulus (Dawson et al., 2007; Levenson and Edelberg, 1985). Additionally, a minimum amplitude criterion (e.g., 0.05 μS) is often applied.
This scoring technique, however, can be complicated in the case of closely superposing SCRs. Presuming an additive superposition of subsequent SCRs, the shape of an SCR could be altered by the trails of preceding phasic activity (Boucsein, 1992). The degree of alteration would depend on the amplitude and proximity of preceding SCRs (Grings and Schell, 1969). For standard peak detection, the non-consideration of the declining trails of preceding activity is expected to result in an underestimation of the amplitude of subsequent SCRs. This methodological effect, which may cause artificial response attenuation, must not be confounded with potential refractory processes of the sweat gland, which may cause factual attenuation of later responses. However, experiments applying intraneural stimulation do not show significant response attenuation for repeated stimulation (Kunimoto et al., 1992a,b), which indicates that refractory processes may not have a strong impact on SCR amplitude.
The issue of superposing responses motivated the proposal of several methodological developments aiming at more precise assessments of the SCR amplitude. Lim et al. (1997) proposed a curve-fitting method for the decomposition of 10-s segments of SC data. A four- to eight-parameter model accounts for the SCL, the slope of preceding phasic activity and the shape of one or two overlapping SCRs. After the appropriate model is determined by visual inspection of the respective data segment, the model will be fitted to the data using a least-squares method. Lim et al. (1997) reported significant increases of SCR amplitude and latency as compared to the standard trough-to-peak method, and demonstrated the applicability of the method to settings with short ISIs in studies involving normal adults as well as a patient group (Lim et al., 1999a,b).
Alexander et al. (2005) introduced a decomposition method by means of deconvolution. The method is based on the assumption that sudomotor nerve activity originally shows peaks (sudomotor bursts) with short time constants which trigger SCRs exhibiting larger time constants. The deconvolution of SC data with an appropriate impulse response function (IRF; also called transfer function) is intended to reverse this transformation. The IRF represents the basic SCR shape that would result from a unit impulse. A Bateman function (i.e., a biexponential function) with the parameters τ1 = 0.75 s and τ2 = 2 s was found to represent an adequate IRF in this deconvolution procedure. Schneider (1987) originally proposed a physiological rationale for the biexponential shape based on a two-compartment diffusion process. The resulting driver showed predominantly distinct impulses2 (i.e., peaks), which could be extracted from the signal and used to reconstruct the corresponding SCRs. The scores derived from the reconstructed SCRs were shown to compare favorably to the trough-to-peak method. Bach et al. (2009) also assume that one single canonical IRF could represent the average response shape. A canonical IRF extracted by means of PCA over all available participants and trials, and fitted with a gamma distribution was found to account for 52% of the variance in responses. They propose to employ this IRF in an efficient time-series analysis, which is akin to the common analysis of event-related functional resonance imaging data. Since this analysis collapses all data to one score per condition, which comes in arbitrary units, differences of this method as compared to previous measures are not directly testable.
Deconvolution relies on the precondition that there exists a stable IRF (i.e., SCR shape). Research on differences in SCR rise-time and recovery-time, however, indicates that the SCR shape shows not only a significant inter-individual variability but also a significant intra-individual variability (Breault and Ducharme, 1993; Edelberg and Muller, 1981; Janes et al., 1985). It can easily be shown that deviations of the data from a model IRF result in implausible driver responses (Benedek and Kaernbach, 2010). If the assumed recovery process of the IRF is slow (i.e., the time constant τ2 is high), the driver may become negative for some SCRs. A negative driver, however, cannot be interpreted in terms of sudomotor activity. On the other hand, if the recovery process is chosen fast, the deconvolution analysis results in less compact impulses in the driver function.
Benedek and Kaernbach (2010) addressed this problem and put forward the decomposition of SC data by means of nonnegative deconvolution. This method claims nonnegativity of the driver and maximal compactness of the impulses. It offers a technique for the estimation of the tonic activity (i.e., SCL) based on a fit of the inter-impulse intervals of the driver resulting from standard deconvolution. Phasic activity can then be extracted by subtracting the SCL from the SC data. Nonnegative deconvolution, applied to the phasic SC data, results in two phasic signals, a nonnegative phasic driver and a remainder. The phasic driver is found to exhibit a zero baseline intermitted by predominantly distinct peaks. The remainder signal captures all deviations from the standard SCR shape. These deviations were found to show a specific pattern contingent to the SCR peak. Benedek and Kaernbach hypothesized that they reflect a pore opening process (Edelberg, 1993). The method accounts for inter-individual differences in the SCR shape and selects the most adequate τ parameters for the IRF in the course of an optimization procedure. The average estimate for the IRF shows a comparable τ1 parameter (0.46 s) and a τ2 parameter which is markedly larger (29.06 s) as compared to the parameters used by Alexander et al. (2005). The slow SCR recovery process revealed by this method seems to correspond more closely to the sweat diffusion from the skin. With this method, the SCL appears to be a nearly constant function of time, varying over minutes rather than seconds. The re-composition of all extracted components results in a valid reconstruction of the original SC data.
This approach is based on the assumption that variations of the shape of the SCR are due to pore opening processes occurring in close temporal vicinity to the SCR peak (Edelberg, 1993). While the results of this study supported this view, microscopic observations in parallel to SC recordings would be needed in order to further corroborate this hypothesis.
2. Aims of the proposed method
Probably the most common reason for assessing SC is to obtain an indicator of phasic sympathetic activity (i.e., sudomotor nerve activity; SMNA). Integrated SMNA is usually conceived as a continuous measure reflecting the spike density of relevant sudomotor neurons and was found to show a stable baseline activity with quite compact peaks of increased activity (Macefield and Wallin, 1996; Mano et al., 2006). The continuous signal of integrated SMNA could be conceived to carry the essential information on sympathetic activity for any given point in time. SC is thought to basically reflect SMNA to some extent, but the original signal properties of SMNA are blurred, presumably amongst other things by the influence of slow sweat diffusion processes. Therefore, SC no longer shows distinct peaks of phasic activity, but rather is characterized by the superposition of extended responses, which eventually complicates the assessment of responses (Boucsein, 1992).
There have been different valuable approaches to decompose SC data in order to obtain more precise estimates of SCR amplitudes (Alexander et al., 2005; Benedek and Kaernbach, 2010; Lim et al., 1997), all of them trying to reduce the impact of superposition effects and to get a more adequate indicator of sympathetic activity. The present approach does not focus at a further enhancement of SCR amplitudes, but aims at establishing a continuous measure that reflects more closely the original properties of the underlying SMNA (i.e., continuous signal with stable baseline activity and compact peaks of increased activity). The obtained measure should allow for the computation of straightforward indicators of phasic response magnitude, acknowledging the de facto continuous shape of apparently discrete single responses.
The proposed method is based on a standard deconvolution algorithm. It addresses the problem of the varying SCR shape differently from the former approach by Benedek and Kaernbach (2010). It is not based on the poral valve model of Edelberg (1993) and hence is more parsimonious as to its theoretical assumptions. The temporal vicinity of the SCR peak is examined in terms of Bateman functions, attributing the variability of the SCR shape to the trail of the SCR and consigning it to a more variable SCL. By employing inter-individually adjusted IRFs with short time constants combined with a technique for the estimation and subtraction of tonic activity, one continuous estimate of phasic activity is obtained, which is compatible with a stable IRF. The present approach abandons the concept of single, discrete responses in favor of a continuous measure of phasic activity, which is assumed to be an adequate indicator of sympathetic activity. It allows for the computation of a straightforward indicator of event-related activity by means of response window integration. The adequacy of the proposed method is examined on basis of empirical as well as simulation data.
3. Extracting continuous phasic activity: rationale and procedure
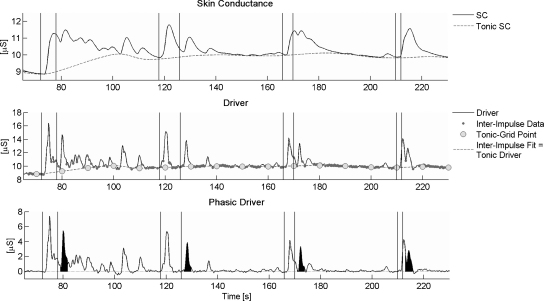
The extraction procedure basically involves three steps: the deconvolution of SC data and the subsequent estimation of tonic and phasic activity. The procedure is initially performed for a predefined parameter set (e.g., τ1 = 0.75, τ2 = 2), and a value for the goodness of the model is determined. In order to increase the goodness of the model, the initial parameters will be optimized, which involves rerunning all three steps for each new parameter set. In the following, the single steps of the extraction procedure are described in more detail and exemplified on basis of a sample of SC data (see Fig. 1). The entire extraction is performed using self-developed SC analysis software (Ledalab 3.2.2) written in MATLAB, which is available online (www.ledalab.de).
Fig. 1.
Phasic driver extraction illustrated for a SC data section of 165 s including four trials with pairs of stimuli realizing ISIs of 6, 8, 4 and 2 s (stimulus times are indicated by vertical lines). The upper row shows the original SC data. The middle row shows the driver signal which results from deconvolution of the SC data. Inter-impulse data are used to estimate the tonic part of the driver at 10-s intervals (tonic grid points). The tonic driver is used to compute the tonic SC (see upper row). Subtraction of the tonic part from the driver results in the phasic driver (lower row). The phasic driver shows a virtually zero baseline and distinct phasic responses. The time integral of the phasic driver for the second stimulus per trial is shaded in black (response window 1–4 s after stimulus onset).
3.1. Deconvolution of SC data
Sudomotor nerve activity causes sweat secretion and thus triggers a specific change in skin conductivity. In mathematical terms, sudomotor nerve activity can be considered as a driver, consisting of a sequence of mostly distinct impulses (i.e., sudomotor nerve bursts), which trigger a specific impulse response (i.e., SCRs). The IRF describes the course of the impulse response over time. The result of this process can be represented by convolution of the driver with the IRF:
| (1) |
Phasic SC activity is assumed to overlie a slowly varying tonic SC activity (Boucsein, 1992; see Fig. 1, upper row). SC activity thus can be assumed to be composed as follows:
| (2) |
Tonic SC activity can equally be represented as the convolution of some sort of tonic driver function convoluted with the same IRF. Although mathematically correct, this procedure is not physiologically motivated. This is, however, not relevant, because the process of deconvolution is reversible and we will resort to the convoluted tonic activity when estimating the phasic activity. SC data can then be represented by:
| (3) |
Deconvolution reverses the process of convolution. Deconvolution of SC data results in a driver function which encompasses a phasic as well as a tonic fraction. If one of them can be estimated, the other results implicitly:
| (4) |
3.2. Estimation of tonic activity
Tonic EDA can be observed in the absence of any phasic activity (Boucsein, 1992). However, SCRs (representing phasic SC activity) have a slowly recovering trail which may obscure any tonic SC activity. For the driver, the time constant of phasic responses is markedly reduced and so is their overlap. Time intervals between distinct phasic impulses can then be used to estimate tonic activity.
The estimation of the tonic proportion in the driver is performed similar as previously described for the method of nonnegative deconvolution (Benedek and Kaernbach, 2010). Convolution can be conceived as a smoothing operation. Deconvolution has the reverse effect and amplifies error noise. Therefore, the resulting driver is smoothed by convolution with a gauss window (σ = 200 ms). Then, peak detection is performed on the smoothed driver by finding zeros in the first time-derivative. A significant peak is detected if a local maximum has a difference of δ ≥ 0.2 μS from its preceding or following local minimum.3 An impulse section is defined by the local minima preceding and succeeding the significant peak in time. All time sections that are not part of detected impulses (inter-impulse sections) are considered to reflect the non-overlapped tonic driver. An interpolation procedure is applied in order to extend the estimation of the tonic driver to the total time range. To this end, a time grid of 10-s spacing is defined and the tonic driver values at these intermittent time points are estimated by averaging the driver values of available inter-impulse sections within the range of one grid spacing before and after the grid points. A cubic spline fit is used to interpolate the tonic driver based on the grid data (see Fig. 1, middle row). Finally, the tonic SC activity is retrieved by convolution of the tonic driver with the IRF.
3.3. Estimation of phasic activity
According to Eq. (4), the phasic driver can now be computed by subtracting the tonic driver from the total driver signal. This subtraction results in a signal, which shows a virtually zero baseline and positive deflections (see Fig. 1, lower row), reflecting the time-constrained nature of the phasic activity underlying the original SC data. In contrast to nonnegative deconvolution, this phasic driver can take on negative values. These negativities may arise from the selection of a sub-optimal IRF or from artifacts in the recorded SC data. They thus give information on the quality of the extraction algorithm and of the original SC data. Again, phasic SC data could be retrieved by convolution of the phasic driver with the IRF. Adding phasic and tonic SC data perfectly adds up to the original SC data.
3.4. Optimization
The most adequate realization of the IRF is unknown and thought to depend on inter-individual differences in skin characteristics. Therefore, the initial parameter set is optimized according to criteria which evaluate the quality of the obtained model. First, the phasic driver should show distinct, compact impulses with a short support (i.e., time or sample number with non-zero values) and approach zero between deflections. As an indicator of indistinctness (indist), the numbers of succeeding samples with values above a predefined threshold (5% of maximum of phasic driver) are counted and the result is divided by the sampling rate. These values represent the length of non-zero sections in seconds. For reasons of standardization, they are squared, summed and finally divided by the total duration of the data. This measure comes out in units of square seconds per second (s2/s) and returns high values when there are long time sections above threshold. Second, the negativity of the phasic driver should be as low as possible. The RMS of the negative proportion of the phasic driver can be considered as an adequate measure of its negativity (neg). Finally, a compound criterion c was defined as a weighted sum of both indicators:
| (5) |
According to the empirical data of the experimental study, comparable variance contributions were given, when the negativity measure was multiplied by a factor of α = 6 s2/(s μS). The solution is optimized by minimizing the criterion c. Low criterion scores are obtained for a solution based on a phasic driver featuring a zero baseline intermitted by short compact impulses. The optimization is achieved by means of a gradient descent method (e.g., Snyman, 2005), which essentially changes parameters in direction of highest criterion improvement until no further significant improvement can be obtained.
4. Study 1: experiment on variation of the interstimulus interval
4.1. Methods
4.1.1. Participants
Forty-eight healthy student volunteers (36 females) were recruited at the Christian-Albrecht University of Kiel by means of advertisement. Mean age of the participants was 23.5 years (SD = 6.04). Prior to the experiment, the participants were presented with single noise bursts of 85, 90 and 95 dB SPL. They were told that the experiment comprised a series of noise bursts of 95 dB. After this instruction, participants could decide upon participation. No participant refused to participate. All participants gave their written informed consent and were paid for their participation. The procedure was approved by the ethics committee of the German Psychological Society.
4.1.2. Equipment and data acquisition
The experiment took place in a soundproof cabin. The stimuli were presented via a closed Beyerdynamic DT 770 PRO headphone (Heilbronn, Germany). A 16-channel bioamplifier (Nexus-16; Mind Media B.V.; Roermond-Herten, The Netherlands) providing 24 Bit A/D conversion was used for data acquisition. A customer-specific sensor was used for EDA recording, ensuring the acquisition of completely raw, unfiltered EDA data. A constant current method was applied (Boucsein, 1992), using a voltage source of 10 V connected in series with 13.2 MΩ. Thus, for SC in a typical range of 1 μS or higher the sensor maintained a voltage of less than 0.8 V between the electrodes. The recorded voltage reflects changes in skin resistance (SR). SC data was obtained by computing the reciprocal of SR. The two flat Ag–AgCl electrodes of 10 mm diameter were placed at the medial phalanges of the digits III and IV of the non-dominant hand. According to common recommendations (Fowles et al., 1981), the electrodes were prepared with an isotonic paste (EC33, Grass Technologies). SC data was sampled at 32 Hz. As part of a standard routine, blood volume pulse was recorded via a photoplethysmograph placed on digit II of the non-dominant hand (sampled at 128 Hz), respiration was assessed via a respiration belt placed on the chest (sampled at 32 Hz) and EMG was recorded at the musculus orbicularis oculi (sampled at 2048 Hz). The data of these additional sensors, however, were not analyzed.
4.1.3. Experimental task and procedure
After a rest period of 1 min the participants were presented with a series of noise bursts (white noise, 95 dB SPL, 120 ms total duration with 20 ms linear ramps). The stimuli were grouped into three blocks of four trials. One trial consisted of two noise bursts exhibiting an interstimulus interval (ISI) of 2, 4, 6, or 8 s. Each ISI was realized exactly once within each block. The ISIs within each block were randomized with the only condition that the first ISI of each block was not the same as the last of the preceding block, thus ensuring that two consecutive ISIs were different from each other for the whole sequence. The inter-trial interval was 40 s.
Participants were seated in a chair with a neck-rest, with their non-dominant forearm placed on a soft armrest. After attachment of the physiological sensors, the participants were asked to find a comfortable position and to avoid any unnecessary movement during the experiment. During the experimental session, the experimenter sat outside of the cabin and monitored the stimulus presentation and the recorded physiological data. The experiment took about 30 min in total.
4.1.4. Analysis of general response characteristics
Let us first consider typical characteristics of single SCRs as represented in the phasic driver. While such an analysis is not required for most experimental questions related to electrodermal activity, its result may be interesting for understanding the relation between the phasic driver and its neural correlate. The typical phasic driver response was usually represented by a single distinct impulse in the phasic driver signal. The computation of response characteristics referred to the dominant impulse within a five seconds interval following stimulus onset. To this end, the data within this 5 s time interval was smoothed by convolution with a gauss window (σ = 200 ms) and the maximal response within this time window was identified by means of standard peak detection. The impulse section was then defined as the time between the local minima preceding and succeeding the peak with the maximal amplitude. The identified maximum and the length of the impulse section already represent coarse estimates of impulse latency and duration. In order to allow for more robust estimates, which consider the entire course of the impulse, the impulse latency and duration were estimated by means of the first and second moment of the impulse section. The calculation of the moments for distinct distributions P(x) was defined as follows (Papoulis and Pillai, 2002):
| (6) |
The first moment about zero μ1(0) equals the expected value or mean and is usually simply denoted or μ; the second moment around the mean μ2 = μ2(μ) is equal to the variance and is usually simply denoted μ2. Hereby, is a robust measure of the response latency which rather refers to its peak time than to the onset time. The variance μ2 can be considered as a robust measure of response extension. The response duration d thus can be estimated by taking four standard deviations (i.e., square root of the variance μ2):
| (7) |
4.1.5. Scoring of the response magnitude
A major advantage of the extraction of a continuous measure of phasic activity (the phasic driver) is the possibility of using a time integral of this continuous measure over the entire response window instead of relying on the detection of distinct peaks. The phasic driver time integral reflects the cumulative phasic activity, underlying SC data, within a specified response window (compare Fig. 1, lower row). This measure could thus be labeled integrated skin conductance response (ISCR). As the phasic driver shows a zero baseline, the computation of the ISCR simply involves the integration (i.e., area under the curve) of the phasic driver signal over a specified response window. The ISCR then is given in the unit of μS s. This scoring method is straightforward. It does not only decrease biases due to superposing SCRs, but it also considers the continuous shape of phasic responses, and circumvents tricky issues such as the localization of local minima and maxima. It is the method that we propose for the scoring of the response magnitude in skin conductance data.
For reasons of better comparability with the classic trough-to-peak analysis (CTTP; i.e., peak detection) the data were in addition analyzed with what could be called “improved trough-to-peak analysis” (ITTP). For this analysis, the phasic SC data were reconstructed from the phasic driver, taking into account only the driver within the predefined response window. This part of the driver data was convoluted with the IRF, thus restoring the phasic SC data resulting from within the response window. The reconstructed signal is comparable to the original signal except that it is rid of any tonic activity and of the influence of SCRs occurring before or after the response window. The reconstructed signal starts at 0 μS and the amplitude could therefore be assessed by taking the signal's maximum. The ITTP can be assumed to co-vary closely with the actually proposed ISCR measure, since both are derived from the continuous phasic driver signal and restricted to that part of the driver that lies within the response window. ITTP uses the same assessment principle and scaling as CTTP and it is, therefore, better suited for direct comparisons of the methods. For CTTP, the amplitude was assessed by the sum of amplitudes of all SCRs with onset (defined by a local minimum) within the response window.
The response window was defined to range from 1 to 4 s after the stimulus and the minimum amplitude criterion was set to 0.05 μS.
4.1.6. Statistical analysis
In order to account for the positively skewed distributions of SCR amplitudes, all scores were standardized with the formula y = log(1 + x) (Venables and Christie, 1980). The same standardization procedure was applied to displayed raw data, before averaging across participants. For raw phasic driver data, the procedure was adapted to y = log(1 + |x|)*sign(x), in order to account for the possibility of negative values. The respective units were labeled with log μS.
For ANOVA analyses, degrees of freedom were corrected by means of the Greenhouse-Geisser method where appropriate and Bonferroni post hoc tests were used for pair-wise comparison of means.
4.2. Results
4.2.1. Phasic driver extraction
Phasic driver extraction was automatically processed for all data. The optimization of τ parameters was performed for six different sets of initial values (all possible combinations of τ1 = 0.75 or 1.5 s and τ2 = 2, 4, or 6 s), which reliably converged toward a common solution as indicated by good absolute agreement of optimized τ-values (ICC(3,1) = .70 for τ1 and ICC(3,1) = .78 for τ2, respectively). For each data set, the solution with the overall lowest model error was kept. The optimized values ranged from 0.24 to 2.56 for τ1 and from 0.73 to 7.80 for τ2; the average optimized parameters were τ1 = 0.96, and τ2 = 3.76 (SD = 0.56 and 1.88, respectively). The average negativity score (before adjustment of variance, see methods section) was 0.05 μS (SD = 0.03) and the average indistinctness was 0.39 s2/s (SD = 0.21). A further examination of the distribution of the phasic driver showed that 75% of the data ranged between ±0.20 μS, while the phasic driver maximum was on average 6.50 (SD = 3.37). These distribution characteristics appear typical for a signal which predominantly varies around a zero baseline but shows some large deflections. The variability of the tonic activity was assessed by averaging the tonic activity for intervals of ten seconds and computing the mean absolute difference of succeeding time intervals (Benedek and Kaernbach, 2010). The tonic activity showed a mean variation of 0.11 μS (SD = 0.06) per 10 s.
4.2.2. Event-related activation
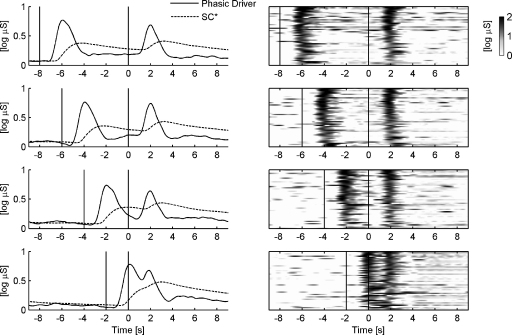
Fig. 2 displays the electrodermal response to the experimental trials with varying ISI (2, 4, 6, and 8 s). For the averaged SC data, the SCRs to the two stimuli were highly overlapped for all ISI conditions. For an ISI of only 2 s, both responses were merged so closely that the latter did no longer show a local minimum and thus no distinct peak in the averaged SC data. For the average phasic driver, however, both responses were discriminable at all ISI conditions as they featured distinct peaks. While for an ISI of only 2 s, responses of the phasic driver were visibly overlapped, these responses appeared to be clearly non-overlapped for ISIs of 6 or 8 s. The depiction of non-averaged single sequences of phasic driver data (Fig. 2, on the right) illustrates the characteristics of the raw driver data underlying the averaged phasic driver. The single phasic driver responses occurred largely contingent on the ISI condition. However, the consideration of raw driver data also disclosed the typical variability of onset latency and duration of single responses. This variability appeared to be constrained by the fact that the response onset was typically found no earlier than about one second after stimulus onset.
Fig. 2.
Event-related responses to stimulus pairs (trials) with an interstimulus interval of 8, 6, 4 and 2 s are depicted in rows one to four, respectively. On the left side, the averaged phasic driver and the averaged SC data (* after subtraction of the minimum within the respective trial) are displayed for the respective ISI condition. On the right side, the 50 most powerful responses are depicted for each ISI condition. Stimulus onset latencies are indicated by vertical lines.
4.2.3. Analysis of general response characteristics
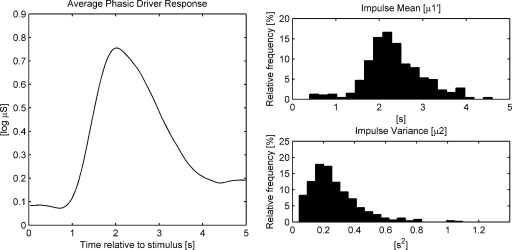
In the following, the characteristics of the phasic driver response (i.e., event-related driver impulses) will be examined in more detail. This analysis referred to both single stimuli of trials with an ISI of 6 or 8 s (50% of all stimuli), since inspection of Fig. 2 suggested that for these ISI conditions phasic responses were not overlapped. The average phasic driver response relative to stimulus onset is depicted in Fig. 3 (left side) together with the distribution of (i.e., impulse mean, reflecting the impulse peak latency) and μ2 (i.e., impulse variance, reflecting the impulse extension). The average driver response showed a steep incline starting at 0.87 s and a somewhat less steep decline ending at 4.44 s as determined by detection of local minima in the averaged response function. The average impulse mean was 2.30 s (Mdn = 2.23, SD = 0.48) and the average impulse variance was 0.25 s2 (Mdn = 0.21; SD = 0.09). Due to the skewed distribution of μ2 (see Fig. 3), the median appears to be a more meaningful estimator of the average variance. The average impulse duration estimated according to Eq. (7) and based on the median of impulse variance was 1.85 s (SD = 0.32). Assuming a symmetrical shape of the impulse, the average impulse had an onset latency of 1.38 s and an offset latency of 3.23 s after stimulus onset.
Fig. 3.
Event-related average phasic driver response for 0–5 s after stimulus onset (averaged over all stimuli of trials with ISIs of 6 or 8 s; left side), and distribution of mean () and variance (μ2) of the underlying single phasic driver responses (N = 576; right side).
Considering the average driver value at the zero-latency (0.08 log μS) as a baseline value that could be subtracted from the averaged driver response, the first five single-second intervals of the averaged driver signal encompassed 0.0, 30.5, 43.4, 18.0 and 8.1% of the total driver response area within this time range after stimulus onset. The 3-s time interval of 1–4 s after stimulus onset thus captured almost 92% of the response.
4.2.4. Comparison to the classic trough-to-peak method
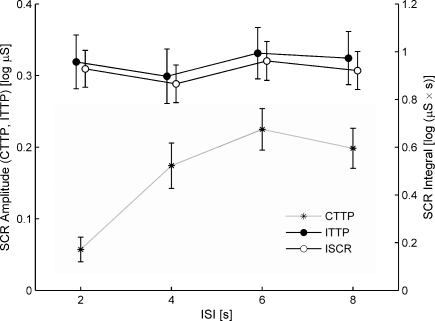
The effect of the four ISI conditions on the SCR amplitude of the second stimulus of each trial was examined by means of an ANOVA using the within-subject factor ISI (2, 4, 6 and 8 s) and the within-subject factor method (CTTP vs. ITTP). The integrated measure ISCR was not directly comparable to CTTP and ITTP as it comes in different units. It was therefore analyzed in a separate analysis. The data of six participants (12.5%) did not show any significant SCRs and thus were excluded from further analysis. The ANOVA returned a significant main effect for method (F[1,47] = 98.90, p < .001, η2 = .68, ɛ = 1) indicating that SCR amplitudes are lower by 49% when assessed using CTTP (M = 0.16 log μS, SD = 0.15) as compared to the ITTP (M = 0.32 log μS, SD = 0.24; see Fig. 4). The analysis also yielded a significant main effect ISI (F[3,141] = 7.17, p < .001, η2 = .13, ɛ = .81) and a significant interaction (method*ISI: F[3,141] = 18.95, p < .001, η2 = .29, ɛ = .82). Post hoc tests revealed that, for the CTTP method, the SCR amplitude was significantly lower for an ISI of 2 s (M = 0.06 log μS, SD = 0.11, p < .001) and tended to be lower for an ISI of 4 s (M = 0.17 log μS, SD = 0.17, p = .15) as compared to ISIs of 6 or 8 s (M = 0.21 log μS, SD = 0.15), but did not depend on ISI for ITTP. The relative difference of the assessed amplitude for CTTP as compared to ITTP was −82% for an ISI of 2, −42% for an ISI of 4 and −35% for ISIs of 6 or 8 s, respectively. A separate ANOVA for ISCR again revealed that responses according to this score did not differ for the ISI conditions (M = 0.92 log μS s, SD = 0.51; F[3,141] = 1.44, ns., η2 = .03, ɛ = .91; see Fig. 4). Inspection of Fig. 4 also indicates that the ISCR shows a lower standard error of mean as compared to the other scores. This suggests that for this integration measure the error variance is reduced.
Fig. 4.
The effect of different ISIs ranging from 2 to 8 s on the magnitude of the SCR amplitude for classic trough-to-peak (CTTP) as compared to the improved trough-to-peak (ITTP), and compared to the integrated skin conductance response (ISCR). Note, that ISCR uses different units and scaling as indicated by the ordinate on the right side.
A complementary analysis considered the relative frequency of no-response trials (i.e., trials for which no SCR met the minimum amplitude criterion in the response window relative to the second stimulus) depending on ISI. For CTTP, non-significant responses were obtained in 64, 33, 5 and 7% of the trials with an ISI of 2, 4, 6 and 8 s, respectively. For ITTP, this frequency was below 7% for all ISI conditions.
4.3. Discussion
The phasic driver derived from the experimental data shows a virtual-zero baseline with burst-like phasic responses, as indicated by the data distribution characteristics and by low values of the negativity and the indistinctness criteria. Inter-individual differences in the typical shape of SCRs are accounted for by the selection of an inter-individually optimized IRF (i.e., optimized τ parameters). The shape parameters show a considerable variability across participants and could reliably be assessed. It is assumed that these shape parameters display stable inter-individual characteristics. A retest analysis would, however, be helpful to examine this assumption.
The event-related analysis of the phasic driver reveals a well-defined response characteristic (see Figs. 2 and 3). Single responses show an average impulse peak latency of 2.30 s after stimulus onset and average impulse duration of less than 2 s. In spite of a considerable variability of single phasic responses, they almost never occur earlier than about one second after stimulus onset. This virtual hard limit is a typical characteristic of all reaction time measures and reflects the minimal time needed for preceding psychophysiological processes such as stimulus processing, nerve conduction time and neuroeffector transfer time (Lim et al., 2003). It results in the positively skewed distribution of the peak latencies and contributes to the skewed shape of the averaged phasic driver response. The onset latency of the average phasic driver response is 0.87 s after stimulus onset, which should represent the overall lower limit of response onset latencies. The data smoothing, which was necessary in the course of deconvolution, will have exerted some bias on this onset latency. By addition of twice the standard deviation of the smoothing window (for a Gauss window with σ = 200 ms this corresponds to 400 ms) physiological realities should be met more closely. The resulting onset latency of close to 1.3 s is in line with previous estimates of the onset latency (Lim et al., 2003).
Inspection of the average phasic driver response (Figs. 2 and 3) reveals that the phasic response does not immediately fully return to the pre-trial baseline after a response. The pre-trial baseline is lower than 0.1 μS and is supposed to represent the average result of spontaneous activity. The phasic driver level attained directly after a response is somewhat higher. This may have two different reasons. First, it may reflect the increased average activity due to an enhanced excitability directly after a stressing stimulus such as a noise burst. Second, it may also reflect a residual of the overshoot which is associated with the deconvolution of SC data by an IRF using short time constants (see Fig. 2 in Benedek and Kaernbach, 2010). The latter effect, however, was accounted for by using an adequate (inter-individually optimized) IRF and by estimation of the tonic activity at shorter time intervals.
The averaged phasic driver response shows a second minimum at 4.44 s marking the overall upper limit of the response offset. If we want to define a response window for phasic responses according to this phasic driver extraction, an inclusive response window would range from 0.8 to 4.5 s after stimulus onset. A more conservative response window, ranging from 1 to 4 s after stimulus onset, can still be considered to capture the essential response. For longer stimuli the definition of the response window has to consider the stimulus duration. While the lower limit refers to stimulus onset, the upper limit actually has to refer to stimulus offset and thus will have to be extended accordingly. In the case of variable stimulus duration, resulting in variable response windows, it would be advisable to divide the response window integral of the phasic driver by the duration of the response window. The ISCR would then be expressed in the unit of μS.
The observed response range is compatible with the common recommendations for response windows for the trough-to-peak method, which typically range from 1 to 3 s up to 1 to 5 s after the stimulus (Dawson et al., 2007; Levenson and Edelberg, 1985). It has to be kept in mind, however, that these windows aim at capturing only the onset of elicited SCRs, while the response range defined for the phasic driver response captures the entire response from onset to offset. The compact response range of less than four seconds, taken together with the low susceptibility to typical bias errors for short inter-SCR latencies, represent desirable preconditions for experimental paradigms involving short ISIs.
The event-related SCR amplitude was compared for the classic trough-to-peak method and two measures based on phasic driver extraction (improved trough-to-peak method and integrated skin conductance response). The CTTP method results in overall lower SCR amplitudes than the ITTP following phasic driver extraction. This is in line with previous evidence using decomposition approaches (Lim et al., 1997; Benedek and Kaernbach, 2010), suggesting that decomposition of SC data successfully reduces the assumed underestimation bias caused by close superposition of SCRs. Moreover, the CTTP method yields especially low SCR amplitudes for an ISI of 2, but also for an ISI of 4 s. This effect could be attributed to physiological or psychological recovery processes, which might attenuate responses coming in brief succession. However, ITTP did not result in especially low SCR amplitudes for these short ISI conditions. This suggests that the impact of physiological recovery processes or habituation might not have been paramount in this stimulation sequence. In this context, Baltissen et al. (1989) showed that lower SCR amplitudes for lower ISIs are only found when it was possible to anticipate a stimulus to come after short ISI (e.g., in a regularly alternating sequence of short and long ISIs) but not if the ISI was randomized. This result also conforms to evidence from studies using intraneural stimulation, which usually do not find lower SCR amplitudes for higher stimulation frequency but in some cases even find response potentiation (Kunimoto et al., 1992a,b). The differences observed by CTTP, therefore, could rather be attributed to an underestimation bias involved in trough-to-peak assessment of SCR amplitudes. This bias is expected to be highest for the shortest ISI condition, for which the trail of the preceding SCR should be steepest at the time of the following SCR.
Considering that the ISI condition of 2 s resulted in an especially high percentage of trials without any significant SCR for CTTP, another explanation should also be taken into account: the very close superposition of two SCRs might obscure the onset of the latter (i.e., the second SCR within the trial). Employing CTTP, the two SCRs then might appear as one, which would result in a misclassification of the second SCR with respect to the response window. Very close superposition of SCRs thus might result in underestimation bias for CTTP in two ways. First, the SCR amplitude may be underestimated by the ignorance of the declining remainder of preceding responses. Second, an SCR may be entirely misclassified with respect to the response window, when its onset was obscured by preceding responses. The following simulation study was designed to examine the potential impact of biases caused by these types of superposition effects.
5. Study 2: simulation on the variation of the inter-SCR interval
5.1. Methods
A simulation was set up, simulating the superposition of SCRs at varying inter-SCR latencies and comparing the effects on the SCR amplitude for scores assessed with classic trough-to-peak analysis (CTTP) as compared to improved trough-to-peak (ITTP) analysis after phasic driver extraction. The simulated SC data considered a time interval of 30 s (−10 to +20 s) and consisted of a tonic baseline activity which was superposed by an SCR with fixed position in time and by a second SCR with variable position. The baseline SC data was represented by a linear function declining by −0.02 μS/s (approximating the typical characteristic of slowly declining SC data in the absence of phasic activity). It was assumed that a stimulus at t = 0 evoked an elicited SCR which could be represented by a phasic driver response with a peak latency of 2.3 s and an impulse duration of 1.8 s. The IRF was set to τ1 = 1, τ2 = 4. These characteristics represent the average phasic response to a noise burst (see results section on event-related activity). For reasons of simplicity, the amplitude of this elicited SCR was set to 1 μS. Given the declining baseline and the predefined response characteristics, CTTP detected the onset of the (non-superposed) elicited SCR at 1.53 s. The baseline and the elicited SCR represent the default data which were kept fixed throughout the simulation. This default setting was complemented by a biasing SCR. This biasing SCR showed identical SCR characteristics as the elicited SCR except for the onset latency. The time-lag of the onset latency of the biasing SCR to the elicited SCR ranged from −6 s (i.e., the biasing SCR preceded the elicited SCR by 6 s) to +6 s (i.e., the biasing SCR followed the elicited SCR by 6 s). The variation of the time-lag was performed for steps of 0.1 s, which resulted in 121 different data scenarios. For every scenario, the SCR amplitude was assessed in a typical response window of 1–4 s after (virtual) stimulus onset (Dawson et al., 2007).
5.2. Results
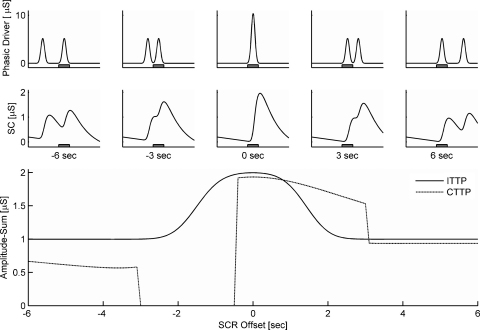
The simulation study simulated the existence of one elicited SCR which was superposed by a biasing SCR with an onset time-lag varying from −6 to +6 s. As illustrated in Fig. 5, the biasing SCR had a significant influence on the SCR amplitude estimated within the response window. Considering CTTP, four different biasing conditions could be distinguished. First, if the biasing SCR preceded the elicited SCR by more than about 3 s both SCRs had distinct onsets as defined by local minima. However, the amplitude of the elicited SCR was underestimated by up to 43% due to non-consideration of the steep decline of the SC data, which was primarily affected by the trail of the preceding SCR. Second, if the biasing SCR preceded the elicited SCR by less than three but more than about half a second only one conjoint minimum was detected (i.e., both SCRs appeared as one). Since this conjoint onset was located previous to the response window, the assessed amplitude was zero. This condition reflects full underestimation of the event-related response due to a closely preceding biasing SCR. Third, if the SCR time-lag ranged from about minus half a second to about three seconds the superposing SCRs again exhibited only one conjoint local minimum which now resided within the response window. The assessed amplitude (close to 2 μS) represented the amplitudes of both SCRs, attenuated by non-consideration of the declining baseline and the superposition of both SCRs. As a special case, for a time-lag of more than 2.5 s and less than about three seconds, the onset of the biasing SCR would actually be outside of the response window. The high amplitude scores in this case thus represented a considerable overestimation of the event-related amplitude. Forth, if the biasing SCR follows the elicited SCR by more than three seconds, both SCR showed distinct onsets defined by local minima. The assessed amplitude reflects only a minor underestimation due to non-consideration of the declining baseline.
Fig. 5.
Simulation of the amplitude of a fixed SCR, which becomes biased by a second SCR with an offset varying from −6 to +6 s. The phasic driver (first row) and SC data (second row) are displayed for −6, 3, 0, +3, and +6 s; the gray box represents the response window. The resulting amplitude-sum for SCRs within the response window is depicted dependent on the SCR offset for the classic trough-to-peak method (CTTP) and for the improved trough-to-peak method (ITTP) after phasic driver extraction (lower part of figure).
Next, the SCR amplitude determined by ITTP analysis following from phasic driver extraction will be considered. If the biasing SCR preceded or followed the elicited SCR by more than about 3 s, the impulses of the phasic driver were fully disjunct and the impulse elicited by the biasing SCR resided outside the response window (see Fig. 5). The extracted phasic response precisely corresponded to the amplitude of the elicited SCR regardless of the superposition found in the SC data. For a time-lag of less than three seconds, a part or the entire phasic response of the biasing SCR was located within the response window. As the total amount of the area of phasic driver within the response window increased, the resulting (reconstructed) SCR amplitude increased accordingly and eventually reached the sum of both amplitudes (2 μS) for the case that both impulses were fully located within the response window.
5.3. Discussion
The simulation study illustrates the impact of typical pitfalls of the classic trough-to-peak method for scoring SCR amplitudes. It shows that increasing proximity of a preceding SCR can easily cause an underestimation of the SCR amplitude of more than 40%. This is perfectly in line with the finding of Study 1 that for ISIs of 4–8 s CTTP shows reduced SCR amplitudes to the second stimulus of up to 42% as compared to ITTP following phasic driver extraction. The simulation study also reveals that if the proximity of the preceding SCR is lower than about three seconds, the second SCR shows no longer a distinct onset in terms of a local minimum and is misclassified with respect to the response window. This condition should frequently occur for responses elicited at an ISI of 2 s. In Study 1, CTTP yielded no significant SCRs in 64% of the trials for an ISI of 2 s. This suggests that the especially low SCR amplitudes obtained for CTTP at this ISI condition may not only be due to underestimation of amplitudes but could largely be attributed to misclassification of entire SCRs.
Finally, the simulation study indicates that close proximity of SCRs can also have an inverse effect. If an SCR is closely followed by a second one, the SCRs appear as one and thus may even result in an overestimation of the SCR amplitude. Since Study 1 only considered the responses to the second stimulus per trial, this effect was not observed directly.
The simulation study thus helped to elucidate some major issues underlying the scoring bias of the classic trough-to-peak method observed in Study 1. It also revealed that the phasic driver extraction method robustly reflects the amount of phasic activity within the given response window and thus is not prone to typical scoring biases.
6. General discussion
6.1. Comparison to the classic trough-to-peak method
The assessment of the SCR amplitude by means of the classic trough-to-peak (CTTP) method requires the detection of a peak which is usually defined by a local maximum (and a corresponding local minimum). The empirical data from study 1 showed that SCRs elicited by stimuli with an ISI of only 2 s often do not exhibit distinguishable peaks. This was supported by the simulation study, which showed that for inter-SCR latencies of less than about three seconds two SCRs will generally appear as one. Failure to discriminate single SCRs may entail severe assessment errors as they may be wrongly attributed either outside or inside the response window. With phasic driver extraction, responses to stimuli at an ISI of two seconds can be distinguished on the basis of two distinct peaks; however, the phasic driver responses are not fully distinct. Simulation data demonstrated that the amplitude of an elicited SCR will be affected by a biasing SCR with inter-SCR latencies of less than 3 s due to the overlap of driver impulses. This influence increases gradually with the increasing proximity of the second SCR but does not show a discontinuous relation as for the CTTP method. For ISIs as low as two seconds, not only do SCRs overlap but also the ranges of expected onset latencies (according to most definitions of response windows). An unambiguous classification of SCRs to either stimulus thus appears impossible due to the variability of the electrodermal response. The partial response overlap then may just reflect the existing uncertainty of attribution of the response to either stimulus. Response overlaps can be avoided by an adequate experimental design; however, the interference with non-specific SCRs can never be precluded.
Finally, the CTTP method is prone to a general underestimation of SCR amplitudes due to ignorance of the declining baseline caused by preceding SCRs. The simulation experiment showed that preceding SCRs even at considerable temporal distance result in marked underestimations of the assessed amplitude. The average reduction of SCR amplitude was previously reported to range from 15 to 17% (Benedek and Kaernbach, 2010; Lim et al., 1997). The empirical experiment as well as the simulation study indicated that for very short inter-SCR latencies and for equal amplitude of the preceding SCR the underestimations may even be more than 40%. The analysis based on phasic driver extraction was not found to be prone to these underestimation errors.
6.2. Comparison with previous deconvolution approaches
The proposed method shows common grounds with the method put forward by Alexander et al. (2005). It is based on a standard deconvolution of SC data and on the assumption that the Bateman function represents an adequate IRF. The current approach takes two additional steps. First, it provides a means for continuous estimation of the tonic activity by applying the technique of inter-impulse fitting of driver data (Benedek and Kaernbach, 2010). The estimation of the tonic activity implicitly returns the phasic activity underlying SC data. As the phasic driver activity shows not only distinct positive deflections corresponding to single SCRs but also exhibits a zero baseline, it apparently corresponds more closely to sudomotor nerve activity than the driver resulting from Alexander et al.’s method, which still reflects a compound of tonic and phasic activity. On all accounts, a direct comparison of phasic driver data and parallel microneurographical recordings of sudomotor units would be helpful to examine the actual correspondence of phasic driver and sudomotor nerve activity. Second, the current approach yields an individual estimate of the typical SCR shape (i.e., impulse response) by optimization of the IRF parameters τ1 and τ2. Considering the extensive literature devoted to the topic of inter-individual differences of the SCR shape associated with state and trait characteristics (an overview can be found in Boucsein, 1992), this should represent additional valuable information. If we want to account for the inter-individual variability of the SCR shape, the adaptiveness of this phasic driver extraction is essential for ensuring a plausible result.
In the following, we shall compare the current approach to the method of nonnegative deconvolution (Benedek and Kaernbach, 2010). Both methods have to deal with the fact that standard deconvolution with a single IRF – even if optimized individually per participant – cannot perfectly reverse the underlying convolution process of a neurophysiological process (sudomotor nerve activity) with the processes of sweat secretion and diffusion in the skin. This is assumedly due to a certain variability of the SCR shape within a session. The two methods explore parallel paths how to deal with this problem.
Nonnegative deconvolution assumes that the variability is due to early processes within the SCR (i.e., processes occurring in the temporal vicinity of the SCR peak). These processes are captured by the remainder of the nonnegative deconvolution and were hypothesized to reflect the opening of poral valves. The diffusion process, exempt from this variability, can be described with very slow recovery-time constants.
Phasic driver extraction assumes that the variability is due to final diffusion processes. Early diffusion can be represented by a biexponential IRF with fast recovery-times. A single IRF per participant thus is sufficient to capture the essential phasic response. The remainder is this time part of the SCL, resulting in a tonic activity measure that varies faster than with nonnegative deconvolution. As a consequence, with the current method the average time constant of the IRF (τ2) was nearly eight times lower and the average tonic variability was about three times higher than as previously reported for nonnegative deconvolution (Benedek and Kaernbach, 2010). A more variable SCL is not unknown to EDA researchers but may in the absence of full decomposition primarily reflect the superposition of the trails of preceding SCRs.
Phasic driver extraction does not aim at a further decomposition of phasic activity. It will thus not allow the differentiated study of intra-individual variation of the SCR shape as reflected by the remainder of nonnegative deconvolution. This simplification implicates practical benefits. While nonnegative deconvolution results in two continuous phasic data (driver and remainder data), the current approach results in one single measure of continuous phasic activity. This allows for a more straightforward scoring of phasic activity. Moreover, phasic driver extraction is less computation intensive as compared to the non-standard nonnegative deconvolution. Entire sessions can be analyzed within seconds.
A second practical issue has been put forward in the present paper. A decomposition method which separates single phasic components always has to fall back on some sort of peak detection, even if it applies to data with enhanced signal-to-noise ratio as with deconvolution approaches. Peak detection cannot be conceived as a fully unambiguous issue, since it is based on the assumption of the existence of distinct entities of activations. In practical data analysis, the number of detectable local minima and maxima largely depends on the level of error noise which may introduce additional local extrema, and of the amount of data smoothing which may obscure them. Moreover, we could question if an SCR necessarily represents a compact entity. An SCR is thought to reflect the cumulative effect of the activity of a number of sweat glands (relevant to the electrodes), operating at different activation thresholds (Nishiyama et al., 2001) and being activated by a subset of different sudomotor axons (Kennedy et al., 1994; Riedl et al., 1998), which potentially contribute single spikes (Macefield and Wallin, 1996, 1999; Macefield et al., 2002). The concurrent activity of a high number of sudomotor axons within certain proximity will be identified as a nerve burst in the integrated nerve signal derived from multi-unit recordings, and it will eventually correspond to an apparently uniform SCR (Bini et al., 1980; Lidberg and Wallin, 1981). Following this notion, it may be considered more straightforward to use an integration measure of phasic activity rather than identify single components in the signal and assess their amplitude. It reduces the impact of windowing problems in event-related designs and it avoids delicate issues involved in peak detection. We, therefore, proposed the computation of the integrated skin conductance response (ISCR) as an indicator of response magnitude. It represents the unbiased cumulative phasic activity, derived from the SC signal, within a given response period. The ISCR captures entire responses accounting for their temporal characteristics instead of simply considering response peaks. Moreover, as the area of phasic SC data is not altered by the transformation of deconvolution, the ISCR perfectly equals the area of the represented SCRs. Traxel (1957) already thought of an area measure of SCR to be a more adequate measure for the entire “quantity of affect” (p. 289). Similarly, in the analysis of EMG data (the rectified EMG signal shows a zero baseline just like the phasic driver) the integrated EMG was found to represent overall muscular contraction more accurately than a simple amplitude (Fridlund and Cacioppo, 1986; Lippold, 1967).
The proposed method specifically aims at the analysis of response magnitudes. Since it avoids peak detection, it also does not return response latencies. A technique for the assessment of a robust indicator of event-related response latency based on the calculation of moments was proposed in the description of the method. Additionally, response latencies (i.e., latencies of onset, peak and offset of each phasic response) can still be computed by applying peak detection on the phasic driver (cf. Benedek and Kaernbach, 2010). Apart from the analysis of response magnitudes, the continuous signal of phasic activity could also be employed for correlation studies involving other continuous measures.
Finally, the current approach imposes less restrictive demands which should facilitate a more robust analysis. First, it does not claim strict nonnegativity of the phasic driver but rather tries to minimize negativity. Second, it does not claim that the IRF represents the SCR for the entire temporal extent but rather an essential part of it. To this end, the tonic activity is estimated at shorter time intervals (10 s instead of 100 s as for nonnegative deconvolution) so that it is able to capture late repercussions of SCRs which may be attributed to slow diffusion processes (Edelberg, 1993). These two conceptual differences allow for a higher flexibility in the analysis which should imply a more robust analysis. This is especially important in the face of data artifacts. Artifacts can easily occur if the participant fails to avoid any movements during the experiment. Such artifacts may have a strong impact on the computation of a detailed decomposition of SC data considering all underlying components while holding up strong restrictions to the model. They can however be compensated by only local biases when the analysis is allowed more degrees of freedom.
7. General conclusions
The proposed method allows for a separation of SC data into continuous data of tonic and phasic activity. The resulting phasic activity shows a zero baseline and compact, predominantly distinct phasic deflections. These characteristics proved especially advantageous for the unbiased analysis of data resulting from short interstimulus intervals with fast succeeding SCRs. An integrative measure of the extracted phasic activity was proposed as a straightforward indicator of the event-related phasic response. The method should hence prove to be useful especially in situations with high phasic activity, whether induced by an experimental setup or relevant in a clinical context.
Acknowledgements
This work was supported by the Austrian Science Fund (FWF): P19276. The authors wish to thank Susanne Gildehaus, Annika Pein, Katrin Hoeldtke and Anna Kanape for their valuable contributions to this research project.
Footnotes
Please note that in this manuscript the term impulse refers to a peak or deflection in the driver function which shows a limited but substantial duration. Hence, it usually does not refer to the special case of a unit impulse, for which the duration approaches zero, unless this is stated explicitly.
As a consequence of the temporal rectification induced by the process of deconvolution, an SCR with given amplitude will correspond to a response of markedly higher amplitude in the driver (cf. Fig. 1). The actual relation between amplitudes in SC data and in the driver depends on the parameters of the IRF as well as on the specific shape of the SCR. Therefore, no constant conversion from SCR amplitudes to driver amplitudes is possible. In general, SCRs with amplitudes lower than the classic amplitude criterion of 0.01 μS are found to correspond to driver responses with amplitudes of less than 0.2 μS.
References
- Alexander D.M., Trengove C., Johnston P., Cooper T., August J.P., Gordon E. Separating individual skin conductance responses in a short interstimulus-interval paradigm. J Neurosci Meth. 2005;146:116–123. doi: 10.1016/j.jneumeth.2005.02.001. [DOI] [PubMed] [Google Scholar]
- Bach D.R., Flandin G., Friston K.J., Dolan R.J. Time-series analysis for rapid event-related skin conductance responses. J Neurosci Meth. 2009;184(2):224–234. doi: 10.1016/j.jneumeth.2009.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baltissen R., Schaefer F., Kimmel H.D. Der Einfluß von zeitlicher Verteilung bei konstanter Häufigkeit der Reize auf die Habituation der Orientierungsreaktion. [The influence of temporal dispersion at constant frequency of stimuli on habituation of the orienting response] Z Exp Angew Psychol. 1989;36(2):181–198. [PubMed] [Google Scholar]
- Benedek M., Kaernbach C. Decomposition of skin conductance data by means of nonnegative deconvolution. Psychophysiology. 2010 doi: 10.1111/j.1469-8986.2009.00972.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bini G., Hagebarth K.-E., Hynninen P., Wallin B.G. Thermoregulatory and rhythm-generating mechanisms governing the sudomotor and vasoconstrictor outflow in human cutaneous nerves. J Physiol. 1980;306:537–552. doi: 10.1113/jphysiol.1980.sp013413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breault C., Ducharme R. Effect of intertribal intervals on recovery and amplitude of electrodermal reactions. Int J Psychophysiol. 1993;14(1):75–80. doi: 10.1016/0167-8760(93)90085-4. [DOI] [PubMed] [Google Scholar]
- Boucsein W. Plenum University Press; New York: 1992. Electrodermal activity. [Google Scholar]
- Dawson M.E., Schell A.M., Filion D.L. The electrodermal system. In: Cacioppo J.T., Tassinary L.G., Berntson G.G., editors. Handbook of psychophysiology. University Press; Cambridge: 2007. pp. 159–181. [Google Scholar]
- Edelberg R. Electrical properties of the skin. In: Brown C.C., editor. Methods in psychophysiology. Williams & Wilkins; Baltimore: 1967. pp. 1–53. [Google Scholar]
- Edelberg R. Electrodermal mechanisms: a critique of the two-effector hypothesis and a proposed replacement. In: Roy J.C., Boucsein W., Fowles D.C., Gruzelier J.H., editors. Progress in electrodermal research. Plenum Press; New York: 1993. pp. 7–29. [Google Scholar]
- Edelberg R., Muller M. Prior activity as a determinant of electrodermal recovery rate. Psychophysiology. 1981;18(1):17–25. doi: 10.1111/j.1469-8986.1981.tb01534.x. [DOI] [PubMed] [Google Scholar]
- Fowles D.C., Christie M.J., Edelberg R., Grings W.W., Lykken D.T., Venables P.H. Publication recommendations for electrodermal measurements. Psychophysiology. 1981;18(3):232–239. doi: 10.1111/j.1469-8986.1981.tb03024.x. [DOI] [PubMed] [Google Scholar]
- Freedman L.W., Scarpa Scerbo A., Dawson M.E., Raine A., McClure W.O., Venables P.H. The relationship of sweat gland count to electrodermal activity. Psychophysiology. 1994;31:196–200. doi: 10.1111/j.1469-8986.1994.tb01040.x. [DOI] [PubMed] [Google Scholar]
- Fridlund A.J., Cacioppo J.T. Guidelines for human electromyographic research. Psychophysiology. 1986;23:567–589. doi: 10.1111/j.1469-8986.1986.tb00676.x. [DOI] [PubMed] [Google Scholar]
- Grings W.W., Schell A.M. Magnitude of electrodermal response to a standard stimulus as a function of intensity and proximity of a prior stimulus. J Comp Physiol Psychol. 1969;67:77–82. doi: 10.1037/h0026651. [DOI] [PubMed] [Google Scholar]
- Janes C.L., Strock B.D., Weeks D.G., Worland J. The effect of stimulus significance on skin-conductance recovery. Psychophysiology. 1985;22(2):138–146. doi: 10.1111/j.1469-8986.1985.tb01575.x. [DOI] [PubMed] [Google Scholar]
- Jänig W. University Press; Cambridge: 2006. The integrative action of the autonomic nervous system. Neurobiology of homeostasis. [Google Scholar]
- Kennedy W.R., Wendelschafer-Crabb G., Brelje T.C. Innervation and vasculature of human sweat glands: an immunohistochemistry-laser scanning confocal fluorescence microscopy study. J Neurosci. 1994;14(11):6825–6833. doi: 10.1523/JNEUROSCI.14-11-06825.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kunimoto M., Kirnö K., Elam M., Karlsson T., Wallin B.G. Neuro-effector characteristics of sweat glands in the human hand activated by irregular stimuli. Acta Physiol Scand. 1992;146:261–269. doi: 10.1111/j.1748-1716.1992.tb09415.x. [DOI] [PubMed] [Google Scholar]
- Kunimoto M., Kirnö K., Elam M., Karlsson T., Wallin B.G. Non-linearity of skin-resistance response to intraneural electrical stimulation of sudomotor nerves. Acta Physiol Scand. 1992;146:385–392. doi: 10.1111/j.1748-1716.1992.tb09433.x. [DOI] [PubMed] [Google Scholar]
- Ledowski T., Bromilow J., Wu J., Paech M.J., Storm H., Schug S.A. The assessment of postoperative pain by monitoring skin conductance: results of a prospective study. Anaesthesia. 2007;62:989–993. doi: 10.1111/j.1365-2044.2007.05191.x. [DOI] [PubMed] [Google Scholar]
- Levenson D.F., Edelberg R. Scoring criteria for response latency and habituation in electrodermal research: a critique. Psychophysiology. 1985;22(4):417–426. doi: 10.1111/j.1469-8986.1985.tb01626.x. [DOI] [PubMed] [Google Scholar]
- Lidberg L., Wallin B.G. Sympathetic skin nerve discharges in relation to amplitude of skin resistance responses. Psychophysiology. 1981;18:268–270. doi: 10.1111/j.1469-8986.1981.tb03033.x. [DOI] [PubMed] [Google Scholar]
- Lippold O.C.J. Electromyography. In: Venables P.H., Martin I., editors. Manual of psychophysiological methods. Wiley; New York: 1967. pp. 245–298. [Google Scholar]
- Lim C.L., Gordon E., Harris A., Bahramali H., Li W.M., Manor B. Electrodermal activity in schizophrenia: a quantitative study using a short interstimulus paradigm. Biological Psychiatry. 1999;45:127–135. doi: 10.1016/s0006-3223(98)00056-0. [DOI] [PubMed] [Google Scholar]
- Lim C.L., Gordon E., Rennie C., Wright J.J., Behramali H., Li W.M. Dynamics of SCR, EEG, and ERP activity in an oddball paradigm with short interstimulus intervals. Psychophysiology. 1999;36(5):543–551. [PubMed] [Google Scholar]
- Lim C.L., Rennie C., Barry R.J., Bahramali H., Lazzaro I., Manor B. Decomposing skin conductance into tonic and phasic components. Int J Psychophysiol. 1997;25:97–109. doi: 10.1016/s0167-8760(96)00713-1. [DOI] [PubMed] [Google Scholar]
- Lim C.L., Seto-Poon M., Clouston P.D., Morris J.G.L. Sudomotor nerve conduction velocity and central processing time of the skin conductance response. Clin Neurophysiol. 2003;114:2172–2180. doi: 10.1016/s1388-2457(03)00204-9. [DOI] [PubMed] [Google Scholar]
- Macefield V.G., Elam M., Wallin B.G. Firing properties of single postganglionic sympathetic neurons recorded in awake subjects. Auto Neurosci: Basic. 2002;95:146–159. doi: 10.1016/s1566-0702(01)00389-7. [DOI] [PubMed] [Google Scholar]
- Macefield V.G., Wallin B.G. The discharge behaviour of single sympathetic neurons supplying human sweat glands. J Autonom Nerv Syst. 1996;61:277–286. doi: 10.1016/s0165-1838(96)00095-1. [DOI] [PubMed] [Google Scholar]
- Macefield V.G., Wallin B.G. Respiratory and cardiac modulation of single sympathetic vasoconstrictor and sudomotor neurons to human skin. J Physiol. 1999;516(1):303–314. doi: 10.1111/j.1469-7793.1999.303aa.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mano T., Iwase S., Toma S. Microneurography as a tool in clinical neurophysiology to investigate peripheral neural traffic in humans. Clin Neurophysiol. 2006;117:2358–2384. doi: 10.1016/j.clinph.2006.06.002. [DOI] [PubMed] [Google Scholar]
- Nishiyama T., Sugenoya J., Matsumoto T., Iwase S., Mano T. Irregular activation of individual sweat glands in human sole observed by videomicroscopy. Auto Neurosci: Basic. 2001;88:117–126. doi: 10.1016/S1566-0702(01)00229-6. [DOI] [PubMed] [Google Scholar]
- Papoulis A., Pillai S.U. McGraw-Hill; New York: 2002. Probability, random variables, and stochastic processes. [Google Scholar]
- Polo A., Aldegheri R., Bongiovanni L.G., Cavallaro T., Rizzuto N. Painless fractures and thermoregulation disturbances in sensory-autonomic neuropathy: electrophysiological abnormalities and sural nerve biopsy. Neuropediatrics. 2000;31:148–150. doi: 10.1055/s-2000-7488. [DOI] [PubMed] [Google Scholar]
- Raine A., Bihrle S., Venables P.H., Mednick S.A., Pollock V. Skin-conductance orienting deficits and increased alcoholism in schizotypical criminals. J Abnorm Psychol. 1999;108:299–306. doi: 10.1037//0021-843x.108.2.299. [DOI] [PubMed] [Google Scholar]
- Riedl B., Nischik M., Birklein F., Neundörfer B., Handwerker H.O. Spatial extension of sudomotor reflex sweating in human skin. J Autonom Nerv Syst. 1998;69:83–88. doi: 10.1016/s0165-1838(98)00016-2. [DOI] [PubMed] [Google Scholar]
- Schmelz M., Schmidt R., Bickel A., Torebjörk H.E., Handwerker J.O. Innervation territories of single sympathetic C fibers in human skin. J Neurophysiol. 1998;79:1653–1660. doi: 10.1152/jn.1998.79.4.1653. [DOI] [PubMed] [Google Scholar]
- Schneider R.L. A mathematical model of human skin conductance. Psychophysiology. 1987;24(5):610. [Google Scholar]
- Snyman J.A. Springer Publishing; Berlin: 2005. Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms. [Google Scholar]
- Storm H. Changes in skin conductance as a tool to monitor nociceptive stimulation and pain. Curr Opin Anaestesiol. 2008;21:796–804. doi: 10.1097/ACO.0b013e3283183fe4. [DOI] [PubMed] [Google Scholar]
- Torigoe K., Numata O., Yazaki S., Hasegawa S., Boku N., Hiura M. Sympathetic skin response in diabetic children: do diabetic children have diabetic neuropathy? Pediatr Int. 1999;41:631–636. doi: 10.1046/j.1442-200x.1999.01146.x. [DOI] [PubMed] [Google Scholar]
- Traxel W. Über das Zeitmaß der psychogalvanischen Reaktion. Z. Psychologie. 1957;161:282–291. [PubMed] [Google Scholar]
- Venables P.H., Christie M.J. Electrodermal activity. In: Martin I., Venables P.H., editors. Techniques in psychophysiology. Wiley & Sons; New York: 1980. pp. 3–67. [Google Scholar]
- Wenger C.B. Thermoregulation. In: Freedberg I.M., Eisen A.Z., Wolff K., Austen K.F., Goldsmith L.A., Katz S.I., editors. Vol. 1. McGraw-Hill; New York: 2003. pp. 119–127. (Dermatology in general medicine). [Google Scholar]
- Yamamoto K., Hornykiewicz O. Proposal for a noradrenaline hypothesis of schizophrenia. Prog Neuro-Psychoph. 2004;28:913–922. doi: 10.1016/j.pnpbp.2004.05.033. [DOI] [PubMed] [Google Scholar]