Abstract
Antibodies are used extensively in diagnostics and as therapeutic agents. Achieving high-affinity binding is important for expanding detection limits, extending dissociation half-times, decreasing drug dosages, and increasing drug efficacy. However, antibody affinity maturation in vivo often fails to produce antibody drugs of the targeted potency1, making further affinity maturation in vitro by directed evolution or computational design necessary. Here we present an iterative computational design procedure that focuses on electrostatic binding contributions and single mutants. By combining multiple designed mutations, a 10-fold affinity improvement to 52 pM was engineered into the anti-EGFR drug cetuximab (Erbitux), and a 140-fold improvement in affinity to 30 pM was obtained for the anti-lysozyme model antibody D44.1. The generality of the methods were further demonstrated through identification of known affinity-enhancing mutations in the therapeutic antibody bevacizumab (Avastin) and the model anti-fluorescein antibody 4-4-20. These results demonstrate novel computational capabilities for enhancing and accelerating the development of protein reagents and therapeutics.
Computational design depends critically on two capabilities: accurate energetic evaluation and thorough conformational search. Previous work has addressed many problems related to the design of improved protein-protein binding affinity, such as the design of stable protein folds2-4, binding pockets for peptides and small molecules5-7, altered protein-protein specificity8-12, and altered enzymatic activity13-15. The design of improved antigen-binding affinity has met with limited success, however16-19. Challenges for protein-protein affinity design include conformational change upon binding, interfacial trapped water molecules, polar and charged side chains, and the trade-off of protein-solvent with protein-protein interactions from the unbound to bound state. Fine free energy discrimination for redesign from nanomolar to picomolar affinities is a particular challenge.
A robust design strategy should both produce a considerable fraction of designs that are successful when tested experimentally, and yield substantial improvements across multiple systems. Though there are potentially many mutations that confer improved binding affinity for a particular interaction, calculations need only identify a subset to be successful. Our approach utilizes thorough optimization techniques that exhaustively rank-order the best solutions in a discretized search space. Although some of these solutions are expected to be improved designs, others will be unsuccessful but may be useful in learning about deficiencies in the energy functions, search procedures, or other methodology.
First we attempted to redesign the model antibody D1.3 for improved binding to its antigen, hen egg-white lysozyme. Single mutations at each of 60 complementarity determining region (CDR) positions to the 20 common side chains, excluding proline and cysteine, were designed using a physics-based energy function and a hierarchical search procedure. (Physics-based refers to an energy function constructed from and parameterized by theoretical and experimental models of the underlying physical interactions; by contrast, knowledge-based refers to potentials statistically derived from observational data, which often takes the form of structure databases.) A striking feature was that predictions for improved binding were dominated by mutations to large amino acids (Supplementary Fig. 1 online), many of which exhibited improved van der Waals packing interactions that outweighed disfavored net Poisson-Boltzmann continuum electrostatic solvation and interaction. Our confidence in these designs was low because many had unsatisfied hydrogen bonding, or a predicted packing improvement of a magnitude uncharacteristically large for a single amino-acid substitution. Nevertheless, 17 single mutations, most with calculated improved total binding free energy, were selected for experimental binding affinity measurement. Only three mutations improved affinity (Supplementary Table 1 online), with 2.4-fold improvement for the best single mutant (Supplementary Fig. 2 online). We found that the calculated electrostatic term of binding was a better predictor for improvement than the total calculated binding free energy, that improvements from mutations to larger amino acids were mostly not realized, and that avoiding potentially destabilizing mutations was important. This led to two questions: Could electrostatics-based predictions alone be used to design binding affinity improvements? Is there a physics-based explanation for the seemingly inaccurate calculated packing improvements?
In our second attempt, we used only the electrostatic term of the computed binding free energy to predict improvements in affinity, but kept the original design procedure and full energy function for side-chain conformational search. Since there were few computed opportunities for improving D1.3 based on electrostatics, new antibodies were chosen to explore both the new method and the possibility that D1.3 is anomalous.
Our second target for redesign was the antibody D44.1. It binds lysozyme, facilitating experiments, but its epitope is different from that of D1.3. In addition, D44.1 has low nanomolar affinity, maintaining the challenge of nanomolar-to-picomolar affinity maturation. Single mutations were designed at all D44.1 CDR positions, and then mutations were ranked by the electrostatic binding free energy term. In contrast to the D1.3 design, there were many computed opportunities for electrostatic improvement. We measured experimental binding affinity for the nine largest-magnitude predictions, choosing no more than two mutations per position. Six of the nine mutants bind tighter than wild type, and the best mutation, L92 Asn-to-Ala, exhibits 8-fold improvement (Table 1A, Fig. 1A). In addition, following the original design procedure, two mutations predicted to increase packing interactions were tested; as expected, neither mutation led to an improvement in affinity (Table 1A).
Table 1. Predicted and experimental antibody mutations.
| A. Predicted and experimental binding affinities in D44.1 | |||||
|---|---|---|---|---|---|
| Position | Mutation | KdWT/Kdmutant | ΔΔGexp* | ΔΔGcalc,total* | ΔΔGcalc,elec* |
| D44.1 (KdWT = 4.4 ± 0.5 nM) | |||||
| Single mutations, selected based on electrostatics energy | |||||
| L32 Asn | Gly | 4.2 ± 0.5 | −0.86 ± 0.07 | +0.99 | −1.03 |
| L92 Asn | Ala | 8.3 ± 1.3 | −1.25 ± 0.10 | −0.02 | −0.86 |
| H28 Thr | Asp | 1.29 ± 0.06 | −0.15 ± 0.03 | −0.30 | −0.26 |
| H31 Thr | Ala | 0.47 ± 0.07 | +0.45 ± 0.09 | +0.31 | −0.97 |
| H31 Thr | Val | 0.41 ± 0.09 | +0.53 ± 0.13 | −2.06 | −0.36 |
| H57 Ser | Ala | 1.9 ± 0.5 | −0.37 ± 0.16 | −0.59 | −1.44 |
| H57 Ser | Val | 2.3 ± 0.4 | −0.49 ± 0.12 | −2.29 | −1.34 |
| H58 Thr | Asp | 2.58 ± 0.16 | −0.56 ± 0.04 | −0.59 | −0.53 |
| H65 Lys | Asp | 0.97 ± 0.12 | +0.02 ± 0.07 | −0.38 | −0.42 |
| Single mutations, selected based on total energy | |||||
| L32 Asn | Tyr | 1.0 ±0.2 | +0.00 ± 0.13 | −0.29 | +2.59 |
| H31 Thr | Trp | 0.8 ± 0.3 | +0.13 ± 0.2 | −3.75 | +1.56 |
| Combinations of single mutations | |||||
| (L32)G, (L92)A | 3.2 ± 0.3 | −0.69 ± 0.05 | +1.23 | −1.68 | |
| (H57)V, (H58)D | 5.3 ± 0.4 | −0.99 ± 0.04 | −2.88 | −1.87 | |
| (L32)G, (L9 2)A, (H57)V, (H58)D | 18.7 ± 1.9 | −1.74 ± 0.06 | −1.65 | −3.55 | |
| (L92)A, (H57)V, (H58)D | 57 ± 5 | −2.40 ± 0.05 | −2.90 | −2.73 | |
| (L92)A, (H28)D, (H57)V, (H58)D | 102 ± 3 | −2.74 ± 0.02 | −3.18 | −2.96 | |
| B. Characterization of D44.1 quadruple mutant | |||||
|---|---|---|---|---|---|
| koff (10−3s−1) | kon (106M−1s−1) | koff/kon (nM) | Kd (nM) | High-salt Kd (nM) | |
| D44.1 | 10.7 ± 1.0 | 2.52 ± 0.13 | 4.3 ± 0.5 | 4.4 ± 0.5 | 3.0 ± 0.8 |
| Quad | 0.466 ± 0.014 | 8.4 ± 1.7 | 0.055 ± 0.012 | 0.0430 ± 0.0013 | 0.18 ± 0.08 |
| C. Double mutant cycle added to D44.1 quadruple mutant | |||
|---|---|---|---|
| Position(s) | Mutation(s) | KdWT/Kdmutant | ΔΔGexp* |
| Quad | 102 ± 3 | −2.74 ± 0.02 | |
| H35 Glu | Ser | < 0.04 | > +2 |
| H99 Gly | Asp | 1.41 ± 0.17 | −0.20 ± 0.07 |
| H35 Glu + H99 Gly | Ser + Asp | 145 ± 17 | −2.95 ± 0.07 |
| D. Predicted and experimental binding affinities in cetuximab (Erbitux) | |||||
|---|---|---|---|---|---|
| Position | Mutation | KdWT/Kdmutant | ΔΔGexp* | ΔΔGcalc,total* | ΔΔGcalc,elec* |
| cetuximab (KdWT = 0.49 ± 0.06 nM) | |||||
| L26 Ser | Asp | 1.4 ± 0.7 | −0.2 ± 0.3 | −0.40 | −0.38 |
| L31 Thr | Glu | 2.4 ± 0.8 | −0.53 ± 0.19 | −0.50 | −0.48 |
| L93 Asn | Ala | 3.5 ± 1.4 | −0.7 ± 0.2 | +1.06 | −0.75 |
| H56 Asn | Ala | 1.1 ± 0.4 | −0.04 ± 0.2 | +2.25 | −0.27 |
| H61 Thr | Glu | 1.1 ± 0.3 | −0.07 ± 0.17 | −0.77 | −0.77 |
| Combinations of single mutations | |||||
| (L31)E, (L93)A | 4 ± 2 | −0.8 ± 0.3 | +0.51 | −1.28 | |
| (L26)D, (L31)E, (L93)A | 9.5 ± 0.3 | −1.33 ± 0.02 | +0.13 | −1.64 | |
| (L26)D, (L31)E, (L93)A, (H56)A, (H61)E |
3 ± 3 | −0.7 ± 0.5 | +1.69 | −2.61 | |
Values in kcal/mol.
Experimental error is the standard deviation from 2 or more (typically 3) independent trials.
Figure 1.


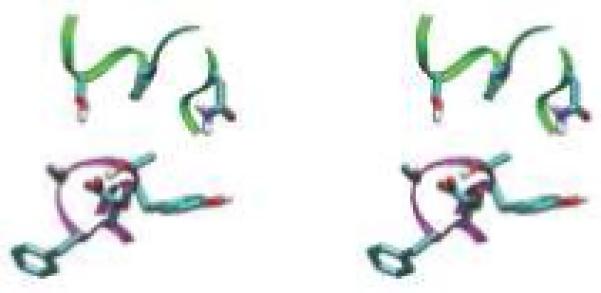
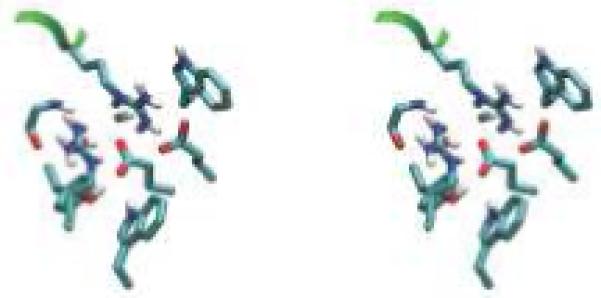
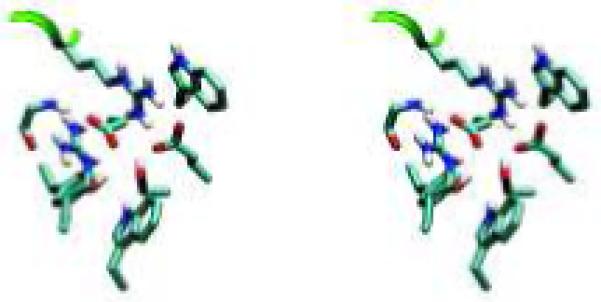
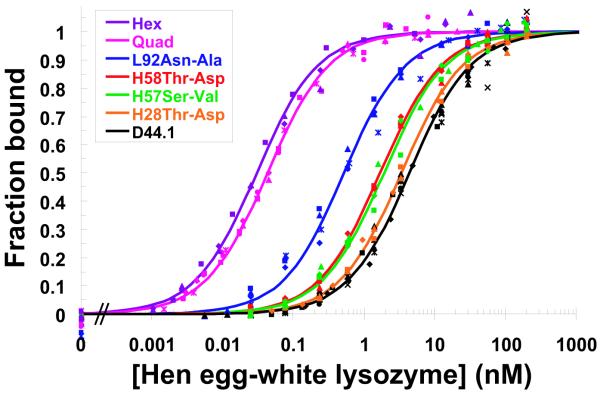
Designed high-affinity mutations in D44.1. (A) Experimental binding affinities, from left to right: 140-fold hex, 100-fold quad, L92 Asn-to-Ala, H58 Thr-to-Asp, H57 Ser-to-Val, H28 Thr-to-Asp, wild type. For each variant, different symbol shapes distinguish independent measurements. (B to D) Predicted structures for single mutations; green ribbon: lysozyme backbone; magenta ribbon: antibody backbone; atom color: design; grey: wild type. (B) L92 Asn-to-Ala. (C) H57 Ser-to-Val, top; H58 Thr-to-Asp, bottom. (D) H28 Thr-to-Asp. (E) Wild type in region of double mutation. The top-center arginine is from lysozyme and all other residues are from the antibody. (F) Designed double mutation: H99 Gly-to-Asp, H35 Glu-to-Ser. The Asp is predicted to displace a crystallographic water molecule.
The successful D44.1 single mutations were combined and tested experimentally. The six favorable mutations span five positions, where L32 and L92 are the only positions in direct contact with each other in the wild-type crystal structure. Contrary to prediction, this double mutant is not as improved as the L92 single mutant alone. The mutations at the other three positions are additive with L92, yielding a quadruple mutant with 43-pM affinity, 100-fold improved over wild type (Table 1A, Fig. 1A). Figure 1B-D displays the designed interactions. Measurements of dissociation and association rate constants for D44.1 and the high-affinity quadruple mutant revealed that both kinetic steps were improved, including a 23-fold slower off-rate (Table 1B). Each ratio of koff to kon is in agreement with the independently measured Kd. Increasing ionic strength from 167 mM to 1.67 M screens the designed quadruple-mutant interaction by approximately 4-fold, in agreement with calculation (+0.9 kcal/mol), whereas the wild type is marginally improved at high salt, in contrast to calculation (+0.3 kcal/mol; Table 1B).
Two sets of calculations were made in an attempt to further improve the high-affinity D44.1 quadruple mutant. First, single mutations were designed based on the predicted structure of the quadruple mutant. These calculations reiterated many predictions seen in the original D44.1 design that had been lower-ranked and not tested experimentally, as well as predictions for mutating position L32, which neighbors the L92 Asn-to-Ala mutation and was found experimentally to not be additive. Second, double mutations were designed at all 93 pairs of contacting positions, and triple mutations were designed at positions H32, H98, and H100, based on cooperative packing at these positions. The double- and triple-mutant designs were filtered for favorable, cooperative predictions, requiring the double or triple mutation to exceed each single mutation and their energetic sum. Four single mutations, three double mutations, and one triple mutation were selected for experimental testing in the quadruple-mutant context (Supplementary Table 2 online). Only the H35+H99 double mutant was improved relative to the quadruple mutant, at 30-nM affinity, 140-fold improved over wild type (Table 1C, Figure 1A). Measurement of the individual H35 and H99 mutations revealed high cooperativity (Table 1C), consistent with the predicted salt-bridge and hydrogen-bond rearrangements (Fig. 1F-G). The diminished success rate of this subsequent design round may be due to smaller magnitude predictions, antibody destabilization, or design in a modeled rather than experimentally-determined structure.
Next, we applied our electrostatics-based methods to the anti-cancer therapeutic antibody cetuximab (Erbitux), which binds epidermal growth factor receptor (EGFR) to block ligand binding20. Calculations revealed nine positions with opportunities for affinity-enhancing single mutations based on improved electrostatics. The five mutations of largest magnitude of predicted affinity improvement were selected for experimental testing in the single-chain antibody format, with one mutation per position, and no two positions in close proximity. The EGFR extracellular domain (EGFR-ECD) mutant used in the assays contains a point mutation that likely interferes with the H56 mutation. Three of the other four mutants bind EGFR tighter than does cetuximab; these three mutations were combined to produce a triple mutant with 10-fold overall improvement, from 490 pM to 52 pM (Table 1D, Fig. 2).
Figure 2.
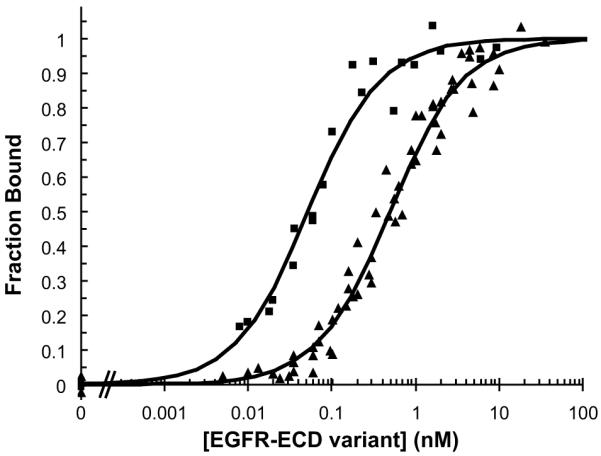
Designed high-affinity cetuximab mutant. Experimental binding affinity titrations as displayed for cetuximab (triangles) and 10-fold improved triple-mutant (squares).
The transferability and utility of these electrostatics-based methods were further demonstrated by designs for which published data validates the predictions. One of our test cases was the antibody 4-4-20, which binds its small-molecule hapten, fluorescein, with 1.2 nM affinity, and was previously engineered using directed evolution to yield the antibody 4M5.3 with over 1,000-fold affinity improvement and 14 mutations21. Our designed single mutations in 4-4-20 revealed opportunities for improvement based on computed electrostatics at nine positions. Two of the predicted mutations, H31 Asp-to-His and H101 Ser-to-Ala, have already been shown to improve binding affinity as single mutations in 4M5.322. Interestingly, the design missed the H102 Tyr-to-Ser mutation in 4M5.3 due to the rigid backbone constraint. Another test case was bevacizumab (Avastin), a therapeutic antibody that binds vascular endothelial growth factor (VEGF)23, where we found five positions suitable for electrostatics-based improvement. The mutation H28 Thr-to-Asp and mutations at H31 and H101 are found in a published high-affinity variant of bevacizumab24. Our other electrostatics-based predictions in both test systems remain to be tested.
The single mutations designed and experimentally validated in this work lead to enhanced binding affinity through one of two electrostatic mechanisms. In one mechanism, the removal of a poorly-satisfied polar group, a polar residue calculated to lose more free energy from desolvation than is recovered by interaction is mutated to a hydrophobic residue. These mutations account for the majority of improved energetics. In a second mechanism, the addition of a charged residue, net charge is changed to increase electrostatic interaction, often at the periphery of the antibody-antigen interface where desolvation is minimal. Unlike previous work using electrostatics to guide design25, 26, these methods explicitly model the mutation, calculate a binding free energy relative to wild type, include positions that are partially or fully buried upon binding, and avoid opportunities where the mutation is predicted to destabilize the mutant protein.
The modeled structures result from optimization with the full energy function, yet the van der Waals and nonpolar solvation energies are then discarded to predict improvement based on only the net electrostatic term. A potential problem is that different/wrong van der Waals parameters would produce altered equilibrium distances and hence altered electrostatic energies, particularly for short-range interactions. The specific mutations predicted and tested here may be less susceptible to this potential problem because they involve the calculation of solvation and medium-range electrostatic energies, which are not especially sensitive to precise atom locations. The energy for substitution of an unsatisfied polar group is dominated by its desolvation penalty, and the addition of a charged group at the interface periphery is not sensitive to precise side-chain placement. However, designs involving the introduction of a new short-range electrostatic contact, such as a new hydrogen bond, could be susceptible to this potential problem. Further work is necessary, but it could be that the energetic terms are actually appropriate for identifying low-energy structures for any sequence, but not for comparing energetics between sequences. Indeed, we think that the packing and nonpolar interactions are not balanced in some situations for accurate comparison of one amino acid to another, as described next.
We investigated the underlying physical model to address the seemingly inaccurate calculated packing interactions. The majority of problematic designs were at the binding site periphery, where mutation to a larger amino acid was predicted to be favorable due to increased intermolecular van der Waals interactions. In some cases, hydrogen-bonding groups were buried, but the unfavorable electrostatic term was outweighed by improved packing. In principle, a larger amino acid at the interface periphery will exhibit increased protein-protein interactions in the bound-state, counteracted by increased protein-water interactions in the unbound-state. However, these offseting energetics are calculated asymmetrically, with an atomistic Lennard-Jones potential for the protein-protein interactions, and a simple solvent-accessible surface area (SASA) nonpolar term for the protein-water interactions. The protein-water nonpolar interaction should be a function of the detailed geometry, including volume effects, as well as the particular protein atom types present. We implemented and parameterized an atomically-detailed nonpolar term based on work by Levy and co-workers (Supplementary Fig. 3 online)27, and found that it reduced the magnitude of favorable prediction for many of the counterintuitive designs to larger side chains (Supplementary Fig. 4 online). In addition, unbound-state conformational search attenuated predictions for larger side chains by introducing an energetic cost to adopt the binding conformation (data not shown). Nevertheless, some incorrect predictions remain, and future work should address this issue.
This work presents a computational alternative to directed evolution for affinity maturation. Directed evolution is adept at accumulating successive, additive mutations, but (with the exception of large-scale shuffling) is less well suited for selecting variants whose encoding DNA is further from wild type. Experimental libraries generated using error-prone PCR generally do not cover all single amino-acid mutations, let alone all pairs or greater combinations of mutations, as 13 of the 19 possible single mutations require more than one base pair change, on average. Some classes of mutation require two base pair changes - for example, mutation to either negatively-charged residue from any codon of 10 of the 18 candidate side chains. Of the 12 single mutations found to improve D1.3, D44.1, or cetuximab, 10 required two base pair changes and would therefore have been substantially more difficult to identify by a method that relies on error-prone PCR. Also, the H35+H99 cooperative double mutation required concerted amino-acid mutation and three total base-pair changes. Computation has the capability to search a vastly larger space than accessible to either in vivo maturation or experimental selection techniques, potentially discovering larger and more beneficial evolutionary steps.
Our results present several design lessons. We find that computed electrostatics alone is a better predictor for improved binding than is computed total free energy. Electrostatics-based predictions yielded fewer false positives, more true positives, and a greater than 60% success rate for single mutations from wild type (Fig. 3). Predictions based on improved total free energy were dominated by mutations to larger amino acids that did not experimentally improve affinity; incorporation of improved nonpolar hydration models may improve accuracy of predicted packing changes28-30. We find that designing single and double mutations allows for in-depth conformational search and avoids having any particular design flaw spoiling all results. In addition, avoiding destabilizing mutations based on calculated folding stability was important. Crystal structure resolution did not have a substantial effect, as the D44.1 and cetuximab structures are of 2.5- and 2.8-Å resolution, respectively, whereas the D1.3 structure is 1.8-Å resolution. Calculations in D1.3 showed few opportunities for electrostatics-based improvement, and accumulated evidence indicates that D1.3 is the anomaly, possibly because of the combination of the many large side chains and buried water molecules at the antibody-antigen interface.
Figure 3.
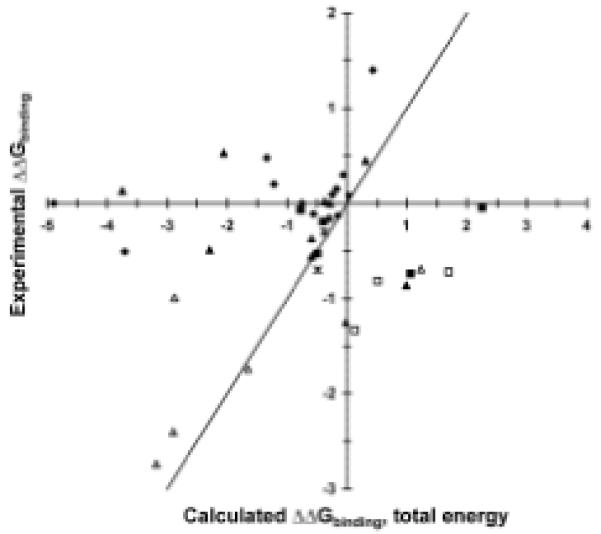
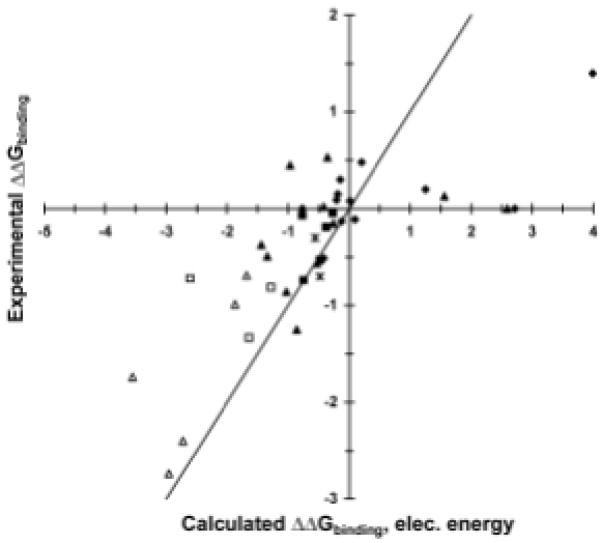
Comparison of calculated and experimental binding free energies. Free energies are in kcal/mol relative to wild type, with the y=x line included to aid interpretation. diamonds: D1.3 mutants; filled triangles: D44.1 single mutants; open triangles: D44.1 combination mutants; filled squares: cetuximab single mutants; open squares: cetuximab combination mutants; asterisks: 4-4-20 mutants. (A) Calculated total free energy. (B) Calculated electrostatic free energy term.
Our results demonstrate novel capabilities for improving protein binding affinity using computational design. Maturation of the model system D44.1 by 140-fold to 30 pM, maturation of the therapeutic antibody cetuximab by 10-fold to 52 pM, and identification of known mutations in 4-4-20 and bevacizumab together indicate that our method is a noteworthy advance for antibody design and should be effective for other antibodies and protein interactions. Computational design holds the promise of far greater exploration of sequence space than possible experimentally, enabling rapid and inexpensive protein improvement.
Methods
Computational design
The design approach used a two-stage hierarchical procedure. First, conformational search was simplified by assuming a rigid protein backbone and allowing only discrete side chain rotamers. The physics-based energy function is pairwise-decomposable, permitting application of dead-end elimination and A* search algorithms. For each protein sequence, we found its global minimum energy conformation (GMEC), and if this energy was within a cut-off of the wild-type GMEC energy, then a continued list of lowest-energy structures was found. Second, we reevaluated the lowest-energy structures of each sequence using more accurate, yet more more computationally-demanding models, including Poisson-Boltzmann continuum electrostatics, continuum solvent van der Waals, unbound-state side-chain conformation search, and minimization. Structures were reranked based on these latter calculations. Binding energy was initially predicted from the bound-state conformation and a rigid binding model. The unbound state search, when applied, approximated flexible binding and estimated a deformation penalty that offset binding. Changes to protein fold stability were approximated from the energetic difference between the folded state and isolated model compounds. Detailed computational methods are provided in Supplementary Methods online.
Experiments
The single-chain format of antibodies were displayed on the surface of yeast. Binding affinities were measured by incubating different vessels of antibody-displaying cells with varying antigen concentration. Secondary reagents were used to detect antibody-antigen complexes, and analyzed with flow cytometry. Detailed exerimental methods are provided in Supplementary Methods online.
Supplementary Material
Acknowledgements
We thank S. L. Sazinsky for the gift of the 404SG material, and D. Lipovsek and R. T. Sauer for comments on the manuscript. This work was supported by a National Science Foundation Graduate Fellowship to S.M.L. and grants from the National Institutes of Health (CA96504 and GM65418).
Footnotes
Competing Interests Statement The authors declare that they have no competing financial interests.
References
- 1.Foote J, Eisen HN. Kinetic and affinity limits on antibodies produced during immune responses. Proc. Natl. Acad. Sci. U.S.A. 1995;92:1254–1256. doi: 10.1073/pnas.92.5.1254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Desjarlais JR, Handel TM. De novo design of the hydrophobic cores of proteins. Protein Sci. 1995;4:2006–2018. doi: 10.1002/pro.5560041006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dahiyat BI, Mayo SL. De novo protein design: Fully automated sequence selection. Science. 1997;278:82–87. doi: 10.1126/science.278.5335.82. [DOI] [PubMed] [Google Scholar]
- 4.Kuhlman B, et al. Design of a novel globular protein fold with atomic-level accuracy. Science. 2003;302:1364–1368. doi: 10.1126/science.1089427. [DOI] [PubMed] [Google Scholar]
- 5.Reina J, et al. Computer-aided design of a PDZ domain to recognize new target sequences. Nat. Struct. Biol. 2002;9:621–627. doi: 10.1038/nsb815. [DOI] [PubMed] [Google Scholar]
- 6.Looger LL, Dwyer MA, Smith JJ, Hellinga HW. Computational design of receptor and sensor proteins with novel functions. Nature. 2003;423:185–190. doi: 10.1038/nature01556. [DOI] [PubMed] [Google Scholar]
- 7.Cochran FV, et al. Computational de novo design and characterization of a four-helix bundle protein that selectively binds a nonbiological cofactor. J. Am. Chem. Soc. 2005;127:1346–1347. doi: 10.1021/ja044129a. [DOI] [PubMed] [Google Scholar]
- 8.Havranek JJ, Harbury PB. Automated design of specificity in molecular recognition. Nat. Struct. Biol. 2003;10:45–52. doi: 10.1038/nsb877. [DOI] [PubMed] [Google Scholar]
- 9.Bolon DN, Grant RA, Baker TA, Sauer RT. Specificity versus stability in computational protein design. Proc. Natl. Acad. Sci. U.S.A. 2005;102:12724–12729. doi: 10.1073/pnas.0506124102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ashworth J, et al. Computational redesign of endonuclease DNA binding and cleavage specificity. Nature. 2006;441:656–659. doi: 10.1038/nature04818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Joachimiak LA, Kortemme T, Stoddard BL, Baker D. Computational design of a new hydrogen bond network and at least a 300-fold specificity switch at a protein-protein interface. J. Mol. Biol. 2006;361:195–208. doi: 10.1016/j.jmb.2006.05.022. [DOI] [PubMed] [Google Scholar]
- 12.Ambroggio XI, Kuhlman B. Computational design of a single amino acid sequence that can switch between two distinct protein folds. J. Am. Chem. Soc. 2006;128:1154–1161. doi: 10.1021/ja054718w. [DOI] [PubMed] [Google Scholar]
- 13.Dwyer MA, Looger LL, Hellinga HW. Computational design of a biologically active enzyme. Science. 2004;304:1967–1971. doi: 10.1126/science.1098432. [DOI] [PubMed] [Google Scholar]
- 14.Lassila JK, Keeffe JR, Oelschlaeger P, Mayo SL. Computationally designed variants of Escherichia coli chorismate mutase show altered catalytic activity. Protein Eng. Des. Sel. 2005;18:161–163. doi: 10.1093/protein/gzi015. [DOI] [PubMed] [Google Scholar]
- 15.Korkegian A, Black ME, Baker D, Stoddard BL. Computational thermostabilization of an enzyme. Science. 2005;308:857–860. doi: 10.1126/science.1107387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dixon RW, et al. Theoretical and experimental studies of biotin analogues that bind almost as tightly to streptavidin as biotin. J. Org. Chem. 2002;67:1827–1837. doi: 10.1021/jo991846s. [DOI] [PubMed] [Google Scholar]
- 17.Song G, et al. Rational design of intercellular adhesion molecule-1 (ICAM-1) variants for antagonizing integrin lymphocyte function-associated antigen-1-dependent adhesion. J. Biol. Chem. 2006;281:5042–5049. doi: 10.1074/jbc.M510454200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sood VD, Baker D. Recapitulation and design of protein binding peptide structures and sequences. J. Mol. Biol. 2006;357:917–927. doi: 10.1016/j.jmb.2006.01.045. [DOI] [PubMed] [Google Scholar]
- 19.Clark LA, et al. Affinity enhancement of an in vivo matured therapeutic antibody using structure-based computational design. Protein Sci. 2006;15:949–960. doi: 10.1110/ps.052030506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sato JD, et al. Biological effects in vitro of monoclonal antibodies to human epidermal growth factor receptors. Mol. Biol. Med. 1983;1:511–529. [PubMed] [Google Scholar]
- 21.Boder ET, Midelfort KS, Wittrup KD. Directed evolution of antibody fragments with monovalent femtomolar antigen-binding affinity. Proc. Natl. Acad. Sci. U.S.A. 2000;97:10701–10705. doi: 10.1073/pnas.170297297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Midelfort KS, Wittrup KD. Context-dependent mutations predominate in an engineered high-affinity single chain antibody fragment. Protein Sci. 2006;15:324–334. doi: 10.1110/ps.051842406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Presta LG, et al. Humanization of an anti-vascular endothelial growth factor monoclonal antibody for the therapy of solid tumors and other disorders. Cancer Res. 1997;57:4593–4599. [PubMed] [Google Scholar]
- 24.Chen Y, et al. Selection and analysis of an optimized anti-VEGF antibody: crystal structure of an affinity-matured Fab in complex with antigen. J. Mol. Biol. 1999;293:865–881. doi: 10.1006/jmbi.1999.3192. [DOI] [PubMed] [Google Scholar]
- 25.Joughin BA, Green DF, Tidor B. Action-at-a-distance interactions enhance protein binding affinity. Protein Sci. 2005;14:1363–1369. doi: 10.1110/ps.041283105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Selzer T, Albeck S, Schreiber G. Rational design of faster associating and tighter binding protein complexes. Nat. Struct. Biol. 2000;7:537–541. doi: 10.1038/76744. [DOI] [PubMed] [Google Scholar]
- 27.Levy RM, Zhang LY, Gallicchio E, Felts AK. On the nonpolar hydration free energy of proteins: surface area and continuum solvent models for the solute-solvent interaction energy. J. Am. Chem. Soc. 2003;125:9523–9530. doi: 10.1021/ja029833a. [DOI] [PubMed] [Google Scholar]
- 28.Gallicchio E, Zhang LY, Levy RM. The SGB/NP hydration free energy model based on the surface generalized born solvent reaction field and novel nonpolar hydration free energy estimators. J. Comput. Chem. 2002;23:517–529. doi: 10.1002/jcc.10045. [DOI] [PubMed] [Google Scholar]
- 29.Gallicchio E, Levy RM. AGBNP: An analytic implicit solvent model suitable for molecular dynamics simulations and high-resolution modeling. J. Comput. Chem. 2004;25:479–499. doi: 10.1002/jcc.10400. [DOI] [PubMed] [Google Scholar]
- 30.Wagoner JA, Baker NA. Assessing implicit models for nonpolar mean solvation forces: the importance of dispersion and volume terms. Proc. Natl. Acad. Sci. U.S.A. 2006;103:8331–8336. doi: 10.1073/pnas.0600118103. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.