Characterizing heterogeneous cellular responses to perturbations

Results

To study the heterogeneous effects of perturbations on cells, we made use of an existing image database of HeLa cells treated with 100 drugs at 13 concentrations and stained by using a multiplexed collection of immunofluorescent markers (DNA/SC35/anillin) (25). However, this dataset did not contain temporal information and additionally lacked consistent numbers of representative drugs in several key categories of drug mechanism. Thus, we created a 25-drug dataset capturing the responses of HeLa cells to drugs at varying concentrations [low or high, as specified in supporting information (SI) Table S1] and time points (3, 6, 12, or 24 h). For this dataset, we selected 5 drugs in each of 5 known functional categories, affecting DNA replication (e.g., methotrexate), histone deacetylation (e.g., trichostatin A), microtubules (e.g., paclitaxel), the glucocorticoid receptors (e.g., dexamethasone), and topoisomerase (e.g., doxorubicin). We additionally included an “other” category containing 10 drugs of miscellaneous (e.g., dichloroacetic acid) or unspecified (e.g., green tea-extracted polyphenols) mechanism. After fixation, cells were stained with 1 of 2 sets of fluorescent markers (DNA/phospho-p38/phospho-ERK or DNA/actin/α-tubulin; see Table S2) selected as general readouts of cell signaling state (25).

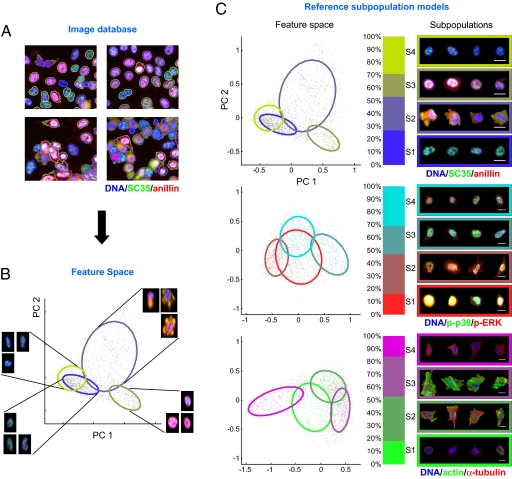
For each image, we identified individual cellular regions and extracted phenotypic features (Fig. 1 A and B). There are multiple approaches for extracting phenotypic information, including detecting either known biological phenotypes [e.g., apoptosis (31) or cell cycle phases (32) or general image properties, e.g., cell morphology and patterns of marker intensities (14, 18)]. Here, we found that a feature set designed to measure the degree of marker colocalization performed well in capturing phenotypic differences in signaling state among visually distinct cells. First, we measured ratios of marker intensities at each pixel to estimate the degree of marker colocalization. To avoid bias due to selection of a “favored” denominator, we measured all 3 possible pairs of marker ratios. Second, we quantized marker ratios into 16 bins. (Bin ranges were empirically chosen based on our data; the highest bin value was set to “infinity” to capture ratios when marker intensities in the denominator were close to background.) Third, we used 6 16 × 16 histograms to tally each of the three quantized marker ratio pairs for both cytoplasmic and nuclear subcellular regions. To down-weight low-intensity pixels, the contribution of each pixel to the histogram was weighted by its total intensity of markers. Finally, each histogram was normalized to have unit mass.

Taken together, these histograms resulted in a 1,536-dimensional (equal to 6 × 16 × 16) feature vector. These high-dimensional feature vectors were subsequently reduced to ≈25 dimensions by principal-components analysis (PCA) (Materials and Methods). Although alternative choices of cellular features could certainly be substituted in the remaining analysis, we found that these ratiometric features performed well at grouping cells with visually similar signaling states in similar regions of feature space.

To enable comparisons of cellular heterogeneity across experimental conditions, a reference training set of 10,000 cells was constructed for each marker set from a uniform sampling of control and drug-treated wells (Materials and Methods). This sample represented only a small fraction (<2%; see Materials and Methods) of our overall datasets. Probabilistic clustering was then applied to this training set to characterize cell heterogeneity as stochastic variation of feature vectors around a collection of distinct phenotypes (Fig. 1 B and C). For a specified number of subpopulations k, expectation maximization (EM) clustering (33) characterized the total population as a weighted mixture of k subpopulations, each defined by a Gaussian distribution around a distinct cellular stereotype and a (prior) overall probability of subpopulation occurrence (30) (Fig. 1C, stacked bar graph). (For convenience of visualization we illustrate our approach with k = 4; the effects of varying k will be discussed subsequently.) The reference subpopulation model is thus defined by this collection of k phenotype means, covariances, and prior probabilities of occurrence.

The heterogeneity of a cell population subjected to a specific experimental condition can be estimated by using the reference subpopulation model. For each cell, the (posterior) probability that it is a member of a given subpopulation can be computed from the subpopulation model by using Bayes' rule. These probabilities for a single cell and all k subpopulations can be represented as a k-dimensional vector whose entries sum to 1. By averaging these k-dimensional vectors over a population of cells, a subpopulation profile is obtained as the expected overall proportion of each subpopulation for a given experimental condition. Replicates produced reproducible subpopulation profiles (Fig. S1), which were averaged to obtain 1 final profile per condition. Thus, the heterogeneity observed within any experimental condition can be concisely encoded by a probability distribution over the reference subpopulations.

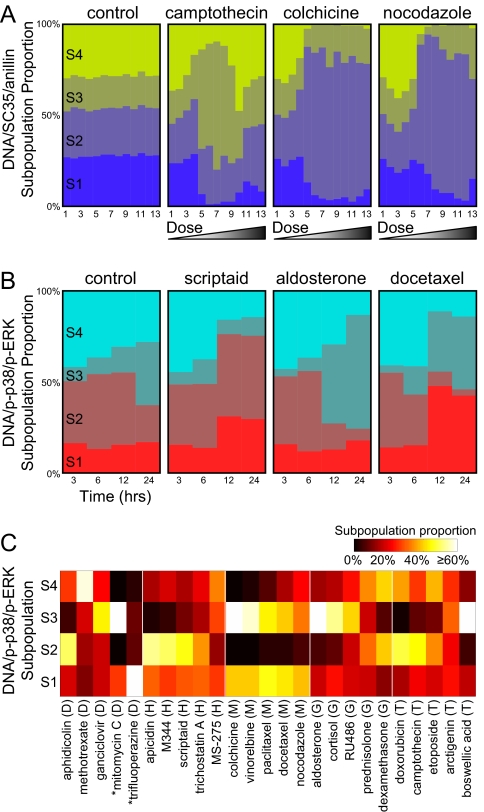
We next examined the degree to which subpopulation profiles can be used to distinguish heterogeneous responses to different drugs (Fig. 2A). We first compared subpopulation profiles for drug-treated conditions to controls. A comparison of camptothecin (topoisomerase) to controls, for example, showed a significant shift to a dominant phenotype (Fig. 2A; e.g., dose 5, population 3). Comparison of colchicine and nocodazole (both targeting microtubules) to controls showed substantial redistributions of phenotypic heterogeneity after drug treatment (Fig. 2A; e.g., dose 9, population 2). We next compared the effects of drugs to one another. We found that drugs of similar mechanism often yielded similar profiles (e.g., Fig. 2A, colchicine vs. nocodazole). Conversely, mechanistically different drugs yielded distinct profiles (e.g., Fig. 2A, camptothecin vs. colchicine).

Dose responses typically revealed sharp transitions in subpopulation proportions as drug concentration increased, whereas untreated populations tended to remain in constant proportions (Fig. 2A). Multiphasic drug effects, such as seen for camptothecin, can be easily discerned as dramatic transitions in subpopulation proportions [Fig. 2A, second image, transitions at doses 5 and 10 in agreement with previous results (18, 25)]. The interpretation of results across time is complicated somewhat by the fact that controls did not maintain constant proportions, likely because of varying exposure times to the drug vehicle DMSO before fixation (Fig. 2B, first image). Although most drugs did not show significant differences from the controls at the 3- and 6-h time points, significant variation was observed at the 12- and 24-h time points (Fig. 2B). We note that analysis of automatically identified subpopulations revealed no significant enrichment for any specific cell cycle stage, as might be expected from our choice of pixel-based features (SI Text and Fig. S2). These observations suggest that subpopulation profiles contain information that may offer insights into drug modes of action.

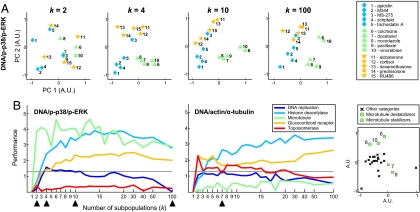
We next wondered whether the significant redistributions of subpopulations were consistent across drug perturbations of similar mechanism. To assess the “information content” of observed patterns of heterogeneity, we computed subpopulation profiles for our 25 annotated drugs at the 24-h time point and grouped the results by category of mechanism (Fig. 2C). (Here, we visualized these results using a heatmap, rather than stacked bar graphs, to provide easier visual comparison among larger numbers of drugs.) Whereas DNA replication-inhibiting drugs showed high variability in their subpopulation proportions, the responses of drugs within all other categories generally showed high concordance. Rigorous assessment of the similarities and differences between drug effects requires a quantitative measure of “distance” between subpopulation profiles. When considered as probability vectors, subpopulation profiles may be viewed as information theoretic descriptions of cell population heterogeneity. Similarities among profiles can be quantitatively compared by using the Kullback–Leibler (KL) divergence (34) and visually displayed by using multidimensional scaling (MDS) plots (SI Text). We observed that profiles showed significant grouping by drug mechanism (Fig. 3A, k = 4). Thus, drugs of similar mechanism appear to induce similar patterns of cellular heterogeneity.

A natural question arose from our analysis: Would increasing the number of subpopulations, k, in the reference model discern finer distinctions between drug effects and thus yield a more accurate classification of drugs? In theory, increasing k allows finer resolution at which to measure cellular heterogeneity, although classification accuracy for very large values of k may fail to improve—or even degrade—because of the introduction of nonbiological separation of cellular phenotypes. We found for the DNA/p-p38/p-ERK and DNA/actin/α-tubulin marker sets that categorization performance for most drug categories sharply improved as k increased from 1 (no predictive power) to ≈5. Afterward, no significant improvement in classification was observed (Fig. 3B). In a few cases, categorization performance was poor. For example, the DNA/actin/α-tubulin marker set showed poor performance for the microtubule category (Fig. 3B Middle). However, as previously shown, this poor performance was due to the fact that the microtubule category was too coarse (18); in fact, subpopulation profiles did distinguish between microtubule-stabilizing taxanes (paclitaxel and docetaxel) and drugs that destabilize microtubules (colchicine, vinorelbine, and nocodazole) (Fig. 3B Right; Fig. S1D). Thus, a small number of subpopulations were sufficient to give accurate classification for most drug categories and both marker sets.

We extended our analysis to include the additional 10 drugs of unspecified or miscellaneous categorization (Table S1). MDS plots for the DNA/p-p38/p-ERK marker set showed these additional drugs to be interspersed with glucocorticoid receptor drugs (Fig. S3, k = 4). We hypothesized that glucocorticoid receptor ligand-like effects would be more likely to be observed for compounds more proximal to drugs in this category. Of 4 proximal compounds tested, 2 induced cytoplasmic-to-nuclear translocation of a GFP-tagged glucocorticoid receptor (35) in COS7 cells (green tea polyphenols and valproic acid), whereas 2 did not (nicotinamide and azelaic acid) (Fig. S4). Neither of the more distal compounds tested (mitoxantrone and methoxyacetic acid) induced glucocorticoid receptor translocation. Of note, the HDAC drug MS-275 closest to the glucocorticoid receptor group also induced translocation, whereas the less proximal HDAC drug trichostatin A did not (data not shown). Interestingly, these insights were derived by using a general signaling marker set, not specific to mechanisms of nuclear receptor regulatory pathways. These results suggest that analyzing patterns of cellular heterogeneity may be useful for generating mechanistic insights into modes of drug action.

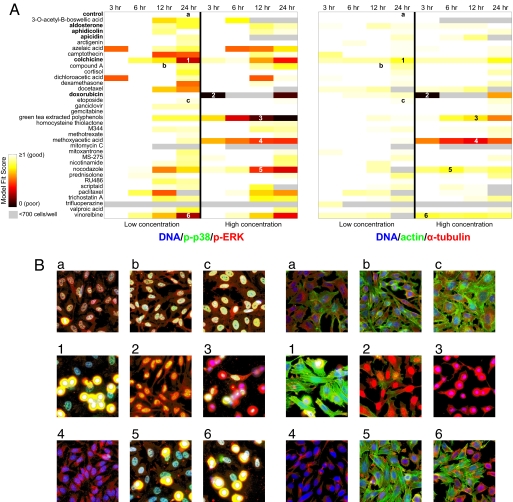
Although our approach effectively captured phenotypic stereotypes common to the entire collection of drug perturbations, we wondered to what extent exceptional (i.e., rare or unmodeled) phenotypes may have been missed (30). To test for exceptional phenotypes in our dataset, we evaluated goodness of model fit for all 35 of our drugs and all treatment conditions based on the ratio of log likelihoods for drug treatment vs. the reference training data (Materials and Methods). We found that only a relatively small number of drug treatment conditions did not fit the reference model reasonably well. To ensure that results were not biased by the inclusion of all 35 drug treatments in our original model, we recomputed model fit using a new reference model based on data sampled from controls and only 5 low-concentration drug treatments, 1 from each category of mechanism (Fig. 4A).

Examining the 6 drugs whose model fit scores were lowest revealed 2 types of exceptional phenotypes (Fig. 4B): (i) microtubule-destabilizing drugs (colchicine, nocodazole, vinorelbine) whose phenotypes were similar to each other but different from most of the remaining drugs; and (ii) 3 drugs at high concentrations (doxorubicin, green tea-extracted polyphenols, methoxyacetic acid) whose phenotypes were visually much different from those seen for any other drug treatment condition. Although colchicine-treated cells were included in the reference model, the phenotypes presented at the 24-h time point were in too low a proportion to constitute 1 of the 4 modeled subpopulations; the other exceptional phenotypes were likely not present in the reference sample. Drugs that induced poorly modeled heterogeneous response in one marker set, tended to also do so in the other marker set. Depending on the application, there are a variety of (supervised and unsupervised) strategies for updating or rebuilding a reference subpopulation model with exceptional phenotypes, such as iterative identification and merging of novel phenotypes in large-scale screens (30). Phenotypic complexity within a collection of perturbations can thus be estimated in a relative sense (i.e., the number of subpopulations required to distinguish the perturbations) or in an absolute sense (i.e., the total number of distinct subpopulations).

Discussion

Phenotypic heterogeneity is often ignored or viewed as an impediment to understanding the effects of perturbations on cellular populations. Traditional measurements of a mean and a variance typically do not capture the complexity of cellular responses to perturbations often observed in microscopy. On the other hand, cell-to-cell variation suggests a potential for limitless cellular complexity. Analysis of our datasets suggested that the effects of perturbations may be characterized largely as redistributions of a limited, but nontrivial, repertoire of underlying states. Subpopulation profiles provided an intuitive and computationally tractable method for identifying functional significance from patterns of heterogeneity. Analysis of subpopulation profiles revealed that drugs of (dis-)similar mechanism induced (dis-)similar patterns of subpopulation redistributions. Thus, our work suggests that patterns of heterogeneity can be quantified and used to extract meaningful biological information.

Our approach for grouping cells is unsupervised, and the identification of subpopulations depends on the composition of the dataset, the markers, the extracted features, and the number of subpopulations. In some cases, subpopulation phenotypes and their redistributions may be interpretable. For example, the microtubule-destabilizing drugs vinorelbine and nocodazole induced a decrease in subpopulations characterized by α-tubulin-positive staining. Our approach also identifies subpopulations whose phenotypes cannot be easily interpreted by current biological knowledge. For example, it is unclear how aldosterone induces an increase in subpopulation 3, characterized by weak diffused p-ERK staining concomitant with clear p-p38 nuclear staining. In general, the best method for interpreting subpopulations and their redistributions may be through relative comparisons with profiles of perturbations with known mechanisms.

GMMs provide a reasonable first approximation for grouping cells in high-dimensional feature space. However, certain subpopulations may still display some degree of phenotypic heterogeneity (e.g., Fig. 1C Upper, subpopulation 2). This may be due to several factors, including: Not all subpopulations will be well modeled by Gaussian distributions; some subpopulations may cover large regions of feature space and need further subdivisions; and automated grouping based on phenotypic features may not agree with visual grouping. Model parameters in future studies of heterogeneity may be optimized to improve visual tightness of identified subpopulation phenotypes.

Our analysis suggests that observed heterogeneity may reflect variation around a discrete set of phenotypic states. Our work provides a framework for future studies with larger sample sizes, greater numbers of perturbations, and higher numbers of markers to rigorously test questions about the nature of heterogeneity, including: Do unperturbed cells occupy essentially the same phenotypic space as cells with significantly perturbed pathways? And, do perturbations induce redistributions among a limited repertoire of underlying stereotypical states? We envision that the ability to identify and interpret information contained in patterns of cellular heterogeneity will provide insights into physiology and disease that may be missed by traditional population-averaged or small-cell-number studies.

Materials and Methods

Similarity Comparison.

Individual profiles were compared by using a symmetrized version of Kullback-Leibler divergence (34). In particular, given subpopulation profiles P and Q for a model with k subpopulations, the similarity measure S(P,Q) is defined as

where

Supplementary Material