Abstract
We have studied the effect of polyethylene glycol (PEG) on the liquid–liquid phase separation (LLPS) of aqueous solutions of bovine γD-crystallin (γD), a protein in the eye lens. We observe that the phase separation temperature increases with both PEG concentration and PEG molecular weight. PEG partitioning, which is the difference between the PEG concentration in the two coexisting phases, has been measured experimentally and observed to increase with PEG molecular weight. The measurements of both LLPS temperature and PEG partitioning in the ternary γD-PEG-water systems are used to successfully predict the location of the liquid–liquid phase boundary of the binary γD-water system. We show that our LLPS measurements can be also used to estimate the protein solubility as a function of the concentration of crystallizing agents. Moreover, the slope of the tie-lines and the dependence of LLPS temperature on polymer concentration provide a powerful and sensitive check of the validity of excluded volume models. Finally, we show that the increase of the LLPS temperature with PEG concentration is due to attractive protein–protein interactions.
Keywords: PEG, ternary mixtures, solubility, partitioning
Polyethylene glycol (PEG) is a hydrophilic nonionic polymer used in many biochemical and industrial applications. Due to its nontoxic character, this chemical can be found in cosmetics, food, and pharmaceutical products. The mild action of PEG on the biological activity of cell components explains the success of this polymer in biotechnological applications. PEG is commonly used for liquid–liquid partitioning and precipitation of biomacromolecules (1, 2). In protein crystallography, PEG is considered the most successful precipitating agent for the production of protein crystals, the crucial step for the determination of the molecular structure of a protein. All these applications make PEG by far the most widely used polymer in aqueous solutions of biological molecules (1, 3).
Due to the extensive practical use of PEG as a precipitating agent for proteins, it is of fundamental importance to understand protein–protein and protein–PEG interactions in protein–PEG–water ternary systems. These interactions are often described in terms of a depletion force, which arises because the polymer is depleted in the region between adjacent proteins (4, 5). Depletion force models have been successful in describing the effect of nonadsorbing polymers on colloidal suspensions (6–10).
Protein–PEG–water solutions have been investigated by several techniques (4, 5, 11–14). Small-angle x-ray- (4) and light-scattering (5) measurements generally confirmed that total protein–protein interactions can be described in terms of depletion effects. The microscopic interpretation used in the above studies is derived from colloid–polymer models. To model the effect of PEG, a depletion component is added to the original protein–protein pair interaction potential. This microscopic modeling, however, does not provide information about the actual protein–PEG interactions in the ternary system. Dialysis experiments, which describe the effect of PEG partitioning (i.e., the difference of PEG concentration) between two solutions separated by a membrane not permeable to protein molecules, give information on protein–PEG interactions only when protein–protein interactions are absent (12, 15). Studies of the solubility of protein crystals in the presence of PEG have been carried out to investigate protein–protein and protein–PEG interactions. However, to interpret the results, assumptions about the properties of the crystal are required. Moreover, simple excluded volume models fail to describe protein solubility as a function of PEG molecular weight (16). The discrepancy between model and experiment becomes particularly large for PEG of lower molecular weights (11). Furthermore, the magnitude of the protein–PEG interactions changes from protein to protein in a way that does not correlate with the simple excluded volume scenario (11, 15).
Liquid–liquid phase separation (LLPS) can be used as a direct tool for probing both protein–protein and protein–PEG interactions. It has been shown that the position of the liquid–liquid boundaries provides insight about the nature and magnitude of the protein–protein interactions (17–20). The advantage of LLPS analysis with respect to measurements of protein solubility is that data interpretation requires no assumptions regarding crystal phase properties (11, 21). LLPS is important also for the analysis of nonequilibrium properties of the system. Because the nucleation of protein crystals is enhanced in proximity of the LLPS, this phase boundary is believed to be implicated in protein crystallization kinetics (22, 23).
We present an experimental investigation of the effect of low molecular weight PEG on the LLPS of aqueous solutions of bovine γD-crystallin (γD). γD is a member of the γ-crystallin family of lens proteins, which are involved in cataract formation (24). The phase diagram of aqueous γ-crystallins has been well characterized, and several members of the family, including γD, have attractive interactions leading to LLPS of the corresponding aqueous solutions (17, 20, 25, 26). γD is a protein with a simple globular structure (27) and is weakly charged at the pH value (≈7) used in our measurements (28). The experiments were performed at a PEG concentration of ≈5% in weight, which falls within the range of concentrations used for protein crystal growth (3).
The LLPS properties of the protein–PEG–water ternary system are described by a coexistence surface in the phase diagram. This coexistence surface represents the LLPS temperature as a function of protein concentration, c1, and PEG concentration, c2. At a fixed temperature, the LLPS properties of the system are described by an isothermal coexistence curve, which gives the concentrations (c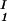 , c
, c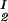 ) and (c
) and (c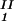 , c
, c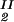 ) of the coexisting phases, I and II. The partitioning of the components in the two coexisting phases is described by tie-lines connecting the points (c
) of the coexisting phases, I and II. The partitioning of the components in the two coexisting phases is described by tie-lines connecting the points (c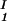 , c
, c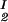 ) and (c
) and (c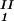 , c
, c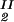 ) of the coexistence curve. The critical point, (c
) of the coexistence curve. The critical point, (c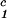 , c
, c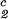 ), is defined as the point of the coexistence curve where the condition (c
), is defined as the point of the coexistence curve where the condition (c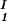 , c
, c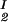 ) = (c
) = (c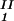 , c
, c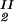 ) occurs. The location of this point as a function of the temperature is described by a critical line on the coexistence surface.
) occurs. The location of this point as a function of the temperature is described by a critical line on the coexistence surface.
Materials and Methods
Bovine γD, which has a molecular mass of 20,700 g/mol, was isolated from 1- to 6-week-old calf lenses, obtained by overnight express from Antech (Tyler, TX). Pure γD was isolated and purified from these lenses by standard procedures described elsewhere (25, 29). The purity of the native sample was at least 95%, based on both ion-exchange and size-exclusion HPLC. The purified γD was dialyzed exhaustively into sodium phosphate buffer (0.1 M, pH 7.1) that contained sodium azide (0.02%).
PEG with molecular masses ranging from 200 to 3,350 g/mol (PEG200–PEG3350) and tetraethylene glycol (TEG, molecular mass 194.2 g/mol) were purchased from Sigma–Aldrich and used without further purification. Sample molecular mass and polydispersity were analyzed by electrospray ionization mass spectrometry at the Biopolymers Laboratory at the Center for Cancer Research at the Massachusetts Institute of Technology. Estimates of the average molecular mass were in agreement with the nominal values provided by the company. All polymers had a narrow molecular mass distribution with a polydispersity of about 1.05.
Protein–PEG aqueous solutions were prepared as follows. Solutions containing dilute γD in phosphate buffer were concentrated by ultrafiltration. When the desired protein concentration was reached, a known weight of PEG was added to the protein solution. The concentration of γD in the samples was determined by UV absorption at 280 nm, using the extinction coefficient value of 2.11 mg−1⋅ml⋅cm−1 (26). The concentration of PEG in the samples was calculated by using the mass of PEG and the total volume of the solution. The volumetric contribution of each component is obtained by multiplying the mass of the component by the corresponding specific volume, i.e., 0.71 ml/g for γD (30), 0.84 ml/g for PEG (15) and 0.992 ml/g for the buffer.
The LLPS temperature for a given protein–PEG aqueous solution was determined by gradually lowering the temperature of the sample until clouding was observed. The cloud point was determined by the examination of the transmitted intensity–temperature profile as previously described by Liu et al. (31). The coexisting phases were obtained by quenching the sample at fixed temperature beneath the coexistence surface. If after about 24 hours the two coexisting phases had not separated by gravity, centrifugation was used for the separation. The protein concentration in each phase was determined by UV absorption. To determine the PEG concentration in each of the coexisting phases, an aliquot of known weight was taken from each phase, and the PEG was separated from the protein by ultrafiltration (Amicon Microcon YM-10). The protein-free solution was weighed and the corresponding concentration of PEG determined by using a standardized refractive index detector (Perkin–Elmer LC-30 RI). The concentration of PEG in each aliquot was then calculated from its measured value in the protein-free solution. To ensure that possible differences in phosphate concentration in the two phases did not affect the results, the refractive index measurements were performed after isocratic elution of the protein-free solution on a size-exclusion HPLC column, by using sodium phosphate buffer (0.1 M, pH 7.1) with a flow rate of 1 ml/min. An Ohpak SB-802.5 HQ column (size 8 mm × 300 ml) from Phenomenex was used for the PEG200 and PEG400 solutions. For PEG1000, the Superdex 75 HR 10/30 column (size 10 × 300 mm) from Amersham Pharmacia Biotech was preferred for its higher resolution. The procedure was verified with protein–PEG aqueous solutions of known composition. In all cases, the measured protein and PEG concentrations in the two coexisting phases were consistent with the protein and PEG concentrations in the original homogeneous samples.
Results
We describe the composition of the γD-PEG-water systems by the protein (component 1) concentration c1 and the PEG (component 2) concentration inside the protein-free volume, c2s. If ν is the protein specific volume and φ = c1ν is the protein volume fraction, then c2s is equal to c2/(1 − φ). The choice of c2s instead of c2 to present our results is justified by the following argument. We consider as a reference system one in which the particles of component 2 have a negligible size and do not introduce specific chemical interactions in the system. In this reference case, the different values of c2 between the two coexisting phases are entirely determined by the exclusion of component 2 from the volume occupied by component 1. Here, the condition of chemical equilibrium is expressed by the relation: c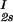 = c
= c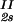 . Thus, in our systems, any observed difference in c2s between two coexisting phases is related to the finite size and specific chemical properties of the PEG molecules.
. Thus, in our systems, any observed difference in c2s between two coexisting phases is related to the finite size and specific chemical properties of the PEG molecules.
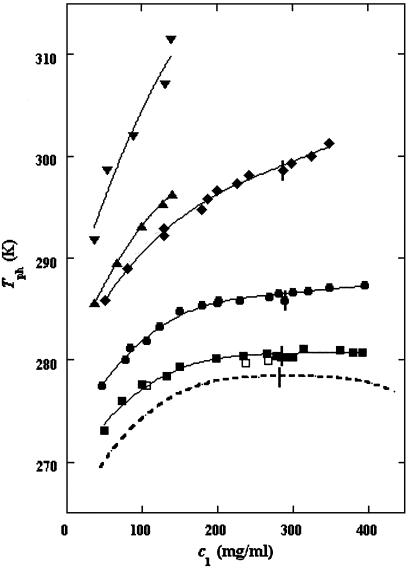
In Fig. 1, we present our measurements of the LLPS temperature, Tph, for γD-PEG-water ternary solutions at constant PEG concentration of c2s ≈ 50 mg/ml and with several polymer average molecular masses: 200 g/mol (filled squares), 400 g/mol (circles), 1,000 g/mol (diamonds), 1,450 g/mol (upright triangles), and 3,350 g/mol (inverted triangles). We also report measurements of temperature of phase separation for the γD-tetraethylene glycol-water at the same value of c2s (open squares). TEG essentially has the same molecular weight as PEG200, but, in contrast to PEG, is monodisperse. We see from the figure that the two sets of measurements, for TEG and for PEG200, overlap within the experimental error and conclude that the effects due to polydispersity are small. In Fig. 1, we also show the coexistence curve for the binary aqueous protein system (dashed curve) (29). The phase boundaries of the ternary systems are located at higher Tph than that of the binary system, and the difference increases with PEG molecular weight. The critical points, shown by vertical bars in Fig. 1, were identified by the examination of the transmitted intensity–temperature profile as previously described by Liu et al. (31). In all cases, the value of protein critical concentration (about 290 mg/ml) is not affected by PEG within the experimental error. On the other hand, the slope of Tph at the critical point, (∂Tph/∂c1)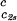 , is positive and increases with the PEG molecular weight, in contrast with the zero slope required for the protein–water binary system. In Table 1, we report the values of the PEG concentration, c2s, the critical temperature, Tc, and the slope (∂Tph/∂c1)
, is positive and increases with the PEG molecular weight, in contrast with the zero slope required for the protein–water binary system. In Table 1, we report the values of the PEG concentration, c2s, the critical temperature, Tc, and the slope (∂Tph/∂c1)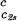 .
.
Fig 1.
LLPS temperature at constant PEG concentration of ≈50 mg/ml for the γD-PEG-water ternary system. The average molecular masses are: 200 g/mol (▪), 400 g/mol (•), 1,000 g/mol (⧫), 1,450 g/mol (▴), and 3,350 g/mol (▾). The solid curves are guides for the eye. The values for the γD-tetraethylene glycol-water ternary system are represented by open squares (□). We draw the coexistence curve for the γD-water binary system (dashed curve). The vertical bars (|) locate the critical point.
Table 1.
The values of the parameters characterizing the ternary coexistence surfaces
| c2s, mg/ml | Tc, K |
(∂Tph/∂c1)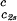 , 10−3 K mg−1⋅ml , 10−3 K mg−1⋅ml |
(∂c2s/∂c1)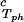 /c /c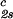 , 10−3⋅mg−1⋅ml , 10−3⋅mg−1⋅ml |
(∂Tph/∂c2s)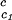 , K−1⋅mg−1⋅ml , K−1⋅mg−1⋅ml |
T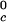 , K , K |
|
|---|---|---|---|---|---|---|
| PEG200 | 54 | 280.6 | 3 ± 2 | −0.5 ± 0.1 | 0.11 ± 0.07 | 275 ± 4 |
| PEG400 | 52 | 286.5 | 9 ± 1 | −1.1 ± 0.1 | 0.17 ± 0.03 | 278 ± 2 |
| PEG1000 | 50 | 299.3 | 33 ± 3 | −2.0 ± 0.3 | 0.33 ± 0.05 | 283 ± 3 |
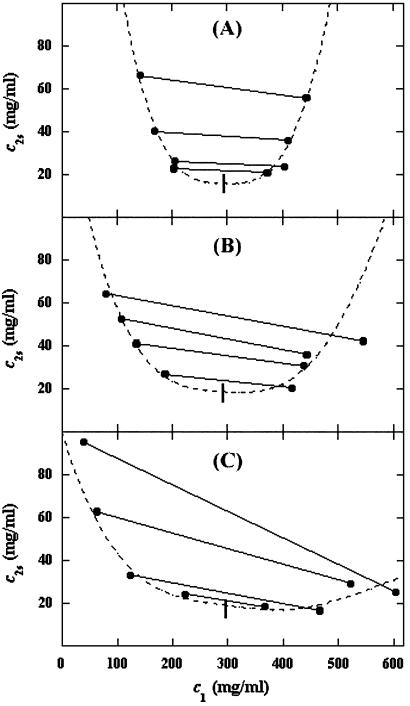
In Fig. 2, we present our experimental data (filled circles) of the coexisting values (c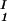 , c
, c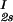 ) and (c
) and (c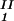 , c
, c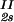 ) for the γD-PEG-water solutions having PEG average molecular weight: 200 g/mol (279.2 K, case A), 400 g/mol (281.7 K, case B), and 1000 g/mol (290.3 K, case C). The pairs of points representing the coexisting phases are connected by straight lines (tie-lines). The dashed curves are eye guides representing the coexisting curves. In all three cases, the coexisting phases were obtained by quenching samples with the same initial protein concentration of 300 mg/ml but with different initial PEG concentrations. The temperatures for the measurements of the coexistence curves were chosen so that they lie above the critical temperature of the protein–water binary system but below the critical temperature of the corresponding ternary system in Fig. 1. Because the protein critical concentration, c
) for the γD-PEG-water solutions having PEG average molecular weight: 200 g/mol (279.2 K, case A), 400 g/mol (281.7 K, case B), and 1000 g/mol (290.3 K, case C). The pairs of points representing the coexisting phases are connected by straight lines (tie-lines). The dashed curves are eye guides representing the coexisting curves. In all three cases, the coexisting phases were obtained by quenching samples with the same initial protein concentration of 300 mg/ml but with different initial PEG concentrations. The temperatures for the measurements of the coexistence curves were chosen so that they lie above the critical temperature of the protein–water binary system but below the critical temperature of the corresponding ternary system in Fig. 1. Because the protein critical concentration, c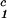 , is equal to the average concentration (c
, is equal to the average concentration (c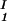 + c
+ c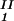 )/2 in the limit of c
)/2 in the limit of c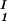 − c
− c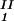 = 0, we determine c
= 0, we determine c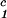 by plotting (c
by plotting (c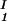 + c
+ c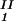 )/2 as a function of c
)/2 as a function of c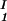 − c
− c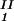 . The resulting values of the critical concentrations (vertical bars in Fig. 2) are, within the experimental error, the same as the value reported for the binary protein–water system. An interesting feature of the phase diagram is that the difference of PEG concentration between the two coexisting phases increases as the PEG molecular weight increases. To describe the effect of PEG molecular weight on PEG partitioning, we consider the normalized slope of the tie-lines at the critical point: (∂c2s/∂c1)
. The resulting values of the critical concentrations (vertical bars in Fig. 2) are, within the experimental error, the same as the value reported for the binary protein–water system. An interesting feature of the phase diagram is that the difference of PEG concentration between the two coexisting phases increases as the PEG molecular weight increases. To describe the effect of PEG molecular weight on PEG partitioning, we consider the normalized slope of the tie-lines at the critical point: (∂c2s/∂c1)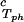 /c
/c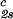 . This quantity can be obtained by plotting the incremental ratio (ln c
. This quantity can be obtained by plotting the incremental ratio (ln c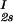 − lnc
− lnc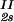 )/(c
)/(c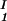 − c
− c ) as a function of c
) as a function of c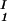 − c
− c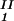 and considering the limit of c
and considering the limit of c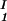 − c
− c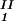 = 0. In Table 1, we can see that (∂c2s/∂c1)
= 0. In Table 1, we can see that (∂c2s/∂c1)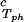 /c
/c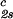 increases with the PEG molecular weight. The protein volume fraction in the protein-rich phase is comparable to the protein volume fraction in the crystal, which is ≈0.4–0.6 (c1 ≈ 600–800 mg/ml) (27, 32). The nonnegligible values of PEG concentration of the protein-rich phases reported for the γD-PEG1000-water system suggest that the crystal phase could accommodate polymer coils with molecular weight equal to or lower than ≈1,000 g/mol.
increases with the PEG molecular weight. The protein volume fraction in the protein-rich phase is comparable to the protein volume fraction in the crystal, which is ≈0.4–0.6 (c1 ≈ 600–800 mg/ml) (27, 32). The nonnegligible values of PEG concentration of the protein-rich phases reported for the γD-PEG1000-water system suggest that the crystal phase could accommodate polymer coils with molecular weight equal to or lower than ≈1,000 g/mol.
Fig 2.
Coexisting surfaces at constant temperature for the γD-PEG-water ternary system with PEG average molecular mass: 200 g/mol (279.2 K, case A), 400 g/mol (281.7 K, case B), and 1,000 g/mol (290.3 K, case C). The pairs of points representing the coexisting phases (•) are connected by the tie-lines (solid lines). The dashed curves are guides for the eye, and the vertical bars (|) locate the critical point.
The behavior of the coexistence surface is described by the three slopes (∂c2s/∂c1)Tph, (∂Tph/∂c2s)c1, and (∂Tph/∂c1)c2s, which are related to each other by the mathematical relationship:
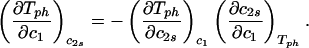 |
It is important to observe that Eq. 1 is true only for ternary systems. Due to the presence of the two buffer salts (dibasic and monobasic sodium phosphate), our protein aqueous solutions contain more than three components. We know that salt partitioning is unimportant if PEG is not in the solution, because the protein-buffer system is well described as a binary system [for example, the critical point is at the maximum of the LLPS curve (26)]. Therefore, in the protein–PEG–buffer system, it is only because of the presence of PEG that salt partitioning may occur. We will show that Eq. 1 successfully describes our experimental results, which suggests that salt partitioning is insignificant insofar as the validity of Eq. 1 is concerned.
We apply Eq. 1 on the critical line of the coexistence surfaces. Because the critical temperature, Tc, of the γD–PEG–water systems (with c2s ≈ 50 mg/ml) is higher than the critical temperature, T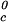 , of the γD-water system (Fig. 1), the quantity (∂Tph/∂c2s)
, of the γD-water system (Fig. 1), the quantity (∂Tph/∂c2s)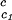 is positive. At the critical point, the slope (∂c2s/∂c1)
is positive. At the critical point, the slope (∂c2s/∂c1)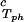 of the coexistence surface is negative because it coincides with the slope of the tie-lines (Fig. 2). Eq. 1 shows that the slope (∂Tph/∂c1)
of the coexistence surface is negative because it coincides with the slope of the tie-lines (Fig. 2). Eq. 1 shows that the slope (∂Tph/∂c1)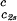 is positive, as found experimentally (Fig. 1 and Table 1).
is positive, as found experimentally (Fig. 1 and Table 1).
The slope (∂Tph/∂c2s)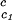 can be calculated, by using Eq. 1, from the values of c2s, (∂Tph/∂c1)
can be calculated, by using Eq. 1, from the values of c2s, (∂Tph/∂c1)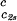 , and (∂c2s/∂c1)
, and (∂c2s/∂c1) /c
/c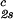 reported in Table 1. We have assumed that the quantity, (∂c2s/∂c1)
reported in Table 1. We have assumed that the quantity, (∂c2s/∂c1)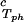 /c
/c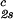 , which is obtained from our measurements of coexistence curves, is not a function of the temperature and PEG concentration within our experimental domain. The calculated values of (∂Tph/∂c2s)
, which is obtained from our measurements of coexistence curves, is not a function of the temperature and PEG concentration within our experimental domain. The calculated values of (∂Tph/∂c2s)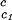 , reported in Table 1, are consistent with the experimentally observed dependence of the critical temperature as a function of PEG molecular weight (Fig. 1). Indeed, we can quantitatively compare the experimental change of critical temperature between the ternary and the binary systems, shown in Fig. 1 for each PEG molecular weight, with the change predicted from the calculated values of (∂Tph/∂c2s)
, reported in Table 1, are consistent with the experimentally observed dependence of the critical temperature as a function of PEG molecular weight (Fig. 1). Indeed, we can quantitatively compare the experimental change of critical temperature between the ternary and the binary systems, shown in Fig. 1 for each PEG molecular weight, with the change predicted from the calculated values of (∂Tph/∂c2s)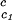 . Specifically, we may estimate the critical temperature, T
. Specifically, we may estimate the critical temperature, T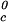 , of the γD-water system from the expression: T
, of the γD-water system from the expression: T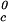 ≈ Tc− (∂Tph/∂c2s)
≈ Tc− (∂Tph/∂c2s)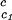 c2s. Thereby, we obtain the calculated values of T
c2s. Thereby, we obtain the calculated values of T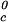 , which are reported in last column of Table 1. These are in acceptable agreement with the experimental value of 278.4 K (29). Hence, using only the information obtained from the properties of the ternary coexistence surfaces, we are able to estimate reliably the location of the binary liquid–liquid phase boundary. This information can be most valuable when LLPS of protein–water systems is not experimentally observable because it is inaccessible due to either the freezing of the system or the denaturation of the protein at high temperature, which is important for proteins with lower consolute critical points (33).
, which are reported in last column of Table 1. These are in acceptable agreement with the experimental value of 278.4 K (29). Hence, using only the information obtained from the properties of the ternary coexistence surfaces, we are able to estimate reliably the location of the binary liquid–liquid phase boundary. This information can be most valuable when LLPS of protein–water systems is not experimentally observable because it is inaccessible due to either the freezing of the system or the denaturation of the protein at high temperature, which is important for proteins with lower consolute critical points (33).
Discussion
Our previous analysis shows that the behavior of the coexistence surfaces at the critical point can be described by two distinct features: the slope of the tie-lines and the dependence of LLPS temperature on PEG concentration. To analyze the physical factors that determine these two features of the coexistence surfaces, we introduce the free energy of the system. We define the quantity F, representing the difference, at constant volume, V, and temperature, T, between the Helmholtz free energy of the virtually incompressible protein–PEG–water system and the pure water system. The changes of F due to the replacement (at constant volume) of γ1 water moles by 1 mole of protein and γ2 water moles by 1 mole of PEG are respectively described by the differences of chemical potentials, μ1 ≡ μprotein − γ1μwater and μ2 ≡ μPEG − γ2μwater. A ternary incompressible system may be equivalently treated as a binary compressible system where μ1 and μ2 are the chemical potentials of the two effective components (17). The quantities μ1 and μ2 will be indicated as the protein and PEG effective chemical potentials.
It is convenient to introduce the reduced free energy f̂ ≡ (F − F0)/RTV, where F0 is the standard free energy, and R is the ideal gas constant. If the concentration of PEG, c2, is relatively small, the reduced free energy is, to first-order approximation with respect to c2, given by the following equation:
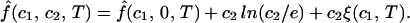 |
In Eq. 2, f̂(c1, 0, T) is the reduced free energy of the binary protein–water system, whereas c2 ln(c2/e) and c2ξ(c1, T) are the contributions to the reduced free energy associated with the replacement of water molecules by PEG molecules at constant V and T. The contribution of PEG to the ideal mixing entropy of the system is represented by the term c2ln(c2/e), whereas the quantity c2ξ(c1, T) is the first term in a series expansion describing the change of the reduced free energy over and above the ideal mixing entropy. This approximation is acceptable because our experimental PEG concentrations are generally well below the threshold for polymer–polymer interpenetration, i.e., we are in the dilute regime (5). If we differentiate Eq. 2 with respect to the concentrations, c1 and c2, at constant V and T, we obtain the following expressions for the reduced effective chemical potentials:
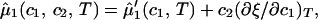 |
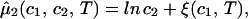 |
where μ̂i ≡ (μi − μ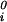 )/RT (with i = 1, 2), μ
)/RT (with i = 1, 2), μ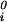 (T) ≡ (∂F0/∂ci)T,V/V, and the quantity μ̂′1(c1, T) ≡ μ̂1(c1, 0, T) is the protein effective chemical potential corresponding to the protein–water binary system. The two crossderivatives of the chemical potentials, (∂μ̂1/∂c2)
(T) ≡ (∂F0/∂ci)T,V/V, and the quantity μ̂′1(c1, T) ≡ μ̂1(c1, 0, T) is the protein effective chemical potential corresponding to the protein–water binary system. The two crossderivatives of the chemical potentials, (∂μ̂1/∂c2)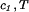 and (∂μ̂2/∂c1)
and (∂μ̂2/∂c1)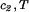 , are both equal to (∂ξ/∂c1)T. This quantity characterizes the protein–PEG interactions. Eq. 3a and 3b fully characterize all the experimental observable features of the coexistence surfaces. Specifically, they enable us to analyze the quantities (∂c2/∂c1)
, are both equal to (∂ξ/∂c1)T. This quantity characterizes the protein–PEG interactions. Eq. 3a and 3b fully characterize all the experimental observable features of the coexistence surfaces. Specifically, they enable us to analyze the quantities (∂c2/∂c1)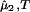 (i.e., the slope of the tie-lines) and (∂Tph/∂c2)c1.
(i.e., the slope of the tie-lines) and (∂Tph/∂c2)c1.
The Slope of the Tie-Lines.
If we differentiate Eq. 3a with respect to c2 at constant c1 and T, and Eq. 3b with respect to c1 at constant μ̂2 and T, we obtain:
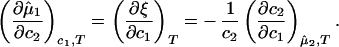 |
Experimentally, the quantity (∂c2/∂c1)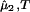 can be found from the limiting value of the slope of the tie-lines at the critical point. If we apply Eq. 4 to our experimental tie-line, we observe that (∂μ̂1/∂c2)
can be found from the limiting value of the slope of the tie-lines at the critical point. If we apply Eq. 4 to our experimental tie-line, we observe that (∂μ̂1/∂c2)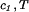 = (∂ξ/∂c1)T is positive and increases with the PEG molecular weight.
= (∂ξ/∂c1)T is positive and increases with the PEG molecular weight.
The slope of the tie-lines can be used to predict the effect of PEG on protein solubility. If protein crystals (solid phase) are in thermodynamic equilibrium with the liquid phase, μ̂1 must be equal to its value in the solid phase, μ̂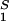 . For relatively low protein concentrations, μ̂′1(c1, T) ≈ln c1. Thus, using the equality of chemical potentials and Eq. 3a, we find: ln c1 ≈ μ̂
. For relatively low protein concentrations, μ̂′1(c1, T) ≈ln c1. Thus, using the equality of chemical potentials and Eq. 3a, we find: ln c1 ≈ μ̂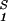 − (∂ξ/∂c1)T c2 (11). This relationship gives the protein solubility, c1, as a function of PEG concentration, c2. The dependence of μ̂
− (∂ξ/∂c1)T c2 (11). This relationship gives the protein solubility, c1, as a function of PEG concentration, c2. The dependence of μ̂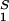 on c1 and c2 is expected to be very weak. Thus the fractional decrease of protein solubility with PEG concentration is fully determined by the value of (∂ξ/∂c1)T, which is proportional to the slope of the tie-line (see Eq. 4). Therefore the magnitude of (∂c2/∂c1)
on c1 and c2 is expected to be very weak. Thus the fractional decrease of protein solubility with PEG concentration is fully determined by the value of (∂ξ/∂c1)T, which is proportional to the slope of the tie-line (see Eq. 4). Therefore the magnitude of (∂c2/∂c1)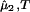 /c2 characterizes the effectiveness of a protein precipitating agent such as PEG.
/c2 characterizes the effectiveness of a protein precipitating agent such as PEG.
The Excluded Volume Model of Protein–PEG Interactions.
We now analyze the experimental coexisting values (φI, c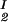 ) and (φII, c
) and (φII, c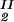 ) to gain insight about the physical factors that determine the quantity ξ and its dependence on c1. We apply a simple excluded volume model that directly relates PEG partitioning to the difference in free volume fractions between the two coexisting phases. If we assume that PEG molecules can be described as ideal polymer coils and that protein molecules have a spherical shape, then due to steric hindrance, each protein will be surrounded by an adjacent region where the centers of mass of the coils are excluded, and the width, δ, of the resulting depletion layer will be proportional to the gyration radius, Rg, of the polymer coil (4–14). If α is the volume fraction available to the centers of mass of the coils, the condition of chemical equilibrium μ̂2(c
) to gain insight about the physical factors that determine the quantity ξ and its dependence on c1. We apply a simple excluded volume model that directly relates PEG partitioning to the difference in free volume fractions between the two coexisting phases. If we assume that PEG molecules can be described as ideal polymer coils and that protein molecules have a spherical shape, then due to steric hindrance, each protein will be surrounded by an adjacent region where the centers of mass of the coils are excluded, and the width, δ, of the resulting depletion layer will be proportional to the gyration radius, Rg, of the polymer coil (4–14). If α is the volume fraction available to the centers of mass of the coils, the condition of chemical equilibrium μ̂2(c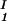 , c
, c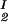 , T) = μ̂2(c
, T) = μ̂2(c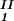 , c
, c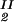 , T) becomes c
, T) becomes c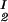 /αI= c
/αI= c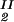 /αII, where c2/α is the polymer concentration in the free volume (9, 34) and the free volume fraction, α, is equal to exp(−ξ) (see Eq. 3b).
/αII, where c2/α is the polymer concentration in the free volume (9, 34) and the free volume fraction, α, is equal to exp(−ξ) (see Eq. 3b).
It has been theoretically shown that, in the case of ideal polymer coils and relatively large hard spheres, δ ≅ 1.1Rg (35). An approximate expression for the free volume fraction, α, as a function of the hard sphere volume fraction, φ, is given by the well established scaled particle theory (34, 36, 37):
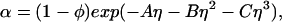 |
where η = φ/(1 − φ), A = 3q + 3q2 + q3, B = 9q2/2 + 3q3, C = 3q3, and q = δ/R is the depletion layer thickness normalized with respect to the hard sphere radius, R. The prefactor, 1 − φ, in Eq. 5, is the volume fraction not occupied by the spheres, whereas the exponential factor describes the effect of the depletion layers. When φ is small, α ≅ 1 − (1 + q)3φ and 4π(1 + q)3R3/3 is the excluded volume connected with each sphere. As φ increases, the average distance between adjacent spheres decreases, and α becomes larger than 1 − (1 + q)3φ because the depletion layers overlap.
Because c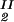 /c
/c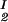 = α(q, φII)/α(q, φI), we substitute the expression for α provided by Eq. 5 into the ratio of the free volume fractions, and thereby we can determine an apparent q value for each experimental tie-line. We find that, within the experimental error, this quantity does not depend on the tie-line position in the coexistence curve. We present the average value of the apparent q as a function of the square root of PEG molecular weight as the filled circles in Fig. 3. We note that the q values calculated by using α = 1 − (1 + q)3φ are only ≈10% smaller than the values calculated by using the complete expression for α and so conclude that the overlapping of depletion layers contributes only marginally to the apparent q values reported in Fig. 3. We have also considered the effect of the PEG molecular weight polydispersity. Because the polydispersity of PEG is given by a narrow Poisson distribution function to be applied to PEG (38, 39), it can be shown that the polymer distribution in each of the two coexisting phases is essentially the same as in the original homogeneous system, and hence polydispersity does not significantly modify the slope of the tie-lines.
= α(q, φII)/α(q, φI), we substitute the expression for α provided by Eq. 5 into the ratio of the free volume fractions, and thereby we can determine an apparent q value for each experimental tie-line. We find that, within the experimental error, this quantity does not depend on the tie-line position in the coexistence curve. We present the average value of the apparent q as a function of the square root of PEG molecular weight as the filled circles in Fig. 3. We note that the q values calculated by using α = 1 − (1 + q)3φ are only ≈10% smaller than the values calculated by using the complete expression for α and so conclude that the overlapping of depletion layers contributes only marginally to the apparent q values reported in Fig. 3. We have also considered the effect of the PEG molecular weight polydispersity. Because the polydispersity of PEG is given by a narrow Poisson distribution function to be applied to PEG (38, 39), it can be shown that the polymer distribution in each of the two coexisting phases is essentially the same as in the original homogeneous system, and hence polydispersity does not significantly modify the slope of the tie-lines.
Fig 3.
Dependence of the size ratio, q, as a function of the square root of the PEG average molecular weight, Mn. The filled circles (•) are the value obtained by fitting the experimental coexisting compositions with Eq. 2; the open circles (○) are the values calculated from the polymer gyration radii and the protein molecular volume. The dashed lines are guides for the eye.
In Fig. 3, we also present the theoretical q values (open circles), calculated by using q = 1.1Rg/R. Rg for PEG is taken from ref. 15, whereas R is estimated from the molecular weight and specific volume of γD. As seen in Fig. 3, both theoretical q and the apparent q vary as the square root of the PEG molecular weight as expected for a Gaussian coil (40). However, the apparent values of q are numerically ≈50% smaller than the corresponding theoretical values. This significant discrepancy represents the deviation of the actual γD-PEG interactions relative to the sphere-ideal coil case.
It has been found that q ≈ Rg/R in the case of bovine serum albumin, chymotrypsinogen, and RNase, whereas q ≈ 0.5Rg/R in the case of β-lactoglobulin and lysozyme (12, 15). The difference between the values obtained for the various proteins suggests that the departure from the excluded volume model is related to direct interactions of PEG with protein surface residues (15). Our results clearly suggest the presence of such specific interactions in the γD-PEG-water systems. It appears that weak attractive interactions between PEG and γD induce a flattening of the polymer coils near the protein surface and a corresponding reduction of the depletion layer thickness.
The Spinodal Boundaries and the Dependence of the LLPS Temperature on PEG Concentration.
The spinodal surface (40), which describes the spinodal temperature, Tsp, as a function of protein and PEG concentrations, defines the boundary between the stable domain ((∂μ̂1/∂c1)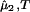 > 0) and the unstable domain ((∂μ̂1/∂c1)
> 0) and the unstable domain ((∂μ̂1/∂c1)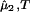 < 0) of a homogeneous protein–PEG–water system. The spinodal condition, (∂μ̂1/∂c1)
< 0) of a homogeneous protein–PEG–water system. The spinodal condition, (∂μ̂1/∂c1)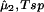 = 0, can be used to determine the spinodal temperature, Tsp, as a function of c1 and c2. Indeed, on differentiating Eq. 3a with respect to c1 at constant μ̂2 and T, we obtain:
= 0, can be used to determine the spinodal temperature, Tsp, as a function of c1 and c2. Indeed, on differentiating Eq. 3a with respect to c1 at constant μ̂2 and T, we obtain:
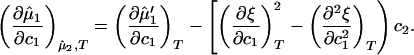 |
In the case of hard sphere-ideal polymer coil excluded volume interactions, α = exp(−ξ), and the difference (∂ξ/∂c1)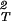 − (∂2ξ/∂c
− (∂2ξ/∂c )T becomes equal to the quantity, (∂2α/∂c
)T becomes equal to the quantity, (∂2α/∂c )T/α. If we use Eq. 5, we find that, when both φ and q are small, (∂2α/∂φ2)T/α is approximately equal to 12q3. Although Eq. 5 is inaccurate insofar as high-order derivatives such as (∂2α/∂φ2)T are concerned, it usefully describes the general features of the excluded volume model. Indeed, due to the overlapping of adjacent depletion layers, (∂2α/∂φ2)T must be positive and must increase as the depletion layer thickness increases. These general features of the excluded volume model can be used to understand the effect of PEG on initially stable protein aqueous solutions. In fact, because (∂ξ/∂c1)
)T/α. If we use Eq. 5, we find that, when both φ and q are small, (∂2α/∂φ2)T/α is approximately equal to 12q3. Although Eq. 5 is inaccurate insofar as high-order derivatives such as (∂2α/∂φ2)T are concerned, it usefully describes the general features of the excluded volume model. Indeed, due to the overlapping of adjacent depletion layers, (∂2α/∂φ2)T must be positive and must increase as the depletion layer thickness increases. These general features of the excluded volume model can be used to understand the effect of PEG on initially stable protein aqueous solutions. In fact, because (∂ξ/∂c1)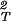 − (∂2ξ/∂c
− (∂2ξ/∂c )T is positive, Eq. 6 predicts that as the polymer concentration increases, (∂μ̂1/∂c1)
)T is positive, Eq. 6 predicts that as the polymer concentration increases, (∂μ̂1/∂c1)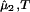 decreases and can be made to reach zero, i.e., a spinodal boundary. Thus, sufficient PEG can in principle induce phase separation at any given temperature. This is true even if the protein–protein interactions are repulsive.
decreases and can be made to reach zero, i.e., a spinodal boundary. Thus, sufficient PEG can in principle induce phase separation at any given temperature. This is true even if the protein–protein interactions are repulsive.
We now use the spinodal condition to analyze the dependence of the LLPS temperature on PEG concentration. We choose the spinodal condition because the spinodal surface is tangent to the coexistence surface on the critical line, and because it is mathematically more convenient than the coexistence condition. If we apply the spinodal condition to Eq. 6 and differentiate the second member with respect to both c2 and Tsp at constant c1, we obtain in the limit of c2 approaching zero:
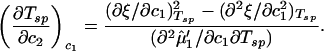 |
The quantity (∂2μ̂′1/∂c1∂Tsp) is equal to −(∂2e′/∂c )Tsp/RT
)Tsp/RT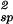 , where e′ is the internal energy per unit volume of the protein–water binary system. On addition of another protein molecule to the system, the mean distance between the proteins must decrease, promoting more protein–protein interactions. From this second-order effect, it follows that the quantity (∂2e′/∂c
, where e′ is the internal energy per unit volume of the protein–water binary system. On addition of another protein molecule to the system, the mean distance between the proteins must decrease, promoting more protein–protein interactions. From this second-order effect, it follows that the quantity (∂2e′/∂c )Tsp is negative for attractive protein–protein interactions, zero for hard-core interactions (i.e., hard spheres), and positive for repulsive interactions.
)Tsp is negative for attractive protein–protein interactions, zero for hard-core interactions (i.e., hard spheres), and positive for repulsive interactions.
Eq. 7 correctly describes the sign of the dependence of the LLPS temperature as a function of PEG concentration for the γD-PEG-water systems. The LLPS temperature increases as the PEG concentration increases because of the attractive nature of the protein–protein interactions [(∂2μ̂′1/∂c1∂Tsp) > 0]. Also, (∂Tsp/∂c2)c1 increases with PEG molecular weight because (∂ξ/∂c1)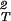 − (∂2ξ/∂c
− (∂2ξ/∂c )T increases as the depletion layer thickness increases.
)T increases as the depletion layer thickness increases.
Conclusion
Our experimental findings and theoretical analysis demonstrate that liquid–liquid phase transition in ternary protein–PEG–water systems is a powerful tool for understanding the effect of PEG as a precipitating agent. We have shown that such studies can be used to locate the phase boundary for binary protein–water systems, which is very useful if this phase separation is hidden. We can also predict the change of protein solubility as a function of the concentration of crystallizing agents. Moreover, the slope of the tie-lines and the dependence of LLPS temperature on polymer concentration provide a sensitive check of the validity of excluded volume models for protein–polymer interactions. The increase of the LLPS temperature with PEG concentration is due to attractive protein–protein interactions.
Acknowledgments
We acknowledge Ajay Pande, Alexander Chernov, Annette Tardieu, Peter Vekilov, and Seth Fraden for useful critical comments. This work was supported by National Aeronautics and Space Administration Grant NAG8-1659 (to G.B.B.) and National Institutes of Health Grants EY05217 (to G.B.B.) and EY10535 (to J.P.).
Abbreviations
PEG, polyethylene glycol
LLPS, liquid–liquid phase separation
γD, γD-crystallin
References
- 1.Albertsson P. A., (1986) Partition of Cell Particles and Macromolecules (Wiley, New York).
- 2.Abbott N. L., Blankschtein, D. & Hatton, T. A. (1991) Macromolecules 24, 4334-4348. [Google Scholar]
- 3.McPherson A., (1999) Crystallization of Biological Macromolecules (Cold Spring Harbor Lab. Press, Plainview, NY).
- 4.Finet S. & Tardieu, A. (2001) J. Cryst. Growth 232, 40-49. [Google Scholar]
- 5.Kulkarni A. M., Chatterjee, A. P., Schweizer, K. S. & Zukoski, C. F. (2000) J. Chem. Phys. 113, 9863-9873. [Google Scholar]
- 6.Asakura S. & Oosawa, F. (1954) J. Chem. Phys. 22, 1255-1256. [Google Scholar]
- 7.Vrij A. (1976) Pure Appl. Chem. 48, 471-483. [Google Scholar]
- 8.Gast A. P., Hall, C. K. & Russell, W. B. (1983) J. Colloid Interface Sci. 96, 251-267. [Google Scholar]
- 9.Lekkerkerker H. N. W., Poon, W. C. K., Pusey, P. N., Stroobants, A. & Warren, P. B. (1992) Europhys. Lett. 20, 559-564. [Google Scholar]
- 10.Ilett S. M., Orrock, A., Poon, W. C. K. & Pusey, P. N. (1995) Phys. Rev. E 51, 1344-1352. [DOI] [PubMed] [Google Scholar]
- 11.Atha D. H. & Ingham, K. C. (1981) J. Biol. Chem. 256, 12108-12117. [PubMed] [Google Scholar]
- 12.Arakawa T. & Timasheff, S. N. (1985) Biochemistry 24, 6756-6762. [DOI] [PubMed] [Google Scholar]
- 13.Abbott N. L., Blankschtein, D. & Hatton, T. A. (1992) Macromolecules 25, 3932-3941. [Google Scholar]
- 14.Vergara A., Paduano, L. & Sartorio, R. (2002) Macromolecules 35, 1389-1398. [Google Scholar]
- 15.Bhat R. & Timasheff, S. N. (1992) Protein Sci. 1, 1133-1143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Edmond E. & Ogston, A. G. (1968) Biochem. J. 109, 569-576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lomakin A., Asherie, N. & Benedek, G. B. (1996) J. Chem. Phys. 104, 1646-1656. [Google Scholar]
- 18.Malfois M., Bonneté, F., Belloni, L. & Tardieu, A. (1996) J. Chem. Phys. 105, 3290-3300. [Google Scholar]
- 19.Lomakin A., Asherie, N. & Benedek, G. B. (1998) Phys. Rev. Lett. 77, 4832-4835. [DOI] [PubMed] [Google Scholar]
- 20.Asherie N., Lomakin, A. & Benedek, G. B. (1999) Proc. Natl. Acad. Sci. USA 96, 9465-9468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yu M., Arons, J. S. & Smit, J. A. M. (1994) J. Chem. Technol. Biotechnol. 60, 413-418. [DOI] [PubMed] [Google Scholar]
- 22.ten Wolde P. R. & Frenkel, D. (1997) Science 277, 1975-1978. [DOI] [PubMed] [Google Scholar]
- 23.Galkin O. & Vekilov, P. G. (2000) Proc. Natl. Acad. Sci. USA 97, 6277-6281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Benedek G. B. (1997) Invest. Ophthalmolo. & Visual Sci. 38, 1911-1921. [PubMed] [Google Scholar]
- 25.Thomson J. A., Schurtenberger, P., Thurston, G. M., Thomson, J. A. & Benedek, G. B. (1987) Proc. Natl. Acad. Sci. USA 84, 7079-7083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Broide M. L., Berland, C. R., Pande, J., Ogun, O. & Benedek, G. B. (1991) Proc. Natl. Acad. Sci. USA 88, 5660-5664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chirgadze Yu. N., Driessen, H. P. C., Wright, G., Slingsby, C., Hay, R. E. & Lindley, P. F. (1996) Acta Crystallogr. D 52, 712-721. [DOI] [PubMed] [Google Scholar]
- 28.McDermott M. J., Gawinowicz-Kolks, M. A., Chiesa, R. & Spector, A. (1988) Arch. Biochem. Biophys. 262, 609-619. [DOI] [PubMed] [Google Scholar]
- 29.Asherie N., Pande, J., Lomakin, A., Ogun, O., Hanson, S. R. A., Smith, J. B. & Benedek, G. B. (1998) Biophys. Chem. 75, 213-227. [DOI] [PubMed] [Google Scholar]
- 30.Schurtenberger P., Chamberlin, R. A., Thurston, G. M., Thomson, J. A. & Benedek, G. B. (1989) Phys. Rev. Lett. 63, 2064-2067. [DOI] [PubMed] [Google Scholar]
- 31.Liu C., Asherie, N., Lomakin, A., Pande, J., Ogun, O. & Benedek, G. B. (1996) Proc. Natl. Acad. Sci. USA 93, 377-382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Matthews B. W. (1968) J. Mol. Biol. 33, 491-497. [DOI] [PubMed] [Google Scholar]
- 33.Galkin O., Chen, K., Nagel, R. L., Hirsch, R. E. & Vekilov, P. G. (2002) Proc. Natl. Acad. Sci. USA 99, 8479-8483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lekkerkerker H. N. W. (1990) Colloid Surf. 51, 419-426. [Google Scholar]
- 35.Tuinier R., Vliegenthart, G. A. & Lekkerkerker, H. N. W. (2000) J. Chem. Phys. 105, 10768-10775. [Google Scholar]
- 36.Widom B. (1963) J. Chem. Phys. 39, 2808-2812. [Google Scholar]
- 37.Lebowitz J. L., Helfand, E. & Praestgaard, E. (1965) J. Chem. Phys. 43, 774-779. [Google Scholar]
- 38.Flory P. J. (1940) J. Am. Chem. Soc. 62, 1561-1565. [Google Scholar]
- 39.Vergara A., Paduano, L., Sartorio, R. & Vitagliano, V. (1999) J. Phys. Chem. B 103, 8732-8738. [Google Scholar]
- 40.Tanford C., (1961) Physical Chemistry of Macromolecules (Wiley, New York).