Abstract
Fluorescence resonance energy transfer (FRET) is a technique used to measure the interaction between two molecules labeled with two different fluorophores (the donor and the acceptor) by the transfer of energy from the excited donor to the acceptor. In biological applications, this technique has become popular to qualitatively map protein-protein interactions, and in biophysical projects it is used as a quantitative measure for distances between a single donor and acceptor molecule. Numerous approaches can be found in the literature to quantify and map FRET, but the measures they provide are often difficult to interpret. We propose here a quantitative comparison of these methods by using a surface FRET system with controlled amounts of donor and acceptor fluorophores and controlled distances between them. We support the system with a Monte Carlo simulation of FRET, which provides reference values for the FRET efficiency under various experimental conditions. We validate a representative set of FRET efficiencies and indices calculated from the different methods with different experimental settings. Finally, we test their sensitivity and draw conclusions for the preparation of FRET experiments in more complex and less-controlled systems.
INTRODUCTION
Förster resonance energy transfer (FRET) is a process by which a fluorophore (the donor) in an excited state transfers its energy to a neighboring molecule (the acceptor) by nonradiative dipole-dipole interaction (Förster, 1948; Lakowicz, 1999). Although not necessary, in most cases the acceptor is also a fluorescent dye. In this case, FRET also stands for fluorescence resonance energy transfer.
In steady-state FRET microscopy, two different approaches are generally used to measure FRET: 1), Emission measurement. Excitation of the donor and detection of the light emitted by either the donor and/or the acceptor in the presence of the other fluorophore. When FRET occurs, the donor emission is decreased and the acceptor emission is increased. 2), Acceptor photobleaching. Excitation of the donor and detection of the light it emits before and after acceptor photobleaching. In both approaches, values can be obtained that represent either a FRET index or the transfer efficiency.
A FRET index is a relative value that varies with changes in energy transfer associated with changes in the donor-acceptor configuration. It should increase when FRET increases, and should decrease when FRET decreases. FRET indices are useful to perform qualitative studies or to take relative measures within the same experiment. However, each FRET index is tuned for specific related experimental needs. A direct comparison between results obtained with different indices can be difficult.
On the contrary, the transfer efficiency (E) is a direct measure of the fraction of photon energy absorbed by the donor that is transferred to an acceptor. It can be calculated as the ratio of the transfer rate kT to the total decay rate of the donor 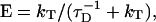 where τD is the lifetime of the donor in the absence of acceptors or any other quenching effects. It can also be measured as the relative fluorescence of the donor in presence (FDA) and absence (FD) of the acceptor E = 1 − FDA/FD or from the lifetimes under these respective conditions E = 1 − τDA/τD (Lakowicz, 1999). Since E depends on the inverse of the sixth power of the distance r between the two fluorophores,
where τD is the lifetime of the donor in the absence of acceptors or any other quenching effects. It can also be measured as the relative fluorescence of the donor in presence (FDA) and absence (FD) of the acceptor E = 1 − FDA/FD or from the lifetimes under these respective conditions E = 1 − τDA/τD (Lakowicz, 1999). Since E depends on the inverse of the sixth power of the distance r between the two fluorophores, 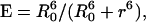 FRET has become the technique of choice to observe protein-protein interaction and to measure distances between fluorophores (Stryer, 1978; Clegg, 1996). R0 is known as the Förster distance and represents a characteristic parameter of every dye pair defining the distance at which the efficiency is 50%.
FRET has become the technique of choice to observe protein-protein interaction and to measure distances between fluorophores (Stryer, 1978; Clegg, 1996). R0 is known as the Förster distance and represents a characteristic parameter of every dye pair defining the distance at which the efficiency is 50%.
As with any proper fluorescence measurement to be quantitative, FRET methods have to account for biases due to 1), bleed-through in excitation, i.e., when a donor is excited by the acceptor's excitation wavelength and vice versa; and 2), cross talk in emission detection, i.e., when the emission of a donor also contributes to the signal measured in a setup for acceptor detection, and vice versa. It is often difficult to separate the contribution of direct cross talk from the contribution of bleed-through signals. We therefore use the term “cross talk” to refer to both kinds of artifacts for the rest of this article.
Various methods introducing different observation strategies for FRET efficiency and indices can be found in the literature. The purpose of the presented work is to validate their performance under various experimental conditions. We have implemented an experimental FRET system, which permits a free selection of the pair and where the donor and acceptor concentrations as well as the average distance between donor and acceptor can be controlled. The system relies on a surface monolayer of biotinylated poly-(l)-lysine-graft-poly-ethylene-glycol (PLL-g-PEG-biotin). This defines a 2D distribution of fluorophores, which can be stochastically modeled. Reference FRET values for the comparison of the analyzed methods are generated by Monte Carlo simulations (MCS) of the transfer process. The simulation accounts for the dynamics and competition in transfer, characteristic for a multi-donor and multi-acceptor system, and considers the kinetics of excitation and relaxation of the fluorophores. Experimental data obtained from microscopy of the surface system are used to calculate the various FRET efficiencies and FRET indices. All the geometric parameters as well as the dye pairs have been varied to test the methods under different conditions. These results are compared with the MCS to determine the sensitivity, biases and uncertainty of each method. We conclude with a practical and objective guide to steady-state FRET microscopy including a few warning about some of the most widespread observation strategies.
FRET EFFICIENCY AND INDEX METHODS
Various methods have been reported to quantify FRET from measured changes in donor and acceptor emission. Table 1 summarizes methods that yield a measure of FRET efficiency and Table 2 those that derive FRET indices, along with examples of applications they were used in. Note that several methods were originally used in flow cytometry (FC) or spectroscopy (S). All of them can, however, be implemented in microscopy (M). The methods are classified according to the number of filter sets necessary, the number of samples and images required, and the level of correction involved. Our notation is largely inspired by the one proposed by Gordon et al. (1998) (see Materials and Methods for further explanations).
TABLE 1.
Different methods to calculate FRET efficiency
| Method | (Filter set/samples/images) | Reference | Application | FRET pair used |
|---|---|---|---|---|
| Emission measurements: | ||||
| 1. E1 = 1 − Db/Dd | (1/2/2) | Turcatti et al., 1996 (S) | Spatial relationship in integral membrane proteins such as receptors and channels | Cyanomethylesther-trimethylrhodamine |
| Ubarretxena-Belandia et al., 1999 (S) | Dimerization of membrane phospholipase | IAEDANS-IANBD | ||
| Lorenz and Diekmann, 2001 (M + S) | Fret in page (DNA in gel) | Fluorescein-rhodamine | ||
| Vallotton et al., 2001 (S) | Mapping of binding sites with micelles | GR-flu-2-dodecylresorufin | ||
| 2. E2 = α2FDb | (2/1/2) | *Bottiroli et al., 1992 (M) | Oligodeosxynucleotide hybridation to mRNA | Bodipy-Cy5 |
| Tsuji et al., 2000 (M) | ||||
| 3. E3 = (FAb − β3a)·β3b | (2/1/2) | Suzuki, 2000 (S) | Swing of lever arm of myosin | BFP-GFP |
| 4. E4/(1 − E4) = α4−1·(Fb −(FDd − FAa·AFd) Db−FAa·Ab)/((1 − FAa·AFd)·Db) with FAa·AFd ≈ 0 | (3/3/8) | *Tron et al., 1984 (FC) | Cell surface staining | Fitc-Tritc |
| (3/3/7) | Mátyus, 1992 (FC) | Single pair (flow cytometry) | Fitc-rhodamine | |
| Kam et al., 1995 (M) | Cytoskeletal components of cell adhesion (actin, vinculin, talin, α-actinin) | Fitc-rhodamine | ||
| 5. E5 = α5·[Fb − FDd·Db−(FAa − FDd·DAa)·Ab]/(FAa·Ab) | (3/3/9) | *Nagy et al., 1998 (M+FC) | Methods | Fitc-Tritc |
6. E6 = FRET/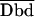 with with |
(3/3/9) | *Gordon et al., 1998 (M) | Bcl-2-Beclin interaction on chromosome | Fitc-rhodamine |
FRET = [Fb − FDd·Db − 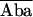 (FAa − FDd·DAa)]/α6 (1 − DFa·FDd) (FAa − FDd·DAa)]/α6 (1 − DFa·FDd) |
Mahajan et al., 1998 (M) | Bcl-2-Bax interaction in mitochondria | BFP-GFP | |
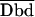 = Db + FRET(1 − α6DAa) − = Db + FRET(1 − α6DAa) − 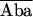 DAa DAa |
Ruiz-Velasco and lkeda, 2001 (M) | Functional expression analysis of proteinsubunits in rat neurons | CFP-YFP | |
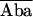 = (Ab − AFd·Fb)/(1 − FAa·AFd) = (Ab − AFd·Fb)/(1 − FAa·AFd) |
||||
| 7. E7 = 1− [Db/(Db + PFRET ·(ψD/ψA)·Qd)] with PFRET = Fb − FDd·Db − FAa·Ab | (3/3/7) | *Elangovan et al., 2003 (M) | Apical endosom in MDCK cells and dimerization of proteins | Alexa 488-Cy3 |
| ψD,A collection efficiency of D, A channels under donor excitation, Qd, quantum yield of the donor. | ||||
| Acceptor photobleaching: | ||||
| 8. E8 = 1 − Db/Db(ab) | (1/1/2) | Wouters et al., 1998 (M) | Nonspecific lipid transfer protein and fatty acid oxidation enzymes in peroxisomes | Cy3-Cy5 |
| Llopis et al., 2000 (M) | Interaction of coactivators and receptor binding protein with nuclear hormone receptor | CFP-YFP | ||
| McLean et al., 2000 (M) | Membrane association and protein conformation in neurons | Fitc-DiL | ||
| A. K. Kenworthy, 2001 (M) | Protein-protein interaction, method | Cy3-Cy5 | ||
| Kinoshita et al., 2001 (M) | Low-density lipoprotein receptor-related protein-Amyloid precursor protein interaction | Fitc-Cy3 EGFP-Ds-Red | ||
| Mochizuki et al., 2001 (M) | Growth-factor-induced activation of RAS and RAP1 | CFP-YFP | ||
| Chan et al., 2001 (M+FC) | Cell surface receptor interactions, flow cytometry | CFP-YFP | ||
| Sato et al., 2002 (M) | Protein phosphorylation | CFP-YFP | ||
A, D, and F denote the acceptor, donor, and FRET channels used for image acquisition, respectively. a, d, and b indicate samples with acceptor only, donor only, and both fluorophores, respectively. In combination, they represent the signal measure in one channel for one sample (e.g., Fa). A term with two capital letters in italic followed by a low-case letter (e.g., FAa) indicates the pixel-by-pixel ratio Fa/Aa. The term (ab) indicates acceptor photobleaching. (αi values are related to concentration and absorption coefficients. βi values are only related to absorption coefficients (cf. original references). References annotated with an asterisk refer to FRET methodological articles and (M), (FC), and (S) indicate the use of the method in microscopy, flow cytometry, or spectrometry, respectively.
TABLE 2.
Different methods to calculate FRET indices
| Method | (Filter set/samples/images) | Reference | Application | FRET pair used | |
|---|---|---|---|---|---|
| Emission measurements: | |||||
| 1. FRET1 = FDb | (2/1/2) | Vanderklish et al., 2000 (M) | Synaptic activity in dendritic spines | CFP-YFP | |
| Arai et al., 2001 (S) | Variable domains homogeneous assay | BFP-GFP | |||
| 2. FRET2 = FDb − FDd | (2/2/4) | Graham et al., 2001 (S) | Interaction between Rac, Cdc42 and binding partners | BFP-GFP | |
| 3. FRET3 = (FDb/FDd) − 1 | (2/2/4) | Damelin and Silver, 2000 (M) | Nuclear transport factors in living cells | CFP-YFP | |
| 4. FRET4 = (Fb − FDa · Ab)/Db | (3/3/5) | Zal et al., 2002 (M) | TCR-coreceptor interactions | CFP-YFP | |
| 5. FRET5 = FDb/(FDd + FAa · ADb) | (3/3/7) | Hailey et al., 2002 (M) | Protein-protein interaction in yeast | CFP-YFP | |
| 6. FRET6 = Fc = Fb − FDd · Db − FAa · Ab | (3/3/7) | Youvan et al., 1997 (M) | Methodological paper focusing on cross talk corrections, verified on a controlled system using beads | BFP-GFP | |
| Sorkin et al., 2000 (M) | Epidermal growth factor receptor (EGFR)-SH2 domain of growth-factor binding protein Grb2 | CFP-YFP | |||
| Normalized with Ab · Db | (3/3/7) | Xia et al., 2001 (M) | Synaptic protein interaction | CFP-YFP | |
| Jin et al., 2001 (M + S) | Protein-protein interaction | CFP-YFP | |||
| 7. FRET7 = Fc/(Db · Ab)1/2 | (3/3/7) | Xia and Liu, 2001 (M) | Controlled system for the evaluation of FRET indices | CFP-YFP |
For an explanation of the notation and acronyms, see Table 1.
Eight different efficiency measures are listed in Table 1. The seven first are based on the measure of emission of either the donor or the acceptor in the presence of the other fluorophore: Method E1 is used in applications where it is possible to observe the sample before and after adding the acceptor. It is assumed that the concentration of the donor remains constant pre- and postaddition of acceptor. Also, cross talk of the acceptor in the donor channel is neglected, and the detected fluorescence intensity is supposed to originate from the donor only.
In contrast to method E1, which is calculated from a ratio of signal originating from two different samples (d and b), the methods E2–E7 all rely on the signal directly obtained in the FRET channel (F) in presence of both fluorophores (b). The methods vary in their schemes for cross talk correction. Method E2 requires prior knowledge of dye concentration and absorption coefficients. It is assumed that the acceptor is not excited at the donor excitation wavelength, and that there is no cross talk of the acceptor in the donor channel. The same assumptions are applied to method E3, but for the donor. The advantage of these two methods over method E1 is that they only require one sample where both fluorophores are present. Therefore, they are most appropriate for monitoring dynamic FRET. Methods E4–E6 provide FRET efficiency calculations with more complete cross talk correction. The principle is to remove the non-FRET contribution of the donor (donor emission observed in the band pass of the acceptor emission filter) and the contribution of the acceptor (emission of the acceptor when excited at the donor excitation wavelength) from the signal measured in the FRET channel in presence of both fluorophores. The underlying assumption is that the amount of cross talk is independent of the absolute intensity of the fluorophores and thus can be calibrated by ratiometric analysis of donor and acceptor signals. This permits the off-line calibration of cross talk ratios in samples containing only one of the two fluorophores at arbitrary concentrations. As with the methods E2 and E3, such precalibration allows the monitoring of FRET in dynamic systems. In contrast, Elangovan et al. (2003) propose a method (E7) where the cross talk ratios are not considered constant but are determined at different fluorescence intensities. They generate an intensity-dependent look-up table, which is then used in the final calculation.
Method E8 relies on the ratio of fluorescence intensity before and after acceptor photobleaching. The efficiency is calculated as the ratio of two intensities generated from two physically different samples (as for method E1) or as the ratio of two intensities measured on the same sample but in two different regions (bleached and unbleached). The application of this method is often delicate in live biological samples due to long bleaching time and phototoxicity. Also, one has to ensure that the donor fluorescent properties are not impaired by photobleaching, and that the acceptor is completely bleached in appropriate time.
In summary, the essential difference between the methods reported in Table 1 consists in the observation strategy: In methods E1 and E8, the efficiency is measured by comparison of a situation with and a situation without acceptor. The actual transfer of energy is never observed directly, but the methods determine FRET indirectly. All other methods (E2–7) rely on a direct measure of FRET that is taken upon the excitation of the donor and the observation of acceptor emission with subsequent correction of potential cross talk.
Six FRET indices are listed in Table 2, each using different cross talk corrections (see references for complete description). All of them involve as their basis the detection of an acceptor signal upon excitation of the donor.
As illustrated in these two tables, the proper use of FRET measurements to characterize molecular interactions requires corrections for 1), cross talk, 2), the fact that each of the measured fluorescence intensities consists of both FRET as well as non-FRET components, 3), the concentration of donor, and 4), the concentration of acceptor (Gordon et al., 1998). Item 1 gets particularly critical with dye pairs that constitute large spectral overlap and thus guarantee high FRET efficiencies. Hence, FRET microscopy suffers the paradox that the higher the signal, the more it is potentially deteriorated by systematic bias.
MATERIALS AND METHODS
Our analysis of FRET efficiency is based on a well-defined coating of a coverslip with a solution containing a controlled amount of donor and acceptor.
Surface preparation
PLL-g-PEG-biotin (Huang et al., 2001; Kenausis et al., 2000) was adsorbed for 30 min on a glass coverslip (96-well with coverslip bottom imaging plates, BD Biosciences, Labware Europe, Le Pont De Claix, France) cleaned by oxygen plasma for 2 min. A solution containing streptavidin (Sa) labeled with donor (Sa-D) or acceptor (Sa-A) fluorophore or unlabeled (Sa-ul) was then adsorbed on the PLL-g-PEG-biotin for 30 min and rinsed three times with Hepes Z1.
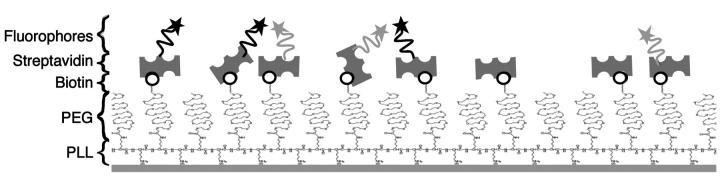
The system was entirely controlled by the three following parameters (Fig. 1):
The ratio RBiot = [PLL-g-PEG-Biotin]/[PLL-g-PEG-Total], which measures the amount of biotin competent for the adsorption of streptavidin. Optical wave-guide light-mode spectroscopy experiments showed that [Sa]Surface, the amount of streptavidin on the surface, can be directly calculated from the ratio RBiot via a linear relationship: [Sa]Surface = 13.27 RBiot [pmol/cm2] (Huang et al., 2001). In our experiments, RBiot is 31%, and therefore [Sa]Surface = 4.01 pmol/cm2.
The ratio RSA = [Sa-Labeled]/[Sa-Total]. By adding unlabeled streptavidin (Sa-ul) to the solution, we can control the mean distance between donors and acceptors.
The ratio RDA = [Sa-D]/[Sa-A] describes the relative population of donors to acceptors in the solution. (e.g., in Fig. 1, RBiot is 0.5, RSA = 0.75, and RDA = 1).
FIGURE 1.
Surface FRET system on a coverslip coated with PLL-g-PEG-biotin. The biotin (black round) is tagged with streptavidin-donor (black star), streptavidin-acceptor (light gray star), and streptavidin-unlabeled.
Fluorophores
Two pairs of fluorophores were examined: Alexa 488-Alexa 546 (R0 = 6.31 nm) and Alexa 488-Alexa 633 (R0 = 5.55 nm) (streptavidin-Alexa Fluor dyes, Molecular Probes, Leiden, The Netherlands). For every set of parameter (RDA, RSA, and R0), three surfaces were coated, one with each of the two dyes alone, and one with both dyes. On the acceptor-alone surface, the donor was replaced by unlabeled streptavidin using the same concentration. On the donor-alone surface, the acceptor was replaced by unlabeled streptavidin using the same concentration.
Notation for distinguishing FRET channels and samples
The notation used in the article is the same as in Gordon et al. (1998), except for two minor modifications. The capital letter indicates the channel (D, A, or F, for donor, acceptor, or FRET channels) used to acquire the image (see Table 3 for microscope setup), and the small letter indicates the sample that was imaged (a, d or b, for samples with acceptor only, donor only, and both fluorophore classes). We introduce a notation with a double capital letter in italic to indicate, for a particular sample, the pixel-by-pixel mean ratio between two channels, e.g., DAa = mean(Da/Aa). The mean of the ratios is calculated over all unsaturated pixels in the two considered channels. In case of acceptor photobleaching, the term (ab) is added. (i.e., Db(ab) indicates the fluorescence measured in the donor channel when both fluorophores are present, but after acceptor photobleaching.)
TABLE 3.
Definition of the three channels
| Channel | Excitation wavelength | Emission filters |
|---|---|---|
| D (Donor) | Argon 488 nm | BI(545) + BP(500–530) |
| A (Acceptor) | 1) He-Ne 543 nm | 1) BI(545) + LP(560) |
| 2) He-Ne 633 nm | 2) BI(545) + LP(630) | |
| F (FRET) | Argon 488 nm | 1) BI(545) + LP(560) |
| 2) BI(545) + LP(630) |
Case 1 corresponds to Alexa 488 paired with Alexa 546. Case 2 corresponds to Alexa 488 paired with Alexa 633.
Fluorescence measurements
Surface imaging was performed using a LSM 510 Confocal Microscope with a 100×/1.4 Plan Apochromat (Zeiss, Jena, Germany). The 8-bit images were normalized to values between 0 and 1 to deliver results independent of the dynamic range. The intensity of the images was controlled for each channel independently by setting of the following parameters:
Pinhole
Fully opened for wide field imaging.
Amplifier gain and offset
Initial investigations with unlabeled streptavidin surfaces showed that in all our experiments, the background level was only dependent on the amplifier settings, but not on the laser power and detection gain (data not shown). This supports that the molecular backbone of our model system does not contribute to the total signal by autofluorescence. Therefore, there was no need to apply any compensation of a background signal by electronic background correction. The amplifier offset was set to 0. On the other hand, we found that the amplifier gain also increased noise. To avoid any complication in reconstructing ratiometric data from different image acquisition channels, we consistently set the gain to 1 (no amplification).
Filter set
Described in Table 3.
Laser power and detector gain
A precalibration of the microscope revealed that detector gains are linear within a certain working range, and therefore each channel can be tuned separately for maximum signal. For each set of experiments (variation of RDA or RSA), we used the donor-only sample (d) with maximum RDA and RSA to set the gain in the donor channel (D), and determined the minimum laser power necessary to acquire a strong signal (Dd) at maximum detector gain. The same process was repeated for the acceptor channel (A) using an acceptor-only sample (a) with maximum RSA but minimum RDA. We set the parameters of the FRET channel (F) by keeping the same laser power as for channel D and by adjusting the detector gain so that the signal measured from the RDA = 1, RSA = 1 sample containing both fluorophores (b) yielded a value around the middle of the dynamic range.
Once set, these parameters were used throughout the entire experiment.
Background subtraction
To eliminate residual background signals that originated from uncompensated dark current of the photo-multiplier tubes, but not from sample autofluorescence (see above), we imaged PLL-g-PEG-biotin surfaces coated with unlabeled streptavidin in all channel combination and subsequently subtracted the mean value from all fluorescence signals.
FRET efficiency and FRET index
Several FRET efficiency and FRET indices have been calculated according to the methods described in Tables 1 and 2. Three types of surfaces were used: surface with acceptor only (a), surface with donor only (d), and surface with both donor and acceptor (b). For each of these surfaces, three quasisimultaneous images were taken in the three channels A, D, and F, (see Table 3), using the multi-tracking function of the microscope. This delivered nine images termed Aa, Da, Fa, Ad, Dd, Fd, Ab, Db and Fb, where Da and Fa, Dd and Fd, and Db and Fb were acquired exactly simultaneous using two separate photo-multiplier tubes. Calculations were made pixel by pixel and a map of FRET (efficiency or index) was reconstructed for each method. We excluded pixels from FRET calculations that were over- or undersaturated in any one of the three channels A, D, or F, for any of the samples a, d, or b. Since our surface was homogenously labeled, the mean efficiency or index over all remaining pixels provided a robust estimate of the amount of energy transfer for one experiment.
Monte Carlo simulation of FRET on surface
Simulations of energy transfer processes in 2D were performed using MATLAB (The MathWorks, Natick, MA, USA). The algorithm (see Appendix for a detailed explanation) implements a competitive scheme between multiple donors and acceptors, taking into account that already excited acceptors are not amenable to energy absorption. The competition between several donors potentially transferring energy to the same acceptor is resolved in a probabilistic sense, where the transfer probabilities depend on the geometry of donor and acceptor distribution. The simulation was controlled by the following parameters: [Sa]Surface = 4.01 pmol·cm−2; RSA = [0.1..1]; RDA = [10−2..102]; R0 = [2..10] nm, Tint, and Nex, where Tint is the integration time and Nex is the number of excitons to be simulated. In our terminology, an exciton is a photon reaching a donor and, dependent on the donor's excitation state upon arrival, potentially participating in the process of donor excitation.
RESULTS AND DISCUSSION
Results of the simulation
To generate reference FRET efficiencies for the experimental conditions of our surface system, we implemented a MCS package (see Appendix). In the following, we establish internal consistency of the MCS and generate predictions of experimental outcomes. All results presented are the mean of 10 runs performed for each of the tested parameter configurations (RDA, RSA, R0) (for a definition of RDA and RSA, see Materials and Methods). Error bars in the graphs reflect the standard deviation of 10 repeated runs.
A system in two dimensions with multiple donors and multiple acceptors cannot be described by the single distance model
The single distance model describes the relationship between the distance r between one donor and one acceptor fluorophore and the transfer efficiency E (Lakowicz, 1999):
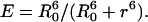 |
(1) |
R0 is the Förster distance, characteristic for the spectral overlap of the donor-acceptor pair (Lakowicz, 1999). In this model, it is assumed that one donor interacts with one acceptor. The model is applicable, for example, in the case where a donor and an acceptor dye molecule are coupled to two different domains of a molecule and variations in FRET efficiencies represent conformational changes (Suzuki et al., 1998; Mochizuki et al., 2001). However, for our situation where several donors and acceptors can interact, the single distance model cannot predict FRET efficiencies. Extensions of the model have been published by Wolber and Hudson (1979) and Dewey and Hammes (1980) for one donor with multiple acceptors. Yet, these more general models still do not describe the situation of multiple donors and multiple acceptors encountered with surface FRET. Here, an appropriate model should account for the following items:
Random distribution of donor and acceptor positions.
Random excitation of donors at random time points.
Already excited donors cannot be excited a second time. The energy is lost in the system.
Competition between excited donors to transfer energy to a nearby acceptor.
Saturation of the system when all acceptors around a donor are already excited and are not able to participate in the transfer process.
It seems difficult to find an analytical solution under all these conditions. However, the system can be elegantly simulated by an MC approach. The algorithm implements the events of fluorescence at the level of single fluorophores: A photon flux reaches the labeled surface. Whereas most of them are lost, those reaching a donor (and potentially participating in the process of its excitation) become “excitons”. In the MCS, each excited donor can then either transfer its energy to an acceptor or emit fluorescence, according to the rules listed above. The simulated efficiency is simply calculated as the number ratio between transfer incidences and the number of used excitons.
MCS stability is flux dependent
The exciton flux is an important parameter for the stability of the MC predictions. Two issues define the stability of our MC FRET simulations:
How many excitons are necessary to guarantee robust statistics providing of FRET in a multi-donor, multi-acceptor system?
What is the maximum flux of exciton such that sufficient donors and acceptors are still excitable at any time point to participate in the competition between donor fluorescence emission and FRET (see Appendix)?
We have performed systematic tests (data not shown) to determine the two parameters defining the exciton flux: Nex, the number of excitons, and Tint, the integration time over which these excitons are randomly released over the simulated sample. It turns out that Nex = 104 excitons guarantee robust statistics, and that for a flux of J = 10 excitons/ns, the donor-acceptor system remains sufficiently unsaturated to ensure a largely undistorted stochastic decision between donor fluorescence emission and FRET. Interestingly, the maximum exciton flux guaranteed experimentally (laser power = 25 mW, at 488 nm, with a 100×/1.4 objective, surface = 104 nm2, extinction coefficient = 78,000 M−1·cm−1, fluorophore concentration = 4.01 pmol/cm2, RDA = 1, RSA = 1) is in the range of 15 excitons/ns, in good agreements with the MCS flux. This flux is dependent on the cross section area of the donor. Implicitly, the more donors, the greater the probability for a photon to become an exciton. Therefore, the exciton flux is proportional to the number of donors, i.e., proportional to the fraction of labeled molecules on the surface RSA, multiplied with the fraction of labeled molecules being donors RDA/(RDA + 1), hence RSA·RDA/(RDA + 1). To be consistent with the experimental setup, the MCS adapts the simulated exciton flux JSim to RDA or RSA as JSim = 2·J·(RSA·RDA/(RDA + 1)).
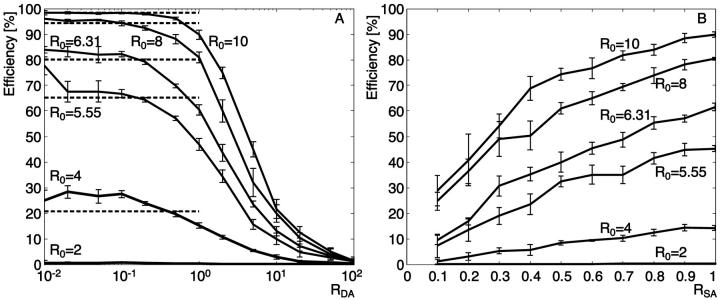
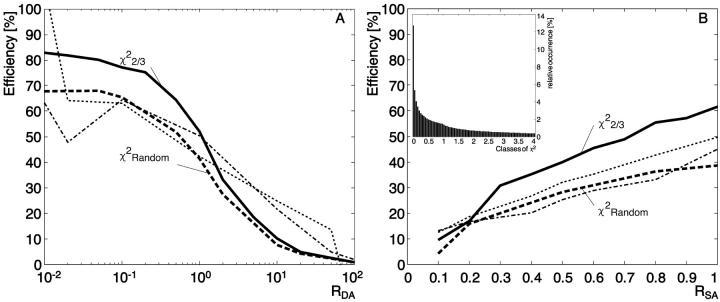
The efficiency increases when the ratio donor/acceptor (RDA) decreases
Fig. 2 A shows the dependence of MC simulated FRET efficiencies on RDA. With low RDA, the surface is almost entirely composed of acceptors. In this configuration, an excited donor has a higher probability to transfer its energy to a neighboring acceptor than to emit energy as fluorescence. The second effect of a high number of acceptors is that the probability that two donors compete for the same acceptor is almost zero. In combination, the two effects yield a high efficiency.
FIGURE 2.
FRET efficiency dependence of fluorophore concentrations for different Förster distances. The exciton flux is set to 10 excitations/ns and the integration time to 1000 ns. (A) The fluorophore concentrations are modified via the donor-to-acceptor ratio (RDA) for a 100% labeling (RSA = 1). The dashed lines represent the value of the efficiency for different Förster distances calculated with the single distance model (Eq. 1), where r = Rc, the distance of closest approach (Rc = 5 nm). (B) The fluorophore concentrations are modified via the labeling ratio (RSA) with constant RDA = 1. The Förster distances R0 = 6.31 nm and R0 = 5.55 nm are those of the dye pairs Alexa 488-Alexa 546 and Alexa 488-Alexa 633, respectively. Data for R0 = 2 nm fall almost onto the abscissa of the graph, since Rc (=5 nm) is so much higher that the efficiency does not exceed 0.4%.
In contrast, at high RDA, a donor has mostly donors as neighbors, and they have to compete for a very low number of acceptors. The probability that a nearby acceptor is already being excited is then high, precluding the transfer of additional energy. The excited donor will emit fluorescence, leading to a decrease of efficiency.
To perform an experiment investigating the effect of changes in the mean distance between donors and acceptors, a good choice for RDA is in the range 1–20. In this range, the efficiency goes almost linear with the concentration ratio and the steep slope predicts high sensitivity in determining donor-acceptor distances from FRET measurements (see Fig. 2 A). For RDA > 20, the efficiency goes to zero, and for RDA < 1, the efficiency reaches a plateau where changes in RDA have little effect on the efficiency. Both ranges preclude a quantification of molecular distances. Note that the RDA range of the plateau depends on the Förster distance R0 (discussed in more detail below). Therefore, in experiments that aim at the detection of small efficiency variations, it might be useful to carefully select the dye pair so that the working range of RDA is in the linear domain.
The efficiency increases when the fraction of labeled molecules (RSA) increases
Fig. 2 B indicates that a decrease of the fluorophore concentration reduces efficiency. In these simulations, RDA is set to 1, and the concentration of both kinds of fluorophores is varied to modulate the mean distance between donor and acceptor. Since the probability of transfer is directly related to r6, we expect a strong dependence of the efficiency on RSA, as is confirmed by the MCS.
The efficiency increases when the Förster distance R0 increases
Six simulations have been run with different Förster distances R0 (2, 4, 5.55, 6.31, 8, and 10 nm). Both graphs, Fig. 2, A and B, show that also in a multi-donor, multi-acceptor system, FRET efficiency is highly dependent on R0.
In Fig. 2 A, efficiency values calculated with the single-distance model (dashed lines) and those simulated at low RDA (RDA < 0.1) (solid lines) yield comparable results for all R0. In this configuration, there is no competition between donors for the same acceptor, leading to a situation where the main parameter influencing the probabilities of transfer is the Förster distance. Interestingly, our multi-donor, multi-acceptor simulation even predicts systematically higher efficiencies than the single-distance model. This underlines the fact that with several acceptors per donor, the cumulative probability for having transfer versus fluorescence is higher than the probability for a single transfer (cf. Appendix).
When RDA increases (Fig. 2 A), the competition between donors for the same acceptor increases and the efficiency drops to zero. The same happens with a decrease of RSA (Fig. 2 B). Here, the reduction in efficiency is related to the increase in distance between the fluorophores.
Experimental performance analysis
For each of the tested parameter sets (RDA, RSA, R0), three surfaces were coated with either donor alone, acceptor alone, or both fluorophores according to the protocol described in Materials and Methods. Per experiment, five independent sets of images were taken in all channel and surface permutations at different positions on the sample, and FRET measures were calculated separately for each set according to the methods described in Tables 1 and 2. The values presented in the following sections represent the mean of the five sets.
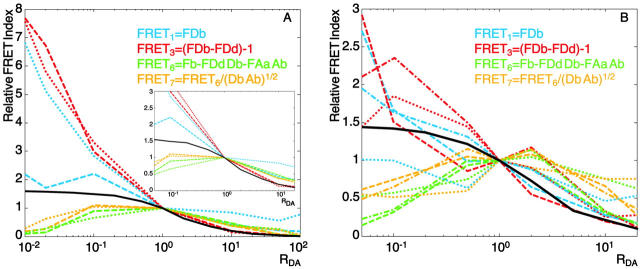
FRET results depend on the method: a comparison of FRET efficiencies
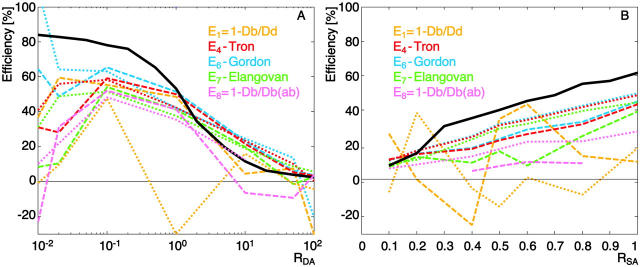
We compare the methods E1, E4, E6, E7, and E8 in Table 1. They include a ratio method using only one filter set and no correction for acceptor cross talk into the donor channel (E1), three methods, which measure energy transfer directly with Fb and account for cross talk corrections with different schemes (E4, E6, E7), and one method involving acceptor bleaching (E8, discussed in a section below). Fig. 3 displays FRET efficiencies calculated with the five methods for changes in RDA (A) and changes in RSA (B). The data comprises two experiments using the dye pair Alexa 488-Alexa 546 (R0 = 6.31 nm). All calculations rely on identical sets of input images, and the differences between the methods only relate to the differences in postprocessing. The methods can be examined in terms of 1), reproducibility between different experiments under identical conditions; 2), their ability to reflect changes in the parameters RDA and RSA consistently, and 3), their agreement with the MCS reference data (overlaid as black lines).
FIGURE 3.
FRET efficiency calculated with five different methods for the dye pair Alexa 488-Alexa 546 (R0 = 6.31 nm). Surface coating parameters have been varied (RDA in A and RSA in B), and results of two experiments are shown as dotted and dashed lines. The black solid line represents the results of the MCS under the same conditions.
Fig. 3 shows that the stability of the curves is highly dependent on RDA. In the range 0.1 < RDA < 10, the results are stable and reproducible between experiments for methods E4, E6, and E7. All three exhibit the expected decrease in efficiency with an increase of RDA (Fig. 3 A) or a decrease of RSA (Fig. 3 B, subject to RDA = 1) in a consistent manner. Although the performances are nearly the same, it occurs that E6 systematically provides results closest to the MCS reference curve. E6 is the method in Table 1 with the most rigorous cross talk correction. We infer that, indeed, these cross talk terms remove essentially all artifacts from the calculated efficiency whereas E4 and E7 are still left with some biases. However, as shown later in this paper, the noise-induced uncertainty amounts to ±12% of FRET efficiency in this range of RDA (“Uncertainty analysis” section). Therefore, the difference between E4, E6, and E7 are statistically not significant, and our interpretation relies on the systematic shift of only two experiments per RDA and RSA settings.
In contrast, the efficiency E1, calculated from the signal ratio of the donor in presence and in absence of acceptor, does not provide repeatable results. In some cases, it even delivers negative efficiencies. Negative efficiency values indicate that the fluorescence of the donor in the presence of the acceptor is enhanced instead of quenched. In our particular case of an experiment with equal donor and acceptor concentrations (RDA = 1), three out of five images showed higher intensity in Db than in Dd. This demonstrates the weakness of indirect measurements of FRET. The method is only stable with absolutely repeatable detection of the donor signal before and after adding acceptor and thus, notably, between two different samples. Small changes in the fluorescence, whether noise- or sample-induced, can dramatically alter the efficiency and yield nonsensical negative values. This behavior is confirmed by the graph in Fig. 3 B when the concentration of fluorophore decreases. Similar concerns apply to method E8, although the weakness of this method will mainly be observable with the results in Figs. 4 and 8. Because of the method-inherent weakness of E1, it is discarded from the rest of the experimental performance analysis.
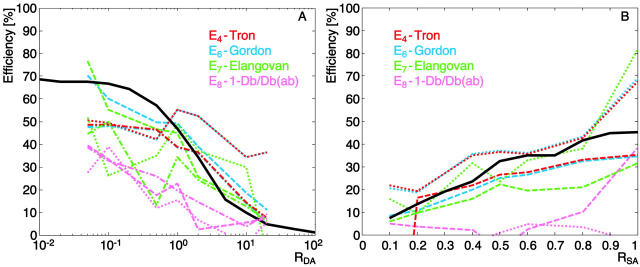
FIGURE 4.
FRET efficiency calculated with four different methods for the dye pair Alexa 488-Alexa 633 (R0 = 5.55 nm). Surface coating parameters have been varied (RDA in A and RSA in B), and results of three experiments are shown as dotted, dashed, and dash-dotted lines. The black solid line represents the results of the MCS under the same conditions.
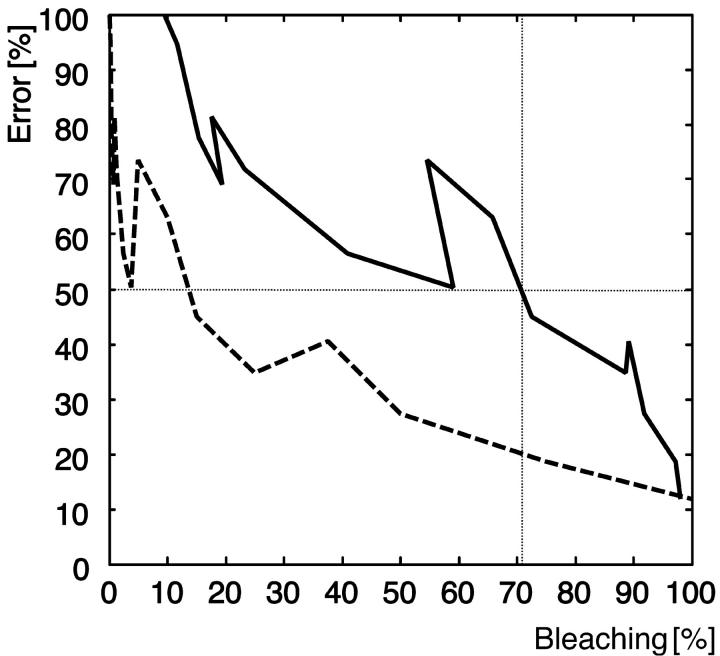
FIGURE 8.
Error of method E8 due to incomplete photobleaching relative to E6. The error is shown as a function of the fraction of bleached acceptor (solid line) and as a function of the fraction of bleaching cycles (dashed line).
Outside the range 0.1 < RDA < 10, the results obtained are unstable, independent of the method. Here, direct observation of Fb with appropriate compensation of cross talk alone does not guarantee accurate efficiency values. For example, for low RDA, method E6 predicts an increase of the efficiency, whereas the other methods suggest a decrease, notably based on identical raw data from the nine image channels. This cannot be explained by the differences in cross talk correction schemes. As will be shown below with the uncertainty analysis, image noise and any irreproducibility of fluorescence between experiments get amplified in an unfavorable manner outside 0.1 < RDA < 10.
The spectral overlap influences FRET sensitivity
Our surface FRET system offers the possibility to exchange the dye pairs (see Material and Methods) and thus to alter the Förster distance. Results from the same set of experiments as discussed before, but for the dye pair Alexa 488-Alexa 633 (R0 = 5.55 nm), are presented in Fig. 4. This new pair tests a donor-acceptor system with on the one hand less spectral overlap and on the other hand higher spectral separation such that cross talk between channels is reduced. A low spectral overlap implies lower probabilities for FRET, and thus a decrease of signal-to-noise ratio (SNR). It also implies that the cross talk ratios are calculated between channels where the cross talk is close to zero. The correction factors become very sensitive to image noise, as illustrated in Fig. 4 A by the substantially weaker reproducibility of the experiments as compared to Fig. 3 A. Only data in the range 0.1 < RDA < 10 is presented (see above). As in Fig. 3 B, the two methods E4 and E6 appear to generate more consistent and stable FRET values than E7 (Fig. 4 B).
Our comparisons of FRET pairs with different R0 lead to the following findings: The instabilities induced by the choice of a well-separated dye pair prevail over the advantages of low cross talk corrections. Actually, Fig. 3 suggests that cross talk can be well corrected, even for a dye pair with a large Förster distance.
Despite the lower reproducibility of the experiments with shorter Förster distance pairs, the data in Fig. 4 B, as compared to Fig. 3 B, are in better agreement with the MCS reference. The effect is less obvious with the comparison between Figs. 4 A and 3 A, although the data in Fig. 3 A exhibit also a trend for systematically lower experimental efficiency in the range RDA = 0.1–1 relative to the MCS predictions. This suggests that the model and experiments suffer a disagreement, which is more severe for long Förster distances. In our model, the Förster distance is a function of the spectral overlap and the geometric factor, χ2, which takes into account the orientation of the donor dipole relative to the acceptor dipole (Lakowicz, 1999). The spectral overlap is characteristic for the spectral properties of the dye pair and is therefore a determined parameter. χ2, however is a free parameter that is dependent on the system. Dale et al. (1979) calculated the average χ2 to be ⅔ in the case where the dyes are freely rotating. We used this value in our initial MCS shown in Figs. 2, 3, and 4. However, the existence of a mismatch between MCS and experiment motivated us to modify our MCS and to introduce a random χ2 for every donor-acceptor pair (see appendix, Eq. A2). The relative orientation of two dyes is calculated using three random angles, and the value of χ2 can range from 0 to 4. This leads to different R0, and thus variable FRET probabilities for every donor-acceptor pair. Fig. 5 shows the results of the modified MCS (dashed line) in comparison to the uncorrected MCS (solid line). The calculations have been made for the same dye pair as in Fig. 3. Lower efficiencies are obtained from an MCS with random χ2 as compared to a fixed χ2 = ⅔, due to the fact that the distribution of random χ2 is skewed toward 0 (Fig. 5 B, inset), accompanied by a decrease of R0.
FIGURE 5.
Role of the orientation factor χ2 in the simulated efficiency. The new simulated efficiency (dashed line) has been calculated with a random orientation factor. The mean of 10 runs is presented for an experiment where RDA varies (A) and where RSA varies (B). The solid line shows the simulated efficiency with χ2 = ⅔ and the dotted and dash-dotted lines depict experimental efficiencies calculated with method E6 as represented in Fig. 3. Inset, relative occurrence of all classes of χ2 between 0 and 4.
Also in Fig. 5, we replot the experimental data, as calculated with method E6. In comparison to Fig. 3, the randomization of χ2 renders experiments and simulation in excellent agreement. This finding clearly reflects the stochastic nature of FRET and underlines the difficulties in representing the determinant statistical distributions by average characteristic parameters, as encountered in analytical predictions. An MCS approach has a fundamentally superior performance in predicting data under such conditions.
FRET indices as qualitative measures of surface FRET
Fig. 6 shows the results obtained for four FRET indices. They have been calculated according to Table 2 for the dye pair Alexa 488-Alexa 546 (A) and for the dye pair Alexa 488-Alexa 633 (B). RDA was varied from 0.01 to 100 for the first dye pair and from 0.05 to 20 for the second dye pair to have more data in the center of the curve. The inset in Fig. 6 A displays the results of the first dye pair for this range and allows immediate visual comparison with the graph in Fig. 6 B. In contrast to efficiency, different indices cannot be compared on an absolute scale. Therefore we have arbitrarily normalized all index values such that the index value equals 1 for RDA = 1. Two behaviors can be distinguished in the results in Fig. 6 A: FRET1 and FRET3 are close to the simulated curve for RDA > 1 and monotonically increase when RDA decreases in good qualitative agreement with the MCS. Interestingly, whereas both MCS and FRET efficiency values exhibit a plateau, the indices seem to amplify its sensitivity in the range 0.01–1. FRET6 and FRET7 perform in a similar manner for RDA > 1, but exhibit a turning point at RDA = 1, which makes them essentially useless, at least for the range RDA < 1.
FIGURE 6.
Relative FRET indices calculated with four different methods for two dye pairs when RDA varies. Results of three experiments for the dye pair Alexa 488-Alexa 546 (panel A, R0 = 6.31 nm) and for the dye pair Alexa 488-Alexa 633 (panel B, R0 = 5.55 nm) are shown as dotted, dashed, and dash-dotted lines. The black solid line represents the results of the MCS under the same conditions.
Results obtained with a dye pair with a shorter Förster distance (Fig. 6 B) confirm these findings, but like with the efficiencies, shorter R0 tend to introduce more instability.
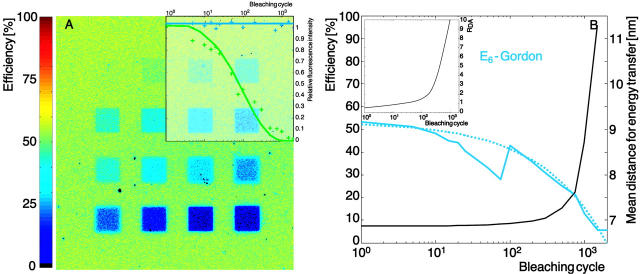
Photobleaching of the acceptor is a method to vary the concentration of acceptors locally
We have tested our system with acceptor photobleaching for the dye pair Alexa 488-Alexa 546. Sixteen regions of interest (ROIs) were defined and photobleaching was performed in these ROIs with 1, 5, 10, 15, 20, 25, 50, 75, 100, 200, 300, 500, 750, 1000, 1500, and 2000 cycles, as shown in Fig. 7. The laser (1 mW He-Ne, 543 nm, maximum power) bleached the acceptor only, as verified with the control experiment illustrated in the inset of Fig. 7 A. The donor signal (blue) is retained, whereas the acceptor signal (green) decays in the expected way. Fig. 7 A represents the efficiency map calculated with method E6. The results are color-coded and clearly display a decrease of FRET with photobleaching of the acceptor (increasing number of cycles from the upper left to the lower right.). The mean value of the efficiency calculated in the ROI is represented in Fig. 7 B as a blue solid line. After 2000 cycles, E6 ≈ 0, suggesting that this is sufficient to completely bleach the acceptor.
FIGURE 7.
Efficiency calculated for an experiment with progressive acceptor bleaching for the dye pair Alexa 488-Alexa 546. (A) False color map of FRET efficiency calculated with method E6 (see Table 1). The range goes from 0 (black) to ∼60% (yellowish green). The squares represent areas where the acceptor was bleached during 1, 5, 10, 15, 20, 25, 50, 75, 100, 200, 300, 500, 750, 1000, 1500, and 2000 cycles (from upper left to lower right). Inset, control experiment with bleaching of the donor alone (blue curve) and with bleaching of the acceptor alone (green curve). (B) FRET efficiency as a function of the bleaching cycle, calculated with method E6 (solid light blue line) and a fit of the curves (dotted light blue line). The relationship between the number of bleach cycles and the mean distance for energy transfer (see text) is illustrated with the black solid line. Inset, relationship between the number of bleaching cycles and RDA (calculated based on the fit curve in B and the interpolated E6 efficiency as a function of RDA taken from Fig. 3 A).
The assumption behind this experimental plan was that bleaching would provide an alternative to altering RDA and RSA for a modulation of the acceptor distance. To test this assumption, we have combined the results of Fig. 3 A (E(RDA)) and Fig. 7 B (dashed line fitted to E(Bleaching cycle)) for E6 to obtain an estimation for RDA as a function of the bleaching cycles (inset of Fig. 7 B). This curve shows that 1000 cycles introduce a reduction of the acceptor concentration of a factor 10. For each of these concentrations, we have derived a mean distance for energy transfer between the donors and the acceptors. The mean distance for energy transfer is calculated by attributing every donor-acceptor distance with a weight that is proportional to the probability that a FRET event occurs 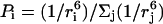 , ∀ j acceptors in the influence area of donor i. Notice that such a distance definition is necessary in a multiple-donor, multiple-acceptor system. Combining these results with those in the inset, we obtained the relationship between the number of bleaching cycles and the mean distance between fluorophores illustrated by the black solid line in Fig. 7 B. The curve shows that the relationship is not linear but the mean distance between donor and acceptor increases exponentially. This is coherent with the fact that for a low number of bleaching cycles, few acceptors are bleached and every donor still has sufficient acceptor for energy transfer. After a certain number of cycles (∼200), the distance suddenly increases dramatically. The point is reached where the number of acceptors in the influence zone of the donor is so low that also longer donor-acceptor distances obtain significant weights. In agreement with our intuition, the curve goes to infinity when the number of bleaching cycles is high enough to destroy all acceptors. This data show that, in principle, it is possible to measure molecular distances also in a multiple-donor, multiple-acceptor system, but that the interpretation of the results is more demanding and much less obvious than with one pair where the single-distance model is applicable. For our system, a theoretical mean distance of 7.2 nm between the center of mass of the streptavidin molecules was predicted from its surface concentration. This predicted value is in good agreement with the mean distance for energy transfer of 6.8 nm shown in Fig. 7 B.
, ∀ j acceptors in the influence area of donor i. Notice that such a distance definition is necessary in a multiple-donor, multiple-acceptor system. Combining these results with those in the inset, we obtained the relationship between the number of bleaching cycles and the mean distance between fluorophores illustrated by the black solid line in Fig. 7 B. The curve shows that the relationship is not linear but the mean distance between donor and acceptor increases exponentially. This is coherent with the fact that for a low number of bleaching cycles, few acceptors are bleached and every donor still has sufficient acceptor for energy transfer. After a certain number of cycles (∼200), the distance suddenly increases dramatically. The point is reached where the number of acceptors in the influence zone of the donor is so low that also longer donor-acceptor distances obtain significant weights. In agreement with our intuition, the curve goes to infinity when the number of bleaching cycles is high enough to destroy all acceptors. This data show that, in principle, it is possible to measure molecular distances also in a multiple-donor, multiple-acceptor system, but that the interpretation of the results is more demanding and much less obvious than with one pair where the single-distance model is applicable. For our system, a theoretical mean distance of 7.2 nm between the center of mass of the streptavidin molecules was predicted from its surface concentration. This predicted value is in good agreement with the mean distance for energy transfer of 6.8 nm shown in Fig. 7 B.
Incomplete photobleaching induces errors in the calculated efficiency
Acceptor photobleaching is also a frequently used approach to measure FRET, as discussed in Table 1. The corresponding efficiency is given by E8 = 1 − Db/Db(ab), relying on the ratio of donor signal before and after complete bleaching of the acceptor. In our case of a homogeneously labeled surface, we chose a slightly different observation strategy. Only a part of the surface was bleached. Thus, the same image showed a region where both fluorophores were still present, providing a measure for Db, and an acceptor-bleached region, providing a measure for Db(ab). This protocol bears the advantage of circumventing problems of sequential observation, e.g., arising from global intensity changes due to focus drift between the acquisition of Db and Db(ab). In a less-controlled sample with inhomogeneous labeling, similar stability can be attained with sequential observation when a control region is coimaged, delivering two donor intensities, Dbc and Dbc(ab) that are unaffected by the acceptor bleaching. The modified method 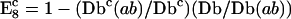 is insensitive to global variation of the intensity and may have the same characteristics as E8 applied to our idealized model sample.
is insensitive to global variation of the intensity and may have the same characteristics as E8 applied to our idealized model sample.
We have investigated the performance of this method in reporting FRET efficiency as a function of RDA, RSA, and R0. Results are shown in Figs. 3 and 4. The reference value Db(ab) was taken after 2000 bleaching cycles, according to our findings in Fig. 7 B.
The results essentially agree with those obtained with the other methods, although in general the values seem to be lower. When R0 decreases (Fig. 4), they exhibit large fluctuations, implying increased sensitivity to noise.
The method bears the advantage of using a single sample and a single filter set but strictly relies on complete photobleaching of the acceptor. In practice, such an approach is often problematic: First, to guarantee proper bleaching, one has to tune the laser power, bleaching wavelength, and bleaching time. Second, bleaching can have cross talk and thus affect the donor signal as well. Third, in live cell imaging, bleaching is known to cause phototoxicity and thus to severely affect the sample viability. It is therefore important to choose an acceptor that can be readily bleached. Our choice of Alexa 546 would obviously be not optimal for life experiments, since Alexa dyes are known to be very stable (as confirmed by the large number of cycles necessary for complete bleaching).
More critical for our performance analysis, however, are errors induced by incomplete bleaching. The method E8 strictly relies on the assumption that the acceptor is entirely bleached. In the practice of, e.g., a live cell experiment, this can frequently not be guaranteed, as acceptor molecules are subjected to diffusion and other protein dynamic processes, and the assessment of the number of cycles necessary for complete bleaching is not straightforward. Fig. 8 shows the relative error estimated under incomplete acceptor photobleaching in comparison to method E6. The results are presented as a function of the fraction of acceptor bleached (solid line) and as a function of the number of bleaching cycles (dashed line). If only 70% of the acceptors are bleached, the error in FRET efficiency is 50%. Even worse, the gradient in the error curve increases between 70% and 100% bleaching, which means that there is no tolerance at all for incomplete bleaching. Fig. 8 shows that despite a 100% photobleaching, the method E8 still provides a 10% error. This error is mainly due to difference in the observation strategy and uncorrected cross talk.
Uncertainty analysis of different FRET methods
Incompatibilities between the different FRET methods can be due to two factors:
Differences in observation strategy and cross talk correction.
Differences in the robustness against uncontrolled changes (irreproducibility) in the intensity measurement of any channel and against noise.
Observation strategies relying on a physical exchange of samples are inferior to those recovering FRET from ratio and difference analysis of samples coimaged in different channels
Depending on the observation strategy, the methods described in Table 1 can be classified into two groups:
Methods E1 and E8 calculate the efficiency from the change of donor fluorescence in images taken from different samples (Db with and Dd or Db(ab) without acceptor). Fig. 3 shows that the efficiencies calculated with these methods can be negative. This problem is inherent to the chosen observation strategy. Any change in the absolute fluorescence intensity between the acquisition of the two images directly affects the FRET efficiency. Such changes are very likely. With method E1, it is almost impossible to ensure twice the same donor distribution in an experiment, one in absence and one in presence of acceptor. With method E8, mainly the bleed-through of the laser line used for acceptor bleaching and mobility of the donor bear the risk of altering the donor fluorescence in an uncontrolled manner. For the same reason, both methods are weak in analyzing FRET in dynamic systems.
In contrast, all other methods derive the efficiency from the signal obtained in the FRET channel in the presence of both fluorophores (Fb). They only differ in the applied cross talk correction factors, but none of them involves an exchange of the sample. To illustrate this, we examine, for example, method E4. It relies on the measure of Fb, from which the cross talk in Db and Ab is subtracted. All three measures are taken from the same sample (b) coimaged in three different channels. The cross talk factors (FDd and AFd for sample d and FAa for sample a) are again calculated from signals comeasured on the same sample (either d or a). Importantly, the equations do not contain any ratio or subtraction that combines the signals of two different samples. Therefore, the only uncertainty of these ratio or subtraction terms arises from dynamic changes of one sample between the observation in two different channels. For many applications and microscope setups, including the one employed for this paper, sample variation during the switch of channels are negligible.
To illustrate the sensitivity of method E1 to changes in the absolute level of fluorescence, we present in Table 4 A an example of intensities obtained for an experiment with RDA = 1 and RSA = 1 yielding negative E1. In this particular case, Db is larger than Dd, most probably because of an uncontrolled increase of donor concentration between the sample d and b. In practice, it is often difficult to guarantee the same range of absolute donor fluorescence for two different samples. In our case, irreproducibilities can occur with different levels of donor protein adsorption and focus shifts. In live cell experiments, the problem gets even more prominent. Different cells will hardly ever express the same amount of protein, and changes in the experimental conditions, e.g., in temperature or pH, can have dramatic effects on the signal. We have measured the sample irreproducibility by taking five independent images per experiment. For the sample b, we found a standard deviation of 16%–38% of the channel mean intensity, indicating that even in our highly controlled surface FRET system, the fluorescence signal is subject to significant variation. These experimental difficulties affect methods E2–E7 much less for the reasons illustrated in the next two sections.
TABLE 4.
SNR analysis of efficiency calculation methods
| Aa | Da | Fa | Ad | Dd | Fd | Ab | Db | Fb | ||
|---|---|---|---|---|---|---|---|---|---|---|
| A. Data noise and irreproducibility for RDA = 1 and RSA = 1 | ||||||||||
| Mean intensity | 0.62 | 0.008 | 0.063 | 0.003 | 0.33 | 0.059 | 0.57 | 0.42 | 0.42 | |
| Std (mean 5 images) | – | – | – | – | – | – | 0.09 | 0.15 | 0.14 | |
| % Irreproducibility | – | – | – | – | – | – | 16 | 38 | 33 | |
| B. Relative influence factors for RDA = 1 and RSA = 1 | ||||||||||
| E1 | 0 | 0 | 0 | 0 | 2.1 | 0 | 0 | −2.1 | 0 | |
| E4 | −0.24 | 0 | 0.24 | −0.003 | 0.3 | −0.3 | −0.24 | −1.5 | 1.7 | |
| E6 | 0.069 | 0.038 | −0.11 | 0.003 | 0.023 | −0.23 | −0.14 | −1.4 | 1.52 | |
| E7 | 0.17 | 0 | −0.17 | 0 | 0.15 | −0.15 | −0.17 | −0.5 | 0.71 | |
| C. Error propagation of method E6 for RSA = 1 | ||||||||||
| RDA = 0.01 | SNR | 16.1 | 4.1 | 11.4 | 27.3 | 4.6 | 2.3 | 8.6 | 6.7 | 6.8 |
| |dE6(Ii)| | 0.096 | 0.15 | 0.19 | 0.002 | 0.016 | 0.048 | 0.19 | 0.12 | 0.36 | |
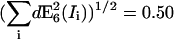 |
||||||||||
dE6(Ii)2/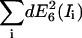
|
0.04 | 0.09 | 0.14 | <0.01 | <0.01 | 0.01 | 0.15 | 0.06 | 0.52 | |
| RDA=1 | SNR | 18.3 | 1.9 | 4.7 | 6.9 | 8.9 | 4.6 | 9.5 | 5 | 6.1 |
| |dE6(Ii)| | 0.009 | 0.03 | 0.031 | 0.001 | 0.010 | 0.023 | 0.021 | 0.065 | 0.084 | |
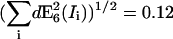 |
||||||||||
dE6(Ii)2/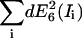
|
0.01 | 0.06 | 0.07 | <0.01 | 0.01 | 0.04 | 0.03 | 0.3 | 0.50 | |
| RDA = 100 | SNR | 3.2 | 30.6 | 1.5 | 1.2 | 16.2 | 10.1 | 9.7 | 3.7 | 4 |
| |dE6(Ii)| | 0.001 | 0.004 | 0.088 | 0.001 | 0.097 | 0.16 | 0.001 | 0.41 | 0.38 | |
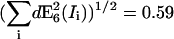 |
||||||||||
dE6(Ii)2/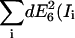 ) ) |
<0.01 | <0.01 | 0.02 | <0.01 | 0.03 | 0.07 | <0.01 | 0.47 | 0.41 | |
Although tending toward the same instability in the presence of uncontrolled changes between Db and Db(ab), E8 yields better results than E1. This owes to the fact that in our model case, Db and Db(ab) are co-observed in two regions of the same, homogenously labeled surface. To a certain extend, this stability can also be rescued into more practical FRET imaging with E8, when compensating global intensity changes with the ratio Dbc(ab)/Dbc of a control region. Nevertheless, the high chances for uncontrolled changes also in these measures and the clearly inferior performance of E8 as compared to E4, E6, and E7 (Figs. 3 and 4) even in our most idealistic case still support the use of a direct observation of FRET in presence of both donor and acceptor.
Influence factors indicate the effect of uncontrolled signal changes
To analyze the effect of uncontrolled signal changes, we have calculated for each of the methods the influence factor of every channel. The influence factor γi of a channel i denotes the change in FRET efficiency induced by a change in the intensity of this channel. In addition, we introduce the relative influence factor, ρi, as a measure of the relative change in efficiency induced by a relative change in the intensity of channel i. γi and ρi are calculated according to:
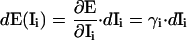 |
(2a) |
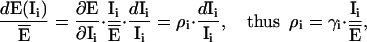 |
(2b) |
where 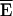 is the nominal efficiency for a certain donor and acceptor configuration and Ii denotes the intensity of the ith channel, i = 1..9. In our case,
is the nominal efficiency for a certain donor and acceptor configuration and Ii denotes the intensity of the ith channel, i = 1..9. In our case,  is estimated by MCS. The relative influence factors ρi are listed in Table 4 B for methods E1, E4, E6, and E7 considering an experiment with RDA = 1 and RSA = 1.
is estimated by MCS. The relative influence factors ρi are listed in Table 4 B for methods E1, E4, E6, and E7 considering an experiment with RDA = 1 and RSA = 1.
For all methods except E7, relative influence factors greater than 1 are obtained for at least one channel. This means that uncontrolled relative changes in the signal propagate adversely, amplifying the relative error of the FRET efficiency, as well. However, there is only a small difference in the magnitude of the relative influence factors between the method E1, which we found unstable in presence of signal irreproducibility, and the clearly more stable methods E4 and E6. The maximum |ρi| of method E1 is 2.1 in both Dd and Db, whereas E4 and E6 both have a maximum |ρi| in Fb of 1.7 and 1.5, respectively. Obviously, the instability in E1 must be associated with the fact that irreproducibilities in Dd and Db propagate independent and uncompensated, whereas the channel contributions of E4 and E6 grant a compensation of irreproducibilities in Fb by other terms.
Methods with ratio and subtraction terms combining the signals of the same sample have compensating relative influence factors and thus are robust against image irreproducibility
It turns out that the fundamental difference between E1 and the more robust methods E4, E6, and E7 consists in the absence versus existence of cross-compensating influence factors. For example, an increase by x% of Db due to an uncontrolled increase in donor concentration of sample b relative to sample d yields a decrease of −2.1·x% in E1. In contrast, the same increase yields a decrease of −1.5·x% in E4, but at the same time, the signals Ab and Fb will increase, nearly canceling the effect of one another. Thus, uncontrolled variation of the sample has little effect on E4 as long as the channels Ab, Db, and Fb are imaged under identical conditions. A similar cross-compensation of relative influence factors is found for the two other samples a and d in all methods listed in Table 4 B except E1. Cross-compensation is indicated by bold numbers grouping the factors of the three channels A, D, and F for each sample a, d, and b. In each of the groups, e.g. {Aa, Da, Fa} the sum of the factors is almost zero, explaining the robustness of E4, E6, and E7 against uncontrolled changes between the samples. The same is true for the groups {Ad, Dd, Fd} and {Ab, Db, Fb}.
The influence of image noise precludes robust analysis in extreme RDA and RSA
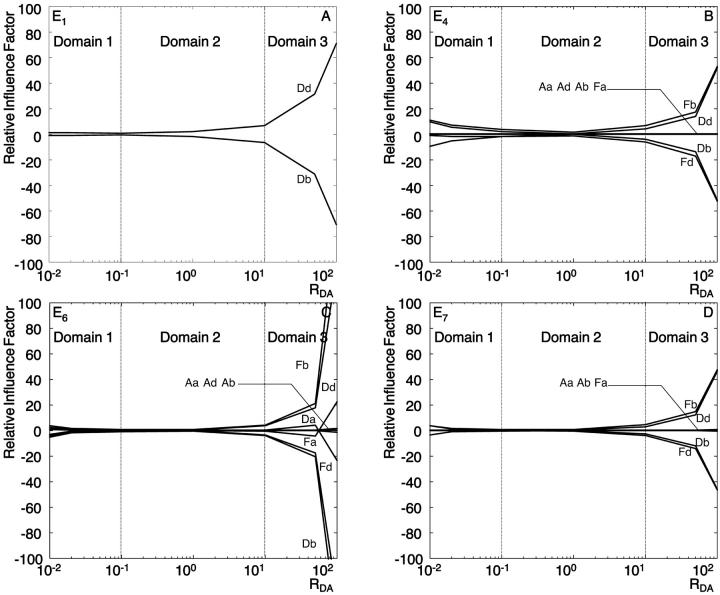
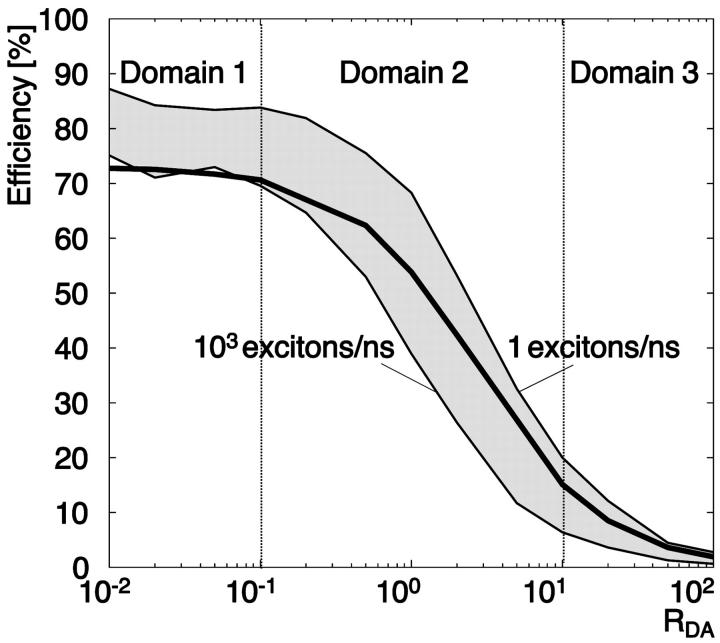
Fig. 9, A–D, illustrate the relative influence factors in the range 0.01 < RDA < 100, RSA = 1 for methods E1, E4, E6, and E7. Three domains can be observed in all panels:
FIGURE 9.
Relative influence factors as a function of RDA for methods E1 (A), E4 (B), E6 (C), and E7 (D).
Domain 1. The relative influence factors are in the range 5–10, implying that a change of 1% in the signal of one channel will yield a change of 5%–10% in the efficiency. Importantly, in the case the signal changes are associated with image noise, there is no cross-compensation between channels. Instead, noise-induced alterations and uncertainties of FRET add up according to the law of error propagation. Table 4 C presents example data for an error propagation in method E6. Noise measurements and influence factors are listed in blocks for the three donor-acceptor ratios RDA = 0.01, 1, and 100, all subject to RSA = 1. The first row in each block contains the SNR of each channel. The SNR was determined experimentally by analyzing the variation in the signal of five images repeatedly taken from the same sample area. The SNR was then defined as the background subtracted mean of the five images divided by the mean of the pixelwise standard deviation of the signal. The second row specifies the magnitude in the FRET uncertainty |dE(Ii)| propagated from the noise in each channel according to Eq. 2a. Quadratic summation, 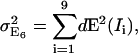 yields the expected overall variance of the FRET efficiency due to image noise. Here, we assume that the noise distributions are mutually independent between the channels. The third row indicates the relative contribution of each channel to the overall FRET efficiency variance
yields the expected overall variance of the FRET efficiency due to image noise. Here, we assume that the noise distributions are mutually independent between the channels. The third row indicates the relative contribution of each channel to the overall FRET efficiency variance 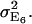 The channels with significantly higher contributions are highlighted as underlined numbers. For the first block with RDA = 0.01, the propagated uncertainty due to noise amounts to 0.50, i.e., the FRET values E6 displayed in Fig. 3 have a confidence interval (p = 66%) E6 = 0.84 ± 0.50. On a relative scale, this corresponds to an uncertainty of ∼60%. Similar values are obtained for the methods E4 and E7 (data not shown). We infer from this that the observed instability in E4, E6, and E7 of efficiency values for low RDA originate in an unfavorable propagation of noise. Interestingly, the channels with the weakest SNR (Da, Dd, and Fd) contribute relatively little to the overall uncertainty, because of low influence factors. For RDA = 0.01, the noise in Fb dominates the behavior of FRET despite a comparably high SNR of 6.8.
The channels with significantly higher contributions are highlighted as underlined numbers. For the first block with RDA = 0.01, the propagated uncertainty due to noise amounts to 0.50, i.e., the FRET values E6 displayed in Fig. 3 have a confidence interval (p = 66%) E6 = 0.84 ± 0.50. On a relative scale, this corresponds to an uncertainty of ∼60%. Similar values are obtained for the methods E4 and E7 (data not shown). We infer from this that the observed instability in E4, E6, and E7 of efficiency values for low RDA originate in an unfavorable propagation of noise. Interestingly, the channels with the weakest SNR (Da, Dd, and Fd) contribute relatively little to the overall uncertainty, because of low influence factors. For RDA = 0.01, the noise in Fb dominates the behavior of FRET despite a comparably high SNR of 6.8.
Domain 2. The influence factors are low (smaller than 5). This indicates that the efficiency calculated in this domain is much less susceptible to noise than in domain 1. Indeed, the data in block RDA =1 in Table 4 C suggest an overall uncertainty of E6 of 0.12, resulting in a confidence interval (E6 = 0.6 ± 0.12, 20% relative uncertainty). This finding is supported by the small variation of FRET efficiencies in this domain in Fig. 3.
Domain 3. The influence factors increase dramatically when RDA increases (e.g., Fig. 9 C, E6). This renders the calculation of FRET efficiency instable. Comparable to domain 1, the uncertainty amounts to ±0.59, but owing to inherently low efficiencies in this domain, the relative uncertainty reaches now a level of up to ∼4000%.
We conclude from this analysis that the cumulated effect of noise propagation of each channel can predict the variation of FRET, calculated with E6, including the nonsensical negative values for extreme RDA found in Fig. 3. Similar conclusions can be drawn for the methods E4 and E7 (data not shown), whereas the instabilities of E1 and E8 originate in the unfavorable propagation of uncontrolled changes in donor concentration between the samples d and b, and focus shifts (see above).
CONCLUSION
There were a number of reasons to undertake the analysis presented in this paper. At the beginning of implementing a FRET assay, it is surprising to see that the literature abounds with methods to measure FRET. They deliver a zoo of numbers, factors, indices, and values, which are difficult to compare. Our first goal was to sort the methods and to rewrite them in a consistent terminology inspired by the one suggested by Gordon et al. (1998). This allowed us to distinguish between methods reporting absolute measures of FRET (FRET efficiencies, Table 1) and those reporting relative measures (FRET indices, Table 2), and to classify them in terms of the data and equipment requirements (filter set per number of samples per number of images). Second, we evaluated their performance using a surface FRET system that could be controlled in terms of absolute and relative fluorophore concentrations, i.e., in terms of sensitivity and mean donor-acceptor distances. In addition, the system could be modeled computationally, providing a reference value for a performance test on an absolute scale.
We have found that FRET efficiencies can only be extracted for RDA in the range 0.1–10. In this range, E6 (Gordon et al., 1998) appears to be the most accurate. For RDA < 0.1, FRET can still be evaluated, although, only qualitatively, with FRET indices (FRET1 or FRET3), which turn out to increase the sensitivity in a low donor regime. For RDA > 10, the number of acceptors is insufficient for a reliable transfer measurement. The exact breakdown depends on the signal-to-noise characteristics.
Comparisons of our results with the predictions made by Kenworthy and Edidin (1998) confirm that in our system, the fluorophores are randomly distributed on the surface and do not cluster: E is dependent on acceptor surface density and E goes to zero at low surface densities.
Our system also allowed an evaluation of one of the most frequently used methods of FRET quantification: acceptor photobleaching. The results obtained with this method are in good agreement with those of other methods, if the photobleaching is complete. The error due to incomplete photobleaching, however, can go up to 100%, and is still 50% if the acceptor is bleached to only 30% of its initial intensity. Incomplete photobleaching will almost always be the reality of a live cell experiment if the acceptor dye is not carefully chosen. We will therefore discard this method for our upcoming measurement in live yeast.
In summary, our main findings with a controlled FRET system, supported by MCS predictions, are the following:
Donor and acceptor concentration should be of the same order of magnitude, and stable FRET measurements can only be achieved in the range of donor-to-acceptor ratios 0.1–10. Outside this range, noise and data irreproducibility propagate unfavorably, rendering accurate efficiency calculations impossible.
The various FRET methods reported in the literature vary greatly in terms of the reported efficiency or indices, and not all of them seem stable inside the range of donor-to-acceptor ratios 0.1–10.
To get stable FRET measurements, the transfer has to be observed in the FRET channel, i.e., by excitation of the donor and a measurement of the acceptor emission. Methods that estimate FRET from the donor signal variation in presence and absence of acceptor (E1 or E8) are less robust.
To get stable FRET measurements, the dye pair with the maximum spectral overlap should be used.
This, however, requires cross talk correction as such dye pairs tend to be accompanied by substantial cross talk in the imaging channels. As written by Gordon and colleagues, there is no need to reject a donor and acceptor combination on the basis that a donor signal can be detected in the acceptor channel. All methods proposing cross talk corrections yield results that are close to the results obtained with the simulation.
Some FRET indices report FRET very reproducibly and still allow qualitative measurements of FRET in cases of donor-to-acceptor ratios <0.1 where efficiency measures fail or are completely insensitive toward distance variations.
Acknowledgments
We are grateful to Dr. János Vörös, from the BioInterface Group, Swiss Federal Institute of Technology, Zurich, Switzerland, for providing the PLL-g-PEG-biotin, and for his appreciated help in the characterization of the polymer. We thank also Julie Mudry for her help in the establishment of the coating protocol and controls.
This project is sponsored by a university internal grant (TH-28/01-1 to G.D.).
APPENDIX
MONTE CARLO SIMULATION ALGORITHM
The simulation involves the following steps (Fig. 10):
The number of excitons Nex is set as a function of RDA and RSA.
A surface is generated and donor and acceptor are placed randomly on the surface according to the parameters [Sa]Surface, RSA, and RDA. In Fig. 10, a gray box indicates the use of the random generator. We take into account that the molecules carrying the fluorophores have a certain size, which defines an exclusion radius Rc (5 nm for streptavidin).
-
The program generates for every donor a list of acceptors in a circular region of radius 10 R0. For distances >10 R0, the probability for transfer is <10−6 and thus negligible. For each acceptor, the distance to the donor ri is calculated, as well as the probability factor
to be excited from this donor by energy transfer.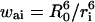
(A1) In the modified algorithm,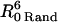 is determined by random generation of χ2 · χRand2 = (sin(θDRand)sin(θARand)cos(φRand) − 2cos(θDRand) cos(θARand))2 (Lakowicz, 1999), where θARand, θDRand, and φRand are random orientation differences between the donor and acceptor dipoles set between 0 and π for θ and between 0 and 2π for φ. This yields new probability factors
is determined by random generation of χ2 · χRand2 = (sin(θDRand)sin(θARand)cos(φRand) − 2cos(θDRand) cos(θARand))2 (Lakowicz, 1999), where θARand, θDRand, and φRand are random orientation differences between the donor and acceptor dipoles set between 0 and π for θ and between 0 and 2π for φ. This yields new probability factors 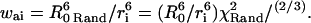
(A2) A time sequence is defined by a random generator, which defines the play time of each exciton in the interval [0, Tint]. Also for each exciton, a target donor is randomly assigned. The experimental clock is set to zero.
All excitons are played sequentially.
The program checks if the donor assigned to the exciton is already involved in either a transfer or fluorescence process. If negative, the algorithm can step directly to point 8.
If the donor is already busy, the program checks at what time it will release its energy. If this time is smaller than the current clock time, the donor is already free and can reparticipate in the game. If this is not the case, the exciton is lost, and the next exciton can be played (point 5).
- A list of the currently free acceptors around the donor is generated. Our assumption is that an already excited acceptor cannot be part of a second energy transfer process. The overall rate
 of energy release for one donor given all free associated acceptors is then calculated as (Demidov, 1999):
of energy release for one donor given all free associated acceptors is then calculated as (Demidov, 1999):
The parameter τD describes the lifetime of the unquenched donor. Notice that with no acceptor in the influence zone of the donor,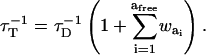
(A3)  i.e., the donor is de-excited by fluorescence emission at a rate
i.e., the donor is de-excited by fluorescence emission at a rate  With acceptors potentially absorbing the energy, the rate of de-excitation increases. The term wai specifies the contribution of an acceptor i to this rate increase.
With acceptors potentially absorbing the energy, the rate of de-excitation increases. The term wai specifies the contribution of an acceptor i to this rate increase. -
With the donor getting excited, its excitation flag is set to “busy”. According to Eq. A3, the probability that the energy is released in a time interval Trelax is given by:
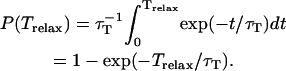
(A4) In an MCS, Trelax for the donor can therefore be determined with a uniformly distributed random generator delivering a value γ = [0,1]:
This defines the time point of energy release for the currently excited donor, i.e., the time point at which the flag is set back to “free”.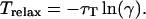
(A5) - Next, it has to be decided in what form the donor will be de-excited. For this, we generate a cumulative histogram with the classes f, a1, …, an, where f represents energy release by fluorescence and aj, j = 1..n denotes energy release by FRET to acceptor j. The probabilities P(ci) for these n + 1 classes are given by
The selection of the class is accomplished by renewed generation of a uniformly distributed random number γ = [0,1] . We select the class S for which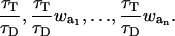
(A6) 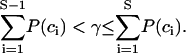
If the selection in point 10 falls in the class f, the variable Fluo is incremented by 1 and the program steps directly to item 14.
If the donor has been selected to transfer its energy to acceptor j, the flag of this acceptor is set to “busy” and the Fret variable is incremented by 1.
The time interval for which the acceptor is busy is determined by yet another MC step, where Trelax = −τA ln(γ) with τA denoting the acceptor lifetime.
The loop 5→6→…→14 is repeated until all excitons are played.
- The simulated efficiency is computed as
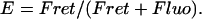
(A7)
FIGURE 10.
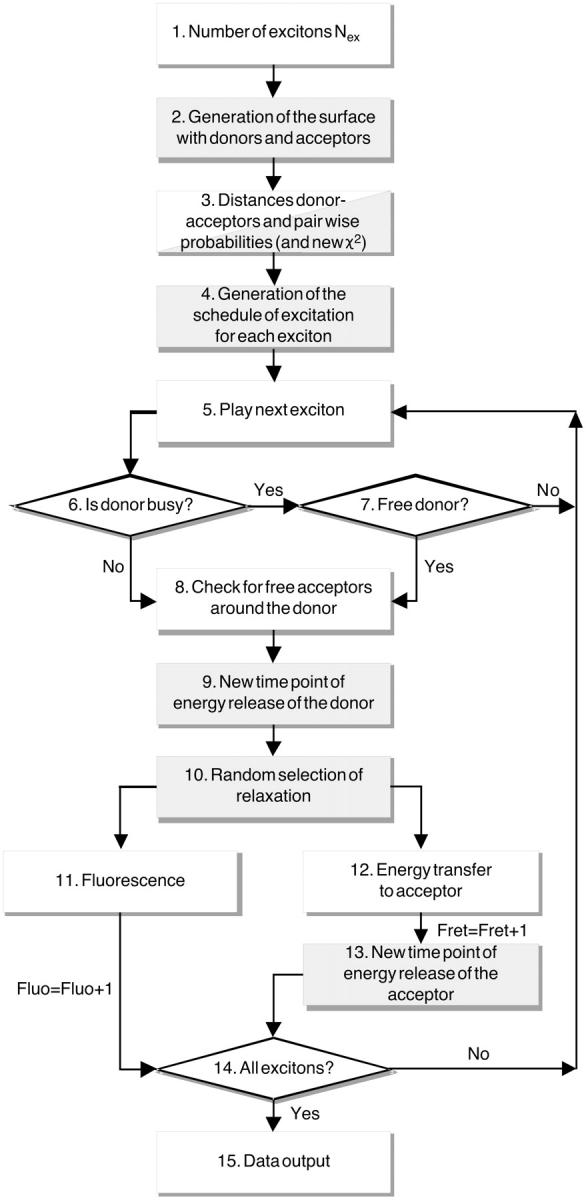
Flow chart of the MCS algorithm. Processes involving the random generator are shown on a gray background.
Similar simulations have already been proposed by Zimet et al. (1995) in the case of energy transfer in biological membranes, by Demidov (1999) in the case of surface coating with fluorophores, and by Frederix et al. (2002) for actin filaments, but they used different strategies as the one proposed in this article. Zimet and colleagues estimated the transfer efficiency by calculating the quantum yield decrease for one donor in the presence of multiple acceptors. Demidov calculated the efficiency of his system from the mean of randomly generated decay rates. Frederix and colleagues randomly generated FRET processes and calculated the efficiency using the generated fluorescence intensities as described in method E2. Although the algorithm presented here is similar to these approaches, we have implemented distinct modifications: 1), Our system accounts for already excited acceptors and excludes them from the game. 2), We perform a quasi-parallel computing of multiple simultaneous events, introducing a fluorescence dynamics in our system and resulting in a competitive FRET scheme, which seems to reflect our situation more realistically. 3), The efficiency is calculated directly as the ratio between the number of excitons transferred to the acceptors and the total number of excitons (transferred and not). The quantum yields, transfer rates, and lifetimes of fluorophores only appear in the calculation of the pairwise FRET probabilities. Once these probabilities are calculated, the final results depend on the random generator only.
The model could easily be completed to account for photobleaching (negligible in our case) or for other routes of relaxation, as shown in the three cited articles. Additional features can also be tested, as we have done with introducing random relative orientation of the donor and the acceptor.
Comparison of MC simulated efficiency with an analytical solution to FRET
An analytical solution for FRET in two dimensions has been proposed by Wolber and Hudson (1979). In their article, they derived a formula to calculate the transfer efficiency for one donor and many acceptors. They studied the special case where each fluorophore is bound to large molecules and cannot come into close contact to another fluorophore. The distance of closest approach Rc is defined by the size of the large molecules. We have reproduced this behavior in our model where the biotinylated fluorophores are bound to streptavidin. Under the assumption that the fluorophores are on average at the center of the streptavidin, Rc is 5 nm.
Fig. 11 shows the analytical solution as a function of RDA in a system with one donor on a surface surrounded by many acceptors. The entire analytical curve is enclosed by the area, whose upper and lower boundaries are defined by extreme flux settings of the MCS.
FIGURE 11.
Analytical solution for FRET efficiency on a surface. The curve has been calculated for different RDA according to the analytical solution by Wolber and Hudson (1979) with a Förster distance of 6.31 nm and a distance of closest approach of 5 nm (ratio Rc/R0 = 0.79). Results from MCS with the same parameters. Curves generated with exciton fluxes of 1 and 103 excitons/ns delimit the gray area.
Three domains can be distinguished in Fig. 11:
Domain 1. In this domain we encounter the biggest differences between the MCS and the analytical model. This result can be explained with the difference between a one-donor, multi-acceptor (analytical model) and a multi-donor, multi-acceptor arrangement (MCS). For low donor concentrations, it is critical for the efficiency that multiple donors can transfer energy to one acceptor. Obviously, this is impossible in the analytical model. Low donor concentrations simply result in an increase of the mean distance between donors and acceptors. Working with multiple donors, acceptors can pair with several donors implying a virtual increase of the acceptor concentration. Therefore, MCS efficiencies tend to be higher for low acceptor concentrations.
Domain 2. Both the MCS and the analytical curve are linear, with the MCS predicting steeper slopes. Again, this is due to the competition of many donors for few acceptors, yielding a tendency for lower efficiency with RDA ≈ 10 for MCS as compared to the analytical solution, whereas at RDA ≈ 0.5, the MCS tends to higher efficiencies for the reasons explained with domain 1.
Domain 3. The analytical model handles the competition between a large number of donors for energy transfer to a low number of acceptors with a low concentration of acceptor in the zone of influence of the donor, yielding low probabilities for transfer. There is a tendency that the analytical curve follows the MCS in better agreement under low flux condition (1–10 excitons/ns). This can be understood with the dynamic behavior of the MCS framework. With predominantly donors in the system and high exciton flux, the competition for unexcited acceptors gets more severe, leading to saturation effects accompanied by a reduction of the efficiency. The analytical model does not account for any of these dynamic effects and thus matches better with low competitive case of a low flux MCS.
To conclude, Fig. 11 indicates the limitations of the model as proposed by Wolber and Hudson (1979). To appropriately predict FRET on a surface with random donor-acceptor distribution requires a multi-donor and dynamic model.
References
- Arai, R., H. Ueda, K. Tsumoto, W. C. Mahoney, I. Kumagai, and T. Nagamune. 2000. Fluorolabeling of antibody variable domains with green fluorescent protein variants: application to an energy transfer-based homogeneous immunoassay. Protein. Eng. 13:369–376. [DOI] [PubMed] [Google Scholar]
- Bottiroli, G., A. C. Croce, and R. Ramponi. 1992. Fluorescence resonance energy transfer imaging as a tool for in situ evaluation of cell morphofunctional characteristics. J. Photochem. Photobiol. B. 12:413–416. [DOI] [PubMed] [Google Scholar]
- Chan, F. K., R. M. Siegel, D. Zacharias, R. Swofford, K. L. Holmes, R. Y. Tsien, and M. J. Lenardo. 2001. Fluorescence resonance energy transfer analysis of cell surface receptor interactions and signaling using spectral variants of the green fluorescent protein. Cytometry. 44:361–368. [DOI] [PubMed] [Google Scholar]
- Clegg, R. 1996. Fluorescence resonance energy transfer. In Fluorescence Imaging Spectroscopy and Microscopy. X. F. Wang and B. Herman, editors. John Wiley, New York. 179–252.
- Dale, R. E., J. Eisinger, and W. E. Blumberg. 1979. The orientational freedom of molecular probes. The orientation factor in intramolecular energy transfer. Biophys. J. 26:161–193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damelin, M., and P. A. Silver. 2000. Mapping interactions between nuclear transport factors in living cells reveals pathways through the nuclear pore complex. Mol. Cell. 5:133–140. [DOI] [PubMed] [Google Scholar]
- Demidov, A. A. 1999. Use of a Monte Carlo method in the problem of energy migration in molecular complexes. In Resonance Energy Transfer. D. L. Andrews and A. A. Demidov, editors. Wiley, New York. 435–465.
- Dewey, T. G., and G. G. Hammes. 1980. Calculation of Fluorescence Resonance Energy Transfer on Surfaces. Biophys. J. 32:1023–1036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elangovan, M., H. Wallrabe, Y. Chen, R. N. Day, M. Barroso, and A. Periasamy. 2003. Characterization of one- and two-photon excitation fluorescence resonance energy transfer microscopy. Methods. J. 29:58–73. [DOI] [PubMed] [Google Scholar]
- Förster, T. 1948. Intermolecular energy migration and fluorescence. Ann. Phys. 2:55–75. [Google Scholar]
- Frederix, P., E. L. de Beer, W. Hamelink, and H. C. Gerritsen. 2002. Dynamic Monte Carlo simulations to model FRET and photobleaching in systems with multiple donor-acceptor interactions. J. Phys. Chem. B. 106:6793–6801. [Google Scholar]
- Gordon, G. W., G. Berry, X. H. Liang, B. Levine, and B. Herman. 1998. Quantitative fluorescence resonance energy transfer measurements using fluorescence microscopy. Biophys. J. 74:2702–2713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graham, D. L., P. N. Lowe, and P. A. Chalk. 2001. A method to measure the interaction of Rac/Cdc42 with their binding partners using fluorescence resonance energy transfer between mutants of green fluorescent protein. Anal. Biochem. 296:208–217. [DOI] [PubMed] [Google Scholar]
- Hailey, D. W., T. N. Davis, and E. G. D. Muller. 2002. Fluorescence resonance energy transfer using color variants of GFP. Methods Enzymol. Pt. C. 351:34–49. [DOI] [PubMed] [Google Scholar]
- Huang, N. P., R. Michel, J. Voros, M. Textor, R. Hofer, A. Rossi, D. L. Elbert, J. A. Hubbell, and N. D. Spencer. 2001. Poly(L-lysine)-g-poly(ethylene glycol) layers on metal oxide surfaces: Surface-analytical characterization and resistance to serum and fibrinogen adsorption. Langmuir. 17:489–498. [Google Scholar]
- Jin, T. Q., L. L. Yue, and J. X. Li. 2001. In vivo interaction between dynamitin and MacMARCKS detected by the fluorescent resonance energy transfer method. J. Biol. Chem. 276:12879–12884. [DOI] [PubMed] [Google Scholar]
- Kam, Z., T. Volberg, and B. Geiger. 1995. Mapping of adherens junction components using microscopic resonance energy transfer imaging. J. Cell Sci. 108:1051–1062. [DOI] [PubMed] [Google Scholar]
- Kenausis, G. L., J. Voros, D. L. Elbert, N. P. Huang, R. Hofer, L. Ruiz-Taylor, M. Textor, J. A. Hubbell, and N. D. Spencer. 2000. Poly(L-lysine)-g-poly(ethylene glycol) layers on metal oxide surfaces: Attachment mechanism and effects of polymer architecture on resistance to protein adsorption. J. Phys. Chem. B. 104:3298–3309. [Google Scholar]
- Kenworthy, A. K. 2001. Imaging protein-protein interactions using fluorescence resonance energy transfer microscopy. Methods. 24:289–296. [DOI] [PubMed] [Google Scholar]
- Kenworthy, A. K., and M. Edidin. 1998. Distribution of a glycosylphosphatidylinositol-anchored protein at the apical surface of MDCK cells examined at a resolution of <100 A using imaging fluorescence resonance energy transfer. J. Cell Biol. 142:69–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinoshita, A., C. M. Whelan, C. J. Smith, I. Mikhailenko, G. W. Rebeck, D. K. Strickland, and B. T. Hyman. 2001. Demonstration by fluorescence resonance energy transfer of two sites of interaction between the low-density lipoprotein receptor-related protein and the amyloid precursor protein: Role of the intracellular adapter protein Fe65. J. Neurosci. 21:8354–8361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakowicz, J. R. 1999. Energy transfer. In Principles of Fluorescence Spectroscopy, 2nd ed. Plenum, New York. 367–394.
- Llopis, J., S. Westin, M. Ricote, Z. Wang, C. Y. Cho, R. Kurokawa, T.-M. Mullen, D. W. Rose, M. G. Rosenfeld, R. Y. Tsien, C. K. Glass, and J. Wang. 2000. Ligand-dependent interactions of coactivators steroid receptor coactivator-1 and peroxisome proliferator-activated receptor binding protein with nuclear hormone receptors can be imaged in live cells and are required for transcription. Proc. Natl. Acad. Sci. USA. 97:4363–4368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenz, M., and S. Diekmann. 2001. Quantitative distance information on protein-DNA complexes determined in polyacrylamide gels by fluorescence resonance energy transfer. Electrophoresis. 22:990–998. [DOI] [PubMed] [Google Scholar]
- Mahajan, N. P., K. Linder, G. Berry, G. W. Gordon, R. Heim, and B. Herman. 1998. Bcl-2 and Bax interactions in mitochondria probed with green fluorescent protein and fluorescence resonance energy transfer. Nat. Biotechnol. 16:547–552. [DOI] [PubMed] [Google Scholar]
- Mátyus, L. 1992. Fluorescence resonance energy transfer measurements on cell surfaces. A spectroscopic tool for determining protein interactions. J. Photochem. Photobiol. B. 12:323–337. [DOI] [PubMed] [Google Scholar]
- McLean, P. J., H. Kawamata, S. Ribich, and B. T. Hyman. 2000. Membrane association and protein conformation of alpha-synuclein in intact neurons. J. Biol. Chem. 275:8812–8816. [DOI] [PubMed] [Google Scholar]
- Mochizuki, N., S. Yamashita, K. Kurokawa, Y. Ohba, T. Nagai, A. Miyawaki, and M. Matsuda. 2001. Spatio-temporal images of growth-factor-induced activation of Ras and Rap1. Nature. 411:1065–1068. [DOI] [PubMed] [Google Scholar]
- Nagy, P., G. Vamosi, A. Bodnar, S. J. Lockett, and J. Szollosi. 1998. Intensity-based energy transfer measurements in digital imaging microscopy. Eur. Biophys. J. 27:377–389. [DOI] [PubMed] [Google Scholar]
- Ruiz-Velasco, V., and S. R. Ikeda. 2001. Functional expression and FRET analysis of green fluorescent proteins fused to G-protein subunits in rat sympathetic neurons. J. Physiol. (Lond.). 537:679–692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato, M., T. Ozawa, K. Inukai, T. Asano, and Y. Umezawa. 2002. Fluorescent indicators for imaging protein phosphorylation in single living cells. Nat. Biotechnol. 20:287–294. [DOI] [PubMed] [Google Scholar]
- Sorkin, A., M. McClure, F. T. Huang, and R. Carter. 2000. Interaction of EGF receptor and Grb2 in living cells visualized by fluorescence resonance energy transfer (FRET) microscopy. Curr. Biol. 10:1395–1398. [DOI] [PubMed] [Google Scholar]
- Stryer, L. 1978. Fluorescence energy transfer as a spectroscopic ruler. Annu. Rev. Biochem. 47:819–846. [DOI] [PubMed] [Google Scholar]
- Suzuki, Y. 2000. Detection of the swings of the lever arm of a myosin motor by fluorescence resonance energy transfer of green and blue fluorescent proteins. Methods. 22:355–363. [DOI] [PubMed] [Google Scholar]
- Suzuki, Y., T. Yasunaga, R. Ohkura, T. Wakabayashi, and K. Sutoh. 1998. Swing of the lever arm of a myosin motor at the isomerization and phosphate-release steps. Nature. 396:380–383. [DOI] [PubMed] [Google Scholar]
- Tron, L., J. Szollosi, S. Damjanovich, S. Helliwell, D. Arndt-Jovin, and T. Jovin. 1984. Flow cytometric measurement of fluorescence resonance energy transfer on cell surfaces. Quantitative evaluation of the transfer efficiency on a cell-by-cell basis. Biophys. J. 45:939–946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsuji, A., H. Koshimoto, Y. Sato, M. Hirano, Y. Sei-Iida, S. Kondo, and K. Ishibashi. 2000. Direct observation of specific messenger RNA in a single living cell under a fluorescence microscope. Biophys. J. 78:3260–3274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turcatti, G., K. Nemeth, M. D. Edgerton, U. Meseth, F. Talabot, M. Peitsch, J. Knowles, H. Vogel, and A. Chollet. 1996. Probing the structure and function of the tachykinin neurokinin-2 receptor through biosynthetic incorporation of fluorescent amino acids at specific sites. J. Biol. Chem. 271:19991–19998. [DOI] [PubMed] [Google Scholar]
- Ubarretxena-Belandia, I., L. Hozeman, E. van der Brink-van der Laan, E. H. M. Pap, M. R. Egmond, H. M. Verheij, and N. Dekker. 1999. Outer membrane phospholipase A is dimeric in phospholipid bilayers: A cross-linking and fluorescence resonance energy transfer study. Biochemistry. 38:7398–7405. [DOI] [PubMed] [Google Scholar]
- Vallotton, P., A. P. Tairi, T. Wohland, K. Friedrich-Benet, H. Pick, R. Hovius, and H. Vogel. 2001. Mapping the antagonist binding site of the serotonin type 3 receptor by fluorescence resonance energy transfer. Biochemistry. 40:12237–12242. [DOI] [PubMed] [Google Scholar]
- Vanderklish, P. W., L. A. Krushel, B. H. Holst, J. A. Gally, K. L. Crossin, and G. M. Edelman. 2000. Marking synaptic activity in dendritic spines with a calpain substrate exhibiting fluorescence resonance energy transfer. Proc. Natl. Acad. Sci. USA. 97:2253–2258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolber, P. K., and B. S. Hudson. 1979. An analytic solution to the Förster energy transfer problem in two dimensions. Biophys. J. 28:197–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wouters, F. S., P. I. Bastiaens, K. W. Wirtz, and T. M. Jovin. 1998. FRET microscopy demonstrates molecular association of non-specific lipid transfer protein (nsL-TP) with fatty acid oxidation enzymes in peroxisomes. EMBO J. 17:7179–7189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia, Z., and Y. Liu. 2001. Reliable and global measurement of fluorescence resonance energy transfer using fluorescence microscopes. Biophys. J. 81:2395–2402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia, Z., Q. Zhou, J. Lin, and Y. Liu. 2001. Stable SNARE complex prior to evoked synaptic vesicle fusion revealed by fluorescence resonance energy transfer. J. Biol. Chem. 276:1766–1771. [DOI] [PubMed] [Google Scholar]
- Youvan, D. C., C. M. Silva, E. J. Bylina, W. J. Coleman, M. R. Dilworth, and M. M. Yang. 1997. Calibration of fluorescence resonance energy transfer in microscopy using genetically engineered GFP derivatives on nickel chelating beads. Biotechnology et alia. 3:1–18. [Google Scholar]
- Zal, T., M. A. Zal, and N. R. Gascoigne. 2002. Inhibition of T cell receptor-coreceptor interactions by antagonist ligands visualized by live FRET imaging of the T-hybridoma immunological synapse. Immunity. 16:521–534. [DOI] [PubMed] [Google Scholar]
- Zimet, D., B. Thevenin, A. Verkman, S. Shohet, and J. Abney. 1995. Calculation of resonance energy transfer in crowded biological membranes. Biophys. J. 68:1592–1603. [DOI] [PMC free article] [PubMed] [Google Scholar]