Abstract
Genomewide linkage analysis has been extremely successful at identification of the genetic variation underlying single-gene disorders. However, linkage analysis has been less successful for common human diseases and other complex traits in which multiple genetic and environmental factors interact to influence disease risk. We hypothesized that a highly heritable complex trait, in which the contribution of environmental factors was relatively limited, might be more amenable to linkage analysis. We therefore chose to study stature (adult height), for which heritability is ∼75%–90% (Phillips and Matheny 1990; Carmichael and McGue 1995; Preece 1996; Silventoinen et al. 2000). We reanalyzed genomewide scans from four populations for which genotype and height data were available, using a variance-components method implemented in GENEHUNTER 2.0 (Pratt et al. 2000). The populations consisted of 408 individuals in 58 families from the Botnia region of Finland, 753 individuals in 183 families from other parts of Finland, 746 individuals in 179 families from Southern Sweden, and 420 individuals in 63 families from the Saguenay-Lac-St.-Jean region of Quebec. Four regions showed evidence of linkage to stature: 6q24-25, multipoint LOD score 3.85 at marker D6S1007 in Botnia (genomewide P<.06), 7q31.3-36 (LOD 3.40 at marker D7S2195 in Sweden, P<.02), 12p11.2-q14 (LOD 3.35 at markers D12S10990-D12S398 in Finland, P<.05) and 13q32-33 (LOD 3.56 at markers D13S779-D13S797 in Finland, P<.05). In a companion article (Perola et al. 2001 [in this issue]), strong supporting evidence is obtained for linkage to the region on chromosome 7. These studies suggest that highly heritable complex traits such as stature may be genetically tractable and provide insight into the genetic architecture of complex traits.
Introduction
Most common diseases are complex genetic traits: not only do multiple genetic loci contribute to susceptibility, but environmental factors also play a major role in determining risk. Understanding how genetic variation influences human complex-trait variation is thus vital to understanding common disease. Genomewide linkage analysis has been used to try to identify the genetic determinants for many common diseases and complex traits. This approach has the advantage of being a genomewide search for genetic factors that does not require a priori knowledge of the underlying biology or risk alleles. However, linkage analysis thus far has had limited success for common disease. Specifically, most studies have failed to generate significant evidence of linkage, and the few regions with significant results have proven difficult to replicate.
Several factors explain the limited success of linkage studies for human complex traits. By definition, multiple genetic alleles contribute to complex traits, and linkage analysis has somewhat limited power for finding genes of modest effect (Risch and Merikangas 1996). Also, environmental variables often significantly affect phenotype and obscure genetic effects, which is reflected in lower heritability. The power of linkage analysis is essentially proportional to the square of heritability (see, e.g., Lander and Botstein 1989; Sham et al. 2000), so significant contributions by environmental influences can severely limit power. Furthermore, phenotype assignment is often ambiguous or uncertain for many common diseases and complex traits. For example, individuals “unaffected” with a late-onset disease may later convert to affected status; affected individuals may also be classified incorrectly, as a result of phenocopy. Finally, for quantitative traits, measurement error or intraindividual variation may degrade the accuracy of phenotype measurement, contributing to nongenetic sources of variance and reducing heritability.
We propose that stature is an example of a complex trait in which some of these problems are minimized. Estimates of heritability range from 76% to 90%, but heritability is generally estimated to be ⩾80% (Phillips and Matheny 1990; Carmichael and McGue 1995; Preece 1996; Silventoinen et al. 2000). In addition, stature is easily, reliably, and accurately measured, reducing phenotypic uncertainty. Finally, it is inexpensive and routine to measure stature in large populations. Of course, it is impossible to know in advance how much any single locus contributes to a complex trait; if stature were significantly more polygenic than other complex traits, these advantages would be partially or completely offset by the increased difficulty of detecting loci with more-modest genetic effects.
The genetics of stature have been studied at least since 1903, when measurements of height in families suggested a high heritability (Pearson and Lee 1903). These studies also revealed that adult height follows a normal distribution, suggesting that multiple factors interact to affect stature, perhaps in an additive fashion. Although changing environmental influences, such as improved nutrition, have led to a progressive increase in height (“secular trend”), the genetic contribution to variation in height is still discernible even where poor nutrition is widespread—as in Gambia (Jepson et al. 1994)—and heritability is high in both old and young cohorts (Carmichael and McGue 1995; Silventoinen et al. 2000).
To our knowledge, no genomewide linkage studies of stature have previously been published. One focused study, using sib-pairs in Pima Indians, identified a region of suggestive linkage on chromosome 20 (P=.0001; Thompson et al. 1995). Also, variation in five genes has been reported to be associated with variation in height: DRD2 (MIM 126450), encoding the dopamine D2 receptor (Miyake et al. 1999); VDR (MIM 601769), encoding the vitamin D receptor (Minamitani et al. 1998); COL1A1 (MIM 120150), encoding collagen type I, alpha 1 (Garnero et al. 1998); ESR1 (MIM 133430), encoding the estrogen receptor, alpha (Lorentzon et al. 1999); and LHB (MIM 152780), encoding luteinizing hormone (Raivio et al. 1996). We are unaware of confirmation of any of these associations or of the linkage to chromosome 20. Thus, stature appears to be an excellent model complex trait, and, as yet, little is known about its underlying genetics. In addition, stature is of clinical interest, as many visits to pediatric endocrine programs are related to short stature, and treatment with growth hormone represents a significant portion of pharmaceutical expenditures for children. Variation in height has also been associated with variation in risk of prostate cancer and coronary artery disease (possibly through common hormonally mediated effects—see Giovannucci et al. 1997; Hebert et al. 1997; Forsen et al. 2000), as well as hip fracture (possibly caused by greater impact velocity—see Hemenway et al. 1994, 1995), suggesting that some variants affecting stature might also affect risk of these diseases. For these reasons, we set out to identify regions of linkage to stature.
We used genomewide scans in four populations for which genotyping, height, age, and gender data were available. We analyzed these populations using a variance-components method (Pratt et al. 2000), using stature as a quantitative-trait locus (QTL), and showed that four regions demonstrate strong evidence for linkage in at least one of the four populations. In data presented in an accompanying article by Perola et al. (Perola et al. 2001 [in this issue]), one of these regions shows strong evidence for linkage in an additional Finnish sample, providing additional support for this region. These initial results suggest that studying highly heritable traits such as stature may provide insight into the genetic architecture of human complex genetic traits.
Subjects and Methods
Study Populations
In total, 2,327 individuals from 483 families were studied (see table 1). Families had been previously identified by ascertaining probands either for type 2 diabetes diagnosed by oral glucose-tolerance tests using WHO criteria (families from Botnia, Sweden, Finland, and Saguenay) or for angiographically proven coronary heart disease (families from Saguenay). Full details of phenotyping and recruitment of patients and families have been described elsewhere (Groop et al. 1996; Parker et al. 2001) or will be described elsewhere, in studies detailing genomewide linkage analysis for type 2 diabetes or coronary heart disease (C.M.L, unpublished data; D.G. and T.J.H., unpublished data; J. Engert, unpublished data). There is no overlap between these samples and those described in the accompanying article (Perola et al. 2001 [in this issue]). Informed consent was obtained from all individuals, and studies were approved by the local institutional review boards and ethics committees. Blood was collected and genomic DNA was extracted from peripheral blood lymphocytes or from whole blood. Height data was obtained by measurement without shoes.
Table 1.
Summary of Populations
|
No. of Individuals |
Normality Tests |
|||||||
| Population and Sex | Genotyped | Phenotyped | Mean ± SD Age(years ) | Mean ± SD Height(cm) | Skewness | Kurtosis | Pa | db |
| Botnia (58 families): | .19 | .85 | >.99 | .03 | ||||
| Female | 207 | 185 | 59±13.6 | 161±6.0 | ||||
| Male | 201 | 194 | 59±14.2 | 174±6.0 | ||||
| Finland (183 families): | .19 | 1.86 | >.99 | .03 | ||||
| Female | 429 | 388 | 60±11.5 | 160±6.3 | ||||
| Male | 324 | 314 | 57±12.1 | 174±7.4 | ||||
| Sweden (179 families): | −.17 | .02 | >.99 | .02 | ||||
| Female | 374 | 334 | 60±12.6 | 164±6.0 | ||||
| Male | 372 | 349 | 60±11.8 | 176±6.6 | ||||
| Saguenay–Lac-St.-Jean (6 families): | −.13 | −.23 | >.99 | .03 | ||||
| Female | 220 | 161 | 55±8.2 | 156±6.0 | ||||
| Male | 200 | 186 | 56±8.8 | 169±6.1 | ||||
P value for Kolmagoroff-Smirnoff test of normality, comparing the observed distribution of height Z scores with an ideal normal distribution.
d, maximal difference statistic for Kolmagoroff-Smirnoff test.
Mean family sizes were as follows: Botnia, 7.0 members (range 2–18); Sweden, 4.2 members (range 2–13); Finland, 4.1 members (range 2–11); Saguenay, 6.7 members (range 3–15). The following number of families, out of the total in each population, represented extended pedigrees (not just single sibships or nuclear families): in Botnia, 47/58; in Sweden, 80/179; in Finland, 89/183; and in Saguenay, 2/63. The number of founders genotyped were: in Botnia, 40; in Sweden, 75; in Finland, 62; and in Saguenay, 17.
Microsatellite Genotyping
For analysis of the Saguenay families, average intermarker spacing was 12 cM, and the markers used were a modified version of the Cooperative Human Linkage Centre (CHLC) Screening Set/version 6.0 that also included Généthon markers (similar to the set described by Rioux et al. [2000]). Fluorescent genotyping was performed as described elsewhere (Rioux et al. 2000). For analysis of the Botnia families, the average intermarker spacing was 6.5 cM, and markers were included from Généthon, the Genome Database (GDB), and the CHLC (see Mahtani et al. 1996 and references therein). Fluorescent and radioactive microsatellite genotyping was performed as described previously (Mahtani et al. 1996). For analysis of the Finland and Sweden families, average intermarker spacing was 8.8 cM, and the marker map was determined, using either CEPH pedigree data and MultiMap (Matise et al. 1994) or information from the GDB; fluorescent genotyping was performed using an ABI 377XL DNA sequencer (Parker et al. 2001).
Analysis of Stature Data
Stature data was available for nearly all of the genotyped individuals. To eliminate individuals from our analysis who might still be growing, phenotype data was discarded for men <23.5 years old and women <21.1 years old; nearly all individuals over these ages have reached final adult height (Roche and Davila 1972). We found that height among the adults was inversely correlated with age in both genders in all populations (slope 0.09–0.14 cm/year, r2=0.02–0.09). This finding is consistent either with a “secular trend” (in which younger individuals are taller because of changing environmental factors) or a loss of height with increasing age. We therefore adjusted the height data by regressing height against age. After the initial regression against age, there was a trend towards higher stature in individuals age >80 years (data not shown). Accordingly, we eliminated data from individuals in that age group (representing <3% of the total data) and repeated the regression. We then calculated a Z score (standard deviations above or below the mean) for height regressed against age, treating each gender separately, so that data from both genders could be combined. These Z scores were generated separately for the Saguenay–Lac-St.-Jean data; the three Scandinavian populations were grouped for this purpose. For calculation of sib-sib and parent-offspring correlations within the Botnia population, 29 families were identified in which Z scores were available for ⩾2 siblings and one parent. Where more individuals were available, 2 siblings and one parent from a family were chosen at random.
These Z scores were used for linkage analysis using a variance-components method implemented in GENEHUNTER 2.0 (Pratt et al. 2000). For each region of the genome, this method estimates parameters to fit a model in which total trait variance is divided into three components: a QTL at the location being tested, other genetic factors, and environmental factors. The method uses nonparametric multipoint approaches developed for GENEHUNTER (Kruglyak et al. 1996). The LOD score at a location reflects the likelihood of the genotype data being observed under the model of linkage (i.e., that a QTL is present at that location) relative to the likelihood of the data being observed under the null hypothesis (i.e., that there is no contribution to variance by a QTL at the location).
The families in which we obtained positive results had been ascertained for type 2 diabetes, and low birth weight is a known risk factor for both type 2 diabetes and short stature (Paz et al. 1993; Phillips 1998; Tuvemo et al. 1999). Thus, we were concerned that, if height were correlated with risk of type 2 diabetes, such a correlation could skew our data. However, no such correlation was observed between height and type 2 diabetes (data not shown).
For estimates of significance for each population, phenotypic and pedigree data were retained, and genotypes were randomly generated within sibships. Variance-component genome-scan simulations were repeated ⩾100 times for each population. Power simulations were also conducted using a model with an additive QTL explaining 20% of the variance of a normally distributed phenotype with 80% heritability. Variance-component simulations were repeated 500 times to calculate the expected distribution of LOD scores, given such a QTL.
Results
Variance-Components Analysis of Stature in Four Populations
To study the genetics of stature, we assembled data for stature and age from individuals in four populations: Finland, Southern Sweden, the Botnia region of Finland, and the Saguenay–Lac-St.-Jean region of Quebec (table 1). DNA from these individuals was originally genotyped for genomewide analysis of type 2 diabetes or coronary heart disease (see Methods). We calculated height Z scores from the stature data, correcting for gender and age (see Methods for details). We used a variance-components method because of increased power for mapping QTLs (Almasy and Blangero 1998; Pratt et al. 2000). Importantly, variance-components methods assume normality of the underlying trait distribution, and certain non-normal distributions can lead to an increased number of false positives (Allison et al. 1999). Height Z scores were normally distributed in all populations—as assessed by Kolmagoroff-Smirnoff tests, using STATVIEW 5.0 (table 1) and χ2 goodness-of-fit tests (data not shown)—which is consistent with earlier studies of height (Pearson and Lee 1903).
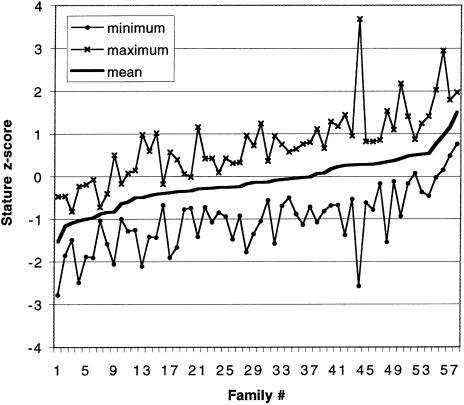
To minimize possible overall environmental variation, we studied each population separately. The heritability estimates were high in all populations (>95% in Finland, >95% in Sweden, ∼80% in Botnia, and ∼70% in Saguenay–Lac-St.-Jean; see fig. 1 for a graphic representation of the clustering of height within Botnia families). To assess for the possible influence of shared environment on heritability, we attempted to compare the correlation coefficients for parent-offspring pairs and sib pairs. Since siblings share more environmental exposures during linear growth than do parent-offspring pairs, shared environmental influences on height should lead to a tighter correlation between siblings than between parents and offspring. This comparison could be made for the Botnia population, where height data were available for at least two siblings and one parent in 29 of 58 families. Correlation coefficients for sib pairs and parent-offspring pairs were essentially identical (0.535 vs. 0.541), consistent with the findings of Pearson and Lee (1903) and suggesting that the high heritability of stature in this population is not due to shared environment. Varying degrees of assortative mating (positive correlation coefficients between spouses) were observed in the three populations where data were available for spouse pairs (r2=0.11 in Botnia, 0.26 in Finland, and 0.03 in Sweden).
Figure 1.
Graph of the heritability of height Z scores in the Botnia population. Each point on the X-axis represents a different family; the families are arranged in increasing order of mean Z score. For each family, the maximum (×), mean (thick line), and minimum (•) height Z scores are shown. Heritability is reflected in the correlation of Z scores within each family. In this population, a difference in Z score of 1 represents ∼6 cm in height.
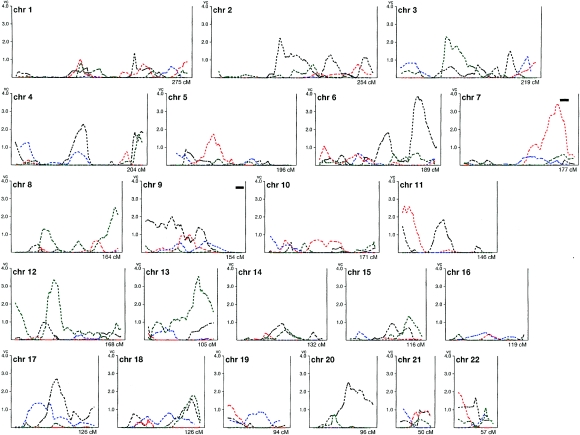
Multipoint variance-components analysis (fig. 2) revealed four regions with multipoint LOD scores >3.3, which is the approximate level of genomewide significance for this method of analysis at α=0.05 (Pratt et al. 2000). The regions are: 6q24-25 (LOD 3.85 at marker D6S1007 in Botnia), 7q31.3-36 (LOD 3.40 at marker D7S2195 in Sweden), 12p11.2-q14 (LOD 3.35 at markers D12S10990-D12S398 in Finland), and 13q32-33 (LOD 3.56 at markers D13S779-D13S797 in Finland). Multiple regions had LOD scores >1.0 (fig. 2; table 2). In addition, five regions showed modest evidence for linkage in at least two populations (fig. 2; table 2).
Figure 2.
Multipoint LOD scores for linkage to stature in each of the four populations. For each chromosome, the total genetic length is shown below the X-axis. The multipoint variance-components (VC) LOD score for each population at markers along each chromosome (proceeding pter→qter) is plotted in dashed lines. Black lines represent data for Botnia, green lines represent data for Finland, red lines represent data for Sweden, and blue lines represent data for Saguenay–Lac-St.-Jean. The two solid bars in the graphs for chromosomes 7 and 9 indicate the locations of the two regions with multipoint LOD scores >2.5 in Perola et al. (2001 [in this issue]). The X chromosome was not analyzed.
Table 2.
Regions of Linkage with LOD Score >1.0[Note]
| Chromosome and Markers | Peak Marker(s) | cM | LOD | Population |
| 1: | ||||
| D1S1665-D1S1665 | D1S1665 | 98 | 1.01 | Sweden |
| D1S210-D1S242 | D1S210 | 189 | 1.35 | Botnia |
| 2: | ||||
| D2S1790-D2S1399 | D2S113 | 104 | 2.23 | Botnia |
| D2S1391-D2S116 | D2S364-D2S116 | 185 | 1.29 | Botnia |
| 3: | ||||
| D3S1766-D3S1752 | D3S1766 | 72 | 2.31 | Finland |
| D3S1763-D3S2427 | D3S3053 | 175 | 1.49 | Botnia |
| D3S2436-D3S2398 | D3S2398 | 204 | 1.19 | Saguenay–Lac-St.-Jean |
| 4: | ||||
| D4S1614-D4S432 | D4S1614 | 0 | 1.30 | Botnia |
| D4S2366-D4S403 | D4S403 | 13 | 1.26 | Saguenay–Lac-St.-Jean |
| D4S1542-GATA4C04 | D4S1564 | 108 | 2.28 | Botnia |
| D4S1540-D4S426 | D4S1540 | 193 | 1.73 | Finland |
| D4S1554-D4S1652 | D4S3051-D4S426 | 201 | 1.89 | Botnia |
| 5: | ||||
| D5S395-D5S650 | GATA67D03 | 60 | 1.75 | Sweden |
| 6: | ||||
| D6S1574-D6S1574 | D6S1574 | 8 | 1.08 | Sweden |
| D6S462-D6S404 | D6S1021 | 111 | 1.82 | Botnia |
| D6S1003-D6S281 | D6S1007 | 159 | 3.85 | Botnia |
| 7: | ||||
| D7S1799-D7S2546 | D7S2195 | 150 | 3.40 | Sweden |
| 8: | ||||
| D8S258-D8S1477 | D8S1752 | 46 | 1.31 | Finland |
| D8S557-D8S373 | D8S1100-D8S373 | 159 | 2.52 | Finland |
| 9: | ||||
| D9S288-D9S175 | D9S1868 | 42 | 2.01 | Botnia |
| 11: | ||||
| D11S1984-D11S2362 | D11S1984 | 0 | 1.47 | Botnia |
| D11S1984-ATA34E08 | D11S2362-D11S1999 | 11 | 2.57 | Sweden |
| D11S905-FGF3 | D11S1337 | 66 | 1.84 | Botnia |
| 12: | ||||
| D12S341-D12S374 | D12S341 | 0 | 2.07 | Finland |
| D12S1042-D12S1072 | D12S1090-D12S398 | 56 | 3.35 | Finland |
| 13: | ||||
| D13S221-GGAA29H03 | D13S221-GGAA29H03 | 13 | 1.01 | Finland |
| D13S788-D13S285 | D13S779-D13S797 | 80 | 3.56 | Finland |
| 15: | ||||
| D15S816-D15S657 | D15S816 | 94 | 1.33 | Finland |
| 17: | ||||
| D17S974-D17S1293 | D17S122 | 40 | 1.35 | Saguenay–Lac-St.-Jean |
| D17S1294-D17S1290 | D17S958 | 66 | 2.69 | Botnia |
| 18: | ||||
| D18S68-D18S554 | D18S541-D18S1121 | 111 | 1.58 | Botnia |
| D18S55-D18S554 | D18S1121 | 116 | 1.77 | Finland |
| 19: | ||||
| D19S878-D19S1034 | D19S878-D19S247 | 2 | 1.25 | Sweden |
| 20: | ||||
| D20S471-D20S173 | D20S96 | 56 | 2.51 | Botnia |
| 21: | ||||
| D21S1437-D21S1437 | D21S1437 | 0 | 1.04 | Saguenay–Lac-St.-Jean |
| 22: | ||||
| D22S420-D22S686 | D22S420 | 0 | 1.95 | Sweden |
| D22S420-D22S283 | D22S281 | 27 | 1.66 | Botnia |
| D22S423-D22S1140 | D22S282 | 44 | 1.10 | Finland |
Note.— For each population and chromosome, regions where the LOD score is ⩾1.0 are listed, as is the maximum LOD score, located within the region at the indicated peak marker(s) and approximate distance in cM. Boxed pairs of rows indicate overlapping regions; boldface italic type indicates regions with empiric genomewide P value <.05.
The regions with LOD scores >3.3 did not overlap among the studies. Indeed, none of these regions were independently replicated within our four populations. However, concurrent studies described in the accompanying article (Perola et al. 2001 [in this issue]) also show strong support for linkage to the chromosome 7 region (LOD 2.9; the solid bars in fig. 2 denote the two regions with LOD >2.5 in the study by Perola et al.). Thus, one of the four regions with strong evidence for linkage in our studies has been replicated in another population.
Previous analysis suggested that a LOD score of ∼3.3 corresponds to significant linkage for a single genomewide scan for this variance-components method (Pratt et al. 2000). To assess the empiric significance of our results, we performed simulations to determine thresholds for significance within each population. We retained phenotypic and pedigree information but randomly generated genotypes under the hypothesis of no linkage. The empiric genomewide levels of significance for the most prominent peaks in our study were: for 6q24-25, P<.06; for 7q31-36, P<.02; for 12p11-q14, P<.05; and for 13q32-33, P<.05. For reference, the empiric levels of significance in the four populations associated with different LOD scores are shown in table 3. These empiric P values differ between populations because the samples we studied vary considerably in terms of family size and structure, total data set size, genotyping efficiency, and percentage of parents/founders available for genotyping.
Table 3.
Empirical P Values for Each Population[Note]
| LOD | Botnia | Finland | Sweden | Saguenay–Lac-St.-Jean |
| 2.5 | .56 | .31 | .11 | .05 |
| 2.6 | .50 | .27 | .08 | .05 |
| 2.7 | .46 | .25 | .06 | .05 |
| 2.8 | .40 | .20 | .05 | .04 |
| 2.9 | .35 | .18 | .04 | .03 |
| 3.0 | .29 | .12 | .04 | .02 |
| 3.1 | .24 | .11 | .02 | .02 |
| 3.2 | .20 | .08 | .02 | .01 |
| 3.3 | .16 | .05 | .02 | .01 |
| 3.4 | .13 | .05 | .02 | <.01 |
| 3.5 | .11 | .05 | .02 | <.01 |
| 3.6 | .09 | .05 | .02 | <.01 |
| 3.7 | .07 | .03 | .02 | <.01 |
| 3.8 | .07 | .02 | .02 | <.01 |
| 3.9 | .05 | .01 | .02 | <.01 |
Note.— P values were determined by performing at least 100 simulations for each population, permuting genotypes under the hypothesis of no linkage. For each LOD score, the reported P value is the fraction of simulations in which that LOD score was exceeded in the indicated population.
Since our study involved a set of four genomewide scans, we evaluated the expected distribution of LOD scores in such a set of scans under the hypothesis of no linkage. From the permuted scans used to generate empiric levels of significance, we drew 100,000 sets of four simulated scans, with each set containing one simulated scan from each of the four populations. These simulations indicated that the probability was small (P<.01) of observing by chance a total of four or more regions with LOD scores >3.0, suggesting that at least some of the four regions observed to have LOD scores >3.3 represent regions of true linkage to stature. In this light, the supporting evidence presented by Perola et al. for chromosome 7 suggests that this region may harbor genetic variation contributing to adult height (Perola et al. 2001 [in this issue]).
Assessment of Variable Linkage Results
One striking feature of our results is that regions with the best evidence for linkage in a given population do not show strong evidence for linkage in other populations. Two possible explanations of these findings are the presence of population-specific effects on linkage and the effect of statistical fluctuation (sampling variation) on LOD scores in the presence of a real, but modest, QTL. Population-specific effects are often invoked to explain variable linkage results, and it is possible that true differences between population (heterogeneity) explain some of the variability we observed. However, we wanted to explore the effects of statistical fluctuation on LOD scores in data sets such as ours, assuming the presence of a QTL that was consistent across all studied populations.
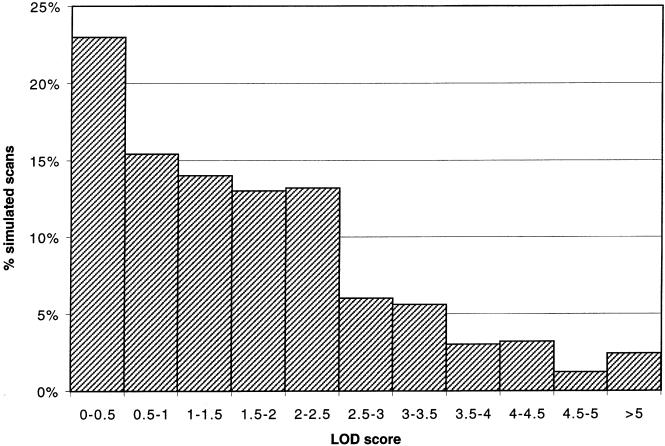
To determine the expected distribution of LOD scores arising from the presence of a QTL of moderate, but significant, effect, we generated 400 simulated data sets with the pedigree structure of our Swedish sample and assumed an additive QTL explaining 20% of the total variance. In the presence of such a QTL, the median LOD score at that QTL was 1.40. In these power simulations, 15% of scans gave a LOD score >3.0, but 37% of scans gave a LOD score <1.0, and fully 10% gave a LOD score <0.1 (fig. 3). Indeed, many of these simulated scans did not generate LOD scores near the “expected” value of 1.40. This slightly counterintuitive result is consistent with LOD scores following a χ2 distribution, which has a large excess of values in both the upper and lower tails, compared with the more intuitive normal distribution. Thus, it is not entirely unexpected to observe widely disparate LOD scores, even in the presence of a consistent QTL. Since significant LOD scores are only expected in a fraction of scans, even for significant QTLs and relatively large data sets, careful interpretation of replication studies is required. Of course, the presence of population-specific effects, should they exist, would only add to the expected variability in LOD scores.
Figure 3.
Expected distribution of LOD scores in the presence of a modest QTL. 500 data sets with the pedigree structure of the Swedish sample used in the study were generated under the assumption of an additive QTL explaining 20% of total variance. A histogram of the percentage of the 500 simulated scans yielding different observed LOD scores is shown.
We also pooled our data from the four populations, using genome-search metaanalysis (GSMA; Wise et al. 1999). In this method, the genome is divided into ∼100 bins, and the bins are ranked according to LOD score for each scan. The rankings are summed across scans, and the P value for this summed ranking is calculated for each bin. We applied GSMA to our four scans; consistent with the wide variability in LOD scores we observed, no region of the genome achieved significance after correction for multiple hypothesis testing across 100 bins. The bin with the best rank sum overlapped the 6q24-25 linkage peak observed in the Botnia population (nominal P value .01).
Study Design Considerations
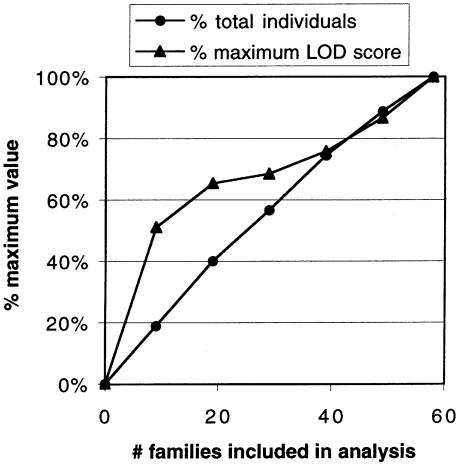
The families we studied using linkage analysis were not ascertained on the basis of extremes of adult height. It is therefore possible that these studies are relatively inefficient because families are included that contribute little to the evidence for linkage. To explore this possibility, we ordered the 58 Botnia families by total stature variance to determine how many of the families were responsible for the linkage to chromosome 6q. We performed an ordered subset analysis by adding in families 10 at a time, ranked in increasing order of intrafamilial variance, and repeating the variance-components analysis for chromosome 6. No subset of families provided markedly disproportionate evidence for linkage (fig. 4), indicating that selective ascertainment of families may provide only modest gains in efficiency. A similar ordered-subset analysis of the Sweden sample for chromosome 7 and the Finland sample for chromosomes 12 and 13 also revealed only modest gains in efficiency (data not shown).
Figure 4.
Ordered subset analysis for linkage to chromosome 6, ranking families by intrafamilial variance in stature. Families from Botnia were ranked by total intrafamilial variance in height Z score, and subsets of families were analyzed for linkage of stature to chromosome 6. Subsets were successively increased in size by ∼10 families, beginning with the families with the greatest variance. The % maximum LOD score (triangles) indicates the LOD score obtained using the number of families indicated on the X-axis divided by the LOD score obtained using the complete set; % of total individuals (circles) is the fraction of the total population contained in the subset of families being analyzed. The difference between the curves reflects the gain in efficiency by considering only a subset of families.
Discussion
Complex traits represent an important area of study for human genetics. Studying highly heritable traits that can be unambiguously phenotyped may advance our understanding of how to dissect the genetic architecture of these traits. As an initial study, we analyzed data from genomewide studies, involving 2,327 individuals from four different populations, and found evidence for linkage to stature in four chromosomal regions. This number of positive results is unlikely to have occurred by chance, as assessed by simulations, suggesting that at least some of the regions represent regions of genuine linkage to stature. Encouragingly, one of the regions (7q31.3-36) showed strong suggestive evidence for linkage both in our studies and in studies described in an accompanying article (Perola et al. 2001 [in this issue]) and therefore is likely to represent a region of true linkage.
One striking feature of our results is that the regions with strongest evidence of linkage in a given study show little evidence for linkage in most or all of the other studies. This inconsistent pattern is similar to those seen in studies of common diseases (e.g., Lernmark and Ott 1998; Lindgren and Hirschhorn 2001). Thus, understanding the source of this variation in linkage may have significant implications for interpreting linkage studies of common disease. For QTLs with modest genetic effects, we have suggested that statistical fluctuation caused by sampling variation may help explain apparently inconsistent linkage results. Indeed, our simulations suggest that a modest QTL (explaining 20% of variance) could give a strong signal in one scan but be essentially undetectable in other scans, simply on the basis of sampling variation. Definitive interpretation of one or a few negative replication studies, therefore, is somewhat difficult. In addition, if multiple QTLs contribute to a trait, it becomes likely that the genetic effect will have been overestimated for the QTL with the best LOD score (the “winner’s curse”). In this case, additional studies with large sample sizes may be required to help clarify the evidence for linkage.
Although sampling variation in the presence of modest QTLs may fully explain our data, there are other possible reasons for the variable LOD scores we observed. In theory, a causal genetic variant may be common in one population but rare in others (as might be seen with founder effects, selection, or even genetic drift), yielding very different linkage results. Similarly, if the evidence for linkage reflects the combined effect of two or more neighboring causal variants, population-specific patterns of linkage disequilibrium between the variants would result in fluctuating power to detect linkage. It is interesting to note that, of the four populations we studied, at least two are known to have founder effects, which could affect allele frequencies and linkage-disequilibrium relationships. It also remains a formal possibility that a genetic variant present in all populations is only functional in one or two, because of interactions with population-specific genetic and or environmental factors. Finally, it is possible that our results represent statistical fluctuations or false positives caused by an unknown artifact, despite results of simulations that suggest that the linkage peaks we observed are unlikely to have occurred by chance. A definitive understanding of the source of variability between studies is likely to require identification of causal variants within implicated regions and examination of frequencies and effects on height of the variants in each population. With improving technology and the potential availability of large follow-up populations for linkage disequilibrium mapping for stature, such studies are now conceivable.
To our knowledge, the studies presented here and in the accompanying article (Perola et al. 2001 [in this issue]) represent the first reported genomewide studies of stature. We did not see evidence of linkage to a previously reported region on chromosome 20 (Thompson et al. 1995), but two of the most interesting regions identified in this study (6q24-25 and 12p11.2-q14) are centered on two of the genes previously reported to be associated with variation in height (ESR1 and VDR; Minamitani et al. 1998; Lorentzon et al. 1999). Although initial studies of these genes did not reveal any evidence of association in our populations (data not shown), we have thus far tested only a few markers around these genes. The availability of the genome sequence and an accompanying dense SNP map will enable more-exhaustive tests of these genes, and we are currently engaged in these follow-up studies.
We have chosen to study stature as a model complex genetic trait, but it is likely that other highly heritable, easily phenotyped traits would be equally suitable. With regard to the selection of such traits, it has been suggested that normally distributed traits (such as stature) should be avoided, since the presence of a major gene will make the distribution deviate from normality (Allison et al. 1999). However, trait values can still be normally distributed, even in the presence of a single locus explaining >50% of the total variance, particularly if the segregating QTL is common in the population and has an additive effect (data not shown). Thus, a normal or near-normal distribution should not exclude a trait from being used in genetic studies.
Finally, the possibility of identifying a genetic variant that affects final adult height raises important ethical issues. Although such issues are relevant to most genetic studies, the general public interest in height as a potential phenotype for genetic engineering makes these issues particularly relevant in this context. For example, genetic modification and/or selection of embryos to “design” taller (or shorter) offspring would be, in our view, unethical, as well as fraught with possible unintended secondary consequences. However, a greater understanding of the genetic basis of stature could have appropriate and beneficial uses, including diagnosis, prognosis, and possible reassurance for children with short or tall stature, as well as contributing to a greater understanding of human biology and the genetic architecture of complex traits.
Acknowledgments
We would like to thank the families for their participation in the studies. This work was supported by research grants from Bristol-Myers Squibb, Millennium Pharmaceuticals, and Affymetrix to E.S.L.; by grants from the Sigrid Juselius Foundation, the J. D. F. Wallenberg Foundation, the Finnish Diabetes Research Foundation, the Swedish Medical Research Council, and the Novo-Nordisk Foundation, as well as a European Community Paradigm grant (BH K99JD-12812-01A) to L.G.; and by grants from the Medical Faculty of Lund University, the Royal Physiographic Society, the Anna-Lisa and Sven Lundgrens Foundation, and the Dir. Albert Påhlssons Foundation to C.M.L. and L.G. J.N.H. and D.A. are both recipients of Howard Hughes Medical Institute Postdoctoral Fellowships for Physicians. C.M.L. is supported by the Foundation for Strategic Research through the National Network of Cardiovascular Research. D.G. is the Canada Research Chair in Preventive Genetics and Community Genetics. T.J.H. is a recipient of a clinician-scientist award from the Canadian Institutes of Health.
Electronic-Database Information
Accession numbers and URLs for data in this article are as follows:
- Authors' Web site, http://www-genome.wi.mit.edu/publications/stature (for LOD scores for the complete genomewide scans)
- Généthon, http://www.genethon.fr/
- Genome Database, http://gdbwww.gdb.org/
- Online Mendelian Inheritance in Man (OMIM), http://www.ncbi.nlm.nih.gov/Omim/ (for DRD2 [MIM 126450],VDR [MIM 601769], COL1A1 [MIM 120150], ESR1 [MIM 133430] and LHB [MIM 152780])
References
- Allison DB, Neale MC, Zannolli R, Schork NJ, Amos CI, Blangero J (1999) Testing the robustness of the likelihood-ratio test in a variance-component quantitative-trait loci-mapping procedure. Am J Hum Genet 65:531–544 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almasy L, Blangero J (1998) Multipoint quantitative-trait linkage analysis in general pedigrees. Am J Hum Genet 62:1198–211 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carmichael CM, McGue M (1995) A cross-sectional examination of height, weight, and body mass index in adult twins. J Gerontol A Biol Sci Med Sci 50:B237–B244 [DOI] [PubMed] [Google Scholar]
- Forsen T, Eriksson J, Qiao Q, Tervahauta M, Nissinen A, Tuomilehto J (2000) Short stature and coronary heart disease: a 35-year follow-up of the Finnish cohorts of The Seven Countries Study. J Intern Med 248:326–332 [DOI] [PubMed] [Google Scholar]
- Garnero P, Borel O, Grant SF, Ralston SH, Delmas PD (1998) Collagen Ialpha1 Sp1 polymorphism, bone mass, and bone turnover in healthy French premenopausal women: the OFELY study. J Bone Miner Res 13:813–817 [DOI] [PubMed] [Google Scholar]
- Giovannucci E, Rimm EB, Stampfer MJ, Colditz GA, Willett WC (1997) Height, body weight, and risk of prostate cancer. Cancer Epidemiol Biomarkers Prev 6:557–563 [PubMed] [Google Scholar]
- Groop L, Forsblom C, Lehtovirta M, Tuomi T, Karanko S, Nissen M, Ehrnstrom BO, Forsen B, Isomaa B, Snickars B, Taskinen MR (1996) Metabolic consequences of a family history of NIDDM (the Botnia study): evidence for sex-specific parental effects. Diabetes 45:1585–1593 [DOI] [PubMed] [Google Scholar]
- Hebert PR, Ajani U, Cook NR, Lee IM, Chan KS, Hennekens CH (1997) Adult height and incidence of cancer in male physicians (United States). Cancer Causes Control 8:591–597 [DOI] [PubMed] [Google Scholar]
- Hemenway D, Azrael DR, Rimm EB, Feskanich D, Willett WC (1994) Risk factors for hip fracture in US men aged 40 through 75 years. Am J Public Health 84:1843–1845 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemenway D, Feskanich D, Colditz GA (1995) Body height and hip fracture: a cohort study of 90,000 women. Int J Epidemiol 24:783–786 [DOI] [PubMed] [Google Scholar]
- Jepson A, Banya W, Hassan-King M, Sisay F, Bennett S, Whittle H (1994) Twin children in The Gambia: evidence for genetic regulation of physical characteristics in the presence of sub-optimal nutrition. Ann Trop Paediatr 14:309–313 [DOI] [PubMed] [Google Scholar]
- Kruglyak L, Daly MJ, Reeve-Daly MP, Lander ES (1996) Parametric and nonparametric linkage analysis: a unified multipoint approach. Am J Hum Genet 58:1347–1363 [PMC free article] [PubMed] [Google Scholar]
- Lander ES, Botstein D (1989) Mapping mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics 121:185–199 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lernmark A, Ott J (1998) Sometimes it's hot, sometimes it's not. Nat Genet 19:213–214 [DOI] [PubMed] [Google Scholar]
- Lindgren CM, Hirschhorn JN (2001) The genetics of type 2 diabetes. The Endocrinologist 11:178–189 [Google Scholar]
- Lorentzon M, Lorentzon R, Backstrom T, Nordstrom P (1999) Estrogen receptor gene polymorphism, but not estradiol levels, is related to bone density in healthy adolescent boys: a cross-sectional and longitudinal study. J Clin Endocrinol Metab 84:4597–4601 [DOI] [PubMed] [Google Scholar]
- Mahtani MM, Widen E, Lehto M, Thomas J, McCarthy M, Brayer J, Bryant B, Chan G, Daly M, Forsblom C, Kanninen T, Kirby A, Kruglyak L, Munnelly K, Parkkonen M, Reeve-Daly MP, Weaver A, Brettin T, Duyk G, Lander ES, Groop LC (1996) Mapping of a gene for type 2 diabetes associated with an insulin secretion defect by a genome scan in Finnish families. Nat Genet 14:90–94 [DOI] [PubMed] [Google Scholar]
- Matise TC, Perlin M, Chakravarti A (1994) Automated construction of genetic linkage maps using an expert system (MultiMap): a human genome linkage map. Nat Genet 6:384–390 [DOI] [PubMed] [Google Scholar]
- Minamitani K, Takahashi Y, Minagawa M, Yasuda T, Niimi H (1998) Difference in height associated with a translation start site polymorphism in the vitamin D receptor gene. Pediatr Res 44:628–632 [DOI] [PubMed] [Google Scholar]
- Miyake H, Nagashima K, Onigata K, Nagashima T, Takano Y, Morikawa A (1999) Allelic variations of the D2 dopamine receptor gene in children with idiopathic short stature. J Hum Genet 44:26–29 [DOI] [PubMed] [Google Scholar]
- Parker A, Meyer J, Lewitzky S, Rennich JS, Chan G, Thomas JD, Orho-Melander M, Lehtovirta M, Forsblom C, Hyrkkö A, Carlsson M, Lindgren C, Groop LC (2001) A gene conferring susceptibility to type 2 diabetes in conjunction with obesity is located on chromosome 18p11. Diabetes 50:675–680 [DOI] [PubMed] [Google Scholar]
- Paz I, Seidman DS, Danon YL, Laor A, Stevenson DK, Gale R (1993) Are children born small for gestational age at increased risk of short stature? Am J Dis Child 147:337–339 [DOI] [PubMed] [Google Scholar]
- Pearson K, Lee A (1903) On the laws of inheritance in man. I. Inheritance of physical characters. Biometrika 2:357–462 [Google Scholar]
- Perola M, Öhman M, Hiekkalinna T, Leppävuori J, Pajukanta P, Wessman M, Koskenvuo M, Palotie A, Lange K, Kaprio J, Peltonen L (2001) QTL analysis of body mass index and stature by combined analysis of five Finnish genome scans. Am J Hum Genet 69:117–123 (in this issue) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips DI (1998) Birth weight and the future development of diabetes. A review of the evidence. Diabetes Care Suppl 21:B150–B155 [PubMed] [Google Scholar]
- Phillips K, Matheny AP (1990) Quantitative genetic analysis of longitudinal trends in height: preliminary results from the Louisville Twin Study. Acta Genet Med Gemellol 39:143–163 [DOI] [PubMed] [Google Scholar]
- Pratt SC, Daly MJ, Kruglyak L (2000) Exact multipoint quantitative-trait linkage analysis in pedigrees by variance components. Am J Hum Genet 66:1153–1157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preece MA (1996) The genetic contribution to stature. Horm Res 45:56–58 [DOI] [PubMed] [Google Scholar]
- Raivio T, Huhtaniemi I, Anttila R, Siimes MA, Hagenas L, Nilsson C, Pettersson K, Dunkel L (1996) The role of luteinizing hormone-beta gene polymorphism in the onset and progression of puberty in healthy boys. J Clin Endocrinol Metab 81:3278–3282 [DOI] [PubMed] [Google Scholar]
- Rioux JD, Silverberg MS, Daly MJ, Steinhart AH, McLeod RS, Griffiths AM, Green T, Brettin TS, Stone V, Bull SB, Bitton A, Williams CN, Greenberg GR, Cohen Z, Lander ES, Hudson TJ, Siminovitch KA (2000) Genomewide search in Canadian families with inflammatory bowel disease reveals two novel susceptibility loci. Am J Hum Genet 66:1863–1870 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risch N, Merikangas K (1996) The future of genetic studies of complex human diseases. Science 273:1516–1517 [DOI] [PubMed] [Google Scholar]
- Roche AF, Davila GH (1972) Late adolescent growth in stature. Pediatrics 50:874–880 [PubMed] [Google Scholar]
- Sham PC, Cherny SS, Purcell S, Hewitt JK (2000) Power of linkage versus association analysis of quantitative traits, by use of variance-components models, for sibship data. Am J Hum Genet 66:1616–1630 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silventoinen K, Kaprio J, Lahelma E, Koskenvuo M (2000) Relative effect of genetic and environmental factors on body height: differences across birth cohorts among Finnish men and women. Am J Public Health 90:627–630 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson DB, Ossowski V, Janssen RC, Knowler WC, Bogardus C (1995) Linkage between stature and a region on chromosome 20 and analysis of a candidate gene, bone morphogenetic protein 2. Am J Med Genet 59:495–500 [DOI] [PubMed] [Google Scholar]
- Tuvemo T, Cnattingius S, Jonsson B (1999) Prediction of male adult stature using anthropometric data at birth: a nationwide population-based study. Pediatr Res 46:491–495 [DOI] [PubMed] [Google Scholar]
- Wise LH, Lanchbury JS, Lewis CM (1999) Meta-analysis of genome searches. Ann Hum Genet 63:263–272 [DOI] [PubMed] [Google Scholar]